将近两个月不学大学物理,现在突击不完了。这一篇也不捋知识点了,直接整理一些有针对性的题目,来进行“Few-shot learning”。
一、考虑宽为$b$长度无限长的导体薄板,点$P$在通过板的中线并与板面垂直的直线距离$h$处。
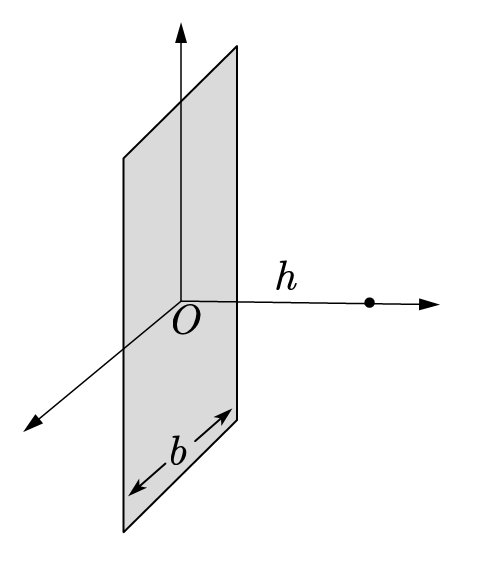
1)当平面薄板的电荷面密度为$\sigma$时,求$P$处电场强度:
2)当平面薄板上有电流$I$均匀流过时,求$P$处磁感应强度:
对于1),我们利用无限长的带电杆的结论,但当时给的是线密度$\lambda$。需要写成$\sigma$的形式:
之后直接计算:
注意给出方向。
对于2),我们仍然利用无限长直杆的结论:
在计算时都需要注意微分算子是否对上了,如果出现了微分算子突然跳跃了,最好检查步骤,一定是哪里列错了。
二、考虑空心单层密绕长直螺线管,总匝数$N$,长为$l$,半径为$R$,$l$远远大于$R$。求螺线管自感$L$
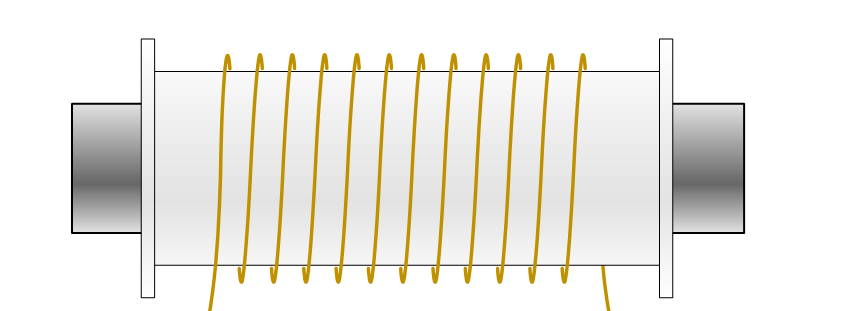
为求自感$L$,先求穿过回路的总磁通量。这样会先求磁感应强度$B$
首先要声明,对于螺线管,不管是圆形还是长直的,我们都将磁场线平行于轴线,管内外磁场均匀,管外磁场为零作为已知结论。这些结论的证明我们就不管了。我们这里要给出两种求解的方法:
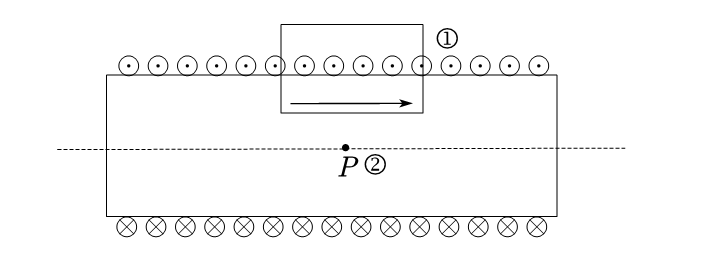
对于①,我们直接利用安培环路定理,因为我们知道管外磁场强度为0,且管内均匀并平行于轴线。此时选取矩形区域即可,设矩形区域长为$\varDelta l$:
对于②,基于对称性,我们计算中心轴线点$P$处的磁感应强度。可将每一匝看作一个环形电流,那么根据环形电流产生的磁感应强度我们即可积分,为了简单,我们取$P$为螺线管正中间的那个点。
如果这个积分没能一眼看出原函数的话,我们需要复习一下换元积分法:
实际上有积分公式:
根据上面的结果可以知道,当$l\gg R$时,$\sin \theta _2-\sin \theta _1\approx 2$,所以$B=\mu _0nI$。
有了磁感应强度$B$,总磁通量可以计算,继而:
这个式子的意义在于告诉我们,自感系数与单位长度的匝数的平方成正比,与螺线管体积成正比。值得一提的是当插入磁介质时,自感系数可以增大$\mu_r$倍。所以当插入的介质是顺磁质$\mu_r > 1$,那么自感系数增大。插入的是抗磁质,$\mu_r<1$,自感系数减小。插入铁磁质,自感系数会大大增大($\mu_r \gg 1$)
三、考虑如下图所示的圆环,圆环带电量$+q$,点$P$在圆环轴线距离中心$h$处。
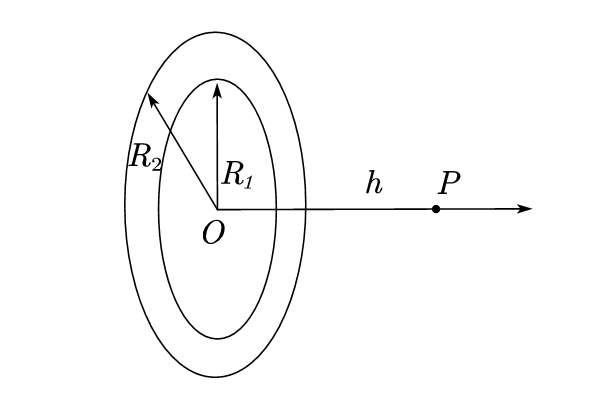
1)计算$P$处电场强度
2)现令圆环以均匀角速度$\omega$绕通过圆心垂直于圆环的轴转动,求$P$处电场强度。
3)在2)的基础上求圆环的磁矩。
对于1),我们看作若干带电圆环直接计算:
调整$R_1,R_2$大小,可以直接得到无限大平板和中间打孔两种特殊情况。
对于2),考虑等效环形电流,那么:
方向沿着$x$轴正向。
注意,上面的那个不定积分并不显然,要用三角换元法来积。
对于3),我们要通过环形电流来计算磁矩。磁矩是从载流线圈中抽出的概念:$\boldsymbol{p}_m=IS\boldsymbol{n}$。在这个问题中我们只需把圆环看成若干小圆环,积分即可:
方向沿着$x$轴正向。
上面三个例题中囊括了四个基本的可用来简化积分计算的几何体:
| 几何体 | 性质 |
|---|---|
| 带电圆环 | $E=\frac{1}{4\pi \varepsilon _0}\frac{qa}{\left( R^2+a^2 \right) ^{\frac{3}{2}}}$ |
| 带电直杆 | $E_x=\frac{1}{4\pi \varepsilon _0a}\left( \cos \theta _1-\cos \theta _2 \right) $ |
| 载流圆环 | $B=\frac{\mu _0IR^2}{2\left( R^2+a^2 \right) ^{\frac{3}{2}}}$ |
| 载流直杆 | $B=\frac{\mu _0I}{4\pi a}\left( \cos \theta _1-\cos \theta _2 \right) $ |
四、分布电容和分布电感,如同所示为两根无限长的圆柱形导线,半径为$r_0$,轴线相距为$d$。$d \gg r_0$
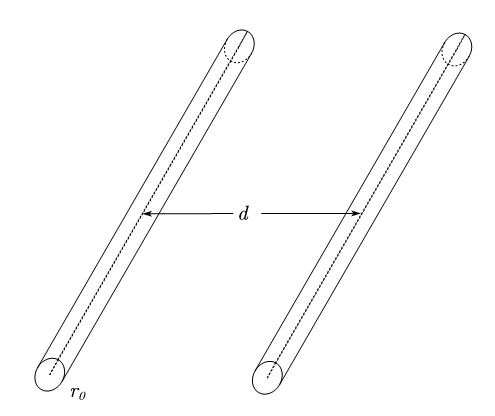
1)设单位长度带电量分别为$+\lambda,-\lambda$。求单位长度上的分布电容。
2)设圆柱中通有方向相反的电流$I$,求单位长度的分布电感。
对于1),先应用高斯定理求出两导线间的电势差(电势叠加),之后应用电容的定义式即可:
这里要穿插一个类似的问题,来对电容器有更清晰的认识:
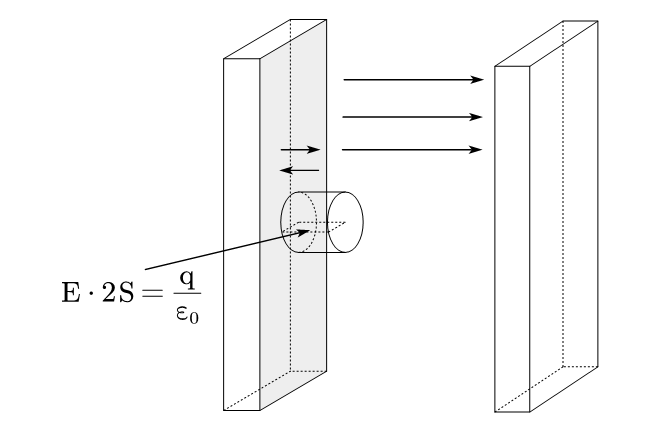
取两块平行平板,相距为$d$,总面积均为$S$,分别均匀带电$+q,-q$,两板线度远大于$d$,则它们的相互作用力大小为$(\frac{q^2}{2\varepsilon _0S})$。这里要注意分母的那个2,原理可以简述成:两块平行平板,实际上是四个带电平面,分别做高斯定理,由静电平衡条件可知中间两个面所带电量必然等量异号。而此时高斯定理是$E \cdot 2S$。所以求解相互作用力时有个$2$。
对于2),要先计算出两个导线间的总磁通,之后即可求出分布电感:
五、地心游记
半径为$R_1$的导体球带有电荷$+q$,球外有一个内,外半径分别为$R_2,R_3$的同心导体球壳,壳上带有电荷$+Q$。
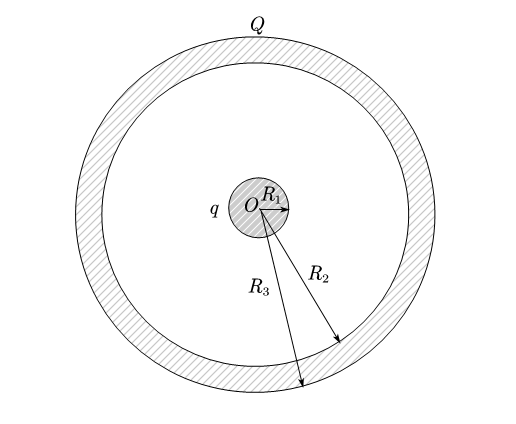
1)计算系统的静电能量
2)若外球壳接地,计算此时球和球壳的各自的电势
3)若内球接地,计算此时球和球壳的各自的电势
对于1),我们利用$w=\frac{\varepsilon _0E^2}{2}$求电场的能量密度。在不接地的情况下,内球和外壳之间有电场,外壳之外也有电场。取无穷远处为零电势点。
对于2),外球壳接地,则外球壳电势为零且接地放电。这不影响内球,内球仍然被外壳屏蔽。(此时正是静电屏蔽)
实际上由于静电平衡,外壳内表面应该受感应得到了$-q$。
对于3),此时要注意,内球的电势为0。无穷远处电势也为0。这种情况下,由于外球壳对内球的感应,内球的带电量并不是0。具体是多少需要结合电势相等条件定量计算。设内球带电量为$q’$,则球壳内表面为$-q’$。外表面由电荷守恒为$Q+q’$。

