“天门中断楚江开,碧水东流至此回。”
前段时间一直没时间写blog,最近换了方向,正在学习一系列前置知识,就有空写一写了。先前鼓捣camera,projection,往mesh上贴3DGS久了,再看这些新方向的内容,有一种朦胧的初恋感。这篇blog主要是对诸多内容进行的复健,毕竟很久不接触,确实很生疏。这篇blog的目的是为了给理解现在的文生图模型的后训练来补充前置知识,故事要从经典的Wasserstein GAN说起,而我们很快会发现“优秀的作品往往都在讲同一件事”。
Wasserstein GAN
Wasserstein GAN(下文简称W-GAN)现在看来已经很早了,我第一次知道这个词的时候,还在本科,那个时候我显然没能看懂它。W-GAN原文里没什么图,有代表性的感觉是这张:
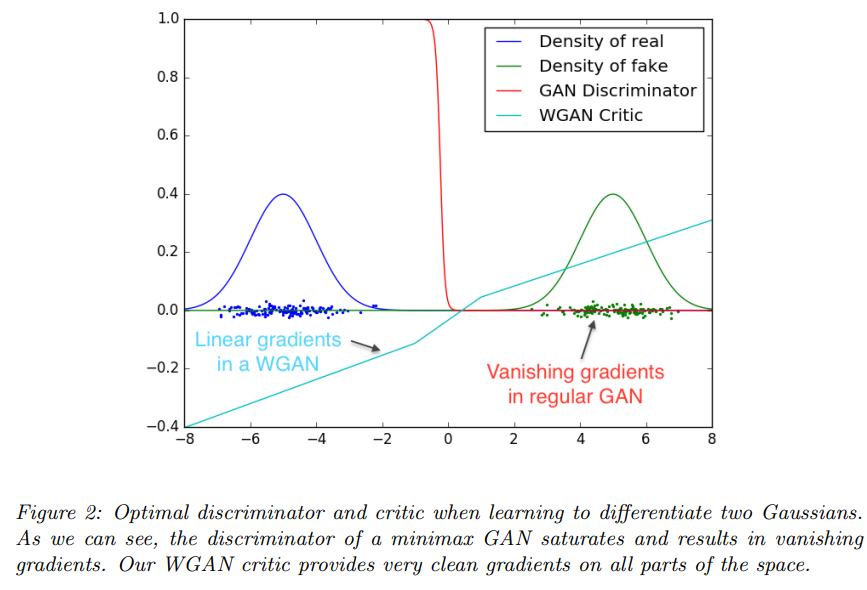
但那个时候也四处搜了搜,知乎几下。确实没咋看懂,然后直接就去用StyleGAN了。
首先广为人知的GAN的训练目标为:
我们可以把$G(z)$的分布在不至混淆的情况下写成$x\sim q$,$q$表示生成的分布;同时将真实数据分布$p_{data}$记作$p$。为了方便叙述,我们把这个极大极小的博弈过程拆成对于生成器和鉴别器各自的损失函数:
这时候如果只考虑在某个样本$x$下,生成器$G$固定时的最优判别器,那就是考虑此时样本$x$对期望的贡献,让$\mathcal{L}_D$关于$D(x)$的导数为零:
我们现在关心在$D^\ast(x)$下,生成器的损失是什么样子。我们把$D^\ast(x)$带入,会得到:
这个形式不好观察,我们在两边加一项$\mathbb{E} _{x\sim p}\left[ \log \left( D^{\ast}\left( x \right) \right) \right]$,我们发现等式右边可以处理成JS散度(Jensen-Shannon Divergence)的形式:
W-GAN指出,由于在最优判别器的条件下,$\mathbb{E} _{x\sim p}\left[ \log \left( D^{\ast}\left( x \right) \right) \right]$相对生成器的优化来说是个常数,这导致如果在计算某些处于$p(x)$和$q(x)$完全不重合的区域的样本时,JS散度会直接为接近零,不提供有效的梯度。
KL散度(Kullback–Leibler Divergence)和JS散度的定义为:
要注意KL散度是非对称的。
有些时候生成器会用非饱和(non-saturating)损失,在这个时候也会有类似的问题,此时的损失为:
类似的,我们在两边加上:
加的这一项正好就是之前分析的在饱和损失的情形下,生成器的损失。所以我们可以把这一项移到右边:
这时候的情况更加复杂,网络被期望拉大分布$p$和$q$的JS散度,同时又要最小化$q$与$p$的KL散度。以及这里的KL散度,其实有些不一样。这里的KL散度是反向(reverse)KL散度,而不是通常情况下的正向(forward)KL散度。
下文对正向和反向KL的约定是:如果期望是在真实分布/教师分布上进行积分,称为正向KL;如果期望是在合成分布/学生分布上进行积分,那就叫反向KL。
其实想重温W-GAN就是为了这叠醋包的饺子,因为对于炼丹爱好者来说,学习W-GAN应该是第一次能接触到反向KL散度和JS散度的机会,这会帮到后面的讨论。
在$KL\left( q\parallel p \right)$下,如果对于某个样本$x\sim q(x)$,其出现在真实分布$p(x)$下的概率很高,而在生成分布$q(x)$下的概率很低,那样这个样本计算出的结果对$KL\left( q\parallel p \right)$贡献很低;而如果其生成的样本在真实分布$p(x)$下的概率很低,而在生成分布$q(x)$下的概率很高,那么这一项会非常大,网络会被优化着竭尽全力避免这种情况的发生。而第一种情况其实是说生成器生成的分布里没能覆盖真实的分布,第二种是说生成器不能生成真实的样本。这是两种错误,而正向KL和反向KL对于这两种错误的行为并不同,在正向KL下,就是反过来的。
在反向KL的行为下,网络会尽量生成真实的样本,如果没能覆盖全真实分布也无所谓。这种行为称之为mode-seeking,而在训GAN时这往往会导致模式坍塌。即网络只需要找到一个真实的样本就好了,然后尽量都生成重复的这一个样本,就不会被惩罚的太狠。
而正向KL则会尽量的覆盖到真实分布,就算覆盖到的区域概率和区域没那么准也无所谓。这种行为称之为mode-covering。在推导VAE和diffusion时,我们往往会关注一个极大似然,这个导出的其实就是正向KL。这一现象从侧面解答了为什么GAN会模式坍塌,以及即使在使用饱和损失下,这一现象仍然存在,本质上是因为鉴别器本身不可能是完美的,我们知道鉴别器实际上是一个二分类:
其中$\sigma(\cdot)$是sigmoid函数。所以最优鉴别器下的$T(x)$其实就是:
我们可以对$T(x)$施加扰动,例如:
这里$\lambda<1$,表示判断的置信度的模糊,$C$表示偏置。现在我们直接把这样假设的$D(x)$带回饱和损失中:
记$a=e^C$,$s=\log \frac{p\left( x \right)}{q\left( x \right)}$,期望里面的式子即为$\log \left( 1+ae^{\lambda s} \right) $。这个式子是一个类似softplus的结构,我们不希望直接消掉这里的指数和对数。考虑到$\lambda<1$,我们将其做一阶展开:
带入原式,然后再进行对数的一阶展开:
所以饱和损失近似为:
这说明在一般情形下的饱和损失里的一个邻域内,GAN仍然表现为mode-seeking,即有模式坍塌的隐患。
为了更好的理解前向KL和反向KL以及他们对应的行为,我们可以利用torch的自动微分,设定一个可学习的单峰高斯分布作为$q(x)$,然后以一个多峰高斯分布作为$p(x)$。我们可以可视化一下优化时的行为:
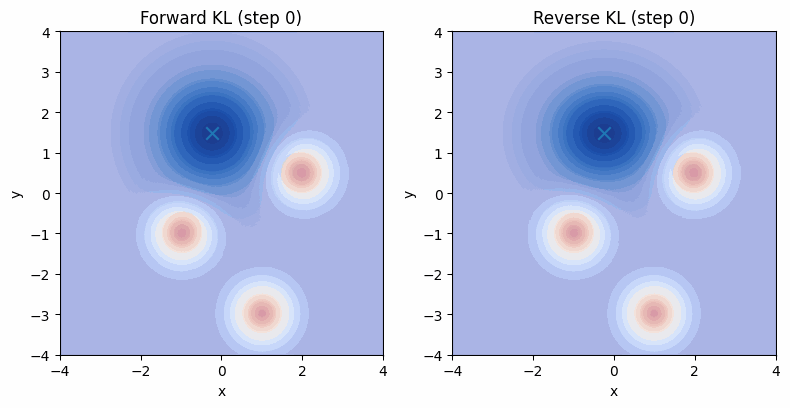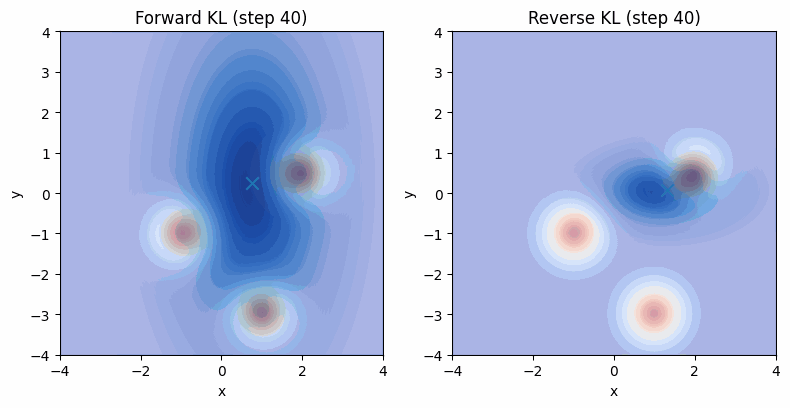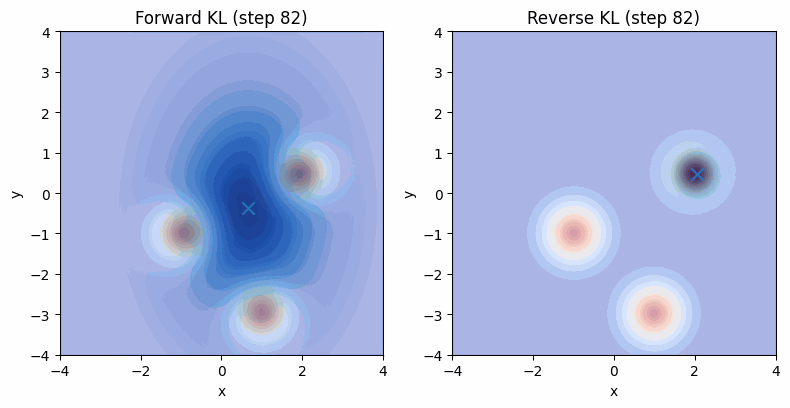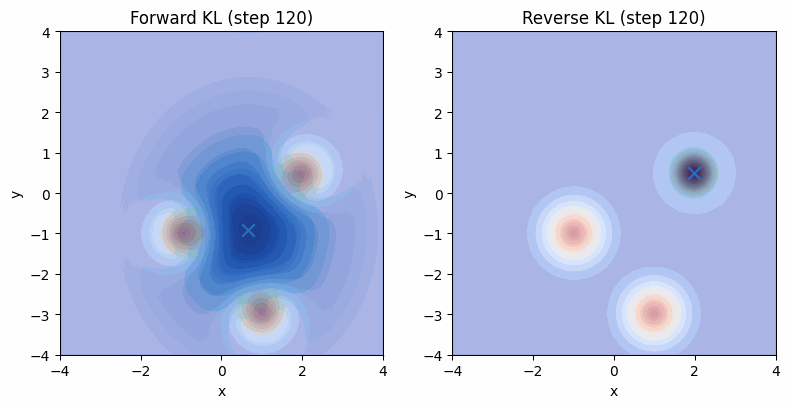
可以看到,在反向KL下,模型倾向于找到高概率的固定的模式,这对应到GAN里就是模式坍塌。其实到这里,提W-GAN的目的已经达到了,应该进行其他部分了。但都写到这儿了,干脆把W-GAN给不严谨的推导一下,算是某种callback一下几年前看不懂的自己。
W-GAN的观点在于,KL散度和JS散度都不能作为很好的距离度量,因为在$p$和$q$完全不重合时,他们的问题都很大。例如考虑在二维平面上的线分布,我们考虑真实分布为:
而待拟合的分布为:
在这种情况下,KL散度和JS散度都不连续,而且没有有意义的监督信号。而如果用Wasserstein距离:
这时候的度量就是连续且有界的了,W-GAN的推导正是在$k=1$的情况下进行的。Wasserstein距离(推土机距离)说的是找到两个集合之间的距离期望的下确界,常在最优传输等问题里也出现。但我们是想用这个距离来进行GAN的训练,而这个形式显然很不好计算。我们可以从离散化时的情形入手,这样会看到一个在推导支持向量机时的很熟悉的形式。
假设真实分布$p(x)$有$m$个离散点$\{x_i\}^m_{i=1}$,概率密度值或者更形象的说“沙子的质量”为$\mu_i$。为了不至于混淆我们记生成分布$q(x)$为$q(y)$,有$n$个离散点$\{y_j\}^n_{j=1}$,概率密度值为$\nu_j$。记运输计划$\gamma_{ij}$为从$x_i$搬运到$y_i$,这要求$\gamma_{ij}$必须大于等于0。而搬运有对应的成本(最常见的就是距离)为$c_{ij}$。所以这时候得到了一个线性规划问题:
就像在推导SVM时那样,我们可以写出其拉格朗日函数:
接下来要求$\mathcal{L} (\gamma ,\alpha ,\beta )$的极大值,由于$\gamma_{ij}$是非负的,所以极大值一定在$c_{ij}-\alpha _i-\beta _j\ge 0$时取,所以对偶问题其实就是:
而这个对偶形式看起来像$\mu_i$和$\nu_j$关于$\alpha_i$和$\beta_j$的期望。我们不严谨的用$f(x_i)$来连续化$\alpha_i$,用$g(y_j)$来连续化$g_y$,将求和换成积分,就得到了连续情形下的对偶形式:
$f(\cdot)$和$g(\cdot)$的选取没有要求,在这里我们直接选取$f^\ast=-g^\ast$的形式,实际上我们是可以说明并保证在这个形式下确实是有更好的解的,但这里我们就不管了。然后选取1-范数作为距离度量:
这就得到了W-GAN里的配置,也就是说只需要给损失函数摘掉$\log$,同时保证鉴别器是Lipschitz连续的,就能更稳定。这一点也很好实现,只要保证鉴别器每次更新时,其参数更新有个截断就好。W-GAN非常经典,但从事后看来,这样稳健的做法其实会降低一些生成质量。以及W-GAN本身是说度量空间性质不好,所以要找更好的度量;但后面我们知道,StyleGAN本身用mapping network去调制latent space,也是一种隐式的来获得更好的度量的方式。而且这一过程是纯data-driven的,而W-GAN就显得是人为的归纳偏置了,StyleGAN加上关于鉴别器的R1正则项,收敛的往往也还好。看样子learning再次打败了inductive bias。
On-policy Distillation
推导W-GAN的练习热身了足够的预备知识,我们现在来关注一个用在自回归的语言模型里的一个经典工作:On-policy Distillation。自回归的语言模型是说,我们将一段序列$x$喂进这个模型,他会输出另一段序列$y$。模型里有一个tokenizer,tokenizer有一个固定的词汇表,词汇表里有$M$个数据(大概是几万的样子)。记$y_{\le n+1}=(y_1,y_2,…,y_n)$为模型生成的到第$n$个token之前的句子,那么自回归的逻辑就是估计$p(\cdot | y_n,x)\in (0,1)^M$这样的一个分布,这个分布往往是通过将网络输出的logits,用拿温度系数调制的softmax来归一化得到的。为了便于叙述,我们记$p\left( y_n|x \right) = p\left( y_n|y_{< n},x \right)$。
这篇工作关注的事情是想让一个学生语言模型$p_S^\theta$,其中$\theta$为可学习参数,尽量能复制教师语言模型$p_T$的行为—即蒸馏。学生模型的容量肯定比教师模型是要低的,在这个settings下,我们往往有一个数据集$X$,如果可以,我们有其配对的下文$Y$组成$(X,Y)$;如果没有,$Y$可以由教师模型生成。在这样一个定义的很好的问题下,我们有许多种直接的策略:
Supervised FT(Supervised Finetuning),即如果有真值的$(X,Y)$,我们直接用这样的高质量数据去训学生模型就好了:
Sequence-Level KD(Sequence-Level Knowledge Distillation),是说如果没有配对的$(X,Y)$,可以用教师网络的输出作为$Y$,形式和SFT是一样的:
Supervised KD(Supervised Knowledge Distillation),在自回归的语言模型中,这种方法是说利用正向KL来对齐token-level的分布:
我们需要指出,SFT和SeqKD的优化目标本质上也是正向KL,只是没有要求要对齐token-level的logits。
而$\log p_T\left( y|x \right)$与$\theta$无关,所以优化前向KL等价于优化负对数似然。
On-policy KD(On-policy Knowledge Distillation),这个方法是让学生网络进行输出,然后用教师网络的logits进行打分,这种方法很像强化学习,有助于最小化训练和推理时的分布不匹配。
Generalized KD(Generalized Knowledge Distillation),是论文提出的一种推广形式:
其中$\lambda$用于调整其中“学生数据”的比例,$\mathcal{D} \left( p_T,p_{S}^{\theta} \right) $可以是各种散度度量,例如正向KL,反向KL,JS散度。可以看到,如果$\lambda$取0,散度取正向KL,那么这一项就是Supervised KD;如果$\lambda$取1,散度取正向KL,那么就是On-policy KD。
JS散度也存在一种广义形式,即:
当$\beta=0.5$时,就是我们熟悉的JS散度。我们发现如果我们直接取$\beta$为0或1,那么这个散度会直接是0。以及在这种形式下:
这说明这种度量是满足某种对称性的。我们现在关注于当$\beta$趋近0时,这个散度的行为:
我们不确定第二项极限的阶数,但大概感觉是趋近于0。严谨的证明非常复杂,可能需要对这个泛函做变分,不好理解。我们可以尝试性的用离散情形下的:
注意我们其实是对一个概率密度函数做扰动,在离散情形下需要满足$\sum_i{\epsilon _i}=0$。然后我们对$\log$做泰勒展开:
带入:
我们取$P=p_2,E=\beta(p_1-p_2)$,得到:
这说明在$\beta$很小时,可以近似认为$JS_{\beta}\left( p_1\parallel p_2 \right) \approx \beta KL\left( p_1\parallel p_2 \right) $,而当$\beta$接近1时,根据对称性,$JS_{\beta}\left( p_1\parallel p_2 \right) =\left( 1-\beta \right) KL\left( p_2\parallel p_1 \right) $。这说明广义的JS散度在$\beta$接近0和1时,有着正向和反向KL的性质。
而这篇工作的主要结论是说,在许多NLP任务下,on-policy,mode-seeking的监督信号,在丧失一些多样性下,会有更好的质量。当我们联系大语言模型的实际后,会发现这个结论非常合理并且具有指导意义。有时候与其用额外的计算去囊括一些质量不一定好的多样性,不如mode-seeking到一些高概率分布的高质量模式。
Distribution Matching Distillation
这个部分是想学习Distribution Matching Distillation系列的工作(DMD,DMD2,Decoupled DMD,DMDR),其中最后的DMDR是最近的一个文本生成图像模型—Z-image能大放异彩的重要设计。但故事的一开始,要先回忆一段往事:
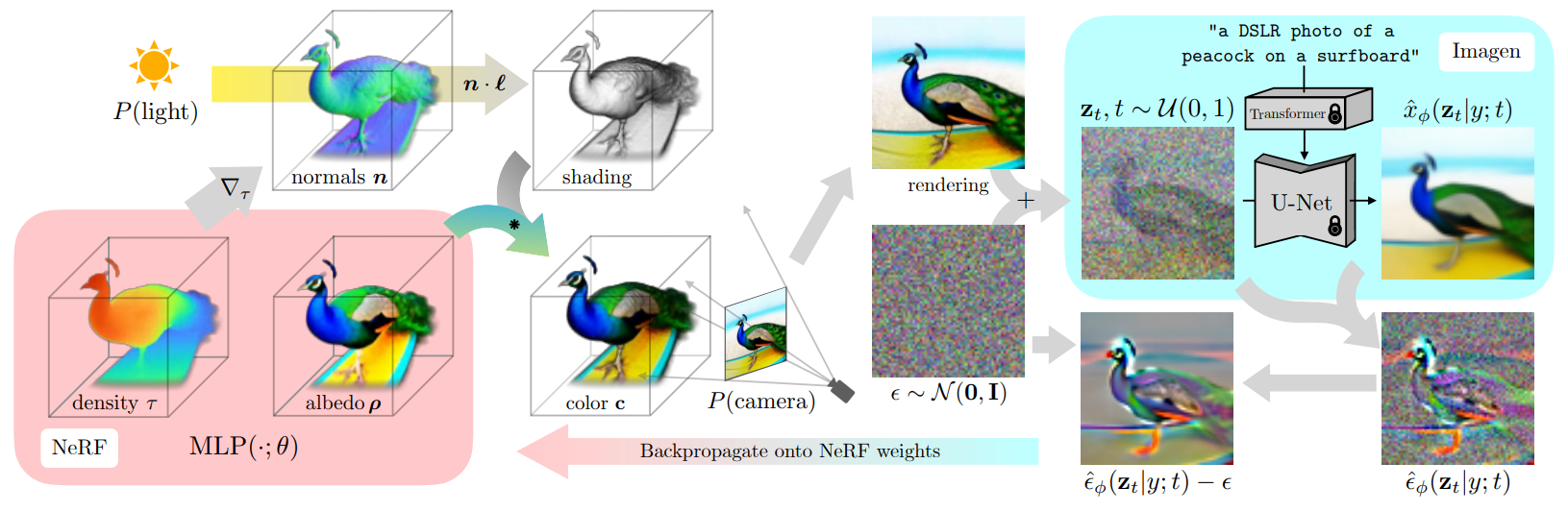
那是在2年多前,我第一次看见Dreamfusion,惊为天人,一眼万年。居然从2D的文生图模型里,可以输出一个3D的物体,自此踏上了一条不归路。当时我对Dreamfusion的理解十分粗浅,好像是说我如果把一张不好的图片加噪,然后送进预训练的diffusion里,diffusion预测的noise会是某种表示“这张图片距离diffusion期望的在指定text prompt下的图还有多远”的度量,然后要让预测的noise和真实加的noise对齐,即Score Distillation Sampling(SDS loss)。但这个思路哪怕现在想起都觉得“不是很透彻”,以及更不用提那诡谲的,忽略掉在这样推导下出现的关于diffusion backbone的梯度。
一个更直接的思路是计算反向KL,我们将用NeRF或者别的表征得到图片的过程记为$x=g(\theta)$(忽略相机位姿,这个不影响讨论),其中$\theta$是可学习参数,以及加噪的过程$z_t=\alpha _tx+\sigma _t\epsilon $看作一个分布$q$。然后我们来衡量这个分布与预训练的扩散模型在指定text prompt $y$和输入$z_t$下的分布的差异:
这个式子难以计算,但如果我们直接在两边求取关于$\theta$的微分:
我们知道在扩散模型中,所谓得分(score)就是对数概率密度函数的梯度,同时score可以根据特威迪公式,从扩散模型预测的噪声中进行估计:
所以关于扩散模型的分布那一项:
而关于加噪得到的那个分布,注意$z_t$和$x$都跟$\theta$有关,此时加噪分布为:
其中$C$是一个常数,求导时可以忽略。然后计算此时关于$\theta$的梯度:
其中的两项偏导恰好可以抵消:
所以所求KL散度的梯度即为:
注意这个梯度是一个期望,一个有用的技巧是我们可以给他减去一个期望为0的随机变量,这样不会影响结果但可以降低方差,有助于优化的稳定。显然加噪的噪声$\epsilon$就很合适,然后我们将$\alpha_t/\sigma_t$吸收进一个权重函数$w(t)$中,就得到了原文的SDS loss:
我们发现在这种情形下自然没有出现diffusion backbone的梯度,非常便于计算。而且我们也不需要解析的计算出$\mathcal{L}_{SDS}$,由于我们可以解析的算出其梯度,我们只需要在自动微分框架下设计一个$\left| x-\mathrm{stop}_\mathrm{grad}\left( x-\nabla _{\theta}\mathcal{L} _{SDS} \right) \right| _{2}^{2}$来进行backward()就可以了。
我们只是觉得$\epsilon$减进来来调度方差是非常自然的,因为他服从单位高斯分布,他的方差固定为1。如果这一项也是可学习的,直觉告诉我们“整个优化目标的方差应该可以再降降,应该会有更好的结果”。换句话说,我们希望估计从$g(\theta)$中得到的分布$q$的这个过程能被可学习的一个过程估计。那么直接的做法就是用另一个扩散模型估计的噪声$\epsilon _{\psi}\left( z_t|y \right)$来代替$\epsilon$。这就是ProlificDreamer的优化目标:
即Variational Score Distillation(VSD)。这个操作意味隽永。
首先这个操作确实降低了方差,在 DreamFusion 中,由于 score-based 梯度估计本身具有较高的方差,实践中往往需要将 classifier-free guidance (CFG) 设置到非常大的数值(如 100)才能获得稳定的优化过程。较大的 CFG 实际上通过放大 conditional score 的相对权重,在一定程度上抑制了梯度中的噪声方向,但这更多是一种以引入偏置换取稳定性的做法。相比之下,VSD 使用常规范围内的 CFG,也能获得稳定且一致的优化行为,这说明这个操作确实抑制了高方差。
我们也可以从分布角度出发来思考这件事,一开始在SDS的角度下出发,我们单纯的认为$q\left( z_t|x \right) =\alpha _tx+\sigma _t\epsilon$,然后其中$x=g(\theta)$表达一个从NeRF中渲染的图片。如果我们单纯的认为我们只想优化最优的$\theta^\ast$,那就是SDS。但VSD指出,在给定条件$y$下,$\theta$不止一个,他应该是一个分布譬如$\mu(\theta|y)$。在这样的假设下,原先的$q(z_t|x)$就不能简单的用高斯分布来表示,当然也写不出先前的解析式,我们只能写出边缘分布$q(z_t|\theta)$为:
这是一个混合高斯分布,其比单个高斯的score复杂的多。但好在我们只需要估计$\nabla _{z_t}\log q\left( z_t|\theta \right)$,而我们知道这个等于$-\frac{1}{\sigma _t}\epsilon \left( z_t|\theta \right) $。也就是说如果有一个扩散模型,其用$g(\theta)$作为$x_0$,然后加噪去噪进行训练,那么就可以帮我们估计$\nabla _{z_t}\log q\left( z_t|\theta \right)$,这自然就引出了用一个额外的$\epsilon _{\psi}\left( z_t|y \right)$来代替$\epsilon$。也就是说SDS就是假设$\mu \left( \theta |y \right) =\delta \left( \theta -\theta ^{\ast} \right) $的特殊情况。
除了从方差和分布两个角度来考虑,另一个角度是我们可以认为$\epsilon _{\phi}\left( z_t|y \right)$是“Real Score Estimator”,他用来指示当前的结果距离$\epsilon _{\phi}\left( z_t|y \right)$所表示的“真实分布”的度量。然后$\epsilon _{\psi}\left( z_t|y \right)$是“Fake Score Estimator”,他表示某个跟某个“虚假分布”的度量。一开始这个虚假分布是不存在的,所以在操作中往往仍会用去噪损失来优化$\epsilon _{\psi}\left( z_t|y \right)$,具体在ProlificDreamer中,是用一个LoRA加到冻结的$\epsilon _{\phi}\left( z_t|y \right)$上来作为$\epsilon _{\psi}\left( z_t|y \right)$。这个过程很像GAN的对抗训练,我们实际上在一开始推导W-GAN时就可以发现:
注意此时$D(x)$是接近最优判别器的,$\mathcal{L}_G$是非饱和情况下的生成器损失,而等号左边的那一项期望是饱和情形下的生成器损失,如果我们把这两项写在一起,记作$\mathcal{L}_G^{KL}$:
然后在两边关于生成器参数$\theta$取梯度,我们会发现形式和VSD Loss是一样的:
相当于只在$t=0$时刻的VSD。而在GAN中会遇到分布$p$和分布$q$不重叠等情况,但在diffusion里,由于加噪过程,初始分布无论怎么样都可以被加噪成布满整个空间的高斯分布,所以总能重叠。以及如果我们把最优判别器$D^\ast(x)$带入$\mathcal{L}_G^{KL}$,我们会发现完全是$\log \frac{q\left( x \right)}{p\left( x \right)}$。这说明,GAN在训练中是需要让鉴别器学到比较好的状态,这时的$\log \frac{1-D\left( x \right)}{D\left( x \right)}$(可以称其为$\log$密度比函数)接近于反向KL,生成器自然接棒,来拉近$p$和$q$分布的距离。而VSD只需要学习score的差即可。
不管是SDS还是VSD,只是想从diffusion里case-by-case的蒸出3D场景或物体。但我们已经看到,其背后有深刻的理论支撑和更抽象的动机,而不是简单的“从2D diffusion里抽取先验”。现在我们把目光移到DMD上,其实就很好理解了:
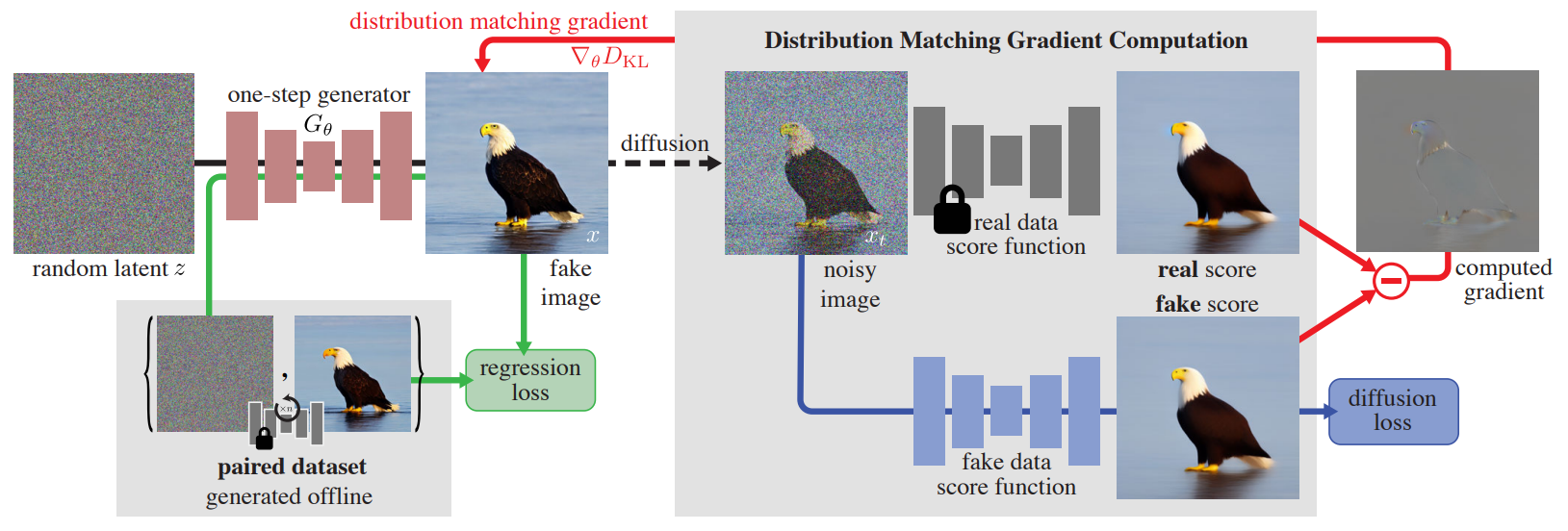
DMD是想蒸馏出一个单步(也可以推广到几步)的生成器,这里的$G_\theta$就是先前3D表示$g(\theta)$的角色。然后冻结的Real data score function就是$\epsilon _{\phi}\left( z_t|y \right)$,Fake data score function就是$\epsilon _{\psi}\left( z_t|y \right)$。$\epsilon _{\psi}\left( z_t|y \right)$用diffusion loss来进行训练,同时作者经验性的设计了一个正则方法,用于稳定质量:即一开始离线cache一些成对的数据集,然后在训练时保证这些成对数据集的噪声在经过更新后的$G_\theta$后,感知距离不要变化太大,来起到一个anchor的作用。在DMD2里,作者移除了这个设计,因为这个设计在数据规模上升后很难实装,同时一旦改下condition,cfg,就都不一样了。转而将Fake data score function的更新转成异步的(即每隔$k$个iters再更新一次Fake score function),同时引入GAN loss来强化$G_\theta$输出图片的真实性。这些都是一些细节上的修饰,大体上仍然是DMD Loss:
我们这里解释一下为什么会出现$z_t$和$\tau$,在多步的settings下。DMD的逻辑是先采样一个$z_t$,然后对其进行多步去噪,得到$G_\theta(z_t)$,在这里进行的去噪是由一个固定的scheduler决定的,他往往只有几步,例如$\{999,749,499,249\}$。再给$G_\theta(z_t)$加到$\tau$强度的噪声上,而这里的$\tau$就连续的多了。这里时间戳为0记作纯噪声,时间戳为1记作无噪声时的干净图片。这个操作叫作“backward simulation”,因为模拟了扩散模型在训练时,其在真实图片上随机加不同强度噪声的行为而得名。
但由于如果只给$s_{\mathrm{cond}}^{\mathrm{real}}\left( x_t \right) $,这个得分的估计其实不是那么准,对于大型的文本生成图像模型来说,需要一个蛮高的CFG值,所以实际上DMD Loss在实践时往往是:
而对于fake score function,不施加CFG。而Decoupled DMD中对这个实践进行了巧妙和深入的分析。我们只需要将$s_{\mathrm{cfg}}^{\mathrm{real}}\left( x_t \right) $带入$\nabla _{\theta}\mathcal{L} _{DMD}$中,会得到:
式子可以拆为两项,第一项是寻常的DMD Loss,第二项论文中称为CFG增强(CFG Aug.)。我们已经知道如果只用DMD Loss,效果并不好;而Decoupled DMD中只应用CFG Aug.进行训练,发现可以得到较高质量的$G_\theta$,但训练过程不稳定。
Decoupled DMD设计了两个巧妙的实验,首先其探索CFG Aug.的功用,先完全训练只靠CFG Aug.训练的单步$G_\theta$,只不过训练时我们严格限制$\tau$的区间:

当$\tau$被限制在高噪声区域时,单步生成器的结果显示CFG Aug.贡献了大致的轮廓。而随着区间逐渐往低噪声区域扩展,更多的细节显示了出来。而当跳过高噪声区域,直接在低噪声区域进行CFG Aug.,训练崩坏。这个现象说明高噪声区域的CFG Aug.支撑了低频结构,低噪声区域的CFG Aug.增添了高频细节。所以作者指出应该在$\tau > t$的区间下做CFG Aug.。因为在$t$时的$z_t$已经有了一些相比于$t$强度的噪声更清晰的低频结构,而我们希望CFG Aug.在这个基础上聚焦于那些没有被解决的部分,即$\tau>t$的那部分。
然后是DMD Loss的功用,作者仍然训练了一个只应用CFG Aug.的生成器。他单纯的用训练好的$G_\theta$推理出图片$G(z_t)$,然后将此时的$G(z_t)$进行重新加噪,再喂给两个打分的模型(其中Fake data score function是在训练$G_\theta$过程中也被训练好了,只是DMD Loss没用来更新$G_\theta$),很神奇:

这时$G_\theta$的结果有一些棋盘伪影,$s^\mathrm{fake}$也有,但$s^\mathrm{real}$没有。这说明如果在训练时启用$s^\mathrm{real}-s^\mathrm{fake}$,就能自然得到一个消去伪影的方向,这说明DMD Loss确实起到了正则化的效果。
还有一篇工作是DMDR,其将强化学习引入了这个过程中。如果将这个部分也用这篇blog的递归深度来记录的话,那这篇blog就太长了,所以这一部分就先暂且按下不表。我们只需知道:我们可以在这个过程中引入一些额外的loss,他们会根据生成的结果来打分,打分的结果反传回来可以让网络沿着打分偏好的方向优化。
Pix2Pix
最后一部分我们留给一个关键的技巧,这一技巧最早来自Pix2Pix,可以概括为在成对的重建/回归损失之上,引入GAN Loss,可以得到更高质量的图像。这个技巧后来在许许多多的任务里都有用过。比如对于有些任务,会用L1 Loss,VGG Loss,GAN Loss来联合优化:
直觉上这很应该取得更好的结果。在有了上文的前置知识后,我们要对这样做为什么能取得更好的效果进行论证。对于重建/回归任务,我们往往有一个$p_{data}$,我们希望能最小化正向KL:
而第一项是一个跟$\theta$无关的常数,所以:
当我们选取高斯分布作为$p_\theta(\cdot)$,那么就会得到L2 Loss,当选取拉普拉斯分布作为$p_\theta (\cdot)$,就会得到L1 Loss。但这些都等价于最小化正向KL,即mode-covering,所以容易产出模糊和平均化的解。而引入GAN Loss,就是引入了一个mode-seeking的项,驱使模型的分布不要那么平均,同时找到一些模式能让像素和特征级别的损失最小。特别地,在这样的上下文下,我们可以认为预训练的VGG网络起到了一个奖励模型(Reward Model)的角色,更全面的叙述我们在下一篇blog再展开。
End
非常感慨,这里的很多概念当时都搞不懂,现在回过头来感觉也没那么复杂。或许是一直以来往mesh上贴3DGS,就像习武之人练蹲马步一样,可能产生了某种“沉淀”基本功的效果。乍一看这记录几个部分,GAN的变式,LLM的蒸馏,text-to-3D,文生图的扩散模型的加速,毫无关系,但他们其实都在讲同一件事。事物之间是存在广泛的联系的,比如象棋里出横車,可能短期内没什么效果,但很多步后可能就可以出奇制胜。但即使一开始理解这个道理,也很难躬行。因为许多关键部分仍然需要仙人指路般提点一手,不然很难串起来;或者找不到合适的切入点,毕竟对着PRML啃的效率确实太低了。但不管怎么说,终于不用往mesh上贴3DGS了。


