Towards 3D Generation

阅读数: 次 2025-03-18

文章目录

Overview
Sparse Structure
1. Sparse Structure VAE
2. Sparse Structure Flow
Structured Latent
Dataset Process
End

“所幸敝屣荣华且把酒，风雨偏洗岳阳楼。“

“直接生成3D物体”是一个听起来像魔法般的操作。给定一些图片或一组文本描述，构造出一个3D物体或场景，的确听起来比生成图像，文本更为“奇迹”。一开始，人们广泛的探索了“得分蒸馏采样”（Score Distillation Sampling），但这种方式在一致性以及效率上还是有短板。之后，“多视角扩散模型”（Multi-view Diffusion）得到了推广，人们在常规的扩散模型基础上加入例如Plücker embedding的相机表示，来生成多视角的图片。再结合经典的稀疏重建的方法，或者单纯将多视角的图片贴（或优化材质图）到已有的mesh上，这样就能生成一个3D物体了。所以后面的工作基本都关注于先训练一个生成mesh的模型，然后再训一个“texture diffusion”，来为mesh贴材质。而这个生成mesh的模型往往是将一个大规模的3D物体数据集，采样成点云的形式。通过去对点的位置做嵌入，来去学习潜在的几何分布。这些工作非常的工程，收集大量私有的数据集，而且往往不开源，很难从中学到什么。

然而，TRELLIS是一个几乎杀死比赛的通用3D生成的工作。这篇工作在精心清洗数据集，力大飞砖的同时，设计了一个大巧不工的管线，整合了多种先进和经典的技术；并且开源了测试代码和数据处理的流程，非常具有学习价值：

现代化的Diffusion
大量值得学习的图形学知识
代码规范

所以，这篇blog旨在通过分析TRELLIS，来记录和扩展一些相关知识。为了更好的理解，读者最好需要了解成熟的生成模型（如Latent Diffusion），常用的3D表达（Mesh，Voxel，NeRF，3DGS），同时对Transformer的工作流程有基础的了解。

Overview

在深入一些细节之前，我们先简要的给出TRELLIS的工作流程。

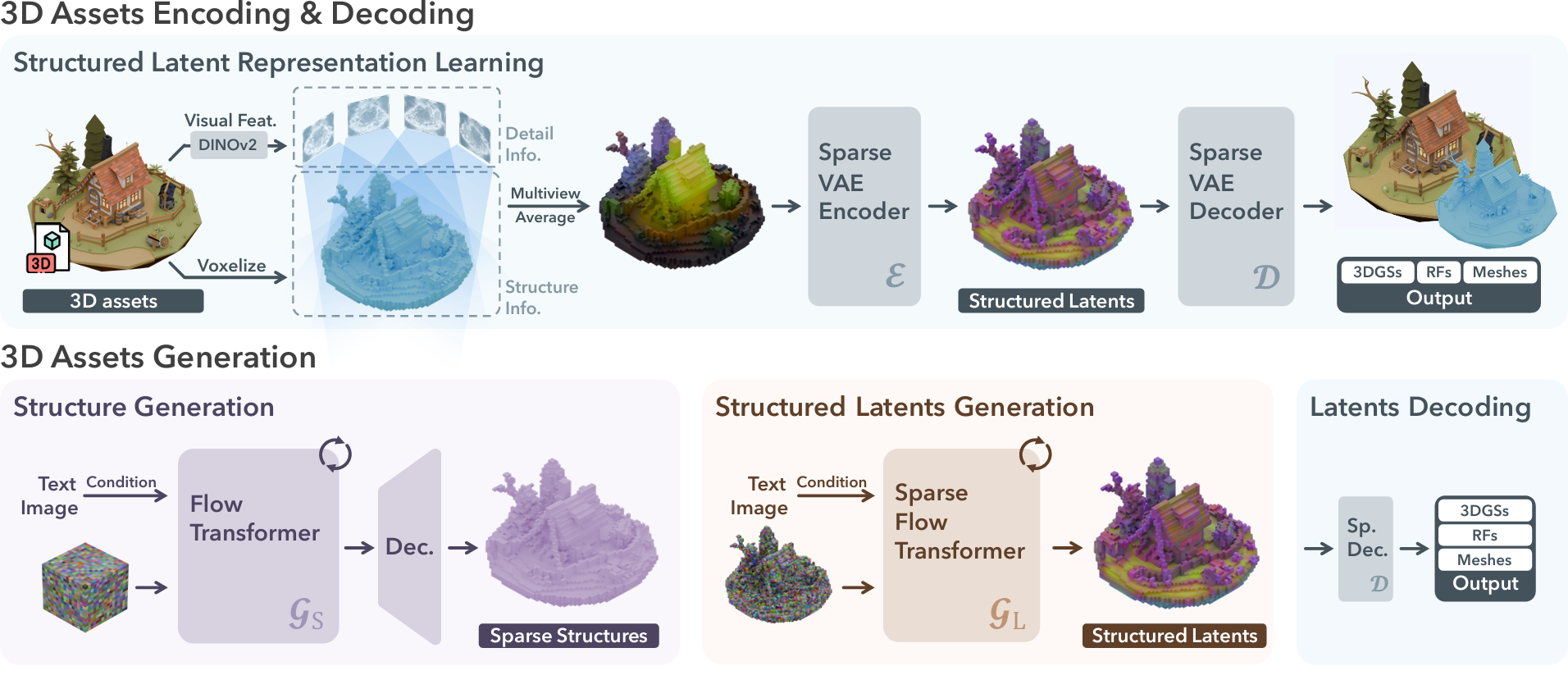
对于一个3D资产，首先从密集的视角（从球面上采150个视角）进行渲染，用DINOv2作为通用的图像特征提取器，对渲染出的图片做特征提取。DINOv2会将图片提取成[1024, 37, 37]大小的patch。同时，我们会对3D资产本身进行处理，将其进行体素化，离散成若干voxel。在TRELLIS的实现中，空间分辨率选取的是64×64×64，在其最后使用的通用数据集上，这样做平均会得到20k个voxel，不同的资产可能导出不同数量的voxel。然后将刚才得到的patch，反投影进这个这些voxel里，每个体素上会有1024维的特征。

接下来，会先训练几何和材质两组VAE。考虑几何，我们会用先前得到的体素，表示成一个形状为[b,1,64,64,64]的占用网格。我们首先训练一对基于3D卷积的$\mathcal{E}_\mathrm{S}$和$\mathcal{D}_{\mathrm{S}}$，其将占用网格压缩成[b,8,16,16,16]的一个紧凑的表示，然后再解码回来，解码出的结果被称为Sparse Structure。考虑材质，则是将先前每个voxel上绑定的1024维的特征，用一个编码器$\mathcal{E}$压缩到8维，压缩得到的结果被称为Structured Latent。后面会专门训练不同3D表示的解码器$\mathcal{D}_{\mathrm{GS}},\mathcal{D}_{\mathrm{RF}},\mathcal{D}_{\mathrm{M}}$来将Structured Latent转换成对应的3D表示，然后通过对应优化目标的监督，来渲染出合理的样子。

关于Structured Latent的VAE：大概率是先用$\mathcal{E}$和$\mathcal{D}_{\mathrm{GS}}$进行的训练，直接以多视角图片做监督训练了一对VAE，然后固定住$\mathcal{E}$，再去训$\mathcal{D}_\mathrm{RF}$和$\mathcal{D}_{\mathrm{M}}$。

在论文中并没有提到KL loss，可能并没有用？也可能是讳莫如深了。

最后，为了生成，会在两组VAE所在的latent space里都训练生成模型$\mathcal{G}$，$\mathcal{G}$的架构主要参考DiT。根据需要来引入对应的控制模态或者扩大模型参数量。

当前，其开源了一个自洽的测试代码，连同数据集预处理的脚本，代码写的非常的整洁。

├── models
│   ├── sparse_structure_flow.py
│   ├── sparse_structure_vae.py
│   ├── structured_latent_flow.py
│   └── structured_latent_vae
│       ├── base.py
│       ├── ...
│       └── __init__.py
├── modules
│   ├── attention
│   │   ├── full_attn.py
│   │   └── ...
│   ├── norm.py
│   ├── sparse
│   │   ├── attention
│   │   ├── ...
│   │   └── transformer
│   ├── spatial.py
│   ├── transformer
│   │   ├── blocks.py
│   │   └── ...
│   └── utils.py
├── pipelines
│   ├── base.py
│   ├── samplers
│   │   ├── base.py
│   │   └── ...
│   └── trellis_image_to_3d.py
├── renderers
│   ├── gaussian_render.py
│   ├── ...
│   └── sh_utils.py
├── representations
│   ├── gaussian
│   │   ├── gaussian_model.py
│   │   └── ...
│   ├── __init__.py
│   ├── mesh
│   │   ├── cube2mesh.py
│   │   └── ...
│   ├── octree
│   │   └── octree_dfs.py
│   └── radiance_field
│       └── strivec.py
└── utils
    ├── general_utils.py
    ├── ...
    └── render_utils.py

models里是网络结构，modules里是构造网络需要的各种模块，其中sparse是相关网络或模块的稀疏变体（后面要用到的妙妙工具）。pipielines实现了一个按diffuser库风格写的一个用于推理的类，renderers和representations分别用来渲染不同3D表示以及构造不同3D表示。

Sparse Structure

我们先从简单的地方入手，先来考虑如何生成占用网格来表示几何。

Sparse Structure VAE

考虑$\mathcal{E}_\mathrm{S}$和$\mathcal{D}_{\mathrm{S}}$。这两者是在Latent Diffusion Model里常用的VAE的直接推广：

SparseStructureEncoder(
  (input_layer): Conv3d(1, 32, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
  (blocks): ModuleList(
    (0-1): 2 x ResBlock3d(
      (norm1): ChannelLayerNorm32((32,), eps=1e-05, elementwise_affine=True)
      (norm2): ChannelLayerNorm32((32,), eps=1e-05, elementwise_affine=True)
      (conv1): Conv3d(32, 32, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (conv2): Conv3d(32, 32, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (skip_connection): Identity()
    )
    (2): DownsampleBlock3d(
      (conv): Conv3d(32, 128, kernel_size=(2, 2, 2), stride=(2, 2, 2))
    )
    (3-4): 2 x ResBlock3d(
      (norm1): ChannelLayerNorm32((128,), eps=1e-05, elementwise_affine=True)
      (norm2): ChannelLayerNorm32((128,), eps=1e-05, elementwise_affine=True)
      (conv1): Conv3d(128, 128, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (conv2): Conv3d(128, 128, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (skip_connection): Identity()
    )
    (5): DownsampleBlock3d(
      (conv): Conv3d(128, 512, kernel_size=(2, 2, 2), stride=(2, 2, 2))
    )
    (6-7): 2 x ResBlock3d(
      (norm1): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
      (norm2): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
      (conv1): Conv3d(512, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (conv2): Conv3d(512, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (skip_connection): Identity()
    )
  )
  (middle_block): Sequential(
    (0): ResBlock3d(
      (norm1): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
      (norm2): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
      (conv1): Conv3d(512, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (conv2): Conv3d(512, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (skip_connection): Identity()
    )
    (1): ResBlock3d(
      (norm1): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
      (norm2): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
      (conv1): Conv3d(512, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (conv2): Conv3d(512, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (skip_connection): Identity()
    )
  )
  (out_layer): Sequential(
    (0): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
    (1): SiLU()
    (2): Conv3d(512, 16, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
  )
)

-------------------------------------------------------------------------

SparseStructureDecoder(
  (input_layer): Conv3d(8, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
  (middle_block): Sequential(
    (0): ResBlock3d(
      (norm1): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
      (norm2): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
      (conv1): Conv3d(512, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (conv2): Conv3d(512, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (skip_connection): Identity()
    )
    (1): ResBlock3d(
      (norm1): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
      (norm2): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
      (conv1): Conv3d(512, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (conv2): Conv3d(512, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (skip_connection): Identity()
    )
  )
  (blocks): ModuleList(
    (0-1): 2 x ResBlock3d(
      (norm1): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
      (norm2): ChannelLayerNorm32((512,), eps=1e-05, elementwise_affine=True)
      (conv1): Conv3d(512, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (conv2): Conv3d(512, 512, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (skip_connection): Identity()
    )
    (2): UpsampleBlock3d(
      (conv): Conv3d(512, 1024, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
    )
    (3-4): 2 x ResBlock3d(
      (norm1): ChannelLayerNorm32((128,), eps=1e-05, elementwise_affine=True)
      (norm2): ChannelLayerNorm32((128,), eps=1e-05, elementwise_affine=True)
      (conv1): Conv3d(128, 128, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (conv2): Conv3d(128, 128, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (skip_connection): Identity()
    )
    (5): UpsampleBlock3d(
      (conv): Conv3d(128, 256, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
    )
    (6-7): 2 x ResBlock3d(
      (norm1): ChannelLayerNorm32((32,), eps=1e-05, elementwise_affine=True)
      (norm2): ChannelLayerNorm32((32,), eps=1e-05, elementwise_affine=True)
      (conv1): Conv3d(32, 32, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (conv2): Conv3d(32, 32, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
      (skip_connection): Identity()
    )
  )
  (out_layer): Sequential(
    (0): ChannelLayerNorm32((32,), eps=1e-05, elementwise_affine=True)
    (1): SiLU()
    (2): Conv3d(32, 1, kernel_size=(3, 3, 3), stride=(1, 1, 1), padding=(1, 1, 1))
  )
)

其工作流很好理解，主体是将2D卷积变成了3D卷积来处理体素。其中的一个频繁使用的类是ResBlock3d，这个类相比于图像里常用的，有着一些有趣的修改：

class ResBlock3d(nn.Module):
    def __init__(
        self,
        channels: int,
        out_channels: Optional[int] = None,
        norm_type: Literal["group", "layer"] = "layer",
    ):
        super().__init__()
        self.channels = channels
        self.out_channels = out_channels or channels

        self.norm1 = norm_layer(norm_type, channels)
        self.norm2 = norm_layer(norm_type, self.out_channels)
        self.conv1 = nn.Conv3d(channels, self.out_channels, 3, padding=1)
        self.conv2 = zero_module(nn.Conv3d(self.out_channels, self.out_channels, 3, padding=1))
        self.skip_connection = nn.Conv3d(channels, self.out_channels, 1) if channels != self.out_channels else nn.Identity()
    
    def forward(self, x: torch.Tensor) -> torch.Tensor:
        h = self.norm1(x)
        h = F.silu(h)
        h = self.conv1(h)
        h = self.norm2(h)
        h = F.silu(h)
        h = self.conv2(h)
        h = h + self.skip_connection(x)
        return h

其一是把一般图像生成里的Group Norm改成Layer Norm，我感觉这样能维护在处理Sparse Structure这个过程时每个体素的“各向同性”。以及ResBlock3d里的一个细节是将self.conv2进行零初始化，保证一开始的残差是零，我记得在2D的latent diffusion model里并没有这样做。但这样做肯定更好训练的，于是就这么干了。

$\mathcal{E}_{\mathrm{S}}$的处理是对空间分辨率进行$64^3 \rightarrow 32^3 \rightarrow 16^3$，同时通道维度先从1用self.input_layer拉到512，然后处理成$512\rightarrow128\rightarrow32$。最后的self.out_layer会将通道数再缩小到8。在$\mathcal{E}_{\mathrm{S}}$里，下采样是很单纯的，直接用卷积把通道数拉大，然后设置步长和卷积核大小就好了，在下采样时这样做并不会产生棋盘伪影（棋盘伪影会反映在梯度上）。

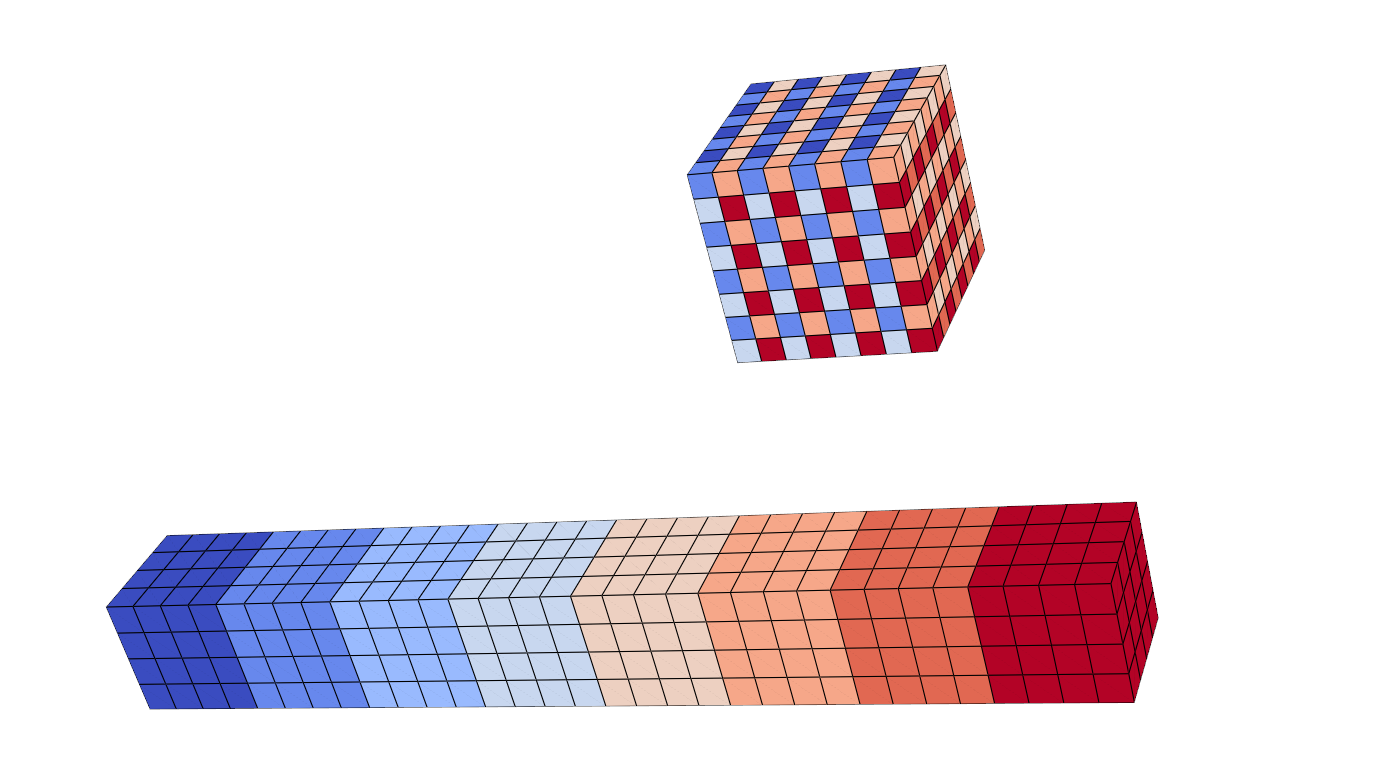
但在$\mathcal{D}_{\mathrm{S}}$里，实现上采样的操作时用的是3D版本的PixelShuffle，这是一个很有趣的操作。这个操作用通道来代换“空间分辨率”，因为CNN强烈假设空间上的局部区域是相关的，通过共享卷积来计算局部特征。然而对通道间的假设较弱，所以可以用不同通道上的滤波器来为空间上的相邻位置提供更“复杂”的插值。

def pixel_shuffle_3d(x: torch.Tensor, scale_factor: int) -> torch.Tensor:
    """
    3D pixel shuffle.
    """
    B, C, H, W, D = x.shape
    C_ = C // scale_factor**3
    x = x.reshape(B, C_, scale_factor, scale_factor, scale_factor, H, W, D)
    x = x.permute(0, 1, 5, 2, 6, 3, 7, 4)
    x = x.reshape(B, C_, H*scale_factor, W*scale_factor, D*scale_factor)
    return x

PixelShuffle是一个很酷的想法，其示意图完全值得一个精良的动画。这里可以借pyvista绘制一下，如图所示：

Sparse Structure Flow

然后我们关注一下生成部分$\mathcal{G}_{\mathrm{S}}$的实现，其主体是一个DiT，但其实也并没有完全沿用DiT里的设计。其训练了一个Rectified Flow，个人觉得训一个DDPM还是Flow Matching在这里区别不大，只不过Rectified Flow在实现起来确实简洁清爽。DiT是一个将Transformer适配进Diffusion的一个设计，生成Sparse Structure的SparseStructureFlowModel基本是DiT的朴素推广：

SparseStructureFlowModel(
  (t_embedder): TimestepEmbedder(
    (mlp): Sequential(
      (0): Linear(in_features=256, out_features=1024, bias=True)
      (1): SiLU()
      (2): Linear(in_features=1024, out_features=1024, bias=True)
    )
  )
  (input_layer): Linear(in_features=8, out_features=1024, bias=True)
  (blocks): ModuleList(
    (0-23): 24 x ModulatedTransformerCrossBlock(
      (norm1): LayerNorm32((1024,), eps=1e-06, elementwise_affine=False)
      (norm2): LayerNorm32((1024,), eps=1e-06, elementwise_affine=True)
      (norm3): LayerNorm32((1024,), eps=1e-06, elementwise_affine=False)
      (self_attn): MultiHeadAttention(
        (to_qkv): Linear(in_features=1024, out_features=3072, bias=True)
        (q_rms_norm): MultiHeadRMSNorm()
        (k_rms_norm): MultiHeadRMSNorm()
        (to_out): Linear(in_features=1024, out_features=1024, bias=True)
      )
      (cross_attn): MultiHeadAttention(
        (to_q): Linear(in_features=1024, out_features=1024, bias=True)
        (to_kv): Linear(in_features=1024, out_features=2048, bias=True)
        (to_out): Linear(in_features=1024, out_features=1024, bias=True)
      )
      (mlp): FeedForwardNet(
        (mlp): Sequential(
          (0): Linear(in_features=1024, out_features=4096, bias=True)
          (1): GELU(approximate='tanh')
          (2): Linear(in_features=4096, out_features=1024, bias=True)
        )
      )
      (adaLN_modulation): Sequential(
        (0): SiLU()
        (1): Linear(in_features=1024, out_features=6144, bias=True)
      )
    )
  )
  (out_layer): Linear(in_features=1024, out_features=8, bias=True)
)

由于后面的SLatFlowModel主体也是一个DiT，但那时候我们需要关注一些其他部分。所以在这里我们在介绍SparseStructureFlowModel的同时，也介绍DiT作为铺垫。

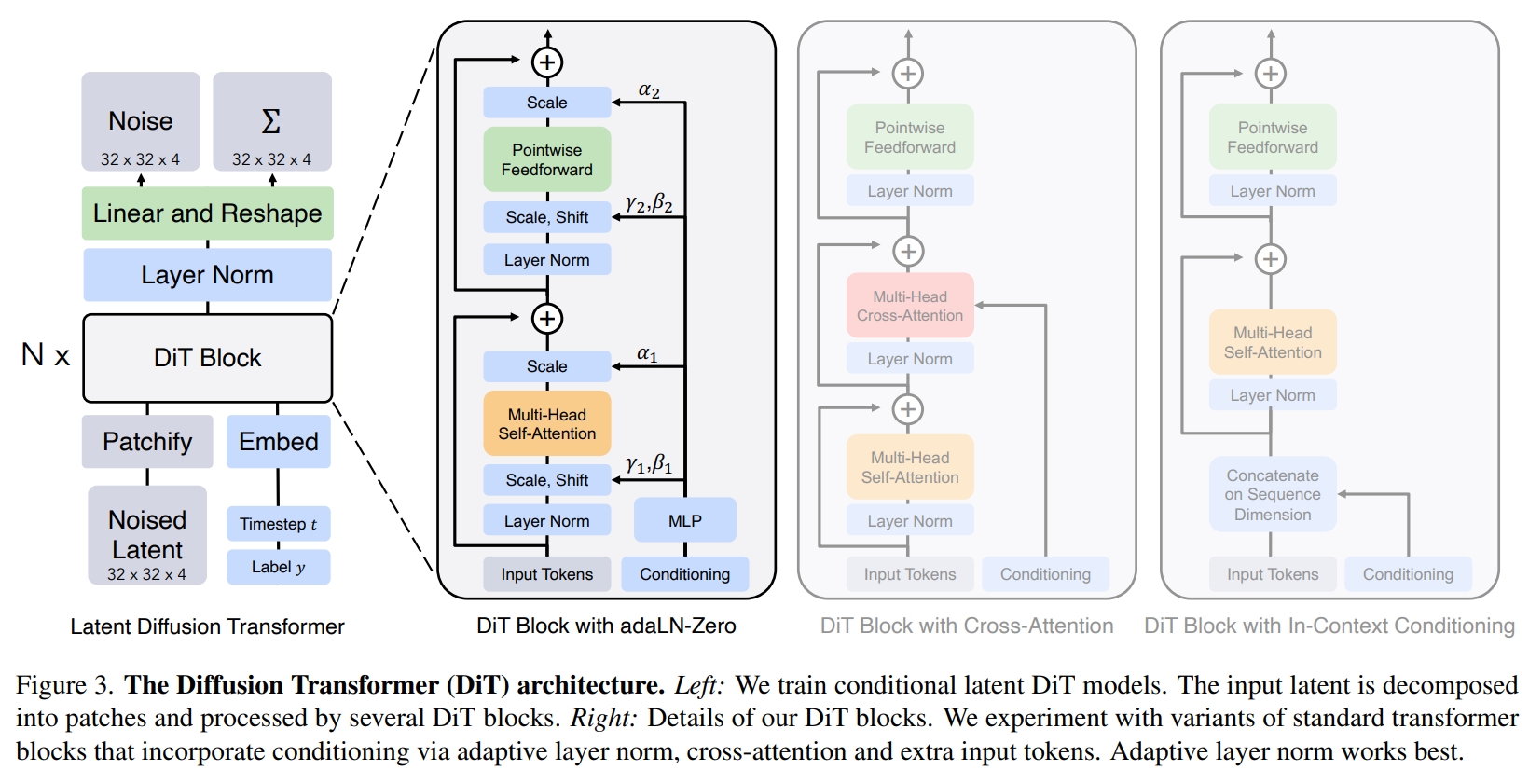
在最初的扩散模型中，一个基于CNN的U-Net，混有attention算子的，具有长程跳连的网络被认为是最佳实践。DiT的一个特点就是整个架构纯由attention实现，没有卷积算子参与其中，这使得整个网络可以简单地叠加许多block，而不需要像CNN一样调整通道数等操作。从一些意义上讲适合”scaling up“。

DiT沿用了许多ViT的设计，先将二维图像通过patchify打成一维序列，这里patch的大小一般是2，4，8。例如对DiT文中所述的32×32×4的latents，取patch大小为2，就会将其展开成256×16的序列。其中256是$(32/2)^2$，代表token的数量，16是将一个patch下的元素（各自有4个通道）排列在一起。然后一般会用一层MLP将16映射到更高维度，后面进行attention的计算。

在一些实现里，也会是将其处理成$16\times16\times16$，然后以patch大小作为卷积核的尺寸和步长，用卷积层来实现映射，道理是一样的。

但TRELLIS这里的pathify是支持更高维输入的，道理其实是一样的：

def patchify(x: torch.Tensor, patch_size: int):
    """
    Patchify a tensor.

    Args:
        x (torch.Tensor): (N, C, *spatial) tensor
        patch_size (int): Patch size
    """
    DIM = x.dim() - 2
    for d in range(2, DIM + 2):
        assert x.shape[d] % patch_size == 0, f"Dimension {d} of input tensor must be divisible by patch size, got {x.shape[d]} and {patch_size}"

    x = x.reshape(*x.shape[:2], *sum([[x.shape[d] // patch_size, patch_size] for d in range(2, DIM + 2)], []))
    x = x.permute(0, 1, *([2 * i + 3 for i in range(DIM)] + [2 * i + 2 for i in range(DIM)]))
    x = x.reshape(x.shape[0], x.shape[1] * (patch_size ** DIM), *(x.shape[-DIM:]))
    return x

这个的影响其实最后的self.input_layer和self.output_layer里，由于其处理的是三维体素，输出维数需要是patch大小的三次方：

1
2
3

self.input_layer = nn.Linear(in_channels * patch_size**3, model_channels)
...
self.out_layer = nn.Linear(model_channels, out_channels * patch_size**3)

但其实，由于TRELLIS里在次数的latent是[b,8,16,16,16]，支持$16^3=4096$的序列长度也不是不行，所以其patch大小取的是1。self.input_layer将8维映射到1024维，即1个token的长度是1024。

然后需要对计算的token进行位置编码，DiT里采用的是最基本的绝对位置编码（Absolute Position Encoding），实际上NeRF里有一个同名的操作，甚至形式也很接近。在NeRF或者INR（Implicit Neural Representation）里，那里的位置编码是用来将坐标投影到高维空间，由于通过三角函数构造的这些不同分量的基他们不能互相线性表示，从而放大了坐标间的差异。而在Transformer里，是用于建模不同token之间的位置的关系的。例如对于序列$x\in\mathbb{R}^{4096\times1024}$，其中4096是token数量，1024是token维度。经典的绝对位置编码按：

$p_{\left( t,2i \right)}=\sin \left( \frac{t}{10000^{\frac{2i}{d_{model}}}} \right) \\ p_{\left( t,2i+1 \right)}=\cos \left( \frac{t}{10000^{\frac{2i}{d_{model}}}} \right)$

其中1024就是$d_{model}$，$t$指代索引$t$处的token，$i$指对应token的分量。这样计算得到的值会直接加到$x$。TRELLIS中也是用的绝对位置编码，然而其代码里额外实现了“旋转位置编码”（Rotary Position Encoding，RoPE），这是一种精妙的结合了绝对位置编码和相对位置编码的技术，虽然最后并没有实装，但我们在这里也介绍一下。

如果你顺着代码定义看下来，你会发现RoPE的加入方式好像和我们意识里的位置编码不太一样。我们顺着ModulatedTransformerCrossBlock→MultiHeadAttention往下找，会在forward里找到计算的过程：

def forward(self, x: torch.Tensor, context: Optional[torch.Tensor] = None, indices: Optional[torch.Tensor] = None) -> torch.Tensor:
    B, L, C = x.shape
    if self._type == "self":
        qkv = self.to_qkv(x)
        qkv = qkv.reshape(B, L, 3, self.num_heads, -1)
        if self.use_rope:
            q, k, v = qkv.unbind(dim=2)
            q, k = self.rope(q, k, indices)
            qkv = torch.stack([q, k, v], dim=2)
        if self.attn_mode == "full":
            if self.qk_rms_norm:
                q, k, v = qkv.unbind(dim=2)
                q = self.q_rms_norm(q)
                k = self.k_rms_norm(k)
                h = scaled_dot_product_attention(q, k, v)
            else:
                h = scaled_dot_product_attention(qkv)
        elif self.attn_mode == "windowed":
            raise NotImplementedError("Windowed attention is not yet implemented")
    else:
        Lkv = context.shape[1]
        q = self.to_q(x)
        kv = self.to_kv(context)
        q = q.reshape(B, L, self.num_heads, -1)
        kv = kv.reshape(B, Lkv, 2, self.num_heads, -1)
        if self.qk_rms_norm:
            q = self.q_rms_norm(q)
            k, v = kv.unbind(dim=2)
            k = self.k_rms_norm(k)
            h = scaled_dot_product_attention(q, k, v)
        else:
            h = scaled_dot_product_attention(q, kv)
    h = h.reshape(B, L, -1)
    h = self.to_out(h)
    return h

我们发现self.rope起效在了计算出Q和K以后，而编码操作的对象也从序列变成和Q和K。这其实就是一种相对位置编码的实现。为了理解这一点，我们先考虑在绝对位置编码时，计算第$i$个token和第$j$个token（记作$x_i,x_j$）计算自注意力（忽略归一化）的过程，其在具有位置编码$p_i,p_j$：

$q_i=\left( x_i+p_i \right) W^Q,k_j=\left( x_j+p_j \right) W^K,v_j=\left( x_j+p_j \right) W^V \\ \alpha _{ij}=\mathrm{soft}\max \left( \left( x_i+p_i \right) W^Q\left( W^K \right) ^T\left( x_j+p_j \right) ^T \right) \\ \mathrm{Att}\left( x_i \right) =\sum_{j=1}^n{\alpha _{ij}\left( x_j+p_j \right) W^V}$

我们会发现，本质上当引入位置编码后，在自注意力运算中多出了一些项：$p_iW^Q,(p_jW^K)^T,p_jW^V$，而相对位置编码就是希望这些项可以被一个相对位置向量$R_{ij}$所替代。而RoPE是一个很精妙的设计，他使用了绝对位置编码来实现相对位置编码。简单来说，如果我们是这样操作$q_i$和$k_i$：

$q_i=x_iW^QR_i,k_j=x_jW^KR_j$

这里$R$是一个正交阵，在token的特征维度只有二维的情形下，其就是一个可交换的旋转矩阵。那样在计算$q_i\cdot k_j$时，其很自然的就成为了$q_i R_{i-j} k_j$，就隐含了相对位置的信息。当token特征维度更高时，我们只需让特征两两一组，每组在他们两个组成的子空间内进行旋转，然后我们只需要像绝对位置编码那样，不同的位置来获取不同的频率。

一般来说，相对位置编码的开销会更大，但其能提供更好的位置泛化。绝对编码计算更快，但变长序列下表现就会下降，所以现在的一些大语言模型往往都选择RoPE。而具体到3D生成这里目前还没有这样的问题。

另外，这里实装了QK normalization。一些技术报告指出，大型transformer在训练时，有时会出现其attention score几乎变成one-hot，然后导致训练崩溃。所以一种缓解的办法就是对Q和K做归一化，TRELLIS是跟SD3的技术报告对齐，使用一组可学习缩放倍数的RMS Norm来进行归一化：

class MultiHeadRMSNorm(nn.Module):
    def __init__(self, dim: int, heads: int):
        super().__init__()
        self.scale = dim ** 0.5
        self.gamma = nn.Parameter(torch.ones(heads, dim))

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        return (F.normalize(x.float(), dim = -1) * self.gamma * self.scale).to(x.dtype)

特别地，DiT对如何注入控制信号做了特别的设计。如之前那张框图里所示，原先的版本都采用的是所谓In-Context Conditioning，就是把驱动信号在一开始就加到tokens里（或者拼在一起）。然后另一种经典的实现就是用cross-attention，驱动信号提供K和V。DiT中探索了用零初始化的AdaLN（Adaptive Layer Norm）来进行驱动信号的注入。这个操作在StyleGAN系列中很常用，StyleGAN里是Adaptive Instance Norm），但道理差不多，只是前者作用于所有特征维度（因为处理的是序列）而后者作用于每个通道（因为是图片）。DiT中声称这样做效果是最好的，于是大家也就这么follow了。

不过这种归一化会有一个问题，因为这种操作对于网络来说，信号$x$和信号$2x$归一化后就都是一样的了。但$x$和$2x$其实根本不一样。在StyleGAN里网络为了抵消这个影响，会在某个通道放置一个非常大的像素点，造成水滴状的伪影。这个问题在DiT里应该也会存在？

但上述condition的方法是适配于向量的（因为驱动信号一般都是向量，例如timestep，标签，CLIP等模型输出的feature），而TRELLIS里的图像condition是DINOV2处理成的token，其维度是[1374, 1024]，所以在TRELLIS实现里，只有时间步用AdaLN-Zero，而图像condition仍然用cross-attention。

我们会注意到，真正计算注意力的函数是scaled_dot_product_attention，如果我们进入这个函数会在modules/attention/full_attn.py里发现这样的写法：

@overload
def scaled_dot_product_attention(qkv: torch.Tensor) -> torch.Tensor:
    """
    Apply scaled dot product attention.

    Args:
        qkv (torch.Tensor): A [N, L, 3, H, C] tensor containing Qs, Ks, and Vs.
    """
    ...

@overload
def scaled_dot_product_attention(q: torch.Tensor, kv: torch.Tensor) -> torch.Tensor:
    """
    Apply scaled dot product attention.

    Args:
        q (torch.Tensor): A [N, L, H, C] tensor containing Qs.
        kv (torch.Tensor): A [N, L, 2, H, C] tensor containing Ks and Vs.
    """
    ...

@overload
def scaled_dot_product_attention(q: torch.Tensor, k: torch.Tensor, v: torch.Tensor) -> torch.Tensor:
    """
    Apply scaled dot product attention.

    Args:
        q (torch.Tensor): A [N, L, H, Ci] tensor containing Qs.
        k (torch.Tensor): A [N, L, H, Ci] tensor containing Ks.
        v (torch.Tensor): A [N, L, H, Co] tensor containing Vs.

    Note:
        k and v are assumed to have the same coordinate map.
    """
    ...

def scaled_dot_product_attention(*args, **kwargs):
    arg_names_dict = {
        1: ['qkv'],
        2: ['q', 'kv'],
        3: ['q', 'k', 'v']
    }
    num_all_args = len(args) + len(kwargs)
    assert num_all_args in arg_names_dict, f"Invalid number of arguments, got {num_all_args}, expected 1, 2, or 3"
    for key in arg_names_dict[num_all_args][len(args):]:
        assert key in kwargs, f"Missing argument {key}"

    if num_all_args == 1:
        ...

    elif num_all_args == 2:
        ...

    elif num_all_args == 3:
        ...

    if BACKEND == 'xformers':
        ...
    elif BACKEND == 'flash_attn':
        ...
    elif BACKEND == 'sdpa':
        ...
    elif BACKEND == 'naive':
        if num_all_args == 1:
            q, k, v = qkv.unbind(dim=2)
        elif num_all_args == 2:
            k, v = kv.unbind(dim=2)
        out = _naive_sdpa(q, k, v)
    else:
        raise ValueError(f"Unknown attention module: {BACKEND}")
    
    return out

然而，Python里并不存在真正的重载。这里的@overload只是类型提示的一部分。这样写在针对这种情景（有许多后端来完成同一件事）时，是很方便的。在TRELLIS项目里，后面还有多处这样的实现。

现在我们关心一下其构造的latent space的性质。在2D图像生成里，我们知道其VAE近乎是一个下采样的作用，我们期望能在3D里看到一样的结果。TRELLIS提供了一个接受图像condition的$\mathcal{G}_{\mathrm{S}}$，我们给出一张在3DV里具有深远意义的图片：

然后来看看得到的[1, 8, 16, 16, 16]是什么样的：

对8通道作PCA降维，然后越小的值分配越低的不透明度。我们可以看到，紧凑的立方体内部确实有一个挖掘机的结构。当进一步过$\mathcal{D}_{\mathrm{S}}$后，我们可以得到整个的sparse structure：

非常惊异的是，我们仅仅只是输入了单张图片，并没有给出对应的相机位姿。在训练时作为condition的图像是被随机抽取的，想不到这样简单的策略居然这么稳健。

Structured Latent

现在我们对粗糙的几何生成有了圆满的答案，我们现在来看如何生成材质。这个事情特别的地方在于，每个样本的体素数量是不一样的，同时每个体素的特征维数是一样的。所以这相比于一般炼丹用的数据结构，需要特殊的处理方法。

Sparse Tensor

对于这样特征维数固定而token数不固定的张量，我们可以先预先考虑一下我们需要对它进行怎样的操作。如果我们只想进行一些非线性激活或者线性映射，只需要用对应的算子去操作其特征就好。如果我们要进行attention运算，attention本身也是支持变长的，也不会有什么问题。但如果我们要实现卷积操作，那就会有一些问题。为了统一这些TRELLIS里实现了一个SparseTensor类，这个类兼容了spconv和torchsparse两个经典的稀疏运算库以及常用的张量操作：

但TRELLIS还是在spconv后端下训的。

class SparseTensor:
    """
    Sparse tensor with support for both torchsparse and spconv backends.
    
    Parameters:
    - feats (torch.Tensor): Features of the sparse tensor.
    - coords (torch.Tensor): Coordinates of the sparse tensor.
    - shape (torch.Size): Shape of the sparse tensor.
    - layout (List[slice]): Layout of the sparse tensor for each batch
    - data (SparseTensorData): Sparse tensor data used for convolusion

    NOTE:
    - Data corresponding to a same batch should be contiguous.
    - Coords should be in [0, 1023]
    """
    @overload
    def __init__(self, feats: torch.Tensor, coords: torch.Tensor, shape: Optional[torch.Size] = None, layout: Optional[List[slice]] = None, **kwargs): ...

    @overload
    def __init__(self, data, shape: Optional[torch.Size] = None, layout: Optional[List[slice]] = None, **kwargs): ...

    def __init__(self, *args, **kwargs):
        # Lazy import of sparse tensor backend
        global SparseTensorData
        if SparseTensorData is None:
            import importlib
            if BACKEND == 'torchsparse':
                SparseTensorData = importlib.import_module('torchsparse').SparseTensor
            elif BACKEND == 'spconv':
                SparseTensorData = importlib.import_module('spconv.pytorch').SparseConvTensor
                
        method_id = 0
        if len(args) != 0:
            method_id = 0 if isinstance(args[0], torch.Tensor) else 1
        else:
            method_id = 1 if 'data' in kwargs else 0

        if method_id == 0:
            feats, coords, shape, layout = args + (None,) * (4 - len(args))
            if 'feats' in kwargs:
                feats = kwargs['feats']
                del kwargs['feats']
            if 'coords' in kwargs:
                coords = kwargs['coords']
                del kwargs['coords']
            if 'shape' in kwargs:
                shape = kwargs['shape']
                del kwargs['shape']
            if 'layout' in kwargs:
                layout = kwargs['layout']
                del kwargs['layout']

            if shape is None:
                shape = self.__cal_shape(feats, coords)
            if layout is None:
                layout = self.__cal_layout(coords, shape[0])
            if BACKEND == 'torchsparse':
                self.data = SparseTensorData(feats, coords, **kwargs)
            elif BACKEND == 'spconv':
                spatial_shape = list(coords.max(0)[0] + 1)[1:]
                self.data = SparseTensorData(feats.reshape(feats.shape[0], -1), coords, spatial_shape, shape[0], **kwargs)
                self.data._features = feats
        elif method_id == 1:
            data, shape, layout = args + (None,) * (3 - len(args))
            if 'data' in kwargs:
                data = kwargs['data']
                del kwargs['data']
            if 'shape' in kwargs:
                shape = kwargs['shape']
                del kwargs['shape']
            if 'layout' in kwargs:
                layout = kwargs['layout']
                del kwargs['layout']

            self.data = data
            if shape is None:
                shape = self.__cal_shape(self.feats, self.coords)
            if layout is None:
                layout = self.__cal_layout(self.coords, shape[0])

        self._shape = shape
        self._layout = layout
        self._scale = kwargs.get('scale', (1, 1, 1))
        self._spatial_cache = kwargs.get('spatial_cache', {})

        if DEBUG:
            try:
                assert self.feats.shape[0] == self.coords.shape[0], f"Invalid feats shape: {self.feats.shape}, coords shape: {self.coords.shape}"
                assert self.shape == self.__cal_shape(self.feats, self.coords), f"Invalid shape: {self.shape}"
                assert self.layout == self.__cal_layout(self.coords, self.shape[0]), f"Invalid layout: {self.layout}"
                for i in range(self.shape[0]):
                    assert torch.all(self.coords[self.layout[i], 0] == i), f"The data of batch {i} is not contiguous"
            except Exception as e:
                print('Debugging information:')
                print(f"- Shape: {self.shape}")
                print(f"- Layout: {self.layout}")
                print(f"- Scale: {self._scale}")
                print(f"- Coords: {self.coords}")
                raise e
        
	......

同时这个类里还仿照标准的torch.Tensor实现了大量的魔法方法来方便使用。其中feats就是寻常的特征，coords是一个[N, 4]的坐标，其中4是由batch id和三维坐标索引构成。data是为了便于跟稀疏运算库对接。

我们需要指出关于shape和batch的定义，SparseTensor里是这样规定张量形状的：

def __cal_shape(self, feats, coords):
    shape = []
    shape.append(coords[:, 0].max().item() + 1)
    shape.extend([*feats.shape[1:]])
    return torch.Size(shape)

例如如果你只有1个样本，那么coords的[:, 0]就会全为0，shape的第一维也就是1，而shape的第二维会是特征维度。所以当我们打印x.shape时，一般只会输出[1, 512], [4, 1024]这样的结果，而不是具体的体素数量。

在这里，batch也并不是那么明显的cat在一起，并且这里的批处理实现与常规的CV和NLP任务有些不同。实际上我们会同时拼接coords和feat，并且维护一个layout来记录哪些索引对应哪个样本：

def __cal_layout(self, coords, batch_size):
    seq_len = torch.bincount(coords[:, 0], minlength=batch_size)
    offset = torch.cumsum(seq_len, dim=0) 
    layout = [slice((offset[i] - seq_len[i]).item(), offset[i].item()) for i in range(batch_size)]
    return layout

例如[slice(0, 18382, None)], [slice(0, 16935, None), slice(16935, 38467, None)]，其中None代表默认步长为1。后面我们会具体看到我们如何让这样的批处理化适应到不同的过程上。

Structured Latent Encoder

现在我们来关心一下在后续实现里具体怎么跟这个SparseTensor结合。我们可以从SLat的编码器$\mathcal{E}$的实现看起，$\mathcal{E}$本身是一个基于Sparse Transformer的结构：

SLatEncoder(
  (pos_embedder): AbsolutePositionEmbedder()
  (input_layer): SparseLinear(in_features=1024, out_features=768, bias=True)
  (blocks): ModuleList(
    (0-11): 12 x SparseTransformerBlock(
      (norm1): LayerNorm32((768,), eps=1e-06, elementwise_affine=False)
      (norm2): LayerNorm32((768,), eps=1e-06, elementwise_affine=False)
      (attn): SparseMultiHeadAttention(
        (to_qkv): Linear(in_features=768, out_features=2304, bias=True)
        (to_out): Linear(in_features=768, out_features=768, bias=True)
      )
      (mlp): SparseFeedForwardNet(
        (mlp): Sequential(
          (0): SparseLinear(in_features=768, out_features=3072, bias=True)
          (1): SparseGELU(approximate='tanh')
          (2): SparseLinear(in_features=3072, out_features=768, bias=True)
        )
      )
    )
  )
  (out_layer): SparseLinear(in_features=768, out_features=16, bias=True)
)

在models/structured_latent_vae/encoder.py的SLatEncoder中。我们可以看到其中先使用了SparseLinear：

1	self.out_layer = sp.SparseLinear(model_channels, 2 * latent_channels)

而如先前的讨论，我们知道这里的Sparse在实现上其实只需要将feats送入寻常的Linear即可：

class SparseLinear(nn.Linear):
    def __init__(self, in_features, out_features, bias=True):
        super(SparseLinear, self).__init__(in_features, out_features, bias)

    def forward(self, input: SparseTensor) -> SparseTensor:
        return input.replace(super().forward(input.feats))

整个Slat_Encoder继承自SparseTransformerBase，我们继续跳转进来查看细节。首先值得一提的是这里也有一个位置编码self.pos_embedder，其发挥作用是在：

def forward(self, x: sp.SparseTensor) -> sp.SparseTensor:
    h = self.input_layer(x)
    if self.pe_mode == "ape":
        h = h + self.pos_embedder(x.coords[:, 1:])

而这里的位置编码就是我们更熟悉的NeRF里的那种了，将形状为[N, 3]的空间坐标用三角函数基映射到高维空间，从而与input_layer的输出维度对齐，如果维度没对齐就直接补零。

现在我们再看回来，关注其中blocks的核心实现SparseMultiHeadAttention：

self.blocks = nn.ModuleList([
    SparseTransformerBlock(
        model_channels,
        num_heads=self.num_heads,
        mlp_ratio=self.mlp_ratio,
        attn_mode=attn_mode,
        window_size=window_size,
        shift_sequence=shift_sequence,
        shift_window=shift_window,
        serialize_mode=serialize_mode,
        use_checkpoint=self.use_checkpoint,
        use_rope=(pe_mode == "rope"),
        qk_rms_norm=self.qk_rms_norm,
    )
    for attn_mode, window_size, shift_sequence, shift_window, serialize_mode in block_attn_config(self)
])

这里的block_attn_config约定了attention的行为：

def block_attn_config(self):
    """
    Return the attention configuration of the model.
    """
    for i in range(self.num_blocks):
        if self.attn_mode == "shift_window":
            yield "serialized", self.window_size, 0, (16 * (i % 2),) * 3, sp.SerializeMode.Z_ORDER
        elif self.attn_mode == "shift_sequence":
            yield "serialized", self.window_size, self.window_size // 2 * (i % 2), (0, 0, 0), sp.SerializeMode.Z_ORDER
        elif self.attn_mode == "shift_order":
            yield "serialized", self.window_size, 0, (0, 0, 0), sp.SerializeModes[i % 4]
        elif self.attn_mode == "full":
            yield "full", None, None, None, None
        elif self.attn_mode == "swin":
            yield "windowed", self.window_size, None, self.window_size // 2 * (i % 2), None

于是在SparseTransformerBlock，self.attn根据具体的模式实例化了具体的attention计算：

self.attn = SparseMultiHeadAttention(
    channels,
    num_heads=num_heads,
    attn_mode=attn_mode,
    window_size=window_size,
    shift_sequence=shift_sequence,
    shift_window=shift_window,
    serialize_mode=serialize_mode,
    qkv_bias=qkv_bias,
    use_rope=use_rope,
    qk_rms_norm=qk_rms_norm,
)

对于$\mathcal{E}$和后面的各种表示的$\mathcal{D}_{\ast}$，这里的模式是windowed，即滑窗，借鉴自曾经的Swin Transformer。然而在Flow的训练里，用的是full。为了便于理解，我们这里先解读full模式下的行为，在后面提到解码器的时候，我们再来分析windowed下的行为。

我们以按qkv整体作输入（即计算自注意力）时为例，其他时候是一样的。在这里，qkv是一个sparse tensor：

1
2
3

q_seqlen = [qkv.layout[i].stop - qkv.layout[i].start for i in range(qkv.shape[0])]
kv_seqlen = q_seqlen
qkv = qkv.feats     # [T, 3, H, C]

我们先利用layout将不同batch对应的序列索引拿出来，然后在先进的attention实现里（例如xformers）：

if num_all_args == 1:
    q, k, v = qkv.unbind(dim=1)
elif num_all_args == 2:
    k, v = kv.unbind(dim=1)
q = q.unsqueeze(0)
k = k.unsqueeze(0)
v = v.unsqueeze(0)
mask = xops.fmha.BlockDiagonalMask.from_seqlens(q_seqlen, kv_seqlen)
out = xops.memory_efficient_attention(q, k, v, mask)[0]

这样会用如下图所示的一个mask：

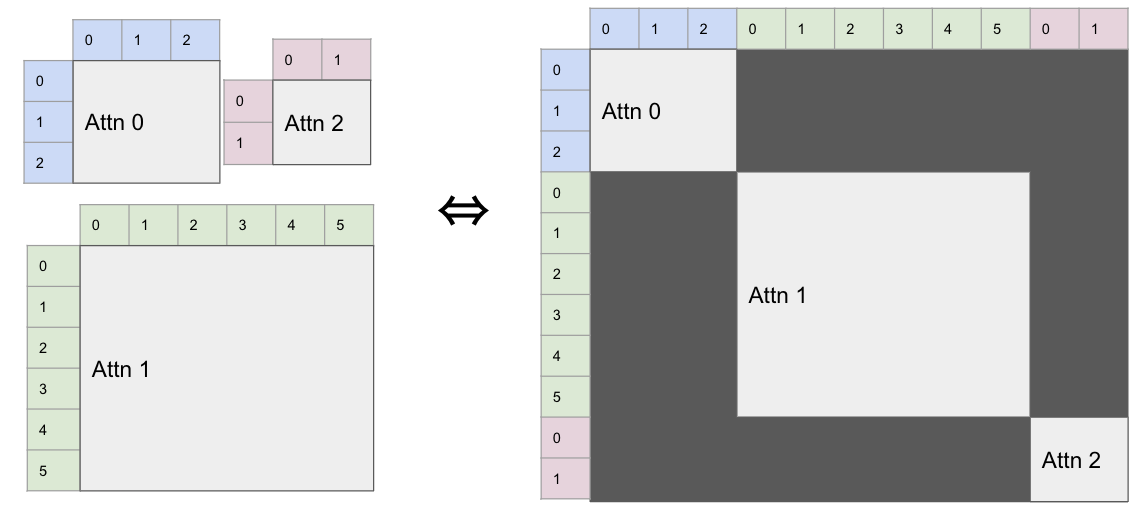
这样就能让不同batch之间互不影响，然后batchify的进行训练。在最后，也会有一个self.out_layer来将特征映射到8维，从而完成压缩。

Structured Latent Flow

$\mathcal{G}_{\mathrm{L}}$的实现主体仍然是DiT：

SLatFlowModel(
  (t_embedder): TimestepEmbedder(
    (mlp): Sequential(
      (0): Linear(in_features=256, out_features=1024, bias=True)
      (1): SiLU()
      (2): Linear(in_features=1024, out_features=1024, bias=True)
    )
  )
  (pos_embedder): AbsolutePositionEmbedder()
  (input_layer): SparseLinear(in_features=8, out_features=128, bias=True)
  (input_blocks): ModuleList(
    (0): SparseResBlock3d(
      (norm1): LayerNorm32((128,), eps=1e-06, elementwise_affine=True)
      (norm2): LayerNorm32((128,), eps=1e-06, elementwise_affine=False)
      (conv1): SparseConv3d(
        (conv): SubMConv3d(128, 128, kernel_size=[3, 3, 3], stride=[1, 1, 1], padding=[0, 0, 0], dilation=[1, 1, 1], output_padding=[0, 0, 0], algo=ConvAlgo.MaskImplicitGemm)
      )
      (conv2): SparseConv3d(
        (conv): SubMConv3d(128, 128, kernel_size=[3, 3, 3], stride=[1, 1, 1], padding=[0, 0, 0], dilation=[1, 1, 1], output_padding=[0, 0, 0], algo=ConvAlgo.MaskImplicitGemm)
      )
      (emb_layers): Sequential(
        (0): SiLU()
        (1): Linear(in_features=1024, out_features=256, bias=True)
      )
      (skip_connection): Identity()
    )
    (1): SparseResBlock3d(
      (norm1): LayerNorm32((128,), eps=1e-06, elementwise_affine=True)
      (norm2): LayerNorm32((1024,), eps=1e-06, elementwise_affine=False)
      (conv1): SparseConv3d(
        (conv): SubMConv3d(128, 1024, kernel_size=[3, 3, 3], stride=[1, 1, 1], padding=[0, 0, 0], dilation=[1, 1, 1], output_padding=[0, 0, 0], algo=ConvAlgo.MaskImplicitGemm)
      )
      (conv2): SparseConv3d(
        (conv): SubMConv3d(1024, 1024, kernel_size=[3, 3, 3], stride=[1, 1, 1], padding=[0, 0, 0], dilation=[1, 1, 1], output_padding=[0, 0, 0], algo=ConvAlgo.MaskImplicitGemm)
      )
      (emb_layers): Sequential(
        (0): SiLU()
        (1): Linear(in_features=1024, out_features=2048, bias=True)
      )
      (skip_connection): SparseLinear(in_features=128, out_features=1024, bias=True)
      (updown): SparseDownsample()
    )
  )
  (blocks): ModuleList(
    (0-23): 24 x ModulatedSparseTransformerCrossBlock(
      (norm1): LayerNorm32((1024,), eps=1e-06, elementwise_affine=False)
      (norm2): LayerNorm32((1024,), eps=1e-06, elementwise_affine=True)
      (norm3): LayerNorm32((1024,), eps=1e-06, elementwise_affine=False)
      (self_attn): SparseMultiHeadAttention(
        (to_qkv): Linear(in_features=1024, out_features=3072, bias=True)
        (q_rms_norm): SparseMultiHeadRMSNorm()
        (k_rms_norm): SparseMultiHeadRMSNorm()
        (to_out): Linear(in_features=1024, out_features=1024, bias=True)
      )
      (cross_attn): SparseMultiHeadAttention(
        (to_q): Linear(in_features=1024, out_features=1024, bias=True)
        (to_kv): Linear(in_features=1024, out_features=2048, bias=True)
        (to_out): Linear(in_features=1024, out_features=1024, bias=True)
      )
      (mlp): SparseFeedForwardNet(
        (mlp): Sequential(
          (0): SparseLinear(in_features=1024, out_features=4096, bias=True)
          (1): SparseGELU(approximate='tanh')
          (2): SparseLinear(in_features=4096, out_features=1024, bias=True)
        )
      )
      (adaLN_modulation): Sequential(
        (0): SiLU()
        (1): Linear(in_features=1024, out_features=6144, bias=True)
      )
    )
  )
  (out_blocks): ModuleList(
    (0): SparseResBlock3d(
      (norm1): LayerNorm32((2048,), eps=1e-06, elementwise_affine=True)
      (norm2): LayerNorm32((128,), eps=1e-06, elementwise_affine=False)
      (conv1): SparseConv3d(
        (conv): SubMConv3d(2048, 128, kernel_size=[3, 3, 3], stride=[1, 1, 1], padding=[0, 0, 0], dilation=[1, 1, 1], output_padding=[0, 0, 0], algo=ConvAlgo.MaskImplicitGemm)
      )
      (conv2): SparseConv3d(
        (conv): SubMConv3d(128, 128, kernel_size=[3, 3, 3], stride=[1, 1, 1], padding=[0, 0, 0], dilation=[1, 1, 1], output_padding=[0, 0, 0], algo=ConvAlgo.MaskImplicitGemm)
      )
      (emb_layers): Sequential(
        (0): SiLU()
        (1): Linear(in_features=1024, out_features=256, bias=True)
      )
      (skip_connection): SparseLinear(in_features=2048, out_features=128, bias=True)
      (updown): SparseUpsample()
    )
    (1): SparseResBlock3d(
      (norm1): LayerNorm32((256,), eps=1e-06, elementwise_affine=True)
      (norm2): LayerNorm32((128,), eps=1e-06, elementwise_affine=False)
      (conv1): SparseConv3d(
        (conv): SubMConv3d(256, 128, kernel_size=[3, 3, 3], stride=[1, 1, 1], padding=[0, 0, 0], dilation=[1, 1, 1], output_padding=[0, 0, 0], algo=ConvAlgo.MaskImplicitGemm)
      )
      (conv2): SparseConv3d(
        (conv): SubMConv3d(128, 128, kernel_size=[3, 3, 3], stride=[1, 1, 1], padding=[0, 0, 0], dilation=[1, 1, 1], output_padding=[0, 0, 0], algo=ConvAlgo.MaskImplicitGemm)
      )
      (emb_layers): Sequential(
        (0): SiLU()
        (1): Linear(in_features=1024, out_features=256, bias=True)
      )
      (skip_connection): SparseLinear(in_features=256, out_features=128, bias=True)
    )
  )
  (out_layer): SparseLinear(in_features=128, out_features=8, bias=True)
)

但由于体素的数量确实比较多，直接做注意力有点吃不住。所以在SLatFlowModel的实现里，使用稀疏卷积进一步做了下采样。当计算完注意力以后再由稀疏卷积上采样回来：

for chs, next_chs in zip(io_block_channels, io_block_channels[1:] + [model_channels]):
    self.input_blocks.extend([
        SparseResBlock3d(
            chs,
            model_channels,
            out_channels=chs,
        )
        for _ in range(num_io_res_blocks-1)
    ])
    self.input_blocks.append(
        SparseResBlock3d(
            chs,
            model_channels,
            out_channels=next_chs,
            downsample=True,
        )
    )
            ...
self.out_blocks = nn.ModuleList([])
for chs, prev_chs in zip(reversed(io_block_channels), [model_channels] + list(reversed(io_block_channels[1:]))):
    self.out_blocks.append(
        SparseResBlock3d(
            prev_chs * 2 if self.use_skip_connection else prev_chs,
            model_channels,
            out_channels=chs,
            upsample=True,
        )
    )
    self.out_blocks.extend([
        SparseResBlock3d(
            chs * 2 if self.use_skip_connection else chs,
            model_channels,
            out_channels=chs,
        )
        for _ in range(num_io_res_blocks-1)
    ])

这里的SparseResBlock3d就是ResBlock3d的稀疏变种：

class SparseResBlock3d(nn.Module):
    def __init__(
        self,
        channels: int,
        emb_channels: int,
        out_channels: Optional[int] = None,
        downsample: bool = False,
        upsample: bool = False,
    ):
        super().__init__()
        self.channels = channels
        self.emb_channels = emb_channels
        self.out_channels = out_channels or channels
        self.downsample = downsample
        self.upsample = upsample
        
        assert not (downsample and upsample), "Cannot downsample and upsample at the same time"

        self.norm1 = LayerNorm32(channels, elementwise_affine=True, eps=1e-6)
        self.norm2 = LayerNorm32(self.out_channels, elementwise_affine=False, eps=1e-6)
        self.conv1 = sp.SparseConv3d(channels, self.out_channels, 3)
        self.conv2 = zero_module(sp.SparseConv3d(self.out_channels, self.out_channels, 3))
        self.emb_layers = nn.Sequential(
            nn.SiLU(),
            nn.Linear(emb_channels, 2 * self.out_channels, bias=True),
        )
        self.skip_connection = sp.SparseLinear(channels, self.out_channels) if channels != self.out_channels else nn.Identity()
        self.updown = None
        if self.downsample:
            self.updown = sp.SparseDownsample(2)
        elif self.upsample:
            self.updown = sp.SparseUpsample(2)

这里的SparseConv3d有两个后端：torchsparse和spconv。传统的卷积是经典的im2col，而稀疏卷积旨在避免白白计算大量值为零的位置，会提前构造好对应关系。在最早的时候是建立输入和输出位置的哈希表，并且维护一个Rulebook来找到滤波器的权重各自对应着哪些输入（以及对应的输出在哪）。在现在，随着相关库的升级，稀疏卷积的具体实现已经没有那么简单了。

先前坐标以[N, 4]储存也正是适配了这里。

一个值得注意的细节是，如果是用spconv来计算，在spconv2.x版本后，在计算时其内部会先对激活的体素进行排序，这样会避免一些无效区域的计算。所以这会导致用spconv计算后输出张量不再连续，我们需要将其按batch id重新排序：

if spatial_changed and (x.shape[0] != 1):
    # spconv was non-1 stride will break the contiguous of the output tensor, sort by the coords
    fwd = new_data.indices[:, 0].argsort()
    bwd = torch.zeros_like(fwd).scatter_(0, fwd, torch.arange(fwd.shape[0], device=fwd.device))
    sorted_feats = new_data.features[fwd]
    sorted_coords = new_data.indices[fwd]
    unsorted_data = new_data
    new_data = spconv.SparseConvTensor(sorted_feats, sorted_coords, unsorted_data.spatial_shape, unsorted_data.batch_size)  # type: ignore

但实际上SLat Flow里用到的SparseConv3d都是stride为1且padding为零的“子流形卷积”SubMConv3d，这种输出的定义是只有卷积核中心覆盖到激活体素时才进行输出。所以在SparseResBlock3d的实现里，self.conv1和self.conv2实际上都不改变坐标数量，坐标数量只有在self.downsample和self.upsample发生改变。

在做降采样时：

class SparseDownsample(nn.Module):
    def __init__(self, factor: Union[int, Tuple[int, ...], List[int]]):
        ...
    def forward(self, input: SparseTensor) -> SparseTensor:
        DIM = input.coords.shape[-1] - 1
        factor = self.factor if isinstance(self.factor, tuple) else (self.factor,) * DIM
        assert DIM == len(factor), 'Input coordinates must have the same dimension as the downsample factor.'

        coord = list(input.coords.unbind(dim=-1))
        for i, f in enumerate(factor):
            coord[i+1] = coord[i+1] // f

        MAX = [coord[i+1].max().item() + 1 for i in range(DIM)]
        OFFSET = torch.cumprod(torch.tensor(MAX[::-1]), 0).tolist()[::-1] + [1]
        code = sum([c * o for c, o in zip(coord, OFFSET)])
        code, idx = code.unique(return_inverse=True)

        new_feats = torch.scatter_reduce(
            torch.zeros(code.shape[0], input.feats.shape[1], device=input.feats.device, dtype=input.feats.dtype),
            dim=0,
            index=idx.unsqueeze(1).expand(-1, input.feats.shape[1]),
            src=input.feats,
            reduce='mean'
        )
        new_coords = torch.stack(
            [code // OFFSET[0]] +
            [(code // OFFSET[i+1]) % MAX[i] for i in range(DIM)],
            dim=-1
        )
        out = SparseTensor(new_feats, new_coords, input.shape,)
        out._scale = tuple([s // f for s, f in zip(input._scale, factor)])
        out._spatial_cache = input._spatial_cache

        out.register_spatial_cache(f'upsample_{factor}_coords', input.coords)
        out.register_spatial_cache(f'upsample_{factor}_layout', input.layout)
        out.register_spatial_cache(f'upsample_{factor}_idx', idx)

        return out

具体的逻辑是将坐标进行整数除法后做哈希，然后得到唯一的索引。这里会在第一次运行时将一开始的坐标等信息存做cache，从而使得后面上采样后可以得到跟下采样之前一样的体素排列：

class SparseUpsample(nn.Module):
    def __init__(self, factor: Union[int, Tuple[int, int, int], List[int]]):
        ...
    def forward(self, input: SparseTensor) -> SparseTensor:
        DIM = input.coords.shape[-1] - 1
        factor = self.factor if isinstance(self.factor, tuple) else (self.factor,) * DIM
        assert DIM == len(factor), 'Input coordinates must have the same dimension as the upsample factor.'

        new_coords = input.get_spatial_cache(f'upsample_{factor}_coords')
        new_layout = input.get_spatial_cache(f'upsample_{factor}_layout')
        idx = input.get_spatial_cache(f'upsample_{factor}_idx')
        if any([x is None for x in [new_coords, new_layout, idx]]):
            raise ValueError('Upsample cache not found. SparseUpsample must be paired with SparseDownsample.')
        new_feats = input.feats[idx]
        out = SparseTensor(new_feats, new_coords, input.shape, new_layout)
        out._scale = tuple([s * f for s, f in zip(input._scale, factor)])
        out._spatial_cache = input._spatial_cache
        return out

这样，Structured Latent的Flow过程的工作流就清楚了。最后还有一处细节，此时训练的Flow是在Structured Latent上的，而在最后送入各自decoder之前，是有一步均值和标准差的变换的。这可能是一开始训VAE训出的空间里的分布直接训Flow不太稳定。

Structured Latent Decoder

现在，流程终于推进到了如何把[N, 8]的Structured Latent给解码成对应的3D表示。如之前所说，$\mathcal{E}$连同不同表示的解码器里也是基于SparseTransformerBase的，同时应用的滑窗注意力。不同表示的解码器派生自SparseTransformerBase，不同之处在于有效的输出维度以及不同的to_representation实现：

def forward(self, x: sp.SparseTensor):
    h = super().forward(x)
    h = h.type(x.dtype)
    h = h.replace(F.layer_norm(h.feats, h.feats.shape[-1:]))
    h = self.out_layer(h)
    return self.to_representation(h)

这里应用滑窗注意力，其实感觉就是显存不够大。在训Flow的时候可以注意力前先降采样，在解码编码的时候这样干损失太大了。虽然滑窗是一个很自然的想法，但TRELLIS其实也探索了一种更纯粹的序列化的方法，即serialized。通过将体素按Z-order或hilbert曲线来映射到一维序列里，然后再进行分块注意力。由于这跟滑窗注意力相比，其实分治（partition）策略的不同，这里我们就不管了。

在modules/sparse/attention/windowed_attn.py里，我们可以找到calc_window_partition：

def calc_window_partition(
    tensor: SparseTensor,
    window_size: Union[int, Tuple[int, ...]],
    shift_window: Union[int, Tuple[int, ...]] = 0
) -> Tuple[torch.Tensor, torch.Tensor, List[int], List[int]]:
    """
    Calculate serialization and partitioning for a set of coordinates.

    Args:
        tensor (SparseTensor): The input tensor.
        window_size (int): The window size to use.
        shift_window (Tuple[int, ...]): The shift of serialized coordinates.

    Returns:
        (torch.Tensor): Forwards indices.
        (torch.Tensor): Backwards indices.
        (List[int]): Sequence lengths.
        (List[int]): Sequence batch indices.
    """
    DIM = tensor.coords.shape[1] - 1
    shift_window = (shift_window,) * DIM if isinstance(shift_window, int) else shift_window
    window_size = (window_size,) * DIM if isinstance(window_size, int) else window_size
    shifted_coords = tensor.coords.clone().detach()
    shifted_coords[:, 1:] += torch.tensor(shift_window, device=tensor.device, dtype=torch.int32).unsqueeze(0)

    MAX_COORDS = shifted_coords[:, 1:].max(dim=0).values.tolist()
    NUM_WINDOWS = [math.ceil((mc + 1) / ws) for mc, ws in zip(MAX_COORDS, window_size)]
    OFFSET = torch.cumprod(torch.tensor([1] + NUM_WINDOWS[::-1]), dim=0).tolist()[::-1]

    shifted_coords[:, 1:] //= torch.tensor(window_size, device=tensor.device, dtype=torch.int32).unsqueeze(0)
    shifted_indices = (shifted_coords * torch.tensor(OFFSET, device=tensor.device, dtype=torch.int32).unsqueeze(0)).sum(dim=1)
    fwd_indices = torch.argsort(shifted_indices)
    bwd_indices = torch.empty_like(fwd_indices)
    bwd_indices[fwd_indices] = torch.arange(fwd_indices.shape[0], device=tensor.device)
    seq_lens = torch.bincount(shifted_indices)
    seq_batch_indices = torch.arange(seq_lens.shape[0], device=tensor.device, dtype=torch.int32) // OFFSET[0]
    mask = seq_lens != 0
    seq_lens = seq_lens[mask].tolist()
    seq_batch_indices = seq_batch_indices[mask].tolist()

    return fwd_indices, bwd_indices, seq_lens, seq_batch_indices

如果理解了之前spconv那里的操作，这块就会更好理解了。我们先考虑batch size是1的时候，对于一个坐标形状为[20527, 4]的稀疏张量。我们会先按照是否需要shift来更新其坐标。

滑窗大小采用的是(8, 8, 8)，实现时会交替的以(0, 0, 0)和(4, 4, 4)做shift_window，来使得相邻层的滑窗可以重叠。

然后，会先计算当前X，Y，Z三方向上索引的最大值MAX_COORDS，然后计算沿X，Y，Z三方向的滑窗数量NUM_WINDOWS，然后我们会按行优先的顺序进行展开（注意NUM_WINDOWS[::-1]）。即我们的NUM_WINDOWS如果是$[W_X,W_Y,W_Z]$：

1	>>torch.cumprod(torch.tensor([1] + NUM_WINDOWS[::-1]), dim=0).tolist()

会输出$\left[ 1,W_Z,W_Y\times W_Z,W_Y\times W_Z\times W_X \right] $，然后再倒序，那样对于一个三维坐标$(x,y,z)$，索引就会是：

$\mathrm{index}=x\times \left( W_Y\times W_Z \right) +y\times W_Z+z$

以及此时$W_Y\times W_Z\times W_X$的那个偏移，会保证不同batch id的坐标被散列到不重叠的位置。在代码里，我们会先将三维坐标整除窗长，找到他们在哪些滑窗内：

1	shifted_coords[:, 1:] //= torch.tensor(window_size, device=tensor.device, dtype=torch.int32).unsqueeze(0)

然后作刚才所说的散列，得到索引：

1	shifted_indices = (shifted_coords * torch.tensor(OFFSET, device=tensor.device, dtype=torch.int32).unsqueeze(0)).sum(dim=1)

例如，对刚才[20527, 4]的例子，我们会计算出：

>> MAX_COORDS
[63, 51, 50]
>> NUM_WINDOWS
[8, 7, 7]
>> OFFSET
[392, 49, 7, 1]

然后，散列表shifted_indices里就是计算好的索引值：

1 2	>> shifted_indices tensor([ 8, 8, 8, ..., 387, 386, 386], device='cuda:0')

对他们做argsort，就能得到按滑窗滑动的顺序了：

1 2	>> fwd_indices tensor([ 0, 1, 2, ..., 20516, 20520, 20524], device='cuda:0')

后面我们会用这个索引重新排列qkv，从而进行批量的滑窗注意力。在计算结束后，我们需要把得到的结果给恢复成原来的顺序，所以这里构造了bwd_indices：

1 2	bwd_indices = torch.empty_like(fwd_indices) bwd_indices[fwd_indices] = torch.arange(fwd_indices.shape[0], device=tensor.device)

这个过程可能有一点绕，举个例子就是比如你和一个人站在桌子的两边，然后面前有一排盒子。对面的人一顿操作把盒子重新排列了一遍，然后递给你一张纸条fwd_indices，然后你读这个纸条，第一行是从左到右第三个盒子，第二行是第五个盒子。然后你找着这个纸条把这些盒子依次取出来从左到右再放好，就是bwd_indices。

然后，用torch.bincount统计一下每个滑窗索引出现的次数，其中有一部分会是零，因为有的时候滑窗会访问一个没有被激活体素的位置。seq_lens.shape[0]可以得到滑窗索引的最大值，再整除OFFSET[0]，就可以得到batch的索引，不过后面也不需要用到。最后去除seq_lens为零的那些索引，就可以用seq_lens再生成对角线式的mask，然后批量进行注意力计算了。计算注意力前后，用fwd_indices和bwd_indices进行重排：

qkv_feats = qkv.feats[fwd_indices]      # [M, 3, H, C]

if DEBUG:
    ...

if all([seq_len == window_size for seq_len in seq_lens]):
    ...
else:
    if ATTN == 'xformers':
        q, k, v = qkv_feats.unbind(dim=1)                       # [M, H, C]
        q = q.unsqueeze(0)                                      # [1, M, H, C]
        k = k.unsqueeze(0)                                      # [1, M, H, C]
        v = v.unsqueeze(0)                                      # [1, M, H, C]
        mask = xops.fmha.BlockDiagonalMask.from_seqlens(seq_lens)
        out = xops.memory_efficient_attention(q, k, v, mask)[0] # [M, H, C]
    elif ATTN == 'flash_attn':
        ...
out = out[bwd_indices]      # [T, H, C]

在多层block之间，这个滑窗的索引是固定不变的，所以也实现了一个cache机制。

现在我们可以说回解码器了。解码器的主体是和编码器一样的12层SparseTransformerBlock，由于mesh的性质，mesh的decoder在Transformer后面接了基于稀疏卷积的上采样模块。由于在这里只需要单纯的按最近邻实现上采样，并不存在之前分析SparseUpsample里的cache，也不需要保证体素数量严格等于什么。所以这里上采样用的是一个新定义的SparseSubdivide类：

class SparseSubdivide(nn.Module):
    """
    Upsample a sparse tensor by a factor of `factor`.
    Implemented as nearest neighbor interpolation.
    """
    def __init__(self):
        super(SparseSubdivide, self).__init__()

    def forward(self, input: SparseTensor) -> SparseTensor:
        DIM = input.coords.shape[-1] - 1
        # upsample scale=2^DIM
        n_cube = torch.ones([2] * DIM, device=input.device, dtype=torch.int)
        n_coords = torch.nonzero(n_cube)
        n_coords = torch.cat([torch.zeros_like(n_coords[:, :1]), n_coords], dim=-1)
        factor = n_coords.shape[0]
        assert factor == 2 ** DIM
        # print(n_coords.shape)
        new_coords = input.coords.clone()
        new_coords[:, 1:] *= 2
        new_coords = new_coords.unsqueeze(1) + n_coords.unsqueeze(0).to(new_coords.dtype)
        
        new_feats = input.feats.unsqueeze(1).expand(input.feats.shape[0], factor, *input.feats.shape[1:])
        out = SparseTensor(new_feats.flatten(0, 1), new_coords.flatten(0, 1), input.shape)
        out._scale = input._scale * 2
        out._spatial_cache = input._spatial_cache
        return out

对于GS，输出的维数是448。这是由于一个voxel约定32个GS，每个GS有14个属性。输出的位置信息是关于当前体素的相对信息，用tanh激活：

1	offset = torch.tanh(offset) / self.resolution * 0.5 * self.rep_config['voxel_size']

GS的属性做了一些特定的处理，例如激活函数改成不易爆炸的softplus，同时取scaling_bias为0.004和opacity_bias为0.1来定义网络输出的零均值。

对于NeRF，其取材自TensoRF，但只是单纯的用CP分解来构造辐射场。对于每一个激活的体素网格，预测形状为[16, 3, 8]的trivec，表示三个正交的向量，对应$v^X,v^Y,v^Z$。形状为[16]的向量表示体密度，形状为[16, 1, 3]的向量表示颜色，他们组合在一起的[16, 4]对应$v^C$。其16是张量分解的秩，全体加起来正好也是448。所以一个定义在当前体素网格里的$8\times8\times8\times4$的local volume可以由外积之和导出：

$V=\sum_{r=1}^R{v_{r}^{X}\circ v_{r}^{Y}\circ v_{r}^{Z}\circ v_{r}^{C}}$

然后，作者们仿照diff-gaussian-rasterization实现了一个diff-octree-rasterization！其实可以理解，八叉树的优化确实是必要的，但这直接把ray casting，CP重建，一套过程都写成cuda扩展是否太夸张了。对于接触晚的人（比如我）NeRF那套早就相忘于江湖了，顶多会个triplane乱弹琵琶了，这太狠了。

对于Mesh，一般的做法都是直接Marching Cubes就完了。但这里沿用了一种更复杂的预测mesh的方法——FlexiCubes，相比于Marching Cubes的固定查表，FlexiCubes引入了更多的参数来支持拓扑的调整。

不过我感觉在这种generative-manner下……感觉可能差别不会很大，这种更适合那种subject-specific时的重建之类的。

在一个体素下，FlexiCubes一共需要预测45个参数。同时Mesh的解码器也预测了8个顶点的颜色，法线和SDF，加起来一共101个参数。然后这些在nvidiffrast的支持下可以直接进行可微渲染，从而优化。

现在我们可以看看最后生成出来的挖掘机是什么样子了，这里就只展示GS render的效果了：

虽然有可能这样的乐高模型已经在数据集里面了，但单张图片能出这样的效果还是很令人欣喜的。

TRELLIS里提供了一系列工具函数来导出.glb，导出以后你可以把它放到blender或meshlab里去看一看：

那一系列工具函数都写的很好，连同在数据预处理时作者们编写的utils3d，都很值得借鉴。

其逻辑是用Mesh Decoder出的Mesh来当作Mesh，用GS Decoder出的GS进行多视角渲染得到图片，然后反投影，烘焙材质图，最后导出为.glb。

至此，整个流程就有了圆满的答案。

Dataset Process

预处理TRELLIS所需的数据也是一个浩大的工程，TRELLIS提供了完整的预处理脚本，适合多结点的服务器运行，在临近最后我也想关于这一部分记录一些内容。无论是渲染用于训练的512尺寸的图像还是用于作图像condition的1024尺寸图片，其都是用Blender渲染，用CYCLES作渲染引擎。这当然是标准解决方案，可以很好的渲染出那些3D资产。

但如果你并没有那么多的服务器来当作“rendering farm”，那么你可以考虑做这样的一些处理，在其blender_script/render.py的init_render中，你可以将bpy.context.scene.cycles.samples调低，这样会降低做光线追踪时一个像素点采样的次数。同时，你可以把一些次级反射统统关了试试：

bpy.context.scene.cycles.max_bounces = 1
bpy.context.scene.cycles.diffuse_bounces = 1
bpy.context.scene.cycles.specular_bounces = 1
bpy.context.scene.cycles.transmission_bounces = 1

bpy.context.scene.cycles.use_transparent_shadows = False
bpy.context.scene.cycles.use_reflections = False
bpy.context.scene.cycles.use_refraction = False

bpy.context.scene.cycles.use_volumetrics = False
bpy.context.scene.cycles.use_glossy_refraction = False

有的时候你会发现你的服务器可能缺少了一些blender运行的必要依赖，你可以试试运行这个脚本。

如果你的计算资源还是不那么充裕，你可以考虑把渲染引擎换成EEVEE，但EEVEE并不是那么好支持单机多卡。以及其后端是OpenGL，如果你的解决方案里有nvidia-docker，你需要特别地在启动容器时输入--gpus 'all,"capabilities=compute,utility,graphics"'，不然OpenGL将不会在GPU上渲染。

如果EEVEE来渲染还是有一些困扰，那么你可以选择重写渲染脚本，选用更轻量和简单的渲染器（例如pyrender）来渲染。

在用blender渲染时，每渲染一个asset会保存一个对应的mesh.ply，这个mesh.ply相比于原来的资产的区别是blender施加的一个旋转。注意在后续体素化，抽特征的时候不要给搞的张冠李戴了。

在提取特征时，TRELLIS选取的是dinov2_vitl14_reg，这个预训练模型的参数量大概是300M。虽然在当时是L，但以现在的角度来看其实也没那么大。但大概率也选用不了更大的模型了，因为方便起见训练图像condition时，DINOv2的特征是online-inference来的，离线存储的话成本反而更大。如果你仔细的话，你会发现在抽特征时，有一个切片操作：

1	patchtokens = features['x_prenorm'][:, dinov2_model.num_register_tokens + 1:].permute(0, 2, 1).reshape(bs, 1024, n_patch, n_patch)

这是大型Transformer的一个特别的现象，会有某些token的值非常大，他们起到的作用有点像NLP里的CLS，表示整张图片的某些全局信息。DINOv2就采取了这样的“寄存器”设计，训练的时候考虑这些token，推理的时候移除。但一些其他的预训练ViT中不一定有这样的设计。

End

虽然从应用效果上看，这样做可能不会比那种寻常DiT方案然后疯狂灌数据，出来mesh以后一顿后处理好。但TRELLIS的管线确实是精巧，涵盖了好多技术栈。TRELLIS给我的感觉就像生化危机6（游戏），各代主角全齐了，故事线交织在一起，直接粉丝向的那种。“这怎么什么都会啊？”，懂DiT，懂稀疏卷积，懂CUDA，懂Blender，懂写代码，很难想象这都是一作一个人做出来的，太狠了。我感觉，如果多年后会有新的三维视觉的教材，估计都会把TRELLIS写上去。这太帅了，我什么时候也能整这么个大活就好了。