From Diffusion Model to Flow Matching


阅读数: 次   
文章目录
  1. Continuous Diffusion
  2. Stochastic Process
  3. Turn Back the Clock
    1. Fokker-Planck Equation
    2. Kolmogorov Backward Equation
    3. Reverse-time SDE
  4. Probability ODE
  5. Flow Matching
  6. Appendix
  7. End

“遥想当年愿，终也只成念，无非梦醒言成谶。“

​ 很久以来我就想写一篇关于更先进的扩散模型的blog，但其发展速度实在是太快了。我上次动手训扩散模型甚至都是2年前了，2年过去，有了翻天覆地的变化。在现在的数据规模下，我们已经知道一个高质量的生成模型，可能更取决于构造的latent。而至于DDPM还是流匹配，可能没那么重要。所以这篇blog其实只是想借着学习这一套东西的由头，复健一下看公式的感觉。

Continuous Diffusion

​ 对扩散模型最直接的理解就是”一步一步的加噪，一步一步的去噪。“，在加噪时，从第$i-1$步加噪到第$i$步的过程为：

下面我们尝试对这个过程进行连续化。我们希望每“一步”尽可能的小，那样我们会增加总的步数$N$，这会导致$\beta_i$的取值相应地变小。在DDPM里，$\beta_i$如下计算：

我们发现，随着$N$的增加，$\beta_i$逐渐变小，而$\beta_i\cdot N$始终不变，构成一个稳定的方差序列。当$N\rightarrow \infty$时，$\beta_i \cdot N$构成一个连续函数，我们记$t=\frac{i-1}{N-1}\in \left[ 0,1 \right] $。不致以混淆，我们记这个连续函数为$\beta(\cdot)$。同时，我们记连续函数$x(t),\epsilon(t)$，他们都等于先前的离散值：

我们取$\Delta t=\frac{1}{N}$，先前的加噪过程即可表示为：

由等价无穷小：

移项后，可得：

这个方程的形式非常接近于一个微分方程，只不过$\sqrt{\beta \left( t \right) \mathrm{d}t}\epsilon \left( t \right) $这一项我们仍然无法处理。为了解决这一项，我们需要引入一些随机过程的基本知识。

Stochastic Process

​ 考虑样本空间$\varOmega$和一个指标集$T$，指标集$T$往往具有时间的含义。随机过程是定义在$\varOmega \times T$上的二元函数$X(\omega,t)$，固定样本点$\omega$，则$X(\omega,t)$就是一个关于$t$的函数，称为轨道；如果固定时间$t$，那么$X(\omega,t)$就是一个我们熟悉的随机变量，服从于某个概率分布。很多时候我们略去$\omega$，将随机过程直接记作$\left\{ X\left( t \right) \right\} $，而一般用小写的$x_t$表示某个样本点或具体取值。那样，在每个时间$t$下，其概率密度函数记作$f(x;t)$，概率分布函数记作$F(x;t)$。

​ 跟概率论时一样，我们也可以定义一些数字特征来描述一个随机过程：

其中$R(t_1,t_2)$称作自相关函数，$C(t_1,t_2)$称作协方差函数，他们用于刻画随机过程自身在两个时间状态之间的关系。

​ 在机器学习课中，我们学过一种非参数化的模型：高斯过程。下面我们回顾一下这个经典的模型，来对随机过程这个概念加深印象。高斯过程指的是一个无限维的高斯分布，对于指标集$T$，如果我们选取$t_1,t_2,…,t_n\in T$，使得得到的$n$维向量$\{\xi_1,\xi_2,…,\xi_n\}$服从一个$n$维的高斯分布，那么我们就说$\{\xi_t\}$是一个高斯过程。我们无法采样无限多的样本点，所以一般我们会先采样足够多的样本构造一个先验分布。我们用核函数$K(\cdot,\cdot)$来建模先验中的自相关关系。最常用的例如径向基核（RBF kernel）：

径向基核张成的协方差矩阵如下图所示：

这个基函数的含义即相邻时间戳下的样本值应该越接近。当我们选择不同性质的核函数，协方差矩阵的会呈现不同的性质，例如周期性，线性等。同时我们一般会给定先验分布是零均值的，即$\mu(t)\equiv0$​。我们采样100个样本点（即我们构造了一个100维的特征空间），通过生成许多组服从高斯分布的样本，通过$K(\cdot,\cdot)$和$\mu(t)$的线性变换，我们可以采样出许多组轨迹：

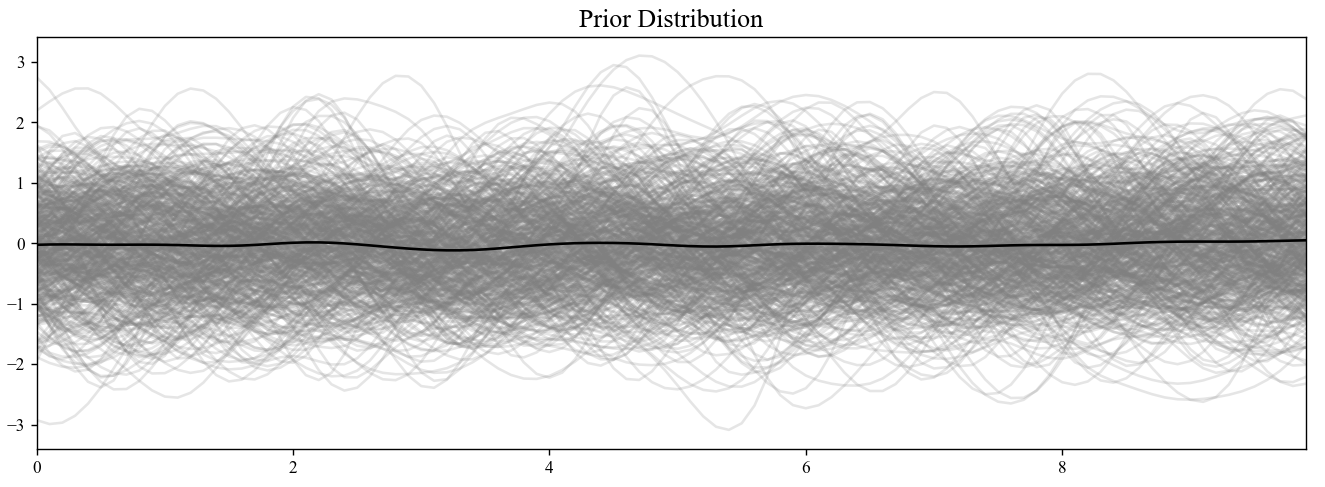
当我们有观测数据后，我们就可以计算后验分布了。根据条件高斯分布的性质：

其中$x_a$是我们观测到的数据，$x_b$是先验分布。

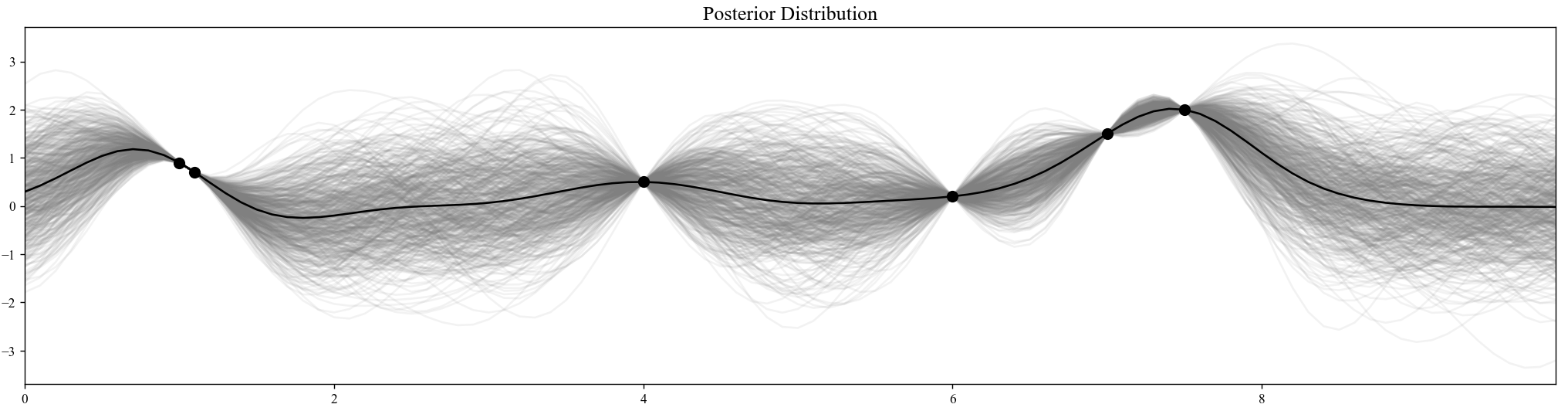
我们就可以直接计算回归后的结果。

​ 现在我们考虑一个非常重要的随机过程：布朗运动，也叫维纳过程。考虑一个对称的一维随机游动，每经过$\Delta t$时间，其等概率地向左或向右移动一步，步长大小为$\Delta x$，记$X(t)$为时刻$t$的位置，则：

当$\Delta t$和$\Delta x$都变得越来越小直至趋于极限，就得到了布朗运动。由于$E\left( X_i \right) =0,\mathrm{Var}\left( X_i \right) =1$​，可以得到：

为了让该随机过程是有意义的，需要使$\Delta x$的阶数是$\Delta t$的根号阶，即$\Delta x = c \sqrt{\Delta t}$。这样$\mathrm{Var}\left[ X\left( t \right) \right] =c^2t$。我们可以可视化一下：

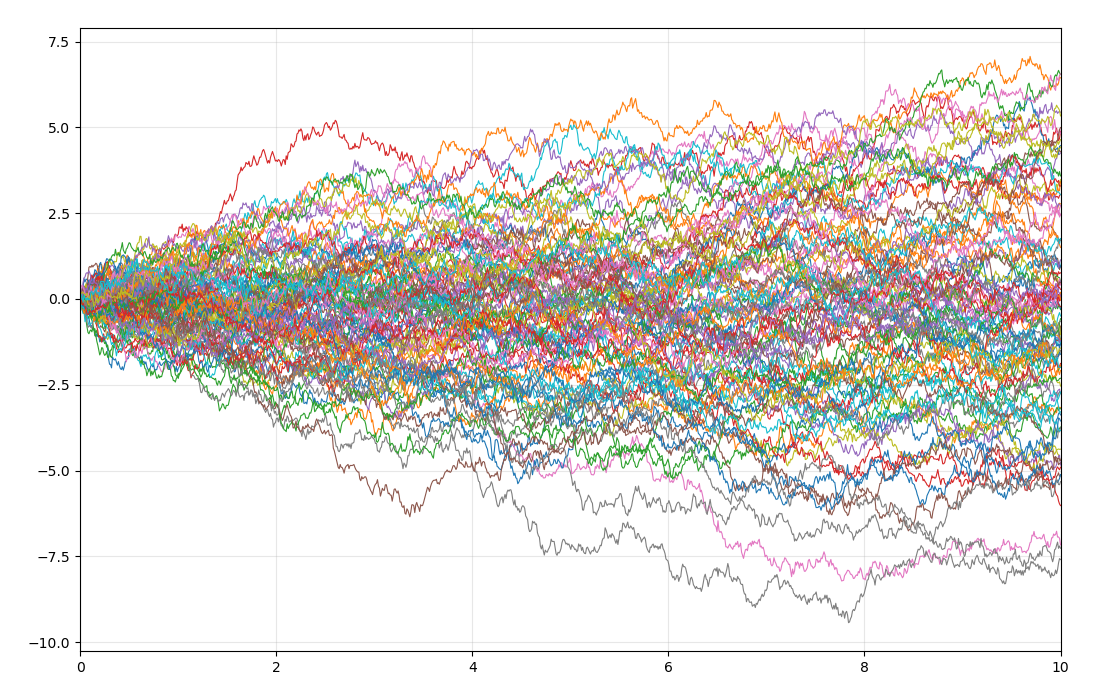
以及，我们可以尝试，如果我们不选取$\Delta x$为$\Delta t$的根号阶，例如我们选取$\Delta x=\Delta t$：

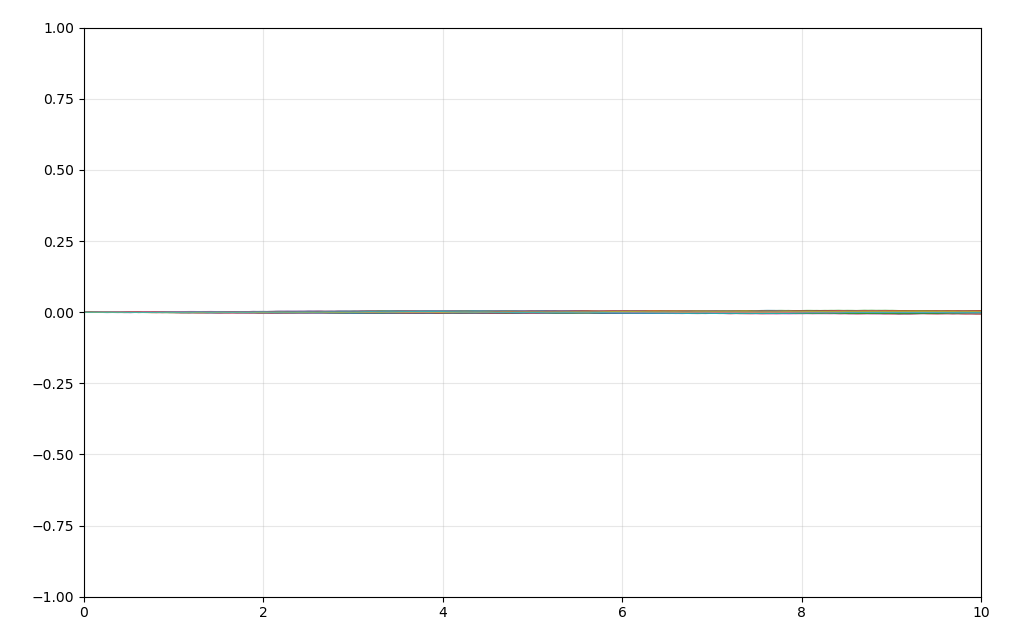
这时候，整个过程就没什么意义了。

同时，随着时间间隔的减少，单位时间内移动的次数越来越多。以及$X(t)$可以看作$X(t_i)-X(t_{i-1})$​这一系列的随机变量之和，他们是独立同分布的，所以根据中心极限定理：

所以$X(t)$服从正态分布，以及我们能发现，给定当前的$X(t)$以及过去的$X(u)$，将来的$X(t+s)$只依赖于现在，所以布朗运动是马尔可夫过程。同时，$X(t)$也是一个独立增量过程。更进一步，我们有：

这可以通过直接计算得到：

我们现在可以看出一些端倪，这里奇怪的$\sqrt{\Delta t}$阶在$\sqrt{\beta \left( t \right) \Delta t}\epsilon \left( t \right) $也出现了，以及$X\left( t+\Delta t \right) -X\left( t \right) \sim \mathcal{N} \left( 0,c^2\Delta t \right) $，正好对应$\sqrt{\Delta t}\epsilon \left( t \right) $，这并不是偶然。我们如果能也建模一个$\mathrm{d}X$，之前推导的连续的前向扩散过程就能有一个完整的答案。

​ 在初学微积分的时候，我们都有知道一些直观的例子，比如求积分其实是无数个离散求和$f(x_{k+1})-f(x_k)$。积分成立的条件是那个求和级数收敛，但对于布朗运动，并不存在这样的条件。因为$X\left( t+\Delta t \right) -X\left( t \right) \sim \mathcal{N} \left( 0,c^2\Delta t \right) $​，随着时间的累积，其“变差”并不是有界的，我们称之为无界变差：

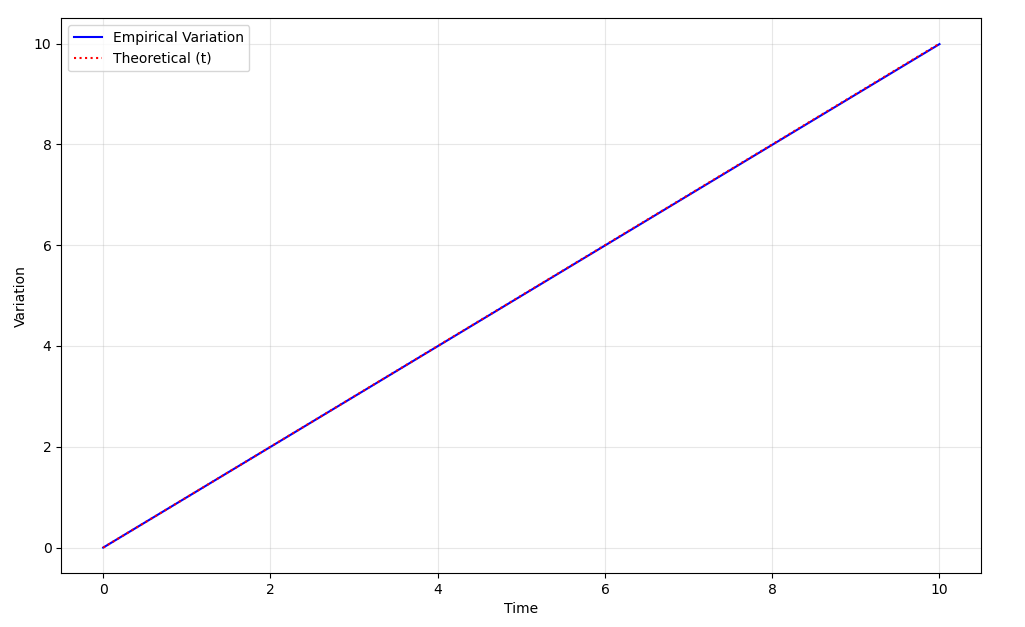
但一个事实是，布朗运动的二阶变差是存在的，并且增量的平方和最终趋近于关于时间的线性函数。我们用标准布朗运动（$c$​取1）来说明这个事实，考虑：

下面我们说明其方差趋近于零，由于独立增量过程是高斯的，其$D(X^2)$的计算并不那么容易，我们先给出：

于是我们就可以直接计算了：

当$\delta$​够小时，方差可以认为是0，所以，我们得到：：

我们也可以简单可视化一下：

接下来，为了不至混淆，我们取其提出者维纳的首字母$W(t)$来表示布朗运动$X(t)$：

此时，等号右侧可以看作一个$0$到$t$上的常规积分。而对于左侧，我们定义$W\left( t_{i+1} \right) -W\left( t_i \right) $为$\mathrm{d}w$​，那么就有：

我们称$\mathrm{d}w$是$\mathrm{d}t$的半阶项，这引导出了与常规微积分中不同的一个本质性的变化。首先，直观上感觉，如果$\mathrm{d}t$趋近于零，此时$\mathrm{d}w\mathrm{d}w$趋近于零，如果将其中一个$\mathrm{d}w$替换为$\mathrm{d}t$​，则当然也趋近于零。不过为了放心，我们在上面求二阶变差时进行一下替换，来看一下：

所以，我们可以说$\mathrm{d}w\mathrm{d}t=0$。现在，我们就能把$\sqrt{\beta \left( t \right) \Delta t}\epsilon \left( t \right) $写作$\sqrt{\beta \left( t \right)}\mathrm{d}w$​了，即：

这样，我们就得到了连续化的DDPM，它是一个一阶随机微分方程。更广义的看，上述微分方程可以写作：

此时对于该微分方程描述的随机过程$\{X(t)\}$，我们称其为伊藤过程。该方程称为伊藤随机微分方程，或扩散方程。$f(\cdot,\cdot)$和$g(\cdot,\cdot)$是两个确定的函数，$f(\cdot,\cdot)$称为漂移（shift）函数，$g(\cdot,\cdot)$称为扩散（diffuse）函数。我们连续化DDPM得到的就是一组特殊的$f(x(t),t)$和$g(x(t),t)$。

​ 对于伊藤过程$X(t)$​，我们有伊藤引理。简单来说，由于半阶项的性质，我们有：

即对于$f(X(t),t)$，在泰勒展开时，我们要多展开一项，这样其他的高阶项在积分意义上才为0。

Turn Back the Clock

我们现在对扩散模型的前向过程有了完整的答案，现在我们要考虑其逆向过程。这个任务是很艰巨的，我们要利用一些工具。首先我们先可视化一个简单的伊藤过程：

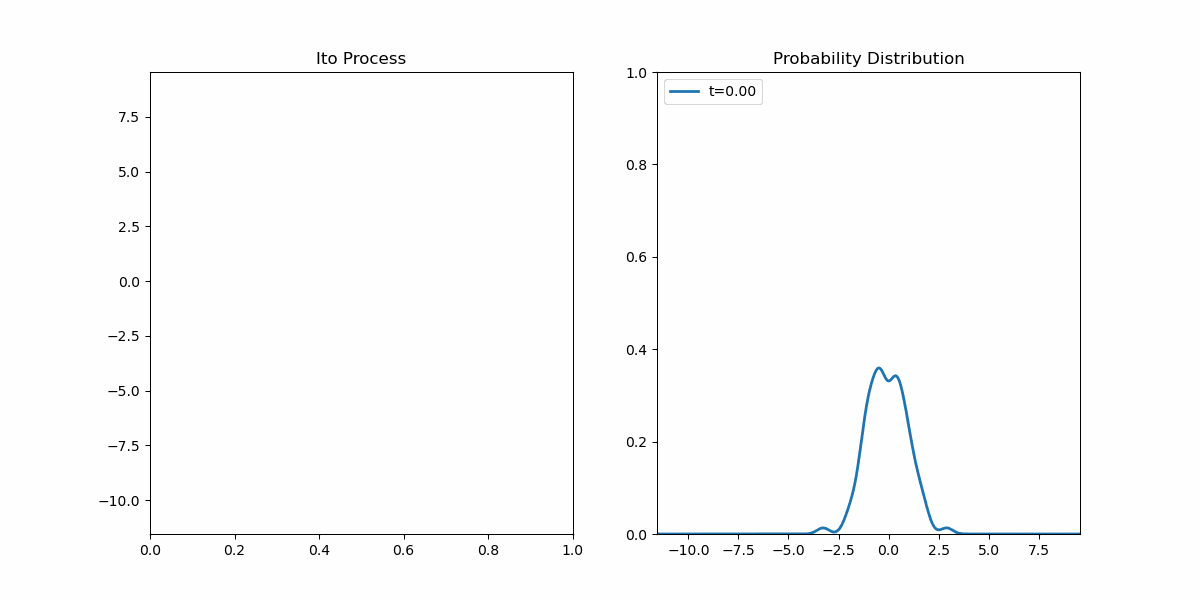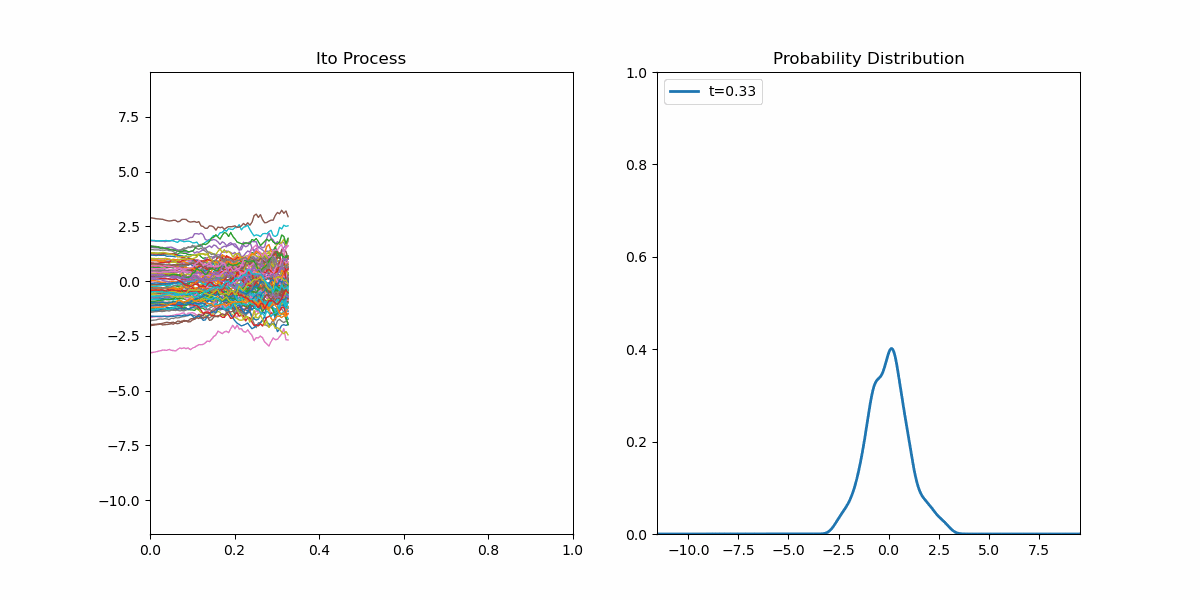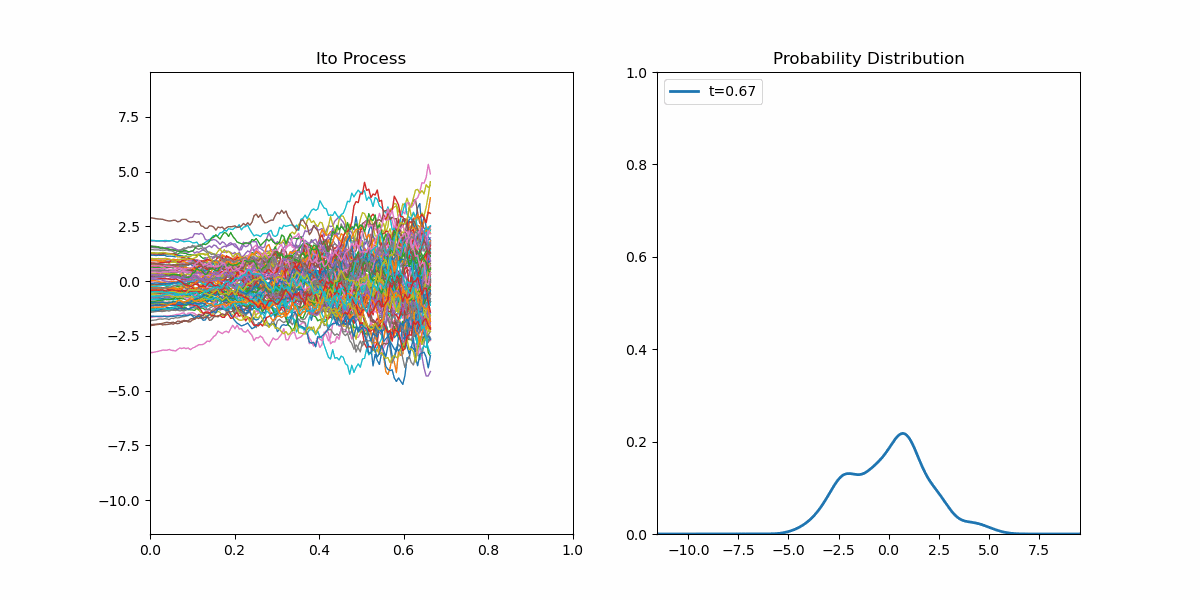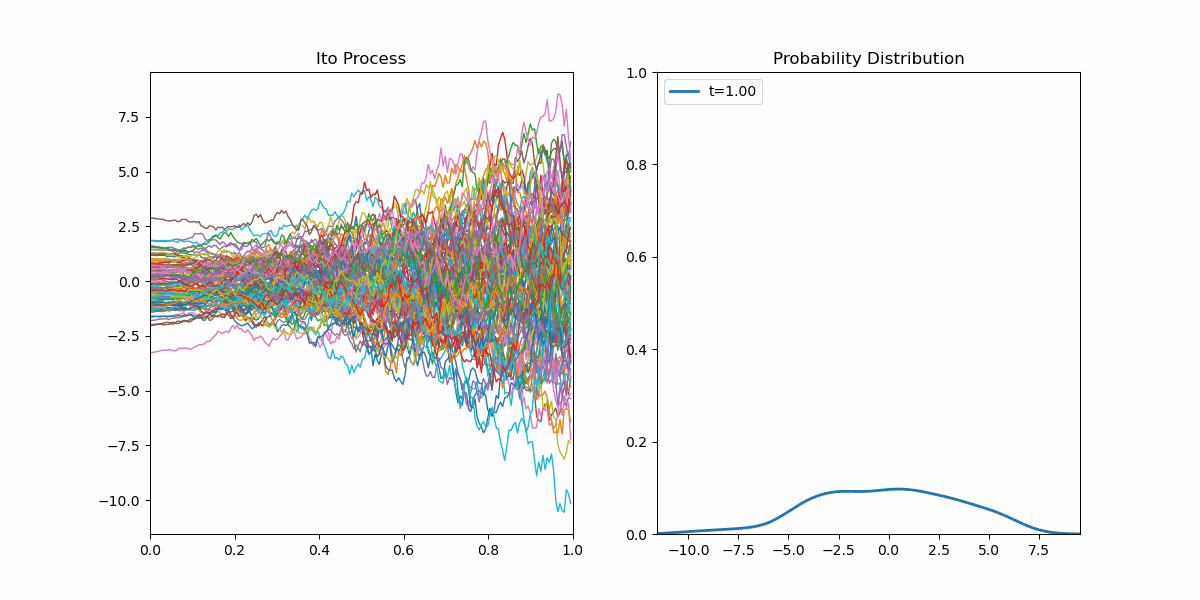
左侧是许多样本轨迹，右侧是每个时刻$t$时由当前的样本点估计出的概率密度函数。我们很自然的发现一件事情，给定随机微分方程，这个方程侧重于描述单个样本的性质；而有时我们很想知道在某个时刻$t$​时全体样本的概率分布。

Fokker-Planck Equation

​ 我们首先所要引入的工具是福克-普朗克（Fokker-Planck）方程，记作FP方程。这个方程将给出随机微分方程的边际分布$p(x_t,t)$，在下文中为了简洁，我们省略显式的时间依赖，如将$p(x_t,t)$记作$p(x_t)$​。推导这个方程需要用到分部积分，而高维情形下的分部积分会给理解这个过程带来不必要的麻烦，所以我们下面就只在一维情形下进行推导。对于一个伊藤过程：

在后面的内容中有时会出现例如$\mu(X_t,t)$和$\mu(x_t,t)$这样的不同，他们具有不同的涵义当我们用大写的$X_t$书写时，往往指代整个随机过程。用小写的$x_t$则表示某一时刻或状态下的具体样本，一般用于描述随机微分方程。

​ 常用的方法是构造辅助函数，我们记$p(x_t,t)$是$X_t$在$t$时的概率密度函数，给定$t_1 < t_2$，我们定义一个函数$F(t,x)$，其满足$F(t_1,x)=F(t_2,x)=0$。出于后面推导的目的，我们还需要$\lim _{x\rightarrow \pm \infty}F\left( t,x \right) =0,\lim _{x\rightarrow \pm \infty}\frac{\partial F\left( t,x \right)}{\partial x}=0$。那么显然，$F\left( t,x_t \right) =\left( t-t_1 \right) \left( t-t_2 \right) p\left( x_t,t \right) $满足这个要求。

​ 由伊藤引理：

然后我们在两边求期望，这样会消去维纳过程那一项：

我们在两边同时从$t_1$积分$t_2$​，不讲武德地交换积分和期望的性质，等式的左侧会是0：

而等式的右侧，会构成三项积分：

注意，当期望展开的时候，第一次出现了$p(x_t)$​。下面我们会继续不讲武德的进行轮换和分部积分：

在计算$I_2$时就用到了$\lim_{x\rightarrow \pm \infty} F\left( t,x \right) =0$：

在计算$I_3$时，用到的就是$\lim_{x\rightarrow \pm \infty} \frac{\partial F\left( t,x \right)}{\partial x}=0$：

由于$I_1+I_2+I_3=0$，我们有：

由于$F\left( t,x_t \right) $是任意选取的，这就引导里的那一项为零：

这个方程就是一维的FP方程，对于多维的情形，可以直接将偏微分推广至梯度算子：

这就是一般情形下的FP方程。也就是说我们给定这个偏微分方程的边界条件，即$p(x_0)$，我们可以通过解这个偏微分方程来直接得到$p(x_t)$。对应到熟悉的DDPM里，就是所谓前向过程的重参数化技巧，可以直接从$x_0$加噪到$x_T$。但我们并不会去解这个偏微分方程，只是用这个方程去导引一些等价变换。

​ 我们在这里先预热一个例子：在扩散模型中，扩散函数$\sigma(\cdot,\cdot)$一般与$x_t$无关，例如我们可以取一个满足$g^2(\cdot)\le\sigma^2(\cdot)$的函数，作下面的代换：

这说明，如果我们将$\mu \left( x_t,t \right) $换成$\mu \left( x_t,t \right) -\frac{1}{2}\left( \sigma ^2\left(t \right) -g^2\left(t \right) \right) \nabla _{x_t}\log p\left( x_t \right) $，将$\sigma ^2\left(t \right) $换成$g ^2\left( t \right) $​，其描述的是两个边际分布完全等价的随机过程。也就是说：

这个事实非常深刻。因为他告诉我们，我们可以人为的改变方差，而不影响$p(x_t)$。我们在后面给出逆向过程的随机微分方程后，这会带来更大的功用。

​ 以及，在推导中，出现了$\nabla _{x_t}\log p\left( x_t \right) $​​，他是当前的对数概率密度函数的梯度。在这个推导里，他的出现看起来很生硬，因为他正好是对数微分的直接结果，我们稍后会看到一个关于这一项更直接的来源，以及其背后的含义。

Kolmogorov Backward Equation

​ 我们已经知道的是，我们可以通过FP方程来等价出一系列的随机过程。但我们仍然没能回答逆向过程，我们可以先形式化上写出我们希望得到的逆向过程：

这里的问题在于，我们并不知道逆向过程的漂移函数$\bar{f}(\cdot,\cdot)$和扩散函数$\bar{g}(\cdot,\cdot)$。在1982年的那篇Reverse-time diffusion equation中，作者使用了许多引理来严谨的给出逆向过程的表达，其用到的技术比较复杂。但其在最后也指出了一个便于理解的证明，理解这个证明我们只需要额外再补充一个关于柯尔莫哥洛夫（Kolmogorov）后向方程的知识。实际上，刚才推导的FP方程也叫柯尔莫哥洛夫前向方程，其简记为KFE（Kolmogorov Forward Equation），后向方程则就简记为KBE。

​ KBE关注的是过渡概率密度函数，即之前的GIF中，右侧的分布是怎么变化的。给定时间$t_0 < t$，过渡概率密度函数记作$p(x,t|x_0,t_0)$，即给定$t_0,x_0$下，$x$和$t$的分布。所以KBE关注的是$\frac{\partial p\left( x,t|x_0,t_0 \right)}{\partial t_0}$，这个式子会很令人困惑。因为我们要取微分的$t_0$，同时出现在了条件里。我们可以这样理解这个偏导数：当概率分布逐渐在时间上向后演化并以$x_0$为条件时，$x$在更晚的时间$t$​上的概率分布将如何变化？

​ 类似地，我们选取$t_0 < t_1 <t$，取$t_1=t_0+\Delta t$。由扩散过程的性质，此时样本的状态也满足$x_1=x_0 + \Delta x$。我们可以写出在这个微小的时间步里的状态转移方程：

我们将其带入到KBE关注的偏导数的定义中去：

由过渡概率密度函数的性质：

于是有：

对$p\left( x,t|x_0+\Delta x,t_1 \right) $进行泰勒展开，展到二阶：

带回原来极限里的那个积分里，就有：

我们可以发现，现在积分和$\Delta t$构成的那两项分别代表着随机过程在时间上的均值和方差，考虑：

由于维纳过程均值为0方差为1，可以计算：

由变上限积分的求导可得：

另一方面，对其取偏微分，我们先操作均值：

我们发现这自动引出了一个条件期望，而这其实就对应着我们控制$x_0,t_0$时向$x_1,t_1$​的演化。其实就对应着想求的极限里的积分项。

对于方差，道理是一样的：

于是，我们就得到了：

在$t_0$和$t_1$差距很小时，我们就可以将等号右边的$t_1$改写为$t_0$：

这就是KBE方程。关于这个方程的功用和意义很令人困惑，我们可以将KBE方程与FP方程放在一起，来直观的理解一下：

我们现在考虑这几个值：在时间$t$时的$x_t$，以及在$s$时的$x_s$，其中$t\le s$。那么对于KFE/FP方程，其中$\partial t$和$\partial x_t$对应的就是$s$和$x_s$，相当于固定$t$时的$x_t$，将其作为初始条件，然后“前向”地计算$s\ge t$时的分布。而对于KBE方程，其中的$\partial t_0$和$\partial x_0$就对应我们选取的$t$和$x_t$。而$s$和$x_s$就被固定，作为边界条件，所以“后向地”计算$t\le s$时的分布。更简洁的说：

前向方程指的是：假如我知道现在的初始条件，未来会发生什么？

后向方程指的是：假如我知道未来的目标状态，现在的条件如何影响这个目标？

举一个很形象的例子，假如你站在一个河流旁边，看到从上游流下来了一个小纸船。前向方程可以用来计算在下游这个小船之后会怎么漂，而后向方程是用来推测这个小船是怎么在上游流下来的，这就是“backward”的来源。所以这并不是“逆转时间”，我们不应把“backward”理解成“reverse”。

Reverse-time SDE

​ 通过刚才的两个推导，我们已经知道，描述$x_t$的随机微分方程和由Kolmogorov方程给出的概率分布$p(x_s,s|x_t,t),s\ge t$是一一对应的。所以，一个随机微分方程的逆向过程，也可以通过先找到其Kolmogorov方程，然后对应过来。

​ 下面为了推导时的简洁，我们不显式的写出概率分布和漂移/扩散函数对于时间$t$的依赖。自然地，我们希望拿到一个关于$p(x_t)$的描述，注意这里的$p(x_t)$与KFE时的并不一样，这里$t\le s$，此时的$p(x_t)$之于之前的讨论，确实是“过去”的状态。

​ 考虑贝叶斯公式：

对两边求取关于$t$的偏导：

然后我们就可以把KBE方程和KFE方程代入进去：

对于等号右侧中的三个偏导，可以进一步展开：

我们先只将前两项的展开进行代入，先不要代入$p(x_t)\sigma^2(x_t)$关于$x_t$的二阶偏导，在复杂的化简后可以得到：

回忆我们的目的，我们希望推导出一个关于$p(x_t)$的偏微分方程，这个偏微分方程的形式要和KFE/FP方程一致，这样我们就能找到对应的逆向过程了。观察上式，我们已经凑出了关于概率分布和漂移函数的乘积的偏微分，下面我们需要凑出$\frac{1}{2}\frac{\partial ^2\left[ p\left( x_{s,}x_t \right) \sigma ^2\left( x_t \right) \right]}{\partial ^2x_t}$，我们考察要凑的这个式子，我们可以通过贝叶斯公式找到他和我们想代换的那两项的关系：

我们可以将$p(x_s|x_t)$记作$u$，$p(x_t)\sigma^2(x_t)$记作$v$，那么由莱布尼茨公式：

我们想构造的那一项即变为了：

我们联立上面的式子：

我们在两边对$x_s$作积分，我们无脑认为我们可以交换微分和积分的顺序，这样将积分符号移到里面不影响结果，终于得到了：

这个偏微分方程描述了$t\le s$时的$p(x_t)$​的分布，

根据KFE方程，这个偏微分方程对应的随机过程是：

我其实不是很好解释那个负号的“吸收”，我不确定认为逆向维纳过程$\mathrm{d}\bar{w}$跟正向的$\mathrm{d}w$这样差个负号是不是对的。但考虑$\mathrm{d}w$其实就是白噪声，差个负号好像也没啥影响……

在扩散模型的情形下，扩散函数往往与$x_t$​无关，所以可以把扩散函数从偏微分里拿出来，然后就又出现了对数微分的结构：

我们用梯度算子替代偏导，推广到多维情形：

这就是逆向时候的随机微分方程。如同Score-Based Generative Modeling through Stochastic Differential Equations中的teaser一样，我们可以模拟一下一个简单的正向和逆向过程：

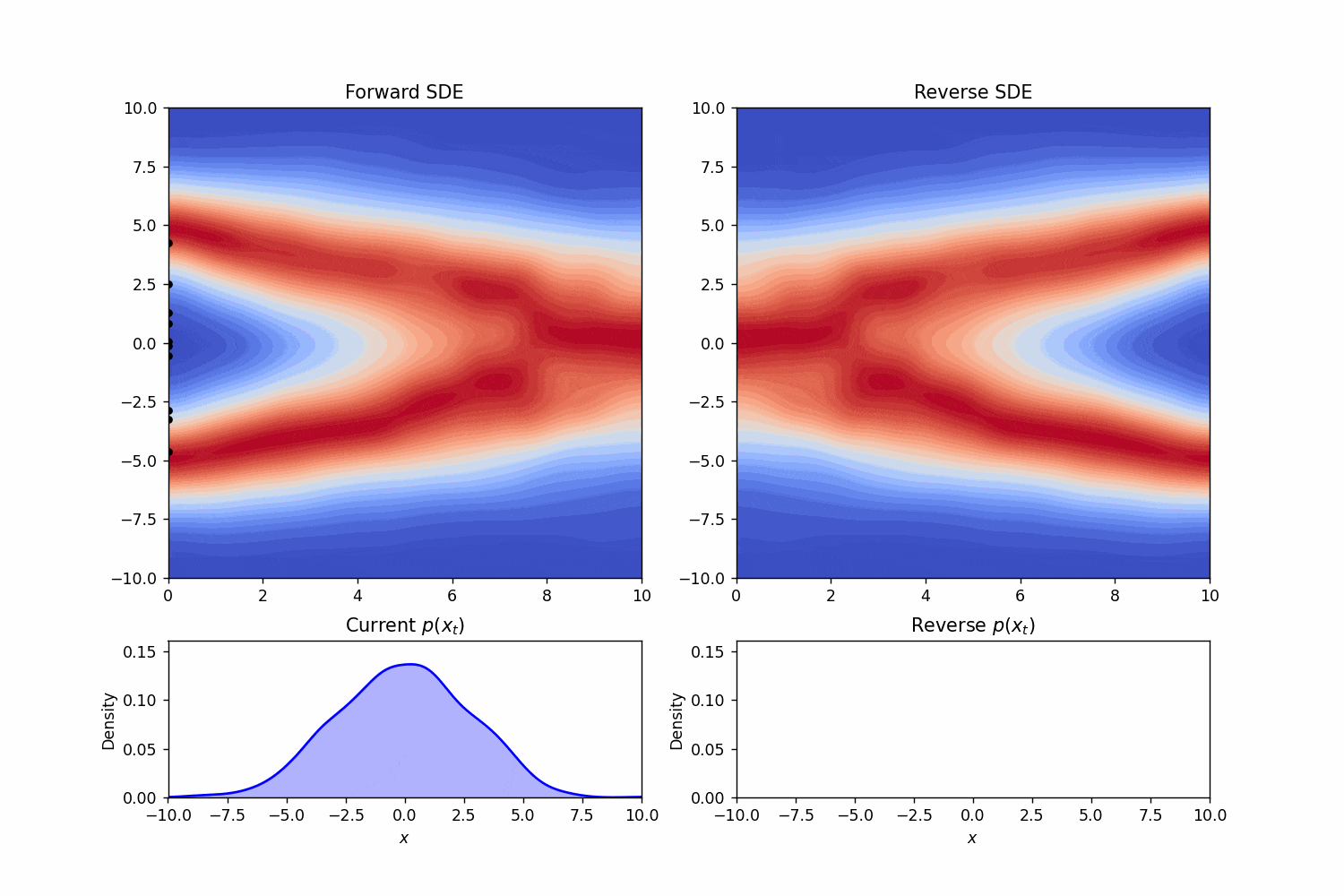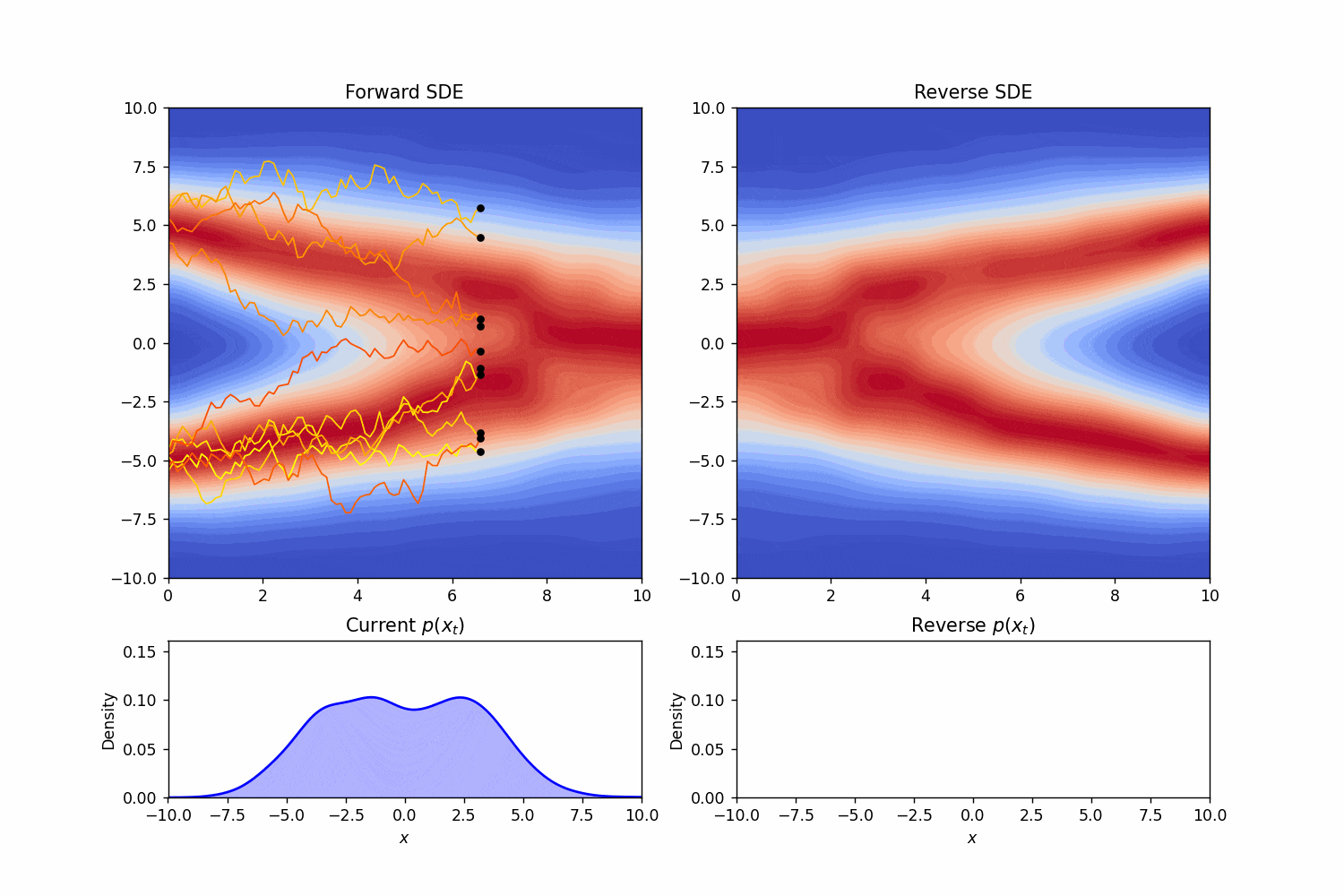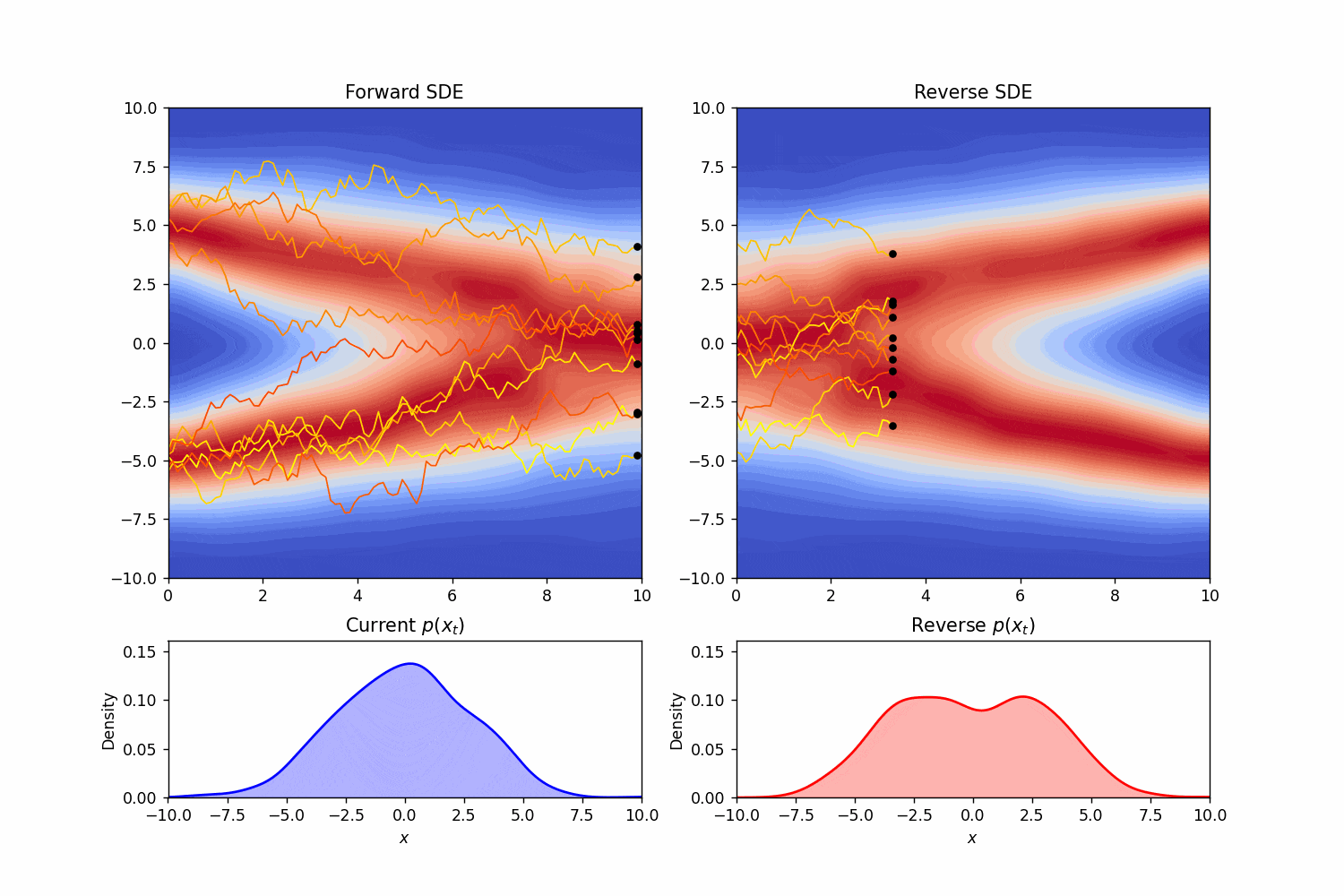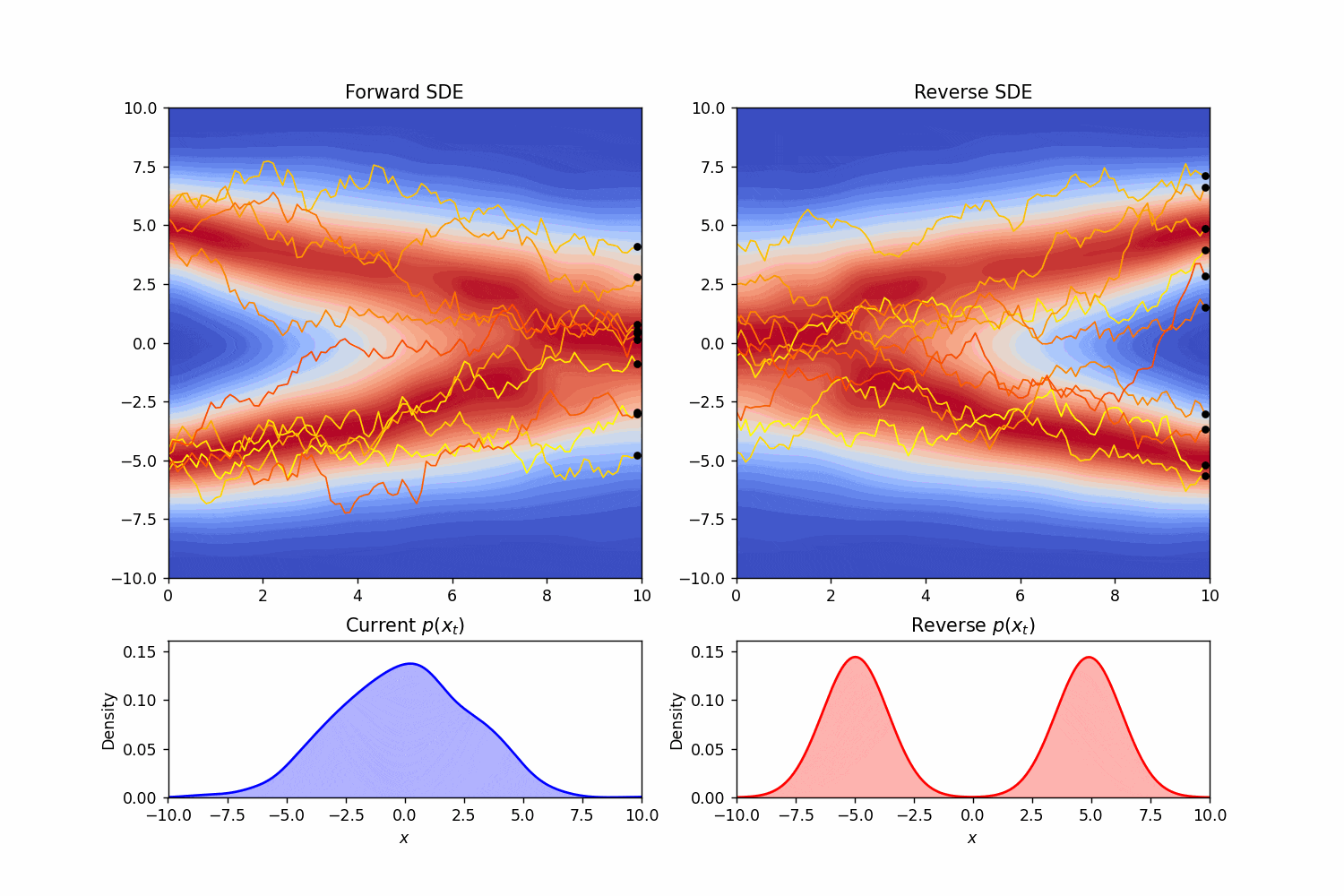
我们又一次看见了对数概率密度函数的梯度。这一项的出现并不是偶然。
先前，我们人为构造了这样的前向过程：

其中$g^2(\cdot)\le\sigma^2(\cdot)$，那么我们可以根据刚才的推导写出其逆向过程，只需要用$\mu \left( x_t,t \right) -\frac{1}{2}\left( \sigma ^2\left( t \right) -g^2\left( t \right) \right) \nabla _{x_t}\log p\left( x_t \right) $替代前向过程里的$\mu(x_t,t)$：

我们把这两个式子写在一起：

忙了这么久，就为了中间差的这个正负号。如果我们增加$g(t)$，在前向过程里，这会导致$\nabla _{x_t}\log p\left( x_t \right) $这一项变小；而在逆向过程里，这会导致$\nabla _{x_t}\log p\left( x_t \right) $变大。以及对于逆向过程，只有$\nabla _{x_t}\log p\left( x_t \right) $是我们不知道的。一个自然的推断是，这一项一定跟扩散模型里神经网络要预测的噪声有关，因为在DDPM的前向和反向里，我们也是只不知道$\epsilon_t$。

​ 我们不禁好奇$\nabla _{x_t}\log p\left( x_t \right) $的意义，我们将$\mu(x_t,t)$和$g(t)$都先置为0，然后取$\sigma(t)$为2来忽略掉这一项的系数。我们得到了这样的一个方程：

根据梯度的意义，$\nabla _{x_t}\log p\left( x_t \right) $是驱使$x_t$沿着概率密度函数上升最快的方向移动，从而将样本移动到高概率密度的区域。如果我们选取$p(x_t)$为某种高斯分布，可以更直接的感受到这一点。因为在高斯分布下，$\mathrm{log}p(x_t)$的结果就是一个L2-范数，把所有常系数都记作$k$：

那么就自然展开成了一个关于分布均值的滑动平均。$\nabla _{x_t}\log p\left( x_t \right) $被称为得分（Score），在Generative Modeling by Estimating Gradients of the Data Distribution中，作者提出Score Model Langevin Dynamics（SMLD）通过Noise Conditional Score networks（NCSN）来估计得分，这里我们不再展开了。我们仅指出得分与噪声的关系，我们先指出一个参数估计的工具：特威迪（Tweedie）公式，这个公式是关于参数估计，他在意的是给定观测数据${x_i}$时对分布参数$\theta_i$的估计。其考虑条件期望$\mathbb{E} \left[ \theta |x \right] $，假设分布$p(x|\theta)\sim \mathcal{N}(\theta,\sigma^2)$，可以从观测数据里估计$\sigma^2$，我们记高斯分布的概率密度函数为$f(x)$，有：

进一步，我们计算条件期望$\mathbb{E} \left[ \theta |x \right] $：

这个公式的意义是说，后验期望和先验分布$p(\theta)$无关，我们可以用样本估计$p(x)$的分布，然后计算$\sigma ^2\frac{\mathrm{d}}{\mathrm{d}x}\log p\left( x \right)$来进一步修正估计的$\theta$。而在DDPM里，我们知道，对于加噪过程$q(x_t|x_0)$，其服从于$\mathcal{N} \left( x_t;\sqrt{\bar{\alpha}_t}x_0,\left( 1-\bar{\alpha}_t \right) \right) $，那么我们带入Tweedie公式：

而我们又知道，在去噪过程中：

所以，我们得到了：

所以预测的噪声其实就对应于反方向的得分，这是非常自然的。

Probability ODE

现在我们考虑逆向过程的SDE：

其实最美妙的事情是我们可以直接选取$g(t)\equiv 0$，这样整个方程就变成了一个普通的常微分方程：

我们可以可视化此时的逆向轨迹：

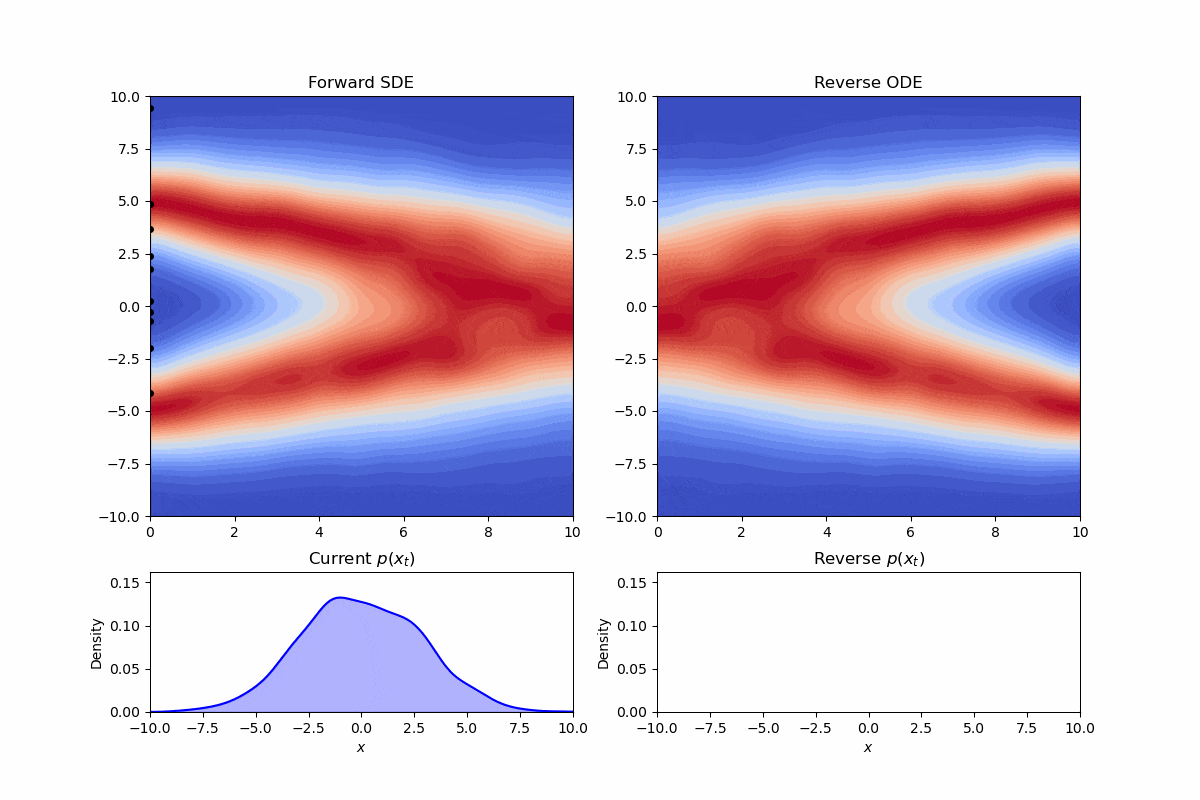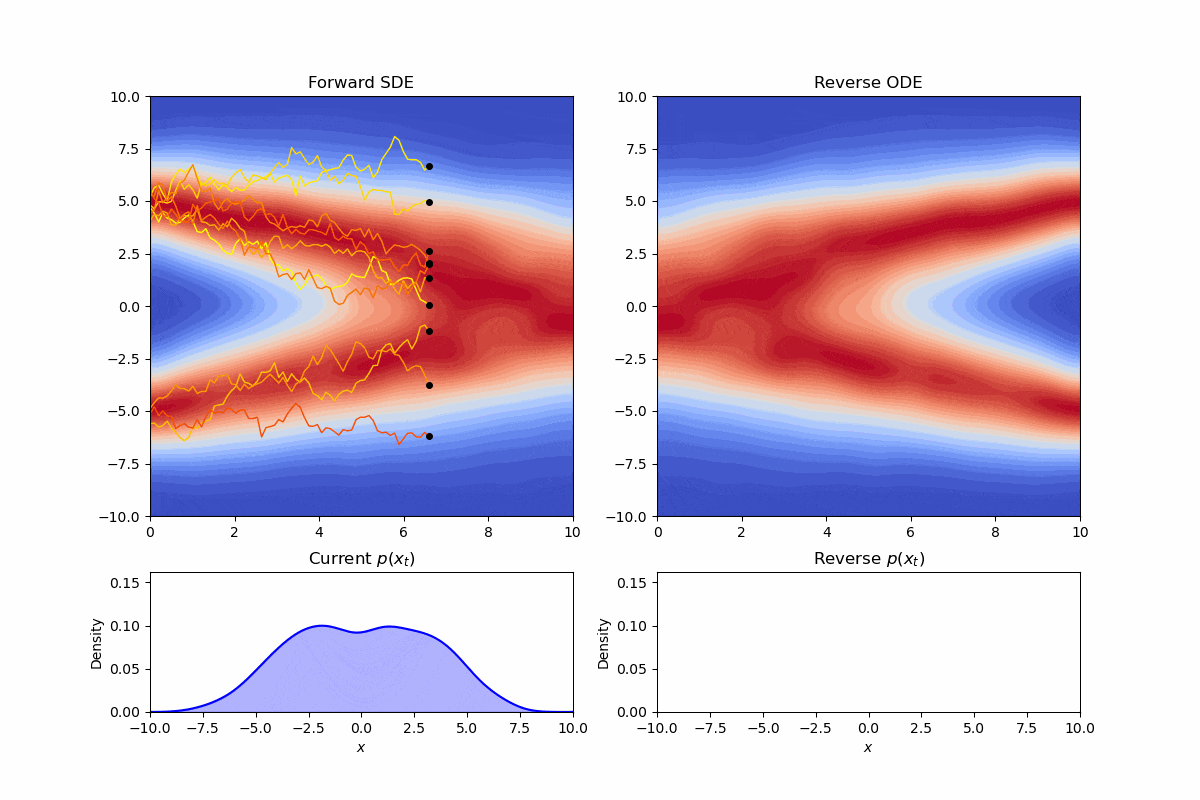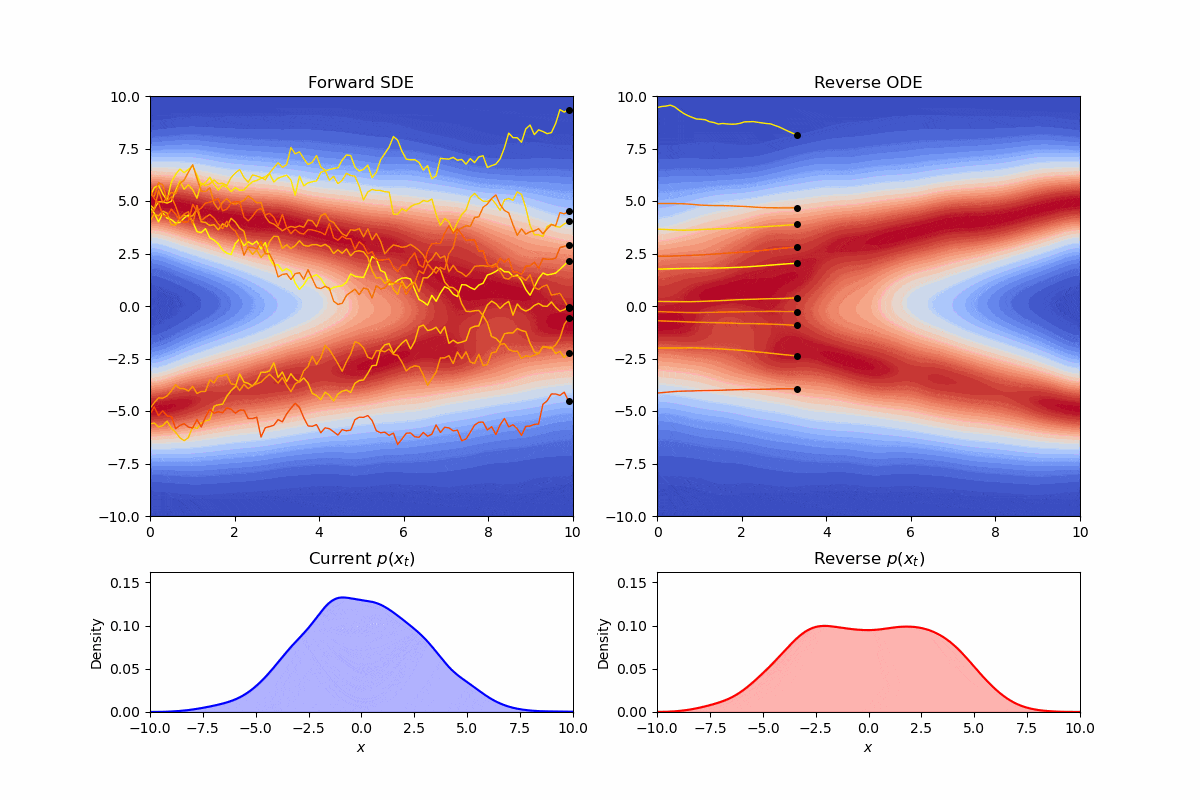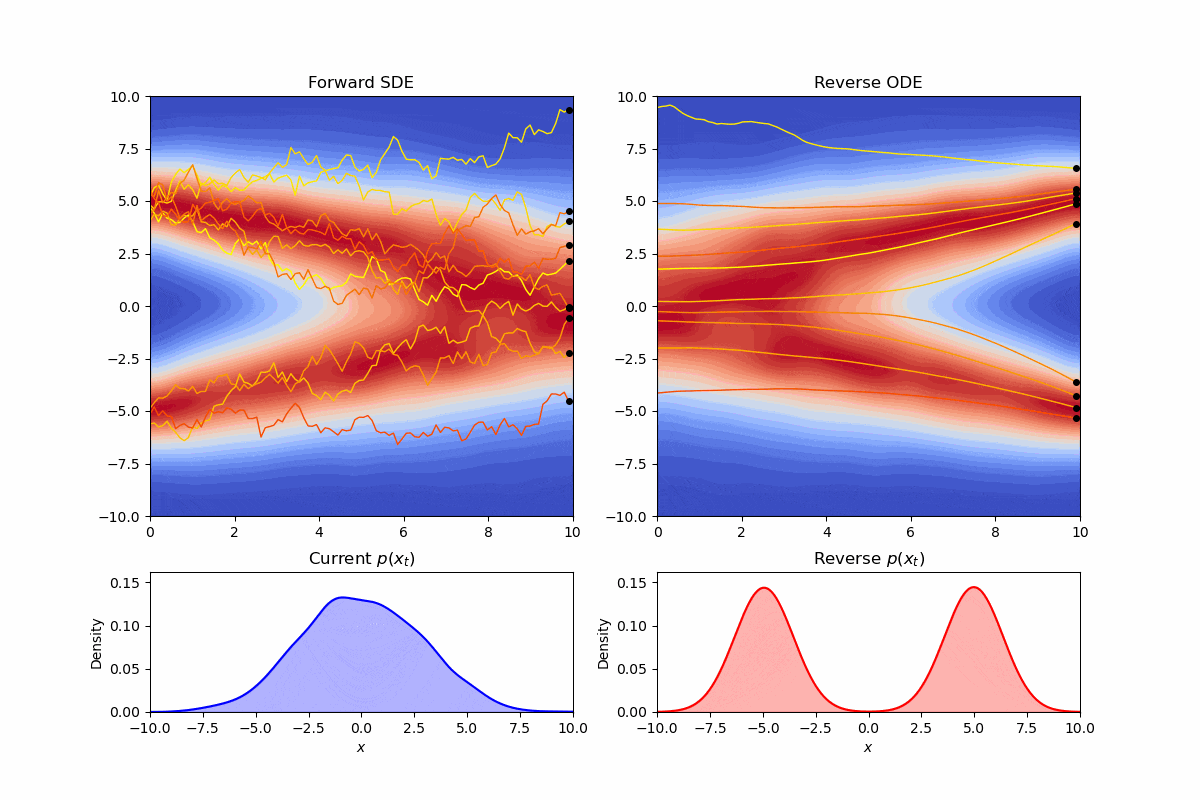
可以看到我们修改了采样时的方差，但边际分布仍然保持不变。这样的常微分方程，我们称为概率流（Probability Flow）微分方程。实际上，省略掉维纳项的形式，就对应着diffusion加速的经典策略—DDIM。通过微分方程的框架，我们可以很自然的理解为什么我们可以在训练时按照DDPM，而采样时按照DDIM，因为他们的边际分布是一样的。同样DDIM可以进行“跳步”现在看来也有一个直觉的理解：“在没有噪声项时，轨迹可以变得更“直”。就像数值分析里解微分方程那样，就不需要迭代那么多次了”。

​ 如何让轨迹变得更“直”这个想法非常的深刻，他直接导向了这篇blog的最终目的：Flow-matching。但在此之前我们先简单的提及单纯地从解微分方程出发，来加速diffusion的一系列工作：DPM-Solver。

在此之前，我们引入的例子是线性方差调度的DDPM，但实际上方差调度和均值的变化是可以更灵活的。例如现在人们都喜欢用余弦式的方差调度器。我们考虑更一般的加噪情形$q\left( x_t|x_0 \right) =\mathcal{N} \left( x_t|\alpha _t x_0,\sigma ^2_t \right) $​，现在我们需要计算这个过程对应的漂移函数和扩散函数，我们考虑加噪过程：

由条件高斯分布的性质：

代入加噪过程后，在等式两边求取微分：

对应到我们希望的正向SDE的形式，这里形式有一点小小的变化，我们规定漂移函数的形式是$\mu(x_t,t)=f(t)x_t$，规定扩散函数的形式是$\sigma(x_t,t)=g^2(t)$，实际上在炼丹中人们选取的也都是这种形式：

于是我们有：

则对应的逆向时的概率流ODE即为：

将得分替换为噪声，最后整理为：

那么由常数变易法，这个微分方程的通解是：

我们在时间区间里选取$t<s$，可以将常数$C$赋为$s$，这样逆向过程的解就是：

实际上到了这一步，我们就可以应用一些传统的ODE求解器来进行求解了，例如龙格库塔，隐式欧拉等。但DPM-Solver的作者进一步指出，在这种通解下，仍然有待挖掘的部分。

​ $f(t)$是已知的，所以$e^{\int_s^t{f\left( \tau \right) \mathrm{d}\tau}}=e^{\int_s^t{\frac{\mathrm{d}\log \alpha _{\tau}}{\mathrm{d}\tau}\mathrm{d}\tau}}=\frac{\alpha _t}{\alpha _s}$。同时我们清理积分项以内的内容，记$\lambda _t=\log \frac{\alpha _t}{\sigma _t}$，那么可以验证：

$\lambda_t$也被记作“半对数信噪比”，因为在扩散模型中习惯定义$SNR=\frac{\alpha _{t}^{2}}{\sigma _{t}^{2}}$为信噪比（Signal-Noise-Ratio）。

于是逆向过程的解可以化为：

所以实际上概率流方程的解呈现一种“半线性（semi-linear）”结构，前面那一项是纯粹的线性项。那么我们考虑相邻的$x_{t_{i-1}}$到$x_{t_i}$的过程，那么很自然的我们可以考虑对积分项进行近似，具体来说就是对预测出的噪声项作$k$阶泰勒展开：

那么代入原式就会得到：

关于估计预测噪声的高阶导数的方法是很成熟的，而这个推导出的结果就是DPM-Solver。特别地，对于$k=1$时：

此时的DPM-Solver，他其实就是DDIM

Flow Matching

其实为了理解Flow Matching，并不需要引入SDE，逆向过程等复杂的内容，可以直接从ODE的角度来切入。但我们马上会看到其实我们前面的推导并没有白费。

​ 在做了前面的准备工作以后，我们就可以以一个更广义的视角来切入Flow Matching了。实际上Flow并不是一个新的词，在先前有一类“Flow-based”的生成模型，在Normalizing Flow（NF）里，是用多个神经网络模拟多步的概率变换，通过变量替换定理，通过设计估计雅可比行列式，来通过这种逐步的方法来最大化似然。在Continuous Normalizing Flow（CNF）中，作者构造了所谓“瞬时换元公式”，来连续化了这个过程。使得在NF里使用的多个神经网络变成一个与时间相关的神经网络。他们都是为了直接最大化似然函数，而后者第一次提出了“Neural ODE”这一概念：

不管是先前的Flow-based model还是现在的Flow matching，他们的都估计一个向量场$u(x,t)$，只不过相比于NF和CNF直接去优化极大似然，Flow matching是想通过指定一种概率路径$p(x_t)$，然后用神经网络将与这个概率路径对应的向量场学出来，概率路径与向量场的关系由连续性方程来描述：

这个方程具有深刻的物理意义，其描述了在没有源或出口的情况下，分布在时间上的变化和空间上的变化是守恒的。

NF和CNF被称为“simulation-based”，因为他们确实是在硬杠$\mathrm{log}p(x)$，但这种方法的效果并不好，而且非常复杂，并没有引发很多人的关注。我对这种方法的细节知之甚少，他们还没凉的时候我都没上大学呢。但直觉上，他们效果没那么好的原因，可能是因为从一个分布到另一个分布的路径可以是无限多的，也对应着无限多的向量场。然而直接优化似然函数相当于同时要拟合这个路径和向量场，这背后的复杂程度可能导致这种方法没办法得到进一步扩展。而Flow matching则被称为“simulation-free”。

然而我们会发现，FP方程中$g(t)\equiv0$时恰好也有这样的形式：

到了这一步我们可以感受到，扩散模型似乎是Flow matching的某种特例。

​ 在Flow matching中，作者推广了这一结果。在下面的讨论里往往约定$t\in[0,1]$，起始分布记作$p_0$，目标分布记作$p_1$，中间任意时刻的分布记作$p_t(x)$。即理解为0下标是“噪声”，1下标是数据，和扩散模型的推导正好反着。而由于$u(x,t)$在物理意义上，其实就是速度场，所以记作$u_t(x)$，即某时刻下描述整个场的速度分布。

​ 所以最直接的办法就是用神经网络学一个对应的速度场$v_{\theta}(x,t)$，然后优化：

即Flow Matching Loss，但就如同Score-Matching，以及推导DDPM的时候一样，由于我们根本不知道真实的$u_t(x)$，直接虚空打靶了。所以作者巧妙地构造了一系列条件分布，来使得这个目的是可达的。

​ 首先，考虑概率路径：

​ 其中$q(\cdot)$是一个用于采样的分布（可以是均匀分布，高斯分布）。对于下面这种形式的速度场：

可以证明，条件速度场$u_t(x|z)$可以替代边缘速度场$u_t(x)$。

“边缘速度场”是作者起的名字。

这个证明的逻辑是，如果可以通过条件速度场$u_t(x|z)$可以导出条件概率分布$p_t(x|z)$（即满足连续性方程），那么从“边缘速度场”$u_t(x)$也能导出边缘概率分布$p_t(x)$：

即我们通过验证，在这种情况下，连续性方程仍然成立。在此基础上，作者进一步给出了Conditional Flow Matching Loss：

并且证明$\mathcal{L} _{\mathrm{CFM}}$​和$\mathcal{L} _{\mathrm{FM}}$​在优化上是等价的。由于二范数展开后实际上就是两项的二范数以及他们的内积，速度场/条件速度场是真值，我们只需验证：

​ 所以，事情开始起了变化。我们现在并不是要考虑“加噪”，“去噪”层面上的问题，也不是“正向”“逆向”。我们发现通过引入$z$，我们只需要设计一个$u_t(x|z)$，只要他能满足连续性方程（推出$p_t(x|z)$，并且保证$p_0$和$p_1$可以通过边缘化$q(z)$得到：

这就是Flow matching。

​ 特别地，如果我们取$z=x_1$​，考虑像扩散模型一样加噪去噪：

这个概率路径被称为“高斯概率路径”，那么代入进连续性方程，可以得到其对应的条件速度场是：

而如果我们选取先前推导扩散模型时用的常用方案，取$\mu_t(x_1)=\alpha_t x_1, \sigma_t(x_1)=\sigma_t$​，那么其实得到的就是DDIM。从结果上看，这样的Gaussian Flow Matching相当于DDPM训练时加入了关于信噪比的权重。

不过对于扩散模型这样的过程，我们以前可以从逆向SDE和概率流ODE里直接得到速度场的表达，而不需要用条件速度场：

“随机过程已经帮我推导过了。”——佚名

比如对于DDIM，其实就有：

也能像DDPM那样采样，只不过由于维纳过程的存在，在真正采样的时候要记得追加噪声：

​ 然而，在扩散模型中，我们都是取初始分布为高斯分布，并没有考虑初始分布与目标分布的联系。我们如果取：

这个的结果令人震惊，那些繁杂的关于方差的权重都消失了。然而这个结果导致的事实是，我们在训练时，只需要采样一个噪声$X$和一个目标（例如图片）$Y$，然后再采样一个时间$t$，就能用$tY+(1-t)X$来表示从$p_t(x|z)$里采样；然后我们只需要让神经网络的输出跟$\left| Y-X \right| ^2$接近即可，这个结论实在是简洁优雅。这就是Rectified Flow。

​ 一个直接的想法是，如果按照Rectified Flow这样构造，假设一开始噪声和数据是“成对”的，那么这个过程会变得更加的完美。然而我们每次都是随机的噪声，噪声与数据的匹配也是随机的，这是不现实的。所以在其文中提出了一种“Reflow”的策略，即先训一个Flow Matching出来，然后用训出来的噪声与数据的配对来“拉直”整个演化的过程。不过这种形式自然会将讨论的方向引导到最优传输（Optimal Transport）理论，会牵扯到更多复杂的内容，等到有时间再去学了。

​ 我们现在可以做一些有趣的实验，模拟一个二维的过程，来可视化一下整个过程。我们可以选取一个自己希望模拟的分布，然后用一个简单的神经网络来模拟一下演化过程：

Appendix

​ 至此，讨论接近尾声。其实在最后，我还想讨论一个很概念的事情，就是“为什么总是有各种神奇的“条件”构造？”。思考这个问题对炼丹毫无任何帮助，恰如”朝菌不知晦朔，蟪蛄不知春秋”。但我不是朝菌，也不是蟪蛄，所以要至少记录下对这个问题的思考。

​ 在一开始学diffusion的时候，先是那神之一手$p(x_{t-1}|x_t,x_0)$，然后在Flow matching里，是这个“条件速度场”里的$z$；在Score Matching里，则是我们因为不知道真实分布的对数概率梯度，然后对分布$x$进行加噪扰动，得到$\tilde{x}$，然后用$\nabla _x\log p\left( \tilde{x}|x \right) $进行优化。所以为什么会有这么多“条件”？

​ 我的一个推测是：给定一个数据集，数据集里有许多样本。我们不知道他的分布$p_{data}$，但我们知道里面的每个样本。通过拟合以单个样本为条件的分布，我们总是可以得到整个分布的。例如，Flow matching中由连续性定理证明的如果$u(x|z)$能推导出$p(x|z)$，那么$u(x)$就能推导出$p(x)$，这其实就是说通过拟合以某个样本为条件的速度场，最终会完成整个速度场的拟合。从这个角度上看，GAN，VAE，Diffusion，Flow matching的训练，都是在求解某种“margin”。

​ 另一个角度上看，以及以样本为条件，会限制整个过程的自由度，令其更稳定（至少更容易收敛）。例如CNF就因为有“无限多”概率路径而很难扩展，另一个现象是在DDPM的推导里，鲜为人知的是，如果直接用ELBO一条道走到黑，是会得到一个结果的。这在Understanding Diffusion Models: A Unified Perspective被记载，如果直接推导，则最后的需要求解关于$q\left( x_{t-1},x_{t+1}|x_0 \right) $的期望。而如果引入$x_0$，就会变成我们寻常认识里的关于$q(x_t|x_0)$的期望。而这个期望实践起来非常简单，我们只需要抽数据，加噪，就可以了。而前者就复杂的多了。

End

​ SDE是可以reverse的，但很可惜的是人生没法reverse，因为没有人会为你估计$\nabla_x\mathrm{log}p(x)$。这几天很难绷，如果当时去做General 3DV，会不会面试就过了；或者，如果当时大四抓紧时间，去follow diffusion相关的，而不是去乱猜w2c, c2w和有没有transpose，事情会不会有些转机。现在论文论文没有，实习实习被挂，只能说是短视了。

“笑言今日事，何苦旧时痴，皆为年少风流思。”

赏

谢谢你请我吃糖果

微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

挟飞仙以遨游，抱明月而长终。<br />知不可乎骤得，托遗响于悲风。