Understanding Facial Tracker


阅读数: 次   
文章目录
  1. Landmarks Alignment
  2. VHAP
    1. Add Teeth
    2. Laplacian Matrix
    3. Monocular Video Datasets
    4. Optimization
    5. Loss Function
      1. landmark loss
      2. photometric loss
      3. regularization terms
      4. Total
    6. Nersemble Video Datasets
  3. End

​ “再回首，读来路；少年轻狂，犹如南柯一梦。”

​ 前段时间一直在瞎忙，没什么时间写blog。最近开摆了，可以有时间写点了。这篇blog计划学习一下一个最近开源的脸部追踪器VHAP，这个tracker实现的非常好，可以看出作者（们）功力之深厚。VHAP相比之前开源的tracker有了很大的改进，包括但不限于推广到多视角视频，实现FLAME几何的估计，更准确的关键点监督。

​ Facial tracking是一个历史悠久的需求，具体来说是输入一段视频，需要逐帧地知道每一帧时人脸的状态。人脸的“状态”一般由参数化模型描述，在当下的语境里一般是FLAME。其一般通过对齐人脸检测出的关键点和FLAME的关键点来实现近似的估计，然后进一步用光度损失（photometric loss），结合可微渲染来进行精细的优化。

实际上，还存在另外一种facial tracking的方案，尤其针对多视点的数据集：通过多视图立体视觉（multi-view stereo）来从多视角图片中估计一个稠密的mesh，然后将这个mesh通过关键点对齐配准到标准模板上。这种方案并不涉及任何光度损失，但无法估计头发的几何。

在介绍VHAP之前，我想先记录基于关键点反投影来对齐的一些细节，然后再进入VHAP的细节。对于关键点对齐部分，主要是一些理论推导；对于VHAP部分，则主要记录一些实践细节和代码技巧。实际上，VHAP的实现具有规范的项目结构，并且以前所未有的力度对一些细节进行了实现。对其他基于可微渲染的优化都具有很好的指导意义。

Landmarks Alignment

​ 通过优化Landmark来进行追踪在很早的时候就被采用了，那时候还没有FLAME，用的是BFM。也没有PyTorch，计算依靠CPU。当时的优化是需要显式的来求解析解的。这样的结果虽然不是很精细，但能满足实时性的要求。这个过程现在完全可以通过PyTorch的可微渲染来实现，并且可以以很快的速度执行，但知道其细节还是比较重要的。

​ 考虑投影到的landmark与检测到的landmark的残差向量$\mathbf{r}\left( \mathbf{X} \right) $，我们希望优化：

一般用的是预定义的68个关键点，所以$\mathbf{r}\left( \mathbf{X} \right) \in \mathbb{R} ^{136\times 1}$。其中$\mathbf{X}\in \mathbb{R} ^{n\times 1}$​，表示参数化模型的系数（如表情，形状等）。这是一个最小二乘问题，可以直接用高斯牛顿法来进行优化，我们先进行一阶线性近似：

​ 其中$\mathbf{X}^t$是当前的参数化模型的系数，雅可比矩阵$\mathbf{J}\in \mathbb{R} ^{136\times n}$定义为：

​ 一阶近似后，代价函数变为：

​ 将其展开：

​ 省略常数项，优化目标即近似为：

​ 这个式子以$\Delta \mathbf{X}$为自变量，系数矩阵$\mathbf{J}^T\mathbf{J}$是半正定的。其极值的必要条件是：

​ 其中$\mathbf{J}^T\mathbf{J}$记作伪海塞矩阵$\mathbf{H}$，$\mathbf{J}^T\mathbf{r}\left( \mathbf{X}^t \right) $记作梯度$\mathbf{g}$。所以更新步长为：

​ 此时$\mathbf{H}\in \mathbb{R}^{n\times n}$，当$n$很大时求解这个矩阵的逆是复杂的，有时会采用共轭梯度法或者其他优化方法。

​ 进一步，我们考虑$\mathbf{X}=\left[ \mathbf{p};\mathbf{s};\mathbf{e} \right] $的一个具体情形，其中$\mathbf{p}\in \mathbb{R}^{n_p},\mathbf{s}\in \mathbb{R}^{n_s},\mathbf{e}\in \mathbb{R}^{n_e}$。得到投影坐标点的过程可以记作：

$\mathbf{x}^{\mathrm{proj}}\in \mathbb{R} ^{2\times 68}$为投影得到的坐标，为了和上文一致我们用$\mathrm{vec}\left( \cdot \right) $记号将其重排成$\mathbb{R} ^{136\times 1}$：

$\mathbf{V}(\cdot)\in\mathbb{R}^{}$是3DMM生成的那些被当作landmark的顶点。$\mathcal{P}\in\mathbb{R}^{2\times3}$为投影矩阵，$\mathbf{t}\in\mathbb{R}^{2\times1}$是平移向量，计算时自动广播成$\mathbf{t}\in\mathbb{R}^{2\times68}$。记人脸检测器得到的landmark向量为$\mathbf{x}^{\mathrm{det}}\in \mathbb{R} ^{136\times 1}$，那么实际上雅可比矩阵的每一列（残差分量对某一个系数$\mathbf{X_j}$的偏导）：

下面我们给出在系数$\mathbf{X}_j$表达不同3DMM系数时$\mathbf{J}_j$的形式，为了简洁就省去向量化算符$\mathrm{vec}$了。

当$\mathbf{X}_j=\mathbf{s}_i$时：

当$\mathbf{X}_j=\mathbf{e}_i$时：

当$\mathbf{X}_j=\mathbf{p}_i$时，姿态往往由$\mathbf{p}_i$构成的旋转$\mathbf{R}$和平移$\mathbf{t}$决定：

其中$\frac{\partial \mathbf{R}}{\partial \mathbf{X}_j}$的计算由具体的旋转表示给出，此处从略。而针对平移向量，结果是简单的单位向量：

据组里的传奇大师兄所说，当时他做这一块的时候还是要拿C++手写雅可比矩阵来作tracking。今天手推一下简单情形的$\mathbf{J}$，聊表敬意。如果将上面的过程其实换成FLAME，述公式的形式会复杂的多。因为涉及一堆blendshape，推一遍没什么意义，直接皈依自动微分就好了。另外，FLAME提供了BFM到FLAME的映射，这样可以把在BFM上追踪的结果直接换算到FLAME上。

VHAP

​ VHAP提供了单目视频和nersemble数据集两种模式，作者为这两种模式写了统一的接口：

1
2
tracker = GlobalTracker(cfg)
tracker.optimize()

​ 在不同的cfg下会触发不同的调用。我们先从单目视频的情形下入手。这样一方面是比较简单，另一方面是我们可以借助单目视频下的情形把优化项都看一遍，这样在多视角的情况下我们就不需要关心优化函数了。

Add Teeth

​ GlobalTracker继承自FlameTracker，在其初始化方法中会先调用FlameTracker的构造方法。在FlameTracker中，执行了FLAME的实例化FlameHead以及渲染后端render的构造。作者这里使用的是FLAME2023，并且在常用的FLAME类的基础上进行了修改。第一个逆天操作是给FLAME增加牙齿，为什么说这是个逆天操作呢，因为我丝毫做不到这样实现。一种最简单的方法是用blender把mesh上下嘴唇部手动给连上面，然后进行UV映射，调整成合适的UV布局。这样当然并不是真的牙，但为了单纯表达牙和口腔内部也能凑合用了。

在GaussianBlendshapes里，一个高年级博士生实现的方法是，先手动构造两个近似牙齿形状的面（如下图所示）

然后测出一个合适的offset，在代码里把这两个面塞进mesh上合适的位置。由于GaussianBlendshapes的设计，这只是一个简单的面，没有构造UV映射。为了让其能跟着下巴的运动而动，还需要写一些代码将每次下巴的刚体变换拿出来，然后分别给这两个面用，这带来了不少麻烦。处理的已经很巧妙了但仍然有些不优雅。

​ 然而VHAP，也就是GaussianAvatars做法：

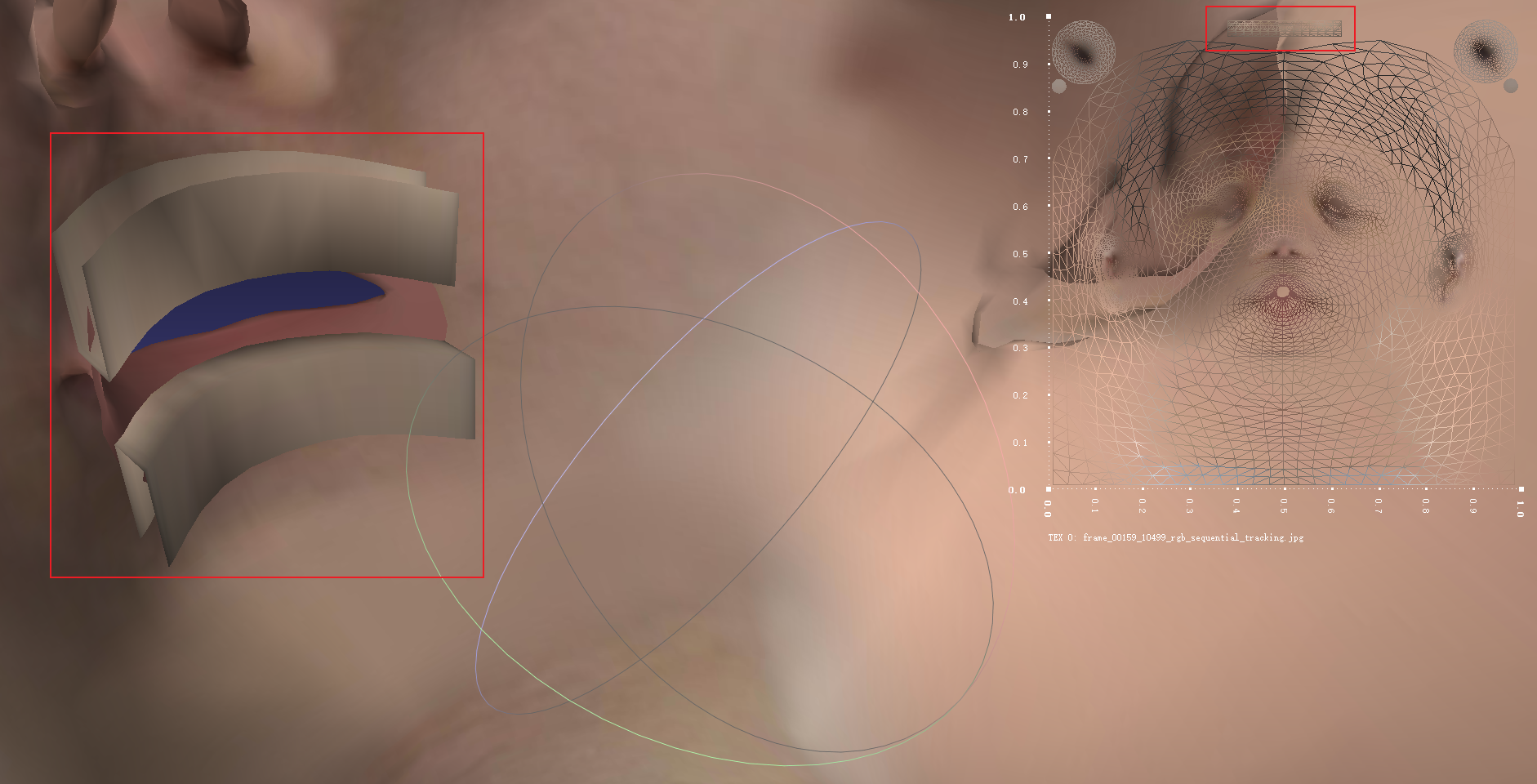
是一个形状非常像牙的“牙”，而不是瓦楞纸或者一层膜，以及还构造了一个很均匀的UV坐标（哪怕按照GaussianAvatars的做法这并不是必须的）。而这个操作纯粹是在代码中实现的，不需要引入第三方的工具，这个补牙的操作的实现充满着作者对FLAME的理解。首先的起手式是FLAME提供的关于顶点的masks：

FLAME在一个*.pkl中提供了如下部分的masks：

1
2
3
{face, neck, scalp, boundary, right_eyeball, left_eyeball, 
right_ear, left_ear, forehead, eye_region, nose, lips,
right_eye_region, left_eye_region.}

在构造FlameHead时，会构造一个FlameMask，在FlameMask的初始化时，会执行self.process_vertex_mask(flame_parts_path)来读取保存了masks的pkl文件：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def process_vertex_mask(self, flame_parts_path):
    """Load the vertex masks from the FLAME model and add custom masks"""
    logger.info("Processing vertex masks for FLAME...")

    part_masks = np.load(flame_parts_path, allow_pickle=True, encoding="latin1")
    """ Available part masks from the FLAME model: 
            face, neck, scalp, boundary, right_eyeball, left_eyeball, 
            right_ear, left_ear, forehead, eye_region, nose, lips,
            right_eye_region, left_eye_region.
    """

    self.v = BufferContainer()
    for k, v_mask in part_masks.items():
        self.v.register_buffer(k, torch.tensor(v_mask, dtype=torch.long))
    
    self.create_custom_mask()

这里有两处玄机，一个是self.v = BufferContainer()：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class BufferContainer(nn.Module):
    def __init__(self):
        super().__init__()

    def __repr__(self):
        main_str = super().__repr__() + '\n'
        for name, buf in self.named_buffers():
            main_str += f'    {name:20}\t{buf.shape}\t{buf.dtype}\n'
        return main_str
    
    def __iter__(self):
        for name, buf in self.named_buffers():
            yield name, buf
    
    def keys(self):
        return [name for name, buf in self.named_buffers()]
    
    def items(self):
        return [(name, buf) for name, buf in self.named_buffers()]

这个类继承自nn.Module，这个类通过重写__repr__，用来让注册进缓冲区（register_buffer）的变量在被打印出来的时候有我们希望的格式。这里的self.v在追加part_masks后，如果我们将其打印出来，会得到：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(Pdb) self.v
BufferContainer()
    eye_region                  torch.Size([751])       torch.int64
    neck                        torch.Size([253])       torch.int64
    left_eyeball                torch.Size([546])       torch.int64
    right_eyeball               torch.Size([546])       torch.int64
    right_ear                   torch.Size([588])       torch.int64
    right_eye_region            torch.Size([287])       torch.int64
    forehead                    torch.Size([133])       torch.int64
    lips                        torch.Size([254])       torch.int64
    nose                        torch.Size([379])       torch.int64
    scalp                       torch.Size([489])       torch.int64
    boundary                    torch.Size([114])       torch.int64
    face                        torch.Size([1787])      torch.int64
    left_ear                    torch.Size([588])       torch.int64
    left_eye_region             torch.Size([287])       torch.int64

而如果不用BufferContainer来管理的话，会打印出每个变量的全体索引，非常不方便查看。这个小细节非常贴心，我自己写的时候很少考虑这个。

​ 第二处是self.create_custom_mask，在这个函数成员里进一步追加了大量自定义的顶点mask，这些mask在之后计算损失的时候有很大的功用。对于追加牙齿这一feature，我们要关注的是'lip_outside_ring_upper'和'lip_outside_ring_lower'，这两者后面会用到。

​ 在处理完顶点的mask后，会处理面索引的mask和纹理坐标的mask：

1
2
3
4
5
6
if self.faces is not None:
    self.construct_vid_table()
    self.process_face_mask(self.faces)
    self.process_face_clusters(self.face_clusters)
    if self.faces_t is not None:
        self.process_vt_mask(self.faces, self.faces_t)

这几个函数基本囊括了对FLAME面，索引，纹理坐标索引之间的所有变换。其中self.construct_vid_table()构造顶点坐标和区域语义的映射（因为一个顶点可能既属于“脖子”也属于“皮肤”），其遍历每个顶点的索引，找到每个顶点都属于哪个部分：

1
2
(Pdb) self.vid_to_region[15] 
['neck', 'scalp', 'neck_upper', 'left_half', 'skin']

然后，根据构造的这张表self.vid_to_region，可以进一步计算process_face_mask，这个函数输入形状为[9976, 3]的faces，是每个面片对应的顶点索引。在process_face_mask中，我们利用self.vid_to_region查询每个面片属于的3个顶点都属于哪些面：

1
2
3
4
5
6
7
8
9
10
11
face_masks = defaultdict(list)  # region name -> face id
for f_id, f in enumerate(faces):
    counters = defaultdict(int)
    for v_id in f:
        for region_name in self.vid_to_region[v_id.item()]:
            counters[region_name] += 1
    
    for region_name, count in counters.items():
        if count >= 3:  # create straight boundaries, with seams
        # if count > 1:  # create zigzag boundaries, no seams
            face_masks[region_name].append(f_id)

这里的count >= 3也是一处细节，保证了face_masks边界的“光滑”。因为如果选取count > 1，在count=3的面片附近的那个面总是至少有count >= 2的，会产生锯齿状的区域。如果选取count >= 1，那么一些孤立的线也会被认为是区域，这是不合适的。在最后，像处理顶点时一样，构造了一个self.f = BufferContainer()：

1
2
3
self.f = BufferContainer()
for region_name, f_mask in face_masks.items():
	self.f.register_buffer(region_name, torch.tensor(f_mask, dtype=torch.long))

计算纹理坐标上面片的mask与上述原理相同。做了这些准备工作以后，就可以追加牙齿了。追加牙齿的逻辑全部封装在了FlameHead的add_teeth中，首先通过之前自定义的'lip_outside_ring_upper'和'lip_outside_ring_lower'来在标准模板上构造关于牙齿的顶点，其结果如下图所示：

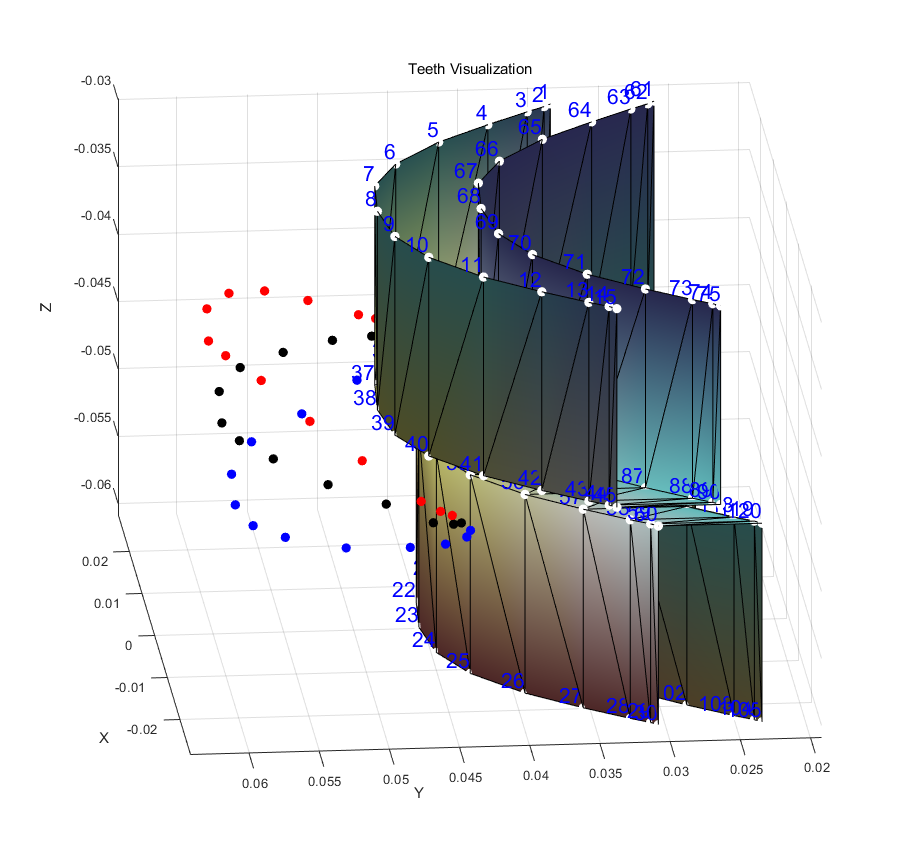
其中红色是v_lip_upper，蓝色是v_lip_lower，黑色是将上下唇顶点求平均得到的v_teeth_middle。通过平移Y轴和Z轴，可以得到右侧所示的八排顶点。

​ 注意在将顶点和后面的各种属性拼进FLAME时，我们都是在末尾追加，这样会带来许多便利，例如landmarks的映射不会被影响等等。

​ 得到顶点只是第一步，除了简单的把顶点拼到标准模板以外，还需要修改FLAME的一系列属性，这样牙齿的顶点才能跟着FLAME一起移动，对于混合形状基$B_E $，考虑将其填充为上下唇顶点对应的基的均值：

1
2
3
4
5
6
7
# shapedirs copy from lips
self.shapedirs = torch.cat([self.shapedirs, torch.zeros_like(self.shapedirs[:num_verts_teeth])], dim=0)
shape_dirs_mean = (self.shapedirs[vid_lip_outside_ring_upper, :, :self.n_shape_params] + self.shapedirs[vid_lip_outside_ring_lower, :, :self.n_shape_params]) / 2
self.shapedirs[vid_teeth_upper_root, :, :self.n_shape_params] = shape_dirs_mean
self.shapedirs[vid_teeth_lower_root, :, :self.n_shape_params] = shape_dirs_mean
...
self.shapedirs[vid_teeth_lower_edge_back, :, :self.n_shape_params] = shape_dirs_mean

​ 对于$B_P$，可以简单的置零：

1
2
3
4
# posedirs set to zero
posedirs = self.posedirs.reshape(len(self.parents)-1, 9, num_verts_orig, 3)  # (J*9, V*3) -> (J, 9, V, 3)
posedirs = torch.cat([posedirs, torch.zeros_like(posedirs[:, :, :num_verts_teeth])], dim=2)  # (J, 9, V+num_verts_teeth, 3)
self.posedirs = posedirs.reshape((len(self.parents)-1)*9, (num_verts_orig+num_verts_teeth)*3)  # (J*9, (V+num_verts_teeth)*3)

​ 同样，我们也不希望增加的牙齿影响用于估计结点的回归矩阵$J$：

1
2
# J_regressor set to zero
self.J_regressor = torch.cat([self.J_regressor, torch.zeros_like(self.J_regressor[:, :num_verts_teeth])], dim=1)  # (5, J) -> (5, J+num_verts_teeth)

​ 但对于LBS权重$\mathcal{W}$，我们希望牙齿结点跟着下巴和脖子的转动而转动：

1
2
3
4
# lbs_weights manually set
self.lbs_weights = torch.cat([self.lbs_weights, torch.zeros_like(self.lbs_weights[:num_verts_teeth])], dim=0)  # (V, 5) -> (V+num_verts_teeth, 5)
self.lbs_weights[vid_teeth_upper, 1] += 1  # move with neck
self.lbs_weights[vid_teeth_lower, 2] += 1  # move with jaw

​ 这样解决了顶点本身的一些要求，按照作者在嘴唇处标记的点的数量，我们一共会为牙齿增加$15\times4\times2=120$个顶点。下面就是要给增加的顶点补拓扑。我们需要追加面片和纹理坐标的关系，对于面片，我们只需要把增加的点按顺序连在一起就好：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# add faces for teeth
f_teeth_upper = torch.tensor([
    [0, 31, 30],  #0
    [0, 1, 31],  #1
    [1, 32, 31],  #2
	...
    [88, 43, 44],  # 110
    [88, 44, 89],  # 111
])
f_teeth_lower = torch.tensor([
    [45, 46, 15],  # 28           
    [46, 16, 15],  # 29
	...
    [118, 59, 58],  # 166
    [118, 119, 59],  # 167
])

这个逻辑是直接的，如果担心写错了其实也可以把顶点导出来，然后在blender里手动标。

对于纹理坐标，作者的处理比较草率，因为那样做也完全够用了：

1
2
3
4
5
6
7
8
9
10
# construct uv vertices for teeth
u = torch.linspace(0.62, 0.38, 15)
v = torch.linspace(1-0.0083, 1-0.0425, 7)
# v = v[[0, 2, 1, 1]]
# v = v[[0, 3, 1, 4, 3, 2, 6, 5]]
v = v[[3, 2, 0, 1, 3, 4, 6, 5]]  # TODO: with this order, teeth_lower is not rendered correctly in the uv space
uv = torch.stack(torch.meshgrid(u, v, indexing='ij'), dim=-1).permute(1, 0, 2).reshape(num_verts_teeth, 2)  # (#num_teeth, 2)
num_verts_uv_orig = self.verts_uvs.shape[0]
num_verts_uv_teeth = uv.shape[0]
self.verts_uvs = torch.cat([self.verts_uvs, uv], dim=0)

手动选出UV layout里的空余的地方，然后用meshgrid做一下网格，就可以了。最后更新了面和纹理坐标以后，再用之前的逻辑（process_vertex_mask等）更新一下mask：

1
2
3
4
5
self.faces = torch.cat([self.faces, f_teeth_upper+num_verts_orig, f_teeth_lower+num_verts_orig], dim=0)
self.textures_idx = torch.cat([self.textures_idx, f_teeth_upper+num_verts_uv_orig, f_teeth_lower+num_verts_uv_orig], dim=0)

self.mask.num_verts = self.v_template.shape[0]
self.mask.update(self.faces, self.textures_idx)

这样就完成了给FLAME里加牙齿的壮举！

Laplacian Matrix

​ 另一个操作是拉普拉斯矩阵$L$​，这个矩阵往往用来平滑mesh。在图论中对该矩阵的定义为：

其中$D$是度矩阵，$A$​是邻接矩阵（如果顶点之间有相连，则为1，否则为0）。在该定义下的拉普拉斯矩阵可以写作：

然而在PyTorch3D中，拉普拉斯矩阵的定义为：

这个矩阵实际上是：

这样归一化拉普拉斯矩阵，是为了适配对mesh的操作。例如在一个单独的三角面片上，可以有：

我们可以计算：

那么给定对应的顶点$V=[v_0,v_1,v_2]$，那么作矩阵乘法$\hat{L}V$，会得到：

这个结果实际上以$1/\mathrm{deg}(i)$的权值来描述了对应顶点和其周围点的加权值之间的差。在PyTorch3D中，这被直接用来优化，即pytorch3d.loss.mesh_laplacian_smoothing。在调用这个正则项时，每次都会重新计算一次拉普拉斯矩阵。对于FLAME/SMPL等拓扑固定的情况来说，这是没有必要的。我们总可以预先计算好拉普拉斯矩阵：

1
2
3
4
5
6
7
# laplacian matrix
laplacian_matrix = Meshes(verts=[self.v_template], faces=[faces.verts_idx]).laplacian_packed().to_dense()
self.register_buffer("laplacian_matrix", laplacian_matrix, persistent=False)

D = torch.diag(laplacian_matrix)
laplacian_matrix_negate_diag = laplacian_matrix - torch.diag(D) * 2
self.register_buffer("laplacian_matrix_negate_diag", laplacian_matrix_negate_diag, persistent=False)

我们注意到了上述矩阵的另一个变种laplacian_matrix_negate_diag，他其实是将主对角线从-1调整成1。这样操作的矩阵可以用于模拟一些类似扩散的平滑。因为此时矩阵乘出来的将是周围顶点的加权和与顶点自身的和（而不是差）。

​ 在VHAP中计算的拉普拉斯平滑实际上是：

1
2
3
4
5
6
7
8
def compute_laplacian_smoothing_loss(self, verts, offset_verts):
    L = self.flame.laplacian_matrix[None, ...].detach()  # (1, V, V)
    basis_lap = L.bmm(verts).detach()  #.norm(dim=-1) * weights

    offset_lap = L.bmm(offset_verts)  #.norm(dim=-1) # * weights
    diff = (offset_lap - basis_lap) ** 2
    diff = diff.sum(dim=-1, keepdim=True)
    return diff

这个损失用于对齐“有offset的FLAME曲面的变化”与“无offset的FLAME曲面的变化”，并不是单纯的让曲面变得平滑。

Monocular Video Datasets

当构造好FlameHead，完成FlameTracker的构造方法后，GlobalTracker会先初始化数据集。对于单目视频，会调用vhap/data/video_dataset.py里的VideoDataset。这个类的作用是将预处理得到的图片，mask和landmark都打包好，并且为单目视频初始化一个相机位姿：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def load_camera_params(self):
    self.camera_ids =  ['0']

    # Guessed focal length, height, width. Should be optimized or replaced by real values
    f, h, w = 512, 512, 512
    K = torch.Tensor([
        [f, 0, w],
        [0, f, h],
        [0, 0, 1]
    ])

    orientation = torch.eye(3)[None, ...]  # (1, 3, 3)
    location = torch.Tensor([0, 0, 1])[None, ..., None]  # (1, 3, 1)

    c2w = torch.cat([orientation, location], dim=-1)  # camera-to-world transformation

    if self.cfg.target_extrinsic_type == "w2c":
        R = orientation.transpose(-1, -2)
        T = orientation.transpose(-1, -2) @ -location
        w2c = torch.cat([R, T], dim=-1)  # world-to-camera transformation
        extrinsic = w2c
    elif self.cfg.target_extrinsic_type == "c2w":
        extrinsic = c2w
    else:
        raise NotImplementedError(f"Unknown extrinsic type: {self.cfg.target_extrinsic_type}")

    self.camera_params = {}
    for i, camera_id in enumerate(self.camera_ids):
        self.camera_params[camera_id] = {"intrinsic": K, "extrinsic": extrinsic[i]}

    return self.camera_params

正常情况下self.cfg.target_extrinsic_type都是w2c，因为实际上w2c才是相机外参（extrinsic），c2w是相机位姿（pose）。这段代码会初始化一个这样的相机模型：

相机外参和内参会在后面的优化中被调整。特别的是，在这个类的实现里有这么一个函数成员吸引了我的注意力：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def define_properties(self):
    self.properties = {
        "rgb": {
            "folder": f"images_{self.cfg.n_downsample_rgb}"
            if self.cfg.n_downsample_rgb
            else "images",
            "per_timestep": True,
            "suffix": "jpg",
        },
        "alpha_map": {
            "folder": "alpha_maps",
            "per_timestep": True,
            "suffix": "jpg",
        },
        "landmark2d/face-alignment": {
            "folder": "landmark2d/face-alignment",
            "per_timestep": False,
            "suffix": "npz",
        },
        "landmark2d/STAR": {
            "folder": "landmark2d/STAR",
            "per_timestep": False,
            "suffix": "npz",
        },
    }

因为在很多时候，我们编写炼丹代码都会有一些类似保存snapshot的需求，比如训练每隔若干iteration保存一些中间结果。如果做的任务对这种保存的需求比较固定，比如生成图像之类的，那可能这样还好。但对于3DV里的任务，可能我们想保存图片就有很多种，更别说还可能希望保存视频，mesh，点云之类的多种“media”。我之前写的时候没意识到这种定义一个self.properties的行为，如果这样做了，会带来很多的便利，例如我们可以在trainer里写这样一个字典，专门管理要保存的各种路径，前缀等。这样就避免了在保存snapshot的工具函数中频繁出现hard-code的路径。

后面还有一个小细节我很喜欢，就是这样来实现张量的一个常见操作：

1
2
3
4
5
6
7
8
@staticmethod
def to_batch(x, indices):
    return torch.stack([x[i] for i in indices])

@staticmethod
def repeat_n_times(x: torch.Tensor, n: int):
    """Expand a tensor from shape [F, ...] to [F*n, ...]"""
    return x.unsqueeze(1).repeat_interleave(n, dim=1).reshape(-1, *x.shape[1:])

在炼丹里，张量矩阵有1没1是个很烦的事情，这样相比于value.unsqueeze(0)等写法要优雅多了。

Optimization

​ 在GlobalTracker的构造方法里，init_params初始化了需要优化的变量：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
def init_params(self):
    train_tensors = []

    # flame model params
    self.shape = torch.zeros(self.cfg.model.n_shape).to(self.device)
    self.expr = torch.zeros(self.n_timesteps, self.cfg.model.n_expr).to(self.device)

    # joint axis angles
    self.neck_pose = torch.zeros(self.n_timesteps, 3).to(self.device)
    self.jaw_pose = torch.zeros(self.n_timesteps, 3).to(self.device)
    self.eyes_pose = torch.zeros(self.n_timesteps, 6).to(self.device)

    # rigid pose
    self.translation = torch.zeros(self.n_timesteps, 3).to(self.device)
    self.rotation = torch.zeros(self.n_timesteps, 3).to(self.device)

    # texture and lighting params
    self.tex_pca = torch.zeros(self.cfg.model.n_tex).to(self.device)
    if self.cfg.model.tex_extra:
        res = self.cfg.model.tex_resolution
        self.tex_extra = torch.zeros(3, res, res).to(self.device)

    if self.cfg.render.lighting_type == 'SH':
        self.lights_uniform = torch.zeros(9, 3).to(self.device)
        self.lights_uniform[0] = torch.tensor([np.sqrt(4 * np.pi)]).expand(3).float().to(self.device)
        self.lights = self.lights_uniform.clone()
    else:
        self.lights = None

    train_tensors += (
        [self.shape, self.translation, self.rotation, self.neck_pose, self.jaw_pose, self.eyes_pose, self.expr,]
    )

    if not self.cfg.model.tex_painted:
        train_tensors += [self.tex_pca]
    if self.cfg.model.tex_extra:
        train_tensors += [self.tex_extra]

    if self.lights is not None:
        train_tensors += [self.lights]

    if self.cfg.model.use_static_offset:
        self.static_offset = torch.zeros(1, self.flame.v_template.shape[0], 3).to(self.device)
        train_tensors += [self.static_offset]
    else:
        self.static_offset = None

    if self.cfg.model.use_dynamic_offset:
        self.dynamic_offset = torch.zeros(self.n_timesteps, self.flame.v_template.shape[0], 3).to(self.device)
        train_tensors += self.dynamic_offset
    else:
        self.dynamic_offset = None

    # camera definition
    if not self.calibrated:
        # K contains focal length and principle point
        self.focal_length = torch.tensor([1.5]).to(self.device)
        self.RT = torch.eye(3, 4).to(self.device)
        self.RT[2, 3] = -1  # (0, 0, -1) in w2c corresponds to (0, 0, 1) in c2w
        train_tensors += [self.focal_length]

    for t in train_tensors:
        t.requires_grad = True

在单目视频优化的配置里，有一些值得注意的事项。

  • 对于self.shape和self.expr，VHAP和INSTA tracker一样，都是用了所有的FLAME系数（n_shape为300，n_expr为100）。而基于DECA的tracker由于训练DECA时只选取了一些主成分（n_shape为100，n_expr为50），所以精度略差一些。

  • 其标记为’rigid pose’的self.rotation和self.translation，描述的是FLAME的全局旋转和平移。对于旋转，实际上就是根结点的旋转，也是用轴角式来表示。而平移self.translation会在FLAME做完LBS后施加给所有顶点。

  • FLAME官方曾为FLAME制作了一个简易的纹理空间，对应在上边代码里的即是self.tex_pca。VHAP里为了更好的photometric loss，并没有用这个简易的纹理空间，其使用的是self.tex_extra，作者手工构造了一个平均纹理，然后在后面逐像素的来优化这张图纹理图。代码里使用的self.tex_extra实际是在平均纹理上学习的残差。

  • 这里self.lights用二阶球谐来模拟打光，这个参数作用于渲染后端（默认的是nvdiffrast）。注意一阶光照被初始化为了$\sqrt{4\pi}$，这是为了总能量的归一化，考虑球谐光照中的光照强度：

    而$Y_{0}^{0}\left( \theta ,\phi \right) =\sqrt{\frac{1}{4\pi}}$，所以为了能量的归一化，$c_{0,0}$即取为$\sqrt{4\pi}$。

  • 参数中有两项可学习的offset，即static_offset和dynamic_offset。这两种offset都是3自由度的，用于在FLAME曲面的基础上学习头发等结构。所谓dynamic_offset是说对于每一个帧，都学习一组offset，用于实现更好的追踪结果。

  • 单目视频的输入下，self.calibrated是False，因为单目视频里其实不存在相机标定。所以这里会将相机焦距作为可学习的参数，至于相机位姿就仍然用默认值，即相机不动，用self.rotation和self.translation来表示人头的刚体变换。

  • VHAP采用基于球谐的漫反射光照模型，这个并不是特别显然，这里我们稍作解释。在标准情形下，漫反射光照的计算公式为：

    其中$\mathrm{p}$是空间中用于着色的某个点，$\omega_0$是视线方向，$\omega_i$是入射光方向，$N_p$为$\mathrm{p}$处法线。但考虑环境光，我们可以认为光源无限远，从而忽略待着色点的位置$\mathrm{p}$以及观察方向$\omega_0$（由于光源无限远，我们总是可以认为着色点位置位于中心）。这样漫反射光照就简化为了：

    那么一个直接的做法就是用球谐函数来构造右边的球面积分：

    所以在代码里的实现是：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    def get_SH_shading(normals, sh_coefficients, sh_const):
        """
        :param normals: shape N, H, W, K, 3
        :param sh_coefficients: shape N, 9, 3
        :return:
        """
        N = normals
        # compute sh basis function values of shape [N, H, W, K, 9]
        sh = torch.stack(
            [
                N[..., 0] * 0.0 + 1.0,
                N[..., 0],
                N[..., 1],
                N[..., 2],
                N[..., 0] * N[..., 1],
                N[..., 0] * N[..., 2],
                N[..., 1] * N[..., 2],
                N[..., 0] ** 2 - N[..., 1] ** 2,
                3 * (N[..., 2] ** 2) - 1,
            ],
            dim=-1,
        )
        sh = sh * sh_const[None, None, None, :].to(sh.device)
        # shape [N, H, W, K, 9, 1]
        sh = sh[..., None]
        # shape [N, H, W, K, 9, 3]
        sh_coefficients = sh_coefficients[:, None, None, :, :]
        # shape after linear combination [N, H, W, K, 3]
        shading = torch.sum(sh_coefficients * sh, dim=3)
        return shading
    ...
    diffuse = get_SH_shading(normal, self.lights, self.sh_const)
    ...
    rgb = albedo * diffuse

    在优化时，我们会优化self.lights来拟合光照，因为我们一开始并不知道环境光具体是怎么样的。

    但值得一提的是，在经典的图形学管线中，我们往往是先知道环境光的贴图（所谓“天空球”，“天空盒”），然后想从贴图里拿到环境光。球谐函数对于这个目的也有着优越的性质，考虑到$L(\omega_i)$和$N\cdot \omega_i$都是关于$\omega_i$的函数，并且$\omega_i$​是在球坐标系上采样的。可以很自然的对这两个函数进行球谐展开（为了不至混淆，我们省去$\omega_i$的下标$i$）：

    带入$L(N)$中，由于球谐函数的正交性：

    而系数$l_i$和$m_i$是方便计算的：

    上述球面积分可以在天空球/盒上做蒙特卡洛采样进行计算。

在后面真正优化的时候，作者做了更加细节的处理，堪称艺术！我们整体地看一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
def optimize(self):
    """
    Optimizes flame parameters on all frames of the dataset with random rampling
    :return:
    """
    self.global_step = 0

    # first initialize frame either from calibration or previous frame
    # with torch.no_grad():
        # self.initialize_frame(frame_idx)

    # sequential optimization of timesteps
    self.logger.info(f"Start sequential tracking FLAME in {self.n_timesteps} frames")
    dataloader = DataLoader(self.dataset, batch_size=None, shuffle=False, num_workers=4)
    for sample in dataloader:
        timestep = sample["timestep_index"][0].item()
        if timestep == 0:
            self.optimize_stage('lmk_init_rigid', sample)
            self.optimize_stage('lmk_init_all', sample)
            if self.cfg.exp.photometric:
                self.optimize_stage('rgb_init_texture', sample)
                self.optimize_stage('rgb_init_all', sample)
                if self.cfg.model.use_static_offset:
                    self.optimize_stage('rgb_init_offset', sample)

        if self.cfg.exp.photometric:
            self.optimize_stage('rgb_sequential_tracking', sample)
        else:
            self.optimize_stage('lmk_sequential_tracking', sample)
        self.initialize_next_timtestep(timestep)

    self.evaluate(make_visualization=True, epoch=0)

    self.logger.info(f"Start global optimization of all frames")
    # global optimization with random sampling
    dataloader = DataLoader(self.dataset, batch_size=None, shuffle=True, num_workers=4)
    if self.cfg.exp.photometric:
        self.optimize_stage(stage='rgb_global_tracking', dataloader=dataloader, lr_scale=0.1)
    else:
        self.optimize_stage(stage='lmk_global_tracking', dataloader=dataloader, lr_scale=0.1)

    self.logger.info("All done.")

整个优化过程分为逐帧（sequential）优化和全局（global）优化两大块。逐帧优化时逐张图片进行优化，当完成逐帧优化后，再打乱整个数据集，随机一些图片进行优化。训练分为若干stage：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def optimize_stage(
        self, 
        stage: Literal['lmk_init_rigid', 'lmk_init_all', 'rgb_init_texture', 'rgb_init_all', 'rgb_init_offset', 'rgb_sequential_tracking', 'rgb_global_tracking'],
        sample = None,
        dataloader = None,
        lr_scale = 1.0,
    ):
    params = self.get_train_parameters(stage)
    optimizer = self.configure_optimizer(params, lr_scale=lr_scale)

    if sample is not None:
        num_steps = self.cfg.pipeline[stage].num_steps
        for step_i in range(num_steps):
            self.optimize_iter(sample, optimizer, stage)
    else:
        assert dataloader is not None
        num_epochs = self.cfg.pipeline[stage].num_epochs
        scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.9)
        for epoch_i in range(num_epochs):
            self.logger.info(f"EPOCH {epoch_i+1} / {num_epochs}")
            for step_i, sample in enumerate(dataloader):
                self.optimize_iter(sample, optimizer, stage)
            scheduler.step()

            if (epoch_i + 1) % 10 == 0:
                self.evaluate(make_visualization=True, epoch=epoch_i+1)

不同的stage有不同的优化策略：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
PipelineConfig(
    lmk_init_rigid=StageLmkInitRigidConfig(
        disable_jawline_landmarks=False,
        num_steps=500,
        optimizable_params=('cam', 'pose')
    ),
    lmk_init_all=StageLmkInitAllConfig(
        disable_jawline_landmarks=False,
        num_steps=500,
        optimizable_params=('cam', 'pose', 'shape', 'joints', 'expr')
    ),
    lmk_sequential_tracking=StageLmkSequentialTrackingConfig(
        disable_jawline_landmarks=False,
        num_steps=50,
        optimizable_params=('pose', 'joints', 'expr')
    ),
    lmk_global_tracking=StageLmkGlobalTrackingConfig(
        disable_jawline_landmarks=False,
        num_epochs=30,
        optimizable_params=('cam', 'pose', 'shape', 'joints', 'expr')
    ),
    rgb_init_texture=StageRgbInitTextureConfig(
        disable_jawline_landmarks=False,
        align_texture_except=('hair', 'boundary', 'neck'),
        align_boundary_except=('hair', 'boundary'),
        num_steps=500,
        optimizable_params=('cam', 'shape', 'texture', 'lights')
    ),
    rgb_init_all=StageRgbInitAllConfig(
        disable_jawline_landmarks=True,
        align_texture_except=('hair', 'boundary', 'neck'),
        align_boundary_except=('hair', 'bottomline'),
        num_steps=500,
        optimizable_params=('cam', 'pose', 'shape', 'joints', 'expr', 'texture', 'lights')
    ),
    rgb_init_offset=StageRgbInitOffsetConfig(
        disable_jawline_landmarks=True,
        align_texture_except=('hair', 'boundary', 'neck'),
        align_boundary_except=('bottomline',),
        num_steps=500,
        optimizable_params=('cam', 'pose', 'shape', 'joints', 'expr', 'texture', 'lights', 'static_offset')
    ),
    rgb_sequential_tracking=StageRgbSequentialTrackingConfig(
        disable_jawline_landmarks=True,
        align_texture_except=(),
        align_boundary_except=('bottomline',),
        num_steps=50,
        optimizable_params=('pose', 'joints', 'expr', 'texture', 'dynamic_offset')
    ),
    rgb_global_tracking=StageRgbGlobalTrackingConfig(
        disable_jawline_landmarks=True,
        align_texture_except=(),
        align_boundary_except=('bottomline',),
        num_epochs=30,
        optimizable_params=('cam', 'pose', 'shape', 'joints', 'expr', 'texture', 'lights', 'static_offset', 'dynamic_offset')
    )
)

当优化开始时，我们先进行逐帧优化，一开始时间戳是第零帧。我们依次进行了lmk_init_rigid和lmk_init_all两个阶段的优化。根据optimizable_params的不同，一开始我们只通过关键点损失来优化'cam'和'pose'（焦距，根节点的旋转和平移）。然后再加上对形状，表情，姿态的优化。其中有一个参数是disable_jawline_landmarks，当其为True时，计算关键点损失时会将脸颊边缘处的18个点移除，因为这些点往往准确率比较差。这个设置在单目条件下并没有真的起效，而在多视点的情况下被启用了。这可能是由于多视角下的关键点检测会存在歧义。

​ 通过这两个阶段，我们可以在第零帧里构造一个稳定的初始状态。在一般情况下，self.cfg.exp.photometric和self.cfg.model.use_static_offset都是True，所以接下来还会初始化rgb_init_texture，rgb_init_all和rgb_init_offset。在关于光度损失的配置里，我们会注意到align_texture_except和align_boundary_except，这两个tuple也非常的细节。在优化光度损失时，会有：

1
2
3
4
5
6
align_texture_except_fid = self.flame.mask.get_fid_by_region(
    self.cfg.pipeline[stage].align_texture_except
) if stage is not None else None
align_boundary_except_vid = self.flame.mask.get_vid_by_region(
    self.cfg.pipeline[stage].align_boundary_except
) if stage is not None else None

这样来得到两组索引，这两组索引在vhap/util/render_nvdiffrast.py中的NVDiffRendered类里被用到，具体是在其render_rgba函数中：

1
2
3
4
5
6
7
8
9
10
11
12
# ---- uv-space attributes ----
texc, texd = dr.interpolate(verts_uv[None, ...], rast_out, faces_uv, rast_db=rast_out_db, diff_attrs='all')
if align_texture_except_fid is not None:  # TODO: rethink when shading with normal
    fid = rast_out[..., -1:].long()  # the face index is shifted by +1
    mask = torch.zeros(faces.shape[0]+1, dtype=torch.bool, device=fid.device)
    mask[align_texture_except_fid + 1] = True
    b, h, w = rast_out.shape[:3]
    rast_mask = torch.gather(mask.reshape(1, 1, 1, -1).expand(b, h, w, -1), 3, fid)
    texc = torch.where(rast_mask, texc.detach(), texc)
...
if align_boundary_except_vid is not None:
    verts_clip = self.detach_by_indices(verts_clip, align_boundary_except_vid)

被这两组索引选中的面片和顶点将会被detach。这非常的自然，在刚开始优化纹理的时候，我们不希望头发处的offset开始移动，因为此时的光度损失并不准。由于此时FLAME的位置基本是被校准的，所以('hair', 'boundary', 'neck')三个区域被detach，从而使rgb_init_texture阶段纹理图专注于拟合脸部外貌，同时顶点的('hair', 'boundary')也被屏蔽，使得此时先不要学习头发处的几何。之后在rgb_init_offset阶段，align_boundary_except中的'hair'被移除，并且optimizable_params追加了static_offset，允许顶点开始拟合头部几何。为了更好的理解整个过程，且看此图：

如图所示，在lmk_init_rigid阶段，会先进行关键点的策略对齐。绿色是脸部检测器检测出的关键点，红色是FLAME反投影出的关键点。一开始只优化了相机和全局的刚体变换，对齐的并不好。然后在lmk_init_all阶段，优化了FLAME的形状系数，表情系数，关键点变得更加对齐。然后在rgb_init_texture阶段，纹理得到了初步的优化。由于此时align_boundary_except=('hair', 'boundary')，由于'boundary'处的顶点被detach，此时脖子处有一些伪影。在rgb_init_all阶段，boundary变成了bottomline，脖子部分的伪影得到了优化。最后在rgb_init_offset阶段，在先前良好初始化的情况下，我们优化出了头发的几何。

注意，在后续的逐帧优化rgb_sequential_tracking时，static_offset并没有被优化。如果逐帧优化时同时优化偏移量，会干扰形状，表情等系数的拟合。

在optimize_stage函数的开始，会用self.configure_optimizer来定义优化器。如果是逐帧优化，那么每一帧的优化器都是新创建的，如果是全局优化，那么优化时一直维护同一个优化器。优化器采用的是经典的Adam优化器，默认（对于形状，纹理，全局旋转，左右眼球，下颚，脖子）的学习率为$5e^{-3}$​，对于其他一些待优化的量的学习率被精心调整。

Variables Learning rate Variables Learning rate
translation $1e^{-3}$ dynamic offset $5e^{-4}$
expression $5e^{-2}$ camera $5e^{-3}$
static offset $5e^{-4}$ light $5e^{-3}$

当进行逐帧优化时，对于那些需要逐帧优化的系数（例如表情），第$i$帧时的参数将从第$i-1$帧继承：

1
2
3
4
5
6
7
8
9
10
def initialize_next_timtestep(self, timestep):
    if timestep < self.n_timesteps - 1:
        self.translation[timestep + 1].data.copy_(self.translation[timestep])
        self.rotation[timestep + 1].data.copy_(self.rotation[timestep])
        self.neck_pose[timestep + 1].data.copy_(self.neck_pose[timestep])
        self.jaw_pose[timestep + 1].data.copy_(self.jaw_pose[timestep])
        self.eyes_pose[timestep + 1].data.copy_(self.eyes_pose[timestep])
        self.expr[timestep + 1].data.copy_(self.expr[timestep])
        if self.cfg.model.use_dynamic_offset:
            self.dynamic_offset[timestep + 1].data.copy_(self.dynamic_offset[timestep])

Loss Function

​ 现在我们单列一小节来细数VHAP里用到的损失函数，其基本就是关键点损失，光度损失，以及（致死量的）正则项。

landmark loss

VHAP在关键点损失$\mathcal{L} _{landmarks}$里加入了先前提到的对脸颊的考虑：

1
2
3
4
5
6
7
8
9
10
if not self.cfg.w.always_enable_jawline_landmarks and disable_jawline_landmarks:
    diff = lmk2d[:, 17:68] - pred_lmk2d[:, 17:68]
    confidence = confidence[:, 17:68]
else:
    diff = lmk2d[:, :68] - pred_lmk2d[:, :68]
    confidence = confidence[:, :68]

    # increase weight for nose landmarks since they are usually robust
    # https://ibug.doc.ic.ac.uk/media/uploads/images/300-w/figure_1_68.jpg
    confidence[:, 27:36] *= 10

当always_enable_jawline_landmarks为True时，计算关键点时会将鼻子附近的关键点的置信度拉大（其实这已经算某种变相的disable_jawline_landmarks了）。这一定程度上也避免了错误的关键点对优化的影响。值得注意的是，在计算loss时，人脸检测器对每个关键点的置信度也作为权重纳入了计算：

1
lmk_loss = torch.norm(diff, dim=2, p=1) * confidence

​ VHAP中为计算landmark提供了两个后端，一个是常用的face_alignment，另一个是STAR。后者精度高一些。

photometric loss

在VHAP中采用$L_1$损失作为光度损失$\mathcal{L} _{photo}$，并没有采用蒙皮损失（silhouette loss）：

1
2
3
4
5
6
7
8
9
10
pred_rgb = render_out['rgba'][:, :3]
pred_alpha = render_out['rgba'][:, 3:]
pred_mask = render_out['rgba'][:, [3]].detach() > 0
pred_mask = pred_mask.expand(-1, 3, -1, -1)

results_dict = render_out

# ---- rgb loss ----
error_rgb = gt_rgb - pred_rgb
color_loss = error_rgb.abs().sum() / pred_mask.detach().sum()
regularization terms

​ 针对全局旋转和平移，有平滑项来令第$i$帧的旋转与平移与第$i-1$​帧的均方损失最小：

实际上，从代码痕迹里可以感觉出来，作者一开始是希望在逐帧优化时保证第$i$帧和第$i-1$帧的连续性，然后在全局优化时再保证第$i$帧和第$i-1$，第$i+1$的连续性。但这个设置最后没有实装。

​ 对于FLAME的剩下的四个结点（脖子，下颚，左右眼），作者在$L_2$正则化的基础上给每个部位增加了额外的正则项：

对于下颚，额外惩罚了沿$x$轴负方向（即下颚向上颚方向旋转）和沿$y$轴$z$轴的旋转；对于左右眼球，额外惩罚了左右眼姿态估计的不一致。同样，针对结点的姿态也有平滑项​：

​ 对于表情，也存在正则项$\mathcal{R}_{expr}$和平滑项$\mathcal{E}_{expr}$：

​ 对于形状，存在正则项$\mathcal{R}_{shape}$：

​ 对于纹理图，我们这里优化的是逐像素的纹理图而不是FLAME提供的纹理空间，作者施加了变分损失来迫使纹理图变得光滑：

$\mathcal{T}$是学习到的残差纹理图，对于牙齿和巩膜（即眼白，sclera，是的没错，在这里你甚至可以学到生理学知识），作者为这些区域的纹理额外施加了$L_2$正则项：

这样保证在优化过程中这两个细节的部位不会被劣化（实际上牙齿和眼白的颜色沿用平均材质一点问题都没有，这还到不了那么细致的程度）。

​ 对于光照，我们同时将球谐系数约束在均匀光照，同时施加正则项来保持着色出的漫反射材质的合理性：

这里$\mathcal{D}$是渲染出的漫反射图，他具有三个通道。$\mathrm{var}(\mathcal{D})$的操作是求取其逐通道的方差，然后求平均。通过对通道间方差进行惩罚，提高打光的稳定性。值得注意的是$\mathcal{D}$的正则项是纯粹针对球谐系数的，跟法线无关：

1
2
3
# ---- shading ----a
diffuse = self.shade(normal, lights)
diffuse_detach_normal = self.shade(normal.detach(), lights)

这里diffuse_detach_normal是用于计算正则项的$\mathcal{D}$，这是很直接的，因为在优化环境光时我们不希望其影响几何。

​ 接下来是对于顶点位置的各种正则项，第一项是拉普拉斯平滑，如前文所说，其迫使施加了offset $d$的mesh和没施加前的具有相似的局部性质：

其中$v_{w/o}$是没有offset的顶点，它是由当前顶点$v$减去offset $d$得到的。我们不希望执行平滑时影响FLAME本身的形状，所以$v_{w/o}$​在计算平滑项时也做了detach()。拉普拉斯平滑并没有被施加到所有部位，self.cfg.w.reg_offset_lap_relax_for标记出了hair和ears两个区域。在这两个区域拉普拉斯平滑的强度会被缩放0.1倍。

​ 第二项是对偏移的$L_1$正则项，用于让offset不要过大：

这个正则项均匀地施加到了所有顶点上，虽然代码里也实现了对不同区域作用不同正则强度的机制，但对于这一项，强度缩放倍数均是1。

​ 第三项是对于特定区域的刚性正则项，它用于让一些区域的偏移尽可能均匀：

计算的方差是关于顶点的方差，得到特定区域若干顶点在$x,y,z$三个方向上偏移的波动，然后再平均，作为待优化的正则项。作者在left_ear，right_ear，neck，left_eye，right_eye，lips_tight六个区域施加了这一正则项。这非常的合理，因为在一般的优化中，这几个部位的几何往往会被附近的结构“淹没”，因为这几个区域往往都比较小并且不易被监督到。

​ 最后针对逐帧的dynamic_offset（如果用到了），作者也施加了平滑项，平滑项不仅约束帧间的变化，还约束第$i$帧跟第$0$帧的变化，防止几何随时间的漂变：

Total

​ 可以看出，作者为了优化过程的顺利进行，设计了相当多的正则项，并且还细节考虑了在哪些地方进行detach()。更加艰巨的任务是给每个优化项准备合适的权重，在单目情形下，总的损失函数为：

调出这些超参需要丰富的经验……我根本想象不到他们花了多久调出来的，以及他们有多少计算资源。

​ 在多视点数据集的情况下，权重会发生一些改变。具体来说，多视点的数据集中，关键点的监督会存在误差，所以关键点对齐的权重会被调低；当存在多个相机位姿时，有必要在一个batch内优化所有位姿，但这样会导致变分损失过平滑（类比于标准炼丹中的batchsize变大，学习率也应该跟着变大），所以变分损失的权重也应该拉大；最后一个设置是在多视点下，作者减轻了对表情的正则和平滑，这可能是为了拟合一些夸张表情（另一个角度来看，在多视角下，有着更准确的几何描述，形状和表情解耦的是比较彻底的，对于表情的约束就可以放低一些）：

nersemble数据集使用了16个视角，如果自己采集的数据并没有使用那么多视角，应将变分损失的权重再调小。

Nersemble Video Datasets

​ nersemble是一个经典的多视点数据集，为了能够处理自己的多视点数据集，我们需要了解VHAP中在追踪nersemble时的一些事项。

​ nersemble数据集在拍摄时，记录了每个相机的颜色校正矩阵，NeRSembleDataset在读取的时候会先根据对应的矩阵进行颜色校正：

1
2
3
4
5
6
7
8
9
10
def apply_transforms(self, item):
    if self.cfg.use_color_correction:
        color_correction_path = self.cfg.root_folder / 'color_correction' / self.cfg.subject / f'{item["camera_id"]}.npy'
        affine_color_transform = np.load(color_correction_path)
        rgb = item["rgb"] / 255
        rgb = rgb @ affine_color_transform[:3, :3] + affine_color_transform[np.newaxis, :3, 3]
        item["rgb"] = (np.clip(rgb, 0, 1) * 255).astype(np.uint8)

    super().apply_transforms(item)
    return item

如果拍摄的数据集之前已经做好了颜色校正，此处可以略去。

​ 多视角下对相机不做任何优化，nersemble读取出来的是w2c，在load_camera_params会将其先处理成c2w，然后进行一些对齐，最后再转回w2c。一个值得提到的对齐操作是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def align_cameras_to_axes(
    R: torch.Tensor,
    T: torch.Tensor,
    target_convention: Literal["opengl", "opencv"] = None,
):
    """align the averaged axes of cameras with the world axes.

    Args:
        R: rotation matrix (N, 3, 3)
        T: translation vector (N, 3)
    """
    # The column vectors of R are the basis vectors of each camera.
    # We construct new bases by taking the mean directions of axes, then use Gram-Schmidt
    # process to make them orthonormal
    bases_c2w = gram_schmidt_orthogonalization(R.mean(0))
    if target_convention == "opengl":
        bases_c2w[:, [1, 2]] *= -1  # flip y and z axes
    elif target_convention == "opencv":
        pass
    bases_w2c = bases_c2w.t()

    # convert the camera poses into the new coordinate system
    R = bases_w2c[None, ...] @ R
    T = bases_w2c[None, ...] @ T

    return R, T

这个对齐是为了将平均相机位姿与世界坐标系对齐。

​ 整个tracker写的“开箱即用”，将数据集按路径准备好了就可以一键启动了。

总的来说，整个tracker实现了针对人头来说非常惊艳的效果。

End

​ 整个项目的实现，完全就像一场“对见习炼丹师进行的指导课”。标准的type hint，规范的doc-string，可扩展性好，方便修改，甚至可以媲美一些由许多人维护的开源炼丹仓库（例如diffuser，transformer）。我起初只是以为我不会做科研，看完了以后我发现我其实连代码也不会写，哪怕是Python。自从入门3D Vision，已经有一年半了，科研上颗粒无收，多少有点麻；然后看了这个项目，我的内心：

“好玩不能当饭吃，要不转Java吧，现在还来得及。”——佚名

回想当时按下推免按钮，“少年轻狂，犹如南柯一梦。”。后来只剩下调了一天camera convention，窝在出租屋蜷着被子刷着手机看见同学该实习的实习，该顶会的顶会，这下更麻了。

​ 算了，扯点别的吧。“我永远喜欢罗小涵！”

赏

谢谢你请我吃糖果

微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

挟飞仙以遨游，抱明月而长终。<br />知不可乎骤得，托遗响于悲风。