“莫名那时今天,你我皆少年。”
这篇blog想讨论并整理一些从毕设题目出发的杂七杂八的东西。
“以这篇blog纪念我的本科毕业设计。“——沃兹基·硕德
“In memory of my undergraduate thesis with this blog.” — Wozki Shod
我的毕设做了这样的一个事情:“利用3D Gaussian Splatting(3DGS),从单目视频中重建一个可驱动的三维人头”。得益于3DGS和FLAME,以及PyTorch和CUDA这种杀手级的工具箱,实现的难度并不大,可以很容易的重建出高保真的人头化身。得到的人头的效果是“photorealistic”的,而且渲染速度非常的快。
但只需要稍微往前回退几年,是几乎不可能取得这么好的效果的。然而从2024年看,可能并不能理解这个任务的困难之处,就像这个段子一样:
小孩问大人手机上的“📞”图标是什么,大人说“这不是电话吗?”,小孩诧异:“电话不应该是这样“📱”的吗?”,大人这才明白,原来现在的小孩从小到大都没见过座机的电话听筒。
所以下文会以一个“re-invent”的逻辑来尽力叙述一下这整个事情是怎么回事。下文以这样的组织进行:
- 在Reconstruction部分,将会简单介绍如何从图像得到人头的mesh,从而理解FLAME等3DMM模型是怎么来的。
- 然后会介绍关于Blendshape的一些内容,Blendshape是在实际应用中的一个重要工具。
- 之后回到毕设本身,分析以NeRF作为表达的一系列工作。
- 最后分析一些Point-based的方法,然后扩展到用3DGS表征人头的这件事上。
Reconstruction
为了建模三维人头,第一个要解决的事情就是如何把人头表示进计算机里。在3D数据的各种表示方法中,将人头建模为mesh网格是最合适的,mesh适配于GPU的管线,同时支持各种应用。一个经典的构造人脸mesh的管线如下:
- 使用相机对人从多个视角进行拍摄,通过运动恢复结构(Structure from Motion, SfM),重建出稀疏点云。
- 然后再通过一些多视图立体视觉(Multi-view Stereo, MVS)中的技术,从稀疏点云中得到稠密点云。
接着应用曲面重建(Surface Reconstruction)技术来得到mesh网格,通过一些简化网格的算法来固定面数和顶点数。
为了让所有的网格有一致的拓扑结构(对应顶点有相同的意义,顶点与三角面的连接关系相同),所以会先创建一个大致的模板人脸,然后将网格与这个模板人脸进行配准(Registration)。
这一段话里涵盖了许多经典的图形学中的算法,涵盖了三维重建,几何处理以及多种方面。所以下面只是简单整理一些资料,从而对这个过程有一个直观和符合直觉的认识。
第一步要考虑的,是如何从多视角的图片中得到稀疏点云。需要先了解对极几何中的一个简单用例。由于多视角的人脸数据比较涉及隐私,下文用一个初音未来的公式服fufu来进行举例。
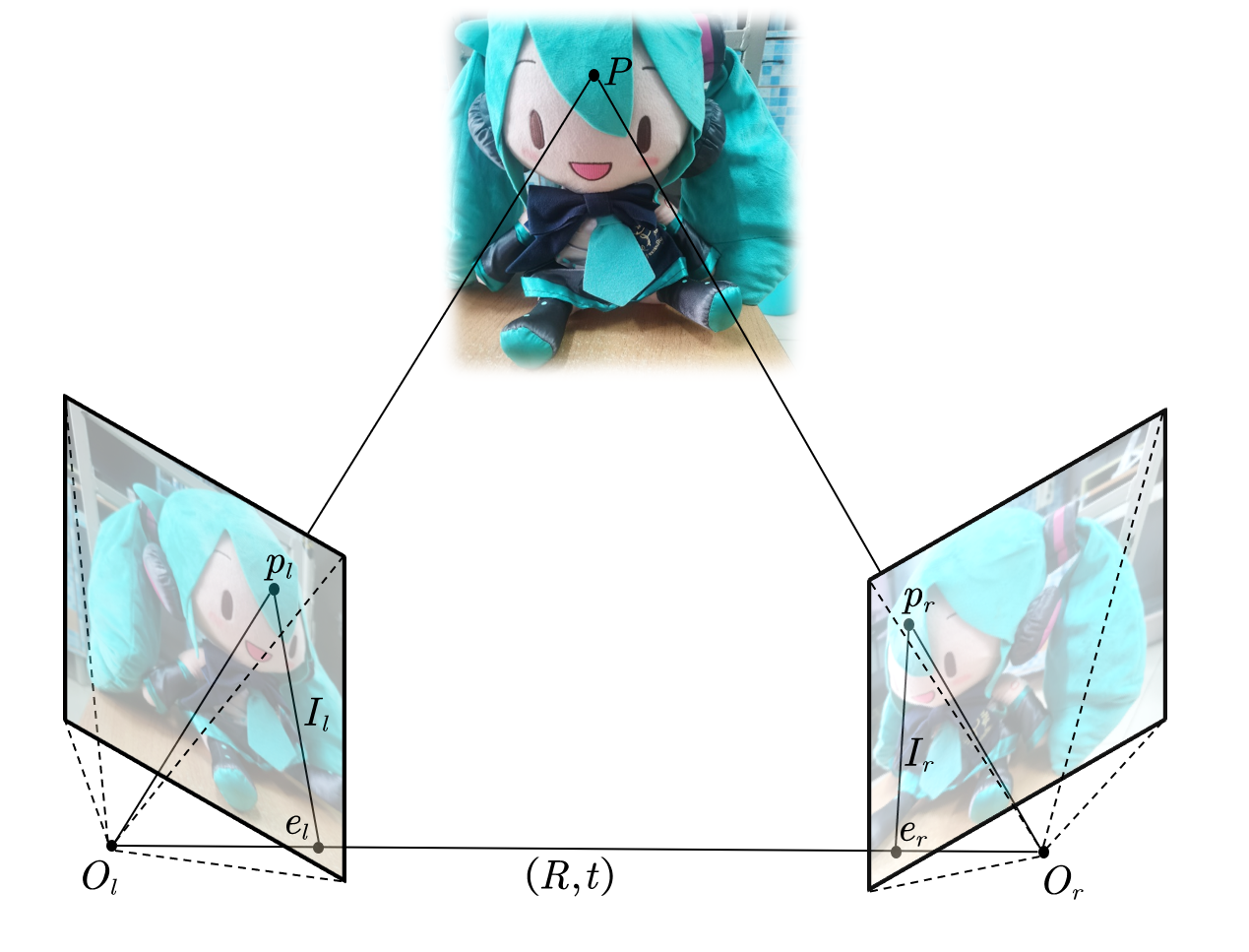
取3D场景中fufu刘海处一点为$P$,我们从左侧和右侧用同一个相机拍摄了两张图片,相机位置记作$O_l$和$O_r$,左侧和右侧相机的位姿和内参分别为为$R_l,t_l,K_l$和$R_r,t_r,K_r$。两者之间的相对位姿由$R$和$t$导出:
刘海在左图和右图中的对应点记作$p_l$和$p_r$,称作同名像点。连接$O_l$与$O_r$,连线称作基线$O_lO_r$。基线与左图右图两个像平面交于极点$e_l,e_r$。$e_l$和$x_l$,$e_r$与$x_r$的连线称作极线$I_l,I_r$。
首先,如果我们知道左侧相机和右侧相机的位姿,事情会变得很自然,我们可以直接得到$P$的坐标$(X,Y,Z,1)$。根据针孔相机的投影过程,我们记$p_l=\lambda_l (u_l,v_l,1)$,$p_r=\lambda_r (u_r,v_r,1)$。可以得到:
我们将内参矩阵和外参矩阵的乘积,记作$P$,那么实际上我们有两个等式:
我们可以用这两组中的第三行等式来作一个变形,为了简洁我们先忽略角标$l$和$r$:
将$p_{14}$和$p_{34}$移到一边:
将第二行乘$u$与第一行作差:
所以我们可以把刚才的两个线性方程变形为如下的形式:
通过解这个线性方程组,我们就可以解出$P$的坐标了。由于真实测量存在误差,上面的线性方程组未必有解,所以一般是用数值方法进行处理(如最小二乘)。
所以给定两个视图,我们只要能确保找到两张图片中相同的“刘海位置的像素就好了。这一般是用SIFT(尺度不变特征变换)和SURF(加速稳健特征)等特征提取技术来做的。这些特征提取的方法被称作描述子(descriptor)。通过处理两个视图,然后对提取的特征点进行两两匹配,从而找到同名像点。
然而一个必要的讨论是在相机姿态未知时的处理,虽然在真实的采集系统中相机位姿都是已知的。这个步骤叫作“运动恢复结构”。实际上,平面$PO_l O_r$形成了对极约束。为了方便,我们将坐标系原点定在$O_l$处。注意向量$t$与$p_l$共面,那么根据向量叉乘和点乘的定义,有:
$t$可以写成一个反对称矩阵$T$:
于是我们有:
同时,又因为$p_l=Rp_r+t$,将其带入上式,得:
注意$t\times t=0$,所以上述约束就可以化简为:
我们将中间两个矩阵的乘积记作本质矩阵(Essential Matrix),标作$E$,于是有:
如果能计算出$E$,通过对$E$进行矩阵分解,我们就能恢复$R$和$t$。我们发现,我们可以把上述二次型转化成向量相乘:
根据齐次线性方程组的解理论,未知数数量为$n$的齐次线性方程组的解的维数为$n-r$。所以为了得到关于$E$的唯一非零解,需要8对同名像点。所以也叫八点法(eight-point algorithm):
但由于采集时存在误差,大部分时候用的点都多于8对,此时系统是过约束的,严格按照线性方程组求解只有零解。所以这时一般是用最优化的思路,最小化$\frac{\left| A\mathbf{e} \right|}{\left| \mathbf{e} \right|}$(分母用于规避零解)。
关于本质矩阵$E$其实还需要进行一些讨论,但这里就不展开了。我们最后指出一点:通过这种重建,得到的是两个视图之间的相对变换,由于我们并不知道其中任何一个相机真正的位姿(当然,我们可以假设其中一个是平移为零,旋转为单位阵的),这会导致真实的重建结果与实际差一个变换。
总之现在我们知道,给定两张图片,通过用一些描述子进行特征匹配,可以得到若干对同名像点。如果此时已知相机位姿,那么可以直接恢复同名像点对应的三维坐标,用像素的颜色作为坐标点处的颜色,可以恢复一个稀疏点云。如果不知道相机位姿,我们可以根据对极几何,来估计本质矩阵,通过对本质矩阵进行分解,来恢复相机位姿。
我们对两个视图时的情况做出了解答,但更一般的时候我们有更多视角的图片,综合这些多视角的图片可以得到更准确的稀疏点云。一般有两种做法:增量式(Incremental)和全局式(Global)。
无论是增量式还是全局式,都需要做一个很重要的操作:捆绑调整(bundle adjustment),这个名字很奇怪,有的翻译叫作“光束法平差”,感觉更怪了。但从现在的角度看,这只是一个损失函数:
其中$n$是当前三维点的总数量,$m$是相机数量,$\mathcal{X}_{i,j}$表示第$i$个点在第$j$个相机下是否可见,如果可见则取1,否则取0。$\mathcal{P}(\cdot)$表示相机投影的过程。下面的过程中会多次优化这个损失,来进一步优化相机参数,三维点坐标,从而提高多视角一致性。这个过程简记作“BA”。
当采用增量式时,会先挑选匹配质量高的一对视图进行特征匹配,然后重建,从而得到一些三维点,然后进行BA。之后加入第三张图片,与前两张图片进行特征匹配,然后根据刚才得到的三维点,和第三张图与前两张图的匹配点,来优化第三张图的位姿,最后通过重建第一张图片和第三张图片,第二张图片与第三张图片,来得到一些新的三维点,然后再重复BA。依次类推,每一个新的视图进入计算时,都进行匹配,重建和BA,同时剔除一些误差过大的点。
而全局式是在一开始就完成所有视图的两两重建,然后统一进行BA。实践表明这样的效率更高,但稳定性低。著名的三维重建开源软件COLMAP,使用的就是增量式SfM。如下图所示:
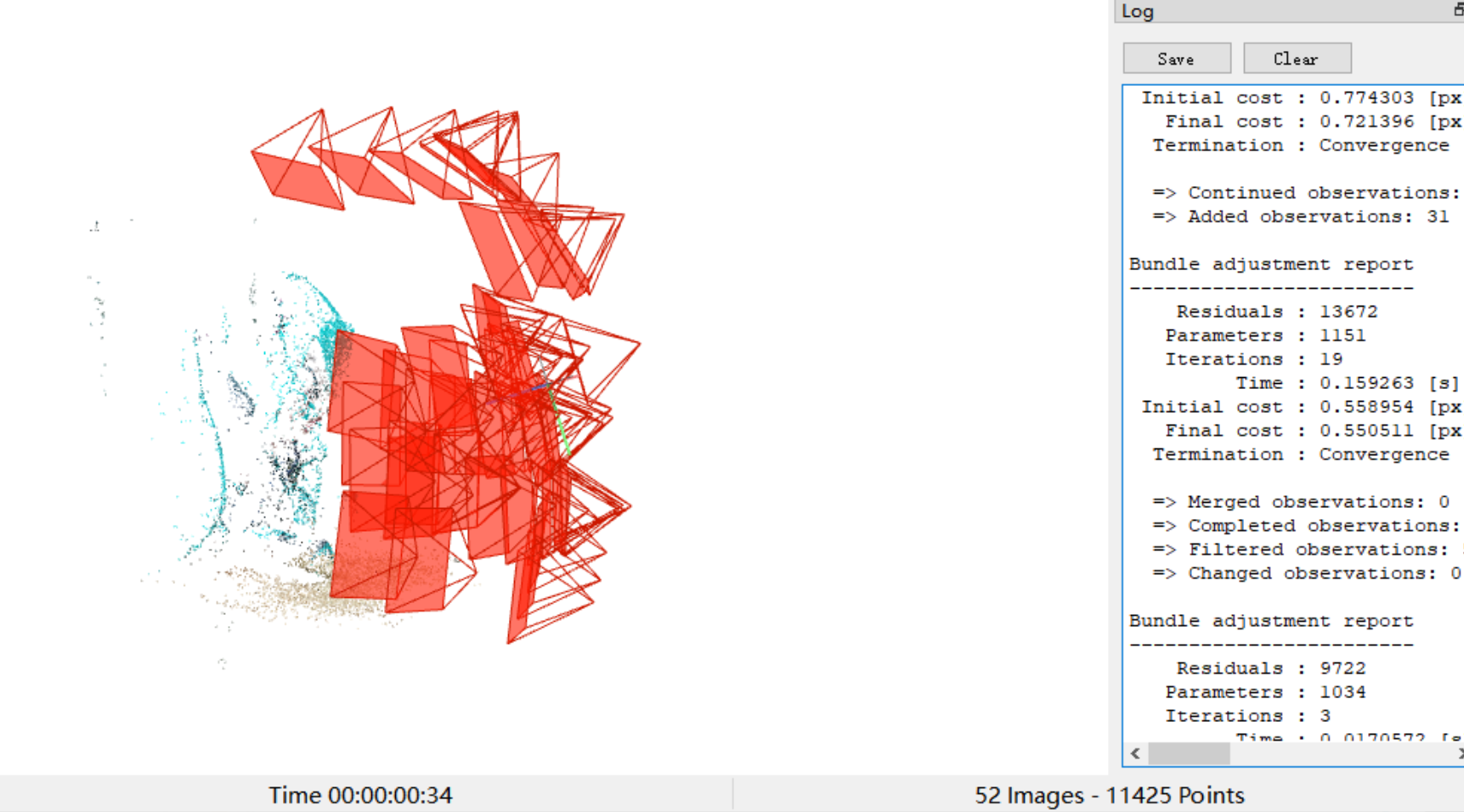
从多视角图片中,我们可以得到一个稀疏点云。
下一步要从稀疏点云中恢复稠密点云,这是一个更加复杂的技术,我们这里只进行简要的讨论,其核心思想在于匹配搜索(Correspondence Search):
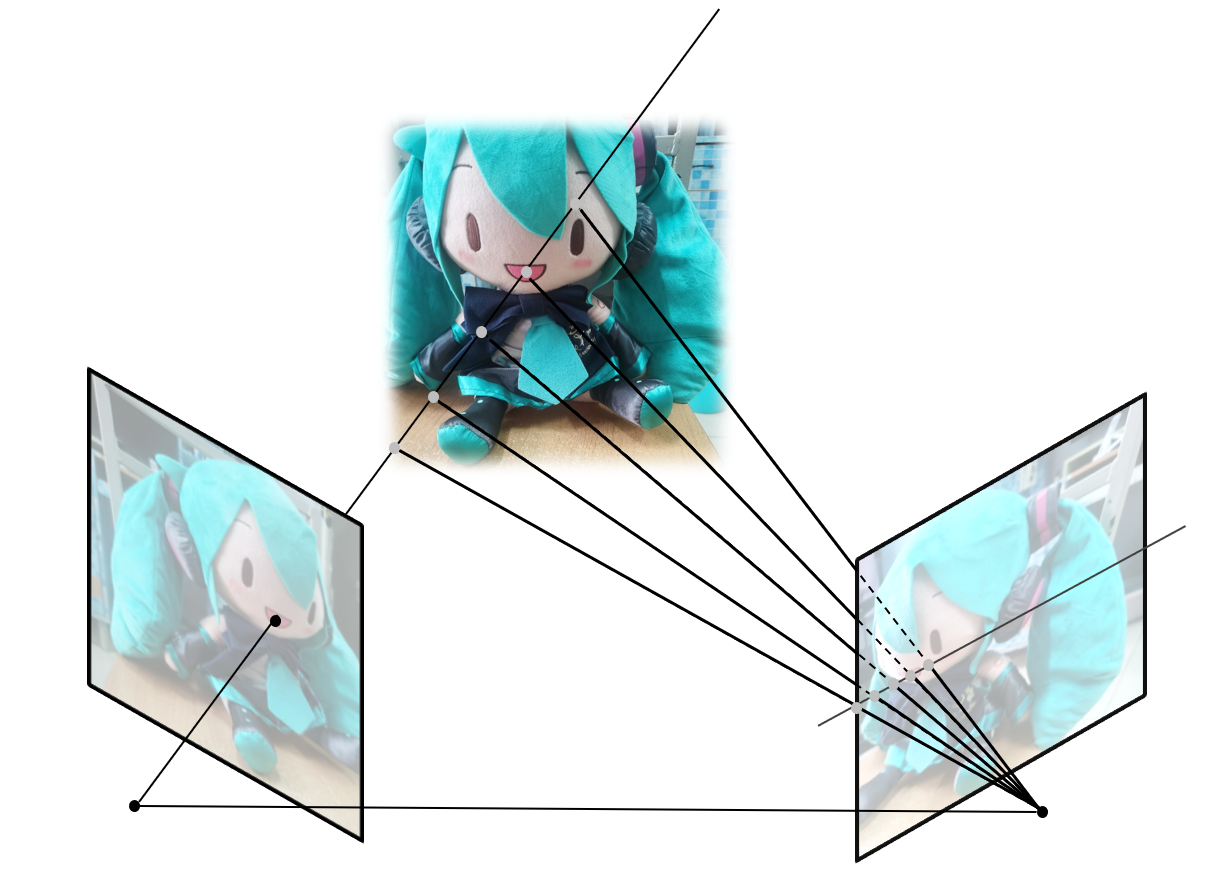
首先从图片中挑选一张图作为参考帧,然后循环读取每一张图片。遍历当前图片中的所有像素,考察当前像素和参考帧上的极线上的点哪些最匹配,这样就得到了一对同名像点,继而得到了每个像素的深度。注意在上图图示中,参考帧上作出的极线是平行的,这并不是显然的,我们需要针对这一对图片构造单应矩阵来进行校正,这里不再展开,我们可以认为图片已经完成了校正。
这里一般会使用归一化互相关NCC(Normalization Cross Correlation)等指标来完成匹配,但这样朴素地用单点匹配的结果并不好,会有很多噪声以及不好的匹配。为了结果的平滑,一般会沿着扫描像素周围展开一个小窗口,也叫支撑窗口(Support Window),来进行计算。后续也开发了一些自适应权值和自适应窗口大小的设计,但尽管如此,仍然存在一个很直接的问题:
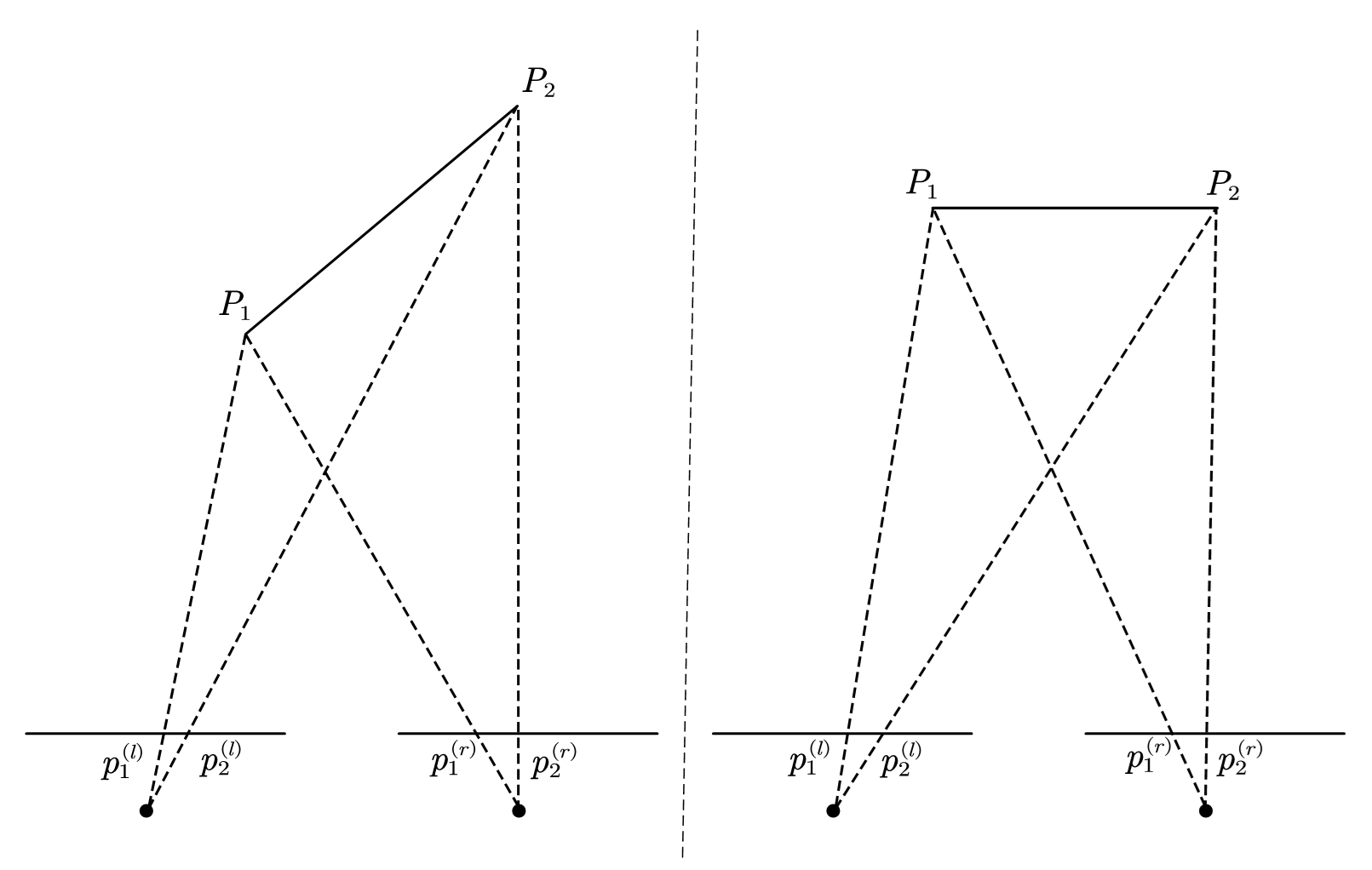
根据中学几何,我们很容易知道左边的$p_{1}^{\left( l \right)}p_{2}^{\left( l \right)}\ne p_{1}^{\left( r \right)}p_{2}^{\left( r \right)}$,而右侧$p_{1}^{\left( l \right)}p_{2}^{\left( l \right)}= p_{1}^{\left( r \right)}p_{2}^{\left( r \right)}$,所以,朴素的按窗口来进行匹配,隐含的假设就是这样的“平行窗口”(Fronto-parallel windows),然而,由于窗内部的不同物体可能来自不同的深度平面,单个物体也不一定平行于像平面,其深度可能像左侧的$P_1P_2$一样是渐变的。所以我们需要建模所谓“倾斜窗口”(Slanted support windows)。
一条线上的研究开启于PatchMatchStereo,其受一篇经典的图像处理论文PatchMatch的启发。我们这里不展开细节,简单来说,在完成极线校正的两个视图中,存在这样的几何关系:
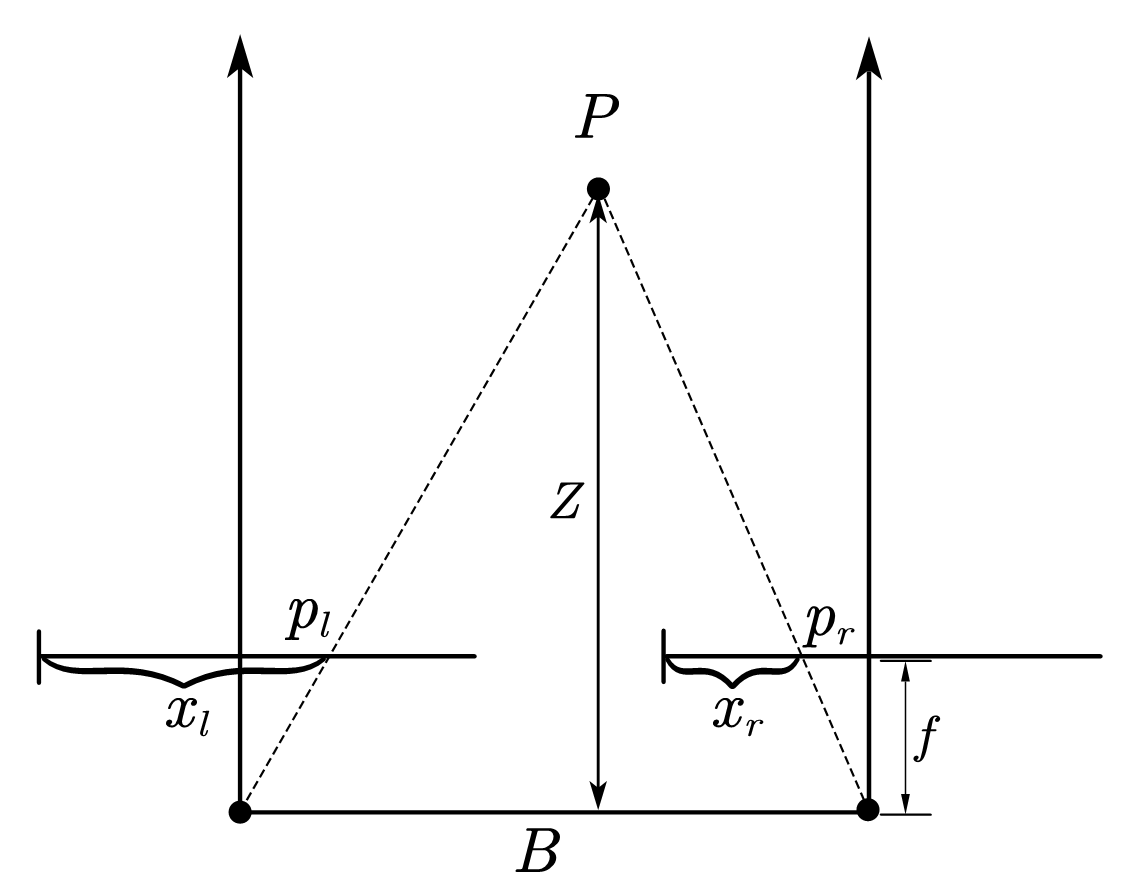
定义所谓视差为$d=x_l-x_r$,根据相似三角形,可以得到深度$Z$与视差$d$的关系:
所以,校正后,$p_r$可以表示为$p_l - d$。PatchMatchStereo中为每个像素随机分配了一个视差平面:
然后问题就转化为了:
这里$w(\cdot,\cdot)$是自适应权值,这个设计可以用来处理窗内物体深度明显不同的情况。$W_p$是以$p$为中心的窗口,$d_p$实际上是$f$的函数,$F$则是全体倾斜平面的集合。这个优化问题是复杂的,所以PatchMatchStereo用了类似PatchMatch中的策略,认为随机的这数以千计个斜平面总有匹配的好的,然后用一些策略(空间上相邻的像素可能有相同深度的平面)来将匹配好的解进行传播,同时对解施加扰动来跳出局部最优。
后来,PatchMatch Based Joint View Selection and Depthmap Estimation在PatchMatchStereo上进行了扩展,建立了一个完善的概率图模型来进行优化,再后来Pixelwise View Selection for Unstructured Multi-View Stereo在此基础上做了进一步的改进,加入了对“光学”(其实就是指RGB)和“几何”一致性的约束,同时估计了法线,而这其实也就是COLMAP其中的MVS实现。此处细节从略。

通过在COLMAP中执行”dense reconstruction“,等待一段时间后,我们可以得到稠密点云。
稠密点云可以进一步进行表面重建,这又是另一个图形学中的话题了,例如泊松表面重建,Delaunay三角化。以我的教育背景,我更喜欢泊松重建,其背后的思想是从稠密点云的法线向量上估计一个向量场,而这个向量场应该和所谓“示性函数”的梯度有关。我们说待重建的物体为$M$,其表面记为$\partial M$,定义一个示性函数$\mathcal{X}_M(\cdot)$,当输入的坐标$p$在$M$内部时,$\mathcal{X}_M(p)=1$,否则$\mathcal{X}_M(p)=0$。这个示性函数在$\partial M$处有无穷大的梯度,这个性质并不好进行实际上的计算,一个信号处理中常用的操作是将其与一个光滑函数$\mathcal{F}$(例如高斯函数)作卷积,来使得“阶跃”平滑。光滑后的$\mathcal{X}_M(\cdot)$记作$\mathcal{X}(\cdot)$:
现在的问题在于如何建立$\mathcal{X}(\cdot)$和表面$\partial M$上的法向量的关系。首先回顾高斯定理:
对于一个向量场$\mathbf{F}$,其向量场散度在一个区域内的体积分等于向量场在这个区域表面的面积分。
这个定理更广为人知的是在大学物理中:“穿过一封闭曲面的电通量与封闭曲面包围的电荷量成正比。”
那么求取$\mathcal{X} $在$p$处的梯度$\nabla _p \mathcal{X}$:
由于$\mathcal{F}$的局部性质,最后的积分只会在$p$附近有效,所以$\nabla _p \mathcal{X}$事实上很好的估计了$p$的法向量,其形成的向量场记作$\overrightarrow{V}(p)$,最终就推导出了:
两边再作用一次$\nabla$,就得到了泊松方程:
泊松方程是一类经典的偏微分方程,在许多领域有着应用。求解上述方程就可以得到一个表面的隐表示$\mathcal{X}$,求解细节此处略去,然后通过构造等值面,再用Marching Cubes,就可以得到最后的mesh了。

mesh通过简化,可以固定面数和顶点数。这些简化的原理一般都是通过构造一种指标,然后判断删除哪些顶点/面/拓扑,对这些指标的影响最小。例如用open3d库:
1 | import open3d as o3d |
网格处理也是一个图形学中比较大的课题,其背后的原理细节在此不作展开。
最后就是所谓的“配准”,这个过程是将现在得到的mesh,按照一个预先定义好的模板人脸(比如手工制作的)进行逼近,然而在这个逼近中,我们不希望真实mesh完全变成模板人脸,我们希望其保存它自己的特点,所以会有一些限制形变的正则项,以及一些例如拉普拉斯平滑的正则项,让mesh变得“在模板人脸的基础上保留大部分真实细节”。我找了很久,找到了一张示意图,原图来自这里:
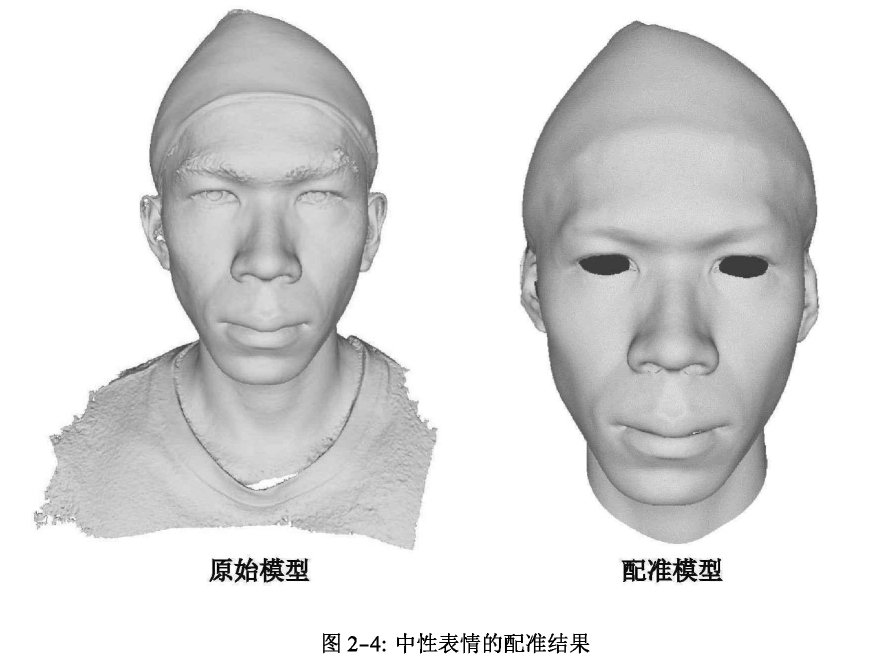
至此,我们就了解了如何从多视角图片中,处理出人脸的mesh。在写这篇blog的时候,这一章节是写起来最为困难的。因为整个pipeline涉及到的内容太多,有些也比较早,网上不太能搜得到,其中的有些工作也不存在“开源代码”这种说法,所以只能比较粗浅的进行理解。但实际上,可以有其他的采集方式,例如结构光,ToF。数据集FaceWarehouse就是用Kinect深度相机采集的,只不过这种相机的精度肯定了差了一些。下面将讨论如何让人脸/头mesh可以被驱动。
[点击以查看一些废话]
历史的车轮滚滚向前,揪着上面的那些环节的细节也意义不大。不如相忘于江湖,抓紧时间多快好省的炼丹。滚雪球的效应是恐怖的:比如有同学选择上大模型的车,已经猛发机器学习三大会了;有的同学早早就知道去找外校intern,然后猛搓螺旋丸了;你还搁这儿横竖转置、透视变换看不明白,那只能一步错步步错,到时候一路生花的名单里就没有你。不过如果你和我一样一开始就从名单里被除名了,那你至少获得了几年的“追求自己喜欢的事情”的豁免。毕竟卷也卷不赢,躺也躺不平,总得找点精神寄托。至少对于我,多年以后,确认接单骑上电动车后,我会想起遥远的大三暑假的某天下午,我把fufu放在椅子上,拿着手机拍了一圈,然后在autodl上跑出了个NeRF新视角的fufu.mp4。
Blendshape
我第一次遇到这个词是在阅读FLAME中,冷不丁就来这么一个“blendshape”(FLAME中其实指的是corrective blendshape),我当时并不理解他什么意思,他被翻译成什么“混合变形”,我其实后来也不是很理解他为什么要叫“blendshape”。然后我看他们都在用这个词,我也就跟着用这个词了。如果非要给blendshape下定义,那大概是:
对于一个$\mathcal{M}$,对其作顶点数不变的变形,得到$\mathcal{M}^\prime$,那么说$\mathcal{M}^\prime$是$\mathcal{M}$的一个blendshape。
但实际上在人头中,blendshape更多被视作一个“语义参数化”(Semantic Parameterization)模型。回忆一开始通过“BFM->FLAME”这个路线来学习参数化人头时,一个经常的论断是“用主成分分析(PCA)来获得可解释性的成分”。但PCA得到的基其实并不是“可解释性”的,当然他们在哲学和理论意义上是“可解释的”,但并不能具有实际意义上的“解释性”。例如一个艺术家想将FLAME通过调整系数,将标准人脸变成某个特定的表情,他会无从下手。
在Blendshape中,基向量被替换为了具有实际意义的表情模板,例如“下巴向左”,“撅嘴”,“抬眉”等,有经验的艺术家可以直接从标准模板里变形出所需要的表情模板,当然也可以用上面所说的采集数据的管线,让受试者做出相应的动作,然后得到其表情模板。记表情模板为$\mathbf{b}_k$,对应权重为$w_k$,则对应的blendshape model为:
这里$\mathbf{f}\in \mathbb{R}^{3v\times 1}, \mathbf{b}_k\in \mathbb{R}^{3v\times 1}$,在更通常的情景下,$\mathbf{b}_0$代表中性表情,所以一种blendshape的形式为:
这样的形式化提供更符合直觉的控制。如果将上式写成矩阵乘的形式:
$\mathbf{B}\in \mathbb{R}^{3v\times n}, \mathbf{w}\in \mathbb{R}^{n\times 1}$,$n$即blendshape的数量。从一个稀奇的角度看,我们构造一个关于$\mathbf{w}$的函数$f(\cdot)$,我们取$f(\mathbf{0})=\mathbf{b}_0$,$f(\mathbf{w})=\mathbf{b}_0 +\mathbf{Bw}$,作一阶近似有:
那么实际上$\frac{\partial f}{\partial \mathbf{w}}$就是$\mathbf{B}$,从这种类似泰勒展开的形式上,我们可以看到Blendshape的局限性。譬如Blendshape其实是$f(\mathbf{w})$在零向量处的展开。理想情况下,如果用足够多的blendshape的模板,$f(\mathbf{w})$在应用上的性质就会好一些。
一个更直观的问题在于,如果在两个形状$\mathbf{f}$之间进行插值,例如$f(\mathbf{w}_1)$和$f(\mathbf{w}_2)$,每个顶点的变化也是线性的。然而实际的人脸形变通常不是线性的,这样直接的操作会导致动画时的不自然。这一点即使在只单独调整$\mathbf{w}$的某一维度时也存在,在这种情况下,往往是插入一些中间位置的模板(Intermediate Blendshape);在更一般的情况下,会采用blendshape的组合(Combination Blendshape)来构造一些交叉项:
这等价于给上面的泰勒展开补充一些高阶项,来模拟一些非线性的操作。正是因为这样的修修补补,好的blendshape模型甚至需要上百个甚至近千个模板。
这里的权重$w_k$,也叫“slider”,意为滑杆,因为在交互界面中,$w_k$往往是通过下面这样的滑杆控件来改变的。
在早期的时候,有一些工作应用Blendshape和上一章的重建技术,实现了一些从单目视频中重建可驱动的人头。例如2015年SIGGRAPH中的Dynamic 3D Avatar Creation from Hand-held Video Input:
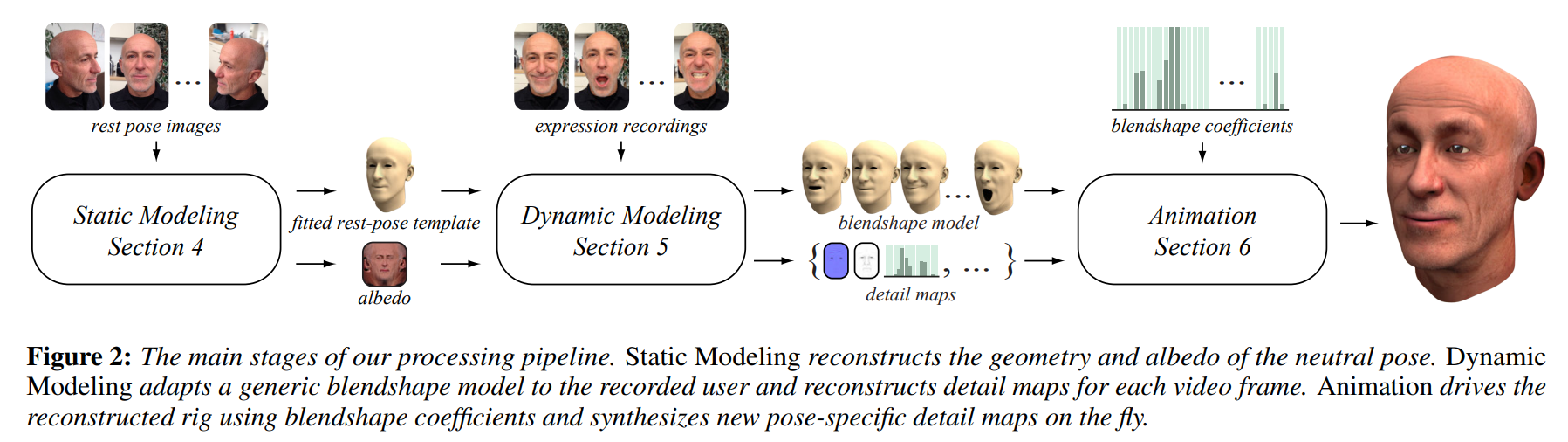
可以看出,其先通过多角度的中性表情时的图片,重建出中性时的模板人头;然后记录不同表情时的图片,制作成不同的blendshape,然后就可以animation了。
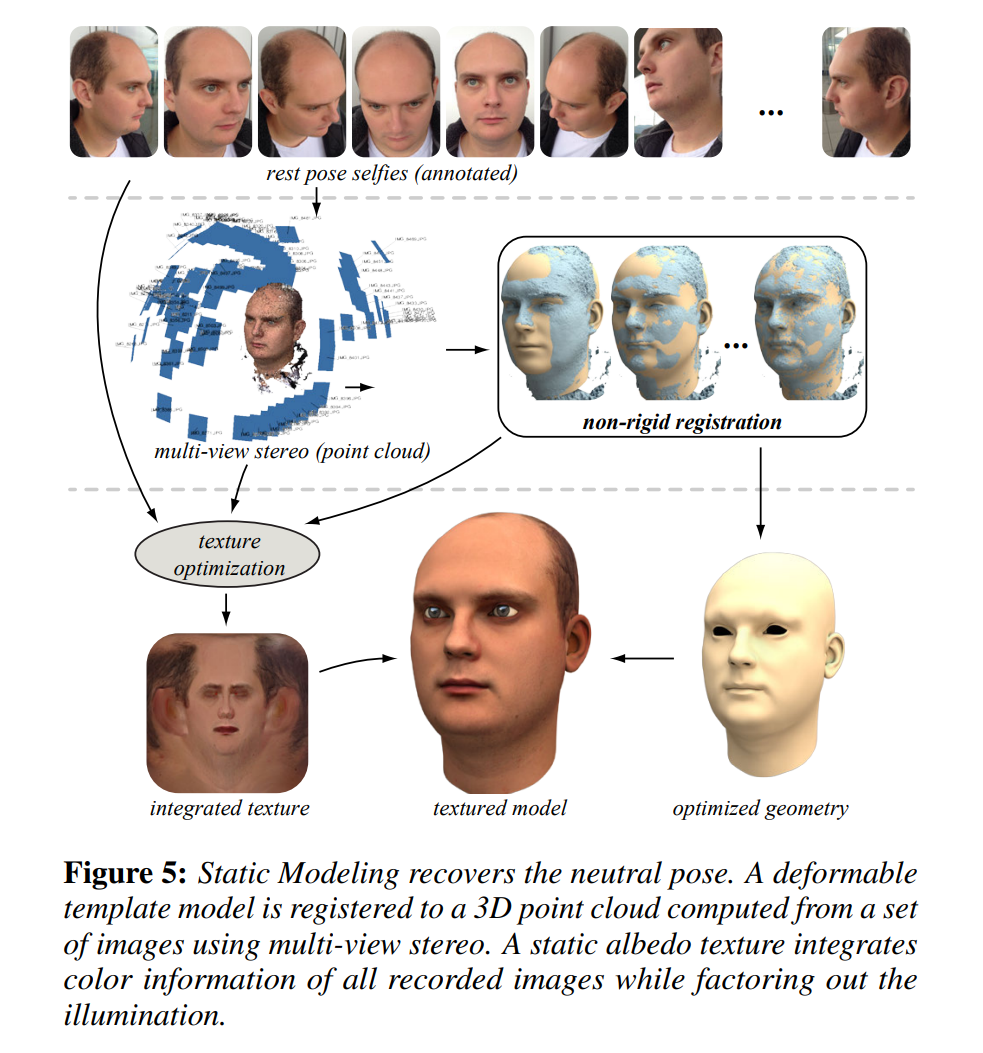
例如这里,建模静态人头的部分,整个流程就是上一章节的内容(除去纹理的优化)。
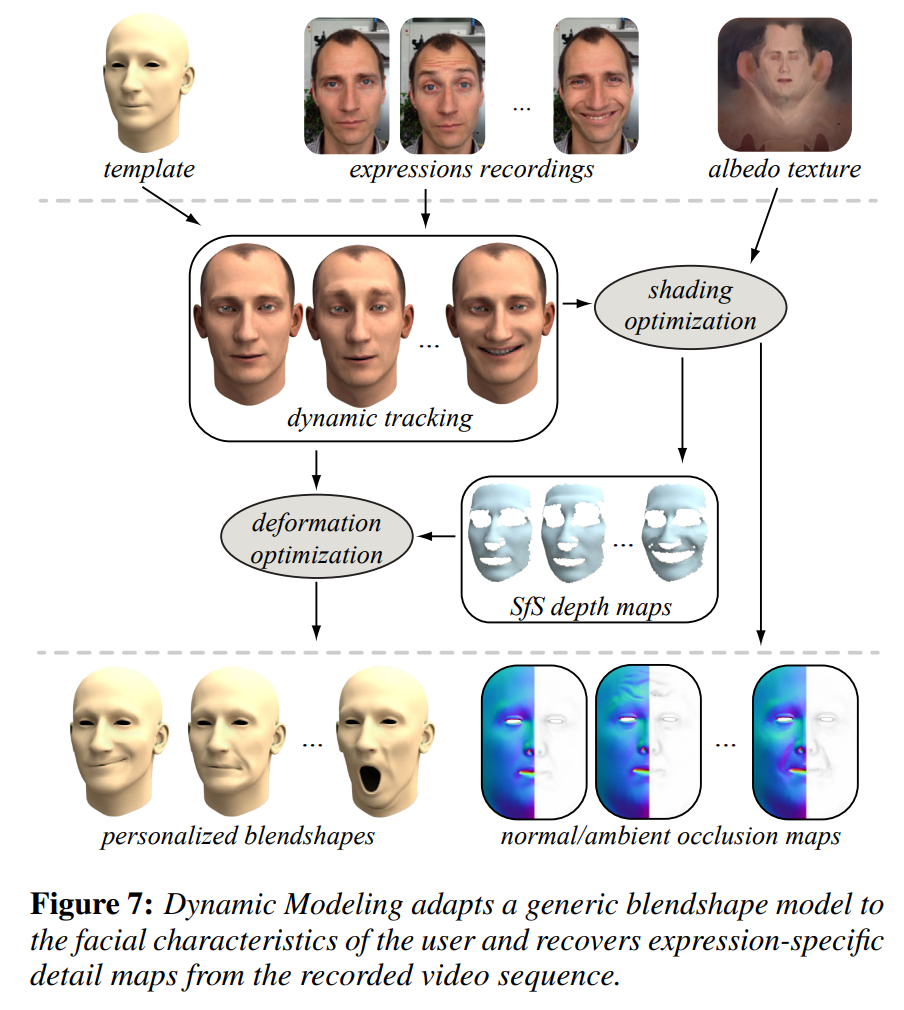
这篇工作中构造blendshape的方法有点类似model transfer,和常规的构造方法有些区别。
一个Blendshape的伴生物就是对各种其他部分(如眼球,牙齿)的建模,我记得我大四实习的时候,我的mentor曾说过一些“贴上去一个预置的牙齿/后脑勺”这种类似的话,我当时听完感觉很抽象,现在看来是我见的少了。例如在2016年的SIGGRAPH,Real-time Facial Animation with Image-based Dynamic Avatars,这篇工作里就单独建模了肩膀,头发,眼球,牙齿:
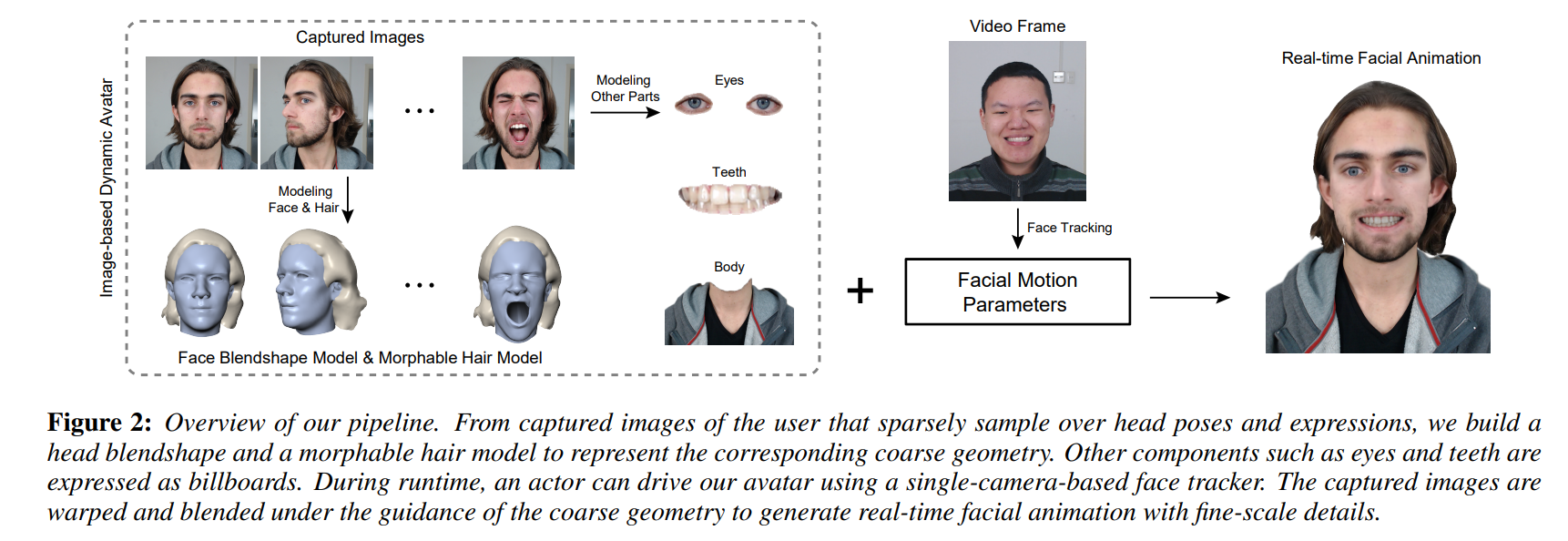
如果用现在的视角来看,除了眼球不用单独处理(FLAME里做了),牙齿,头发,肩膀都应该各自八仙过海各显神通的进行单独建模。
总之,Blendshape是一个很好的思想,简单的线性加和就可以构成表现力丰富的表情表示,这个思想在一些比较新的工作(NeRFBlendshape,3DGS Blendshape)里也有用到。
NeRF-based
在这一章我们转过来关注”单目视频重建可驱动人头“这个事情,一个很明显的不同是,许多关于这个任务的研究工作,并没有沿用上述的”Blendshape“,大抵是因为为了研究目的,其实并不需要”语义可解释性“那么强的先验,BFM和后来的FLAME这类基于PCA或张量分解的3DMM模型完全够用。这个任务旨在通过输入一段单目视频,然后预处理得到单目视频里每帧的3DMM系数,在这些的基础上建立一个高质量的,可驱动的人头。
在许多年里,研究者们致力提升重建的人头的质量。但如一篇很有名的综述3D Morphable Face Models - Past, Present and Future中的teaser所示:

截止到2019年,得到的效果仍然不能说是“photorealistic”的,即使有精细displacement map来雕刻几何,细节的texture map,以及各种photorealistic的loss,甚至是结合了GAN的对抗训练来补充一些高频细节,其结果看上去,还是那么差点意思;另一方面,头发的问题仍然不容易解决,至少没有(以及很难有)一个发型的参数化模型。其中一个原因是,表达的人头都是基于mesh的,这天然具有一些局限性。
后来,在2020年的ECCV上,出现了NeRF,从某种意义上带来了一种范式的改变:“可微”+“体渲染”,这种颇具“量大出货”方式计算出来每个像素的颜色,能带来很好的渲染质量。于是在2021年的CVPR上,NeRFace将3DMM的系数作为condition,训了一个condition NeRF,效果拔群!
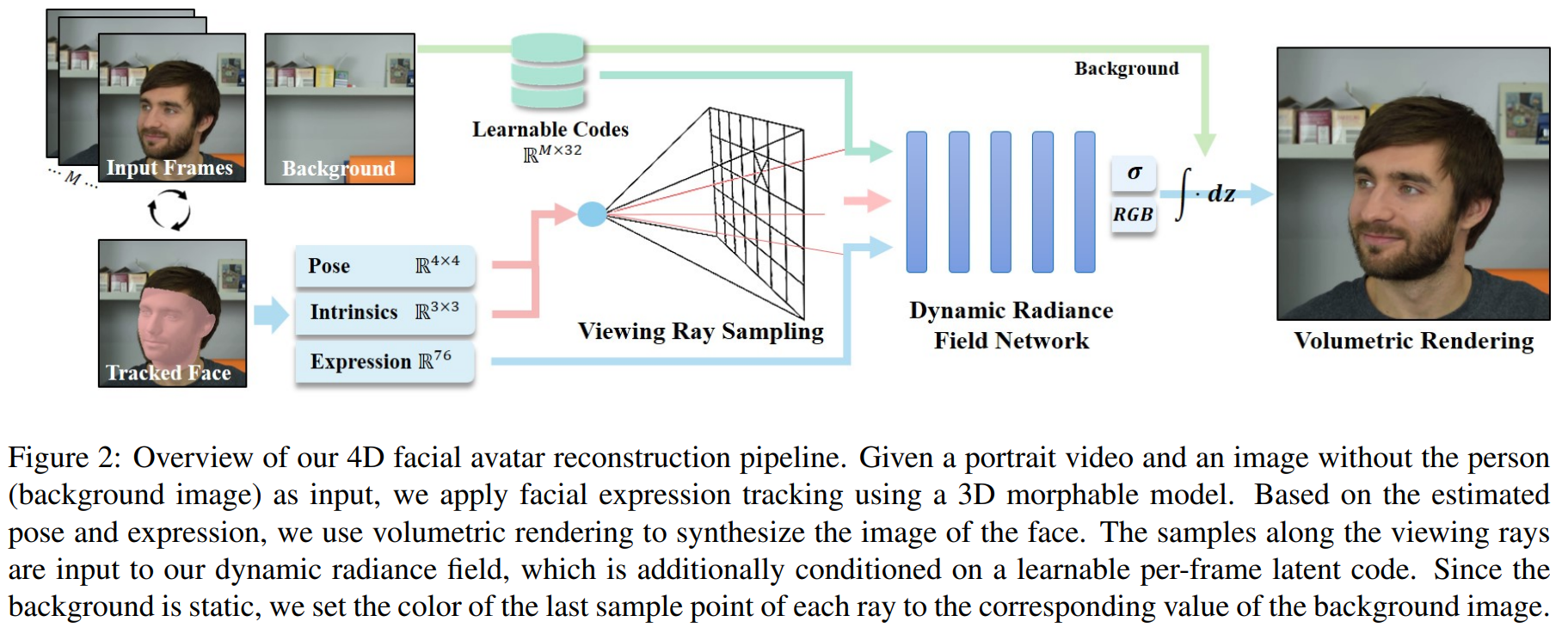
然而NeRFace只是一个很符合直觉的尝试,其本身并没有能够结合人脸本身的几何先验。以及用这种方式做出来的人头,也并没有一般意义上的“几何”,如果尝试提取法线,只会得到类似NeRF中的嘈杂的法线。另外,由于其单纯的应用了朴素的NeRF,其训练速度和推理速度都十分感人。
实际上在那时候,为了实现可驱动的人头,并不是只有3D人头这一条路线。还有一些image-based的方法,可以将输入的图片进行动画化。例如出现在NeRFace中采用的一个baseline:FOMM。这是一个非常有趣的将图片动画化的工作。
所以一个很直接的思路就是应用NeRF中的一些加速技术,例如Instant-NGP。2023年CVPR中的INSTA
就是这么做的:
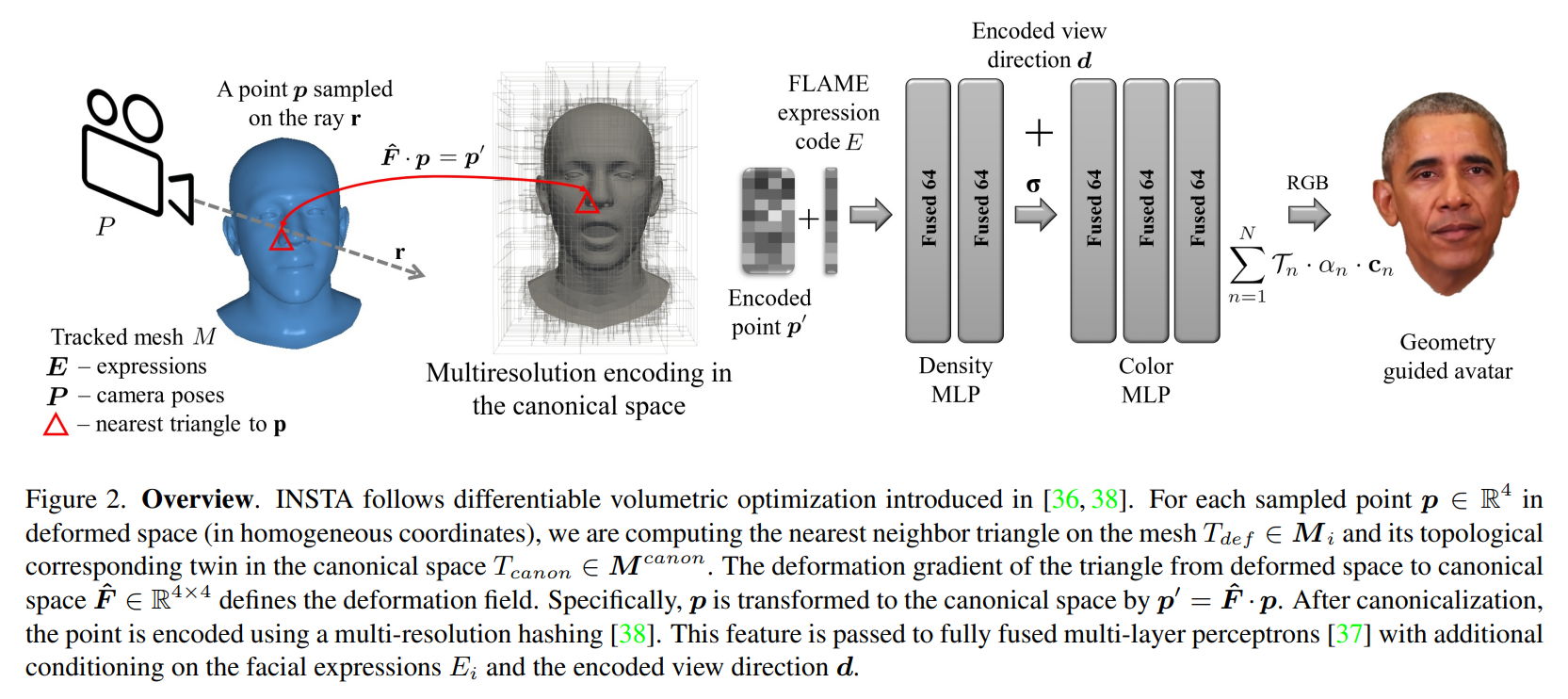
INSTA采用Instant-NGP的表达方式,间接的利用了人脸的几何先验,应用了一些经典的技术(AABB,BVH)来进一步加速了。其还是在canonical的基础上,用MLP来进行变形。然而这样的变形其实也没有用到3DMM的参数化。
所以一个矛盾在于,预处理得到每一帧的FLAME系数本身可以恢复一个不错的在特定表情和姿态下的几何,我们称作“deformation space”,然而在NeRF的范式下,这个先验很难被利用。NeRF本身需要作光线投射,这个操作本身是“backward”的。换句话说,投射一根光线,然后在体积结构里采样再积分,可以看作是一次“测量”。我们在发射光线时,很难有一个类比3DMM之于mesh的机制,来让投射的光线的积分产生一样的变化(从对应于canonical space里的某些triangles变为deformation space里的triangles)。
2022年CVPR中的IMAvatar设计了相当复杂的机制来作这件事,这篇工作同时实现了两点,一个是让表征出的avatar也可以像3DMM被输入参数驱动,另一个是实现了从“deformation space”里进行优化。这个工作实现起来非常的复杂:
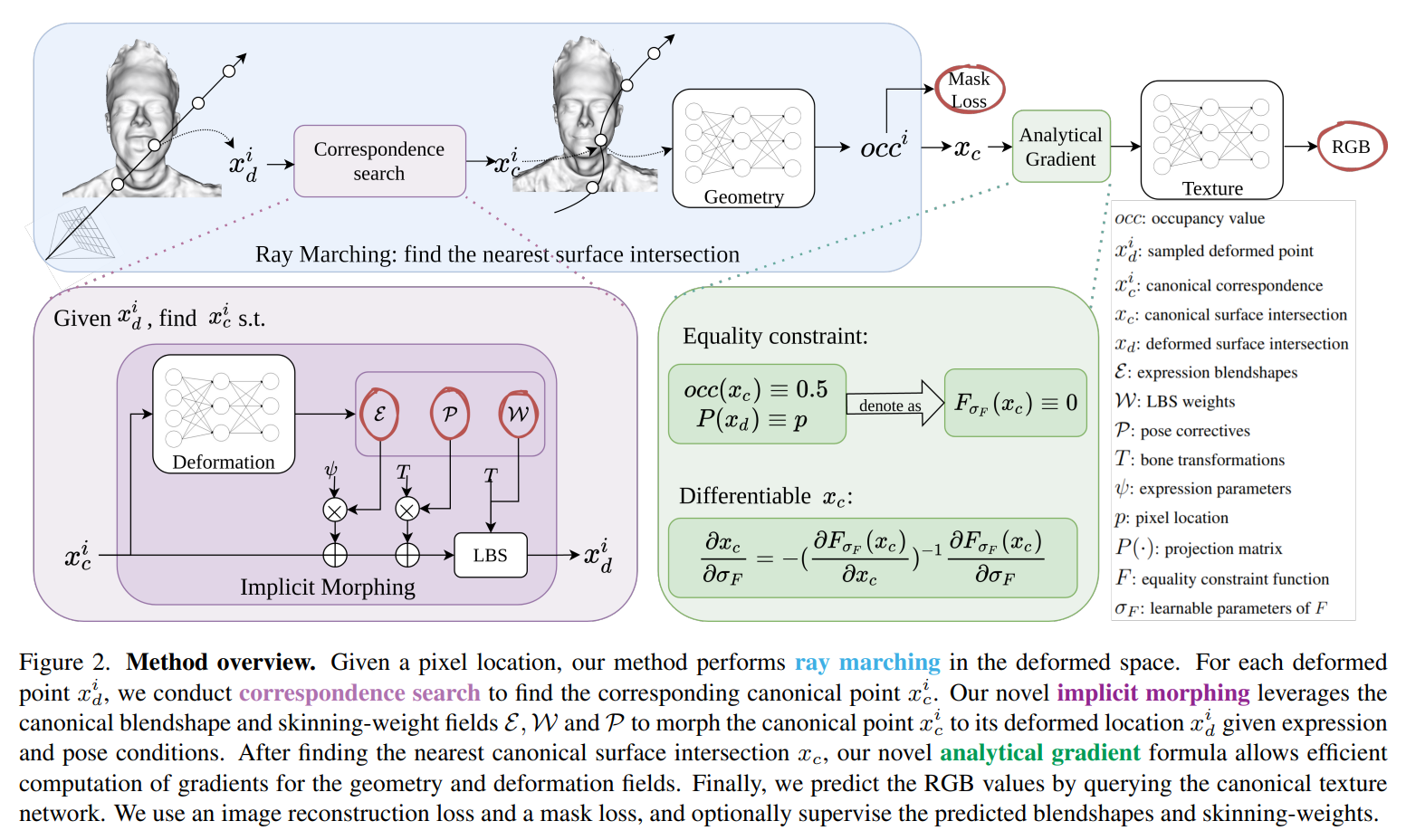
首先注意到我们谈论的mesh,其实都是离散的,而在这个操作里,我们需要“连续的”mesh,它的表现形式其实是SDF。IMAvatar首先应用了SNARF的研究成果,将deformation space表示成一个连续的SDF,用NN建立一个SDF中$x_d$与$x_c$的映射,所以“Correspondence Search”其实指的是SNARF里的一个环节。然后IMAvatar同时用NN参数化了FLAME的LBS方程中的基($\mathcal{E},\mathcal{P},\mathcal{W}$)。
于是,整个过程即是:我们在NeRF里架好相机位置和姿态,发射出一条光线,然后在这条光线上进行采样,得到若干$x_d$(即直接在deformation space里进行采样),此时是有这一帧的表情$\psi$,姿态$\theta$的,所以可以由FLAME来作inverse skinning来得到一个初始的$x_{c}^{\left( init \right)}$,即“如果是FLAME,在这个$\psi$和$\theta$下,会是哪个$x_c$这么变换到当前的$x_d$的”。然后由于在这里还学习了一个deformation network来输出估计的$\mathcal{E},\mathcal{P},\mathcal{W}$,所以接下来会从刚才的$x_{c}^{\left( init \right)}$作为初始点,来找到”如果是这个deformation network输出的$\mathcal{E},\mathcal{P},\mathcal{W}$,那么会是哪个$x_c$“,之后会拿这个$x_c$作为geometry network和texture network的输入,然后来表达这个人头。
所以如果细看这个过程,作者是尽力在NeRF框架下想办法用上了deformation space里的先验,只不过整个管线确实是复杂,以及作者在代码里老喜欢写闭包,让过程更加复杂了。
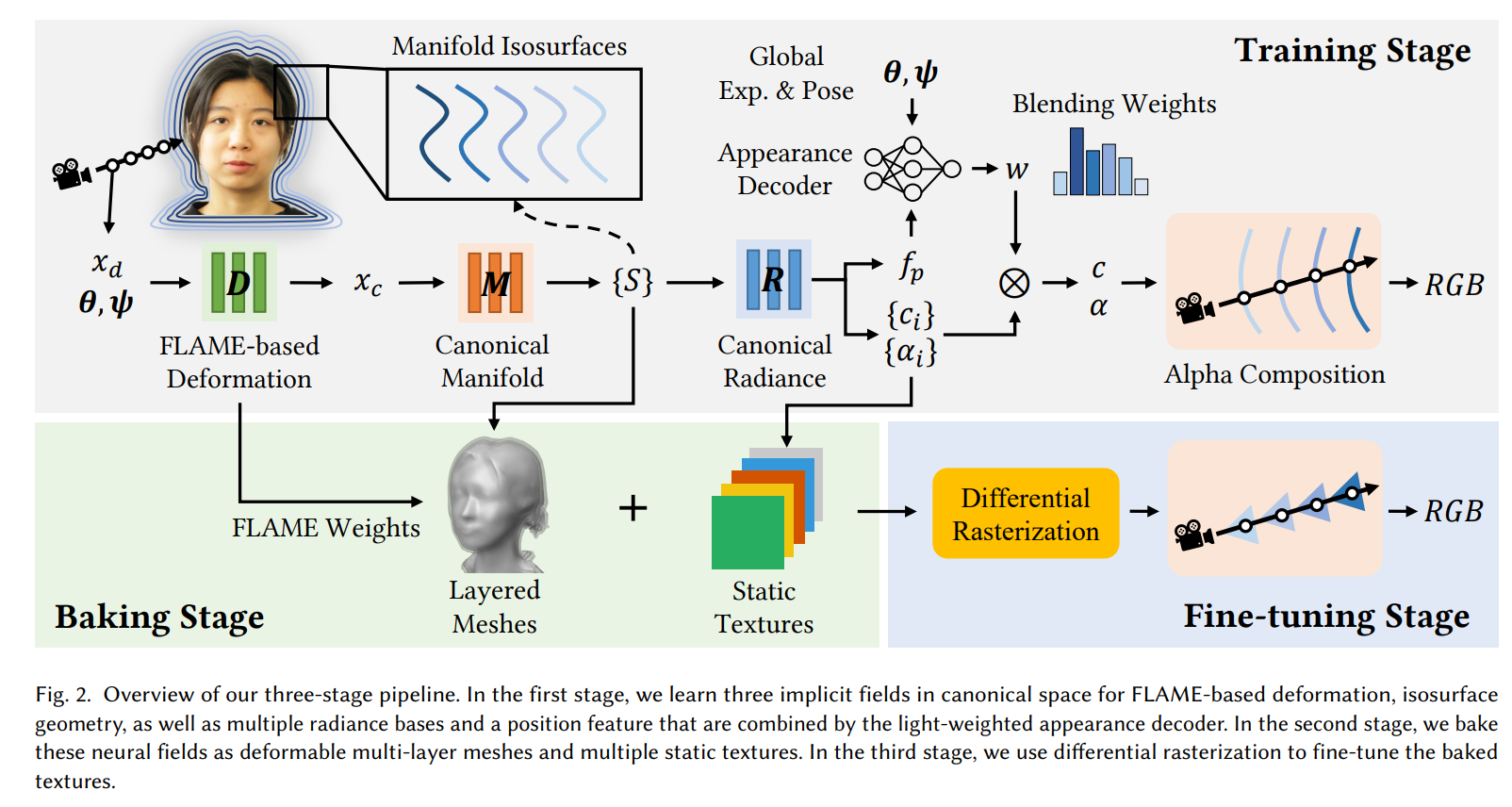
在NeRF的框架下,基本就是这两种方式了,一个从canonical到deformation,另一个从deformation到canonical。后续主要是一些在效率上的改进,例如SIGGRAPH Asia 2023里的BakedAvatar,其沿用了IMAvatar的deform方式,然后后续做了baking,把表达形式从NeRF换成多层mesh,提高了渲染效率。
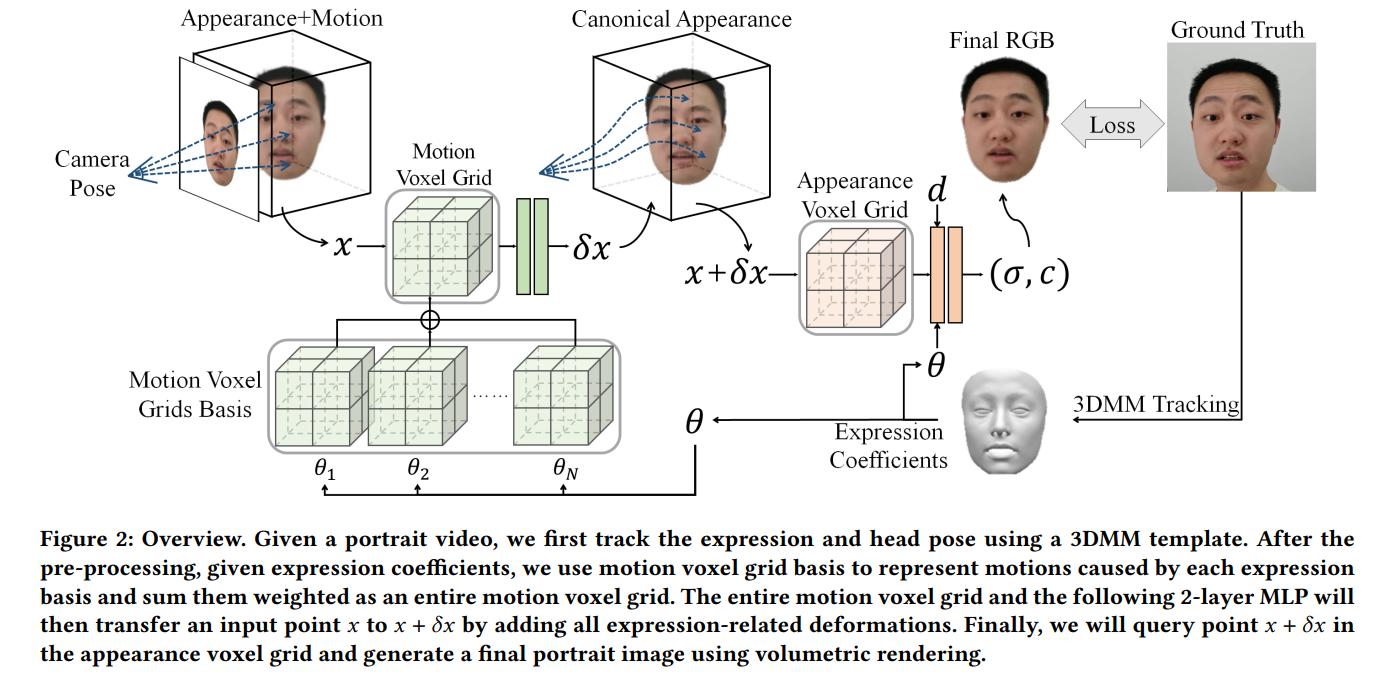
以及一些基于Grid-based的方式来进行加速的,如AvatarMAV,NeRFBlendshape:
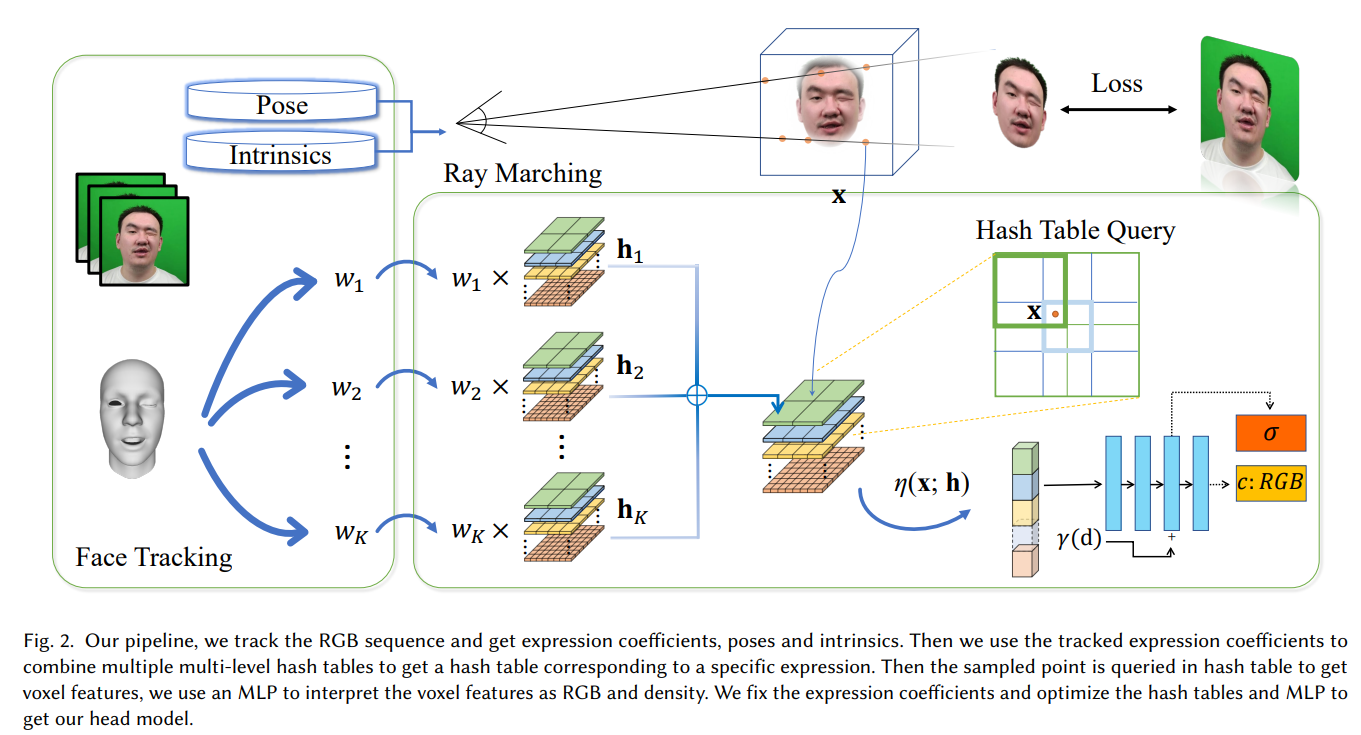
总的来说,这些基于NeRF的方法,大幅提高了重建人头的效果,至于优缺点,我们会在下面介绍完Point-based的方法后再进行讨论。
Point-based
基于点的渲染其实也是图形学里的一个课题,只不过没有那么为人所知。实际上在3DGS出现之前,IMAvatar的作者是用更朴素的splatting来做了这个任务的,即CVPR2023里的PointAvatar:
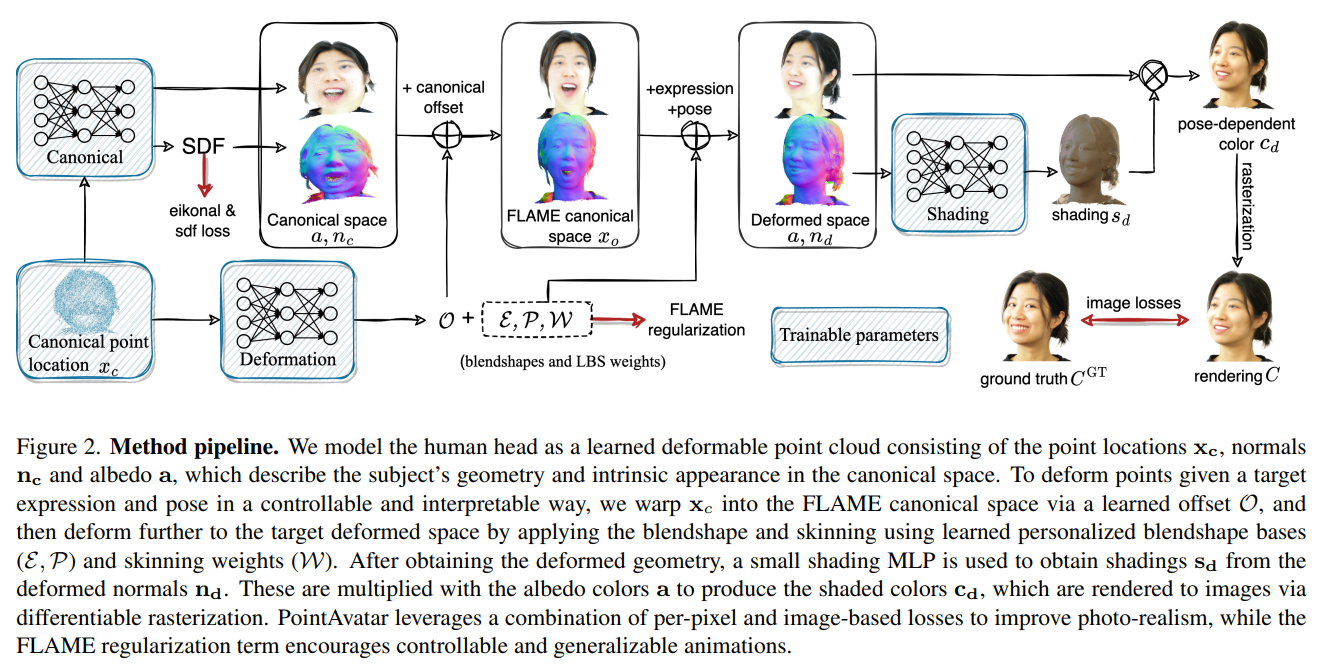
以后来人的视角,我推测作者当时其实已经意识到了用NeRF做人头的某些局限性。但我进一步推测作者当时为了”有领子的人头“的执念,以及一些效率上的权衡,才设计了这样的管线。为了说明白这一点,我们先来介绍PointAvatar的管线:首先在所谓canonical space里在一个球面上随机采一些点$x_c$,得到一个球面点云。然后用一个canonical network来预测albedo和SDF,这里要预测SDF其实是为了估计法线,albedo是为了给出漫反射下的颜色。
然后$x_c$会用一个deformation network来预测$\mathcal{E},\mathcal{P},\mathcal{W}$,就像IMAvatar一样,同时给一个偏移$\mathcal{O}$,来将$x_c$移到更像FLAME人头的空间中。然后通过用可学习的$\mathcal{E},\mathcal{P},\mathcal{W}$进行LBS,人头就被驱动到了deformation space里了,这里作者还额外用了一个NN来预测阴影$s$,然后用$c=a\cdot s$来简单建模颜色。
在训练过程中,点会按照一个固定的scheduler来进行增加,增加的方式是在已有的点附近以一个半径随机采样。然后会删除一些没有投影到任何一个像素上的点以及一些透射率过低的点。
现在我们来谈论一些幕后的事情,在PointAvatar中,splatting是通过PyTorch3D的API来做的。每个点的尺寸$r$是固定的,其不透明度$\alpha$被显式定义为符合平方反比$\alpha=1-d^2/r^2$。所以跟3DGS相比,这个表达方式是很简单的,每个小球的半径,不透明度和位置都是不可优化的。然后透射率定义为:
在PyTorch3D的API中,$T_i$可以很容易被返回,可惜在3DGS的原版实现中,这是困难的。以及,PointAvatar需要相当多的显存,我推测这是由于PyTorch3D中实现可微点渲染是用自动微分实现的,这与3DGS直接把每项的结果推出来比,带来了相当大的开销。
另外一个要讨论的是:为什么要这么设计?PointAvatar要从一个类球面的点云中,先变形为一个像FLAME的,为什么不直接在FLAME上采样?我觉得一个原因是作者想通过NN导引的变换(canonical network)来构造法向量,毕竟点云的法向量估计起来并不容易。另一个是,如果从FLAME上采,那些有领子甚至有大量躯干的avatar将不是很好重建,例如名为soubhik的数据集:

所以这其实牵扯出了,如果用基于点的方式,一些参数化模型覆盖不到的地方就没法直接建模。这个问题在NeRF-based的方法里虽然也有,但暴露的不那么明显。一个很暴力的解决方案是直接把衣服看作背景,或者干脆训练的时候用分割掉衣服的图像来训练。但PointAvatar的作者可能还是在这方面决定坚守些完美主义。
IMAvatar和PointAvatar的一作是同一个人,Yufeng Zheng。这两篇工作非常的厉害,很具有启发性。以及她录制了一段自己的单目视频用于研究目的(dataset yufeng),成为了一个这一小任务里的benchmark之一,我在毕业设计的时候最开始也是从这个数据集开始训练和调试的,然后看的时间长了,遂转成颜粉了。
后来这些,当3DGS出现以后,就都不是什么问题了。在Look Closely at Head 3,我们分析了一些基于3DGS的单目视频重建人头任务,核心就是把splat按某种方式绑定到mesh上,然后随着LBS的驱动,这些splat的位置自然而然的发生变化,然后光栅化,就能有非常好的效果。这种方式可以完全借助参数化人脸的先验,不需要像NeRF-based的方法一样绞尽脑汁的构造,同时高斯点的也具有丰富的表达能力,弥补了单纯用mesh和NeRF,一些细节(例如发丝)的缺失。所以,当有了GS以后,从单目视频中重建人头获得了更有力的工具,算是为这一任务给出了一个圆满的答案。
“GS在手,论文我有。”——佚名
“With Gaussian Splatting in tow, my thesis will glow.”——Anonymous
在这里我们就不详细展开那些用3DGS从单目视频中重建人头的工作的细节了,同时我们扩大一下讨论的范围,变成结合3DMM与3DGS来表征人头。我们可以根据mesh被绑定的方式汇总出下面的这样一个表格:
| method | work |
|---|---|
| Affine Transformation | GaussianAvatars Gaussian Head & Shoulder HeadStudio |
| UV / Barycentric Coordinate | FlashAvatar PSAvatar GGHead SplattingAvatar |
| Blendshape | 3DGS Blendshape |
这三种方法很难说谁比谁好多少,各自有可取之处。值得注意的是,一些工作往往需要学习关于GS属性的残差,例如$\varDelta s,\varDelta r,\varDelta \mu$等,与一般的炼丹情景时不同,在关于GS的任务里,这些残差属性的学习往往需要特殊的初始化(最后一层的权重和偏置一开始都置零),甚至需要用一些技巧控制一下数量级。以及GS的属性本身也是有“激活”(activated)一说的,例如rotation本身储存的并不是一个归一化的四元数,是在用之前自行用norm作为“激活函数”的;以及scale因为数量级的原因,是转化在对数轴上来训的,所以要$\exp \left( \cdot \right) $;不透明度$o$是用$\mathrm{sigmoid}\left( \cdot \right) $来约束到$(0,1)$的,所以残差$\varDelta$是加到激活前还是激活后,也是一个trial and error的事情。
回过头来看从单目视频中重建的这件事,其实有许多槽点,例如一般情况下重建不出完整的360°人头;不能做到audio-driven,限制了其应用(不过那个算是另一个任务了);对不同的person需要重训;以及受单目条件的限制,表情和人头形状往往没能很好的解耦,所以几乎所有单目重建的工作为了让拟合的效果更好,都会学习一个基于输入的表情系数的函数,这其实让不同的人头具有了不同的“表情空间”(基底都不一样了),而这一点在做cross reenactment的时候就会暴露出弊端。如果有能力采集多视角视频,那么预处理的时候就可以更好地解耦表情和形状,带来更好的效果。然而采集多视角视频需要昂贵的设备,普罗大众肯定不会这么做。
目前大众喜闻乐见的在人头上的应用,往往是那种用diffusion力大飞砖出来的,例如一个应用软件call annie,以及VASA-1。其实人们并不是那么关心“你这个是不是3D的?”,只要屏幕上的人头能按照预想的说话,摇头,同时有很好的质量。跟这种范式下的产物相比,单目重建只能孔乙己般的声称“我这个更能person-specific”,然而没准人家那些大号pretrained如果做一些例如DDIM-inversion的事情,效果也几乎一样好。从这种角度看,做这种条件下单目视频重建,多少有些一厢情愿的意思。
在最后,我们讨论一下NeRF-based的方法和Point-based(其实就是3DGS)在表征人头上的一些优劣。首先最明显的是,3DGS比NeRF快。即使有些用了3DGS的工作同时结合了一些MLP进去,基于3DGS的也还是快,因为gemm的优化下,MLP/CNN的时间开销反而没那么大。但在NeRF里,像素和像素之间没有那么强的“关联”,比如假设在一个视角下,NeRF计算出的两个像素具有不同方向的梯度,那在MLP的高维空间里,这两个方向的需求并不会“冲突”,即如果想train,总能train出个东西。这在一些3D-aware GAN的工作里是非常必要的特点,因为这样才适配于炼丹的方法论。然而如果把3DGS换进去,一个splat影响的可能是个多个像素,一群splat溅射的结果互相耦合,这会带来一些困扰。以及如果用3DGS作为可微渲染的部件,放入炼丹框架(如GAN,diffusion)中,容易某个属性(例如scale)一崩,剩下的属性都连着崩,然后再也回不来正常量级。
另外,在NeRF的设定下,“留不留衣领/肩膀”是一个无所谓的事情,然而在3DMM+3DGS的情况下,这一点就比较微妙了,可以选择单独建模,可以选择让mesh“长”到肩膀上去(通过学习一组新的blendshape bias)。然后对于一些细节的刻画,例如发丝,3DGS有着很自然的表示的方法:“斜的,细的,高斯核”,这某种意义上比NeRF-based的方法用positional encodeing逼出来的高频表示要更可控一些。
最后,基于3DGS来建模人头,某种意义上作为之前用mesh来显式建模的精神续作,也会单独建模一些棘手的,非刚性的部分。例如GaussianAvatars手动补加了牙齿的面,FlashAvatar将FLAME嘴部的面连在一起,让口腔处可以嵌入一些splat, 3DGS Blendshape单独用一个静态的GS来建模口腔,MeGA设计了一个机制来解耦头发与人头。
End
这篇blog从经典的人头mesh采集开始,介绍了在参数化人头中常用的Blendshape机制,同时对基于NeRF和3DGS的单目视频重建人头方法进行了简要的分析,最后将讨论的范围扩大到表征人头,记录了一些自己的理解。


