Between Extrinsics and Intrinsics


阅读数: 次   
文章目录
  1. EG3D
  2. NeRF-PyTorch
  3. 3DDFA
  4. 3D Gaussian Splatting
  5. Lie theory of rotations
  6. End

​ “说书人或许会留恋，但故事毕竟有终点。”

​ “相机系统是一个非常令我头疼的事情，我真的很不擅长这个。”

​ 这篇blog是为了“解析”我遇到的一些仓库中的关于相机系统的代码，这么说可能会很奇怪，因为对于比较专业的人来说，这些根本不能算是问题；但由于我是一个只知道PyTorch的文盲，所以这对我来说，是问题，而且很大。

​ 哪怕在这里语境下的“相机”只是最最简单的理想模型，但即使这样，想修改与其相关的代码对没有受过相关训练的人来说还是有些困难的。尤其当需要对相机系统做一些更“定制化”的操作时候，浅显且不够直接的理解就不太能支持继续推进下去了。

​ 我曾将我的窘况诉说给一位学长，他听完非常震惊“不是吧这都不会”（此处自动脑补“虾头座椅电脑”表情包）。他建议我去回炉重造，去看GAMES101或者洋人的公开课。但我没看几分钟就睡着了，睡醒以后我不禁陷入思考：在那个田园的时代，人们或许是通过看一些关于3DV的课或者书从而掌握了其理论基础，然后可能在OpenCV，OpenGL，Unity等库里进行实践，由于那些库写的都很严谨，所以很快就可以将理论与实际匹配上，然后熟悉这一套东西。

​ 但在2024年，在新时代图形学的背景下，我如果再这么做可能有点缘木求鱼了。所以有没有一种顺应新时代的掌握这些的方法呢？大部分DL+3D项目都是缝来缝去，作者可能自己都不知道我的coordinates convention是什么。所以我觉得更适合新时代的方法是头铁的去硬看那些代码，把这些都看明白了，自然就会了。

​ 这篇blog以这样的组织进行：

  • 会先从EG3D的相机系统出发，这里提供了一种构造相机位姿矩阵（下文简称为c2w）的方法，同时可以让我们对NeRF-based的方法有个可视化的认识。在这个部分我们可以对c2w有一个直观的认识。
  • 然后我们会返回去解决初学NeRF-PyTorch时不太关心的那些相机代码。相当于对上一部分的练习，同时温习一下透视投影。
  • 之后我们会阅读PanoHead的预处理部分，其基于3DDFA_V2。这个预处理本质上和EG3D的预处理做的事情是一样的，只是这个基于3DDFA的预处理被PanoHead的作者整理的更自洽。在这套代码里，我们会正好遇到相机外参（下文简称为w2c）和c2w的关系。这一套预处理比较复杂，涉及正交投影和一些琐碎的数字图像处理。相当于某种程度的过关考核。
  • 再然后我们会解读3D Gaussian Splatting的代码。这个如今大热的显式表示可以让我们复习一下在NeRF里常常被忽略的透视投影。
  • 最后，我们会从更深入的角度下讨论在代码中经常出现的旋转操作，用李群和李代数的视角进行一些浅显的讨论，来从某种意义上“升华”一下我们的理解。

​ 所以这篇blog至少需要读者大概了解上述工作，可能咿呀学语般的玩过其中一些的代码，大概能稀里糊涂的说出什么相机内外参，刚体变换之类的名词，对情况有大致的了解。（天哪这简直是我.jpg）

EG3D

​ 在EG3D那一套代码里，我们经常可以看到c2w是这么被召唤出来的，先是有一个地方定义了一个：

1
camera_lookat_point = torch.tensor([0, 0, 0.2], device=self.device)

​ 然后在需要c2w的地方，会有：

1
2
cam2world_pose = LookAtPoseSampler.sample(3.14/2 + 2 * 3.14 * frame_idx / num_frames, 3.14/2,
camera_lookat_point, radius=2.75, device=self.device)

​ 类似这样的操作，然后就神奇的得到一个有效的4×4矩阵了。例如：

1
2
3
4
5
>>> cam2world = LookAtPoseSampler.sample(math.pi/4, math.pi/4, torch.tensor([0, 0, 0]), radius=2.5)
>>> tensor([[[ 0.7071, -0.3536,  0.6124, -1.5309],
             [ 0.0000, -0.8660, -0.5000,  1.2500],
             [ 0.7071,  0.3536, -0.6124,  1.5309],
             [ 0.0000,  0.0000,  0.0000,  1.0000]]])

​ 现在我们关心LookAtPoseSampler.sample的实现，这个实现展示了一个很经典的用look, at, up构造相机外参的方法。EG3D中，整套代码是在这样的一个settings下：

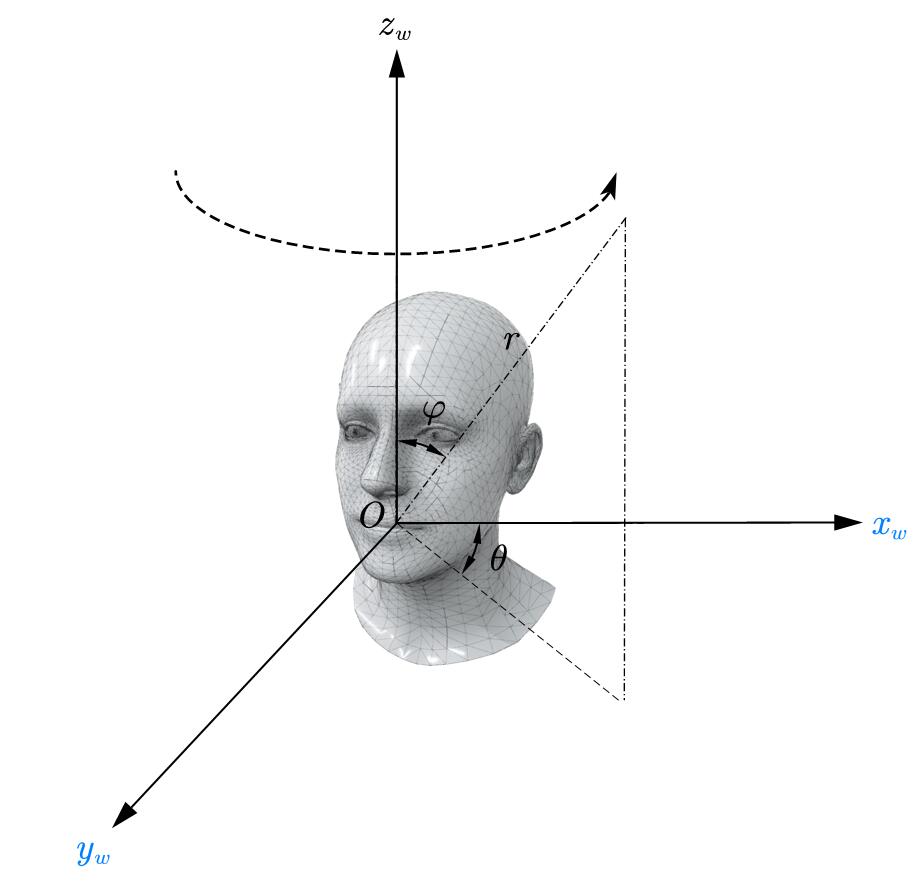
​ 这里用的是左手系，不过影响不大。整套代码的实现是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class LookAtPoseSampler:
    """
    Same as GaussianCameraPoseSampler, except the
    camera is specified as looking at 'lookat_position', a 3-vector.

    Example:
    For a camera pose looking at the origin with the camera at position [0, 0, 1]:
    cam2world = LookAtPoseSampler.sample(math.pi/2, math.pi/2, torch.tensor([0, 0, 0]), radius=1)
    """

    @staticmethod
    def sample(horizontal_mean, vertical_mean, lookat_position, horizontal_stddev=0, vertical_stddev=0, radius=1, batch_size=1, device='cpu'):
        h = torch.randn((batch_size, 1), device=device) * horizontal_stddev + horizontal_mean
        v = torch.randn((batch_size, 1), device=device) * vertical_stddev + vertical_mean
        v = torch.clamp(v, 1e-5, math.pi - 1e-5)

        theta = h
        v = v / math.pi
        phi = torch.arccos(1 - 2*v)

        camera_origins = torch.zeros((batch_size, 3), device=device)

        camera_origins[:, 0:1] = radius*torch.sin(phi) * torch.cos(math.pi-theta)
        camera_origins[:, 2:3] = radius*torch.sin(phi) * torch.sin(math.pi-theta)
        camera_origins[:, 1:2] = radius*torch.cos(phi)

        # forward_vectors = math_utils.normalize_vecs(-camera_origins)
        forward_vectors = math_utils.normalize_vecs(lookat_position - camera_origins)
        return create_cam2world_matrix(forward_vectors, camera_origins)

​ 最开始，是先构造出球坐标系下的$\theta$和$\phi$。然后，我们会根据半径$r$给出相机的位置camera_origins：

​ 由于$x_w$和$y_w$与标准的右手系下的球坐标系不太一样，所以这里变成了$\pi-\theta$。之后，我们会计算一个forward_vector，这个其实就是LookAt。通过将输入的lookat_position和camera_origins的差归一化，我们会得到一个从相机位置指向look at位置的一个方向。然后就进入了create_cam2world_matrix(forward_vectors, camera_origins)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def create_cam2world_matrix(forward_vector, origin):
    """
    Takes in the direction the camera is pointing and the camera origin and returns a cam2world matrix.
    Works on batches of forward_vectors, origins. Assumes y-axis is up and that there is no camera roll.
    """

    forward_vector = math_utils.normalize_vecs(forward_vector)
    up_vector = torch.tensor([0, 1, 0], dtype=torch.float, device=origin.device).expand_as(forward_vector)

    right_vector = -math_utils.normalize_vecs(torch.cross(up_vector, forward_vector, dim=-1))
    up_vector = math_utils.normalize_vecs(torch.cross(forward_vector, right_vector, dim=-1))

    rotation_matrix = torch.eye(4, device=origin.device).unsqueeze(0).repeat(forward_vector.shape[0], 1, 1)
    rotation_matrix[:, :3, :3] = torch.stack((right_vector, up_vector, forward_vector), axis=-1)

    translation_matrix = torch.eye(4, device=origin.device).unsqueeze(0).repeat(forward_vector.shape[0], 1, 1)
    translation_matrix[:, :3, 3] = origin
    cam2world = (translation_matrix @ rotation_matrix)[:, :, :]
    assert(cam2world.shape[1:] == (4, 4))
    return cam2world

​ 之后需要从forward_vector出发，建立一组正交的基向量。具体的做法是，先给定一个参考向量up_vector$[0, 1, 0]$，通过计算up_vector与forward_vector的叉乘，可以得到一个正交于forward_vector的right_vector，然后再计算forward_vector与right_vector的叉乘，就可以得到一个与forward_vector和right_vector都正交的up_vector。这一组正交向量自然的形成了一个正交阵，描述了一个$\mathbb{R}^3$上的旋转变换。然后再和平移矩阵相乘，就得到了最终的结果。这个过程有点类似施密特正交化。

​ 这个矩阵很直接的描述了如何从相机坐标系下的某个点，变换回世界坐标系。我们可以带入$[0, 0, 0, 1]$，$[1, 0, 0, 1]$这两个特殊的点：

​ 可以看到，这个变换将原点平移到了相机位置，将$x$轴方向的单位向量旋转到right_vector的方向，并且也平移了一个相机位置。所以实际上$\vec{r}$就是$x$轴被旋转后的样子，$\vec{u}$是$y$轴，$\vec{f}$是$z$轴。真是一个有用的矩阵。

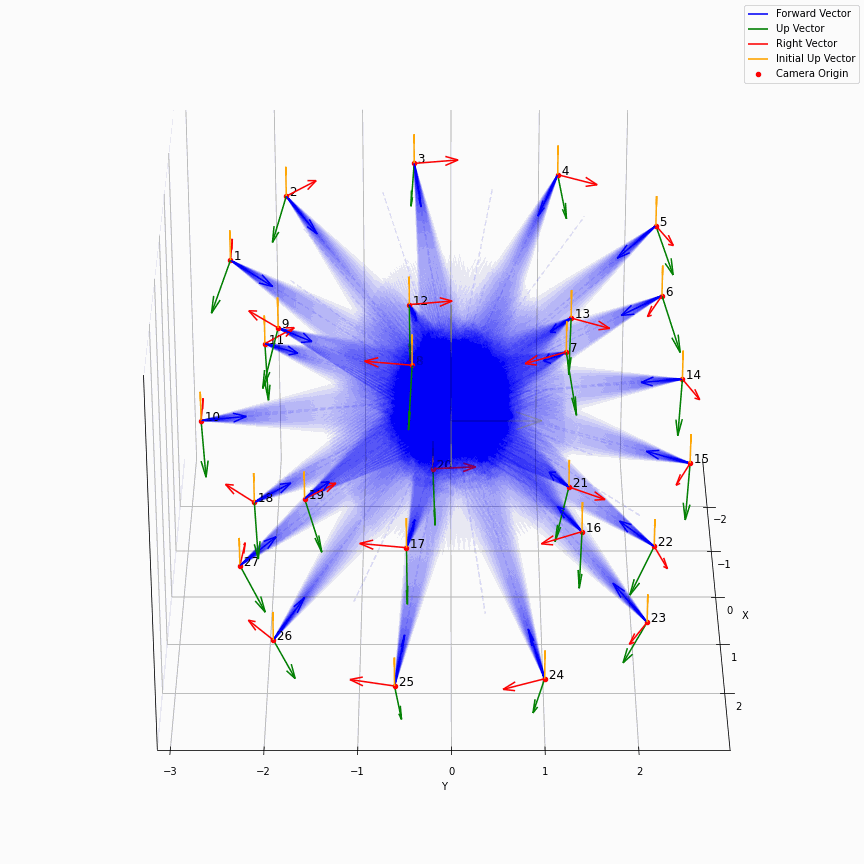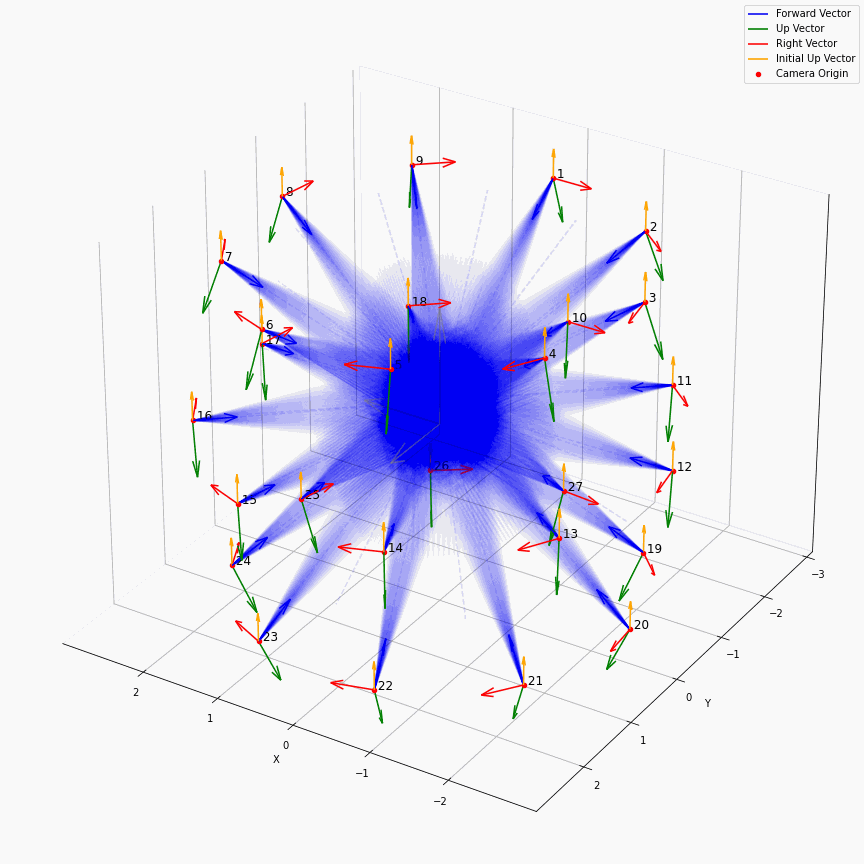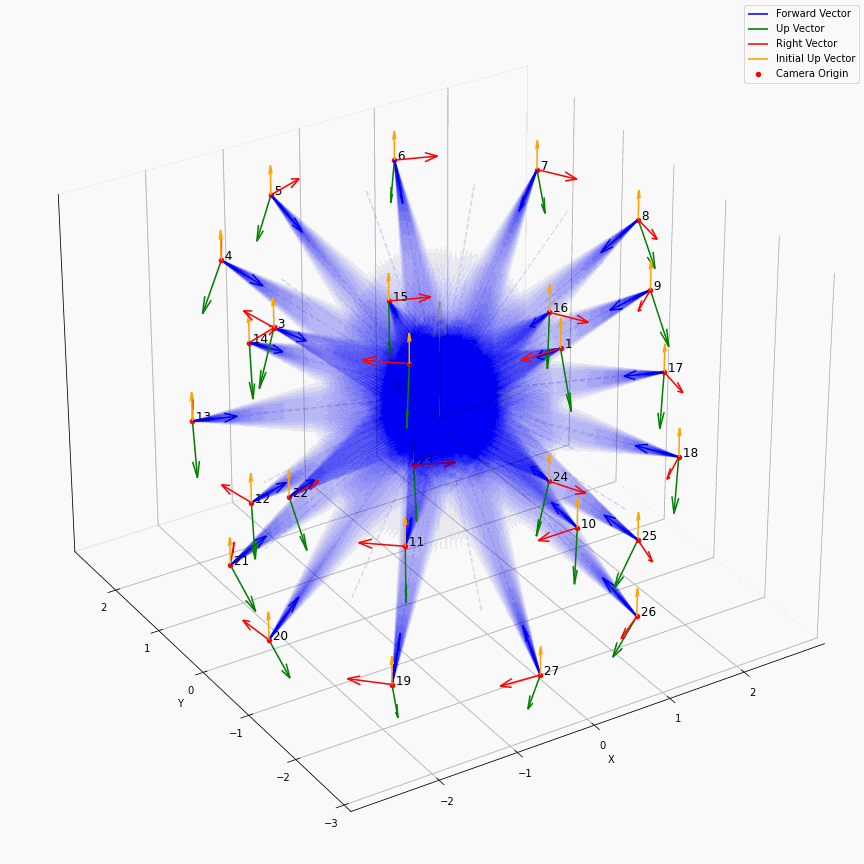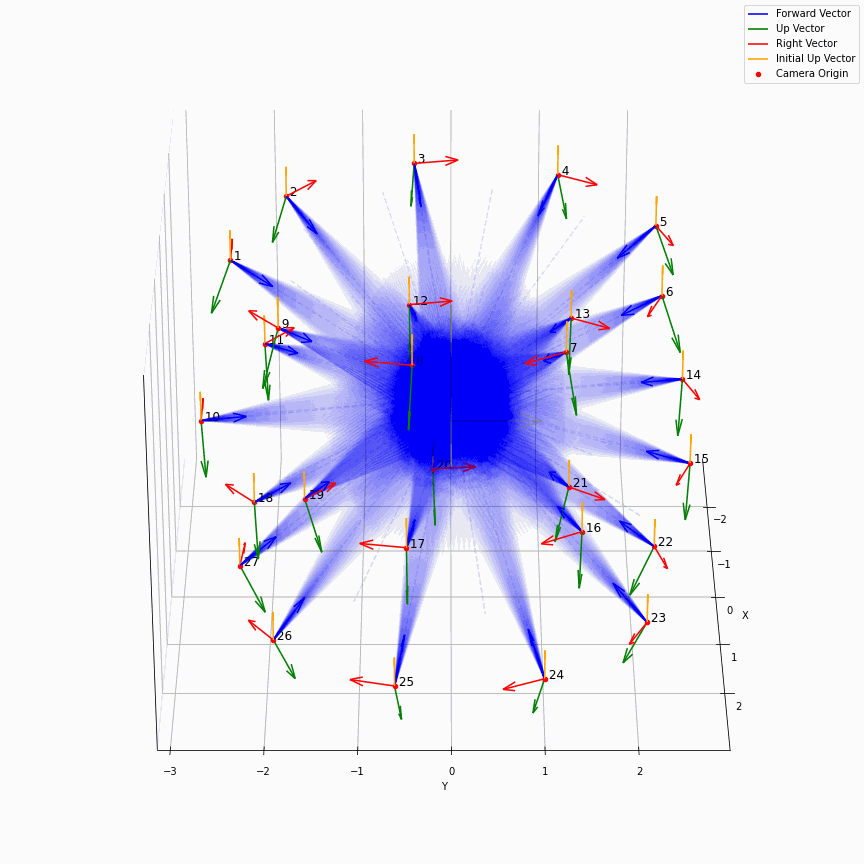
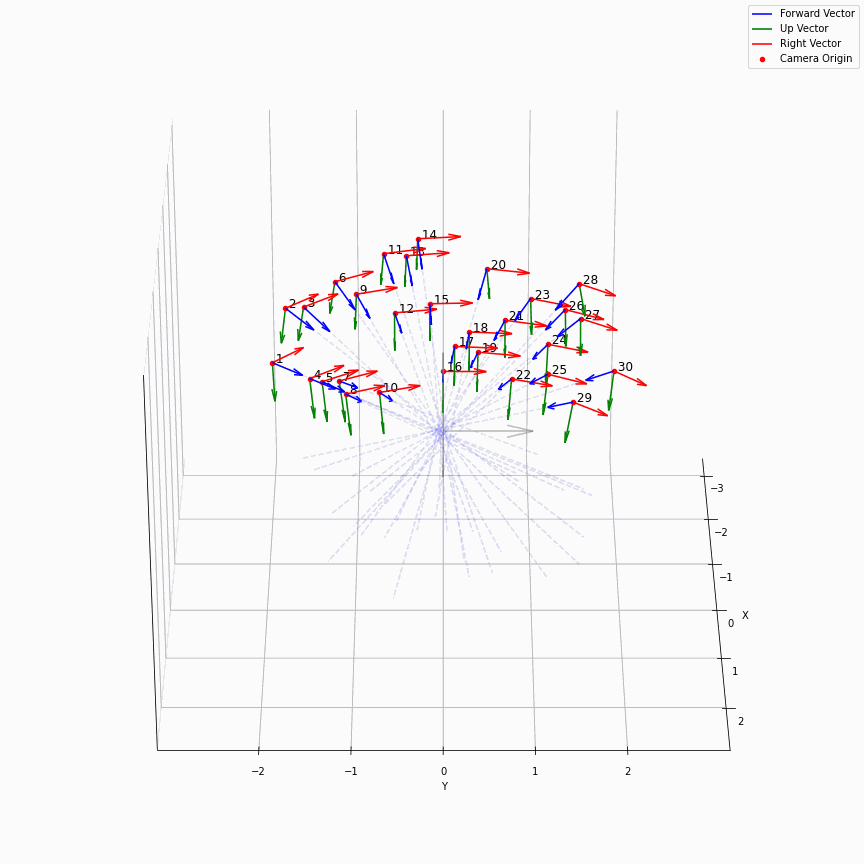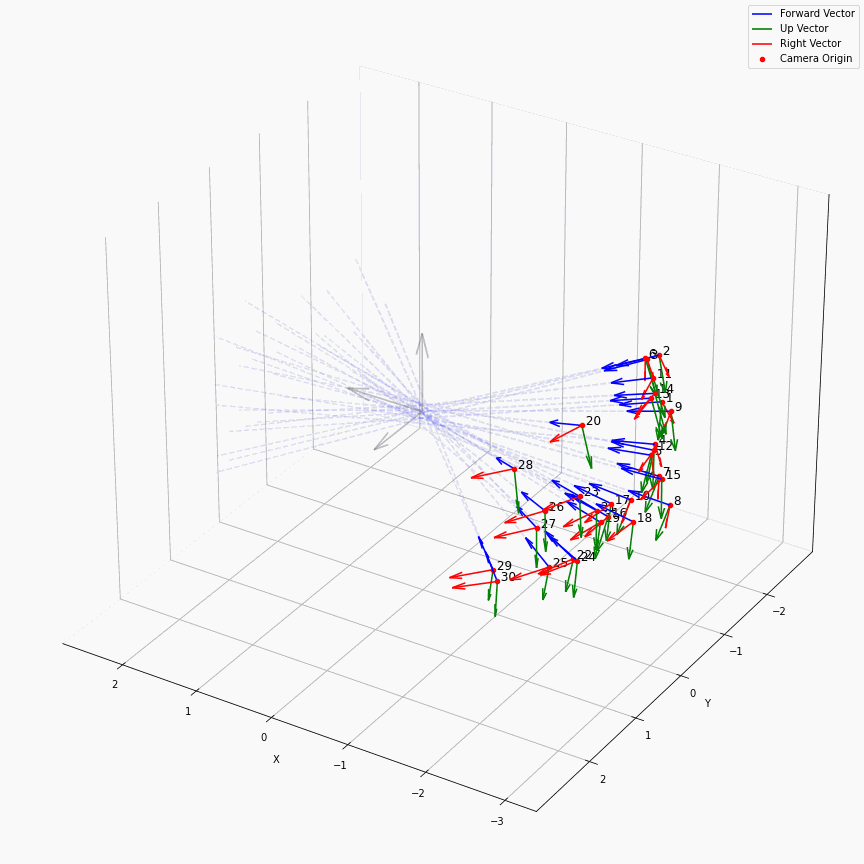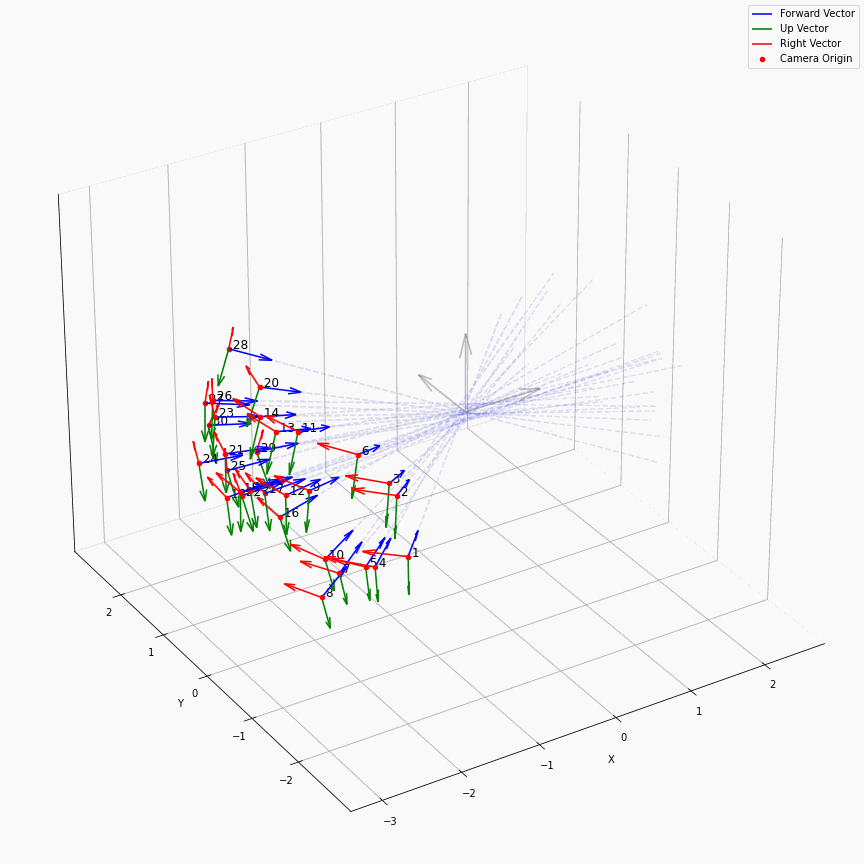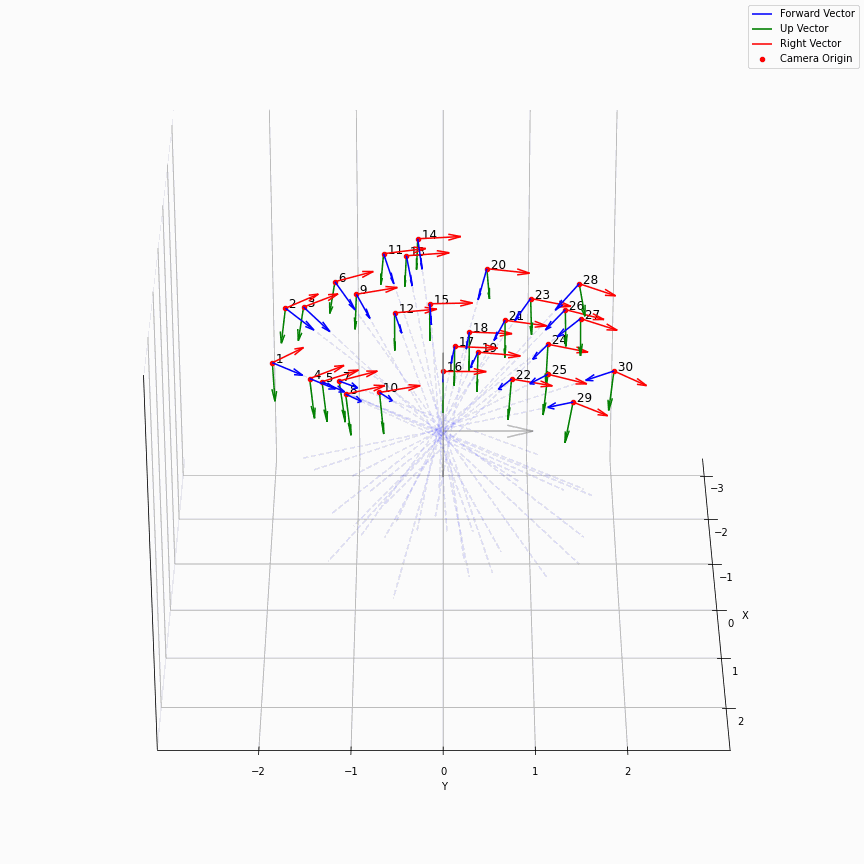
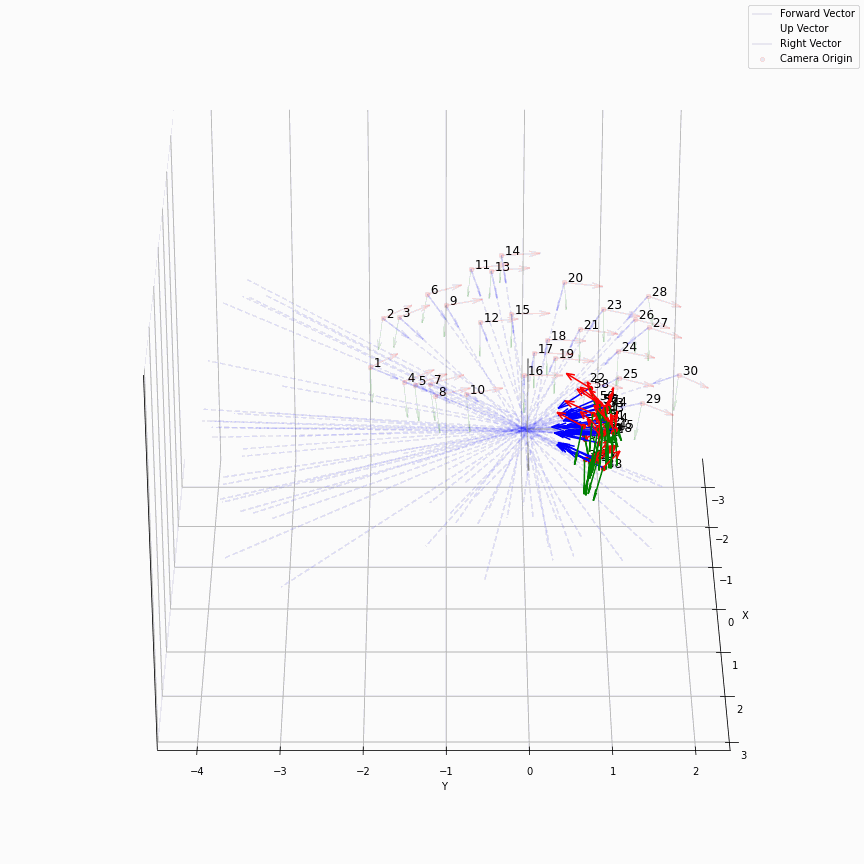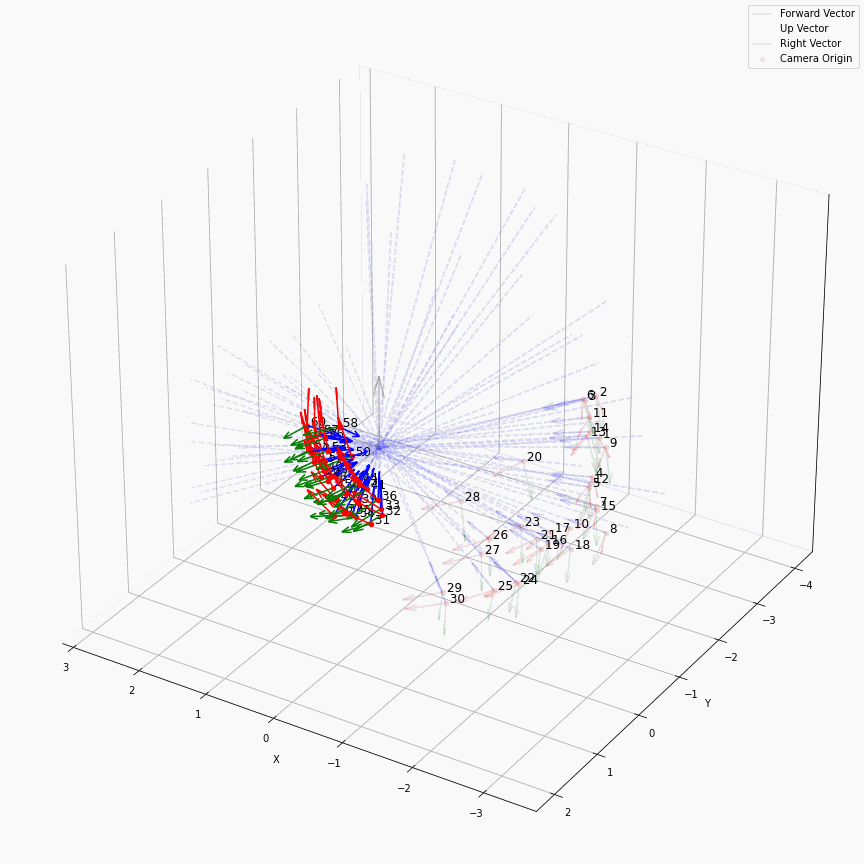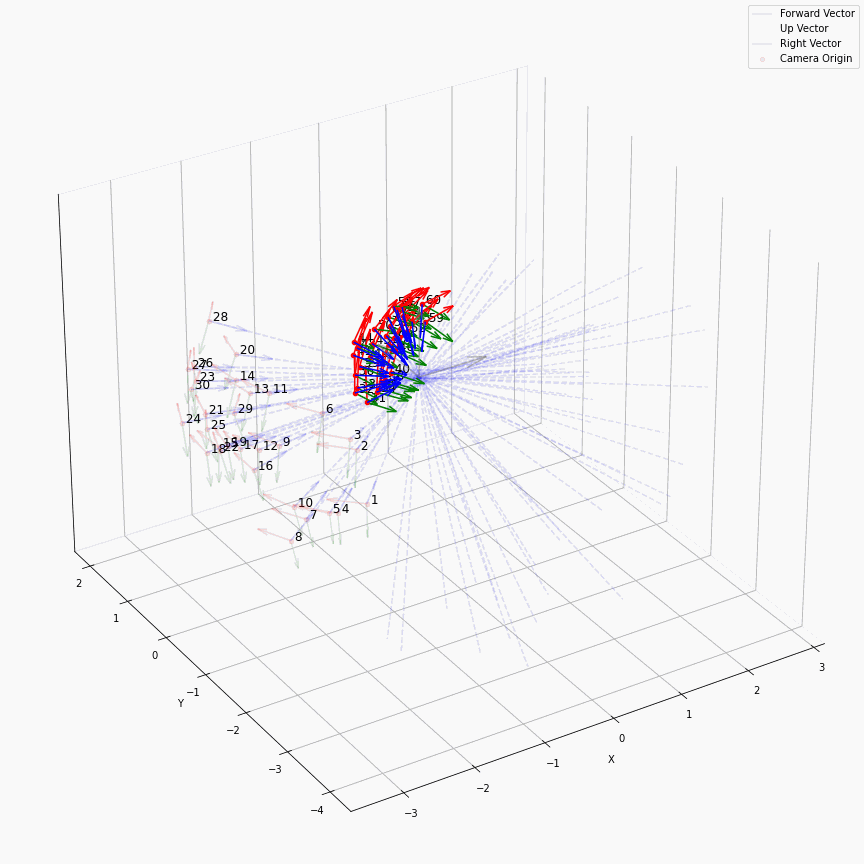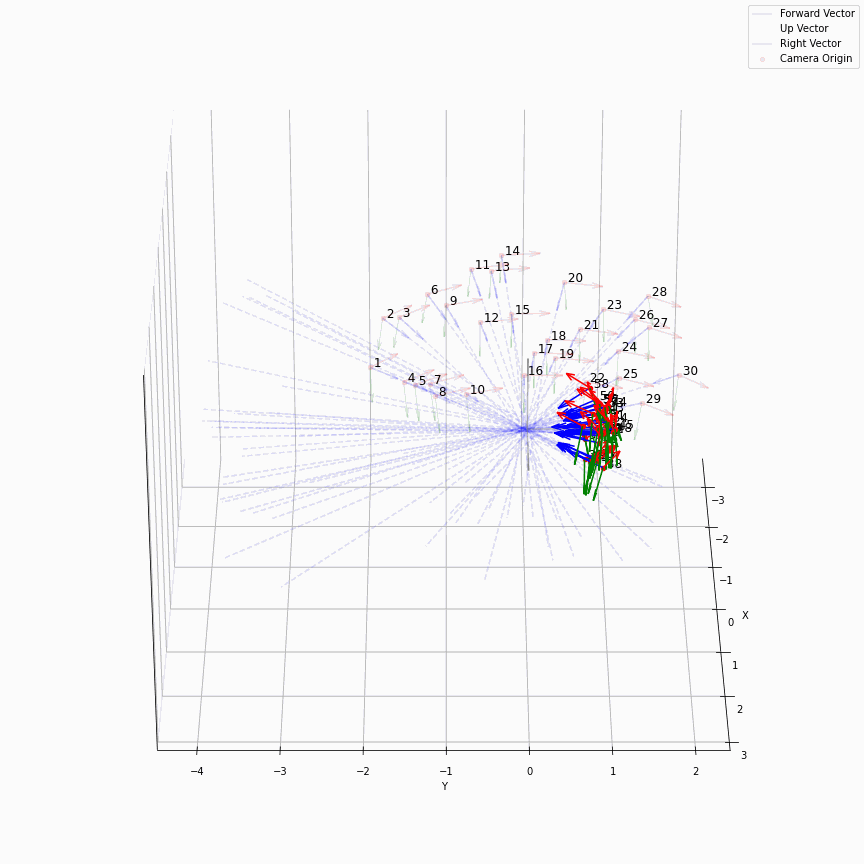
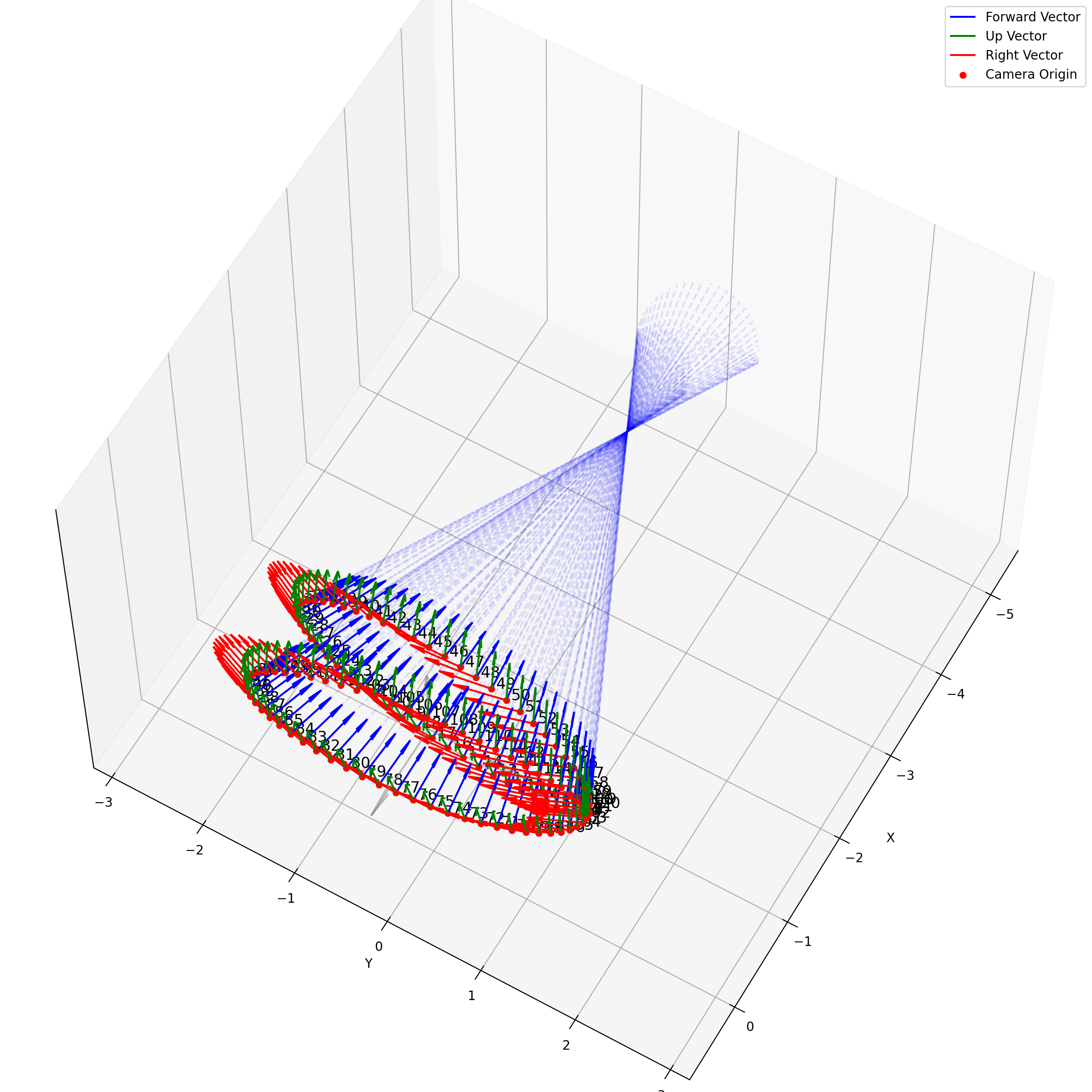
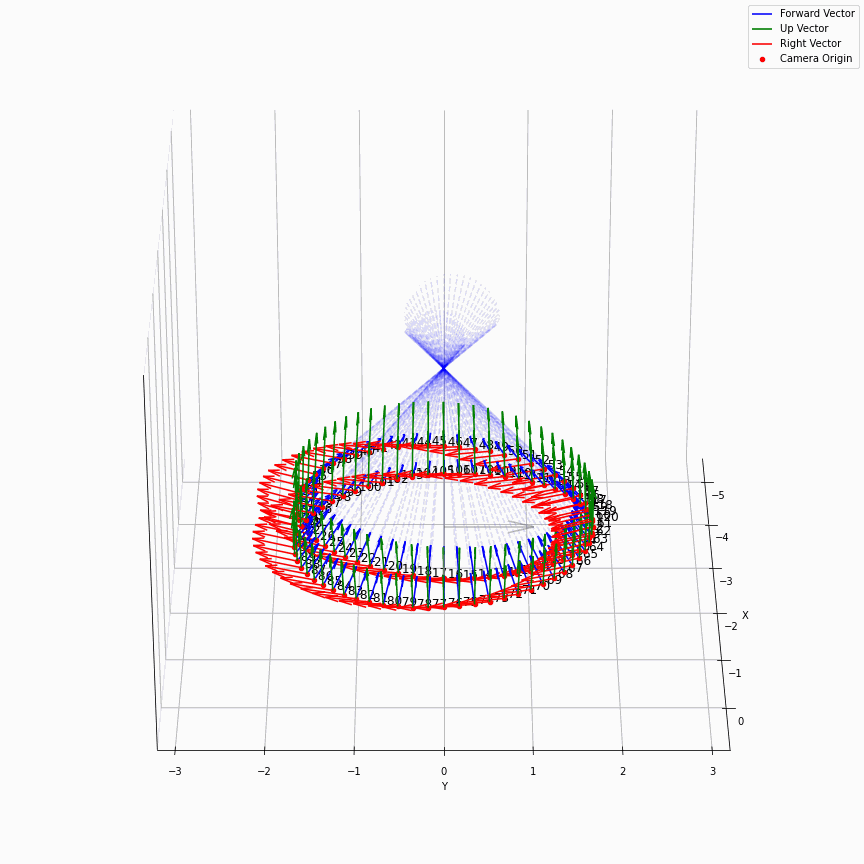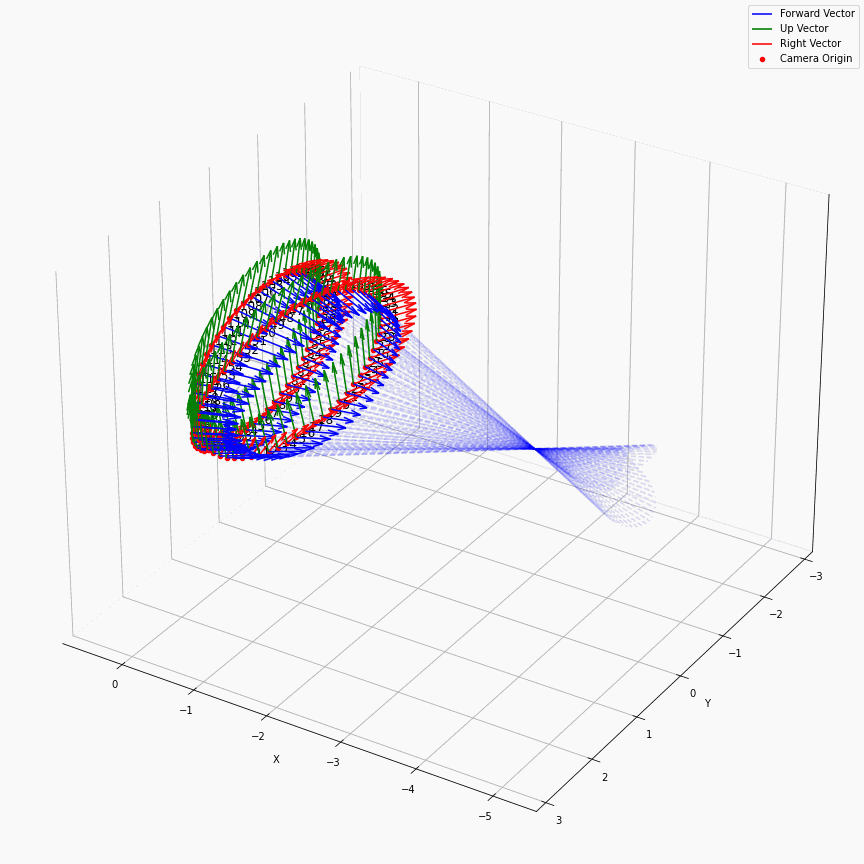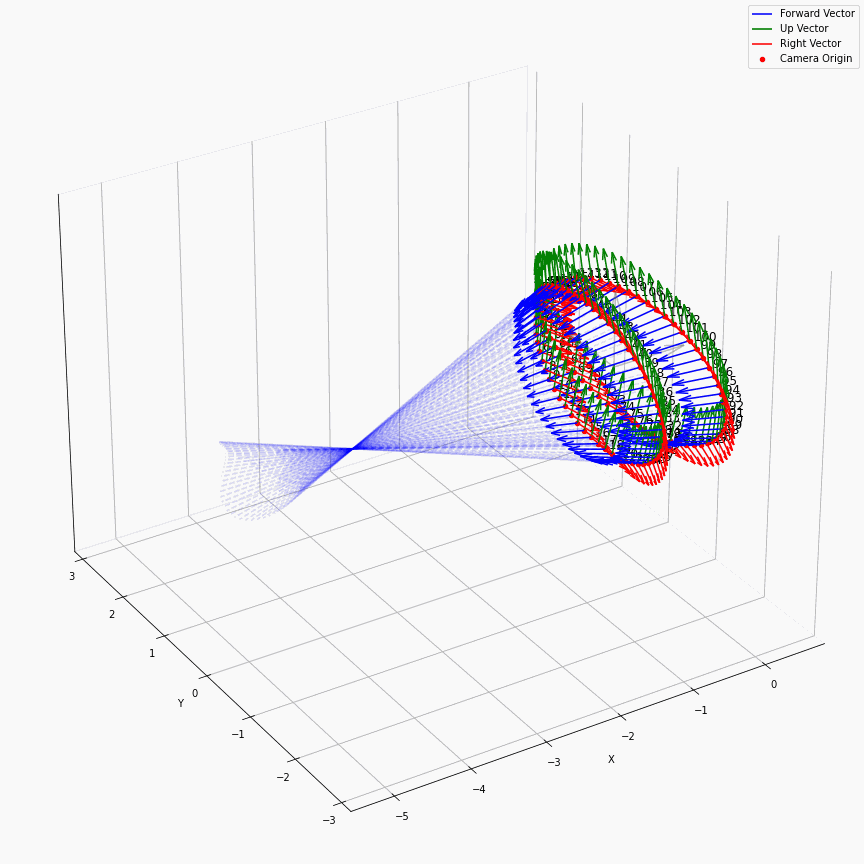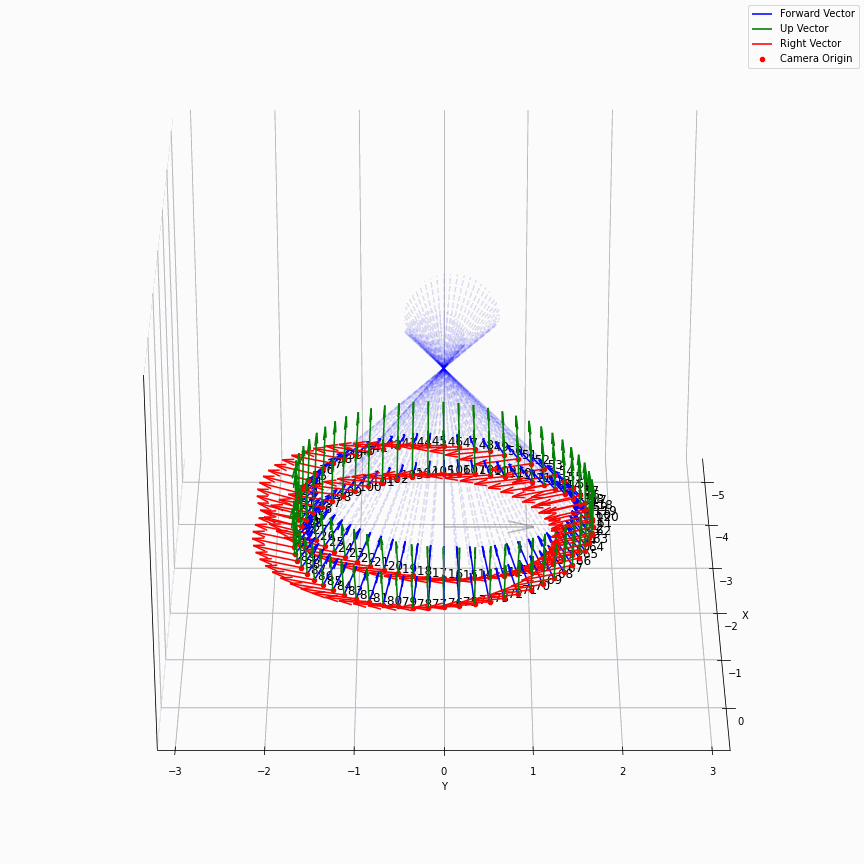
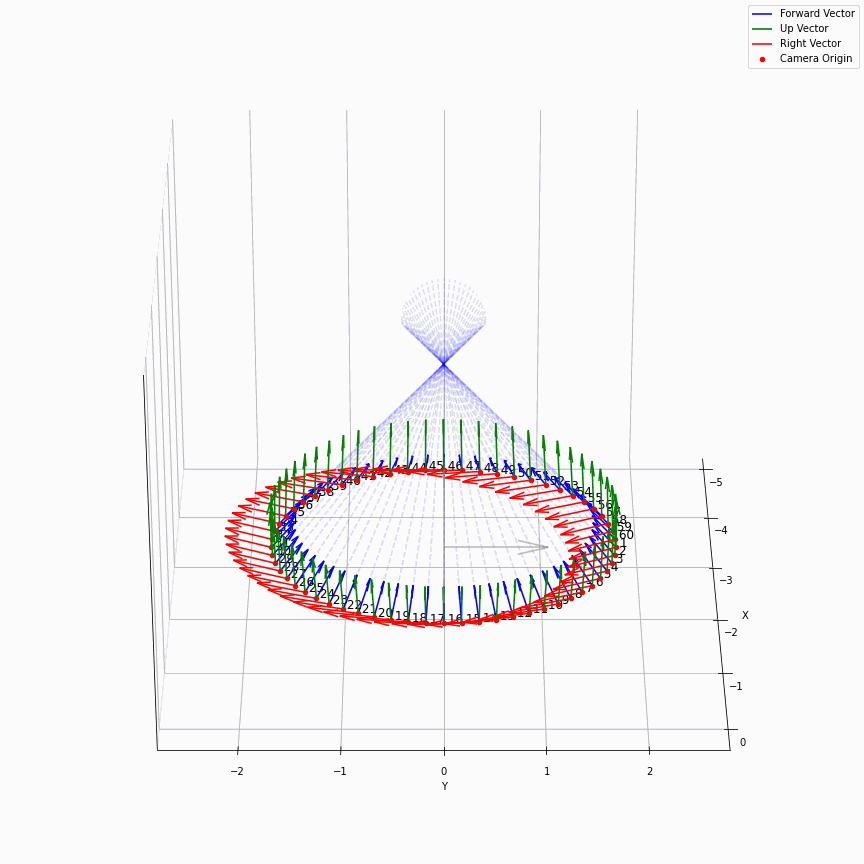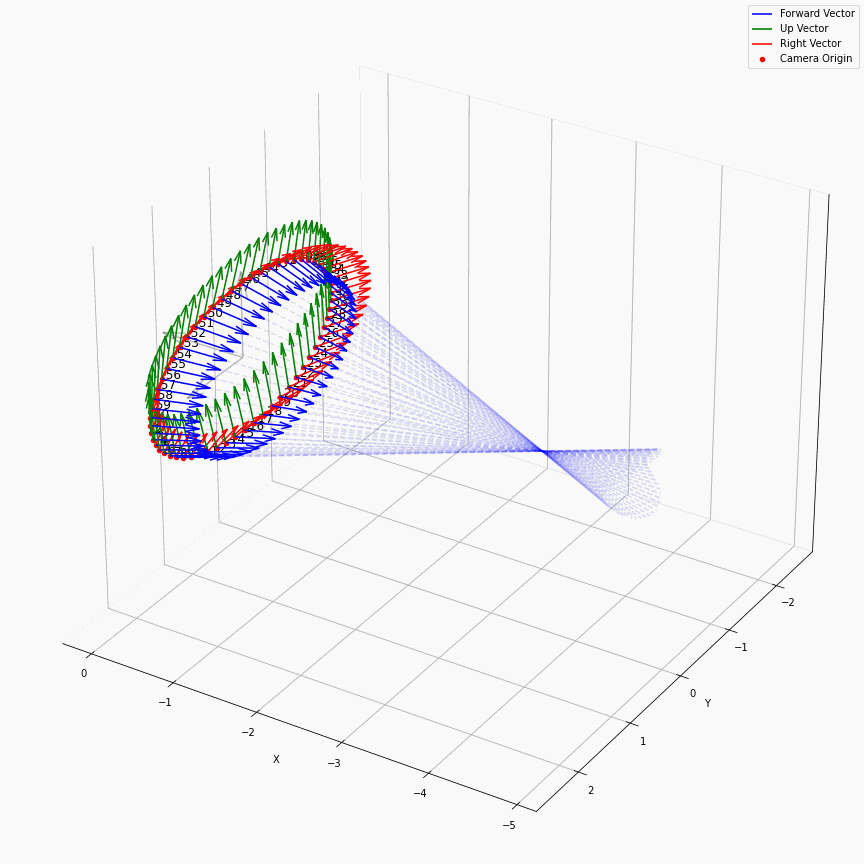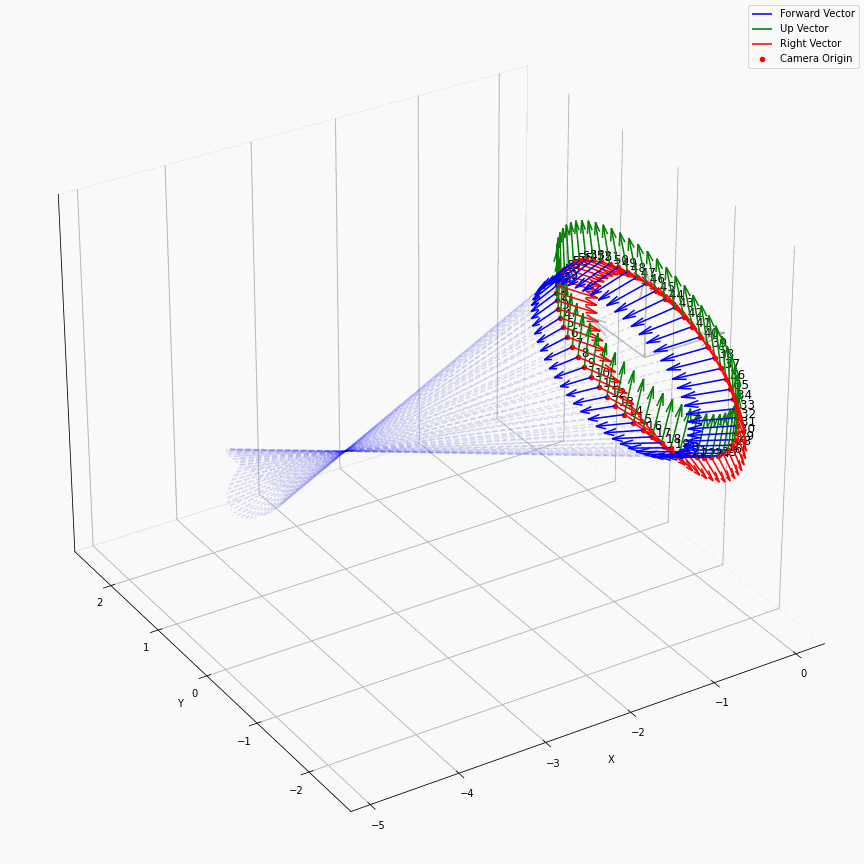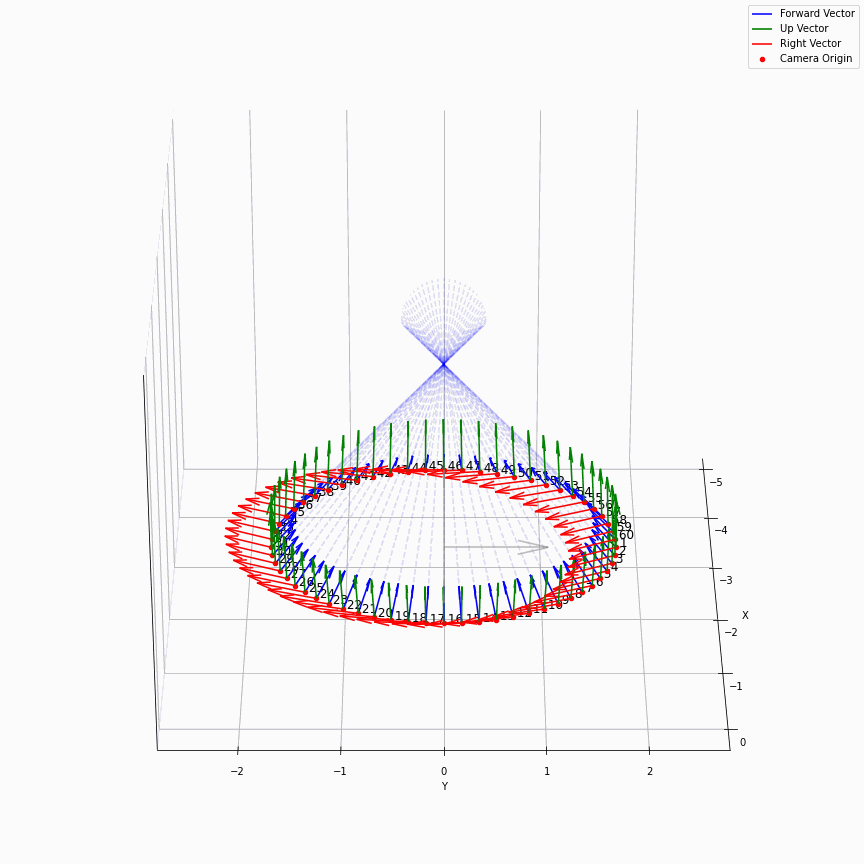
​ 相机外参实际上是这个矩阵的逆，即w2c。从坐标系变换来理解c2w和w2c，总是有些困难的。更倾向于用这种方法理解了c2w，然后将相机外参当作这个矩阵的逆就好了。可以做一些简单的可视化来加深印象，下图画一个对于人头前半部分和整个部分的相机：

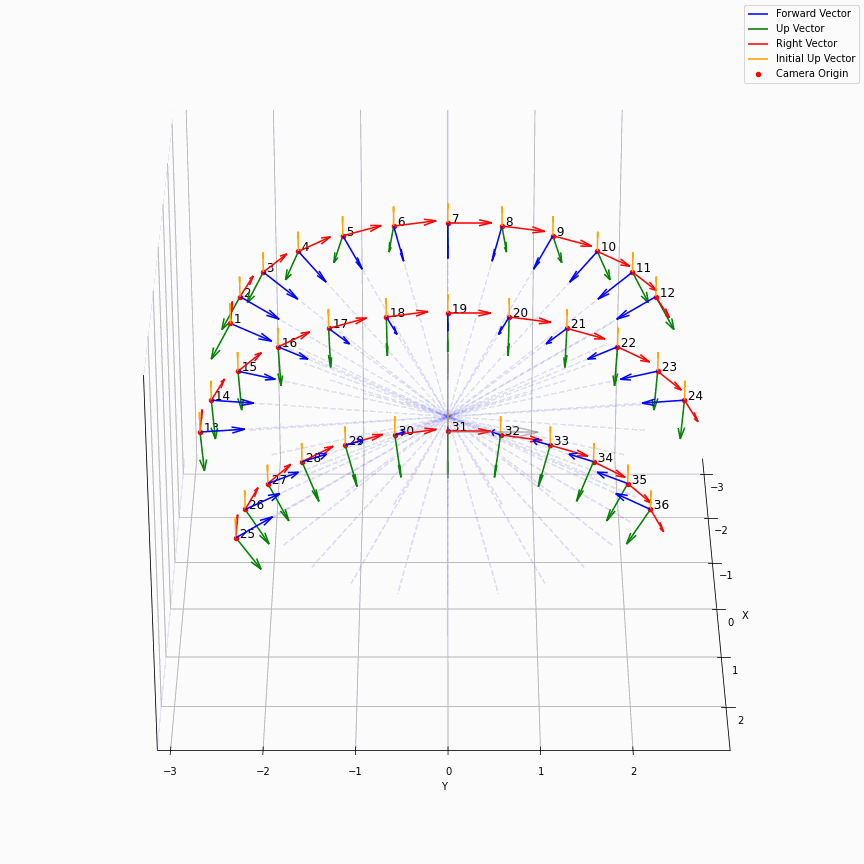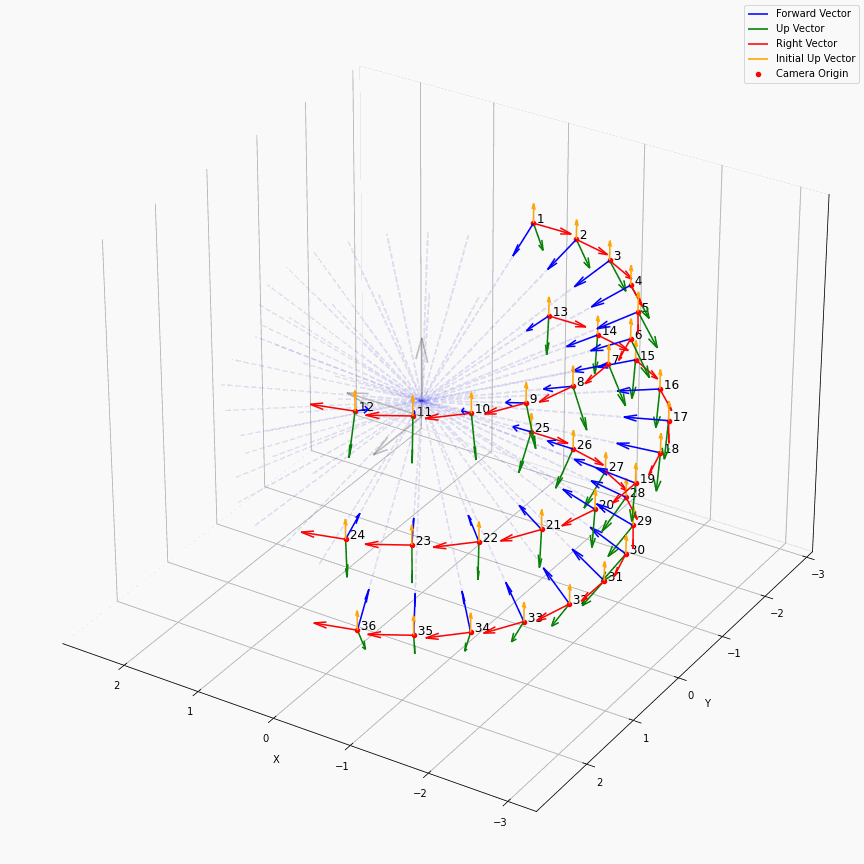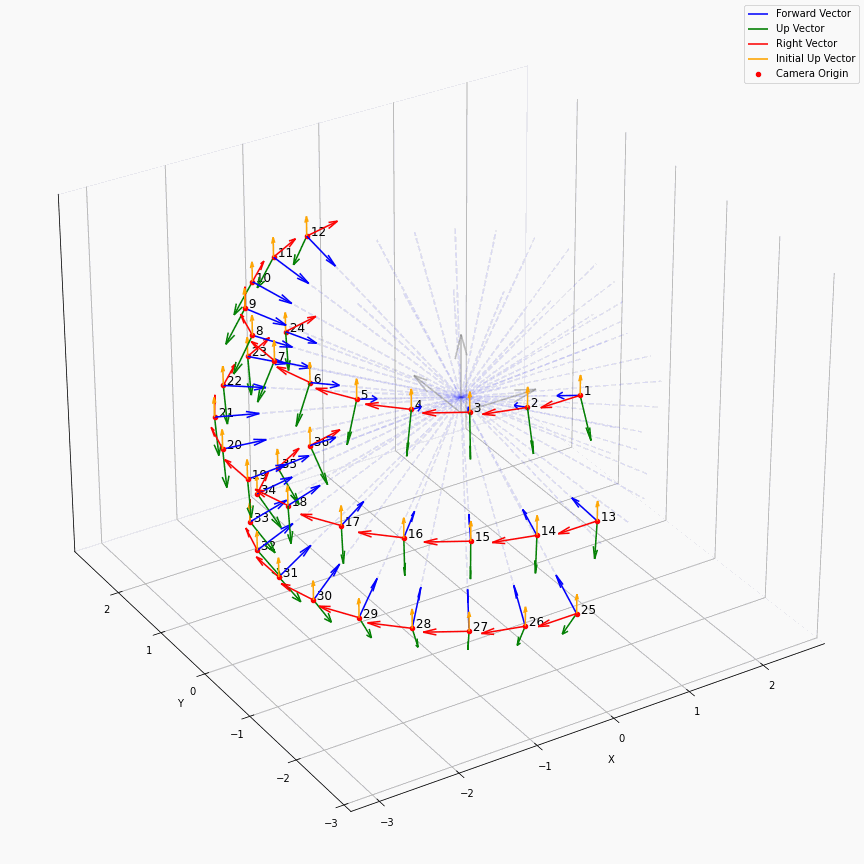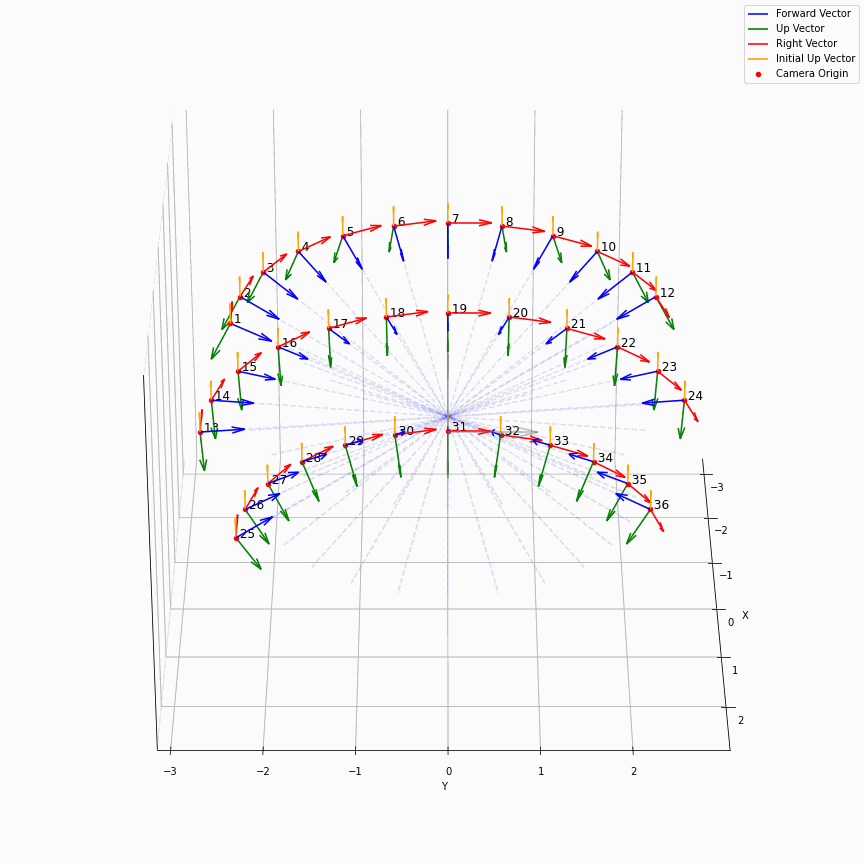
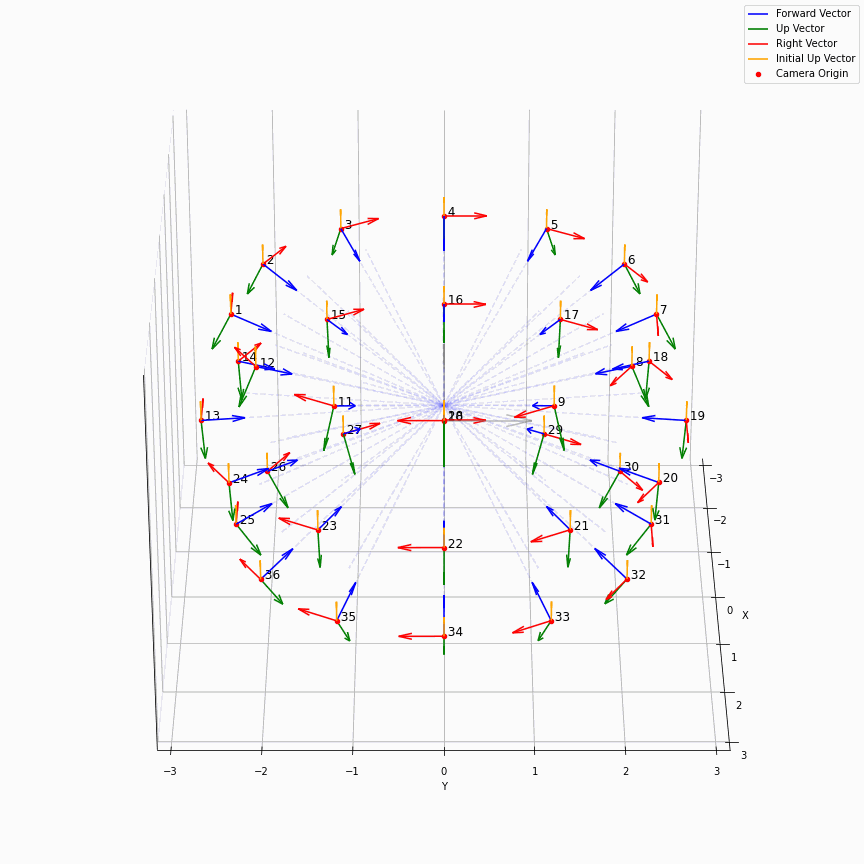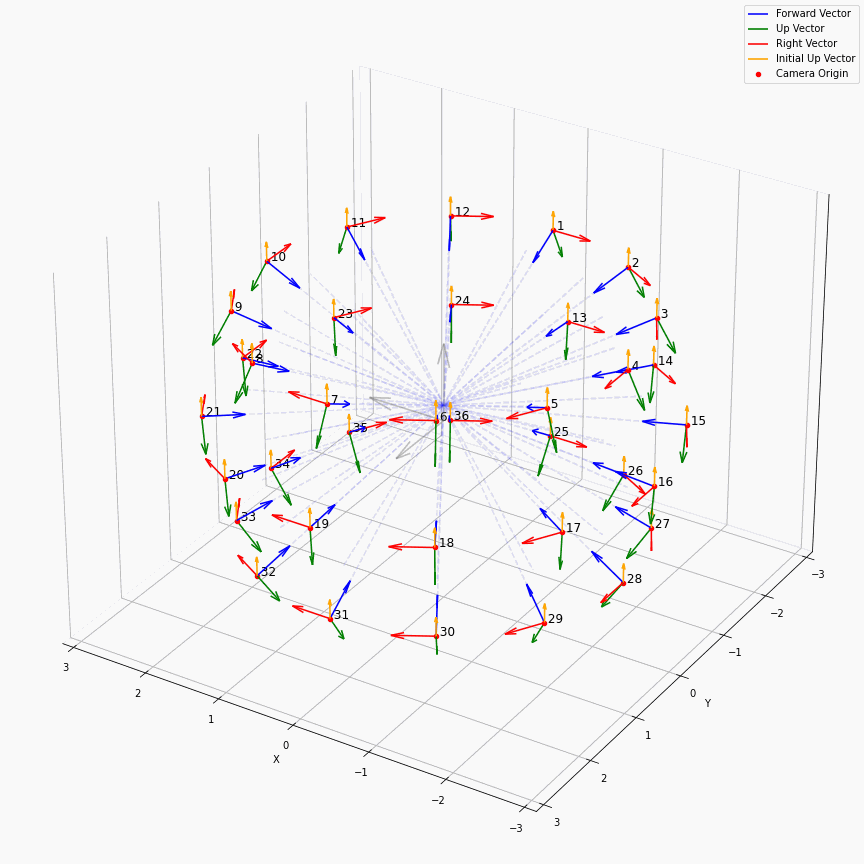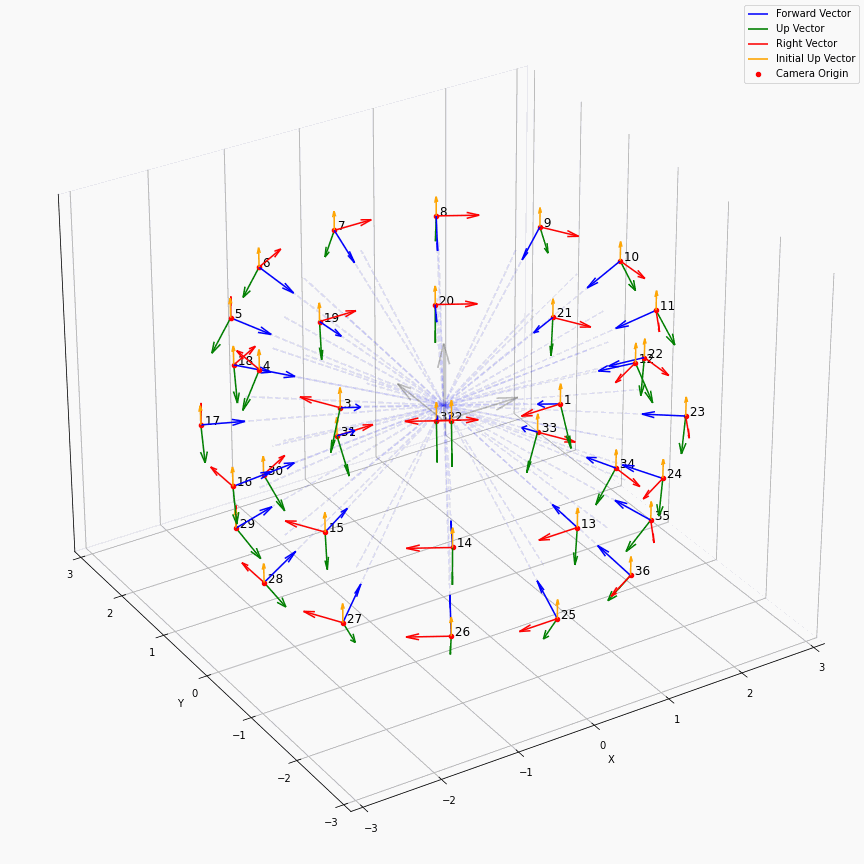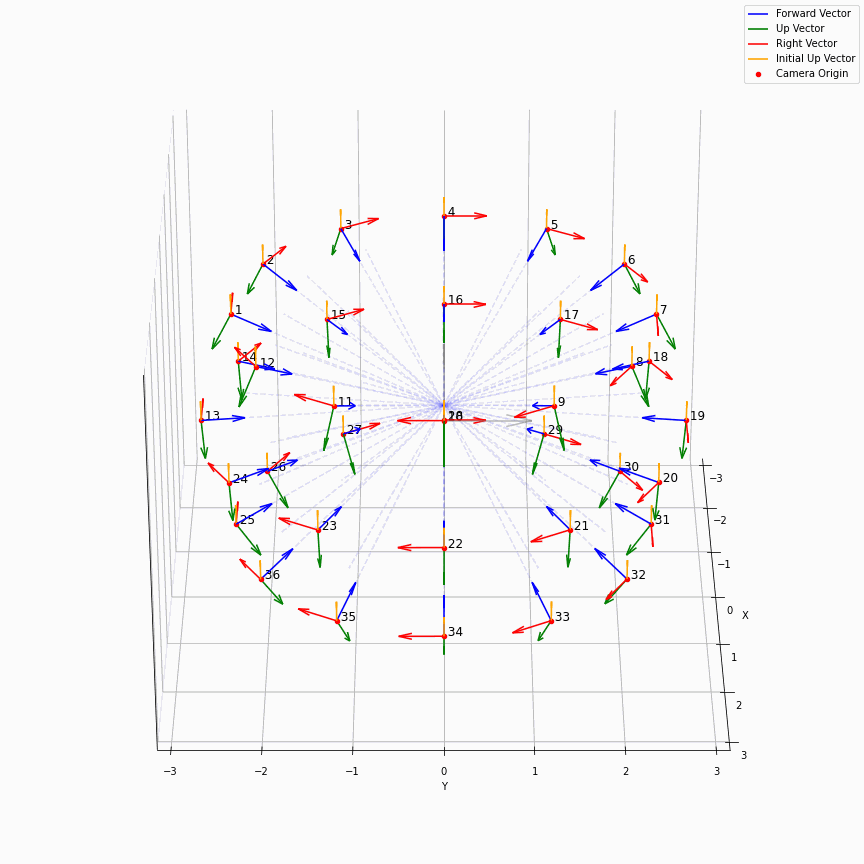
​ 上述脚本中设置了lookat_position为[0, 0, 0.2]，所以可以看到这些相机的延长线汇聚到了$z$轴上方的一个点。

​ 然后是关于相机内参的事情，在EG3D里相机内参是在预处理阶段直接给定的。其本身没有什么特殊的，只是选取了一个视场角比较小的内参，在EG3D的代码中，可以看到：

1
intrinsics = torch.tensor([[4.2647, 0, 0.5], [0, 4.2647, 0.5], [0, 0, 1]], device=device)

​ 上面的4.2647是归一化后的内参：

​ 所以：

​ 这个值算出来只有$13°$左右，所以相当于是那种怼着脸拍的长焦镜头，背景基本是虚化的。

​ 内参在这套代码里的目的，是用来决定发射光线的方向的。具体来说是起到“视口变换”的逆变换，即从归一化平面坐标系转移到相机坐标系：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def raysampler(cam2world_matrix, intrinsics, resolution=16):
    """
    Create batches of rays and return origins and directions.

    cam2world_matrix: (N, 4, 4)
    intrinsics: (N, 3, 3)
    resolution: int

    ray_origins: (N, M, 3)
    ray_dirs: (N, M, 2)
    """
    N, M = cam2world_matrix.shape[0], resolution**2
    cam_locs_world = cam2world_matrix[:, :3, 3]
    fx = intrinsics[:, 0, 0]
    fy = intrinsics[:, 1, 1]
    cx = intrinsics[:, 0, 2]
    cy = intrinsics[:, 1, 2]
    sk = intrinsics[:, 0, 1]

    uv = torch.stack(torch.meshgrid(torch.arange(resolution, dtype=torch.float32, device=cam2world_matrix.device), torch.arange(resolution, dtype=torch.float32, device=cam2world_matrix.device), indexing='ij')) * (1./resolution) + (0.5/resolution)
    uv = uv.flip(0).reshape(2, -1).transpose(1, 0)
    uv = uv.unsqueeze(0).repeat(cam2world_matrix.shape[0], 1, 1)
    
    x_cam = uv[:, :, 0].view(N, -1)
    y_cam = uv[:, :, 1].view(N, -1)
    z_cam = torch.ones((N, M), device=cam2world_matrix.device)

    x_lift = (x_cam - cx.unsqueeze(-1) + cy.unsqueeze(-1)*sk.unsqueeze(-1)/fy.unsqueeze(-1) - sk.unsqueeze(-1)*y_cam/fy.unsqueeze(-1)) / fx.unsqueeze(-1) * z_cam
    y_lift = (y_cam - cy.unsqueeze(-1)) / fy.unsqueeze(-1) * z_cam

    cam_rel_points = torch.stack((x_lift, y_lift, z_cam, torch.ones_like(z_cam)), dim=-1)

    world_rel_points = torch.bmm(cam2world_matrix, cam_rel_points.permute(0, 2, 1)).permute(0, 2, 1)[:, :, :3]

    ray_dirs = world_rel_points - cam_locs_world[:, None, :]
    ray_dirs = torch.nn.functional.normalize(ray_dirs, dim=2)

    ray_origins = cam_locs_world.unsqueeze(1).repeat(1, ray_dirs.shape[1], 1)

    return ray_origins, ray_dirs

​ sk是一个用于校正$x$和$y$轴不垂直的系数，我们可以认为其是0。我们可以看出整个代码的逻辑是创建一个[0, 1]的uv，实际上就是一个1×1的grid上的坐标。他们现在需要被换算到相机坐标系：

​ 大多数时候，平面$z$都是1。然后这些相机坐标系下的点左乘刚才的c2w，就可以变换到世界坐标系。继而求出ray_dirs。

​ 求出每个像素上光线的方向后，下面就是要考虑沿光线方向采样。在EG3D中，其对于FFHQ数据集，经验性质的选择了ray_start=2.25，ray_end=3.3。不同的数据集这个采样的上下限不一样，我推测是试+大概齐估计的。所以对于一个相机，它发出的光线大概就是下面这样：

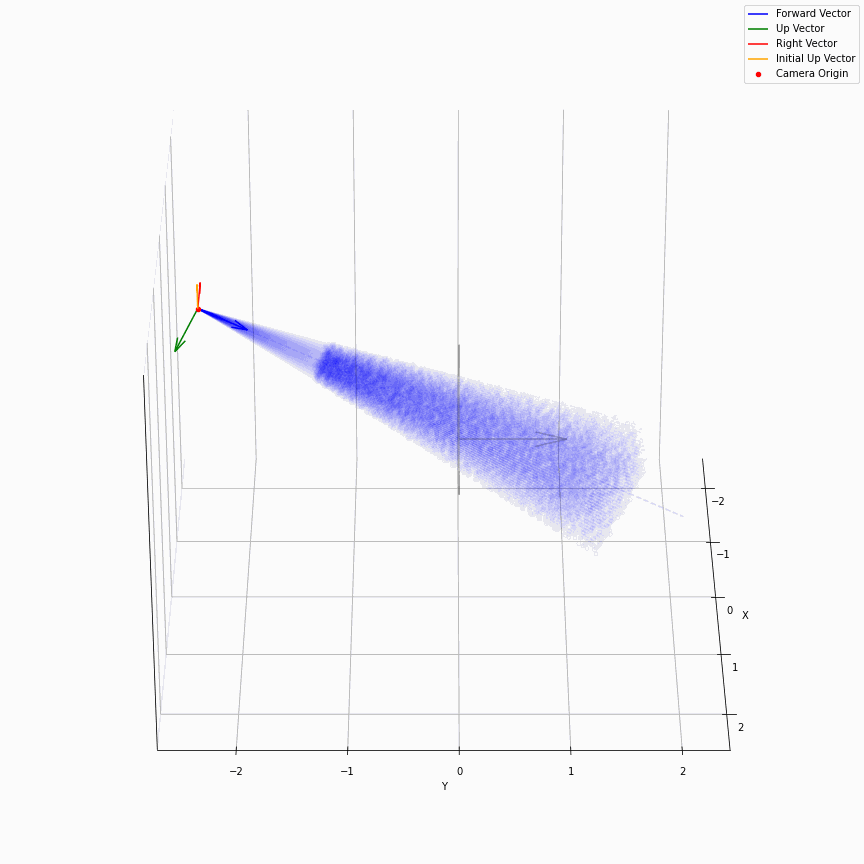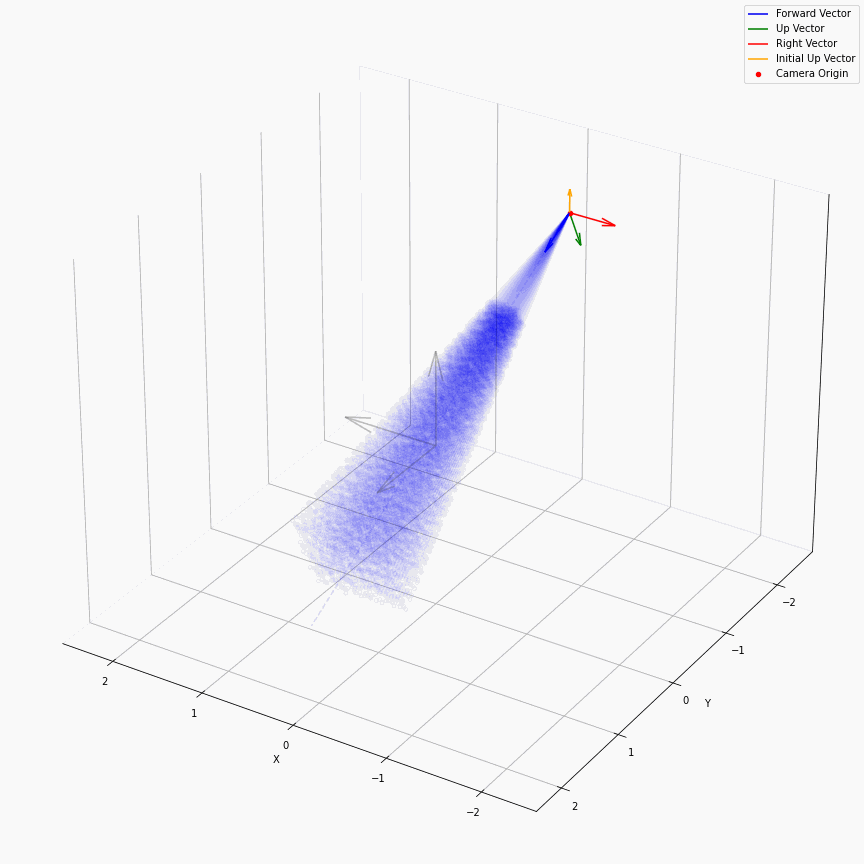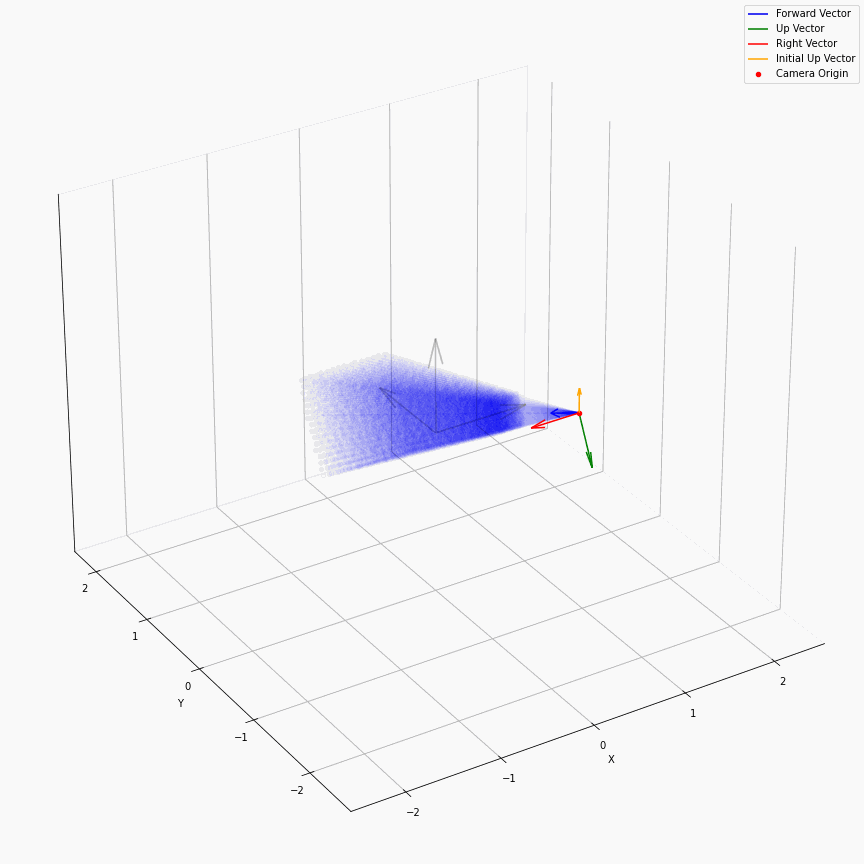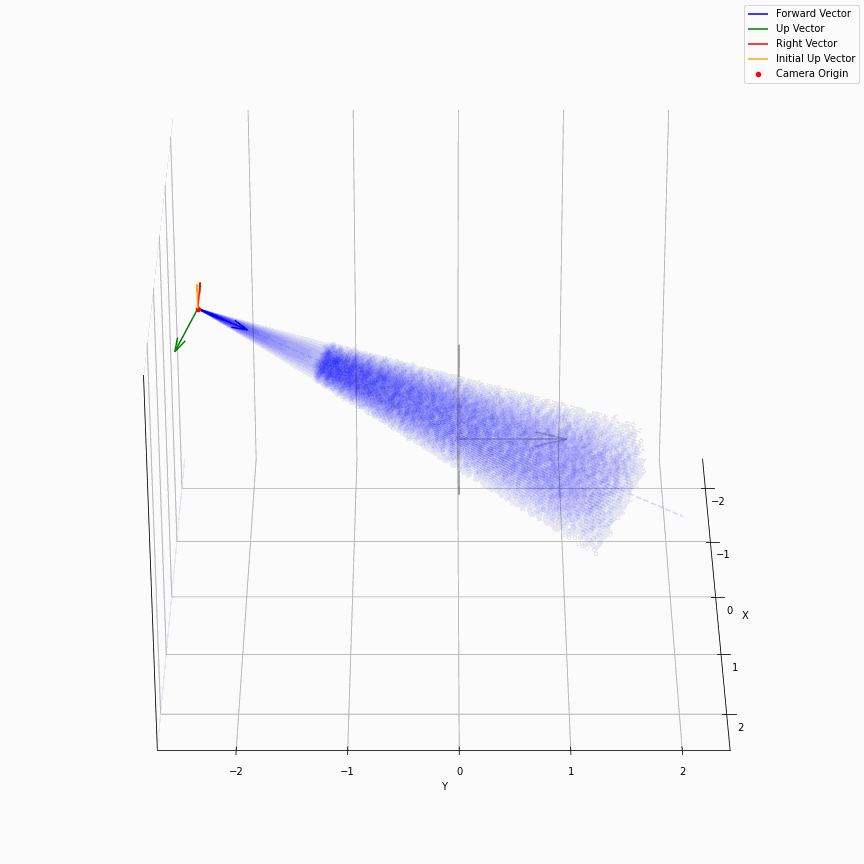
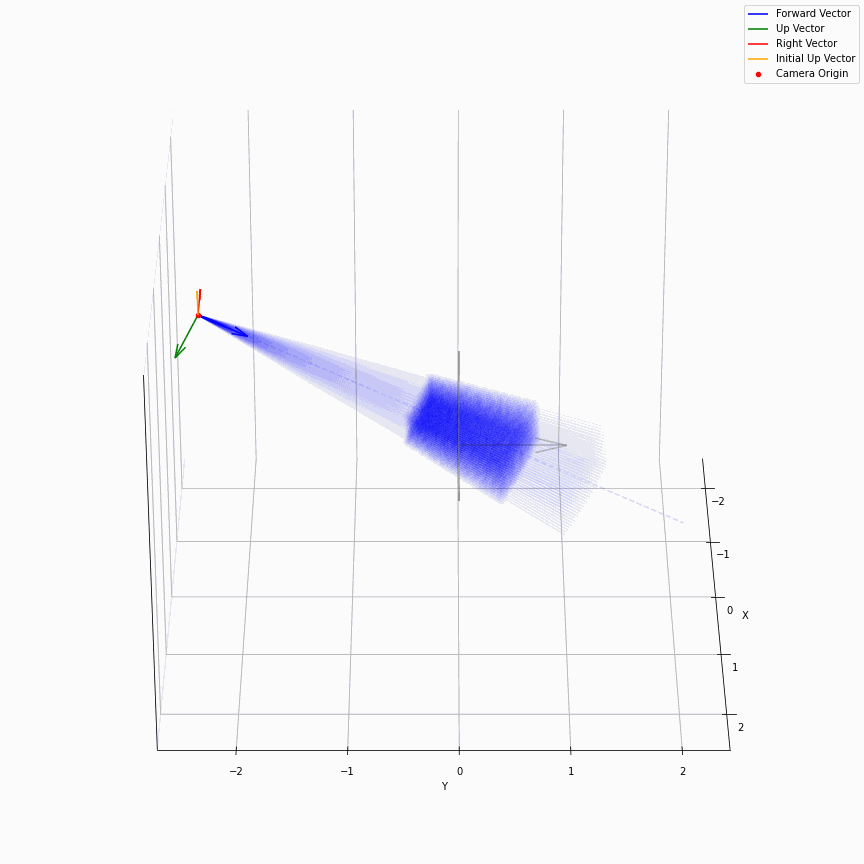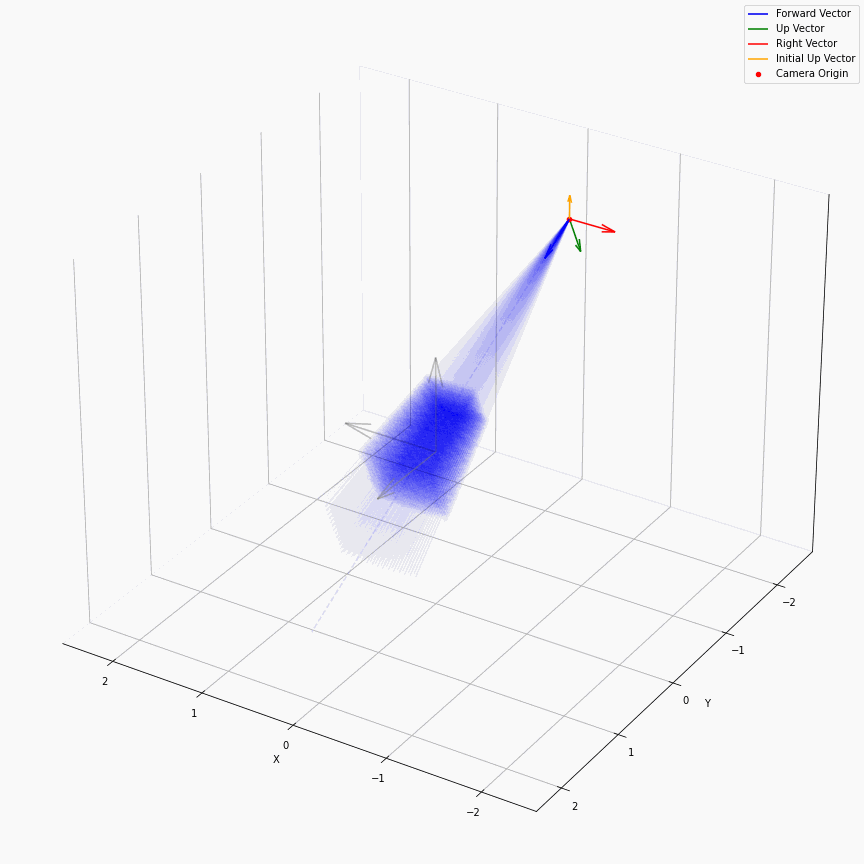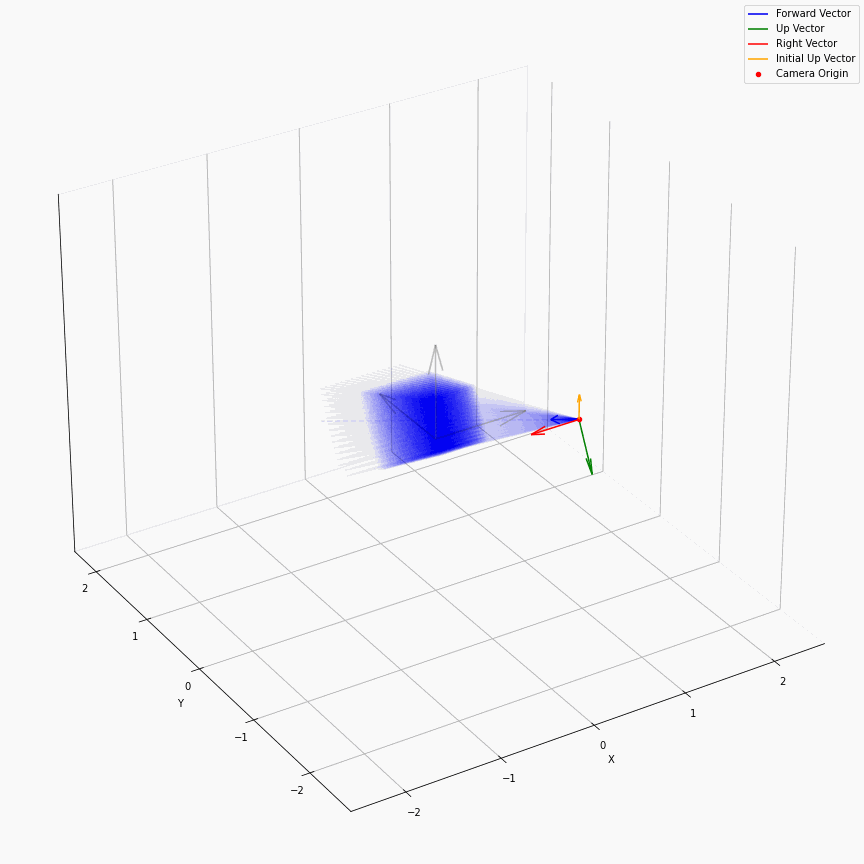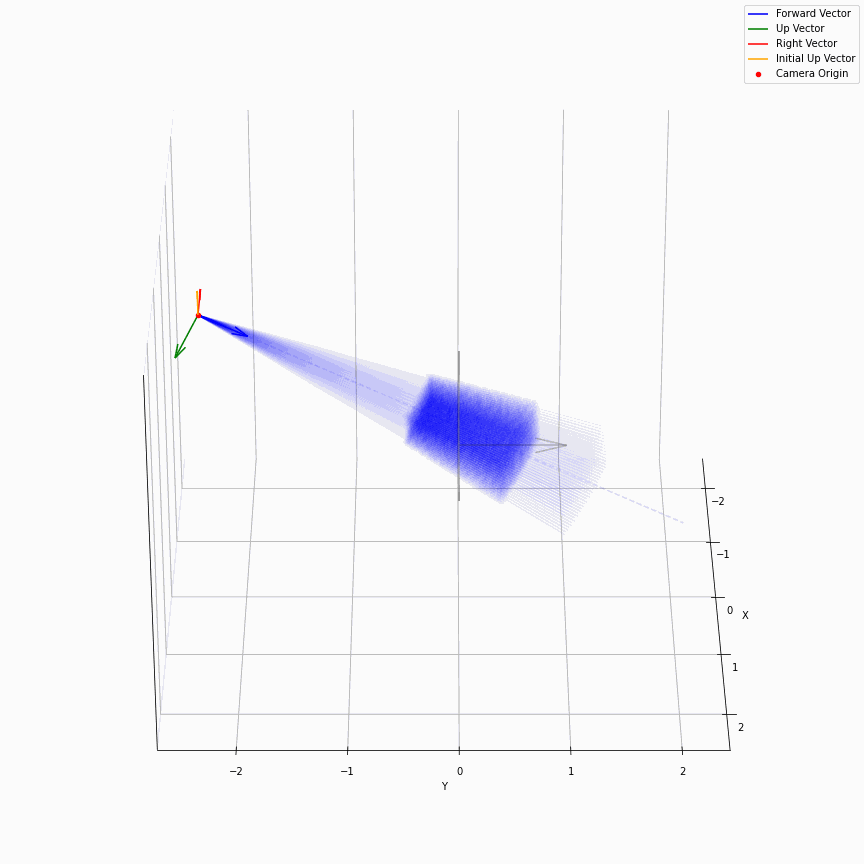
​ 我们可以看到采样出的那个光锥，以及视场角确实很小。给定一个预训练模型后，这里能改动的地方其实不多。首先更改ray_start和ray_end大概率会有一些无效的值，感觉能做的操作只剩下修改采样点数，和换成那个“倒数线性插值”。

​ 以及ray_start=2.25，ray_end=3.3也和相机半径$r$在EG3D训练FFHQ被指定为2.75有关，可以看到图中的坐标基本是在-0.5~0.5，因为后续需要在triplane里去插值。

​ 最后画一个多个相机发出光线的样子：

​ 这个动图还是挺有意思的。所有EG3D生成出来的图，都来自于中心那蓝色区域，蓝色区域会由不同的$z$所导引出的不同的特征图$f$按照triplane的方法来产生不同的响应，仿佛一个在涌现着什么的水晶球，从某个角度看过去就会有一张又一张的人脸。

“视锥之内，即是NeRF。”

​ 所以在这个settings下，“透视变换”的概念就比较弱，相机内参给定焦距，焦距给定光线方向，除此以外就没有“透视投影”的事情了。

NeRF-PyTorch

​ 上述EG3D的管线中，并没有使用“透视变换”。但实际上在原版NeRF实现中，我们不应忘记，是有NDC空间的使用的。而从正常的欧式空间变换到NDC空间用的就是透视变换。

​ 对于拍摄的facing-forward的数据集，我们应该在训练时变换到NDC空间，这样深度就被缩放到$[-1,1]$了，有利于NN去拟合。同时在此基础上对$z$进行均匀采样，在NDC空间里自动变成了对近处多采一些对远处少采一些的倒数线性采样。

​ 对于拍摄的$360°$的数据集，那么我们需要禁用NDC，因为全景的图片会造成近平面的歧义，同时对相机位姿进行球化，为了避免在这种情况均匀采样会采集很多远处不必要的点，我们手动进行线性视差插值。

​ 在这篇博客中，详细阐述了NeRF之中的NDC和lindisp。我们在这里不作赘述，重点放在解析其他的一些相机工具代码。

​ 我们主要讨论load_llff.py中的一些函数，这个版本的NeRF代码中传递的poses一般为[N, 3, 5]，N为数量，5那儿多出来的那一维是cat了图像的宽高，估计的焦距。中间是3而不是4，是因为存储时舍去了$[0, 0, 0, 1]$这一行。这里我们使用的poses是由LLFF中的imgs2poses.py导出的，其中储存的就是c2w。

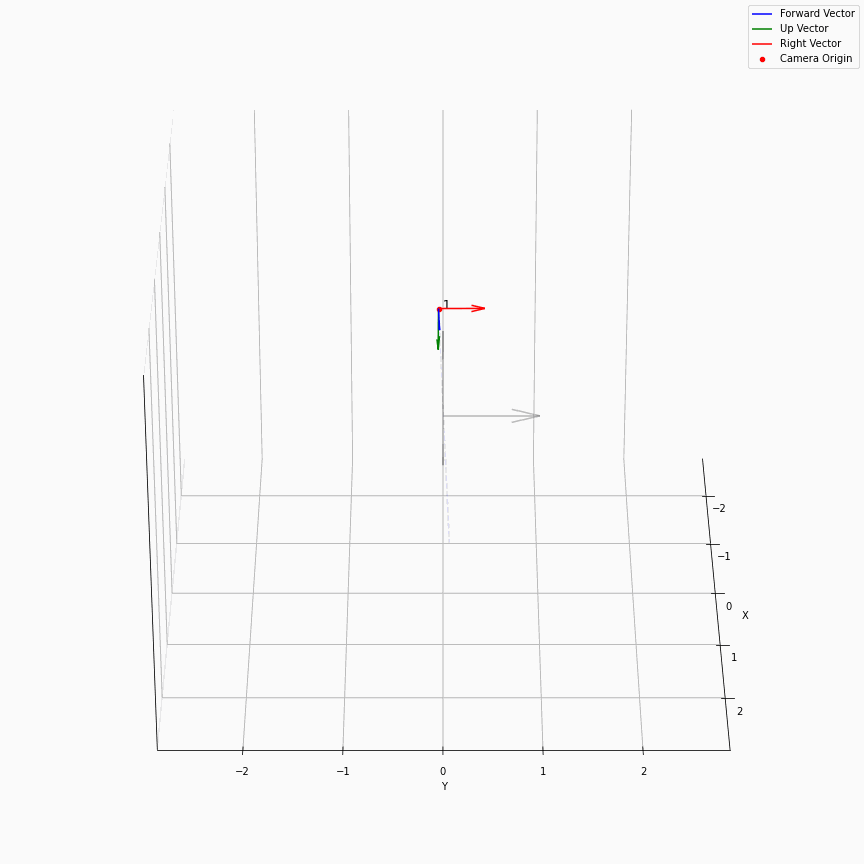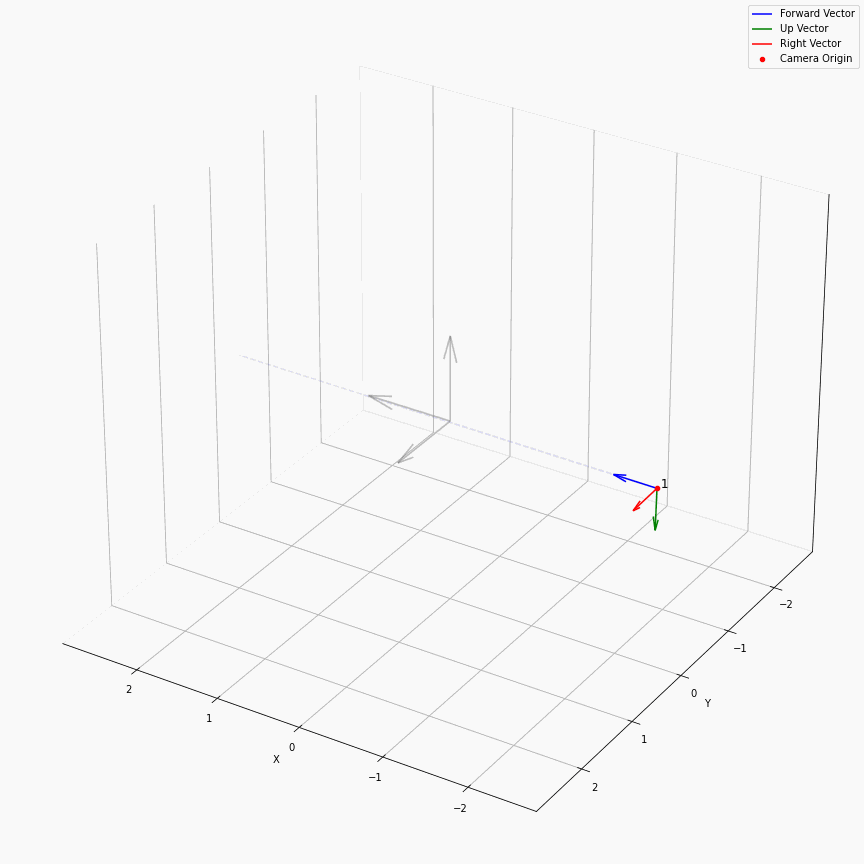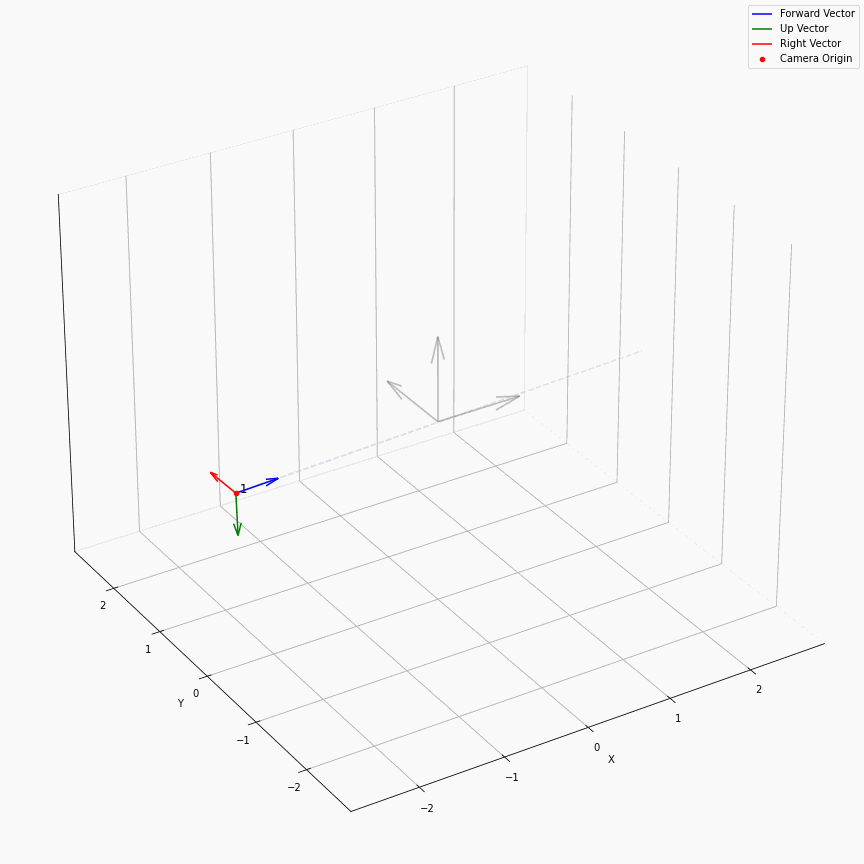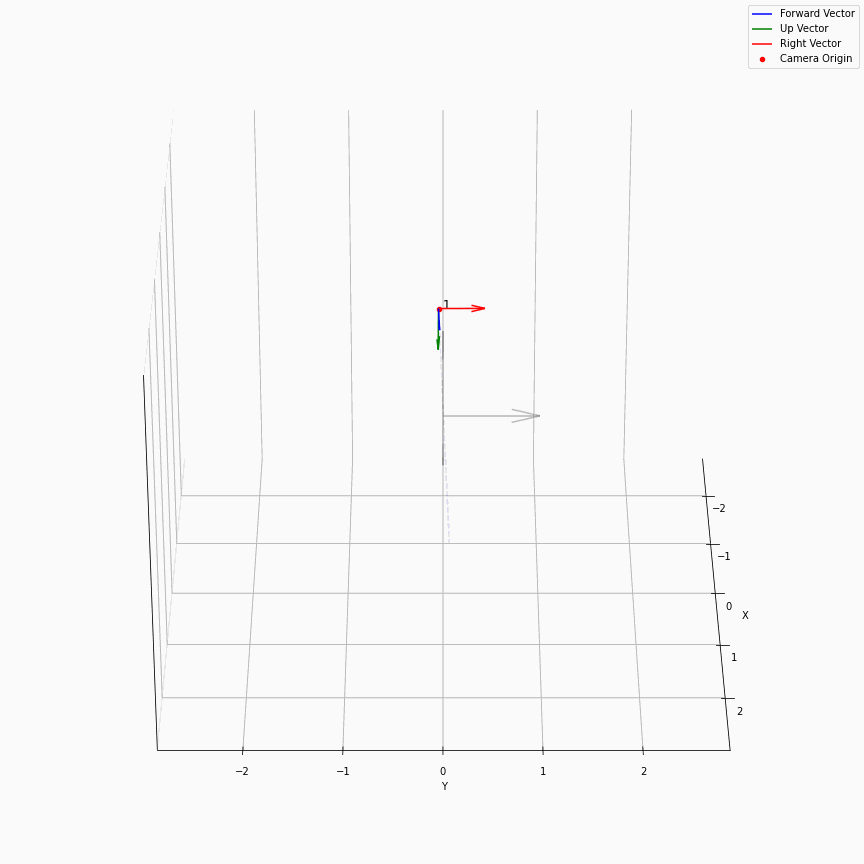
​ 一个常用的函数是求取这些位姿的平均姿态pose_avg：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def viewmatrix(z, up, pos):
    vec2 = normalize(z)
    vec1_avg = up
    vec0 = normalize(np.cross(vec1_avg, vec2))
    vec1 = normalize(np.cross(vec2, vec0))
    m = np.stack([vec0, vec1, vec2, pos], 1)
    return m

def poses_avg(poses):

    hwf = poses[0, :3, -1:]

    center = poses[:, :3, 3].mean(0)
    vec2 = normalize(poses[:, :3, 2].sum(0))
    up = poses[:, :3, 1].sum(0)
    c2w = np.concatenate([viewmatrix(vec2, up, center), hwf], 1)
    
    return c2w

​ 这个是很直接的，我们求取了每个轴方向向量的平均，相机位置的平均，最后得到一个表示相机平均位置的c2w，如下图所示：

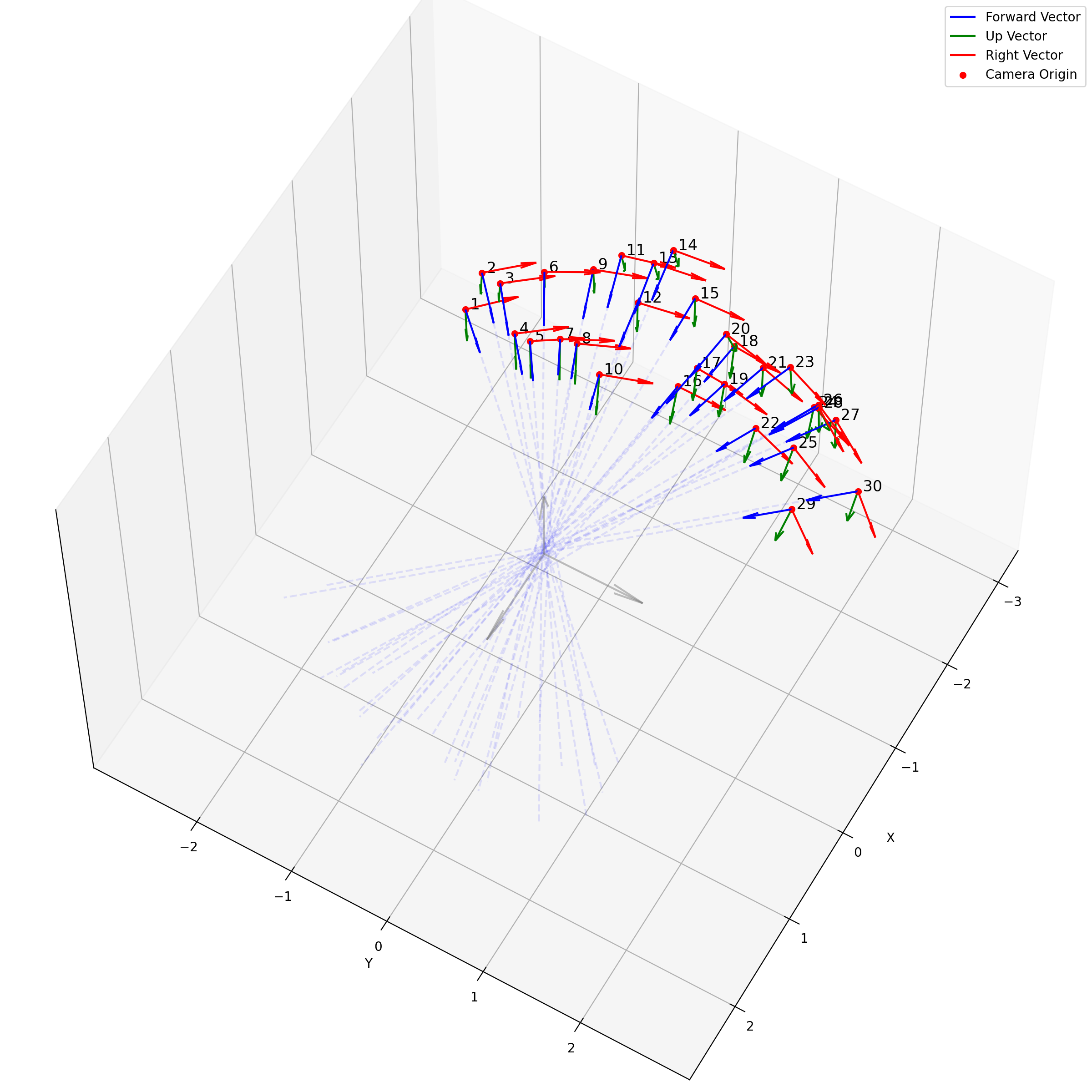
​ 一个在处理facing-forward的数据时的一个很有用的操作是recenter_poses，通过对全体姿态左乘一个平均姿态的逆，可以让任意settings下的相机都转变到一个“跟世界坐标系一致”的样子下：

1
2
3
4
5
6
7
8
9
10
11
12
13
def recenter_poses(poses):

    poses_ = poses+0
    bottom = np.reshape([0,0,0,1.], [1,4])
    c2w = poses_avg(poses)
    c2w = np.concatenate([c2w[:3,:4], bottom], -2)
    bottom = np.tile(np.reshape(bottom, [1,1,4]), [poses.shape[0],1,1])
    poses = np.concatenate([poses[:,:3,:4], bottom], -2)

    poses = np.linalg.inv(c2w) @ poses
    poses_[:,:3,:4] = poses[:,:3,:4]
    poses = poses_
    return poses

​ 这么说可能有点抽象，下面是图示：

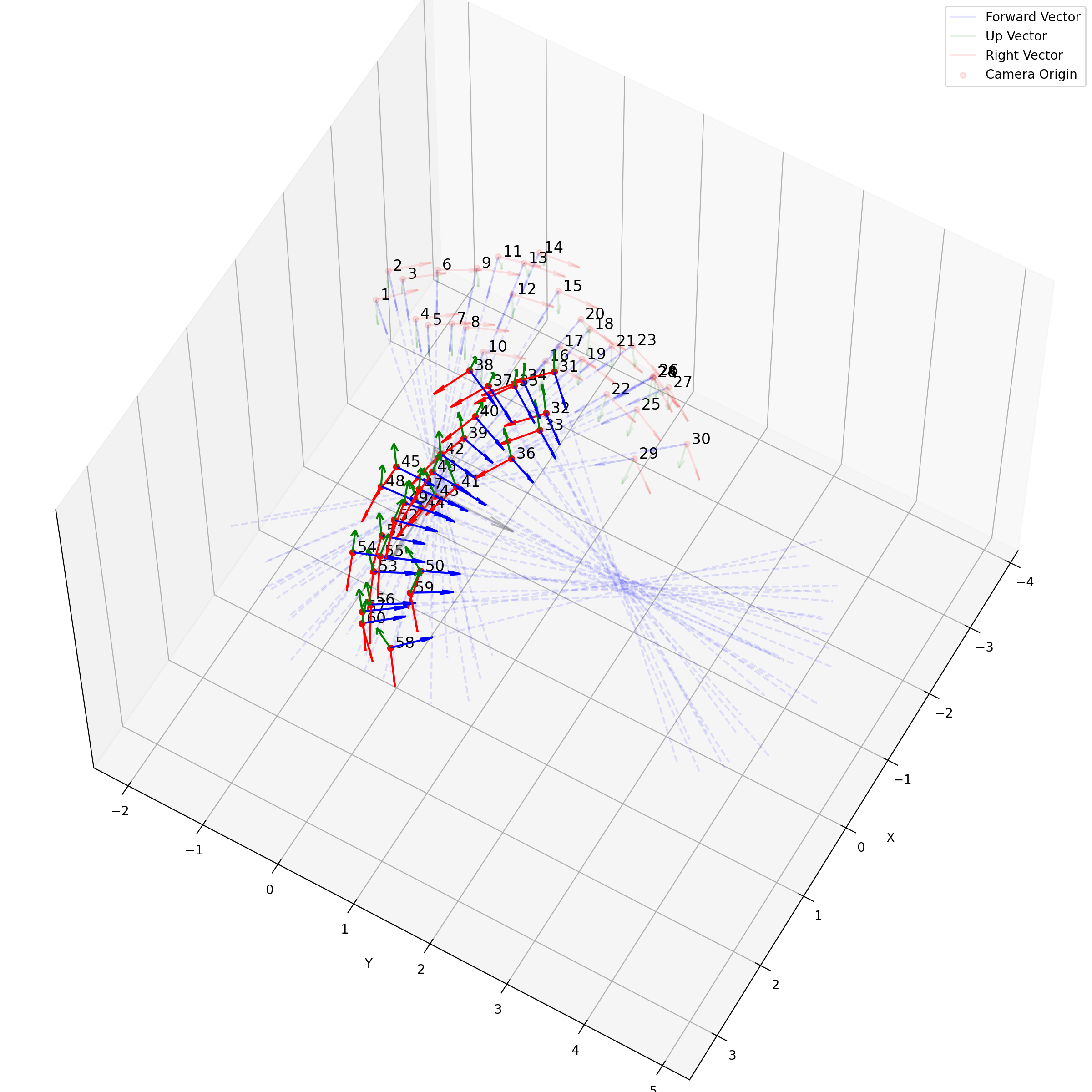
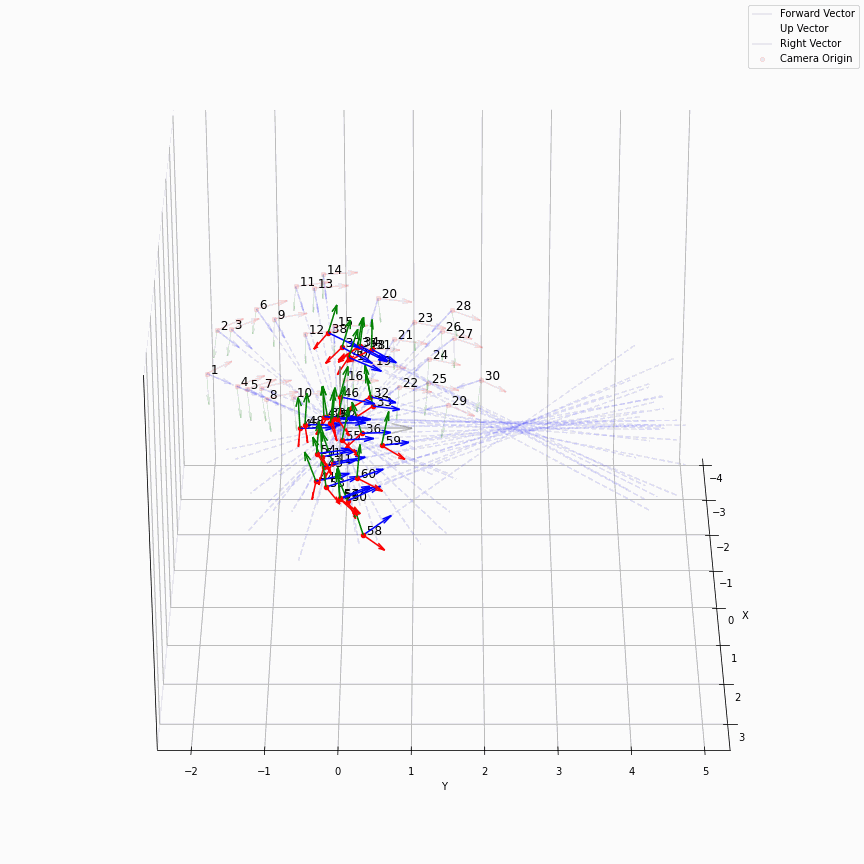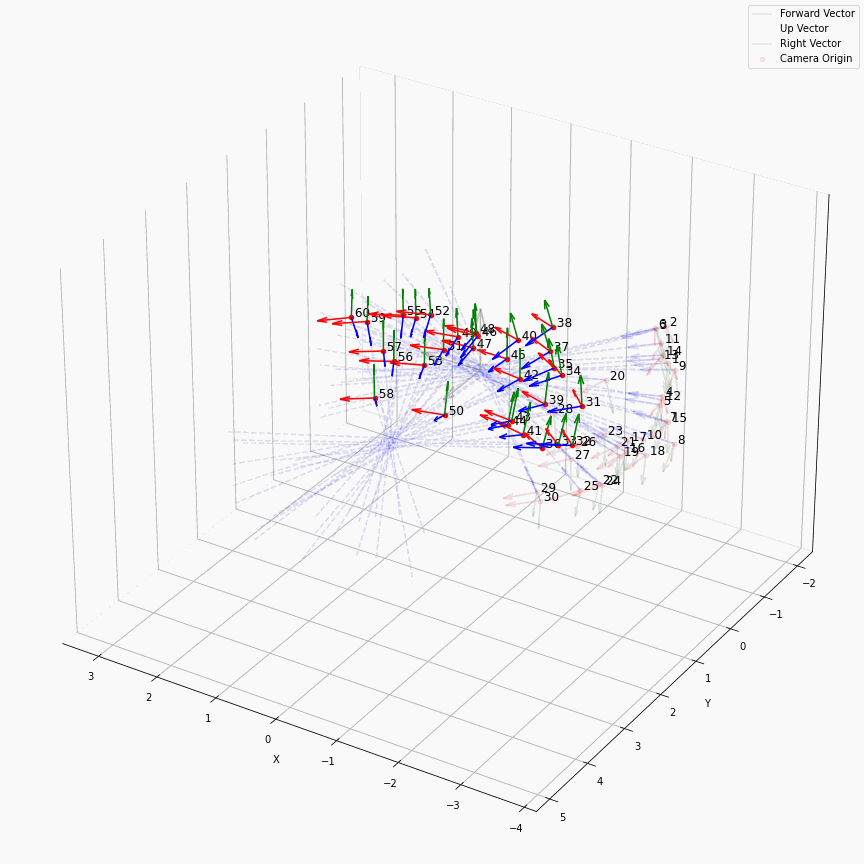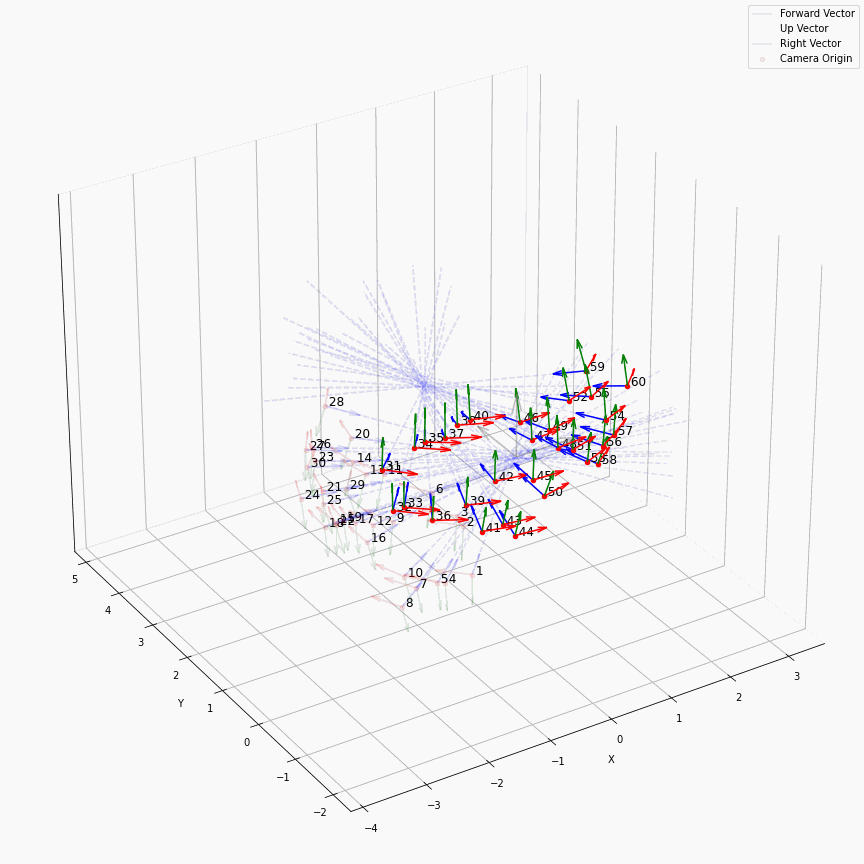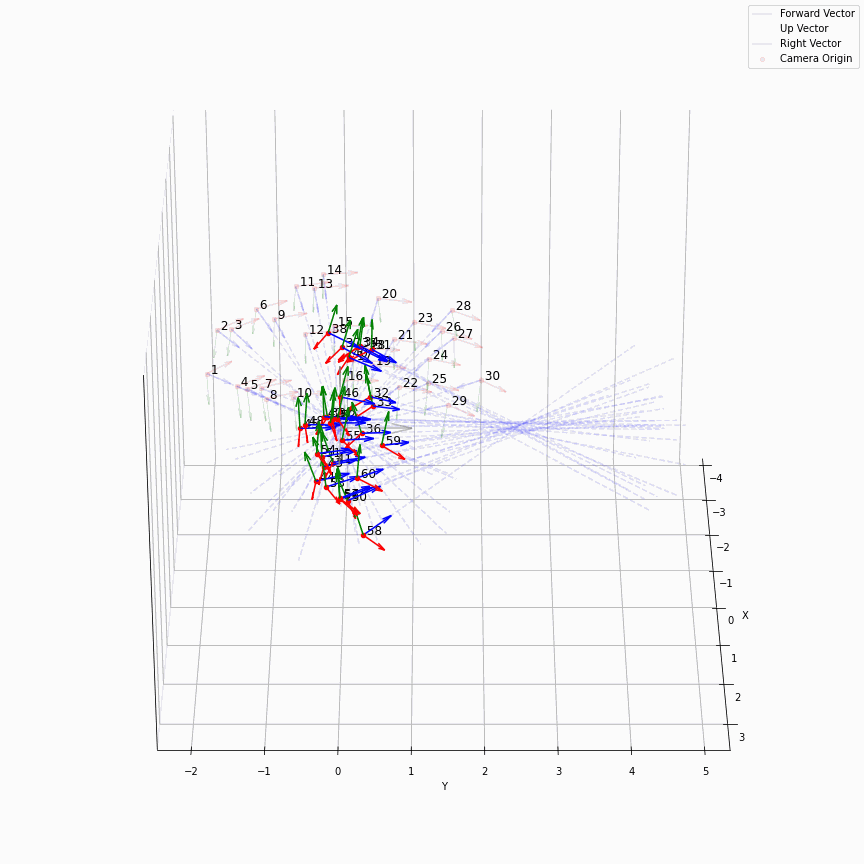
​ 我们可以很轻松的看出哪些是recenter后的相机，可以看到，recenter消除了后面做NDC时的歧义，同时方便了后面生成螺旋轨迹的相机轨迹。

​ 另一个比较复杂的就是spherify_poses，它分为两个部分，先对相机轨迹进行“球化”，然后再其基础上构造新的相机轨迹（用于可视化）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
def spherify_poses(poses, bds):
    
    p34_to_44 = lambda p : np.concatenate([p, np.tile(np.reshape(np.eye(4)[-1,:], [1,1,4]), [p.shape[0], 1,1])], 1)
    
    rays_d = poses[:,:3,2:3]
    rays_o = poses[:,:3,3:4]

    def min_line_dist(rays_o, rays_d):
        A_i = np.eye(3) - rays_d * np.transpose(rays_d, [0,2,1])
        b_i = -A_i @ rays_o
        pt_mindist = np.squeeze(-np.linalg.inv((np.transpose(A_i, [0,2,1]) @ A_i).mean(0)) @ (b_i).mean(0))
        return pt_mindist

    pt_mindist = min_line_dist(rays_o, rays_d)
    
    center = pt_mindist
    up = (poses[:,:3,3] - center).mean(0)

    vec0 = normalize(up)
    vec1 = normalize(np.cross([.1,.2,.3], vec0))
    vec2 = normalize(np.cross(vec0, vec1))
    pos = center
    c2w = np.stack([vec1, vec2, vec0, pos], 1)

    poses_reset = np.linalg.inv(p34_to_44(c2w[None])) @ p34_to_44(poses[:,:3,:4])

    rad = np.sqrt(np.mean(np.sum(np.square(poses_reset[:,:3,3]), -1)))
    
    sc = 1./rad
    poses_reset[:,:3,3] *= sc
    bds *= sc
    rad *= sc
    
    centroid = np.mean(poses_reset[:,:3,3], 0)
    zh = centroid[2]
    radcircle = np.sqrt(rad**2-zh**2)
    new_poses = []
    
    for th in np.linspace(0.,2.*np.pi, 120):

        camorigin = np.array([radcircle * np.cos(th), radcircle * np.sin(th), zh])
        up = np.array([0,0,-1.])

        vec2 = normalize(camorigin)
        vec0 = normalize(np.cross(vec2, up))
        vec1 = normalize(np.cross(vec2, vec0))
        pos = camorigin
        p = np.stack([vec0, vec1, vec2, pos], 1)

        new_poses.append(p)

    new_poses = np.stack(new_poses, 0)
    
    new_poses = np.concatenate([new_poses, np.broadcast_to(poses[0,:3,-1:], new_poses[:,:3,-1:].shape)], -1)
    poses_reset = np.concatenate([poses_reset[:,:3,:4], np.broadcast_to(poses[0,:3,-1:], poses_reset[:,:3,-1:].shape)], -1)
    
    return poses_reset, new_poses, bds

​ 代码的前半部分是一个有趣的线性代数问题（min_line_dist），给定$N$条直线，求出一个点到这些直线的距离和最小。这个问题可以直接直接得到解析解。考虑光线原点$\mathbf{o}$，光线方向$\mathbf{d}$，直线上的点可以表述为$\mathbf{o}+t\mathbf{d}$，考虑直线外一点$\mathbf{p}$，其点到直线距离为（均为列向量）：

​ 最后一个等号是因为方向向量$\mathbf{d}$的内积$\mathbf{d}^T\mathbf{d}$是1，所以$\mathbf{I}-\mathbf{d}\mathbf{d}^T$长成了一个幂等矩阵。

​ 考虑有$N$条光线时，有：

​ 这其实就是一个线性方程组：

​ 于是就有了上面代码里的子函数。接下来，这个函数用不同的叉乘顺序计算了一个类似c2w的矩阵，其位置是刚才估计的直线中心。然后对所有位姿左乘其逆阵，这样就让位姿的lookat对准原点了。同时将相机位置的半径缩放为1，完成“球化”：

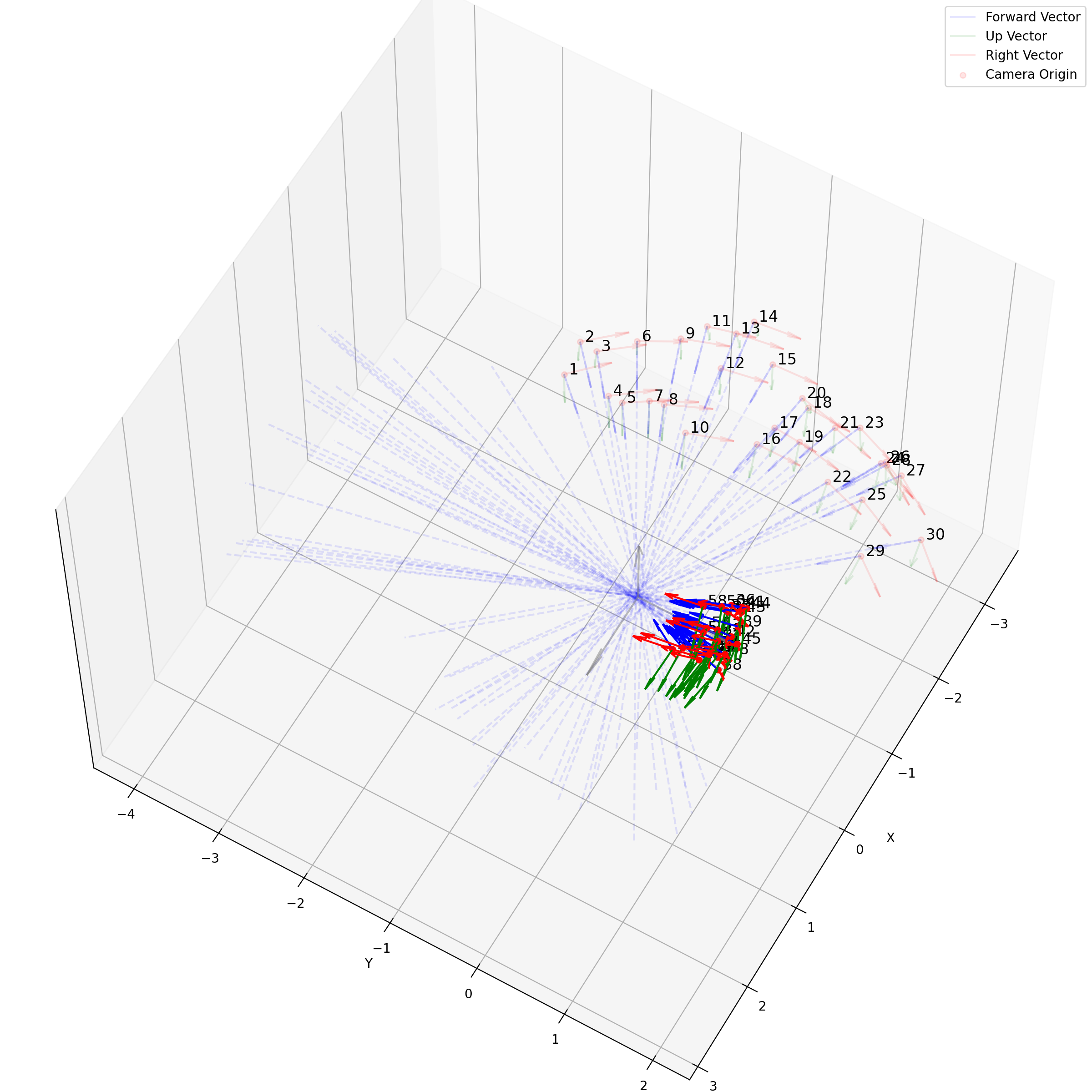
​ （但这个“球化”并不意味着相机姿态真的处理成了一个球面上均匀分布的样子，不要混淆。）

​ 最后一个需要解读的函数是render_path_spiral，这个函数可以生成一个螺旋型的轨迹，来可视化出NeRF在facing-forward时的novel pose：

1
2
3
4
5
6
7
8
9
10
def render_path_spiral(c2w, up, rads, focal, zdelta, zrate, rots, N):
    render_poses = []
    rads = np.array(list(rads) + [1.])
    hwf = c2w[:,4:5]
    
    for theta in np.linspace(0., 2. * np.pi * rots, N+1)[:-1]:
        c = np.dot(c2w[:3,:4], np.array([np.cos(theta), -np.sin(theta), -np.sin(theta*zrate), 1.]) * rads) 
        z = normalize(c - np.dot(c2w[:3,:4], np.array([0,0,-focal, 1.])))
        render_poses.append(np.concatenate([viewmatrix(z, up, c), hwf], 1))
    return render_poses

​ 可以看出是先创建这样的螺旋线：

​ 与解析几何中熟悉的螺旋线不同，这里的$z$是用$\sin(\cdot)$来有确保有界的。这个函数的其他输入来自于load_llff_data函数的一个分支：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
else:

    c2w = poses_avg(poses)
    print('recentered', c2w.shape)
    print(c2w[:3,:4])

    ## Get spiral
    # Get average pose
    up = normalize(poses[:, :3, 1].sum(0))

    # Find a reasonable "focus depth" for this dataset
    close_depth, inf_depth = bds.min()*.9, bds.max()*5.
    dt = .75
    mean_dz = 1./(((1.-dt)/close_depth + dt/inf_depth))
    focal = mean_dz

    # Get radii for spiral path
    shrink_factor = .8
    zdelta = close_depth * .2
    tt = poses[:,:3,3] # ptstocam(poses[:3,3,:].T, c2w).T
    rads = np.percentile(np.abs(tt), 90, 0)
    c2w_path = c2w
    N_views = 120
    N_rots = 2
    if path_zflat:
        #             zloc = np.percentile(tt, 10, 0)[2]
        zloc = -close_depth * .1
        c2w_path[:3,3] = c2w_path[:3,3] + zloc * c2w_path[:3,2]
        rads[2] = 0.
        N_rots = 1
        N_views/=2

    # Generate poses for spiral path
    render_poses = render_path_spiral(c2w_path, up, rads, focal, zdelta, zrate=.5, rots=N_rots, N=N_views)

​ 通过场景的界限bds，我们可以知道一个类似近远平面的度量，将两者进行倒数线性插值，作为一个估计，来给出focal，focal在def render_path_spiral用于计算lookat的那个固定点。当path_zflat为真时，计算出的rads的$z$值会归0，于是刚才的螺旋线将退化为圆。

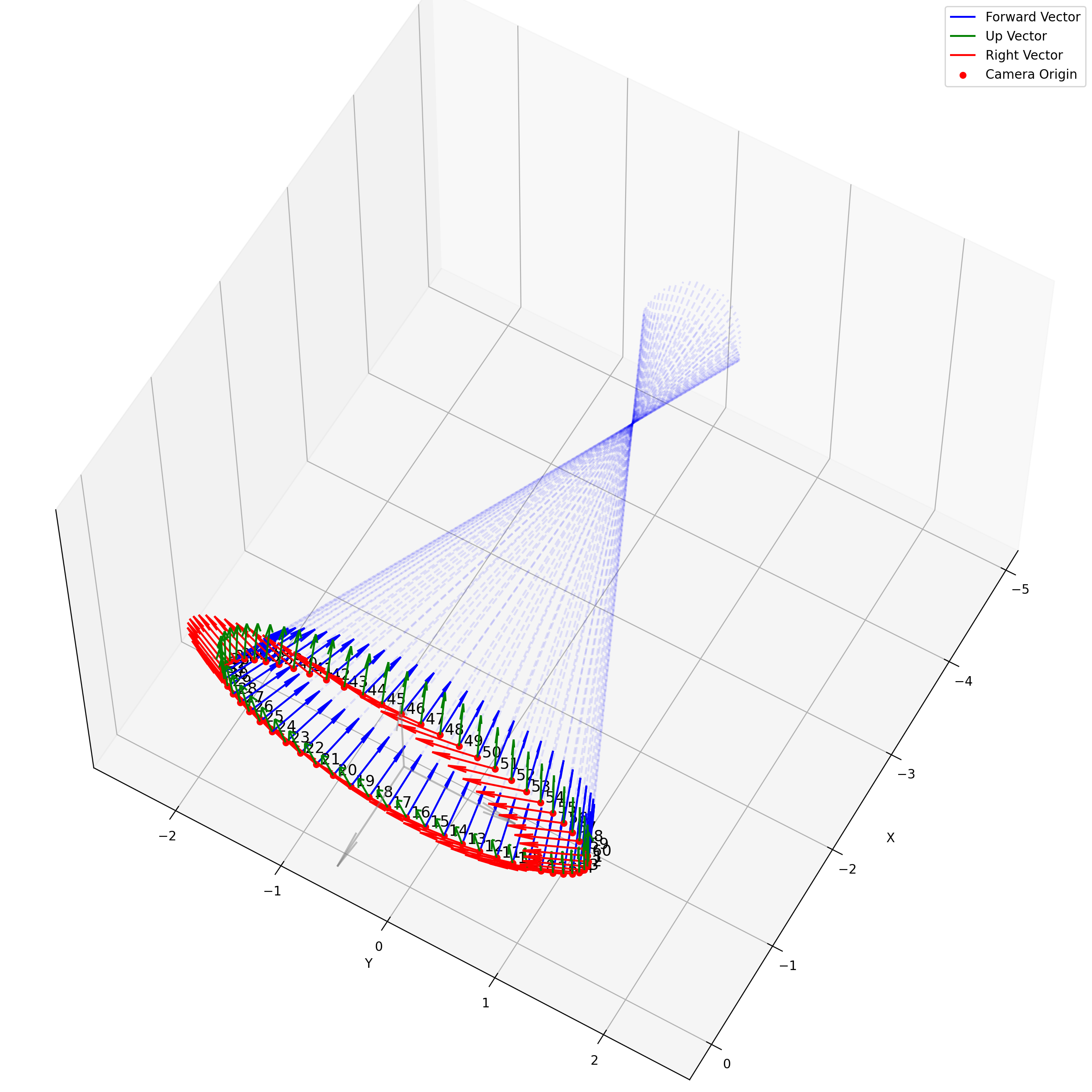
​ 这就是NeRF中的一些关于相机的工具函数了。

3DDFA

​ 在这个部分，我们其实关心的是EG3D中对人脸图片的预处理。这个预处理在处理2D人脸数据时常用的“FFHQ alignment”上更进了一步。但由于EG3D给的预处理代码写的比较分散，不太适合作为“教具”。而基于EG3D的工作PanoHead里提供了一个更自洽和规整的脚本，来让我们可以体会对齐这一步。

​ PanoHead的预处理用到了3DDFA，这篇工作的全称是Face Alignment in Full Pose Range: A 3D Total Solution，它的本意是为了为了提升大角度偏转情况下人脸对齐的效果，在这个预处理中用到它的目的其实和它的本意有点出入，但这个问题不大，我们也可以把这个当作一个熟悉陌生工作中相机settings的例子。我这里用一张3DDFA GitHub仓库里的teaser来图示一下这个工作具体做了什么事情。

​ 我们可以简单总结为它旨在从单张图片中估计一个人脸的姿态，表情。我们从PanoHead项目中提供的recrop_images.py开始看，会对一些事情产生困惑，继而需要先去浏览下3DDFA的原文，我们不需要很清楚其中的技术原理，只需要关心它的输出形式。通过分析，其模型的输出是$p=\left[ q_0,q_1,q_2,q_3,\mathbf{t}_{2d},\mathbf{\alpha }_{id},\mathbf{\alpha }_{exp} \right] $，这里面的$q_i$是四元数的不同部分，他们用于计算旋转矩阵$\mathbf{R}$：

​ 但实际上，$q_i$在3DDFA的实现里并不是一个单位四元数，其本身有一个$\sqrt{f}$作为分母，并没有严格的进行模1的约束。这个$f$是一个缩放系数，因为在3DDFA的settings里，整个系统被表述为：

​ 括号里的那一项是一个3DMM重建出的人脸，然后这个人脸上的每一个点，都被$\mathbf{R}$旋转，然后被$\mathbf{Pr}$做正交投影，这个概念非常的简单，正交投影矩阵只是：

​ 你可以看出它直接忽略掉了$z$，等价于一个焦距非常大的相机，没有近大远小的性质，在这个任务的情景下是非常合适的简化。而它又乘了一个缩放系数$f$，那么实际上$f\ast \mathbf{Pr}$在做的操作有一个专门的名字：弱透视投影。

在一个比较滑稽的情境下，我被指出分不清强投影和弱投影。实际上这个概念非常简单，只是我过于土鳖，没听过。弱投影应该就是上面的“弱透视投影”，我后来又去搜了一下，发现并没有“强投影”这个专有名词，大概率这个强投影只是指普通的透视投影。

​ 然而实际上，$\bar{\mathbf{S}}+\mathbf{A}_{id}\mathbf{\alpha }_{id}+\mathbf{A}_{exp}\mathbf{\alpha }_{exp}$这一项是以BFM参数化模型“自己”为中心的，所以经过旋转变换，弱透视变换后，这个人头会是在画面中央的。这显然不太合理，所以就需要一个$\mathbf{t}_{2d}$的偏置。这里的$\mathbf{t}_{2d}$也叫作translation vector，但它和上面相机外参里的translation vector不是一个东西，但起到了类似的意义。

​ 这里的$f$，你可以把它按照弱透视投影里的那个scaling来理解，或者更简单地，单纯的认为它只是将标准3DMM里那些顶点的量级（大约几百）调整为更符合图像中的量级（可能-1~1）。

​ 所以这里就有了一个很有意思的比较，再看刚才的式子：

​ 从右到左，你可以把它看成“model”，“view”，“projection”三个部分的变换。这个和GAMES101和一些图形学教材非常类似。在模型变换（model transformation）的这个部分，我们把3DMM从标准模板进行形变，把它捏成想要的人的样子（$+\mathbf{A}_{id}\mathbf{\alpha }_{id}$），把它的表情捏成预定的样子（$+\mathbf{A}_{exp}\mathbf{\alpha }_{exp}$）；然后在视图变换（view transformation）里，整个人脸被正交阵$\mathbf{R}$旋转了；然后再作投影变换（projection transformation），这个3D的结果最终被打到的2D的形式，得到了图片。

​ 这个过程被总结为MVP变换，但其实GAMES101上讲的MVP变换描述了一个更正规情况下的事情。比如在GAMES101中的视图变换，其变换矩阵就是用上面说的lookat的事情构造的，并不是单纯的只有旋转$\mathbf{R}$，透视变换时其作的也是正常的透视变换而非简化后的弱透视变换。

​ 根源是我们这里在单纯的描述“从一张图片中重建出一个人脸mesh”时，我们不需要那么详细的描述。我们可以假定焦距无限远，然后不考虑近大远小，因为人头本身就不是一个很长的东西。

​ 只不过在这里，我们需要“意识到”投影变换的存在。正如前文所说，一个滑稽的事情就是：假如你入门3DV只是跟我一样通过NeRF入门的，那么你大概率“意识不到”投影变换的存在，你会把它弱化，结构为初二物理里平面镜成像规律中就能学到的“近大远小”。你虽然知道有这么个东西，但你大概率很难对这个有什么“intuition”。因为在NeRF里每个像素都是ray casting出来的，想象成是某种“投影”并不直接。因为从体渲染的角度来看，NeRF是backward mapping， 是发出光线去查点，你并不需要像forward mapping般的主动的去投影。

​ 意识到这些以后，我们可以看一下代码了。

​ 在recrop_images.py之前，其实每张输入的人脸图片是通过dlib库检测了一波人脸关键点的。如下图所示：

​ 从FFHQ数据集的对齐开始，就一直沿用一种方法：从这些关键点中，提取左眼，右眼，嘴部的关键点，然后整合出一个quad，其包含4个顶点，在图上可以连成一个类似平行四边形的图案，如上图中的红色圆点（灰色区域表示他们在原图外围）。FFHQ对齐的精髓在于以这4个点对图片进行仿射变换，从而将图片拉正。这样可以保证GAN学习到一个更规整的人脸分布，减少一些掉san的伪影。

​ 但在这里，我们不仅要对齐这个人头，我们还想用3DDFA估计出这个人头此时的位姿，这要求我们对quad进行进一步的处理。同时我们希望位姿符合EG3D的相机系统，所以接下来会有更复杂的一些处理。首先，利用已有的，通过关键点计算出的quad对图片进行仿射变换：

1
2
3
bound = np.array([[0, 0], [0, size-1], [size-1, size-1], [size-1, 0]], dtype=np.float32)
mat = cv2.getAffineTransform(quad[:3], bound[:3])
img = crop_image(img_orig, mat, size, size)

​ 然后用3DDFA扫一下仿射变换后的图片img：

1
2
param_lst, roi_box_lst = tddfa(img, boxes)
box_idx = find_center_bbox(roi_box_lst, w, h)

​ 这里find_center_bbox就是单纯的在所有roi_box_lst里，最接近图片中心的那个。但大部分时候图片里只有一张人脸，我们可以认为box_idx就是0。接下来我们会利用第box_idx个param_lst和roi_box_lst来进行处理：

1
2
3
param = param_lst[box_idx]
P = param[:12].reshape(3, -1)  # camera matrix
s_relative, R, t3d = P2sRt(P)

​ 我们可以打印一个P出来，会发现：

1
2
3
4
(Pdb) print(P)
[[ 4.7336455e-04  3.7309933e-06  1.8318256e-05  5.8912811e+01]
 [ 1.1534430e-06  4.8227943e-04  1.3704226e-05  6.9054771e+01]
 [-1.9893454e-05 -1.7727274e-05  4.7678972e-04 -6.6671005e+01]]

​ 这根本不像我们以为的相机矩阵，原因就是$\sqrt{f}$的存在，由于旋转矩阵的每一项可以看成$q_i$的二次型，所以旋转矩阵的每一项相当于被缩小了$f$倍。所以在P2sRt()函数中，我们就是来解算正常的P的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def P2sRt(P):
    """ decompositing camera matrix P.
    Args:
        P: (3, 4). Affine Camera Matrix.
    Returns:
        s: scale factor.
        R: (3, 3). rotation matrix.
        t2d: (2,). 2d translation.
    """
    t3d = P[:, 3]
    R1 = P[0:1, :3]
    R2 = P[1:2, :3]
    s = (np.linalg.norm(R1) + np.linalg.norm(R2)) / 2.0
    r1 = R1 / np.linalg.norm(R1)
    r2 = R2 / np.linalg.norm(R2)
    r3 = np.cross(r1, r2)

    R = np.concatenate((r1, r2, r3), 0)
    return s, R, t3d

​ 注意t3d中，实际上有效的只有前两个数，在tddfa中t3d的最后一位永远是-66.67，因为这里没有任何深度之类的事情（焦距无限远）。然后我们提取第一行和第二行，将其归一化，叉乘出第三行，得到新的正交阵作为旋转R。同时计算第一行和第二行模场的平均值，我们就可以估计出$1/f$，代码中记成了s（scale）。根据3DDFA用的BFM model的量级，其实$f$可以估计出大致是2000。

1
2
3
4
5
6
7
8
(Pdb) print(s_relative)
0.0004781045136041939
(Pdb) print(R)
[[ 0.9992211   0.00787572  0.03866785]
 [ 0.00239068  0.9995937   0.02840398]
 [-0.03842843 -0.02828942  0.9987962 ]]
(Pdb) print(t3d)
[ 58.91281   69.05477  -66.671005]

​ 然后，需要调整一下t3d，在代码中称为”Adjust z-translation in object space”，我推测这么做的原因是3DDFA估计出的结果，是隐含在BFM标准人头的那个坐标系下的：

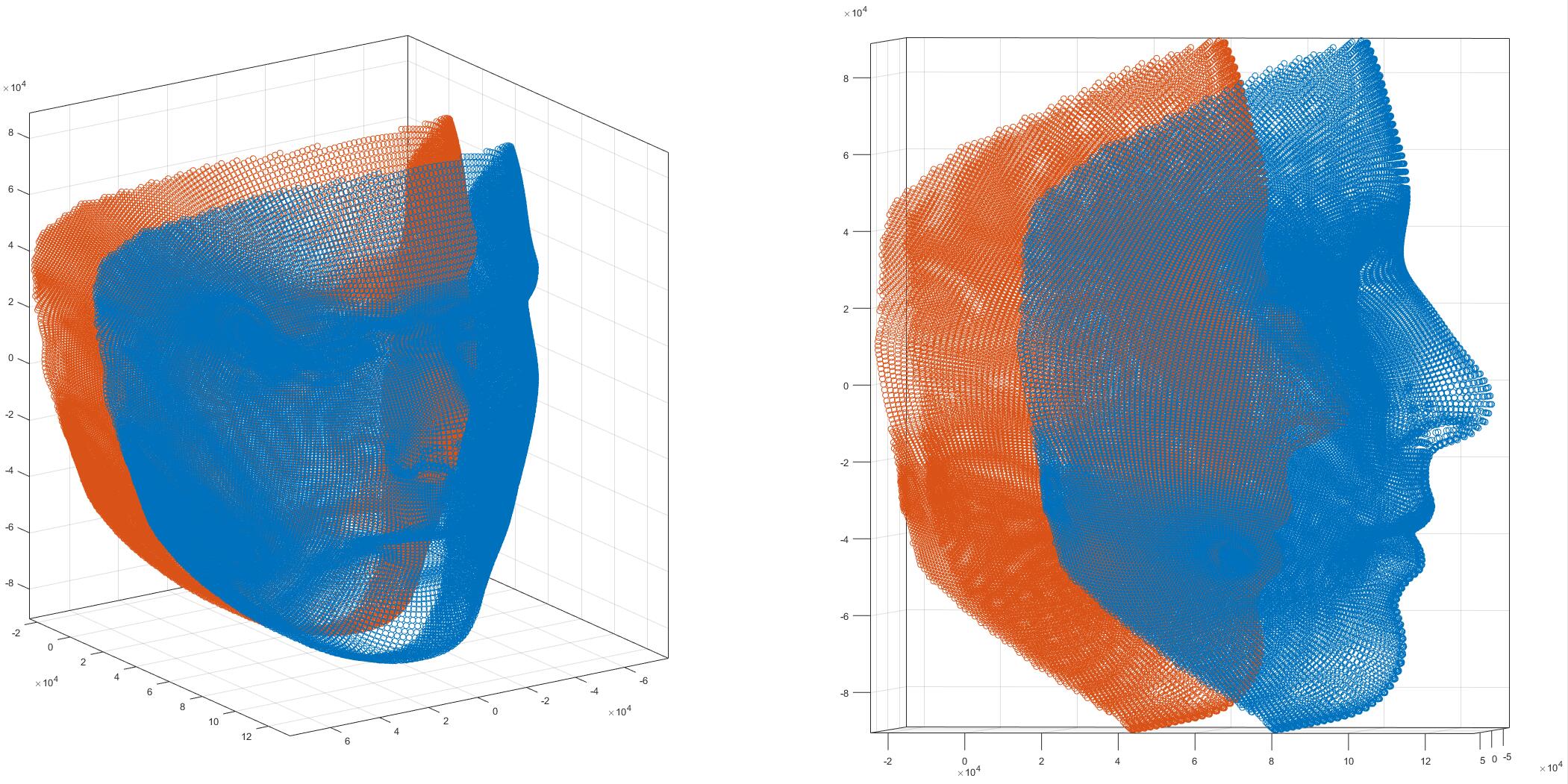
​ 如上图所示，蓝色的人脸是标准的BFM，橙色的是将z轴减去0.5*mean(z)以后的BFM。因为我们想要那个人头（是某种程度上）在原点附近的，0.5*mean(z)作为一个经验值就被作者采用了。可以看到右侧的橙色人脸，如果我们脑补一个完整的脑壳出来，那么差不多就是一个在原点处的人头了。

​ 这样做虽然是调整”z-translation”，但我们这里其实是没有真正的深度的，所以这样做的目的其实是修正t3d中的t2d，即：

1
2
3
4
5
R_ = param[:12].reshape(3, -1)[:, :3]
u = tddfa.bfm.u.reshape(3, -1, order='F')
trans_z = np.array([ 0, 0, 0.5*u[2].mean() ]) # Adjust the object center
trans = np.matmul(R_, trans_z.reshape(3,1))
t3d += trans.reshape(3)

​ 在正脸的时候，trans大概是：

1
2
3
[[ 0.6798876 ]
 [ 0.50863648]
 [17.69619383]]

​ 由于是正脸，所以修正项很小。

​ 在一些侧着头的情况下，大概是：

1
2
3
[[-11.60984414]
 [ -0.08104343]
 [ 14.03402536]]

​ 这时候修正项就不能忽略了。

​ 接下来，我们需要对t3d进行归一化，这一步基本算是数字图像处理课程里的习题，t3d本身是在3DDFA的尺寸下的，其中tddfa.size一般是120，我们需要通过之前Face_Boxes得到的roi_box_lst把t3d先缩放回原始图像上：

1
2
3
sx, sy, ex, ey = roi_box_lst[0]
scale_x = (ex - sx) / tddfa.size
scale_y = (ey - sy) / tddfa.size

​ 由于t3d的坐标系和图像坐标系的$y$轴是反的（如下图）：

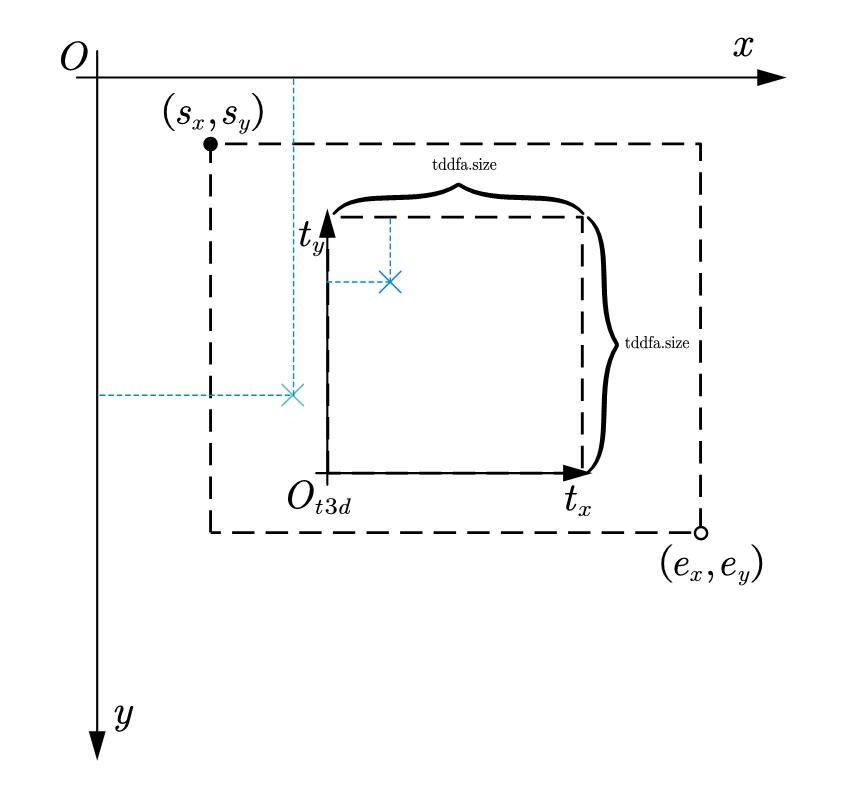
​ 所以进一步换算为：

1
2
t3d[0] = (t3d[0]-1) * scale_x + sx
t3d[1] = (tddfa.size-t3d[1]) * scale_y + sy

​ 然后再根据图片的w和h进行归一化：

1
2
t3d[0] = (t3d[0] - 0.5*(w-1)) / (0.5*(w-1)) # Normalize to [-1,1]
t3d[1] = (t3d[1] - 0.5*(h-1)) / (0.5*(h-1)) # Normalize to [-1,1], y is flipped for image space

​ 同时要对缩放系数s_relative也进行“重缩放”：

1
2
3
4
s_relative = s_relative * 2000
scale_x = (ex - sx) / (w-1)
scale_y = (ey - sy) / (h-1)
s = (scale_x + scale_y) / 2 * s_relative

​ 完成这些以后，我们终于可以对quad进行加工了：

1
2
3
4
5
6
quad_c = quad_c + quad_x * t3d[0]
quad_c = quad_c - quad_y * t3d[1]
quad_x = quad_x * s
quad_y = quad_y * s
c, x, y = quad_c, quad_x, quad_y
quad = np.stack([c - x - y, c - x + y, c + x + y, c + x - y]).astype(np.float32)

​ 我们可以看出，对quad进行修改的目的，是为了让quad圈定的图片中的人头的中心更贴近（TDDFA认为的）图像中心。即争取让每一张图片在对齐后，输入给TDDFA后都能输出近似为[60, 60, -66.7]的t3d（tddfa.size为120）。

​ 最后一步就是要得到c2w矩阵来做训练，由于现在的图像已经被裁剪成没有“translation”了，我们只需要拿来旋转$R$，就可以产生一个符合PanoHead的c2w了。

这里有一个比较不自然的事情，TDDFA输出的$R$其实是将BFM从canonical变换成图像中的姿态。在坐标系规定合适的情况下，它是等价于w2c中的$R$的，但许多时候不一定合适，这样可能$x$或$y$方向就会差个负号。我们下面的讨论里就当这里的$R$是等价于w2c里的$R$的。

​ 但与之前不同，我们并不是很清楚相机的位置，不能直接用角度定义。我们可以先给出相机外参w2c，然后求逆。当谈及相机外参时，我们往往会提到”translation vector”，即$t$。一个关于$t$的表述是：世界坐标系下的原点在相机坐标系下的表示。因为当你将$[0, 0, 0, 1]$左乘w2c后，你会得到$[t, 1]$。

​ 考虑旋转$R$和平移$t$构成的w2c，我们可以构造出其逆阵：

​ 所以考虑c2w中的旋转$R_C$和相机位置$C$，我们有：

​ 在之前的例子中，我们给定半径在球坐标系上采点作为相机的原点$C$，我们假设lookat是原点，那么forward vector其实就是$[-c_x,-c_y,-c_z]/\left| c \right| $，那么我们构造的$R_C$其实就是：

​ 那么直接代入$t=-RC$就会得到（注意向量$r$和向量$u$对于向量$c$都是正交的）：

​ 最后得到的结果即是相机位置的模长，由于相机位置是在球坐标系下采样得到的，所以就是半径。

​ 于是我们直接取t=[0,0,-radius]，即可得到w2c，继而求逆得到c2w：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def eg3dcamparams(R_in):
    camera_dist = 2.7
    intrinsics = np.array([[4.2647, 0, 0.5], [0, 4.2647, 0.5], [0, 0, 1]])
    # assume inputs are rotation matrices for world2cam projection
    R = np.array(R_in).astype(np.float32).reshape(4,4)
    # add camera translation
    t = np.eye(4, dtype=np.float32)
    t[2, 3] = - camera_dist

    # convert to OpenCV camera
    convert = np.array([
        [1, 0, 0, 0],
        [0, -1, 0, 0],
        [0, 0, -1, 0],
        [0, 0, 0, 1],
    ]).astype(np.float32)

    # world2cam -> cam2world
    P = convert @ t @ R
    cam2world = np.linalg.inv(P)

    # add intrinsics
    label_new = np.concatenate([cam2world.reshape(16), intrinsics.reshape(9)], -1)
    return label_new

​ 到这里，才完成了全部。我们终于从一张wild-image出发，得到了对齐后的图像和对应的符合EG3D格式的相机位姿。

3D Gaussian Splatting

​ 在3DGS中，有着更加“practical”的相机系统。由于3DGS是一种显式的表达方法，其跟NeRF在相机实现上的最大不同就是因为其是forward mapping，所以必须手动实现投影的过程。除了这一点以外，由于3DGS的官方代码开发周期比较长，所以里面很多令人困惑的地方，下面我们一并过一下。

​ 3DGS中将相机的一些属性组织进一个Camera类中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Camera(nn.Module):
    def __init__(self, colmap_id, R, T, FoVx, FoVy, image, gt_alpha_mask,
                 image_name, uid,
                 trans=np.array([0.0, 0.0, 0.0]), scale=1.0, data_device = "cuda"
                 ):
        super(Camera, self).__init__()

        self.uid = uid
        self.colmap_id = colmap_id
        self.R = R
        self.T = T
        self.FoVx = FoVx
        self.FoVy = FoVy
        self.image_name = image_name

        try:
            self.data_device = torch.device(data_device)
        except Exception as e:
            print(e)
            print(f"[Warning] Custom device {data_device} failed, fallback to default cuda device" )
            self.data_device = torch.device("cuda")

        self.original_image = image.clamp(0.0, 1.0).to(self.data_device)
        self.image_width = self.original_image.shape[2]
        self.image_height = self.original_image.shape[1]

        if gt_alpha_mask is not None:
            self.original_image *= gt_alpha_mask.to(self.data_device)
        else:
            self.original_image *= torch.ones((1, self.image_height, self.image_width), device=self.data_device)

        self.zfar = 100.0
        self.znear = 0.01

        self.trans = trans
        self.scale = scale

        self.world_view_transform = torch.tensor(getWorld2View2(R, T, trans, scale)).transpose(0, 1).cuda()
        self.projection_matrix = getProjectionMatrix(znear=self.znear, zfar=self.zfar, fovX=self.FoVx, fovY=self.FoVy).transpose(0,1).cuda()
        self.full_proj_transform = (self.world_view_transform.unsqueeze(0).bmm(self.projection_matrix.unsqueeze(0))).squeeze(0)
        self.camera_center = self.world_view_transform.inverse()[3, :3]

​ 具体的逻辑是，当在Scene中加载数据集中的每一张图片时，旋即读取相应的COLMAP或synthesis数据集的transform，对应实例化一个Camera出来。然后会来到scene/dataset_readers.py里，可以看到其为这两种形式的数据集layout提供了两种回调函数：

1
2
3
4
sceneLoadTypeCallbacks = {
    "Colmap": readColmapSceneInfo,
    "Blender" : readNerfSyntheticInfo
}

​ 但无论是哪种，我们都会发现，程序赋值的$R$，都是相机外参的旋转的转置：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def readColmapCameras(cam_extrinsics, cam_intrinsics, images_folder):

	...
	
        R = np.transpose(qvec2rotmat(extr.qvec))
    ...
    
def readCamerasFromTransforms(path, transformsfile, white_background, extension=".png"):

	...

            # get the world-to-camera transform and set R, T
            w2c = np.linalg.inv(c2w)
            R = np.transpose(w2c[:3,:3])  # R is stored transposed due to 'glm' in CUDA code
            
            ...

​ 这个其实是历史遗留问题，我们返回来看Camera实现里关于变换的计算：

1
2
3
4
self.world_view_transform = torch.tensor(getWorld2View2(R, T, trans, scale)).transpose(0, 1).cuda()
self.projection_matrix = getProjectionMatrix(znear=self.znear, zfar=self.zfar, fovX=self.FoVx, fovY=self.FoVy).transpose(0,1).cuda()
self.full_proj_transform = (self.world_view_transform.unsqueeze(0).bmm(self.projection_matrix.unsqueeze(0))).squeeze(0)
self.camera_center = self.world_view_transform.inverse()[3, :3]

​ 查看getWorld2View2：

1
2
3
4
5
6
7
8
9
10
11
12
def getWorld2View2(R, t, translate=np.array([.0, .0, .0]), scale=1.0):
    Rt = np.zeros((4, 4))
    Rt[:3, :3] = R.transpose()
    Rt[:3, 3] = t
    Rt[3, 3] = 1.0

    C2W = np.linalg.inv(Rt)
    cam_center = C2W[:3, 3]
    cam_center = (cam_center + translate) * scale
    C2W[:3, 3] = cam_center
    Rt = np.linalg.inv(C2W)
    return np.float32(Rt)

​ 也就是说输入进Camera的R本身就是w2c转置过的，也就是c2w里的旋转，然后这里又取个转置得到Rt，那么说明Rt应该是w2c，然后这里留了一个修正姿态的废案，给Rt取逆得到c2w。然后再给c2w求逆得到w2c，所以这个函数返回的是相机外参/w2c，这没什么问题。

​ 但在给self.world_view_transform赋值的时候，刚传出来的w2c会再转置一下。所以我们得到的其实是：

​ 同样的，在创建透视投影矩阵时，最后也是将结果转置一下，得到$P^T$。这里如果我们检视getProjectionMatrix()，会发现其和我们熟悉的透视投影矩阵不太一样，代码中实现的是：

​ 而我们更熟悉的投影矩阵是：

​ 原因是因为这里的投影矩阵是将$z$投影到了$[0,1]$，而不是$[-1,1]$，我们可以重新走一下推投影矩阵的过程。根据待定系数法得到$M_{persp\rightarrow ortho}$这一步是没有变化的，这一步的推导在NeRF中考察NDC空间时我们已经做过了。

​ $z_{\mathrm{sign}}$可能为1或-1，这取决于坐标系是左手系还是右手系，更具体的说，近平面$n$和远平面$f$是正还是负。通过$M_{persp\rightarrow ortho}$会将视锥体变换成$[l,r]\times[b,t]\times[n,f]$的长方体，然后我们应用平移变换和缩放变换来得到canonical的表示（注意$z$轴投影到$[0,1]$）：

​ 于是投影矩阵$P$即：

​ 你或许发现第一行的第三个元素和第二行的第三个元素，跟代码实现不符。这应该是代码实现的BUG，但由于函数内定义的视锥是对称的（$r=-l,t=-b$），所以这一项为0，不会影响结果。

​ 为了对这个过程有更加透彻的理解，这里展示了一个透视矩阵视场角，近平面，远平面变化时，视锥体（黑）和canonical（红）的样子：

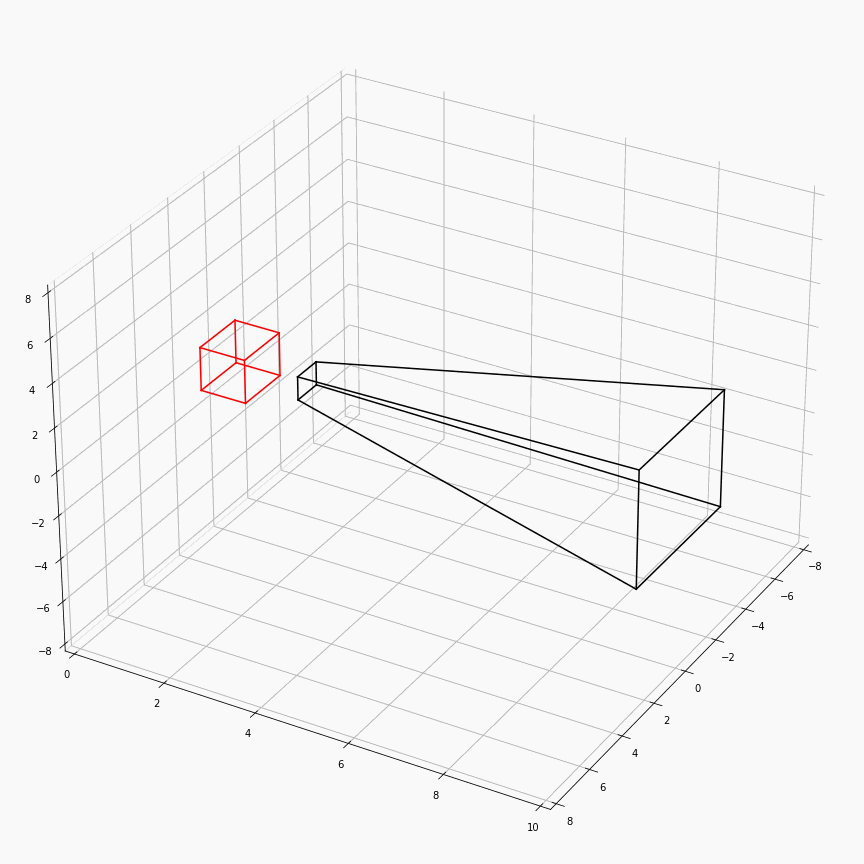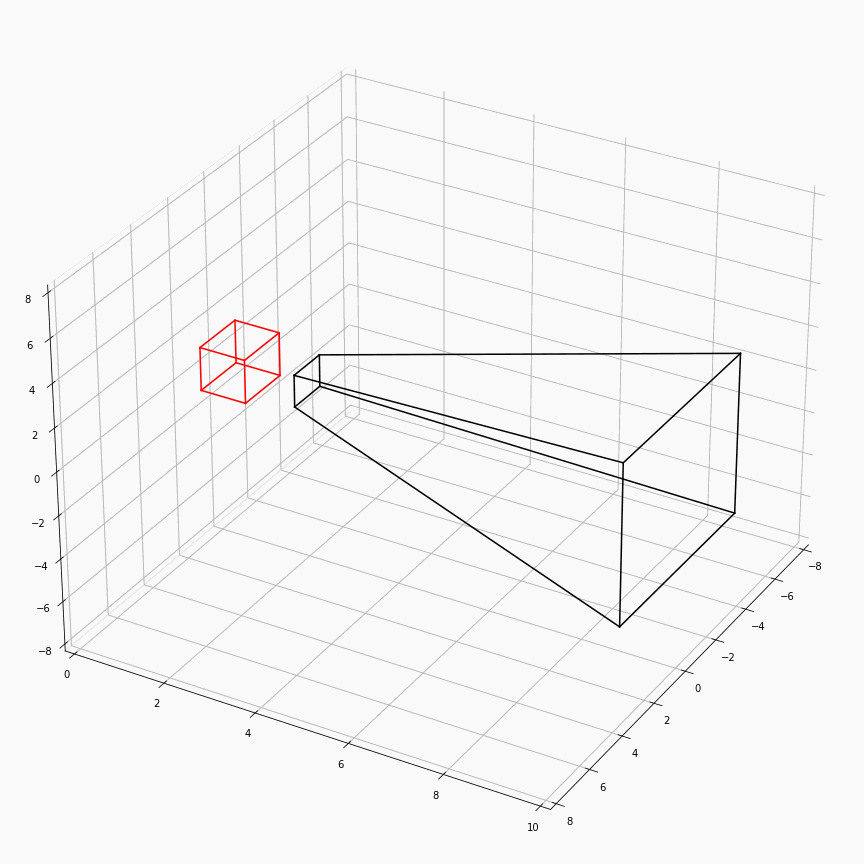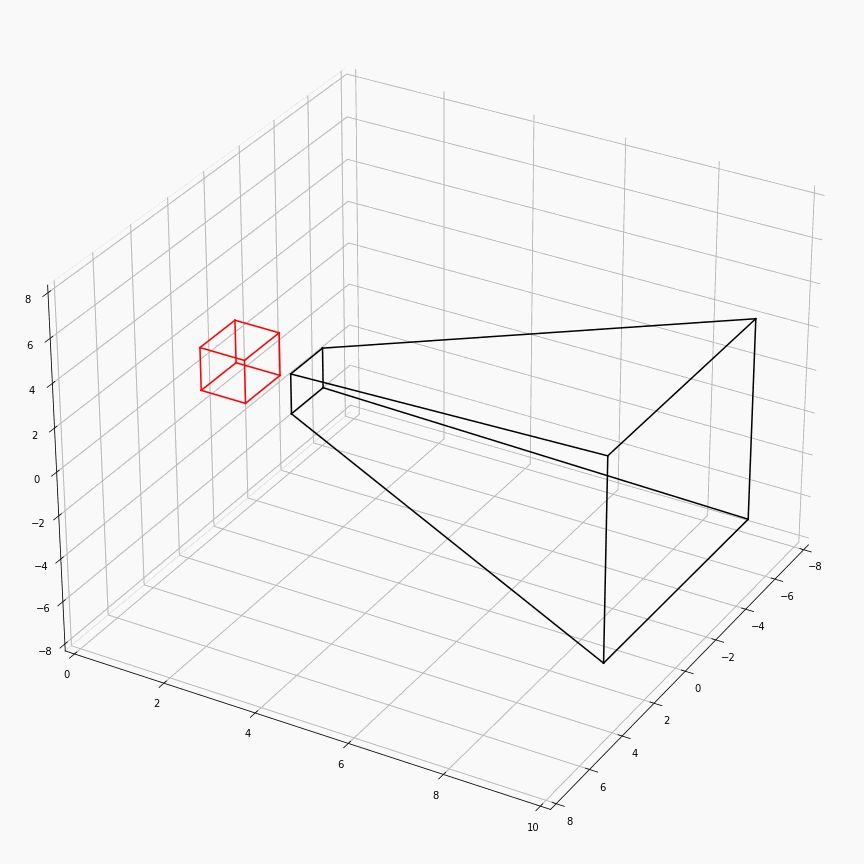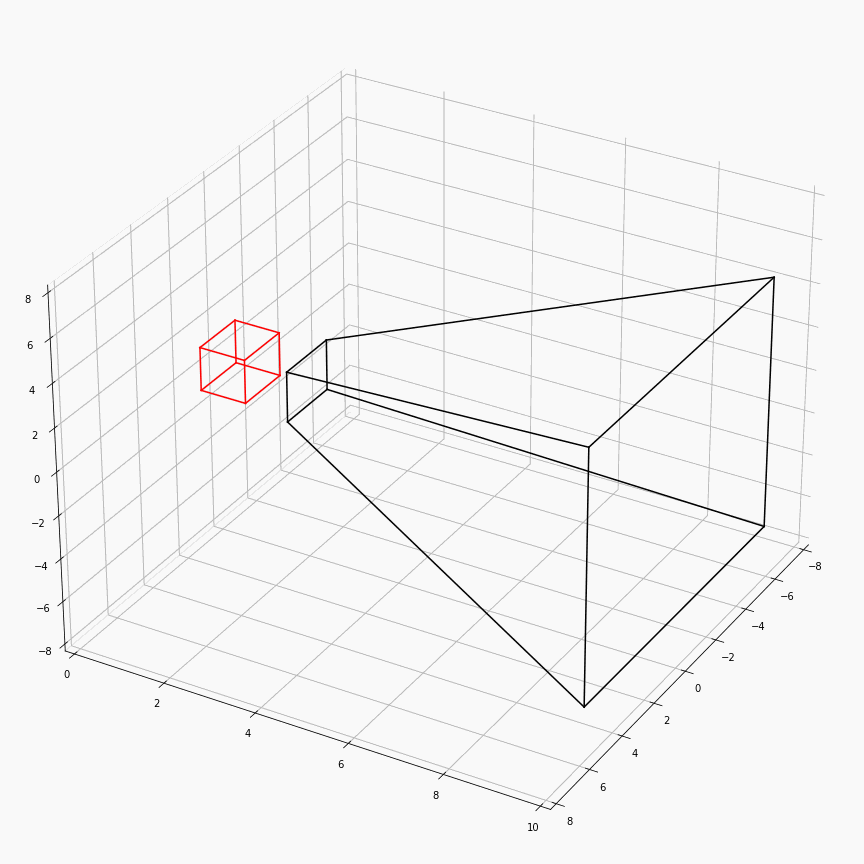
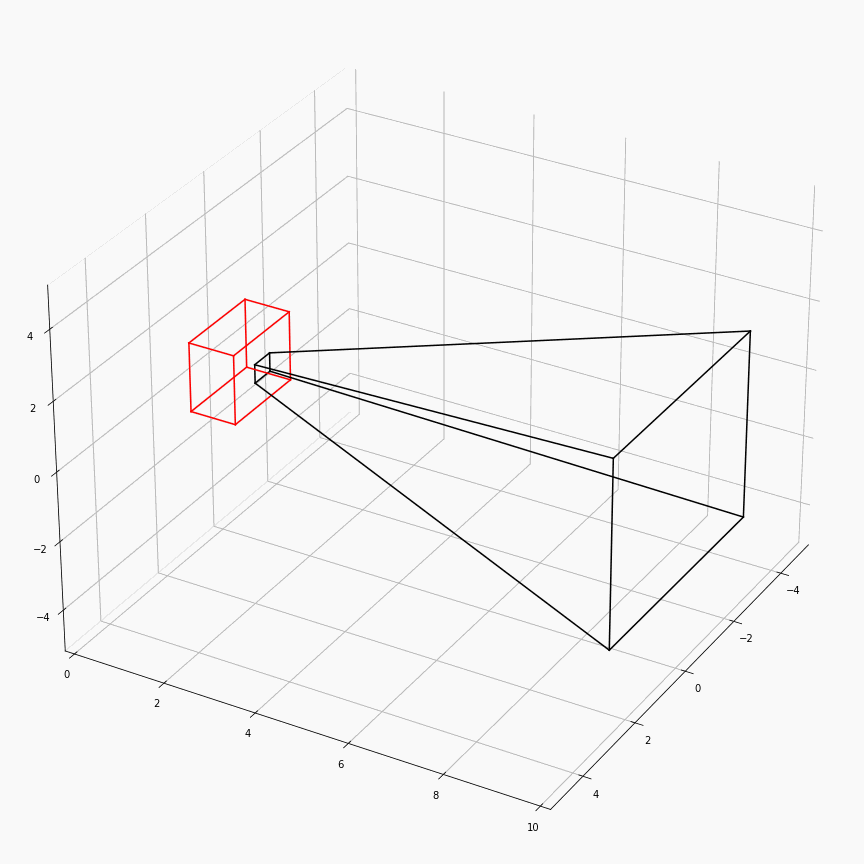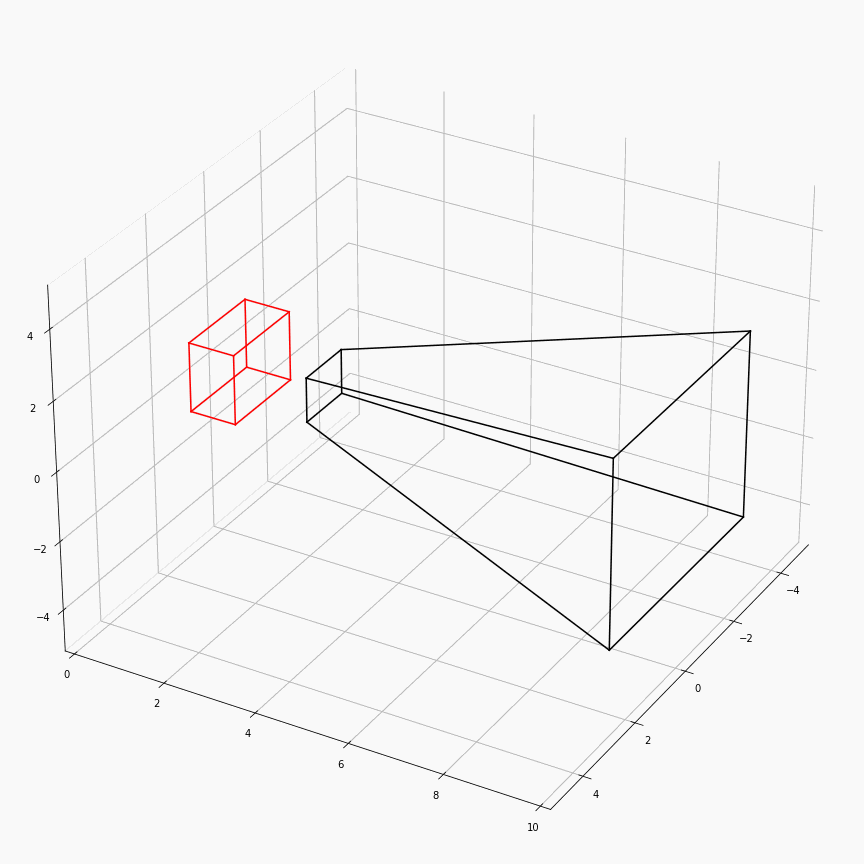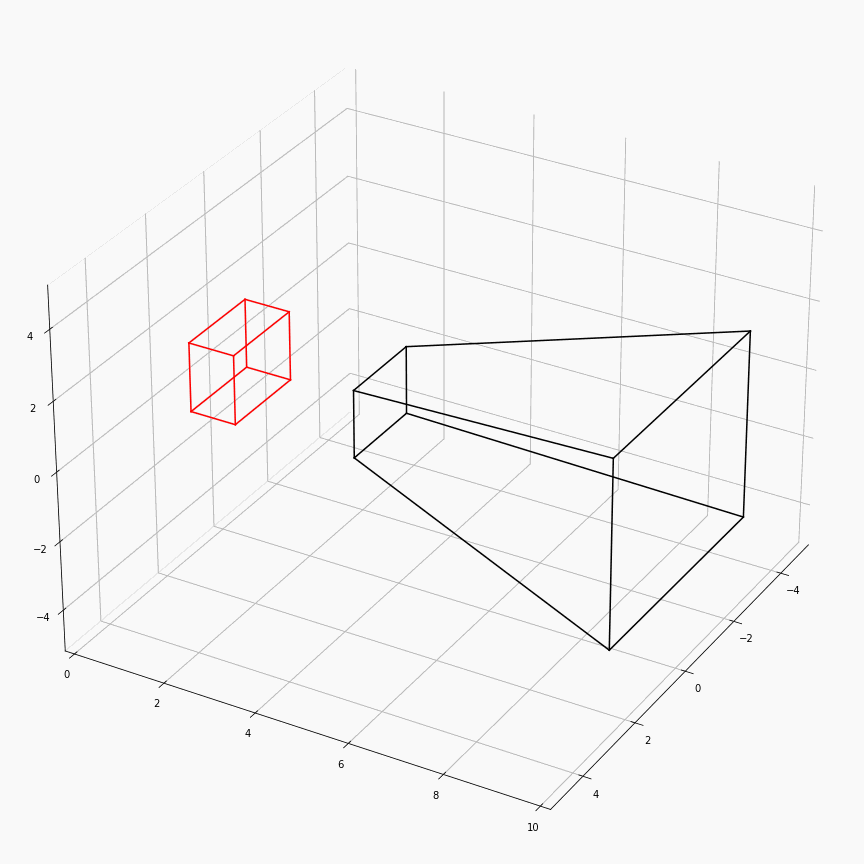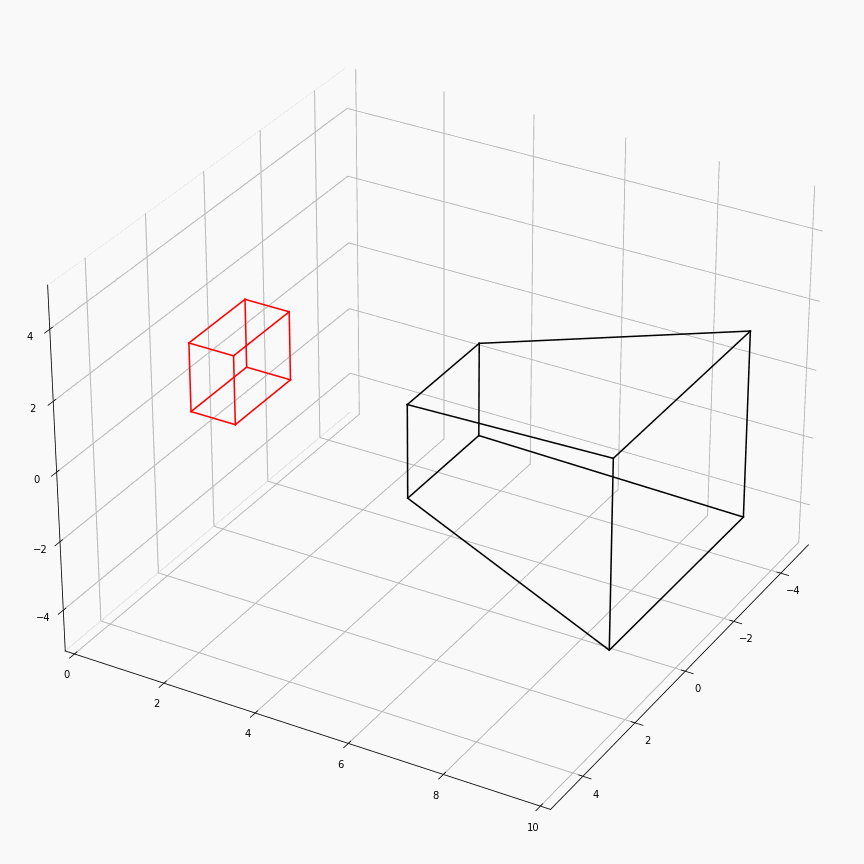
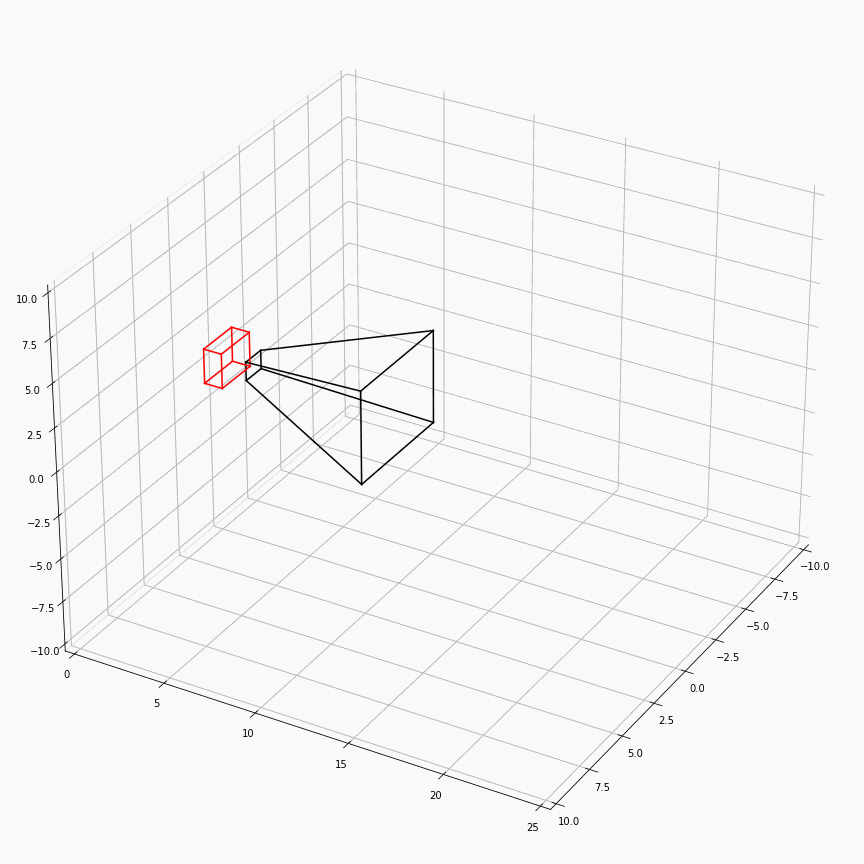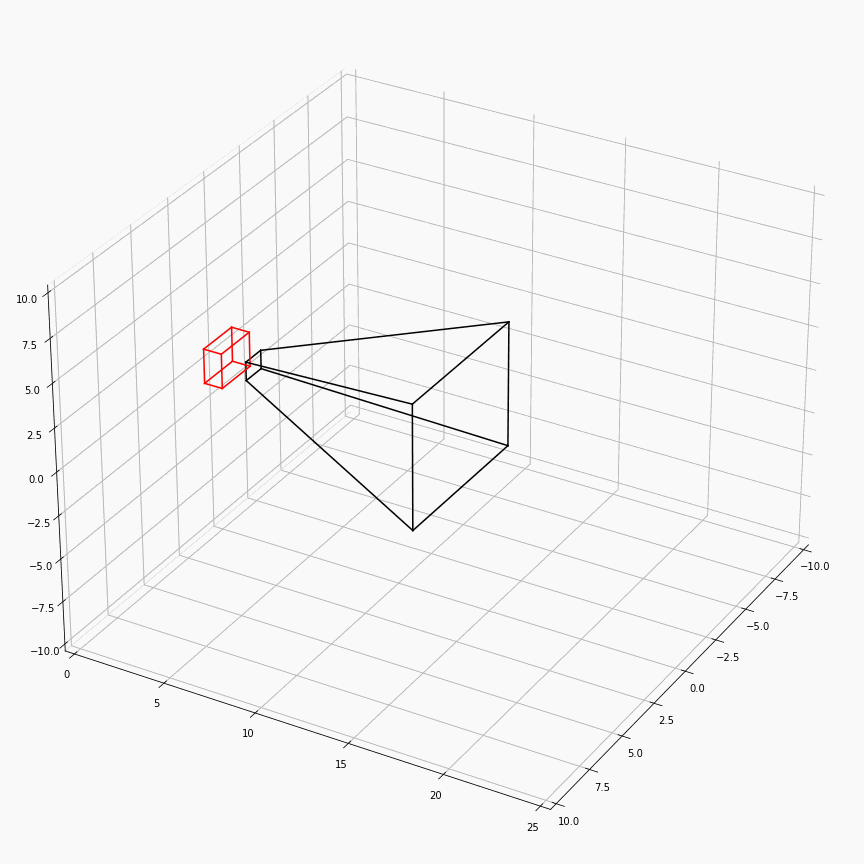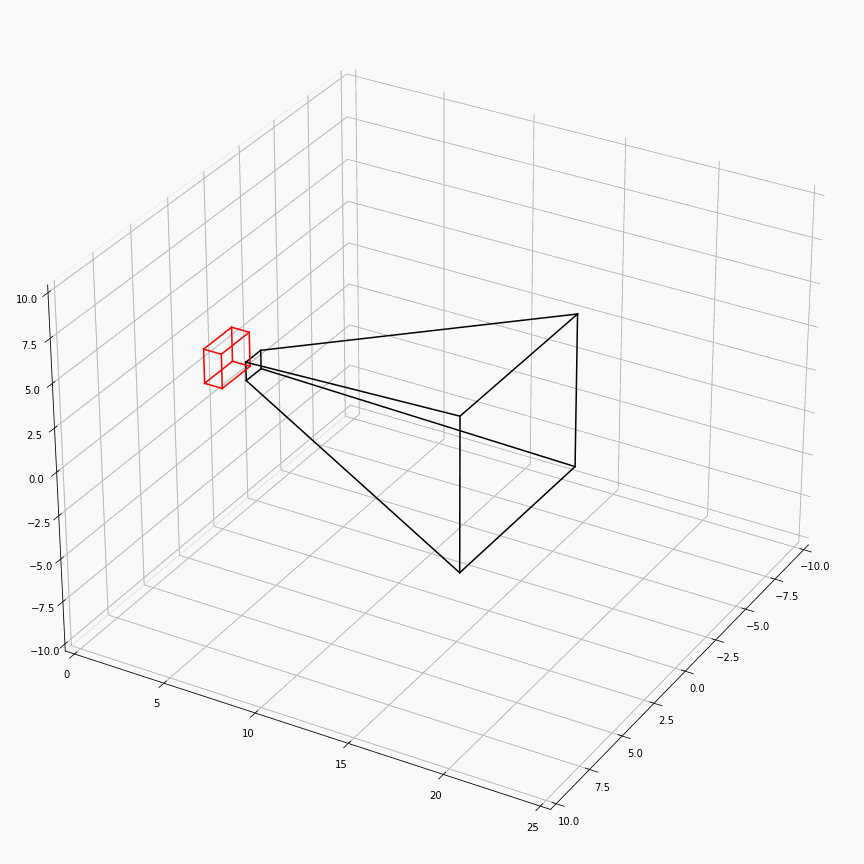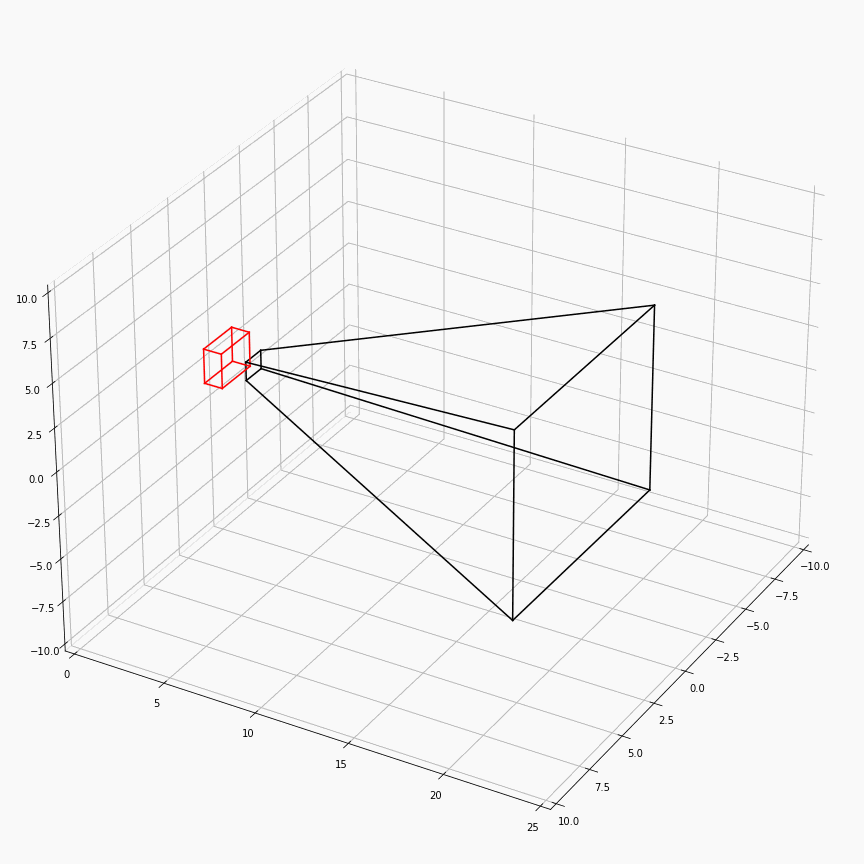
​ 注意这里$z$轴是被缩放到$[0,1]$，所以其看起来是个长方体而非正方体。

​ 我们继续回到代码，之后的self.full_proj_transform是$M^T P^T$，刚才的self.world_view_transform是$M^T$，在render时我们传入CUDA侧的变换都是转置过的。这其实是因为CUDA代码中是按照glm的规范，即列主序实现的矩阵乘。例如在cuda_rasterizer/auxiliary.h中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
__forceinline__ __device__ float3 transformPoint4x3(const float3& p, const float* matrix)
{
	float3 transformed = {
		matrix[0] * p.x + matrix[4] * p.y + matrix[8] * p.z + matrix[12],
		matrix[1] * p.x + matrix[5] * p.y + matrix[9] * p.z + matrix[13],
		matrix[2] * p.x + matrix[6] * p.y + matrix[10] * p.z + matrix[14],
	};
	return transformed;
}

__forceinline__ __device__ float4 transformPoint4x4(const float3& p, const float* matrix)
{
	float4 transformed = {
		matrix[0] * p.x + matrix[4] * p.y + matrix[8] * p.z + matrix[12],
		matrix[1] * p.x + matrix[5] * p.y + matrix[9] * p.z + matrix[13],
		matrix[2] * p.x + matrix[6] * p.y + matrix[10] * p.z + matrix[14],
		matrix[3] * p.x + matrix[7] * p.y + matrix[11] * p.z + matrix[15]
	};
	return transformed;
}

​ 可以看到这些索引并不是按照我们以为的：

1
2
3
...
matrix[0] * p.x + matrix[1] * p.y + matrix[2] * p.z + matrix[3],
...

​ 索引排列。

​ 接下来我们简要讨论下为什么要将这两个变换传入CUDA侧。传入CUDA的两个变换矩阵viewmatrix和projmatrix有不同的作用，首先通过这两个变换，可以判断每个线程处理的高斯核是否在关心的视锥内，如果不在可以直接结束该线程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
__forceinline__ __device__ bool in_frustum(int idx,
	const float* orig_points,
	const float* viewmatrix,
	const float* projmatrix,
	bool prefiltered,
	float3& p_view)
{
	float3 p_orig = { orig_points[3 * idx], orig_points[3 * idx + 1], orig_points[3 * idx + 2] };

	// Bring points to screen space
	float4 p_hom = transformPoint4x4(p_orig, projmatrix);
	float p_w = 1.0f / (p_hom.w + 0.0000001f);
	float3 p_proj = { p_hom.x * p_w, p_hom.y * p_w, p_hom.z * p_w };
	p_view = transformPoint4x3(p_orig, viewmatrix);

	if (p_view.z <= 0.2f)// || ((p_proj.x < -1.3 || p_proj.x > 1.3 || p_proj.y < -1.3 || p_proj.y > 1.3)))
	{
		if (prefiltered)
		{
			printf("Point is filtered although prefiltered is set. This shouldn't happen!");
			__trap();
		}
		return false;
	}
	return true;
}

​ projmatrix计算出的结果p_proj，会联合cov2d，用于计算radii，从而得到该高斯核影响那些像素：

1
2
3
4
5
6
7
8
9
10
11
12
13
// Compute extent in screen space (by finding eigenvalues of
// 2D covariance matrix). Use extent to compute a bounding rectangle
// of screen-space tiles that this Gaussian overlaps with. Quit if
// rectangle covers 0 tiles. 
float mid = 0.5f * (cov.x + cov.z);
float lambda1 = mid + sqrt(max(0.1f, mid * mid - det));
float lambda2 = mid - sqrt(max(0.1f, mid * mid - det));
float my_radius = ceil(3.f * sqrt(max(lambda1, lambda2)));
float2 point_image = { ndc2Pix(p_proj.x, W), ndc2Pix(p_proj.y, H) };
uint2 rect_min, rect_max;
getRect(point_image, my_radius, rect_min, rect_max, grid);
if ((rect_max.x - rect_min.x) * (rect_max.y - rect_min.y) == 0)
return;

​ 计算cov2d时，需要用viewmatrix得到在相机下高斯点的位置，然后用EWA sampling中仿射变换的一阶近似来得到$J$，才能得到cov2d：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// The following models the steps outlined by equations 29
// and 31 in "EWA Splatting" (Zwicker et al., 2002). 
// Additionally considers aspect / scaling of viewport.
// Transposes used to account for row-/column-major conventions.
float3 t = transformPoint4x3(mean, viewmatrix);

const float limx = 1.3f * tan_fovx;
const float limy = 1.3f * tan_fovy;
const float txtz = t.x / t.z;
const float tytz = t.y / t.z;
t.x = min(limx, max(-limx, txtz)) * t.z;
t.y = min(limy, max(-limy, tytz)) * t.z;

glm::mat3 J = glm::mat3(
focal_x / t.z, 0.0f, -(focal_x * t.x) / (t.z * t.z),
0.0f, focal_y / t.z, -(focal_y * t.y) / (t.z * t.z),
0, 0, 0);

glm::mat3 W = glm::mat3(
viewmatrix[0], viewmatrix[4], viewmatrix[8],
viewmatrix[1], viewmatrix[5], viewmatrix[9],
viewmatrix[2], viewmatrix[6], viewmatrix[10]);

glm::mat3 T = W * J;

glm::mat3 Vrk = glm::mat3(
cov3D[0], cov3D[1], cov3D[2],
cov3D[1], cov3D[3], cov3D[4],
cov3D[2], cov3D[4], cov3D[5]);

glm::mat3 cov = glm::transpose(T) * glm::transpose(Vrk) * T;

​ 这就是传入这两个变换的逻辑，如果你对这其中的一些推导感兴趣，可以查阅这篇博客。

​ 在讨论中我们忽略了一个传入CUDA侧的参数：相机位置。它的作用是计算点和相机的方向，从而计算球谐系数。在Python侧，相机位置通过计算：

1
self.camera_center = self.world_view_transform.inverse()[3, :3]

来实现，我们在先前已经讨论过为什么对w2c求逆可以得到相机位置了。

Lie theory of rotations

​ 我们现在已经结合许多实际的项目代码分析并可视化了一些内容，在最后我们需要将目光放在一直以来都被认为习以为常的旋转$R$上。

​ 本科课程上都大概了解过，比如一个正交阵对应一个旋转变换（行列式为-1时还多做了一个镜像变换）。比如我们知道用欧拉角描述旋转，需要注意顺序，会有万向节死锁，然后有了用四元数表示旋转等等。然后在学习参数化模型时我们知道有个很奇怪的公式（罗德里格斯公式）可以把一个轴角式的旋转向量变成熟悉的$R\in\mathbb{R}^{3\times3}$。

​ 了解到这一层对于搬运代码来说完全足够，但这会萌生更多新的问题，比如罗德里格斯公式除了可以几何意义上推导，还可以怎么来？为什么有时候这个公式左侧不叫$R$而叫$\exp(\cdot)$？为什么实际的旋转是四元数表示的旋转的两倍？以及四元数这一堆是什么？

​ 我们需要用一个更抽象但合适的理论来概括一下，即需要借助李群（Lie Group）和李代数（Lie algebra）。由于我不是数学或物理专业出身，所以下面的叙述以建立直觉和认识为主。对于像我这样没有学过数学的人来说，阅读《视觉SLAM十四讲》的第四章是最合适的切入方式，但仅仅阅读那一段还是太过于管中窥豹了，接下来我们先以《视觉SLAM》十四讲的部分引入，然后再此基础上追加一些内容。

​ 在大一的时候，我们学过如何计算向量叉乘（外积）：

​ 右边的结果可以进一步拆成矩阵与向量的乘法：

​ 我们将展成的这个矩阵记作$\boldsymbol{a}^{\land}$，它是一个反对称矩阵。也就是说，对于任意一个向量，都对应着一个唯一的反对称矩阵，从而可以将外积$\boldsymbol{a}\times\boldsymbol{b}$变换成线性变换$\boldsymbol{a}^{\land}\boldsymbol{b}$。同理，对于一个反对称矩阵$A$，我们也能找到一个向量$\boldsymbol{a}$与它一一对应，我们记作$\boldsymbol{a}=A^{\lor}$。

​ 接下来我们这里按SLAM十四讲里的方法来引入“李代数”，考虑旋转矩阵$R$，我们假设其代表某个相机的旋转，即随时间变化。那么根据旋转矩阵的正交性：

​ 非正式地，我们对两边关于时间求导，得到：

​ 这说明$\dot{R}\left( t \right) R\left( t \right) ^T$是一个反对称矩阵，那么一定有一个三维向量$\phi \left( t \right)$与其对应，即$\dot{R}\left( t \right) R\left( t \right) ^T=\phi \left( t \right) ^{\land}$。对上式右乘$R(t)$可以得到$\dot{R}\left( t \right)$，进一步，我们再考虑$R(t)$的一阶泰勒展开：

​ 不失一般性的，我们取$t_0=0$且$R(0)=\mathbf{I}$，于是右边可以写成：

​ 我们看到，向量$\phi \left( t_0 \right) $某种程度上反应了$R$的变化。除此以外，由于：

​ 我们假设在$t_0$附近$\phi \left( t_0 \right) =\phi _0$，那么上式就是一个普通的常微分方程，初始值为$R(0)=\mathbf{I}$：

​ 这里$t$只是我们为了进行上述推理所虚设的一个值，他其实没必要是$0$，只要在$R(t_0)=\mathbf{I}$，那么在$t_0$的邻域内就可以有这样的关系。

​ 我们其实还没有定义这个情景下的指数运算。但我们能感觉到，冥冥之中，好像我如果有一个向量，然后把这个向量写成反对称阵，然后做一下这个“$\exp(\cdot)$”就可以得到$R$了。除此以外，我们其实也并不了解“为什么上面要这么引入”，为什么要构造一个似是而非的“$R(t)$”和凑个微分方程，感觉很生硬。

但其实，李群、李代数的初衷好像就是为了求解微分方程。不过好像不是上面这样。

​ 下面我们先引入群：我们刚才是习惯上想用$R(t)$来描述一组$R$，我们最好引入另一个结构来描述一组$R$，即群。群的定义是：

令$G$是一个非空集合，它有一个运算$\cdot$，考虑$G\times G \rightarrow G$构成的代数结构$(G,\cdot)$，若满足：

  1. 封闭性：$\forall a,b\in G,\quad a\cdot b\in G$
  2. 结合律：$\forall a,b,c\in G,\quad \left( a\cdot b \right) \cdot c=a\cdot \left( b\cdot c \right) $
  3. 幺元：$\exists g_0\in G,\quad s.t. \forall g\in G, g_0\cdot g=g\cdot g_0=g$
  4. 逆：$\forall g\in G,\quad \exists g^{-1}\in G,\quad s.t.\quad g\cdot g^{-1}=g_0$

则称$(G,\cdot)$为一个群。

​ 所以我们一直在处理的旋转$R$，它和矩阵乘法就组成了一个群。显然旋转变换的复合还是旋转变换，且矩阵乘法满足结合律，旋转变换存在幺元即单位旋转，每个旋转变换都存在逆阵。我们将行列式为1的这些旋转矩阵，与矩阵乘法组成的群，称为特殊正交群（Special Orthogonal Group），记作$\mathrm{SO}(n)$：

​ 我们关心的往往是二维和三维上的旋转，即$\mathrm{SO}(2),\mathrm{SO}(3)$。更重要的是，旋转是可以连续变化的。这种具有连续（光滑）性质的群，称为李群。我们可以简单的认为，由于李群的连续性，使得我们比较熟悉的微积分可以作为分析李群的工具。

​ 事实上，每个李群都对应一个李代数，李代数反应了李群在幺元附近的性质，即描述了幺元附近的正切空间。我们可以以二维时的情景举例，考虑复平面上的旋转$e^{i\theta}$，它满足群的定义，同时是光滑的，所以是李群。其幺元为$e^{i0}=1$，我们可以画出：

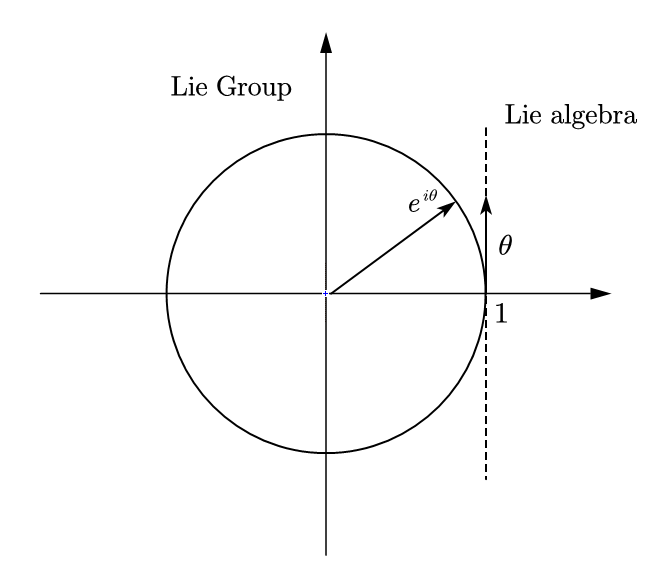
​ 我们作出幺元处的“切线”，如果我们沿着切线方向，取一个长度为$\theta$的向量，那么作$e^{i\theta}$直接就得到了群上的元素。那么切线方向张成的空间，其实就是李代数。这个过程即指数映射，再从群上的元素计算李代数上的元素即对数映射。

​ 这个指数映射是具有一般性的，我们考虑幺元$g(0)=1$附近的无穷小的群：

​ 我们将$J$称作生成元（generator），因为它从幺元处导引出了$g(\epsilon)$，那么对于一个有限的变换$g(\theta)$，只需要有：

​ 那么根据重要极限，我们就有：

​ 所以刚才的例子就是生成元取$J=i$时的情况。所以从生成元和幺元出发，我们可以得到整个李群。这就是为什么，在刚才微分方程背景下的引入中，我们有“只要在$R(t_0)=\mathbf{I}$，那么在$t_0$的邻域内就可以有这样的关系。”。

​ 有了对李群和李代数的更直观的了解，现在我们引入李代数的定义：

考虑向量空间$G^{\prime}$，数域$F$，和一个二元运算$[,]$，如果$G^{\prime}\times G^{\prime} \rightarrow G^{\prime}$构成的结构$(G^{\prime},[,])$满足：

  1. 封闭性：$\forall a,b \in G^{\prime},[a,b]\in G^{\prime}$
  2. 双线性：$\forall a,b,c\in G^{\prime}, f,g\in F\quad \left[ fa+gb,c \right] =f\left[ a,c \right] +g\left[ b,c \right] ,\quad \left[ c,fa+gb \right] =f\left[ c,a \right] +g\left[ c,b \right] $
  3. 自反性：$\forall a\in G^{\prime},\quad \left[ a,a \right] =0$
  4. 雅可比等价：$\forall a,b,c\in G^{\prime},\quad \left[ a,\left[ b,c \right] \right] +\left[ c,\left[ a,b \right] \right] +\left[ b,\left[ c,a \right] \right] =0$

其中二元运算$[,]$称为李括号（Lie bracket），这个运算只要求自反，不要求结合律，用于表达两个元素的差异。

​ 在这里要提及一下Baker-Campbell-Hausdorff公式，这个式子给出了李群上的运算和李代数上的运算的关联，考虑$G^{\prime}$上的元素$a,b$，有：

​ 这个式子的意思是说，考虑李代数上的$a$，作指数映射得到$e^a\in G,e^b\in G$，他们作群上的运算的结果，等价于将$a,b$按那一串无穷级数计算再映射的结果。特别地，在我们刚才举的二维例子里，向量$\theta$上的运算纯是标量的计算，李括号始终是0，所以没有级数后面那些余项。

​ 我们刚才讨论的$\phi \in\mathbb{R}^{3}$其实就是$\mathrm{SO}(3)$对应的李代数，记每个$\phi$代表的反对称矩阵为$\varPhi$：

​ 李括号为$[\phi_1,\phi_2]=\varPhi_1 \varPhi_2-\varPhi_2 \varPhi_1$（我并不清楚李括号的运算是否有其他形式，但群元素为矩阵时的李括号好像就是这个，而我们处理的大部分情况好像也就是矩阵的时候），所以我们可以说$\mathrm{SO}(3)$对应的李代数$\mathfrak{s} \mathfrak{v} \left( 3 \right) $为：

​ 现在我们来考虑计算指数映射$\exp(\phi^\land)$，我们定义对于复方阵$A$，有对应的复方阵$\exp(A)$：

​ 形式上即泰勒展开。对于指数映射出的矩阵$\exp(A)$，这里有一个比较重要的性质：

这是由于任何复方阵$A$都可以作相似变换，得到一个三角阵：

​ 那么两边作指数映射：

​ 两边取行列式得$\det \left( \exp \left( A \right) \right) =\det \left( \exp \left( T \right) \right) $，又因为$\det(\exp(T))=\exp(\mathrm{tr}(A))$，所以上述性质得证明。

​ 后面我们会看到，这个性质提供了一种计算生成元的方法。下面我们考虑$\phi\in\mathbb{R}^3$，将其分解为模长$\theta$和方向$a$，注意$a$的模长是1，考虑其张成的反对称矩阵$a^\land$，有很好的两条性质：

​ 于是我们就可以展开$\exp(\phi^\land)$中的高次项了：

​ 于是我们就得到了罗德里格斯公式，这个公式在SMPL和FLAME都用到了。这事实上说明，$\mathfrak{s} \mathfrak{v} \left( 3 \right) $里的$\phi$其实就是几何意义上的旋转向量。相应地，我们也可以定义对数映射，来将$\mathrm{SO}(3)$中的元素对应到$\mathfrak{s} \mathfrak{v} \left( 3 \right) $上：

​ 这个式子比较难处理，更明智的做法是通过指数映射的结论两边取迹：

​ 现在我们从指数映射上解答了罗德里格斯公式，下面我们开始讨论一下四元数，我们知道四元数是所谓：

​ 一般定义下，我们有$\boldsymbol{i}^2=\boldsymbol{j}^2=\boldsymbol{k}^2=-1,\boldsymbol{ijk}=-1$（左右手系下一些区别会不一样），我们被告知，可以用一个单位四元数$q$，即满足$\sqrt{a^2+b^2+c^2+d^2}=1$的四元数，来指定旋转。具体来说将一个三维点$p$指定为纯虚四元数$p=[0,x,y,z]^T=[0,v]^T$，那么旋转后结果为$p^{\prime}=qpq^{-1}$的虚部（这里的乘法均为四元数乘法）。这个结构具有奇怪的计算方法，理解起来比较抽象。

​ 我们会发现，这个结构可以用矩阵和矩阵乘法来等价描述，下面我们定义这样的复矩阵：

​ 这样，通过用$a,b,c,d$线性组合这四个矩阵，我们也可以得到一个复矩阵$U$：

​ 其行列式为$a^2+b^2+c^2+d^2$，所以如果我们考虑单位四元数，那它对应的$2\times2$矩阵$U$就应满足：

​ 这也是个特殊的群，我们定义：

​ 称之为二阶特殊幺正（unitary）群，实际上，单位四元数以及其乘法构成了一个群，而$2\times2$的幺正矩阵以及矩阵乘法也构成了一个群，并且每个单位四元数都可以对应到某个幺正矩阵中。这种关系正是群的同构，我们可以通过研究$\mathrm{SU}(2)$来研究四元数。

​ 现在，我们将$\mathrm{SO}(3)$和$\mathrm{SU}(2)$放在一起，考察他们的生成元，在$\mathrm{SO}(3)$的定义中，我们有：

​ 我们先前知道，群元素可以写成$\exp(\theta J)$的形式，我们将其带入上式中的$R$，有：

​ 注意，上面第一个式子并不是直接的，我们能利用$\exp(\cdot)$是因为$[J,J^T]=0$，然后对于第二个式子，我们应用刚才的性质，于是有：

​ 如果我们用矩阵来表达生成元，那么满足上面两个条件的一组基矩阵可以是：

​ 那么我们刚才讨论的$\mathfrak{s} \mathfrak{v} \left( 3 \right) $，实际上就是$\phi=[\phi_1,\phi_2,\phi_3]^T$，使得：

​ 以及，我们发现，他们之间的李括号存在这样的关系：

​ 我们再考虑$\mathrm{SU}(2)$上的生成元：

​ 由于此时是复矩阵，所以：

​ 可以验证，如下三个基矩阵可以用来表达生成元：

​ 所以我们其实也得到了$\mathfrak{s} \mathfrak{u} \left( 2 \right) $，即：

​ 此时，这几个基矩阵之间的李括号为：

​ 这其实在抽象意义上说明了一件事，$\mathrm{SU}(2)$上的基生成元之间的“差别”是$\mathrm{SO}(3)$上差别的“两倍”，也就是说，如果在$\mathrm{SU}(2)$上实施了一个变换，从$J_i$转换到了$J_j$，其比在$\mathrm{SO}(3)$上要多“转动”一倍。更技术地说，$\mathrm{SU}(2)$实际上是$\mathrm{SO}(3)$的二重覆盖。我们可以从这个角度理解为什么四元数旋转是我们认为的旋转的两倍。

​ 在这个例子中，我们也能看出，$\mathfrak{s} \mathfrak{v} \left( 3 \right)$和$\mathfrak{s} \mathfrak{u} \left( 2 \right) $是同构的。那么关于$\mathrm{SO}(3)$和$\mathrm{SU}(2)$，我们不加证明的给出$\mathrm{SU}(2)$到$\mathrm{SO}(3)$是2对1的同态（其实这一点可以从二重覆盖里直观的感受到）。

​ 我们直接给出，对于$\mathrm{SO}(3)$上转过欧拉角$(\alpha,\beta,\gamma)$，$\mathrm{SU}(2)$上存在这样的对应：

​ 由$\mathrm{SU}(2)$到$\mathrm{SO}(3)$是2对1的同态这一点，我们可以再往前阐明一件事情。有这样的一个需求，考虑一组基底函数，当他们被群作用时，我们希望这些函数可以变换为其线性组合。我们这么说其实就是为了引出球谐函数$Y_{l}^{m}\left( \theta ,\phi \right) $，因为这个在实际项目中我们确实会用到，哪怕大多数时候我们不需要知道它的原理和细节。

​ 在$\mathrm{SO}(3)$上直接处理是困难的，我们考虑在$\mathrm{SU}(2)$上先进行处理。考虑二维复向量$[u,v]$，我们可以找到这样一个函数：

​ 分子项整体的幂次为$2j$，假设对$[u,v]$作线性变换得到$[u^\prime,v^\prime]$，那么分子仍然还是$u,v$组成的幂次为$2j$的齐次项。也就是说在$\mathrm{SU}(2)$的变换下，$f_{j}^{m}\left( u,v \right) $也将变成其线性组合。由于$m$可以从$-j$取到$j$，所以这一共提供了$2j+1$个函数（或者说$2j+1$维表示）。接下来我们考虑用$\mathrm{SU}(2)$中的矩阵$M$来作用它，$M$是个幺正矩阵，我们就直接将元素写成复数形式，以$\ast$来标记共轭：

​ 我们将变换作用上去：

​ 用二项式定理展开，并整理，可以得到：

​ 其中$k$的上限是$j+m$，$l$的上限是$j-m$，我们注意到由于二项式定理打开后，等式右边实际上是不同$f_{j}^{m}\left( u,v \right) $的线性组合，我们设$m^\prime=j-k-l$，那么$u$上的幂就是$j+m^\prime$，$v$上的幂就是$j-m^\prime$，同时我们将$l$用$j-k-m^\prime$替换，式子于是可以整理为：

​ 这里：

​ 在这样的参数化下，$k$的上限为$\min(j+m,j-m^\prime)$，$k$的下限为$\max(0,m-m^\prime)$。这里的$m^\prime$和$m$都从$-j$取到$j$，所以$D^j$实际上是一个$(2j+1)\times(2j+1)$的矩阵。

​ 之前我们已经给出$\mathrm{SU}(2)$到$\mathrm{SO}(3)$是个同态，我们选取那些对应于$\mathrm{SO}(3)$的元素：

​ 我们将其带入$D_{m^{\prime}m}^{j}\left( a,b \right)$，化简得到：

​ 我们将中间的阶乘项，连同带有半角的项一起，记作$d_{_{mm^{\prime}}}^{j}\left( \beta \right)$：

​ 那么，我们之前讨论的变换即在$\mathrm{SO}(3)$上改写为：

​ 现在我们考虑球坐标系上的点$x_0=(r,0,0)$，我们希望通过欧拉角转动$M\left( \varphi ,\theta ,\gamma \right) $将$x_0$转动到$x=(r,\theta,\varphi)$，这个变换不依赖于$\gamma$。那么我们有：

​ 由于这个变换不依赖于$\gamma$，所以右边含$\gamma$的项必然为$0$，也就是说当$m^\prime \ne 0$时，$f_{j}^{m^\prime}\left( x_0 \right) =0$，于是有：

​ 此时左侧的$e^{im\varphi}d_{_{m0}}^{j}\left( \theta \right) $，乘上一个归一化系数后，就是著名的球谐函数：

​ $f_{j}^{0}\left( x_0 \right) $可以视作关于$x_0$径长的函数$\phi(r)$，而$x$又是从球面上采的，不失一般性我们可以认为$\phi(r)$恒等于1，这样，我们就可以认为：

​ 结合先前的式子，这实际上给出了一种对旋转后的球谐函数进行计算的方法：

​ 所以矩阵$D^j$，就是Wigner D-matrix。

​ 上式给出的复球谐，而我们实际用的其实是实球谐，这里的推导只是为了让我们对球谐函数是怎么来的有一个除开调和分析以外的概念，实际上指导意义不大。

​ 写这一部分的时候还是很艰难的，因为我一直以来代数就不好。以及这一部分讨论的这些理论内容，大部分出自数学或物理教材，他们用的符号标记和说法工科出身很难适应，我在图书馆中找了很久，一个很“elementary”的教材是《李群》（邵丹 邵亮 郭紫 著），这本书帮助很大。

​ 至于为什么要坚持写这个部分，这些推导肯定都是不严谨而且以后也用不到的。但通过学习没学过的东西，然后能有选择性的学和跳过哪些内容，从而构建一个逻辑自洽的roadmap，是很重要的一个能力。这个部分只是为了这碟醋包的饺子。我有时就在想，如果当年高等代数课不逃课，事情会不会有所不同。所以这也算是克服心魔了吧。

End

最好的惊堂木是时间，
就让我合上这书卷。

​ 这篇blog选取了若干先进的与相机系统有关的深度学习项目进行了分析，最后从理论角度讨论了代码中常用的旋转操作的一些性质。

赏

谢谢你请我吃糖果

微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

挟飞仙以遨游，抱明月而长终。<br />知不可乎骤得，托遗响于悲风。