Look Closely at Head 3

阅读数: 次 2024-02-17

“雾蒙蒙，城头上，弦月下。”

春节假期快结束了，这篇blog是用来记录一下探索毕设过程中得到的一些认识。我毕设要做的是基于3D Gaussian Splatting实现三维人脸（头）的合成，

我承认，有那么很短的一瞬间，我有过想把EG3D里的Neural Rendering换成Gaussian Splats的想法，做一个generative manner的东西，但只有那么一瞬间，因为太难了。

于是我就瞄准了“从单目视频中重建人头”这个任务，这个直观看起来难度就比较适中了。该任务可以形式化为给定一段单目视频$I=\left\{ I_i \right\} $，相机内参$\mathbf{K}$，如何得到一个“head avatar”。由于人头先前工作的铺垫，往往可以通过先前工作的pretrained，从每一帧中得到FLAME模型中的mesh曲面$M={M_i}$，表情系数$\varPsi =\left\{ \psi _i \right\} $，用于表示该identity的形状系数$\mathcal{S} =\left\{ s_i \right\} $，FLAME的结点的姿态$\varTheta =\left\{ \theta _i \right\} $，根结点的姿态（或者理解为相机外参）$\mathcal{P} =\left\{ P_i \right\} $。这些前人提取prior的成果是使得这个任务变得“可以做”的重要一环。

这个task，对像我这样想入门的人，除了难度适中，还有不少的好处。

因为这个任务需要在了解了3DGS以后，做出一个可以deform或者叫dynamic的Gaussian Splatting。和更general的4D-scene reconstruction不同的是，FLAME和有意采集的各种姿势下的人头图片，保证了一个很强的先验，这样做完以后可以用一个GUI界面，来实时的调整一个avatar，这个比较好玩。
和用SMPL的人体任务相比，人头相对简单的多，可以借着使用FLAME了解一些在PyTorch中“灵活运用mesh”的艺术。
在这个任务里，用来驱动人头的condition比较简单，只是表情系数。有些audio-based的这个就又是另一回事了，在提取condition的时候要多花一些功夫。
这个任务是朴素意义上的supervised-learning，数据分布全部来自于拍摄的单目视频，只要专注于fit就好了。像有些任务上需要紧密依赖一个pretrain来监督，这个可能太ambiguous了。
而且它是单目的，如果真的多目了，已经有很多有经验的多的人用一堆我来不及学的technique（什么DMTet恢复一个mesh）来做，这个，不太适合入门的人。
用Gaussian Splatting做这个任务还没有可用的开源代码（截止到写这篇blog的时候），可以从零搓一遍。

所以在几个月里，我先是学习了3D Gaussian Splatting[post]，然后了解了FLAME[post]，之后梳理了一下预处理管线[post]，最后搓了初步的demo出来。在实际操作阶段，结合实践出的一些现象，再回过头来看用3D Gaussian Splatting实现这一任务的一些工作，有了一些新的理解和启发。

截止到现在，用3D Gaussian实现这个任务有许多工作，但现在都没有开源（有一个是放出了inference部分，另一个是全放出来了，但缺失了一个挺重要的部分，后面会提到）。它们有MonoGaussianAvatar，PSAvatar，HeadGaS，GaussianHead，flashavatar，GaussianAvatar。下面将会简要的指出这些工作里的一些细节，然后进行总结。

在正式切入主题之前，还需要指出关于3D Gaussian Splatting中的一些细节：

对于每一个splat，scale用于调整这个椭球分布在不同方向的长度，最终得到的图像上，有许多高频细节都是需要很多个某一个轴上的scale很大的splat来合成，他们看起来像许多针。这些scale的范围大概在$10^{-5}\sim 10^{-3}$这个量级，这个数值太“subtle”了，这数值甚至有时候都没学习率大。所以在原版3DGS里，用了torch.exp()来优化在对数尺度下的scale（也就是说大概在$-5\sim-3$这样，这个就是一个对于常规的NN优化时的正常范围了），这个操作有些午夜梦回高中化学选修四——酸碱中和滴定。
原版3DGS是为了合成静态场景的，引入球谐系数来实现“颜色随方向变化”的效果。方向由每个点相对此时的相机中心作差获得。相机中心$C$是外参矩阵求逆来的：
$\left[ \begin{matrix} R& t\\ \mathbf{0}& 1\\ \end{matrix} \right] \left[ \begin{matrix} R^T& \underset{C}{\underbrace{-R^Tt}}\\ \mathbf{0}& 1\\ \end{matrix} \right] =\left[ \begin{matrix} \mathbf{I}& 0\\ \mathbf{0}& 1\\ \end{matrix} \right]$
优化球谐这个操作可以为颜色提供更大的自由度。通俗的认识是说，这种显式定义的让颜色变化的方法，效果没有MLP+camera pose好，但我推测这里有一些别的原因（见后文）。

所以如果你得到$t$或者$C$以后，然后要做coordinate system convention，一定不要只改R，记得平移向量也要改。
每个高斯点的位置$\mu$在原版3DGS里是可优化的，densification操作靠的是追踪梯度${\mathrm{d}L}/{\mathrm{d}\mu}$。不管是做split还是clone，其实一开始注册的新的位置new_xyz都是和densify之前的位置是一样的。真正让他们“动”起来的原因是，有一半的参数的grad是None，然而另一半的是loss.backward()出来的有效值，所以那另一半在调用optimizer.step()时，一半的高斯就会借助优化位置$\mu$而移动开。所以这里并没有显式规定“步长”这一概念。

现在切入正题。

MonoGaussianAvatar

这篇工作follow了PointAvatar，作图什么的都存在明显致敬。

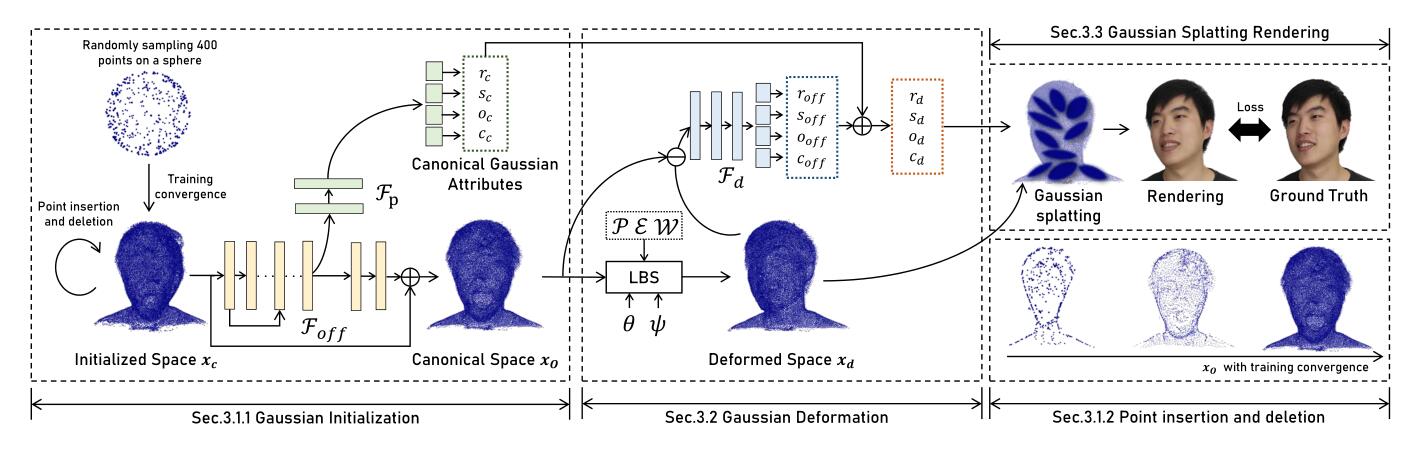
这个流程分为两个阶段，先从一个稀疏的球状点云里，用sphere splat来fit出一个人头形的几何。这个操作大概是直接follow自PointAvatar，用PyTorch3D里的rasterizer实现的。这个fit的过程中，对这些球状的splat，也是要做densify和prune的，prune的机制就是删掉那些不透明度很小的，densify的机制跟3D Gaussian Splatting里的不同，是类比于PointAvatar的，就是在当前点周围，用随机噪声来产生新的点，跟梯度一点关系没有。

然后，得到的这一组点，就固定了，记作canonical space $x_c$，之后进入第二阶段，开始学习Gaussian Splat，点并不会增加和减少，会用MLP来对每一个$x_c$学一组高斯的属性，学一个位置的偏移量$\mathcal{F}_{off}(x_c)$，然后再学一个implicit LBS用于让人头动起来。

这里的问题在于，按照LBS的做法，点动了，高斯本身的旋转$r$是没有动的，这样肯定会导致在一个pose时的解是好的，然后转动到另一个pose后产生模糊的解，所以这里又补了一个Gaussian Deformation Field的MLP，来学高斯属性的偏置$r_{off},s_{off},o_{off},c_{off}$。

其实直觉上，这一步可以用LBS最后得到的旋转变换来直接显式的给出来。因为感觉就只有$r_{off}$的影响是最大的。

这里要注意的一个事情是，这种用MLP学出来的Gaussian Attributes，不一定能对应上这些属性各自的显式的范围，颜色和不透明度好说，都是0到1，用一个Sigmoid()就好了，但scale就不一定了，所以我比较好奇这个工作里的initialized MLP里，为什么$s_c$的激活是Sigmoid()，这样得到一个0~1的值，它不可能满足scale的范围啊，不太清楚了。

以及至于那些偏置$r_{off},s_{off},o_{off},c_{off}$是怎么加的，就更奇怪了。如果按照附录里的图理解，得到的这些偏置也是被激活过的，那直接相加$r_d=r_c+r_{off},s_d=s_c+s_{off},o_d=o_c+o_{off},c_d=c_c+c_{off}$可太奇怪了，比如颜色和不透明度，应该有加出1以外的风险，难道要额外的clamp一下吗？所以我推测应该是把激活前的这些implicit value进行相加。

原文中报告的结果是在100k的$x_c$下取得的，这篇工作对于MLP的输入，也就是那些坐标，没有使用positional encoding，其声称这样是为了得到“较为光滑”的representation，这个操作其实有点反直觉。

在用sphere splat得到$x_c$时，可以看出tune了很久，这说明一个好的$x_c$很重要。

FlashAvatar

这篇工作在FLAME的纹理上进行均匀的UV sampling，这个操作可以用PyTorch3D的rasterizer顺手返回的bary coords实现。

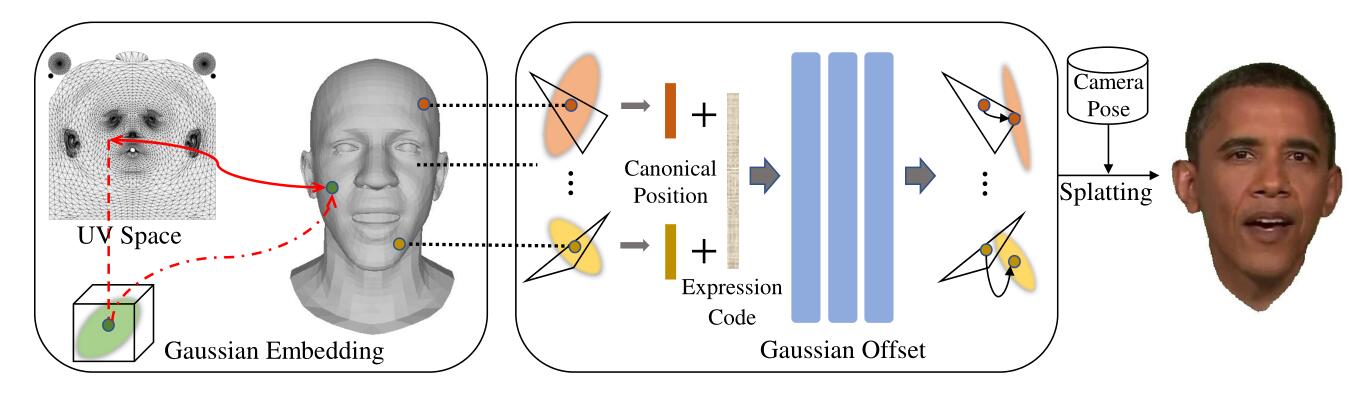
FLAME本身的模板上嘴是不闭合的，所以UV sampling是采不到能表示口腔的那些点的，需要手动的缝一些面。这个操作可以用Blender手工实现，得到一个新的模板。

flashavatar的操作是，对于预处理得到的FLAME下的canonical head，用UV sampling，得到一个模板顶点集$\mu_T$，这个点集是固定的。由于每一帧的mesh曲面$M_i$都已知，所以UV sampling得到的顶点，可以与当前$M_i$上的顶点进行重心插值，得到在这一帧下的位置$\mu_M$。

将$\mu_T$进行位置编码$\gamma(\cdot)$，与FLAME的其他系数一起，送入MLP，得到位置，旋转，缩放的偏移量$\varDelta \mu,\varDelta r, \varDelta s$。此时位置的偏移量$\varDelta \mu$是与$\mu_M$相加，来得到最终的位置。球谐系数和不透明度是各自Gaussian Splat自己point-wise的优化的。

UV sampling是一个很好的操作，因为一般的参数化模型的顶点分布都不太均匀，比如眼球那里有相当多的顶点，多到基于instant-ngp的工作在用FLAME先验之前都要把眼部那里的面简化掉。同时这个操作下对每一帧，有一个很不错的canonical head，很稳定。

我当时觉得这里感觉最不舒服的一点就是$\varDelta \mu ,\varDelta r,\varDelta s=F_{\theta}\left( \gamma \left( \mu _T \right) ,\psi \right) $这种变形的方式，我感觉不如用LBS来引导变形，这样在人头的task里会舒服一些。

按照这篇的做法，只需10k的点数量就能有很高的质量，但我早些时候手搓过一般，没整出来，可能是哪里整的不对了。

GaussianAvatar

这篇工作其实处理的是多目视频条件下的重建，有点黑科技。他们定制化了一个FLAME tracking，让这个tracking能fit出头发形状的mesh，然后在这个mesh的基础上指派高斯点。为了要有牙齿，还手动补了上下牙齿的面，crazy。

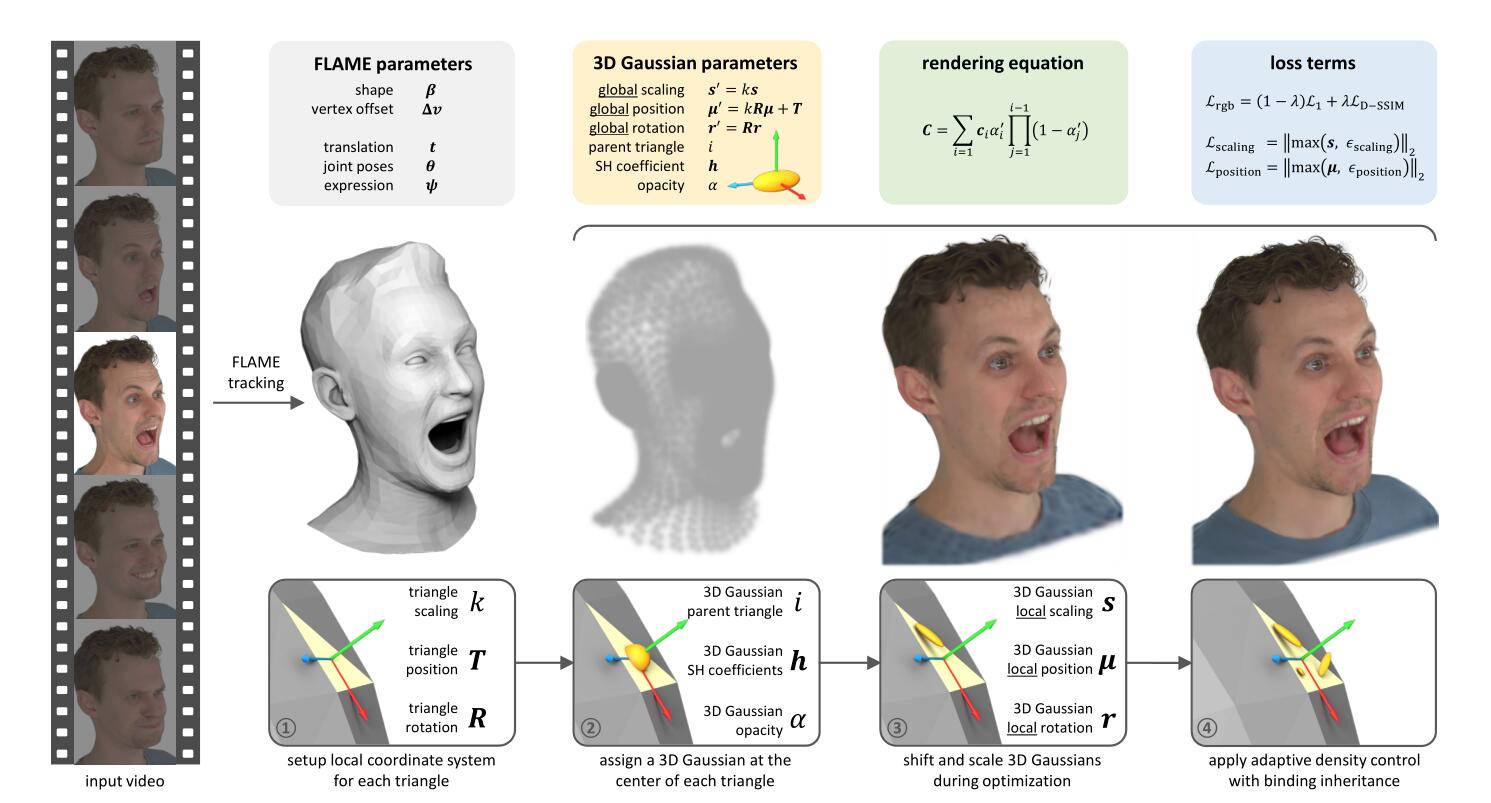
这里把顶点实际上是绑定在了三角面片上，这个实现起来感觉很不容易。每个三角面片都能确定一个坐标系，以其重心位置为中心，可以得到旋转$R$和平移向量$T$。同时，由于在做一些表情时，顶点之间的距离会变，其三角形面积也会变，所以会有一个比例系数$k$来保持局部高斯的不变性。所以整个变换可以导引为：

$s^{\prime}=ks \\ \mu ^{\prime}=kR\mu +T \\ r^{\prime}=Rr$

然后就可以直接训高斯了，还可以直接应用3DGS原版的densification，因为就算有新的点，新的表情，上述线性变换也会忠实的把点映进合适的位置上的。

这篇的代码给出来了，但没有给出来那个神奇的FLAME tracking，所以一键follow是不存在的。

PSAvatar

这篇工作某种意义上很像MonoGaussianAvatar。

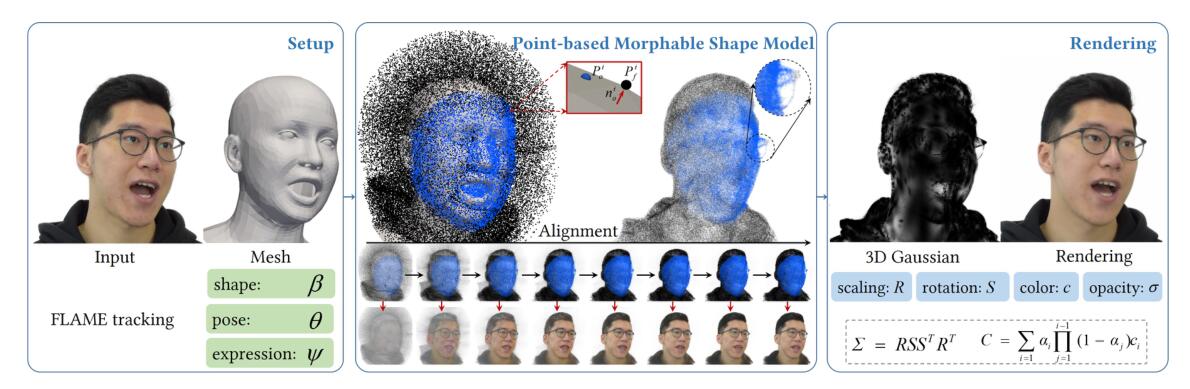
与从400个点生长到一个canonical的人头，这里的办法是先从FLAME的模板顶点中，沿着法线方向，创建新的顶点。然后用这些新的顶点，以他们的面积（PyTorch3D中的mesh_face_areas_normals可以直接算出来）为基准进行加权抽样（torch.multinomial），对得到的索引随机一组重心坐标，来进行采样。最开始用的也是sphere splat，然后得到一个粗糙的点云几何，然后切成gaussian splat进行训练。

我推测在第一步获得那些点的时候，应该没有对其位置进行变化，也就是说又是固定好的了。这一步的好处是，在第二阶段做deformation的时候，LBS要用的基也能用重心插值出来。这样变形可能还差一点，于是又学了一组基向量来修正：

$\mathcal{G} \left( \theta ,\psi \right) =B_P\left( \theta ;\mathcal{P} ^{\prime} \right) +B_E\left( \psi ;\mathcal{E} ^{\prime} \right)$

以及这里就是显式给出高斯的旋转的：

$R=R^{\prime}R^i$

整个部件根本没用到NN，很舒适（其实学$\mathcal{P}^{\prime}$和$\mathcal{E}^{\prime}$的过程等价于学一组linear，无activation）。直觉上这个应该需要相当多的点。

HeadGaS

这篇工作的图画的挺随意。

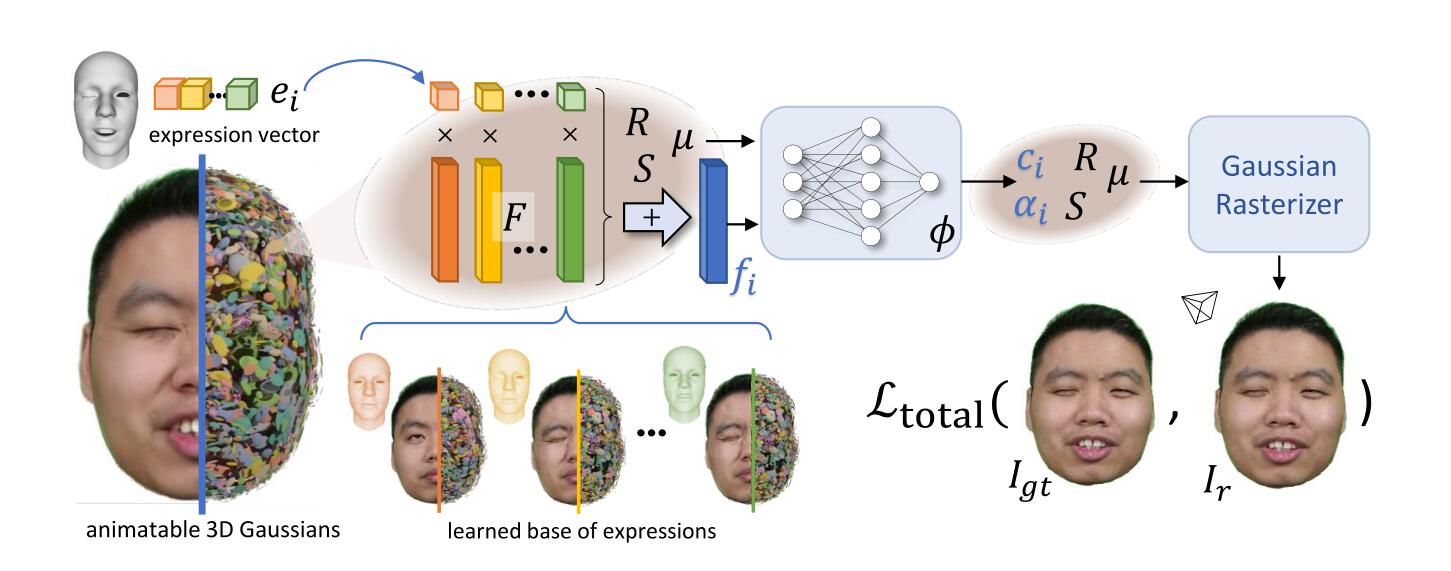
他的操作在于，此时是有表情的基向量和系数的，将基向量当作可学习的参数，然后在给定一组表情系数的情况下，可以合成出一个特征向量$f_i$，然后将其与点的位置拼在一起，输入进一个MLP算出颜色和不透明度。

而高斯的位置，旋转，缩放，全是point-wise的优化的，然后高斯的点随意的densification。

所以，这种做法是舍弃了几何来换取变形。在不同表情的驱动下，MLP会产生不同的颜色和不透明度，然后他们会渲染出不同的样子，但不同的表情下，高斯的几何（位置，缩放，旋转）这些却都是固定的。

值得一提的是，在这个工作的附录里，做了一个消融实验。假如我们认定这个消融实验是客观的，那会带来一些观察。作者比较了三种设定下，推理时间，PSNR，和高斯点数量的变化，我比较关心高斯点数量的变化。

第一个是不用所谓的“feature blending”，也就是输入MLP的是点的位置和表情系数，然后输出颜色和不透明度，这个需要135k个高斯点。第二个是将预测的对象从颜色和不透明度换成$\varDelta \mu$和$R$，这需要更多的高斯点，234k个。最后一个是将MLP撤掉，然后用一种比较朴素的办法，对颜色和不透明度进行加权，最终需要295k个点。然而他们的settings下只需要28k个点。

GaussianHead

这篇工作其实也是牺牲掉几何的一个做法。

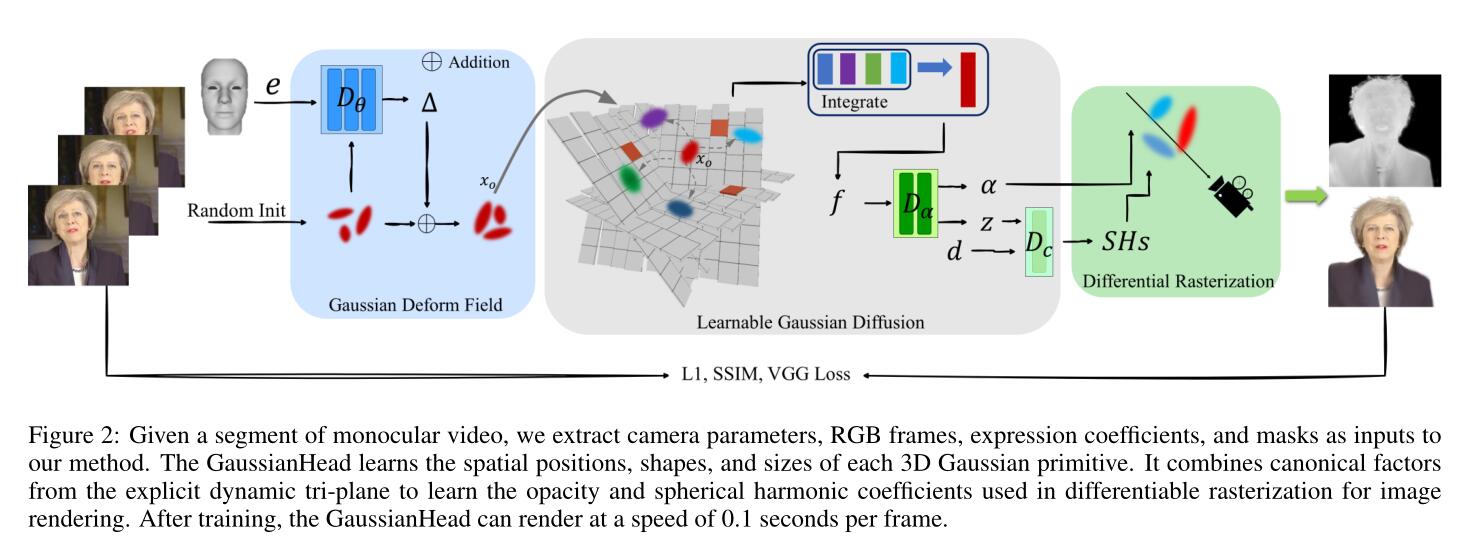
他先用表情系数作为condition，然后学一个几何的偏置$(\varDelta \mu ,\varDelta r,\varDelta s)$。然后将加上偏置以后的高斯点的这个坐标，投影到可以旋转的triplane（这是一篇ICLR里做的工作），然后抽出特征向量，再用别的MLP解算坐标和不透明度，然后得到所有属性后，进行光栅化。

这个工作也支持随意的densification。

这篇工作放出来了一个ckpt，可以打开其中保存为.ply的文件：

可以看见这个点云与人头相差甚远。

这里引入的可旋转的triplane，是一种很有意思的结构。因为triplane本身是没有归纳偏置的，比如对于其中一个面，一个点投影下去，其得到的$f_{i,j}$只和周围四个点有关。有一篇工作PET-NeuS讨论了一下这个事情，挺有意思的。

Summary

呼~

所以可以看出来，这6个工作里，前四个是一类，后两个是一类。他们都是很好的工作，下面所说的内容只是我个人看法和情感。

前四个工作是围绕FLAME的几何进行操作的，核心在于一个好的canonical space。然后在这个canonical space的基础上学deform。后两个工作，其实更像“借着快速光栅化”的NeRF。

这背后是显式的point-wise和用MLP隐式优化的区别，我们做一些不严谨的符号计算来说明这个事情。在此之前，我们最好把Gaussian Splatting说的更加透彻一些。假定一个像素的值是由$N$个splats合成的，那么根据体渲染：

$C_i=\sum_n{c_n\alpha _nT_n},\quad T_n=\prod_{m<n}{\left( 1-\alpha _m \right)}$

这里索引下标从小到大就认为是tile sorting后的索引了，根据Gaussian Splat的定义，$\alpha_n$来自于：

$\alpha _n=o_n\cdot \exp \left( -\frac{1}{2}\left( \mathrm{p}_i-\mu _{n}^{\prime} \right) ^T\Sigma _{n}^{\prime-1}\left( \mathrm{p}_i-\mu _{n}^{\prime} \right) \right)$

这里$\mathrm{p}_{i}$表示该像素的坐标，$\mu _{n}^{\prime}$是投影到2D-space中的高斯点位置。考虑颜色的梯度（为了简洁，忽略RGB三通道的记号了），这个的计算比较简单：

$\frac{\partial \mathcal{L}}{\partial c_n}=\frac{\partial \mathcal{L}}{\partial C_i}\frac{\partial C_i}{\partial c_n} \\ \frac{\partial \mathcal{L}}{\partial C_i}=\nabla \left\| C_{i}^{\mathrm{gt}}-C_i \right\| _2 \\ \frac{\partial C_i}{\partial c_n}=\alpha _nT_n$

然后是不透明度：

$\frac{\partial \mathcal{L}}{\partial o_n}=\frac{\partial \mathcal{L}}{\partial C_i}\frac{\partial C_i}{\partial \alpha _n}\frac{\partial \alpha _n}{\partial o_n}$

注意$\alpha_n$在大于$n$的$T_{i}$中也会出现，所以：

$\frac{\partial C_i}{\partial \alpha _n}=c_nT_n-\frac{\sum_{i>n}{c_i\alpha _iT_i}}{1-\alpha _n}$

由上面$\alpha_n$和$o_n$的关系，可以得到：

$\frac{\partial \alpha _n}{\partial o_n}=\exp \left( -\frac{1}{2}\left( \mathrm{p}_i-\mu _{n}^{\prime} \right) ^T\Sigma _{n}^{\prime-1}\left( \mathrm{p}_i-\mu _{n}^{\prime} \right) \right)$

于是$\frac{\partial \mathcal{L}}{\partial o_n}$就得到了。

接下来，我们记上式中的指数中的项为$\sigma_n$，这一项提供了对几何属性的梯度：

$\sigma _n=\frac{1}{2}\left( \mathrm{p}_i-\mu _{n}^{\prime} \right) ^T\Sigma _{n}^{\prime-1}\left( \mathrm{p}_i-\mu _{n}^{\prime} \right)$

所以式子可以简化为：

$\frac{\partial \alpha _n}{\partial o_n}=\exp \left( -\sigma _n \right)$

在接下来推到关于几何属性的梯度时，我们先回忆在前向过程中，Gaussian Splatting中的位置$\mu$是先将世界坐标系转换到相机坐标系下，然后还在代码里作了一次透视变换把点都规正到NDC space中，最后再做那个投影变换的一阶近似的。

所以其实所有高斯点都是被normalized到NDC空间中的，我们操作的scale和rotation也是在NDC空间中的。

记相机外参为$T_{c}$，NDC变换矩阵为$P$：

$T_c=\left[ \begin{matrix} R_c& t_c\\ \mathbf{0}& 1\\ \end{matrix} \right] \quad P=\left[ \begin{matrix} \frac{2f_x}{w}& 0& 0& 0\\ 0& \frac{2f_y}{h}& 0& 0\\ 0& 0& \frac{\left( f+n \right)}{\left( f-n \right)}& \frac{-2fn}{\left( f-n \right)}\\ 0& 0& 1& 0\\ \end{matrix} \right]$

我们就不用专门的字母表示相机内参了，相机内参中的焦距，主点，就直接用$f_x,f_y,c_x,c_y$表示了。$n$表示near，$f$表示far，这些在3DGS里分别取为0.01和100.0了。$w$和$h$是输出图片的尺寸。

但原版3DGS其实没有用相机主点……

所以对于位置$\mu$的变换即为这三步：

$t=\left[ \begin{matrix} R_c& t_c\\ \mathbf{0}& 1\\ \end{matrix} \right] \left[ \begin{array}{c} \mu\\ 1\\ \end{array} \right] \\ t^{\prime}=Pt \\ \mu ^{\prime}=\left[ \begin{array}{c} \left[ \left( t_{x}^{\prime}/t_{w}^{\prime}+1 \right) \cdot w-1 \right] /2\\ \left[ \left( t_{y}^{\prime}/t_{w}^{\prime}+1 \right) \cdot h-1 \right] /2\\ \end{array} \right]$

最后一步是将$[-1,1]$的NDC空间中的点变换到像素空间中。参见cuda_rasterizer/auxiliary.h中的ndc2pix：

__forceinline__ __device__ float ndc2Pix(float v, int S)
{
	return ((v + 1.0) * S - 1.0) * 0.5;
}

写成矩阵应该是：

$\left[ \begin{array}{c} \mu _{x}^{\prime}\\ \mu _{y}^{\prime}\\ \end{array} \right] =\frac{1}{2}\left[ \begin{array}{l} w/t_{w}^{\prime}& 0& 0& \frac{\left( w-1 \right)}{t_{w}^{\prime}}\\ 0& h/t_{w}^{\prime}& 0& \frac{\left( h-1 \right)}{t_{w}^{\prime}}\\ \end{array} \right] \left[ \begin{array}{l} t_{x}^{\prime}\\ t_{y}^{\prime}\\ t_{z}^{\prime}\\ t_{w}^{\prime}\\ \end{array} \right]$

然后为了让投影变换后的高斯保形，对于$\Sigma$所做的投影变换的一阶近似$J$为：

$J=\left[ \begin{array}{l} f_x/t_z& 0& -f_x\cdot t_x/t_{z}^{2}\\ 0& f_y/t_z& -f_y\cdot t_y/t_{z}^{2}\\ \end{array} \right]$

因为根本用不到第三行，于是就$J\in\mathbb{R}^{2\times3}$了，所以对于$\Sigma$有：

$\Sigma ^{\prime}=JR_c\Sigma R_{c}^{T}J^T$

所以回到$\alpha _n=o_n\cdot \exp \left( -\sigma _n \right) $，有：

$\frac{\partial \alpha _n}{\partial \sigma _n}=-o_n\cdot \exp \left( -\sigma _n \right)$

接下来我们计算$\sigma_{n}$与$\Sigma^{\prime}$和$\mu^{\prime}$的关系：

$\frac{\partial \sigma _n}{\partial \mu _{n}^{\prime}}=\Sigma _{n}^{\prime-1}\left( \mathrm{p}_i-\mu _{n}^{\prime} \right)$

然后这个逆矩阵不是很好处理，我们直接掏出matrix cookbook，可以得到：

$\frac{\partial \mathbf{Y}^{-1}}{\partial x}=-\mathbf{Y}^{-1}\frac{\partial \mathbf{Y}}{\partial x}\mathbf{Y}^{-1} \\ \frac{\partial \mathbf{a}^T\mathbf{Xa}}{\partial \mathbf{X}}=\frac{\partial \mathbf{a}^T\mathbf{X}^T\mathbf{a}}{\partial \mathbf{X}}=\mathbf{aa}^T$

所以就有：

$\frac{\partial \sigma _n}{\partial \Sigma _{n}^{\prime}}=-\frac{1}{2}\Sigma _{n}^{\prime-1}\left( \mathrm{p}_i-\mu _{n}^{\prime} \right) \left( \mathrm{p}_i-\mu _{n}^{\prime} \right) ^T\Sigma _{n}^{\prime-1}$

所以现在我们通过设定为高斯分布的不透明度的计算，已经将chain延申到了2D的screenspace中了。

“只要不停下来，道路就会不断延伸。”

我们先解决好处理的部分，由于：

$\Sigma ^{\prime}=JR_c\Sigma R_{c}^{T}J^T$

所以我们两边求取微分，可以得到：

$\frac{\partial \Sigma ^{\prime}}{\partial \Sigma}=R_{c}^{T}J^TJR_c$

然后至于协方差矩阵$\Sigma$和旋转四元数$q_n$和缩放$s_n$的关系，在这篇blog的最后是推导过的，所以关于旋转和缩放的反向传播的计算图，我们就有了：

$\frac{\partial \mathcal{L}}{\partial q_n}=\frac{\partial \mathcal{L}}{\partial C_i}\frac{\partial C_i}{\partial \alpha _n}\frac{\partial \alpha _n}{\partial \sigma _n}\frac{\partial \sigma _n}{\partial \Sigma _{n}^{\prime}}\frac{\partial \Sigma _{n}^{\prime}}{\partial \Sigma _n}\frac{\partial \Sigma _n}{\partial M_n}\frac{\partial M_n}{\partial \bar{q}_n}\frac{\partial \bar{q}_n}{\partial q_n}$

这里$M$即为协方差矩阵$\Sigma$的Cholesky分解，$\bar{q}$是归一化后的四元数。

对于缩放，道理是一样的：

$\frac{\partial \mathcal{L}}{\partial s_n}=\frac{\partial \mathcal{L}}{\partial C_i}\frac{\partial C_i}{\partial \alpha _n}\frac{\partial \alpha _n}{\partial \sigma _n}\frac{\partial \sigma _n}{\partial \Sigma _{n}^{\prime}}\frac{\partial \Sigma _{n}^{\prime}}{\partial \Sigma _n}\frac{\partial \Sigma _n}{\partial M_n}\frac{\partial M_n}{\partial s_n}$

为了身心健康，这里就不把每一项带入了。

现在，就差关于位置$\mu$的偏导了。我们要注意到，在二次型$-\frac{1}{2}\left( \mathrm{p}_i-\mu _{n}^{\prime} \right) ^T\Sigma _{n}^{\prime}\left( \mathrm{p}_i-\mu _{n}^{\prime} \right) $中，不仅$\mu _{n}^{\prime}$跟位置有关，$\Sigma _{n}^{\prime}$也和位置有关。因为雅可比阵$J$。所以：

$\frac{\partial \mu _{n}^{\prime}}{\partial t_n}=\frac{\partial \mu _{n}^{\prime}}{\partial t_{n}^{\prime}}\frac{\partial t_{n}^{\prime}}{\partial t_n} \\ =\frac{1}{2}\left[ \begin{array}{l} w/t_{w}^{\prime}& 0& 0& \frac{\left( w-1 \right)}{t_{w}^{\prime}}\\ 0& h/t_{w}^{\prime}& 0& \frac{\left( h-1 \right)}{t_{w}^{\prime}}\\ \end{array} \right] P$

然后，我们计算：

$\frac{\partial \Sigma ^{\prime}}{\partial t_n}=\frac{\partial \Sigma ^{\prime}}{\partial J}\frac{\partial J}{\partial t_n}$

这个式子中的两项都不能写成很整洁的形式，我们记$T=JR_c\in\mathbb{R}^{2\times3}$，我们可以将$\Sigma ^{\prime}=JR_c\Sigma R_{c}^{T}J^T$打开：

$\Sigma _{_{00}}^{\prime}=T_{00}(T_{00}\Sigma _{00}+T_{01}\Sigma _{10}+T_{02}\Sigma _{20})+T_{01}(T_{00}\Sigma _{01}+T_{01}\Sigma _{11}+T_{02}\Sigma _{21})+T_{02}(T_{00}\Sigma _{02}+T_{01}\Sigma _{12}+T_{02}\Sigma _{22}) \\ \Sigma _{_{01}}^{\prime}=T_{10}(T_{00}\Sigma _{00}+T_{01}\Sigma _{10}+T_{02}\Sigma _{20})+T_{11}(T_{00}\Sigma _{01}+T_{01}\Sigma _{11}+T_{02}\Sigma _{21})+T_{12}(T_{00}\Sigma _{02}+T_{01}\Sigma _{12}+T_{02}\Sigma _{22}) \\ \Sigma _{_{11}}^{\prime}=T_{10}(T_{10}\Sigma _{00}+T_{11}\Sigma _{10}+T_{12}\Sigma _{20})+T_{11}(T_{10}\Sigma _{01}+T_{11}\Sigma _{11}+T_{12}\Sigma _{21})+T_{12}(T_{10}\Sigma _{02}+T_{11}\Sigma _{12}+T_{12}\Sigma _{22})$

一个不需要借助其他数学工具（如将矩阵展成Frobenius内积来表达矩阵求导）的理解思路是，假设我们根据前面的计算已经得到了$\frac{\partial \mathcal{L}}{\partial \Sigma _{_{00}}^{\prime}},\frac{\partial \mathcal{L}}{\partial \Sigma _{01}^{\prime}}\left( \frac{\partial \mathcal{L}}{\partial \Sigma _{10}^{\prime}} \right) ,\frac{\partial \mathcal{L}}{\partial \Sigma _{11}^{\prime}}$，根据多元函数微积分：

$\frac{\partial \mathcal{L}}{\partial T_{00}}=\frac{\partial \mathcal{L}}{\partial \Sigma _{_{00}}^{\prime}}\frac{\partial \Sigma _{_{00}}^{\prime}}{\partial T_{00}}+\frac{\partial \mathcal{L}}{\partial \Sigma _{_{01}}^{\prime}}\frac{\partial \Sigma _{_{01}}^{\prime}}{\partial T_{00}}+\frac{\partial \mathcal{L}}{\partial \Sigma _{_{10}}^{\prime}}\frac{\partial \Sigma _{_{10}}^{\prime}}{\partial T_{00}}+\frac{\partial \mathcal{L}}{\partial \Sigma _{_{11}}^{\prime}}\frac{\partial \Sigma _{_{11}}^{\prime}}{\partial T_{00}}$

然后根据上面展开的结果逐项求导，这其实也正是3DGS中CUDA代码的来源，然后再用$T=JR_c$如法炮制一遍就好了，对应diff-gaussian-rasterization/cuda_rasterizer/backward.cu中的：

// Gradients of loss w.r.t. upper 2x3 portion of intermediate matrix T
// cov2D = transpose(T) * transpose(Vrk) * T;
float dL_dT00 = 2 * (T[0][0] * Vrk[0][0] + T[0][1] * Vrk[0][1] + T[0][2] * Vrk[0][2]) * dL_da +
	(T[1][0] * Vrk[0][0] + T[1][1] * Vrk[0][1] + T[1][2] * Vrk[0][2]) * dL_db;
float dL_dT01 = 2 * (T[0][0] * Vrk[1][0] + T[0][1] * Vrk[1][1] + T[0][2] * Vrk[1][2]) * dL_da +
	(T[1][0] * Vrk[1][0] + T[1][1] * Vrk[1][1] + T[1][2] * Vrk[1][2]) * dL_db;
...

// Gradients of loss w.r.t. upper 3x2 non-zero entries of Jacobian matrix
// T = W * J
float dL_dJ00 = W[0][0] * dL_dT00 + W[0][1] * dL_dT01 + W[0][2] * dL_dT02;
float dL_dJ02 = W[2][0] * dL_dT00 + W[2][1] * dL_dT01 + W[2][2] * dL_dT02;
...

于是对于$\frac{\partial \sigma _n}{\partial t_n}$我们就有了答案：

$\frac{\partial \sigma _n}{\partial t_n}=\frac{\partial \sigma _n}{\partial \mu _{n}^{\prime}}\frac{\partial \mu _{n}^{\prime}}{\partial t_n}+\frac{\partial \sigma _n}{\partial \Sigma _{n}^{\prime}}\frac{\partial \Sigma _{n}^{\prime}}{\partial t_n}$

由于$t_n$是经过相机变换过的，有$\frac{\partial t_n}{\partial \mu _n}=R_c$，所以，最终关于位置$\mu$的链即为：

$\frac{\partial \mathcal{L}}{\partial \mu _n}=\frac{\partial \mathcal{L}}{\partial C_i}\frac{\partial C_i}{\partial \alpha _n}\frac{\partial \alpha _n}{\partial \sigma _n}\frac{\partial \sigma _n}{\partial t_n}\frac{\partial t_n}{\partial \mu _n} \\ =\frac{\partial \mathcal{L}}{\partial C_i}\frac{\partial C_i}{\partial \alpha _n}\frac{\partial \alpha _n}{\partial \sigma _n}\left( \frac{\partial \sigma _n}{\partial \mu _{n}^{\prime}}\frac{\partial \mu _{n}^{\prime}}{\partial t_n}+\frac{\partial \sigma _n}{\partial \Sigma _{n}^{\prime}}\frac{\partial \Sigma _{n}^{\prime}}{\partial t_n} \right) \frac{\partial t_n}{\partial \mu _n}$

实际上这里还省略了一项，如果球谐系数的分量不为0，那么还会多一项，但这里就省略了。我们把这五个属性放在一起看一下：

$\frac{\partial \mathcal{L}}{\partial c_n}=\frac{\partial \mathcal{L}}{\partial C_i}\frac{\partial C_i}{\partial c_n} \\ \frac{\partial \mathcal{L}}{\partial o_n}=\frac{\partial \mathcal{L}}{\partial C_i}\frac{\partial C_i}{\partial \alpha _n}\frac{\partial \alpha _n}{\partial o_n} \\ \frac{\partial \mathcal{L}}{\partial s_n}=\frac{\partial \mathcal{L}}{\partial C_i}\frac{\partial C_i}{\partial \alpha _n}\frac{\partial \alpha _n}{\partial \sigma _n}\frac{\partial \sigma _n}{\partial \Sigma _{n}^{\prime}}\frac{\partial \Sigma _{n}^{\prime}}{\partial \Sigma _n}\frac{\partial \Sigma _n}{\partial M_n}\frac{\partial M_n}{\partial s_n} \\ \frac{\partial \mathcal{L}}{\partial q_n}=\frac{\partial \mathcal{L}}{\partial C_i}\frac{\partial C_i}{\partial \alpha _n}\frac{\partial \alpha _n}{\partial \sigma _n}\frac{\partial \sigma _n}{\partial \Sigma _{n}^{\prime}}\frac{\partial \Sigma _{n}^{\prime}}{\partial \Sigma _n}\frac{\partial \Sigma _n}{\partial M_n}\frac{\partial M_n}{\partial \bar{q}_n}\frac{\partial \bar{q}_n}{\partial q_n} \\ \frac{\partial \mathcal{L}}{\partial \mu _n}=\frac{\partial \mathcal{L}}{\partial C_i}\frac{\partial C_i}{\partial \alpha _n}\frac{\partial \alpha _n}{\partial \sigma _n}\left( \frac{\partial \sigma _n}{\partial \mu _{n}^{\prime}}\frac{\partial \mu _{n}^{\prime}}{\partial t_n}+\frac{\partial \sigma _n}{\partial \Sigma _{n}^{\prime}}\frac{\partial \Sigma _{n}^{\prime}}{\partial t_n} \right) \frac{\partial t_n}{\partial \mu _n}$

这个链式法则产生的计算图可以与一些实验时的现象结合，带来一些的观察：

如果一个不怎么该出现高斯点的地方有一个高斯点，那么它大概率是不可能通过优化$\mu$来到合适的位置的，它大概率会因为不透明度在几个iteration中变的很小，然后导致$\frac{\partial C_i}{\partial \alpha _n}$也很小，然后中道崩殂。
高斯点们之间唯一“通信”的地方只在不透明度的计算中，因为那里排序的先后顺序会影响穿透率。如果引入一个MLP，其实本质上是建立MLP的输入与这些属性的关系。比如输入坐标，这一定程度上是实现了“location-aware”。因为通过这样操作，神圣的MLP就把这些离散的高斯点联系在一起了，就开始NeRF了。这或许也解释了为什么用一些结构，如最早Plenoxels的这种用显式的球谐比MLP+camera pose要稍次一点，因为“primitives”之间没有“通信”。
当建模动态的事物时，由于上述机制，adaptive-densification是乏力的。因为动态时所重建的对象在不同帧下会反馈比较混沌的梯度信号，$\frac{\partial \mathcal{L}}{\partial \mu _n}$本身参考意义就不是很大。

“adaptive densification只是你的谎言。”——一位一觉醒来发现point居然densification到了500k的学生说。

以及如果在初期时一旦有一些点不透明度接近0了，那他们会“直接死亡”，没法复生。在这种情况下，感觉还不如随机在现在的点周围sampling。
所以一个常识“先学到一个好的canonical，再学deformation”是必要的。这也是前四篇工作一直在想办法找canonical的原因。
当我们有了一个差不多的解的时候，是否还有必要让每个高斯点都是learnable的？用一种progressive manner是不是更合适呢？

所以如果要像前四个工作一样，那就要想办法确定一个canonical，然后再学Gaussian，这也是比较有创意的部分。而后两个工作，其实完全破坏了Gaussian的显式特性，把他们变成了一个“特征寄存器”，我个人不太喜欢这种方法。

我现在能做到的结果已经梦回PointAvatar了，我明明用的是Gaussian splat，然而结果跟sphere splat的没啥区别，这其实就说明在变形的阶段的优化是很ambiguous的。怎么能不落俗套的再搞一个canonical出来，这是一个很有意思的事情。

End

“快过年了，不要再科研了，看那几本论文集。在生活种并不能给你带来任何实质性的作用。朋友
们兜里掏出一大把钱吃喝玩乐，你默默在家远程服务器打开shell，亲戚吃饭问你一个人闷屋子里在干什么，你说我刚改了改了套参数又改了改代码，亲戚们懵逼了你还在心里默默嘲笑他们，不懂得 CCF-A 多闪亮多梦幻，亲戚都在说自己子女一年的收获，儿买了个房，女儿买了个车，闺女出国定居了，你的父母默默无言，说我儿子是科学家，在家对着黑黢黢的屏幕十天动都不带动了。”