“闻听说书人也曾将故事杜撰,听罢取壶酒踏歌去醉意阑珊。”
事情是这样的,我毕业设计打算做三维人脸合成,但其实在2023年的语境下,把“三维”和“人脸”放在一起,其实目的就是整出一个完整的“三维人头”。但当我试图在炼丹里像女巫魔法一样“synthesis”出一个人头的时候,我发现我设想的pipeline里需要一个很强的先验或者约束,以及本着要写开题报告和后面related work的因素,我就打算先整理这么个blog,把人头的这个事情说清楚。
表征一个人头是几十年来图形学和计算机视觉里的不懈追求,从方法论上来看,做到这点其实就是实现“参数化模型”(parameterized model),如果我们可以用一组参数和一些映射关系来表达人体的几何和外观,那么我们也就实现了对人头和人脸的表征。这个过程就像很多游戏里捏人系统一样,希望通过调整一些数值的大小,来得到不同的人脸:

Basel Face Model
基于表示现实人脸的参数化人脸模型的最早尝试应该就是3DMM(3D Morphable Model)。3DMM是一个很经典的方法了,最早可以追溯到1996年。但在当下,当提到3DMM的时候,往往指的是巴塞尔大学的研究人员提出的Basel Face Model,简称BFM。这一部分我想用先用3DMM来引出一些东西,然后用BFM结合一些具体例子,聊作记录。
考虑一个人人脸的数据采集,一种很直接的办法就是在人脸上用激光扫描采集很多很多点(稠密匹配),记录这些点的位置和颜色。位置,换句话说也是形状(shape),可以叫$s=[v,3]^{T}$;颜色,换句话说也叫纹理(texture),记作$t=[v,3]^{T}$。其中$v$是采集的点的数量,形状里的3是$xyz$,纹理里的3自然是RGB三个通道。
当我们采集足够多的$n$张人脸以后,我们把$s$和$t$重排成一维向量,那么对于形状就会有一个大矩阵$\mathbf{S}\in \mathbb{R} ^{n\times 3v}$,对于纹理就有$\mathbf{T}\in \mathbb{R} ^{n\times 3v}$。对整个数据分别做主成分分析,我们可能会得到$M$个成份。3DMM隐含的假设正是想利用这$M$个人脸的线性组合来合成其他人脸:
由于真正在做PCA的时候,会先计算出一个平均脸,然后将人脸数据按这个平均脸中心化,所以我们往往会用中心化后的$\mathbf{S}_i,\mathbf{T}_i$,所以这时候的线性组合写作:
后来的一篇工作3DFace实现了对表情的控制,核心是将表情看作对于形状的偏置,那么在采集的时候,让一个受试者做出不同的表情,然后再走PCA那一套,就可以得到表情的表达了:
我们可以在BFM的网站上下载训练好的模型(也就是那些基,平均脸什么的),里面提供了一些matlab脚本可以玩,我们可以画出里面的标准人脸:

画出这张图,用到的是matlab里的一个trimesh函数,上面的这张图是将01_MorphableModel.mat里的shapeMU,texMU画出来的样子,就是那张“平均脸”。shapeMU和texMU只是单纯的散点,如果不用trimesh,用scatter看作三维点单纯的画的话,是这样的:
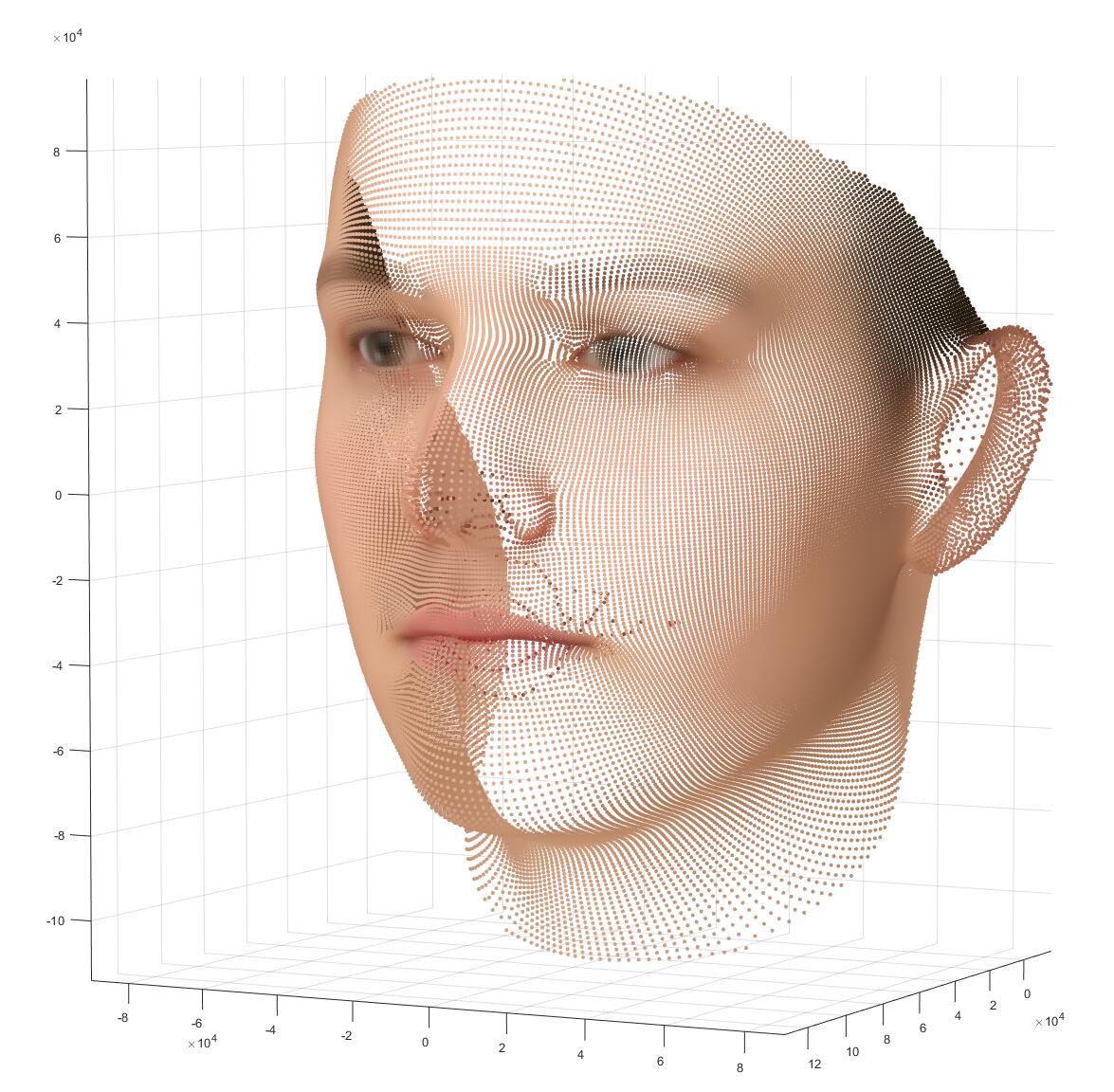
从这些带颜色的点出发,到刚才的那张人脸,经历的过程叫“光栅化”(Rasterization),一个三角形片元的三个顶点之间,会互相插值出颜色,最后得到一个平滑的表示。这是一个图形学里非常基础的概念,但我想指出的是,如果一个人只有炼丹的背景,那么在大多数时候他所接触的数据都是“grid-based”的,比如图像只是$[C,H,W]$的张量,字和词也是是长度为$l$的token。那么光栅化实际上提供了一个从不是那么“structured”的数据,变换到”grid-based”的数据。例如刚才,我们从一堆顶点中出发,渲染出了一张人脸,这张人脸所形成的图片和在寻常深度学习管线中需要处理的图片别无二致。这一点的意义十分重大。
非常幸运,有很厉害的工程师们实现了很高效率的可微的光栅化器,如PyTorch3D,nvdiffrast,他们用一些策略实现了这一过程的前向算子和反向算子,这将光栅化的操作变成了可微分的。这带来了很多的可能,例如我们可以将光栅化后的结果跟一些别的东西联合在一起当loss,作为一种监督;我们可以引入标准人头的mesh来作为一种先验。
用这个仓库,我们可以从单张图片或者视频里来拟合一张脸的3DMM,想实现这点其实需要一个off the shelf的人脸检测器,来先标出哪里是人脸,一般用的都是mtcnn。
从2023年的角度出发,不要用tensorflow版的mtcnn了,用facenet集成的mtcnn吧。
比如,我们用卷福试一下:


这个结果勉强看着还行,但如果换成一个稍微难一点的case,换成《生化危机:IV》重制版中阿什利的脸模小姐姐:


就不太行了。
说到底,这种方式的表达能力还是很有限的,一眼就能看出是那种零几年的电脑游戏里的感觉,而且只能有一张脸皮,没办法有整个头。感觉确实不是那么的“amusing”。
有一篇结合了BFM的工作比较重要:Deep3DFaceRecon,这篇工作在EG3D里被用于预处理FFHQ数据集,EG3D的目的是要每张图片拍摄时的相机位姿$\mathbf{p}$。除此以外,这篇工作的核心是利用可微分渲染,估计出BFM参数后重建人脸,然后渲染,然后用渲染后的图像和原图做损失。应该是最先把可微渲染引入这个过程的工作。它输入是RGB图像,输出是一组向量$\mathbf{x}=\left( \boldsymbol{\alpha },\boldsymbol{\beta },\boldsymbol{\delta },\boldsymbol{\gamma },\boldsymbol{p} \right) \in \mathbb{R} ^{239} $,其中$\boldsymbol{\alpha }\in \mathbb{R} ^{80},\boldsymbol{\beta }\in \mathbb{R} ^{64},\boldsymbol{\delta }\in \mathbb{R} ^{80}$分别是形状,表情,纹理的基系数,$\boldsymbol{\gamma }\in \mathbb{R} ^9$是三阶的球谐系数,用于拟合光照,$\boldsymbol{p}\in \mathbb{R} ^6$是三个角度Yaw, Pitch, Roll和一个平移分量$\mathbf{t}\in \mathbb{R} ^3$。
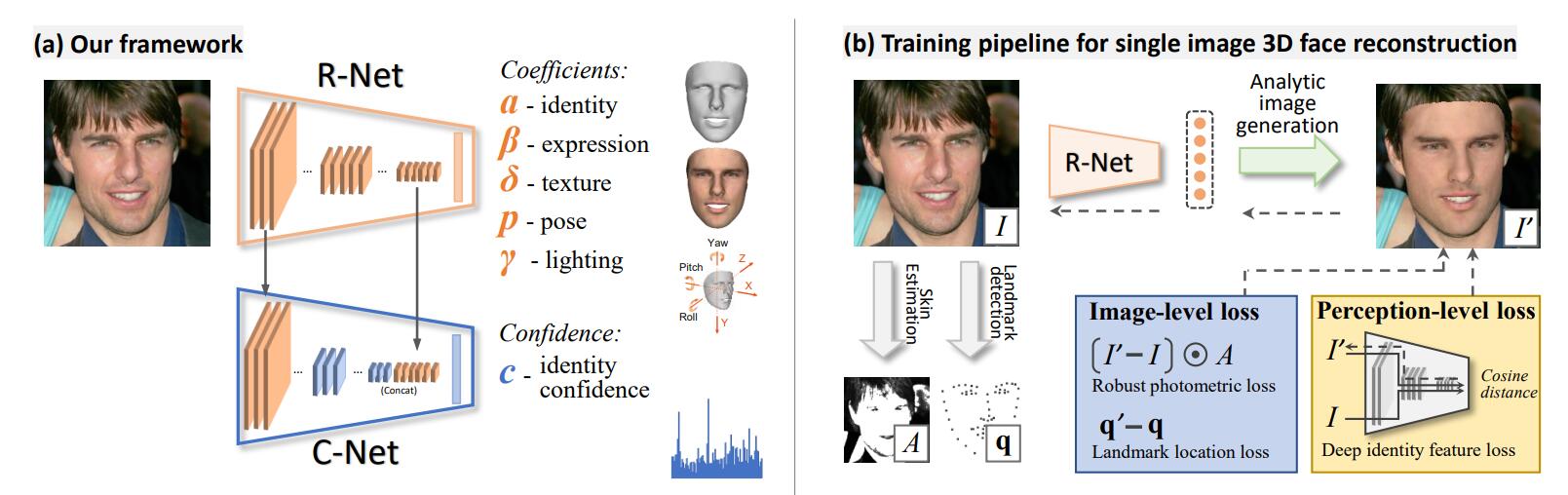
所以这个最后实现的效果还是很“麻雀虽小五脏俱全”的,输入一张图片就可以预测出这么多的东西。
Deep3DFaceRecon最开始是用tensorflow编写的,后来作者们又重写了一版PyTorch的。如果你想玩一下那个库,现在最大的问题是原仓库表明的torch版本一般都比较低,比如torch1.6.0,低版本的torch往往不支持高版本的CUDA,而一些新的显卡也不兼容低版本的CUDA(安培架构的30系显卡,Ada架构的40系显卡,都需要使用11.3版本以上的CUDA)。一个简单的解决办法是租像2080Ti,T40这样的旧一点的显卡,或者就是换新版本的torch,但后者可能会带来一些问题。
那么在没有可微渲染的时候呢?在3DDFA里,那时候的人们需要用各种办法来实现3D信息的监督,这里面就提出了两种,一种是PNCC(Projected Normalized Coordinate Code),另一种是PAF(Pose Adaptive Feature)。在后面有些talking head synthesis的工作里,我曾看见过这个“PNCC”,然后当时给整懵了,论文正文里都会一副仙人派头的写:
实际上这行似公式非公式的写法,说的是:找标准人脸$\bar{\mathbf{S}}$,将$\bar{\mathbf{S}}$的三个维度分别作极大极小归一化,得到:
那么这个$\mathrm{NCC}$就能保证在$[0,1]^3$之间,所以叫它“Normalized Coordinate Code”。这里面的每个$[0,1]^3$中的点,都可以“指认”(assign)一个RGB的颜色。这一点其实蛮有趣的,如果你用一些画图工具,matlab也好python也好,你画出一个$[0,1]^3$的立方体,然后用这种办法来上色,会得到一个挺有意思的正方体,其体对角线可以看出表示了亮度的变化(这就是数字图像处理里的另一种图像空间YCrCb了)。
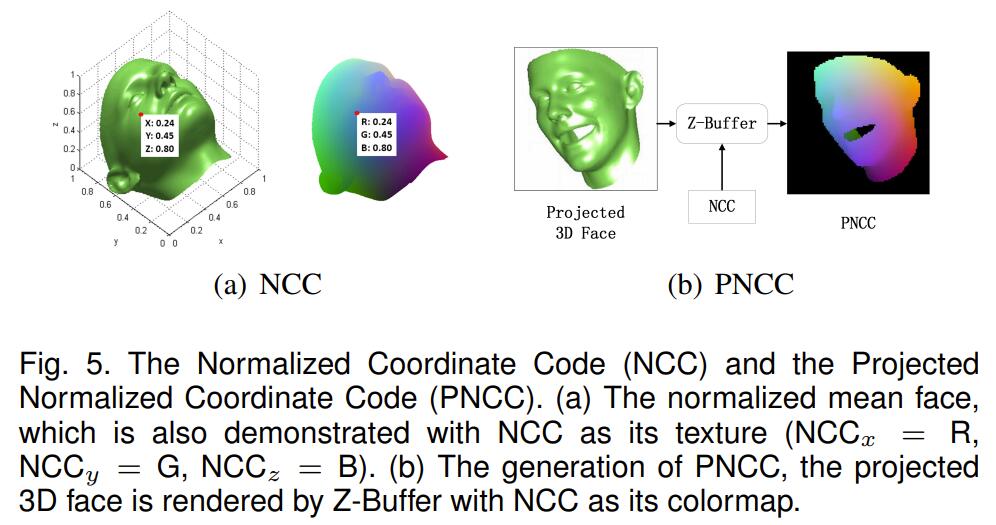
然后对于一个经过旋转,平移后的3D人脸$V_{3d}(\mathbf{p})$,用NCC指认的颜色作Z-buffer,渲染出一张图,这张图就叫PNCC。
Z-buffer是说,对于每一个三角形片元,我们都计算一次他光栅化后会占据哪些像素点,同时也可以得到每个点之于三角形片元的“深度”Z(倒数线性插值)。然后对每个像素点,我们都保留一个z-buffer,按打擂台式的方法找出哪些片元离这个像素是最近的,在更新更近的深度的同时,也在frame-buffer里更新这个点对应的RGB。这个步骤在大多数时候根本轮不到我们来做。
至于PAF说的什么柱面采样之类的,我没有在一些别的任务里见过了,此处就不讨论了。
FLAME
刚才提到的BFM并不能复原出整个人头,同时,对于旋转它其实没有做特殊的处理。也就是说BFM只有一个全局的旋转,但一个人头,有一部分当然是可以发生局部旋转的,比如眼球,下颚等。然后马普所的研究人员就发力了!有了FLAME。直观来看,FLAME有了一整个人头,而且还支持一些部分的局部旋转,但它本身没有提供纹理(如果你愿意,你可以把BFM里的纹理转换过来)。但是FLAME其实相比于BFM要复杂了一些,为了理解FLAME的这盘醋,得包一大盘饺子:要看懂SMPL。
SMPL本身是一个用于表征整个人身体的参数化模型,我们下面需要尽力的从零开始理解SMPL。但有些同学可能像我一样,只能非常羞怯的承认,因为读本科期间好吃懒做忙于看冻鳗小人,没有接触过图形学,没去看过GAMES系列,也没有上过Blender,Maya之类的选修课,连个交互式的viewer都不会写,甚至还没能捋清楚过渡矩阵是从谁变换到谁就要本科毕业了,但依然还想了解一些3D vision和computer graphic的东西。翻遍了图书馆里什么虎书黑皮书,上来一堆什么“蒙皮”,“BlendShape”,“Rigging”,都没能找到自己可以看得懂的资料。但上天被这愚公移山的努力感动,于是GitHub上出现了这个项目,在这个项目提供的UI下,我们可以对SMPL和FLAME等模型进行可视化,从而将公式与具体实际相结合。
首先我们要明确,在我们讨论比较“现代”的数字人时,其实分为两个对象:骨骼(“skeleton”)和表面(“surface”),我们一定听闻过诸如“人体姿态估计”这样的任务,我们会用若干个结点(“joints”)来表达一个人,比如HumanEva-I数据集里是14个结点,Human3.6M里是17个结点。这些结点构成的树就是骨骼,而表面指的就是图形学里的“mesh”。
之前BFM的例子里,有一个事情没能体现出来。可能由于时代原因,BFM模型的数据以.mat的形式储存的。而一般来说这种数据是用一些更通用的3D文件格式,如.obj格式储存的。对于.obj文件,你甚至可以用记事本打开它。打开以后一般会遇到:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
v 0.123 0.234 0.345
v ...
...
vt 0.500 1
vt ...
...
vn 0.707 0.000 0.707
vn ...
...
f 1 2 3
f 3/1 4/2 5/3
f 6/4/1 3/5/3 7/6/5
f 7//1 8//2 9//3
f ...
...当然还有其他声明,上面这四个是最重要的。其中v是最简单的vertex,表示顶点。vt是vertex texture,说的是纹理坐标,第一个数一般记作u,第二个数一般记作v。这两个坐标张成的二维映射,也叫UV mapping,在UV map上会记录该vt的颜色。vn是vector norm,是每个顶点的法向量,其实是用于决定面的朝向的。一个面由三个顶点构成,将这三个顶点对应的vn相加取平均。
最后的f是面,用于记录哪些顶点是在一组的。例如f 1 2 3的意思就是说v中的第一行,第二行,第三行是一个组。如果f记录时有斜杠,例如f 3/1 4/2 5/3,那么句法就是
f 顶点v索引/纹理坐标vt索引,如果有两个斜杠,那么就是f 顶点v索引/纹理坐标vt索引/顶点法向量vn索引。
而这个表面就是很多很多个结点组成的三角面片的集合体,所以当我们给出一个3D模型的表示时,其实并没有mesh内部的那些“joints”。SMPL里是用一个回归矩阵$\mathcal{J} \in \mathbb{R} ^{\left( K+1 \right) \times N}$来从输入的mesh里去估计joints的。这里如前文所说$K=23$,同时顶点数$N=6890$,所以$\mathcal{J}$其实还是个挺大的矩阵。
在姿态估计的范式下,每一个结点代表的是一个二维或者三维的坐标;但在数字人驱动的角度上,这种表达不太好“animation”。一种更合适的做法,是我们预先设定好骨骼里相邻结点之间的距离(即“骨头”的长度),然后我们规定根结点(这个结点一般对应在人体的胯骨附近)为父节点,通过指出父节点的子结点相对父节点的旋转,我们可以链式的计算当给定一组旋转后,此时骨骼上各结点的位置。
我们可以用一个平面上的链杆来说明这件事:
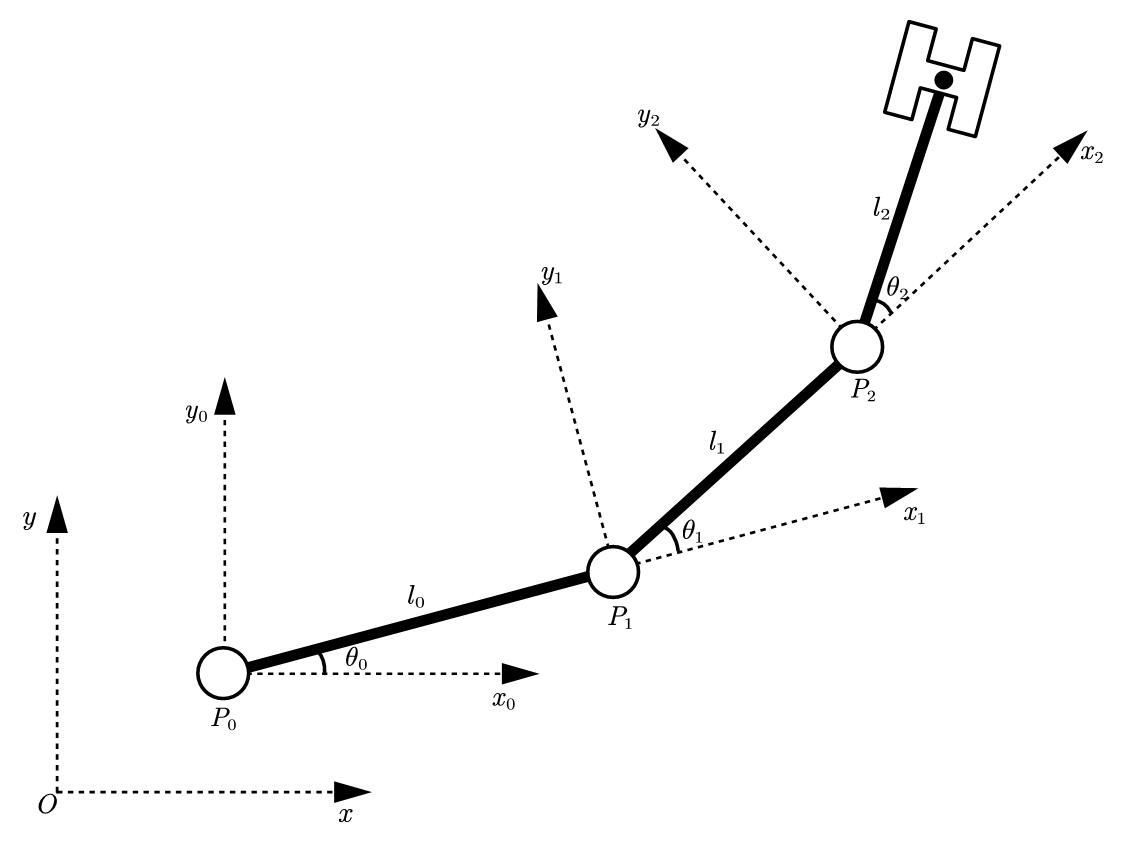
这个结构上有三个点$P_0,P_1,P_2$,我们现在想得到$P_2$在全局坐标系$xOy$下的坐标。这里我们认为$P_0$是根结点,也就是说我们是知道$P_0$的坐标的。同时链杆的初始状态是水平的。我们要意识到,$P_0$处旋转$\theta_0$,会带动$P_1,P_2$一块旋转。然后我们再旋转$P_1$,对$P_1$的旋转也会作用到$P_2$上。我们用$Q$来表示某个点全局的旋转矩阵,用$R$来表示其局部的旋转矩阵,则有:
于是我们就可以给出$P_2$在全局坐标系下的表达了:
所以这个过程就像链条一样“forward”,即前向运动学(“forward kinematic”)。如果我们选择用齐次坐标的表示,那么式子的书写就可以归结为齐次变换的矩阵的连乘。
但有时,我们又是想指定一个pose,比如通过指定一组$(x,y,z)$坐标的方法。那么这时候就是相应的逆向运动学(“Inverse kinematic”)。
现在我们知道了在给定每个结点的旋转下,所有结点的坐标的表示。$l_i$当给定一个骨骼时,它已知的,现在仍需确定的就是$R_i$了。我们知道$R_i$从数学定义的角度看,单纯的做“旋转”,是个正交阵。但是这个正交阵的导出可是有好几种写法的。
我们需要具体的讨论一下SMPL中的“旋转”。与常见的欧拉角描述旋转不同,在SMPL里采用的是“轴角式”(axis-angle)来描述旋转的,这种描述顾名思义,是指给定一个向量$u$和一个角度$\theta$,所作用的旋转就是沿这个向量$u$旋转$\theta$度,方向由右手定则确定。那么为什么要采用这种表示方法呢?因为这种方法避免了在表达人体时出现“万向节死锁”。
我们可以用下面这个例子来体会“万向节死锁”,我们先按Y轴旋转90°,然后再旋转X和Z轴,会发现:

这是由于在代码里:
1 | euler_angle = [val, self._body_pose_joint_y.int_value, self._body_pose_joint_z.int_value] |
隐含的规定了顺序为XYZ的欧拉角表示,而欧拉角表示只会忠实的读入当前的euler_angle然后先绕X轴变换,再绕Y轴变换,再绕Z轴变换。所以当Y轴被设置成90度以后,再调整X或Z轴,仍然相当于先旋转了X轴,然后旋转了90度的Y轴,这导致再旋转Z轴和之前旋转X轴具有一样的效果,即一个自由度的消失。
但欧拉角的好处是方便进行人机交互,这也是UI里给的端口是欧拉角的原因。而轴角式就不会有这样的问题,但这说穿了也只是旋转的几种写法而已,最后作变换的实际上还是旋转矩阵$R$,那么如何用这种轴角式的表示来导出$R$呢?罗德里格旋转公式(Rodrigues formula)可以做到这点 :
理解这个公式,以及理解这个$\mathrm{exp}(\cdot)$为什么乱入进来,可能以后会再写一篇blog(没准是什么“旋转的四种写法”),这里我们先不管了,我们只要知道这个$\exp\mathrm{(}\vec{w}_j)$就是我们朝思暮想的$R$就好了。这里的$\vec{w}_j\in\mathbb{R}^3$,有人可能会疑惑,这轴角式,不是说要一个向量$u$然后一个角度$\theta$么?这不肯定得$\mathbb{R}^4$了?实际上这只是一个写法上的事情,由于旋转轴我们只关心方向不关心模长,所以用一个单位向量表示,然后再将$\theta$点乘进单位向量里,这就凑成了$\vec{w}_j\in\mathbb{R}^3$。所以这里$\theta$其实就是$\left| \vec{w}_j \right| $,旋转轴实际就是$\overline{w_j}=\frac{\vec{w}_j}{\left| \vec{w}_j \right|}$。然后上述公式里的$\widehat{\bar{w}}_j$是一个从$\overline{w_j}$导出的反对称矩阵,至于这个反对称矩阵的具体写作什么也是旋转推导里的,我们这里先不提了。
所以给定一个人体姿态$\overrightarrow{\theta }=\left[ \vec{w}_0;…,\vec{w}_K \right] $,以及此时的骨骼结点$\mathbf{J}\in \mathbb{R} ^{3\times K}$,那么各结点的变换即写作:
$A(k)$是第$k$个结点的祖先结点的集合。同时,注意姿态本身存在一个静止时的姿态$\overrightarrow{\theta ^{\ast}}$(可能是T-pose或者A-pose),静止时的变换记作$G_k\left( \overrightarrow{\theta ^{\ast}},\mathbf{J} \right) $,所以我们需要消除“转移到静止姿态的变换”的影响,于是最终的姿态是:
即我们先左乘静止时的变换的逆,来抵消初始姿态的影响。
那么现在我们对各个结点的位姿变换有了圆满的答案,但我们如何回答构成mesh的那些顶点随这些旋转的变换呢?经典的办法即“线性混合蒙皮”(Linear Blending Skinning,LBS)。即考虑对顶点跟随每个结点的旋转的效果进行线性加权,我们用$\overline{\mathbf{T}}$来表示平均的结点集合,每个顶点记作$\overline{\mathbf{t}_{\mathbf{i}}}$,那么变换后的顶点$\overline{\mathbf{t}_{\mathbf{i}}}^{\prime}$按照LBS即为:
这里的$w_{k,j}$来自于一个权重矩阵$\mathcal{W} \in \mathbb{R} ^{N\times K}$,在动画制作的管线中,$\mathcal{W}$的选取需要手动调整,这个操作也叫“刷权重”。在SMPL里,$\mathcal{W}$是从大量的扫描数据里回归出来的。但在SMPL是用参数可以控制出高矮胖瘦不同的人,对不同状态,不同位姿的人用同一个$\mathcal{W}$是不合适的。与BFM类似,通过对不同体型不同身高的人的顶点进行PCA,我们可以得到若干个具有可解释性的成份:
其中$\overrightarrow{\beta }=\left[ \beta _1,…,\beta _{\left| \vec{\beta} \right|} \right] ^T$即我们可以调整的系数,而$\mathcal{S}$是优化出来的那些成分长成的矩阵,有$\mathcal{S} =\left[ \mathbf{S}_1,…,\mathbf{S}_{\left| \vec{\beta} \right|} \right] \in \mathbb{R} ^{3N\times \left| \vec{\beta} \right|}$。$\left| \vec{\beta} \right|$在最初的一版里仅为10,后续又有一版300的。但10个组份的时候基本就能很好的描述高矮胖瘦了。他们的物理意义即“shape”这一因素对顶点们产生的位移(displacement)。这个处理也叫“Shape blend shapes”,翻译过来,可以叫“基于形状的混合变形”。
与在BFM里我们将表情看作一种对人脸形状的偏置一样,我们可以认为刚才讨论的那些旋转对于人体形状的偏置。从另一个角度看,随着姿态的变化,一些顶点的相对位置也会发生变化。例如当做一些复杂的动作时,一些可能在用力的部分的顶点应该发生一些形变来模拟肌肉的收缩,这一点在做animation的时候会很明显。SMPL里于是又用了“Pose blend shapes”,形式上和刚才的是类似的,但道理上不是那么直接。在刚才的“Shape blend shapes”里,$\beta$作为系数的出现,是PCA的直接结果。但在这里,实际上是将旋转本身作为系数,然后反解出此时需要的基表示。
这里用于作系数的旋转,是将之前的$\overrightarrow{\theta }=\left[ \vec{w}_0;…,\vec{w}_K \right] $,直接用罗德里格旋转公式逐$\vec{w}_j$的计算出旋转矩阵$R$,然后将这个3×3的旋转矩阵展平,最终得到一个$\mathbb{R} ^{9\times K}$的表示作为系数。这里$K=23$,所以即需要$23\times9=207$个基,即:
这里在系数部分减去$R_n\left( \overline{\theta ^{\ast}} \right) $是为了保证在静止姿态时,$B_P\left( \overline{\theta ^{\ast}};\mathcal{P} \right) \equiv 0$。从而在用一些简单姿势进行试验时,$B_P\left( \vec{\theta};\mathcal{P} \right)$其实都不会很大,数量级会显著低于正常顶点坐标的量级。
通过引入这两处修正,我们就可以给出SMPL里提出的蒙皮算法了,只需要对之前LBS里的$\overline{\mathbf{t}_{\mathbf{i}}}$进行修正:
这里的$\mathbf{b}_{S,i}\left( \vec{\beta} \right) ,\mathbf{b}_{P,i}\left( \vec{\theta} \right) $就是从$B_S\left( \vec{\beta};\mathcal{S} \right) ,B_P\left( \vec{\theta};\mathcal{P} \right) $计算出的对应的偏移。
最后就只剩下一个问题没有解决了,随着高矮胖瘦的变化,$\mathbf{J}$也会发生变化。前文里我们说$\mathbf{J}$是通过$\mathcal{J} \in \mathbb{R} ^{\left( K+1 \right) \times N}$来估计的,那么我们现在知道,由于“Shape blend shapes”的作用,这个估计的输入即是$\bar{\mathbf{T}}+B_S\left( \vec{\beta};\mathcal{S} \right) $,所以在不同$\beta$下的骨骼结点即为:
这也是要保证$B_P\left( \overline{\theta ^{\ast}};\mathcal{P} \right) \equiv 0$的原因之一,否则在这一步的估计会变得更困难。“你不能在没有确定结点的情况下就有了poses”。
于是我们就对SMPL有了一个圆满的解释,所谓SMPL模型,就是从一个大量的人体测量数据集里估计$\Phi =\left\{ \bar{\mathbf{T}},\mathcal{W} ,\mathcal{S} ,\mathcal{J} ,\mathcal{P} \right\} $,最终在输入$\vec{\beta},\vec{\theta}$,通过$\mathcal{J}$估计在$\vec{\beta}$下的静止结点$J$,然后用$\vec{\theta}$计算姿态的变换$G_{k}^{\prime}\left( \overrightarrow{\theta },\mathbf{J} \right)$。最终利用其改进的加入了$B_S\left( \vec{\beta};\mathcal{S} \right) ,B_P\left( \vec{\theta};\mathcal{P} \right) $的线性蒙皮混合算法,得到此时的顶点坐标。
眼见为实,我们可以可视化一下$B_S\left( \vec{\beta};\mathcal{S} \right) ,B_P\left( \vec{\theta};\mathcal{P} \right) $的影响。



最左边是测试的姿态,中间是此时的姿态产生的$B_P\left( \vec{\theta};\mathcal{P} \right)$加到模板$\bar{\mathbf{T}}$上的效果,右边是单纯的$\bar{\mathbf{T}}$的效果,可以看见$B_P\left( \vec{\theta};\mathcal{P} \right)$在一些部分有轻微的调整。$B_P\left( \vec{\theta};\mathcal{P} \right)$的效果直接观察比较难看出来,所以只能通过这样来观察了。
莫名想到小说《球状闪电》里,丁仪在众人的嘲笑下,拿出一张围棋棋盘,来看见未激发球闪空泡的轮廓。这个UI项目原本是不支持画出网格线的,但可以在
load_body_model()中进行修改,从而画出网格线。
$B_P\left( \vec{\theta};\mathcal{P} \right)$的效果是更显著的:
终于,我们可以讨论FLAME了。FLAME和SMPL的框架是一样的,只不过结点少了很多,只有4个,只用于驱动左眼球,右眼球的转动,嘴巴张开的角度,以及脖子的旋转。但FLAME多做了关于表情的基,从而让人头更富有表现力。

在我们之前的讨论里,都不涉及对大规模人脸数据的处理,以及人脸参数化模型的具体训练和优化,这些部分往往是难度更大的部分。因为这篇blog的目的其实是为了毕设做人脸合成打前置知识。但值得指出的是,除了类似FLAME这种对人头的参数化方式,还存在一种被称作“双线性模型”的参数化模型,如FaceWarehouse,FaceScape。这种模型采用的方式是在得到大批量人脸的初步的mesh后,对整批数据进行张量分解,来得到独立的成分(形状和表情)。这样天然的保证了形状和表情的解耦,而在FLAME中,这一点是靠大规模数据集来保证的(对同一个人采集若干表情)。从拿一个参数化模型来当先验的角度看,两者的区别不会太大。以及由于双线性模型导引出的结合形式是乘法,而不是加法,所以可能在一些下游任务里用FLAME会安全一些?(只是直觉,没有证据。)
与FLAME结合的有一个很好的工作:DECA,可以看作是之前DeepFaceRecon的升级版。其核心仍然是“参数化人脸+可微渲染”,通过用神经网络来预测出FLAME的系数来从wild image里恢复一个人头,同时佐以描述光照,描述纹理的系数,分别用不同的组件进行解码。
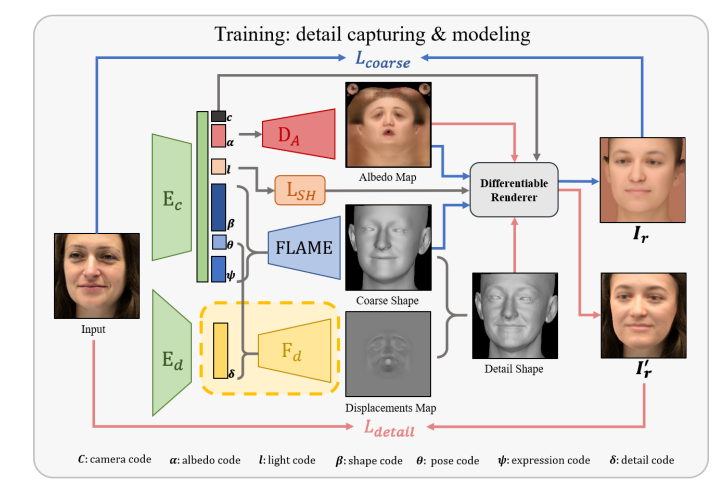
有趣的地方在于,我们知道FLAME本身的模型还是看着“光溜溜”的,为了让它能更贴合真实的人脸几何(一些皱纹等等),这里也有“coarse to fine”的策略。具体表现在会给出一张Displacements Map,其类似UV map,用于对顶点的位置进行微调。微调的方向大概是沿着顶点法向量的方向。
我们可以输入一张稍微out-of-distribution的图片,一张游戏《生化危机:VI》里过场动画里的王阿姨,然后对比一下输出的几何:


可以看到最后的结果还是很好的……捕捉了王阿姨的美的。
无论是FLAME还是SMPL,由于许多前人的努力,他们在PyTorch下有了很完善的封装,他们的类实现继承自nn.Module,可以像使用其他的网络层一样简单的调用他们。在smplx库里,有着SMPL,FLAME的实现。除此以外还有SMPLH,SMPLX,MANO。MANO是一个关于手部的模型,而SMPLH就是SMPL+Hand(MANO)的意思,SMPLX就是SMPL+face(FLAME)+hand(MANO)。
他们使用起来非常方便:
1 | model_output = model( |
model_output是一个实例化的类,里面具体有什么取决于一些其他设置:
1 | output = SMPLOutput(vertices=vertices if return_verts else None, |
而那些令我们头痛的计算过程往往被打包写进了lbs.py的实现里,我们可以大多数时候都不管他们,耶!
Implicit Model
虽然FLAME的效果已经很好了,但它没能解决至少一个很明显的问题:头发。头型是一个很明显的对象,但其是非常多样的,先前的模型都没有处理头发这一问题,因为这确实很困难。但至少,神经网络提供了一个很强的拟合连续变化边界的解决方案。显式的模型很难处理这个问题,于是就只能炼丹了。下面我们会看到,在显式和隐式之间来回横跳,是一门艺术。
但一旦引入neural,那么之前FLAME构建的“mesh-vertex”的这种表示就不能直接用了。需要一些别的表示方法,例如,符号距离函数(Signed Distance Function, SDF)就是一个不错的方法。有许多工作都采取了这种范式,输入坐标$(x,y,z)$,向神经网络查询该坐标下的SDF。其实有一部分工作最开始并没有打算用于建模头发,最开始只是想用这种非线性的拟合能力,把之前FLAME建模产生的误差再降一降;也可能是完整的人头数据不好处理,而一些成熟的管线都处理好了人脸的那张mesh。
例如在Imface中,作者先对FaceScape数据集进行较为复杂的预处理,从mesh中先获取SDF,然后用网络来拟合SDF。
这里有一个事实是,FaceScape数据集里在扫描的时候好像有意避免了头发的影响,每个受试者都戴着一个红色头套,具体原因不详。所以Imface的作者们当时可能是想建模一下头发的,但可能那时候没有更好的数据集。另一个高质量的数据集FaceVerse是2022年了,在那个数据集的扫描数据里是有头发的。
同时,与之前显式模型中人为设定表情和形状的系数类似,网络的输入中还有$\left\{ \mathbf{z}_{\exp},\mathbf{z}_{\mathrm{id}} \right\} $。这里的$\mathbf{z}$虽然也被叫作“latent code”,但其实并不是类似GAN那样从高斯分布里采样的,是设定好输入输出维度,用nn.Embedding()学出来的。从而当训好这个网络后,可以很自然的对$\left\{ \mathbf{z}_{\exp},\mathbf{z}_{\mathrm{id}} \right\} $进行插值来产生unseen的人脸。
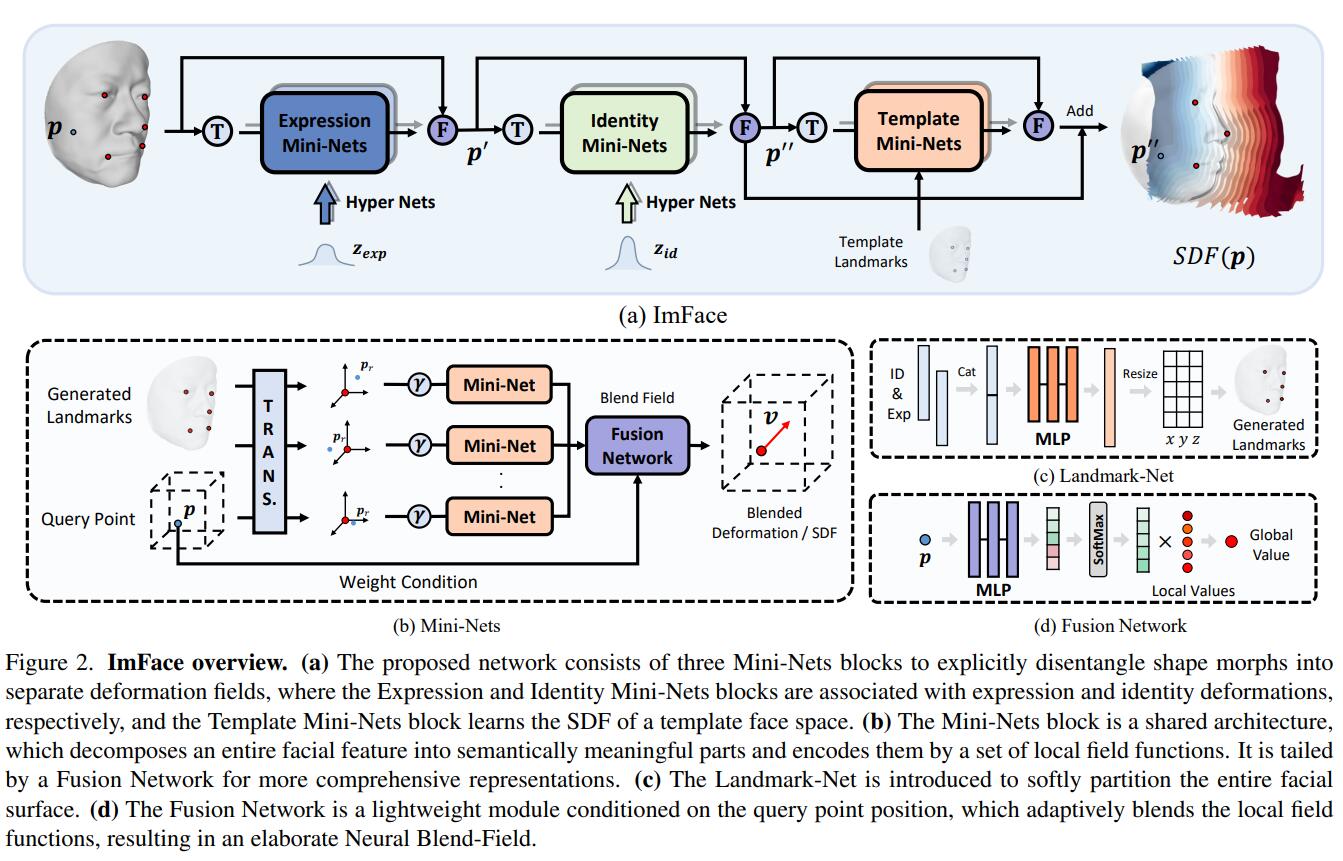
如上图所示,整个管线还是很复杂的,这里我们就不展开了。另一篇工作i3DMM正式向头发发起了冲锋,
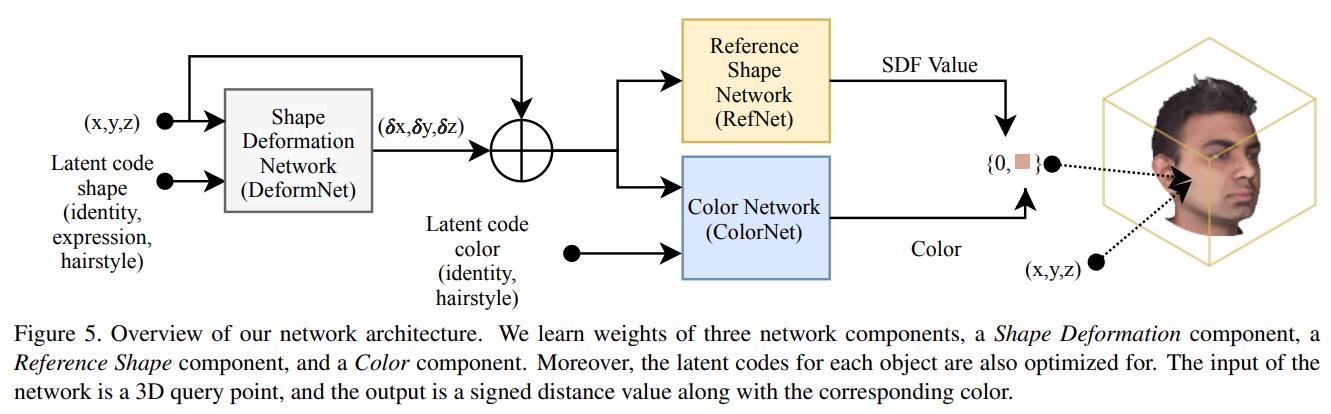
他们使用的是自建的数据集,可以看出其实结果并没有那么喜人,但至少有了头发。在NPHM中,通过提高数据集的粒度以及一些组件的设计,最后呈现的效果明显变好了:
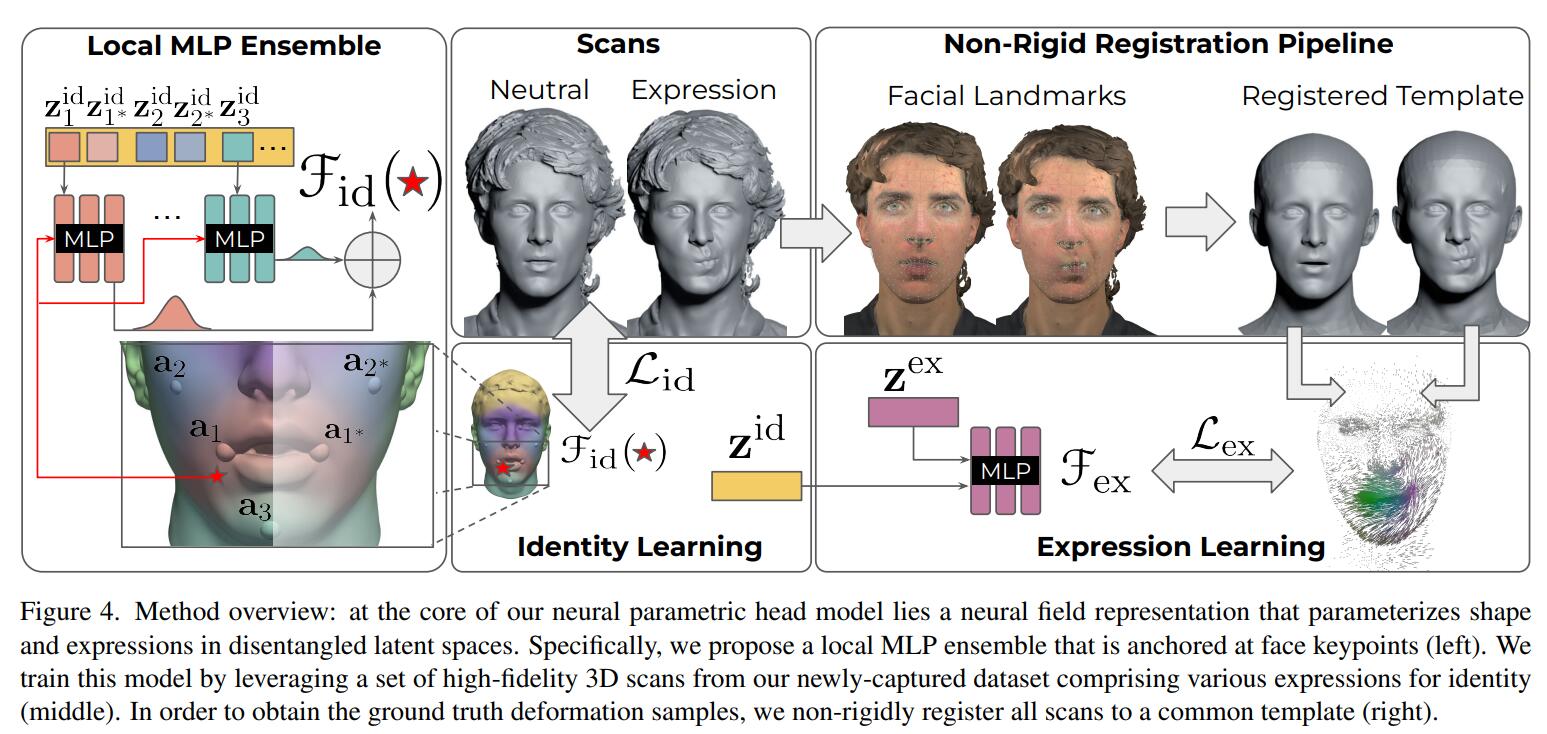
我们可以在NPHM的项目主页上体验一下按这种范式训练后,对$\left\{ \mathbf{z}_{\exp},\mathbf{z}_{\mathrm{id}} \right\} $插值的效果:
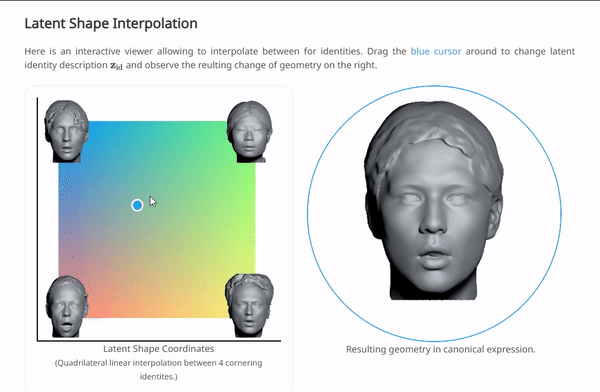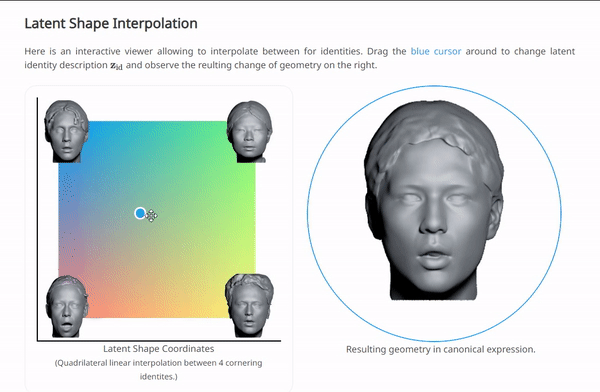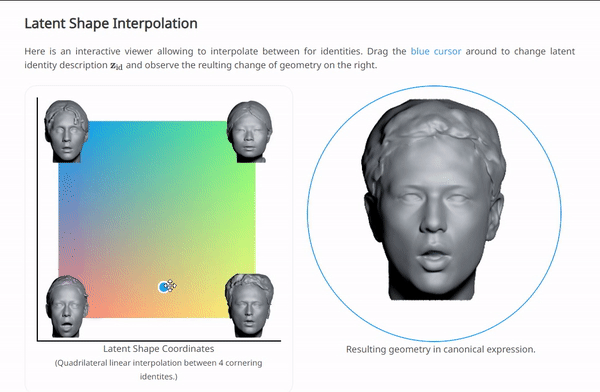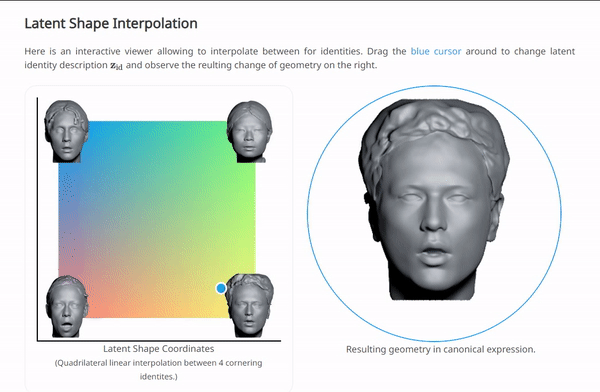
这几种方法都是基于数据集是大规模的人脸数据,所以其实在拟合的同时,也自然的导出了一种“generative manner”。这是由于人脸数据本身就有很好的结构性。这三种方法计算出的结果都是SDF,通过对整个空间均匀采样,计算SDF,再利用一个传统的图形学管线中的方法“marching cube”,可以将SDF转换为mesh:
实际上利用神经网络对人脸数据做参数化的方法不止SDF一种,别的也可以。例如当NeRF兴起后,用基于NeRF的范式,对单目的人头视频,或者怼着一个人不同角度拍的照片。那么NeRF-based的方法也可以给出很好的解决方案。对于人脸上的表情这样的非刚性变换,可以对应于D-NeRF那样的方法来解决。但这种方案最后给出的都是“personalized”的人脸或人头,也就是很难泛化到另一个人身上。例如Nerfies:
NeRF的逻辑是输出体密度和颜色,通过对体密度设置一个阈值,那么也可以用marching cube的办法来得到mesh。但在许多时候这样的方案往往不“专门为了人头/人脸”而生,其实没有用到一些人脸或人头的先验,这就导致可编辑性上就很难做文章了。而从炼丹的方法论上看,想要可编辑性,那就多给网络上condition。例如在刚才的Nerfies里,其实在拟合deformation的部分加上了个latent code的设计,从而使得一些帧间的插值可以实现。
在MoFaNeRF里,在提供每一张图片时,也提供此时的形状,表情,姿态等信息作为condition。解耦的输入自然会带来解耦的输出,那么就可以在以NeRF为参数化的方法下实现很好的可编辑性了。
在刚才基于“大规模数据→SDF”的范式下,我们能够实现一种类似生成式的方案。主观上并没有真的要估计出一个复杂的分布,但客观上也许确实这么做了。在另一条路线里,有人试图将3D的场景引入GAN里,于是就有了pi-GAN,GIRAFFE,之后就是EG3D。这种基于3D-aware GAN的办法,也可以实现对人头的隐式表达。这种方法的特点是从“only collection of 2D image datasets”里来学习3D的表达,相比于前面“3D结构化的数据”和“对一个人,一个物件的拍照采集”,这种数据源的监督强度可确实是弱了不少,所以真正训练出来并不容易。
EG3D有很令人满意的视觉效果,但由于其用的FFHQ数据集只涉及正脸和部分侧脸,同时其三平面的设计会导致$(x,y,z)$和$(x,y,-z)$在投影到$XY$平面时具有相同的值。所以其实并不能完美的给出整个人头,后来字节的PanoHead,通过将一个拍摄发型的数据集(K-hairstyle)和一些拍摄后脑勺的私有数据混合进来,设计一个估计后脑勺位姿的预处理管线,以及引入所谓“tri-grid”,来实现对一个人头的完整的生成。同时在管线里加入了segmentation的先验来使得人头和背景分离,所以实现的细节十分复杂,但效果确实很好:

但这种范式下,很难对生成的人头和人脸做编辑。当然,由于这个路子的核心基于StyleGAN,所以一切对StyleGAN的一些花招都可以招呼上去,例如像InterFaceGAN里通过一个现成的二元分类器,在StyleGAN的空间里用SVM找到个方向来实现对这个分类器对应的属性的编辑(PS:由于现在已经2023年了,这个二元分类器可以直接用CLIP),把这个想法发扬光大,可以得到StyleGAN-NADA。
这种编辑终归不是我们想要的,感觉跟“人头”总是还隔了一层说不清道不明的东西。但只要思想不滑坡,方法总比困难多。Next3D里,引入了FLAME的先验:
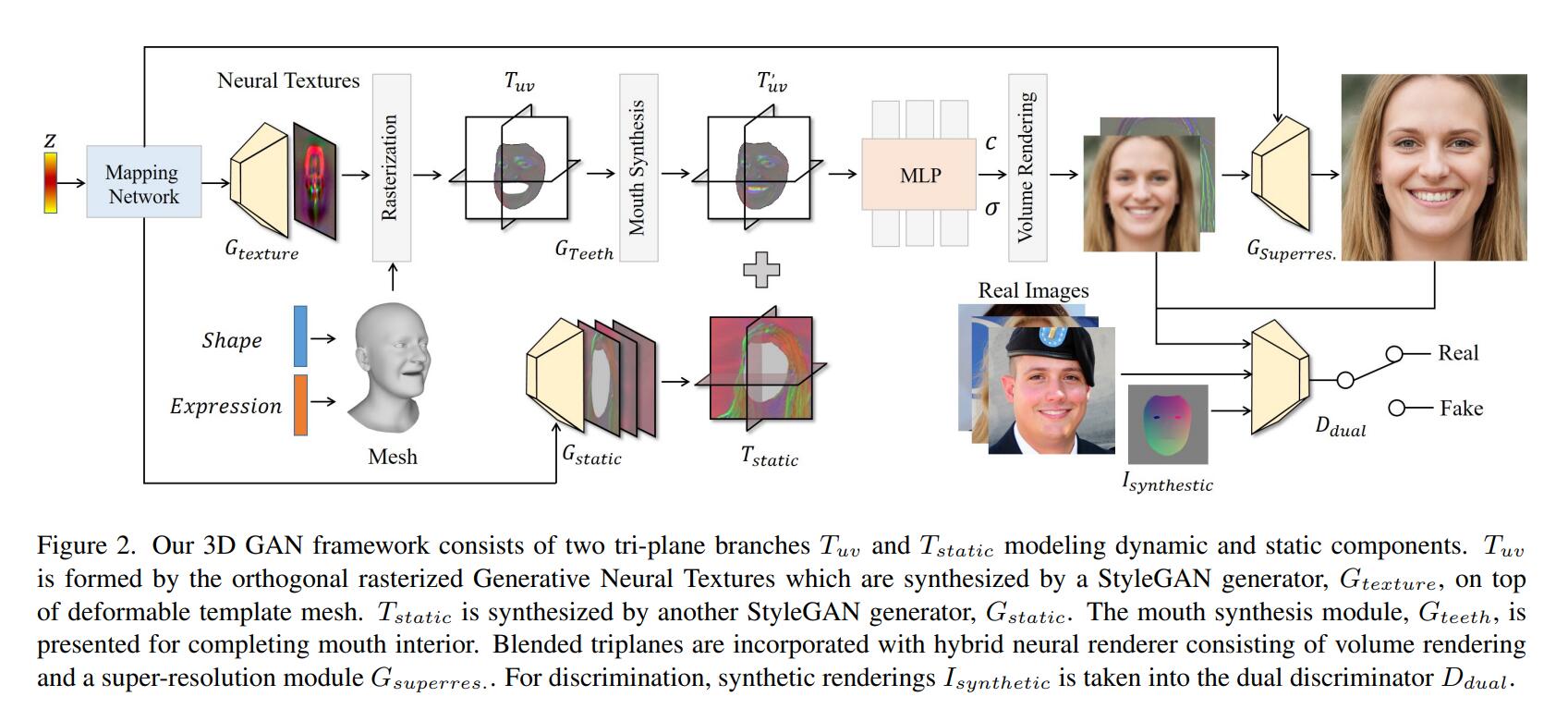
这里引入的办法是将GAN生成器生成的特征图,指认为UV map,然后利用PyTorch3D,从三个互相正交的角度进行光栅化,得到事实意义上的tri-planes。这个部分用于产生人头,而这个部分以外用另一个生成器来生成所谓“static”部分。然而这样做会让嘴的部分空出来,因为FLAME并不涉及对口腔的建模。所以由FLAME导引出的triplane需要再送入一个网络,来“synthesis mouth”。但这里其实不涉及任何所谓牙齿的数据集或者特别设计的loss,只是单纯在那里应用了一个比较对称的结构(style-modulated U-Net),梯度信号会让这个结构学会“inpainting”牙齿那个部分。
有些可能偏商用的工作里,可能会有专门的人对FLAME的模板进行编辑,来把牙齿补出来。
在最后,通过调整FLAME模板的表情和形状系数,就可以达到控制了。那么在训练时,对于每个输入的图片,正是用前文的DECA来估计这张图片的FLAME系数作为输入,由于DECA并不会估计FLAME模板里左右眼球的旋转,所以由用了mediapipe来aug了一下。
UV mapping
在这个部分我想记录一些DECA中用到的一些UV mapping上的内容,这个部分在实际操作中非常重要,而且在我看来,由于一些概念的缺失,这一块不是很好懂。

上图左边是DECA输出的纹理图,右边是FLAME规定的作texture mapping的模板。只要稍微看了GAMES101相关章节,都能大概明白要做什么。比如我们希望从左边的纹理图中,得到右边的图上的各个三角面顶点们的颜色;或者希望从右边的模板里进行采样,然后得到采样的这些uv坐标对应世界坐标系下的那些坐标。如何在当前版本(PyTorch,PyTorch3D)下怎么具体来做这件事,还是得盲人摸象般的看一手函数接口。
我们先来看第一点,这里有许多繁杂的细节。我们先从./decalib/deca.py里看,第一眼就是类内实现的_create_model和_setup_renderer。然后我们观察其他脚本里用到DECA()时,一般都是用的deca.decode()这个函数,所以我们就看这个decode()的实现。首先是:
1 | verts, landmarks2d, landmarks3d = self.flame(shape_params=codedict['shape'], expression_params=codedict['exp'], pose_params=codedict['pose']) |
这里输入的shape_params,expression_params,pose_params都是从输入图像里encode出来的,但返回的值里又包含了landmarks2d和landmarks3d,这在之前的讨论里是不涉及的。我们一步步看,顺藤摸瓜找FLAME()的类实现,我们会在其__init__()方法里发现这样的几行:
1 | # Static and Dynamic Landmark embeddings for FLAME |
这里load的.npy文件,是马普所研究人员的另一个项目RingNet的结果,这里的.npy是RingNet中的flame_dynamic_embedding.npy和flame_static_embedding.pkl二者二合一的结果。
self.register_buffer()是继承自nn.Module里的方法,这个方法回将指定的变量注册为模型的一部分,在模型保存和加载时会带着这些变量一起,但这些变量并不会被认定为是parameters(),也就是说在优化时他们不会被计算梯度。
这里所谓的static,指的是鼻子眼睛嘴巴这种互相相对位置比较固定的landmark。然后dynamic就是脸的轮廓上标注的那些landmark。在很早些时候,人脸关键点检测这个任务就规定了68个landmark,所以这里其实也是要整出68个landmark。
但这里的情况比较复杂,在一些单纯的关键点检测的任务里,关键点往往只是对一个图片预测出一组坐标。这里这个模板的关键点实际上是通过指定该关键点所在的面索引,然后在这个索引上用一组重心坐标插值来合成出来的。例如这里的lmk_embeddings['static_lmk_faces_idx'],它是这样的一个长为51的一维张量:
1 | (Pdb) print(lmk_embeddings['static_lmk_faces_idx']) |
比如我们考虑lmk_embeddings['static_lmk_faces_idx'][2],它是2857,那么在后续的程序里,我们会找到第2857片三角形对应的三个顶点,然后通过lmk_embeddings['static_lmk_bary_coords'][2,:],我们可以看到重心坐标下的系数:
1 | (Pdb) print(lmk_embeddings['static_lmk_bary_coords'][2,:]) |
这样,我们就可以用第2857片三角形的顶点合成出一个坐标了,这个坐标就是这个landmark。
然后我们会发现,在这里lmk_embeddings['static_lmk_faces_idx']形状为(51,),lmk_embeddings['full_lmk_faces_idx']形状为(1, 68),但lmk_embeddings['dynamic_lmk_faces_idx']的形状却为(79, 17),这就是所谓“dynamic”的原因。因为随着人脸的旋转,脸边缘的那些地方的landmark变化幅度比鼻子眼睛嘴巴等landmark要大得多。以及考虑正常人脸的拍照并不会太低头或者抬头,所以只关注其左右偏转。于是就通过从-40°旋转到40°,逐角度建立了79个不同角度时的landmark模板。在这里FLAME()的forward代码里,会有通过之前DECA中估计出的相机位姿来计算landmark的过程,这里并不是重点,所以我们只是简单的提一下这神奇的landmark是怎么来的。
我们回到decode的部分,跳过对landmark的re-projection,我们来到了:
1 | ops = self.render(verts, trans_verts, albedo, h=h, w=w, background=background) |
为了理解这个部分,我们需要调头回_setup_render()那里,在那儿:
1 | self.render = SRenderY(self.image_size, obj_filename=model_cfg.topology_path, uv_size=model_cfg.uv_size, rasterizer_type=self.cfg.rasterizer_type).to(self.device) |
我们结合这个SRenderY的实现:
1 | class SRenderY(nn.Module): |
我们可以注意到load_obj(obj_filename)读入了一个挺重要的东西,通过查utils/config.py,我们可以知道其load的是/data/head_template.obj。那么load_obj()其实是一个来自PyTorch3D库的函数,专门用于读取.obj的。这个函数返回了verts,faces,aux,后两者是个元组,这里我们就只关心我们会用到的几个元素了。首先verts是朴素的[5023, 3],5023就是顶点的数量,然后aux里的verts_uvs,就是我们想要的UV坐标的映射,是[5118, 2],这里5118比5023略大,是因为有些顶点被映射到了多个UV坐标上,但这对后续好像没有什么影响。然后faces里的textures_idx,是和刚才的aux.verts_uvs吻合的,其维度是[9976, 3],意思是一共有9976个面,每个面的三个UV坐标的索引。索引的值从0取到5117,和之前UV坐标为[5118, 2]是对上的。然后faces里的verts_idx,是和原本的verts对应的,其也是9976个面,每个面的三个坐标索引从0取到5022。
这几个变量被重新记作uvcoords,uvfaces,faces,这三个变量都会用self.register_buffer()注册进类内。而表示顶点的变量并不会,因为在forward时会接受新的vertices,其本身可能与标准模板的顶点是不一样的,但UV map这样的映射关系是保持的,这一点叫作拓扑(topology)的不变。
以及这一段代码里还实例化了一个self.rasterizer,假设看这段话的人和我一样没有真的上手过写一个光栅化器,我们需要在这里补充一段话来增加一些直觉,从而帮助理解。这个光栅化器的目的,就是给定一个size,一般是方形,比如256×256,输入一个mesh,然后将这些mesh投影到一个平面上,将投影得到的结果用256×256的粒度进行划分,然后得到这里每一个像素的属性。实际上一个三角面往往会涵盖许多像素,就像网络上介绍光栅化时的时候一样。我们可以做个粗浅的估计,对于FLAME的面数,大约是9000多。假设这些面完全没有前后遮挡,那么投影下来也就是9000多个面。而一个128×128的网格就有16384个像素了,所以一个三角形往往包含许多像素点。
所以这个光栅化的过程其实严格意义上并没有对颜色进行混合,并不是说对于一个mesh上的顶点,我们先有了他们的颜色,然后通过光栅化器得到了纹理;而是我们先进行了光栅化,得到了每个像素的在哪个面上,然后用这个面上的三角形的属性再插值出来。
之后,在forward里,还有一些工作要做。在这里:
1 | # attributes |
这里带有transformed前缀的,是指在NDC空间下进行的操作,因为光栅化实际上是在NDC空间下进行的。这里的face_vertices形状是[1, 9976, 3, 3],最前面的1是为了批处理,我们不用管它。其内容是每个面的三个顶点的坐标,例如:
1 | (Pdb) print(face_vertices[0, 10, :, :]) |
然后会计算normals,这里计算法向量的逻辑是将顶点和面读进去,然后对于每个面,都可以由三个顶点构成的向量来叉乘出面的法向量。然后会根据索引,找到一个顶点在哪几个面上,然后这些不同面的法向量相加,再归一化,得到normals。然后face_normals和face_vertices逻辑是一样的,记录的是一个面上的三个顶点的法向量。之后对于在NDC空间下,也要这么计算一次transformed_normals和transformed_face_normals。
这样计算出一堆变量,为了就是合成一个下面要用到的attributes。注意self.face_uvcoords是在__init__里构造的一个变量,形状为[1, 9976, 3, 3]:
1 | # uv coords |
这里首先是要给之前的uvcoords补个全是1的第三维,然后得到一个表示UV map上每个面的三个顶点的UV坐标的face_uvcoords。然后全部的这些会cat成形状为[9976, 3, 12]的张量,意义就是每个面的三个点的各种属性。我们在下一步的光栅化会看到他们cat起来的原因。
1 | # rasterize |
然后我们就进入class Pytorch3dRasterizer(nn.Module):里,看它的forward,注意此时我们输入的是transformed_vertices,self.faces和attributes。
1 | def forward(self, vertices, faces, attributes=None, h=None, w=None): |
PyTorch3D封装的rasterize_meshes()会返回pix_to_face,zbuf,bary_coords,dists。我们这里只需用到pix_to_face和bary_coords,前者是光栅化后产生的图片上,每一个像素点对应哪个面(的投影)的索引:
1 | (Pdb) print(pix_to_face.shape) |
后者这些像素点在这个面上的具体位置,用重心坐标插值的方式来表示:
1 | (Pdb) print(bary_coords.shape) |
然后在forward这里,会先把attributes的批处理的维度和面数的维度合一下,同时对pixel_to_face也进行变形和复制,整成idx。这样做的目的是为了应用torch.gather()这个函数,这个函数比较抽象,我们一步步来说。attributes.gather(0, idx)表示对attributes沿着第0维,根据idx进行索引。例如当idx[100]时,有:
1 | (Pdb) print(idx[100]) |
那么就是取attributes[7890, 0, 0],...attributes[7890, 0, 11], attributes[7890, 1, 0],...attributes[7890, 2, 11]作为gather下来的第100个元素,然后idx[101],idx[102],一直到idx[-1],在这里idx是[50176, 3, 12],于是最终attributes.gather(0, idx)也就是[50176, 3, 12]的。这里是由于我们要抽取的属性其实都是同一个面上的,所以idx在同一个索引下都一样,实际上这个功能是为了在这种“idx不全是7890”的情况下工作的。
调整形状后即得到了pixel_face_vals,然后下一步里,重心坐标bary_coords会和pixel_face_vals直接对应相乘,然后对倒数第二个维度求和,那个维度为3,其实就是批量完成了重心坐标插值。注意pixel_face_vals包含着attributes里的所有属性,所以那四个属性:法向量,NDC下的法向量,顶点,uv坐标,都同时被重心插值了。这样,对于光栅化后的每个像素,我们终于插值出来了它的uv坐标!
回到SRenderY的forward函数,刚才讨论的pixel_face_vals返回为rendering,根据当时cat时的顺序,rendering的前三维即是对于每一个像素点的uv坐标(有一维是补充的哑元)。
1 | # albedo |
grid里去掉了那一维的哑元,albedos是forward里的输入,大小为[N, 3, 256, 256],是DECA另一个部分解码的结果。然后grid此时已经处理成了[N, 224, 224, 2],然后应用F.grid_sample,就会从albedos里采样224×224个点,坐标按照最后那一维里的2。这样就得到了大小为[N, 3, 224, 224]的albedo_images。
上面写了很多,索引来索引去的,让人脑壳疼。我们抽象的总结一下,当:
1 | rendering = self.rasterizer(transformed_vertices, self.faces.expand(batch_size, -1, -1), attributes, h, w) |
这行代码运行的时候,到底是做了什么。首先,我们输入了在NDC空间下的顶点们transformed_vertices, [N, 5023, 3],以及构成面的结点索引self.faces.expand(batch_size, -1, -1), [N, 9976, 3],和构成每个面的顶点的四种(三个顶点增广过的nv坐标,NDC空间下的法向量,顶点的原始坐标,原始空间下的法向量)三元的属性attributes, [N, 9976, 3, 12]。
然后,光栅化器将transformed_vertices和self.faces组成的mesh进行光栅化,得出了每个像素在哪个面上,以及他们在这个面上的哪个位置(重心坐标系数)。最后,我们用每个像素在面上的索引,找到相应的这个面上的三个顶点的重心坐标系数,从而对attributes里的所有属性进行平滑的插值,完成光栅化,返回结果。
这里的重点在于,我们复用这里的光栅化器,通过改变输入,来实现从UV map上进行采样。例如,我们依次以增广后的顶点的UV坐标self.uvcoords,UV map下的三角面的顶点索引,以及此时顶点们的三维坐标作为输入。我们就会发现,我们会朴素的对UV map进行“光栅化”,此时UV map有恒定的$z$值,所以其实就是在从UV map上均匀的划分网格,然后判断每一个小网格在哪个面上,以及在这个面上的什么位置。什么位置即用重心坐标系数来表示,然后与此时作为attributes的顶点们的三维坐标相乘求和,这样就找到了UV map上的点与空间上的三维坐标的一一映射的关系。
Discussion
在补充了FLAME,BFM等必要的前置知识,以及走马观花了一下一些相关工作。我们可以做一个小小的总结:当我们考虑表征一个人头的时候,我们可以依次思考,输出的是只有一个人脸还是有一个完整的人头,输出的结果是不是“photo-realistic”的,输出的结果能不能做二次编辑(换表情,换姿态),以及输出的结果具不具有泛化性,我们可以比较笼统的做出如下的判断:
| 参数化模型 | 完整性 | 真实性 | 可编辑性 | 泛化性 | e.g. |
|---|---|---|---|---|---|
| BFM | × | × | √ | √ | DeepFaceRecon |
| FLAME | √ | × | √ | √ | DECA |
| Neural Implicit | √ | √ | √ | √ | NPHM |
| 3D-awares GAN | × | √ | × | √ | EG3D |
| NeRF-based | - | √ | × | × | Nerfies |
上表只是一个笼统的判断,因为各种流派之间互相借鉴,例如NerFACE虽然是朴素的基于NeRF-based的方法,但同时输入了3DMM的表情系数做condition,所以也是可以编辑的。
但如果将其中可微渲染的部件从MLP换成3D Gaussian Splatting,那这又是另一回事了。因为不管是3D-awares GAN还是NeRF-based还是Neural Implicit方法里,能取得成功最终收敛,很大程度上都是MLP翩若惊鸿宛若游龙般的拟合连续边界的能力。但3DGS并没有那么强的能力,3DGS拟合连续边界是靠砸雪球砸出来的。这就导致一个像素的颜色会受许多个椭球的影响,同时这些椭球又影响到更多的像素点。这种优化的难度比ray casting可大多了。(3DGS里的scale需要$\exp \left( \cdot \right) $,训练时需要有clone and prune,需要比较精密的lr scheduler)。这就导致像3D-awares GAN那里,从2D image datasets里,用对抗训练这么弱的监督去想整出一个“zero-shot”的3DGS,是困难的。
目前有且仅有一个从2D数据集里来generative 3DGS的工作GaussianShellMaps,由于作者列表过于重量级,不开源根本follow不动。还有许多针对personalized avatars的工作,GaussianAvatars,Relightable Gaussian Codec Avatars,MonoGaussianAvatar,FlashAvatar,GaussianHead,HeadGaS。这些都是最近高斯井喷时的工作,现在都没开源。但看下来,感觉UV map结合一下应该是最靠谱的。
End
“花开花落花开了又一遍,年年岁岁盼过了又一年。”


