NeuS && VolSDF

阅读数: 次 2023-10-22

在NeRF中，我们知道最后MLP预测的体密度其实是“不保真”的。那么有没有什么办法可以让其预测的体密度是符合客观几何的呢？这样就可以满心欢喜的达成事实上的“重建”了。

针对这个问题，有两篇同一时期的工作给出了圆满的答案。NeuS和VolSDF，他们解决的问题比较类似，但切入的视角并不一样。

由于他们都是基于NeRF所构造的“可微+体渲染”框架下的改进，所以这篇blog可能并不会去分析代码和具体实验，主要捋清这两篇工作推导的逻辑（形式与数学上）。

这两篇工作里当然会涉及到很多图形学上的背景知识，但就像不同背景的人对“傅里叶变换”会有不同的理解，没有学过CG也没有关系，我们总能在理解这两篇工作的同时找到乐趣所在。（自我安慰.jpg）

Signed Distance Function

用神经网络来表达一个3D场景，有很多种方法。具体来说，可以通过引入不同的归纳偏置。例如显式的体素网格，点云，网格；隐式的，例如Occupancy Networks以及我们要提到的符号距离函数（SDF）。

神经网络到底应该输出什么“representation”来表征3D场景，早些年间有许多讨论。我在写这篇blog的时候也回顾了一下，挑选了一些代表整理于此，各倾陆海云尔。

体素：3D ShapeNets: A deep representation for volumetric shapes (CVPR 2015)

点云：A point set generation network for 3D object reconstruction from a single image (CVPR 2017)

网格：Pixel2Mesh: Generating 3D Mesh Models from Single RGB Images (ECCV 2018)

占用网格：Occupancy Networks: Learning 3D Reconstruction in Function Space (CVPR 2019)

符号距离场：DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation (CVPR 2019)

这些都是2020年之前的，或许自NeRF出来以后，人们就更关注NeRF那一套框架了。

在NeuS和VolSDF中，都借助了SDF这个工具，用来隐式的表示三维重建中想获得的那个曲面。SDF的定义非常好理解，给定$\varOmega \subseteq \mathbb{R} ^3$是目标物体的点集，那么$\partial \varOmega$是其边界（也就是我们想要的曲面），$d(\cdot,\cdot)$为一个距离函数，对于$\boldsymbol{x}\in \mathbb{R}^3$有：

$f\left( \boldsymbol{x} \right) =\left\{ \begin{array}{c} d\left( \boldsymbol{x},\partial \varOmega \right) , \boldsymbol{x}\in \varOmega ^c\\ -d\left( \boldsymbol{x},\partial \varOmega \right) , \boldsymbol{x}\in \varOmega \,\,\\ \end{array} \right.$

其中$\varOmega ^c$是$\varOmega$关于$\mathbb{R}^3$的补集。也就是说如果$\boldsymbol{x}$在曲面内部，那么计算点到曲面的距离，取负；如果$\boldsymbol{x}$在曲面外部，那么距离取正。给定$f(\cdot)$的情况下，我们就可以将目标曲面转述为：

$\mathcal{S} =\left\{ \boldsymbol{x}\in \mathbb{R} ^3|f\left( \boldsymbol{x} \right) =0 \right\}$

这种写法也叫SDF的零集集合（zero-level set）。

SDF有一个有趣的性质，由于点到面的距离定义的是点到面上一点的最小长度，假设最短距离对应的是曲面上的点$p$，那么$x$到$p$的方向也正好是SDF下降最快的方向。所以考虑其梯度：

实际上这里并不严谨，这里要求$\varOmega$有一些性质，从而保证SDF“几乎处处可微”。“几乎处处可微”这一点在VolSDF的推导中被提到了，我们可以先不管。

$\left| \nabla f \right|=\left| \frac{\partial f}{\partial \boldsymbol{x}} \right|=\sqrt{\left( \frac{\partial f}{\partial x} \right) ^2+\left( \frac{\partial f}{\partial y} \right) ^2+\left( \frac{\partial f}{\partial z} \right) ^2}=1$

其恒等于1。这一点曾经很重要，因为SDF其实是一类重要的偏微分方程的特例：

$\left| \nabla f\left( x \right) \right|=\frac{1}{c\left( x \right)}$

当$c\left( x \right) \equiv 1$时，就是刚才讨论的符号距离函数。这种偏微分方程又叫程函方程（eikonal equation），用于描述波动中波前的传播。如果在这个背景下，$f(x)$则是到达点$x$时波需要行进的时间，而$c(x)$是点$x$处的波速。在后来的一段时间里，人们比较沉迷于用偏微分方程来作图像处理，而当$c(x)$取为常数时，这样的波动方程的梯度的模长又是恒定的，所以带来了较好的数值稳定性。不过随着炼丹的兴起，人们已经不怎么提PDE之于图像处理的那些方法了。

当然，在后面我们会发现，SDF的这个性质会在NeRF的管线下贡献出一个很好的正则项。

这就是我们需要提前知道的关于SDF的知识了。

所以，我们知道，体渲染很好，SDF也很好。在NeRF的框架下，MLP接收输入$\mathbf{r}(t),\mathbf{d}$，得到输出体密度$\sigma(\mathbf{r}(t))$和颜色$c(\mathbf{r}(t),\mathbf{d})$。如果我们让输出的体密度变成SDF此时的值，即$f(\mathbf{r}(t))$，（如果这样能成功）那我们就能得到满意的曲面。但这样就不能直接体渲染了，所以我们需要想一些办法，将输出的SDF转化为某种类似体密度的东西，然后来跑通体渲染。

其实，在NeRF中的MLP，他知道自己的某个头输出的是“体密度$\sigma$”吗？他其实不知道。如果你去采访一下他：“感知器先生，您输出的这是什么啊？”，他大概只能支支吾吾的回答：“我也不知道，我只知道把一百来个这样的东西分别相乘然后全加起来，好像就是一个有意义的颜色了。”

NeuS

我们回顾一下体渲染的公式：

$C\left( \mathbf{r} \right) =\int_0^{+\infty}{T\left( t \right) \sigma \left( \mathbf{r}\left( t \right) \right) c\left( \mathbf{r}\left( t \right) , \mathbf{d} \right) \mathrm{d}t} \\ T\left( t \right) =\exp \left( -\int_0^{t}{\sigma \left( \mathbf{r}\left( s \right) \right) \mathrm{d}s} \right)$

关键在于：

$w\left( t \right) =T\left( t \right) \sigma \left( \mathbf{r}\left( t \right) \right)$

的构造。我们希望$w(t)$取极大值的地方，也是满足$f(\mathbf{r}(t))=0$的地方。这在NeuS中被称为Unbiased。

同时注意体渲染的一个性质：$T(t)$是单调递减的。因为我们会让体密度是大于0的值，所以$T(t)$里的那个积分会变得越来越小，导致$T(t)$随着$t$越大，越接近0。这样，如果沿着光线发射的方向观察，在前面的一个点，对颜色的贡献$w(t_1)$，就会比在后面的一个点的贡献$w(t_2)$大，这在NeuS被称为Occlusion-aware。

我们先说回对SDF进行变换的这件事。在NeuS中，作者们提出对SDF应用如下的变换：

$\phi _s\left( x \right) =\frac{se^{-sx}}{\left( 1+e^{-sx} \right) ^2}$

将$\phi_s(f(\mathbf{r}(t)))$记作S-density，$\phi_s(x)$是我们熟悉的Sigmoid函数的导数：

这里挑Sigmoid函数作为原函数，其实是“便于计算”。因为后面的推导里，我们会发现我们只需要计算钟形曲线$\phi_s(\cdot)$的原函数即可，那，最方便的就是拿Sigmoid算，而Sigmoid的导数，就是上面的了。

$\varPhi _s\left( x \right) =\frac{1}{1+e^{-sx}}, \frac{\mathrm{d}\varPhi _s\left( x \right)}{\mathrm{d}x}=\phi _s\left( x \right)$

这篇blog并不打算去分析NeuS的项目代码，但先简单的检视那几个文件，会对我们之后的理解更有帮助。在NeRF里，我们定义了一个NeRF类，它在计算时的两个输出直接作为sigma和RGB。在NeuS里这稍微被写的复杂了一些（因为后续的可能的提取mesh等功用，整个网络被分开定义了），NeuS里实际定义了一个sdf_network，一个deviation_network，一个color_network。sdf_network忠实的输出$f(\mathbf{r}(t))$，deviation_network只有一个参数，就是刚才的$s$，然后color_network是将sdf_network的输出，以及一些其他输入一起加工，最后得到RGB的网络。

这里的$s$，作用是为了调整$\phi_s(x)$的带宽：

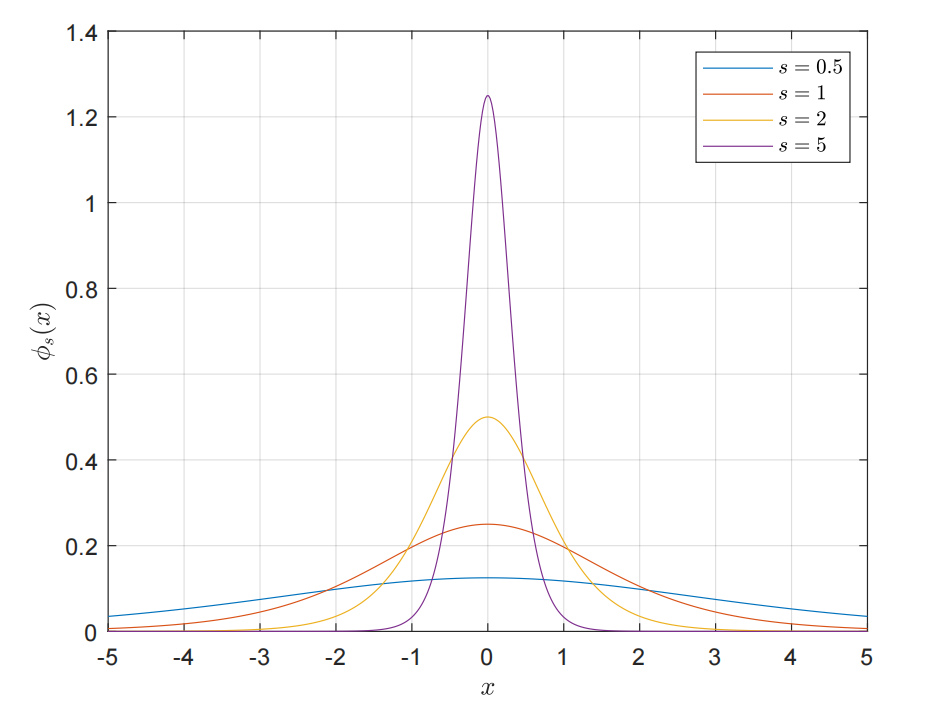
可以看到，$s$越大，$\phi_s(x)$越接近尖峰函数。实际上，我们可以直接推导出$\phi_s(x)$的标准差，NeuS中说“is given by $1/s$”，但作者应该是把常数因子给省略了，或者在书写时混淆了参数化前后的逻辑斯蒂分布。我们这里重新推导一下，注意到由于对称性，$\mathbb{E} \left[ X \right] =0$，那么由方差的定义：

$Var\left[ X \right] =\int_{-\infty}^{+\infty}{x^2\phi _s\left( x \right) \mathrm{d}x}-\left( \mathbb{E} \left[ X \right] \right) ^2 \\ =\int_{-\infty}^{+\infty}{x^2\cdot \frac{se^{-sx}}{\left( 1+e^{-sx} \right) ^2}\mathrm{d}x}$

作第一类换元积分，令：

$u=\frac{1}{1+e^{-sx}}$

则原积分化为：

$Var\left[ X \right] =\int_0^1{x^2\cdot \mathrm{d}u}$

根据$u$的定义，我们可以用$x$来表示$u$：

$-\frac{1}{s}\ln \left( \frac{1-u}{u} \right) =x$

所以将$x$带入积分中：

$Var\left[ X \right] =\int_0^1{\frac{1}{s^2}\ln ^2\left( \frac{1-u}{u} \right) \cdot \mathrm{d}u} \\ =\frac{1}{s^2}\left( \int_0^1{\ln ^2\left( 1-u \right) \cdot \mathrm{d}u}-2\int_0^1{\ln \left( 1-u \right) \ln \left( u \right) \cdot \mathrm{d}u}+\int_0^1{\ln ^2\left( u \right) \cdot \mathrm{d}u} \right)$

对于积分项中的第一项和第三项其实是相等的，反复运用分部积分即可求解：

$\int_0^1{\ln ^2\left( 1-u \right) \cdot \mathrm{d}u}=\int_0^1{\ln ^2\left( u \right) \cdot \mathrm{d}u}=2$

中间的交叉项就比较复杂了，我们可以借助经典级数：

$\ln \left( 1-u \right) =-\sum_{n=1}^{\infty}{\frac{u^n}{n}}$

来对其进行展开，~~同时我们赌一把积分和求和可以交换顺序~~：

$\int_0^1{\ln \left( 1-u \right) \ln \left( u \right) \cdot \mathrm{d}u}=-\sum_{n=1}^{\infty}{\frac{1}{n}\int_0^1{u^n\ln \left( u \right) \mathrm{d}u}} \\ =-\sum_{n=1}^{\infty}{\frac{1}{n}\left[ \frac{u^{n+1}}{n+1}\ln \left( u \right) -\frac{u^{n+1}}{\left( n+1 \right) ^2} \right] _{0}^{1}} \\ =\sum_{n=1}^{\infty}{\frac{1}{n}\frac{1}{\left( n+1 \right) ^2}}$

然后就变成了高数习题里的一个常见的级数和，我们进行裂项：

$=\sum_{n=1}^{\infty}{\frac{1}{n\left( n+1 \right)}}-\sum_{n=1}^{\infty}{\frac{1}{\left( n+1 \right) ^2}} \\ =1-\left( \sum_{n=1}^{\infty}{\frac{1}{n^2}}-1 \right) \\ =2-\frac{\pi ^2}{6}$

所以最终的方差即为：

$Var\left[ X \right] =\frac{1}{s^2}\left( 2-4+\frac{\pi ^2}{3}+2 \right) =\frac{\pi ^2}{3s^2}$

所以严格来说标准差其实是$\frac{\pi}{\sqrt{3}s}$，但有时会进行重参数化，来配凑均值为0，方差为1的逻辑斯蒂分布。所以作者可能以为这个式子是已经参数化后的，所以说标准差是$1/s$，这不重要，我们这里只是做一下积分练习。通过标准差我们可以直观的看出来，$s$越大，其标准差就越小，带宽就越窄。

现在，我们认为$\phi_s(f(\mathbf{r}(t)))$就是一个很好的替代$\sigma(f(\mathbf{r}(t)))$的操作，现在我们考虑，如果MLP输出的$f(\mathbf{r}(t))$已经完美拟合了一个曲面$\mathcal{S}$，此时考察曲面上任意一个点，在这个点附近将曲面近似为平面，我们考察在这个简单的平面上的SDF，即对SDF进行一阶展开，则此时的$f(\mathbf{r}(t))$可以近似为：

$f\left( \mathbf{r}\left( t \right) \right) =-\left| \cos \left( \theta \right) \right|\cdot \left( t-t^{\ast} \right)$

如下图所示：

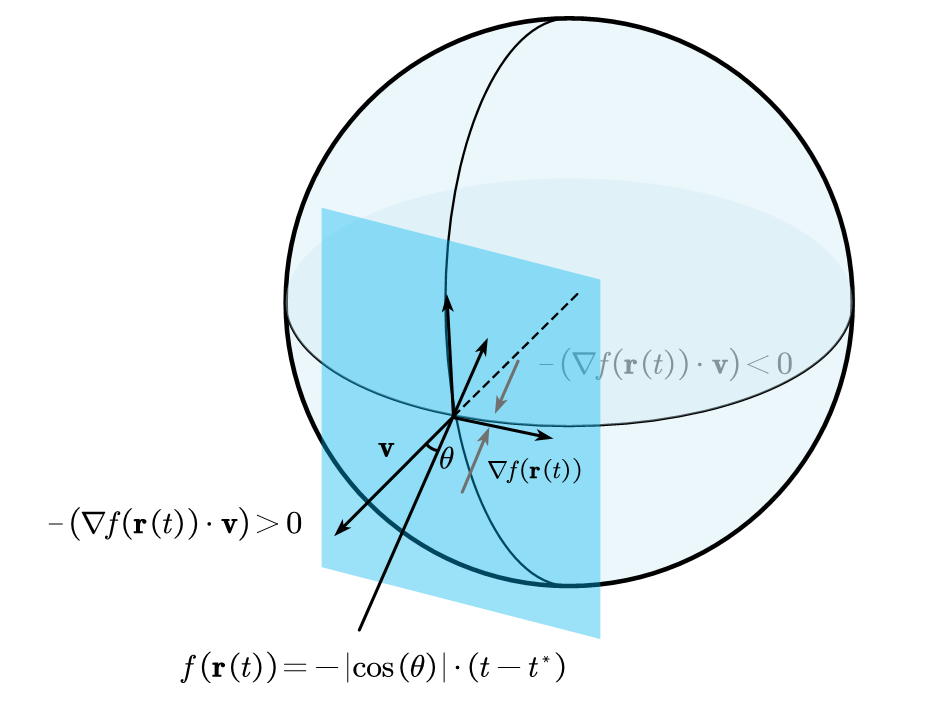
注意到随着光线从外部射入内部，再从内部远离交面，符号距离函数的梯度方向会发生变化。然后如果我们此时直接用$\phi_s(f(\mathbf{r}(t)))$来替代先前的体密度$\sigma(f(\mathbf{r}(t)))$（下文中我们直接将$\mathbf{r}(t)$略写为$t$，这在分析其导数性态时没有影响，因为$\mathbf{r}(t)=\mathbf{o}+t\cdot\mathbf{n}$只是一个简单的线性函数。）：

$w\left( t \right) =T\left( t \right) \sigma \left( t \right) , T\left( t \right) =\exp \left( -\int_0^t{\sigma \left( s \right) \mathrm{d}s} \right) \\ \frac{\mathrm{d}w}{\mathrm{d}t}=\frac{\mathrm{d}T\left( t \right)}{\mathrm{d}t}\sigma \left( t \right) +T\left( t \right) \frac{\mathrm{d}\sigma \left( t \right)}{\mathrm{d}t} \\ =-T\left( t \right) \sigma ^2\left( t \right) +T\left( t \right) \frac{\mathrm{d}\sigma \left( t \right)}{\mathrm{d}t} \\ =T\left( t \right) \left( \frac{\mathrm{d}\sigma \left( t \right)}{\mathrm{d}t}-\sigma ^2\left( t \right) \right)$

然后我们将$\sigma(t)$换为之前讨论的$\phi_s(f(\mathbf{r}(t)))$，由链式法则：

$\frac{\mathrm{d}\phi _s(f(\mathbf{r}(t)))}{\mathrm{d}t}=\phi _s\prime(f(\mathbf{r}(t)))\frac{f(\mathbf{r}(t))}{\mathrm{d}t} \\ =-\left| \cos \left( \theta \right) \right|\phi _s\prime(f(\mathbf{r}(t)))$

所以考虑$f\left( \mathbf{r}(t^{\ast}) \right) =0$，此时权重的一阶导：

$\frac{\mathrm{d}w}{\mathrm{d}t}\left( t^{\ast} \right) =-{\phi _s}^2(0)T\left( t^{\ast} \right) <0$

所以，在SDF取极值的时候，$w(t)$不能取极值。

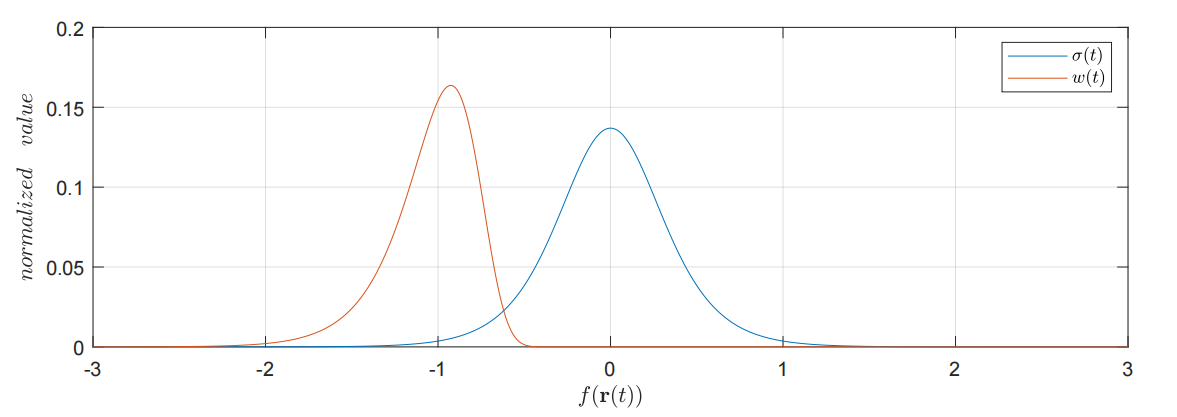
所以NeuS怎么做了呢？他们说：“想让$f\left( \mathbf{r}(t) \right)$取到极值的时候$w(t)$也取极值很简单，我直接：”

$w\left( t \right) \propto \phi _s\left( f\left( \mathbf{r}(t) \right) \right)$

这是很直接的一种办法，这不就是$f\left( \mathbf{r}(t) \right)$取极值然后$w(t)$也就极值了。由于$w(t)$一般都是非负的，并且考虑到一些数量级上的问题，可以将其定义为被归一化后的版本：

$w\left( t \right) =\frac{\phi _s\left( f\left( \mathbf{r}(t) \right) \right)}{\int_0^{+\infty}{\phi _s\left( f\left( \mathbf{r}(u) \right) \right) \mathrm{d}u}}$

注意积分下限是0，这个地方其实闹了两年的乌龙。在NeuS最早的版本和在NIPS上camera ready的版本里，在后面的一步推导里，积分下限变为了$-\infty$，当下限变为$-\infty$时会带来一些数学上的方便（概率密度函数从负无穷积到正无穷为1）。但这显然不太合适，直到23年3月份，arxiv上的版本更新了一版，在正文里用“简单平面入射”的例子里，强加一条“相机在无穷远”处的假设，从而直接取$t^{\ast}$为$+\infty$，然后导致最后要处理的积分相当于上下限是无穷的。

我个人觉得这完全没必要，尤其是$t^{\ast}\rightarrow +\infty$这一步，其实带来了更大的困扰。我有一个更合理的解释，因为我们一直以来用的$t$，其实都是光线那条直线参数方程里的$t$，它当然应该是正的，从0开始积分指的就是从相机坐标处开始发射。然而其实正常情况下，此时的SDF值都会比较大（除非你直接怼着什么东西拍），SDF等于0的点绝对是在沿着$t$增大的方向里，$t$为负的那些点（相机背后）我们肯定是当它没有东西的，所以此时SDF会比在0时的更大，对应的$\phi_s(f(\mathbf{r}(t))$其实很小了。我们可以直接假设从负无穷积到0的这个部分相比于从0积到正无穷的部分，可以忽略。

在这个逻辑下，论文的推导就不会有什么问题。我们可以推导出归一化后的$w(t)$：

$w\left( t \right) =\frac{\phi _s\left( f\left( \mathbf{r}(t) \right) \right)}{\int_0^{+\infty}{\phi _s\left( f\left( \mathbf{r}(u) \right) \right) \mathrm{d}u}} \\ =\frac{\phi _s\left( f\left( \mathbf{r}(t) \right) \right)}{\int_{-\infty}^{+\infty}{\phi _s\left( -\left| \cos \left( \theta \right) \right|\cdot \left( u-t^{\ast} \right) \right) \mathrm{d}u}} \\ =\frac{\phi _s\left( f\left( \mathbf{r}(t) \right) \right)}{\left| \cos \left( \theta \right) \right|^{-1}\int_{-\infty}^{+\infty}{\phi _s\left( u-t^{\ast} \right) \mathrm{d}u}} \\ =\left| \cos \left( \theta \right) \right|\phi _s\left( f\left( \mathbf{r}(t) \right) \right)$

我们会发现，在这样的假定下，这个复杂的分母会变成一个定常数$\left| \cos \left( \theta \right) \right|^{-1}$，所以这种设置是可以实现Unbiased的，但不能实现Occlusion-aware。只要$w(t)$还可以像$w(t)=T(t)\sigma(t)$一样，用一个单调递减的$T(t)$与一个密度表示$\sigma(t)$调制出，即可实现Occlusion-aware。

我们假设这种表述为$\rho(t)$，现在我们通过联立方程来求解它：

$\left| \cos \left( \theta \right) \right|\phi _s\left( f\left( \mathbf{r}(t) \right) \right) =T\left( t \right) \rho \left( t \right)$

注意到：

$\frac{\mathrm{d}T}{\mathrm{d}t}\left( t \right) =-T\left( t \right) \rho \left( t \right)$

于是我们得到了一个很简单的微分方程：

$-\left| \cos \left( \theta \right) \right|\phi _s\left( f\left( \mathbf{r}(t) \right) \right) =\frac{\mathrm{d}T}{\mathrm{d}t}\left( t \right)$

我们记$\phi_s(\cdot)$的原函数Sigmoid函数是$\varPhi_s(\cdot)$，以及$\frac{\mathrm{d}\left( f\left( \mathbf{r}(t) \right) \right)}{\mathrm{d}t}=-\left| \cos \left( \theta \right) \right|f\left( \mathbf{r}(t) \right) $，代换后两边积分，所以可以得到：

$T\left( t \right) =\varPhi _s\left( f\left( \mathbf{r}(t) \right) \right)$

进一步：

$\exp \left( -\int_{-\infty}^t{\rho \left( u \right) \mathrm{d}u} \right) =\varPhi _s\left( f\left( \mathbf{r}(t) \right) \right) \\ \int_{-\infty}^t{\rho \left( u \right) \mathrm{d}u}=-\ln \left( \varPhi _s\left( f\left( \mathbf{r}(t) \right) \right) \right) \\ \rho \left( t \right) =\frac{-\frac{\mathrm{d}\varPhi _s}{\mathrm{d}t}\left( f\left( \mathbf{r}(t) \right) \right)}{\varPhi _s\left( f\left( \mathbf{r}(t) \right) \right)}$

这里积分下限选$-\infty$和0是无所谓的，因为在我们先前的讨论中，我们其实已经默认了相机以及相机背后是没有东西的，所以其$\rho(\cdot)$一定是0。

这其实非常离经叛道，无论是过程还是结果。过程上，我们是直接选择了一种无偏的$w(t)$，然后反推出能支持这个$w(t)$的“渲染方式”。结果上，$\rho(t)$的分子涉及$\varPhi _s\left( f\left( \mathbf{r}(t) \right) \right) $的一阶导，这说明这个$\rho(t)$还会被其邻域内的$\rho \left( t\pm \delta t \right) $所影响，然而在传统体渲染中，这些不应该是相关的。

然而这只是解决了单个平面，当遇到多个平面时会遇到这样的问题：

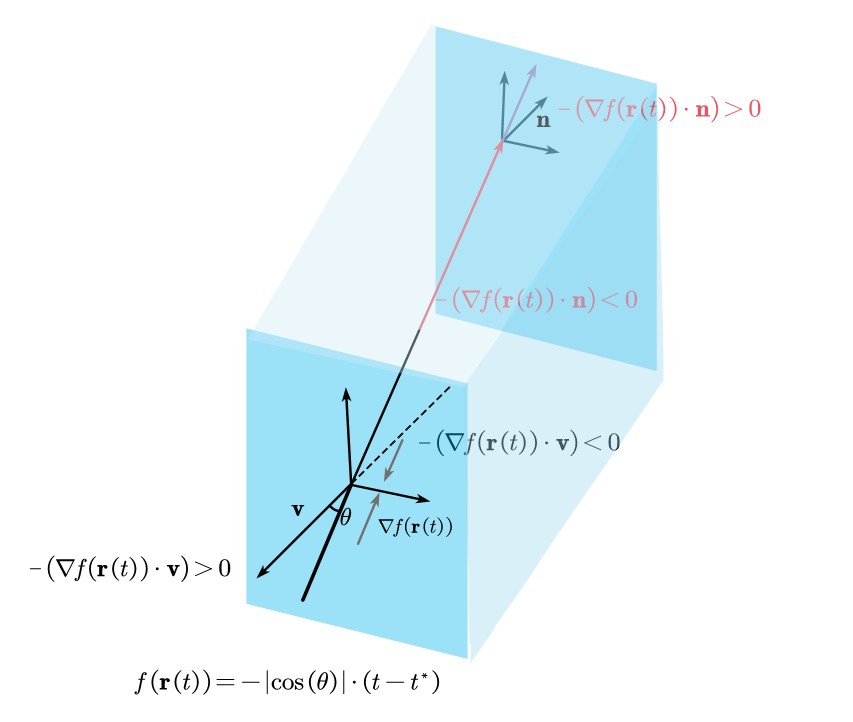
当有两个平面时，$\rho(t)$可能会变成负的，原因是这样的，$\rho(t)$的分母是恒正的，分子，在光线射入一个平面时，SDF从正数逐渐减小到0。所以$\varPhi(t)$的导数值是负的，加上前面那个负号，$\rho(t)$是正的了；当光线远离第一个平面时，SDF从0继续减小到负的，所以没什么问题。但当光线继续前进，距离第二个平面的距离比第一个近时，由于SDF的定义，此时SDF会从一个负数（因为我们此时在一个物体内部）逐渐增大成0，这样就会导致$\varPhi(t)$导数值是正的，导致$\rho(t)$是负的，这可能会产生些问题。

于是作者提议可以直接对计算出的$\rho(t)$进行截断：

$\rho \left( t \right) =\max \left( \frac{-\frac{\mathrm{d}\varPhi _s}{\mathrm{d}t}\left( f\left( \mathbf{r}(t) \right) \right)}{\varPhi _s\left( f\left( \mathbf{r}(t) \right) \right)}, 0 \right)$

这一段内容在作者的叙述里逻辑变得可能不是那么好理解，作者画了一个图，说明第一个平面是“visible surface”，然后说第二个平面是“invisible surface”，很令人困惑。凭什么第二个平面就是“invisible”的？难道我们不该重建第二个平面吗？这样对$\rho(t)$一截断，第二个平面就不可能被反向传播更新了（注意更新的核心还是体渲染的结果与ground truth的二范数）。

我的个人理解是，考虑我们是如何获得NeuS的几何的：

def extract_fields(bound_min, bound_max, resolution, query_func):
    N = 64
    X = torch.linspace(bound_min[0], bound_max[0], resolution).split(N)
    Y = torch.linspace(bound_min[1], bound_max[1], resolution).split(N)
    Z = torch.linspace(bound_min[2], bound_max[2], resolution).split(N)

    u = np.zeros([resolution, resolution, resolution], dtype=np.float32)
    with torch.no_grad():
        for xi, xs in enumerate(X):
            for yi, ys in enumerate(Y):
                for zi, zs in enumerate(Z):
                    xx, yy, zz = torch.meshgrid(xs, ys, zs)
                    pts = torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1), zz.reshape(-1, 1)], dim=-1)
                    val = query_func(pts).reshape(len(xs), len(ys), len(zs)).detach().cpu().numpy()
                    u[xi * N: xi * N + len(xs), yi * N: yi * N + len(ys), zi * N: zi * N + len(zs)] = val
    return u


def extract_geometry(bound_min, bound_max, resolution, threshold, query_func):
    print('threshold: {}'.format(threshold))
    u = extract_fields(bound_min, bound_max, resolution, query_func)
    vertices, triangles = mcubes.marching_cubes(u, threshold)
    b_max_np = bound_max.detach().cpu().numpy()
    b_min_np = bound_min.detach().cpu().numpy()

    vertices = vertices / (resolution - 1.0) * (b_max_np - b_min_np)[None, :] + b_min_np[None, :]
    return vertices, triangles

从代码里可以看出，核心是输入一个$(x,y,z)$去查sdf_network里的值，那么我们关心的是$f\left( \mathbf{r}(t) \right) $，并不是$\rho(t)$和$w(t)$。以及$f\left( \mathbf{r}(t) \right) $本身是NN预测的，并不是有个预先的定义，NN并不会知道哪些是物体内部，哪些是物体外部。假设我们拍摄一个正方体，如果只对着正方体的前侧进行拍摄，那么NeuS最后计算出的只会有一个面。如果我们绕着这个正方体进行拍摄，拍到了它后侧的情况，那么为了让后侧渲染出来的结果符合ground truth。网络会在此时赋予后侧的$(x,y,z)$一个接近0的SDF，但NN此时也并不知道前侧的平面和后侧的平面，代表的是一个“物体”。NN只是由于有了后侧的输入，所以才做出了一个符合后侧拍摄图片的响应。在这个过程里其实并不会涉及到刚才图示中，什么$\rho(t)$变为负的的情况。所以这样，SDF其实并不会按照定义来呈现，它可能会是阶跃的，或者非常杂乱。

所以为了更好的生成几何，最直接的办法是让生成的SDF——“你最好真是SDF”。于是他们应用SDF的梯度模长为1的性质，会补充一项loss，也叫Eikonal term：

$\mathcal{L} _{reg}=\left( \left\| \nabla f\left( \left( \mathbf{r}(t) \right) \right) \right\| _2-1 \right) ^2$

有了这个正则项，NN预测的SDF，就会是连续的。从而就有可能导致$\rho(t)$变成负的，而负的$\rho(t)$所引发的梯度信号，会同时影响前后两个平面的重建。于是干脆就把负的$\rho(t)$截断就好，只要我们拍摄了后侧的图片，那么NN一定会根据这个需要，重建出一个关于这个平面合理的SDF。而这两个SDF之间的阶跃，就会由$\mathcal{L}_{reg}$补上。

最后一步就是推导离散版本下的“渲染积分”，作者可能是想对齐NeRF实现时，用alpha compositing的路子，同时也注意到$\rho(t)$是$-\ln \left( \varPhi _s\left( f\left( \mathbf{r}(t) \right) \right) \right) $求导出的结果吧。选择从$\alpha_i$来进行离散化，我们知道：

$\alpha _i=1-\exp \left( -\sigma _i\delta _i \right)$

所以：

$\alpha _i=1-\exp \left( -\int_{t_i}^{t_{i+1}}{\rho \left( t \right) \mathrm{d}t} \right)$

如果，此时$\rho(t)$是非零的：

$\alpha _i=1-\exp \left[ -\left( -\ln \left( \varPhi _s\left( f\left( \mathbf{r}(t_{i+1}) \right) \right) \right) +\ln \left( \varPhi _s\left( f\left( \mathbf{r}(t_i) \right) \right) \right) \right) \right] \\ =1-\frac{\varPhi _s\left( f\left( \mathbf{r}(t_{i+1}) \right) \right)}{\varPhi _s\left( f\left( \mathbf{r}(t_i) \right) \right)}$

如果此时$\rho(t)$是零，那么$\alpha_i$显然也是0。由于$\rho(t)$在非零时，$f(\mathbf{r}(t))$是单减的，所以$\alpha_i$也是恒正的。于是：

$\alpha _i=\max \left( 1-\frac{\varPhi _s\left( f\left( \mathbf{r}(t_{i+1}) \right) \right)}{\varPhi _s\left( f\left( \mathbf{r}(t_i) \right) \right)},0 \right)$

这就是，NeuS的构造了。其实给人的感觉不是很舒服……感觉作者先是从$w(t)$那个构造入手，然后反推出的这些，其实有些不自然。

VolSDF

“这位更是重量级”——佚名

VolSDF有着很重的“机器学习”色彩，它最开始也是用一个钟形曲线，只不过它取的是拉普拉斯分布：

$\varPsi _{\beta}\left( s \right) =\left\{ \begin{array}{c} \frac{1}{2}\exp \left( \frac{s}{\beta} \right) , s\leqslant 0\\ 1-\frac{1}{2}\exp \left( -\frac{s}{\beta} \right) , s>0\\ \end{array} \right.$

拉普拉斯分布的标准差是$\sqrt{2}\beta$，所以$\beta$越大，曲线越扁平。

然后，不同于NeuS的是，VolSDF的思路非常直接！“体渲染出的体密度不好？体渲染没问题，是对体渲染进行离散化时产生的误差所致。我先给你推个误差界。”

为了避免混淆，我们在这一节沿用VolSDF的符号，在VolSDF中，直接记$\sigma \left( x \right) =\alpha \varPsi _{\beta}\left( f\left( \mathbf{r}\left( t \right) \right) \right) $，所以下文中出现$\sigma(\cdot)$时，均是被转换过的SDF，不再是体密度。

这里$\alpha=\beta^{-1}$，是为了调整尖峰函数的幅度。所以要学习的参数也只有一个$\beta$，和NeuS类似。

在NeRF中，透明度（Transparency）定义为：

$T\left( t \right) =\exp \left( -\int_0^t{\sigma \left( x\left( s \right) \right) \mathrm{d}s} \right)$

那么不透明度（opacity）定义为：

$O(t)=1-T(t)$

我们关心，连续下的$O(t)$和离散估计出的$\hat{O}\left( t \right) $的误差。这很合理，注意此时的$\sigma(x(t))$代表一个尖峰函数，所以容易出现这样的情况：

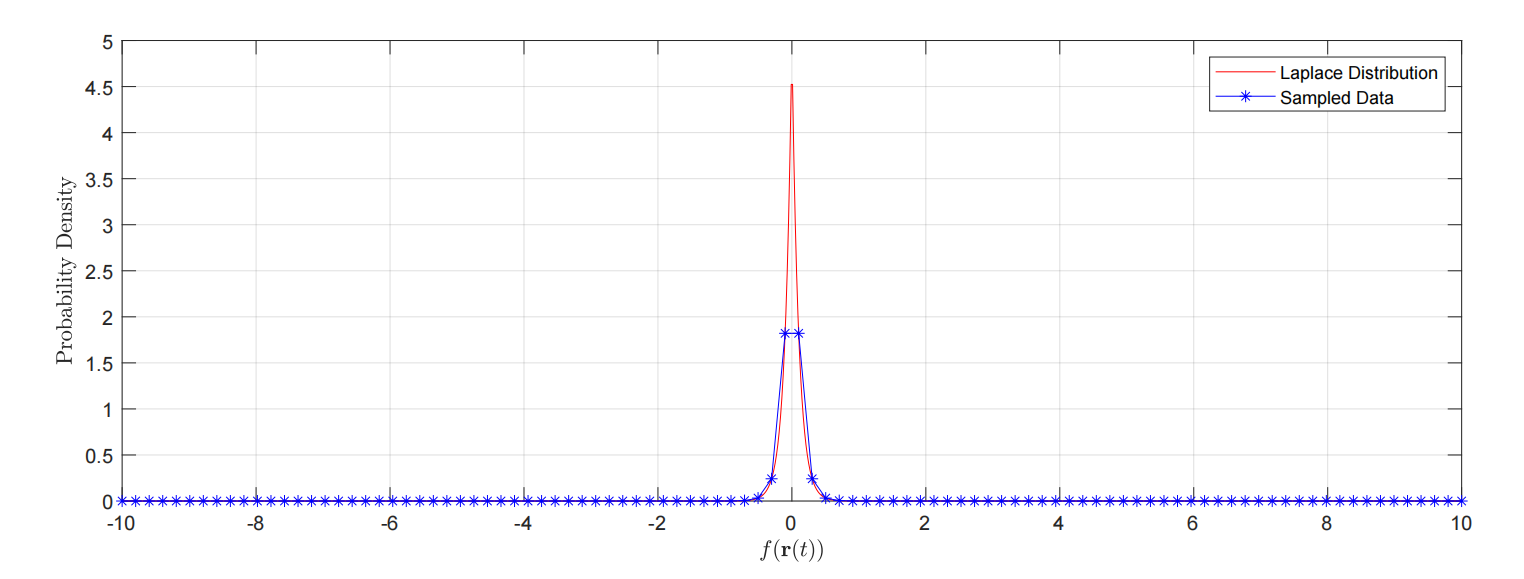
即，由于离散，从而等间距采样，是很难得到尖峰分布的极值点的。也就是说我们关心的是误差$E(t)$：

$E\left( t \right) =\int_0^t{\sigma \left( x\left( s \right) \right) \mathrm{d}s}-\hat{R}\left( t \right) , \hat{R}\left( t \right) =\left( t-t_k \right) \sigma _k+\sum_{i=1}^{k-1}{\delta _i\sigma _i}$

这里$\hat{R}\left( t \right) $是进行寻常离散后的结果。

整个推导误差界的思路可以概括为：

由于$\sigma(x)$是SDF的复合函数，并不处处可微，所以转向推导其利普希茨（Lipschitz）上界
证明在一个积分段中，$\left| \frac{\mathrm{d}\sigma \left( x(t) \right)}{\mathrm{d}t} \right|$存在上界。
从而推出在一个积分段中，$|E(t)|$的绝对值存在上界。
于是推出$\left| O\left( t \right) -\hat{O}\left( t \right) \right|$存在上界。

我们开始吧。

首先对于一个积分段$[t_i,t_{i+1}]$，对于其中任何的$s,t$，我们定义利普希茨常数$K_i$：

$\left| \sigma \left( x\left( s \right) \right) -\sigma \left( x\left( t \right) \right) \right|\le K_i|s-t|$

我们根据$\sigma \left( x \right) =\alpha \varPsi _{\beta}\left( f\left( \mathbf{r}\left( t \right) \right) \right) $对不等式左侧进行推导，希望最后能得到有着$K_i|s-t|$形式的不等式。

$\left| \sigma \left( x\left( s \right) \right) -\sigma \left( x\left( t \right) \right) \right|=\alpha \left| \varPsi _{\beta}\left( f\left( x\left( s \right) \right) \right) -\varPsi _{\beta}\left( f\left( x\left( t \right) \right) \right) \right|$

注意到$\varPsi_\beta(\cdot)$的利普希茨常数是其导数的最大值，记：

$\frac{\mathrm{d}\varPsi _{\beta}}{\mathrm{d}s}\left( s \right) =\varPhi _{\beta}\left( s \right) =\frac{1}{2\beta}\exp \left( -\frac{|s|}{\beta} \right)$

所以我们可以进一步推导为：

$\left| \sigma \left( x\left( s \right) \right) -\sigma \left( x\left( t \right) \right) \right|\leqslant \alpha |f\left( x\left( s \right) \right) -f\left( x\left( t \right) \right) |\underset{t^{\ast}\in \left[ t_i,t_{i+1} \right]}{\max}|\varPhi _{\beta}\left( f\left( x\left( t^{\ast} \right) \right) \right) |$

注意右边因式的第一个部分，我们知道SDF的导数值最大也就是1，所以自然有：

同时，注意$\varPhi _{\beta}\left( s \right)$是恒正，且关于$s=0$对称并向两侧递减。所以最大的$\varPhi _{\beta}\left( s \right)$意味着最接近0的$s$，也就是最接近某个曲面的$f\left( x\left( t^{\ast} \right) \right) $值。这个SDF的值的绝对值，我们记作$d_{i}^{\ast}$，所以式子可以归结为：

$\left| \sigma \left( x\left( s \right) \right) -\sigma \left( x\left( t \right) \right) \right|\leqslant \alpha \varPhi _{\beta}\left( \underset{t^{\ast}\in \left[ t_i,t_{i+1} \right]}{\min}|f\left( x\left( t^{\ast} \right) \right) | \right) \left| s-t \right| \\ \leqslant \alpha \varPhi _{\beta}\left( d_{i}^{\ast} \right) \left| s-t \right|$

我们对齐了不等式！所以我们有：

$K_i\leqslant \frac{\alpha}{2\beta}\exp \left( -\frac{d_{i}^{\ast}}{\beta} \right)$

$d_{i}^{\ast}$是可以求解的，即使它在后面的推导里并不会显式的代入进来，求解$d_{i}^{\ast}$其实很像一道高中数学题。问题的表述是，我们已知$f\left( x\left( t_i \right) \right) $和$f\left( x\left( t_{i+1} \right) \right) $，也就是说对于$t_i$和$t_{i+1}$，我们知道其到曲面的最短距离$d_i$和$d_{i+1}$，那么在已知$d_i$和$d_{i+1}$的情况下，如何求解$[t_i,t_{i+1}]$内的点到曲面的最短距离$d_{i}^{\ast}$的下界？

我们可以进行分类讨论：

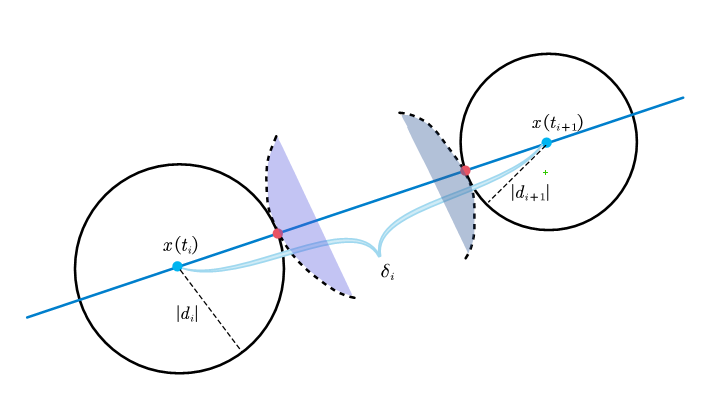
此时，$|d_i|+|d_{i+1}|\leqslant \delta_i$，可以直接看出，如果有曲面恰好能过红点处，那么$d_{i}^{\ast}$下界即为0。如果继续增加$|d_i|$和$|d_{i+1}|$：

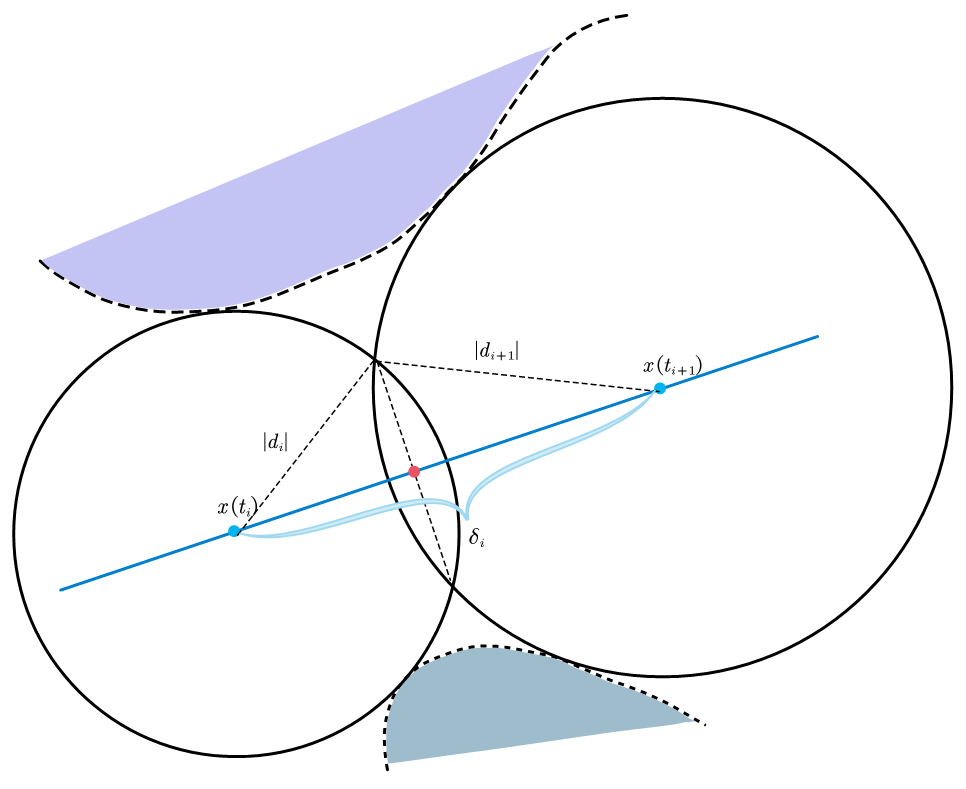
两点的最短距离张成的球面（在图里就是圆了）会有交集，那么会形成一个三角形，这个三角形关于$\delta_i$那条边的高，就是距离下界。结合海伦公式和等面积法，我们可以推导出高$h_i$为：

$p=\frac{1}{2}\left( \delta _i+|d_i|+|d_{i+1}| \right) \\ S=\sqrt{p\left( p-\delta _i \right) \left( p-|d_i| \right) \left( p-|d_{i+1}| \right)} \\ h_i=\frac{2}{\delta _i}\sqrt{p\left( p-\delta _i \right) \left( p-|d_i| \right) \left( p-|d_{i+1}| \right)}$

此时$h_i$就是下界。

如果进一步增加，形成的三角形可能变为钝角三角形，这样高的垂足就落不进$[t_i,t_{i+1}]$了：

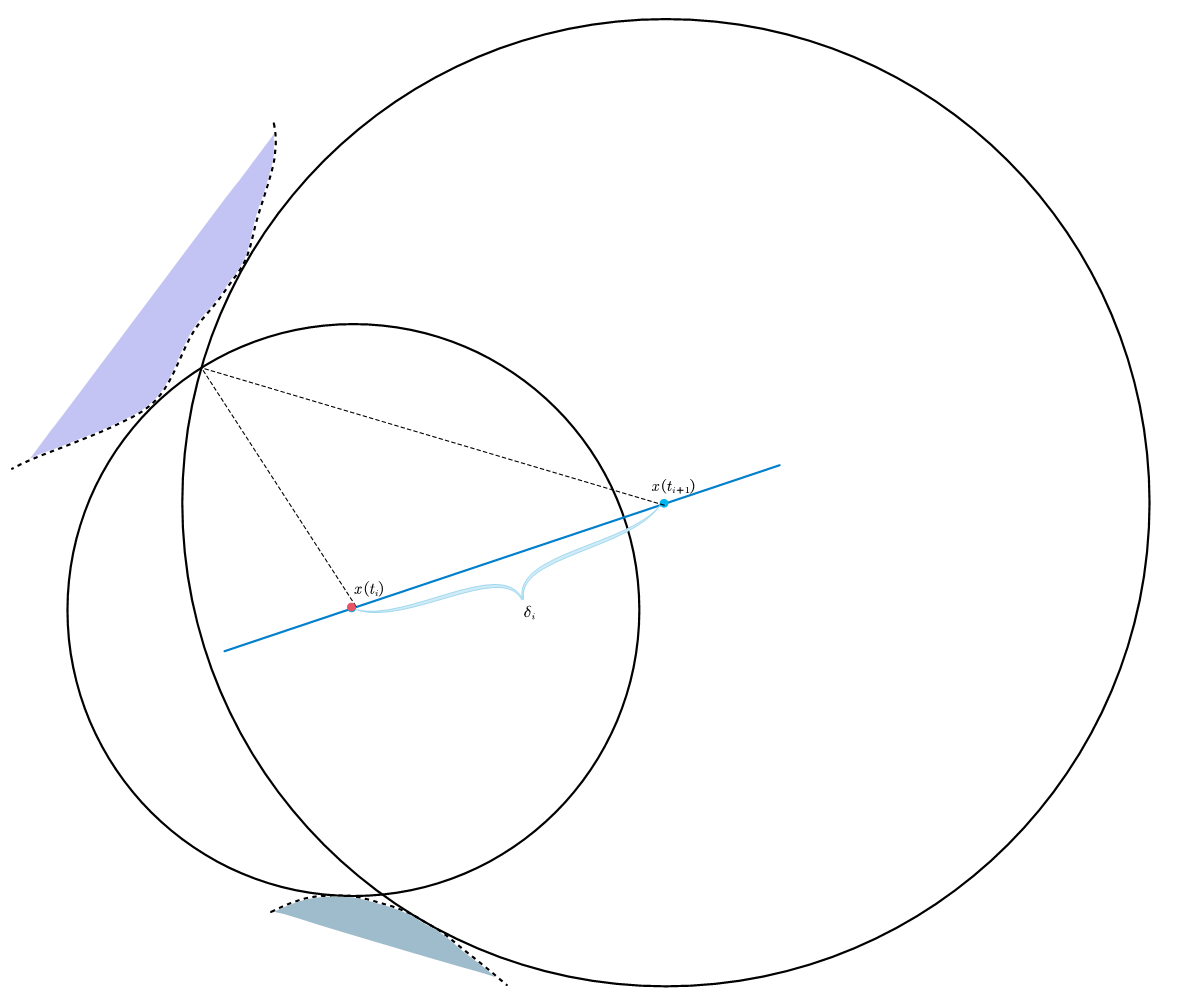
这种时候，距离下界就是$\min \left\{ |d_i|,|d_{i+1}| \right\} $，这种情况的判定，可以由余弦定理，判断$\delta_i$边上的两个角是否为锐角，即：$\left| |d_i|^2-|d_{i+1}|^2 \right|\geqslant \delta _{i}^{2}$，所以，综合三种情况，可以给出$d_{i}^{\ast}$下界：

$d_{i}^{\ast}=\left\{ \begin{array}{c} 0, |d_i|+|d_{i+1}|\leqslant \delta _i\\ \min \left\{ |d_i|,|d_{i+1}| \right\} , \left| |d_i|^2-|d_{i+1}|^2 \right|\geqslant \delta _{i}^{2}\\ h_i, otherwise\\ \end{array} \right.$

现在，我们可以继续往下推导了，我们关注一个积分段$[t_i,t_{i+1}]$上的$E(t)$，根据积分的三角不等式：

$\left| \int_{t_i}^{t_{i+1}}{\sigma}(\boldsymbol{x}(s))\mathrm{d}s-\delta _i\sigma _i \right|\le \int_{t_i}^{t_{i+1}}{\left| \sigma (\boldsymbol{x}(s))-\sigma \left( \boldsymbol{x}\left( t_i \right) \right) \right|}\mathrm{d}s$

进一步，用利普希茨常数进行放缩：

$\int_{t_i}^{t_{i+1}}{\left| \sigma (\boldsymbol{x}(s))-\sigma \left( \boldsymbol{x}\left( t_i \right) \right) \right|}\mathrm{d}s\le \int_{t_i}^{t_{i+1}}{K_i\left( s-t_i \right)}\mathrm{d}s=K_i\frac{\delta _{i}^{2}}{2}$

将这个估计进行离散求和，得到误差$E(t)$的估计$\hat{E}\left( t \right) $，得：

$\hat{E}\left( t \right) =K_i\frac{\left( t-t_k \right) ^2}{2}+\sum_{i=1}^{k-1}{\delta _{i}^{2}K_i} \\ =\frac{\alpha}{4\beta}\left( \sum_{i=1}^{k-1}{\delta _{i}^{2}\exp \left( -\frac{d_{i}^{*}}{\beta} \right)}+\left( t-t_k \right) ^2\exp \left( -\frac{d_{i}^{*}}{\beta} \right) \right)$

注意连续下的误差是要比离散下的更少的，所以有：

$|E\left( t \right) |\leqslant |\hat{E}\left( t \right) |$

现在，准备工作终于要结束了，我们回忆不透明度的连续情形和离散情形：

$O\left( t \right) =1-T\left( t \right) \\ \hat{O}\left( t \right) =1-\exp \left( -\hat{R}\left( t \right) \right)$

我们直接计算：

$\left| O\left( t \right) -\hat{O}\left( t \right) \right|=\left| \exp \left( -\hat{R}\left( t \right) \right) -\exp \left( -\int_0^t{\sigma \left( x\left( s \right) \right) \mathrm{d}s} \right) \right| \\ =\exp \left( -\hat{R}\left( t \right) \right) \left| 1-\exp \left( \hat{R}\left( t \right) -\int_0^t{\sigma \left( x\left( s \right) \right) \mathrm{d}s} \right) \right| \\ =\exp \left( -\hat{R}\left( t \right) \right) \left| 1-\exp \left( -E\left( t \right) \right) \right|$

接下来使用一个不等式$\left| 1-\exp \left( x \right) \right|\leqslant \exp \left( \left| x \right| \right) -1$，这个不等式说实话很巧夺天工，既去掉了不等号，又能给$E(t)$套个绝对值（因为你很难直接操作$E(t)$，你不知道它是正是负）。所以：

$\leqslant \exp \left( -\hat{R}\left( t \right) \right) \left( \exp \left( \left| E\left( t \right) \right| \right) -1 \right)$

同时$|E\left( t \right) |\leqslant |\hat{E}\left( t \right) |$，所以得到上界：

$\left| O\left( t \right) -\hat{O}\left( t \right) \right|\leqslant \exp \left( -\hat{R}\left( t \right) \right) \left( \exp \left( \left| \hat{E}\left( t \right) \right| \right) -1 \right)$

由于$\hat{R}\left( t \right) $单调递增，所以$\exp \left( -\hat{R}\left( t \right) \right) $单调递减，同时由于离散误差的累积效应，$\exp \left( \left| \hat{E}\left( t \right) \right| \right) $单调递增。所以给定一个特定的离散区间$[t_k,t_{k+1}]$，有：

$\underset{t\in \left[ t_k,t_{k+1} \right]}{\max}\left| O\left( t \right) -\hat{O}\left( t \right) \right|\leqslant \exp \left( -\hat{R}\left( t_k \right) \right) \left( \exp \left( \left| \hat{E}\left( t_{k+1} \right) \right| \right) -1 \right)$

最终，作者取所有区间中的最大上界，标记为一个新的界$\mathcal{B} $。

同时定义离散采样的划分$\mathcal{T} =\left\{ t_k \right\} _{k=1}^{n}, 0=t_1<t_2<…<t_n=M$。

所以这个界$\mathcal{B} $可以视为$\mathcal{T}$和$\beta$的函数：

$\underset{t\in \left[ 0,M \right]}{\max}\left| O\left( t \right) -\hat{O}\left( t \right) \right|\leqslant \mathcal{B} _{\mathcal{T} ,\beta}=\underset{k\in \left[ 0,n-1 \right]}{\max}\left\{ \exp \left( -\hat{R}\left( t_k \right) \right) \left( \exp \left( \left| \hat{E}\left( t_{k+1} \right) \right| \right) -1 \right) \right\}$

观察这个上界，可以得到两个结论：

一个是如果固定表征SDF时所用的$\beta$，那么只要$\mathcal{T}$采样足够致密，就可以达到任意的误差：

$\mathcal{B} _{\mathcal{T} ,\beta}\leqslant \left( \exp \left( \left| \hat{E}\left( t_n \right) \right| \right) -1 \right) =\left( \exp \left( \frac{\alpha}{4\beta}\sum_{i=1}^{k-1}{\delta _{i}^{2}\exp \left( -\frac{d_{i}^{*}}{\beta} \right)} \right) -1 \right) \\ \leqslant \left( \exp \left( \frac{\alpha}{4\beta}\sum_{i=1}^{k-1}{\delta _{i}^{2}} \right) -1 \right)$

所以只要$\delta_i$越小，$\mathcal{B} _{\mathcal{T} ,\beta}$就会越小。

另一个结论是，假设均匀采样，固定采样间隔$\delta_i=\frac{M}{n-1}$，足够大的$\beta$也可以实现任意的误差，可以通过构造：

$\beta \geqslant \frac{\alpha M^2}{4\left( n-1 \right) \log \left( 1+\epsilon \right)}$

来获得足够大的$\beta$，这是因为：

$\mathcal{B} _{\mathcal{T} ,\beta}\leqslant \left( \exp \left( \frac{\alpha}{4\beta}\sum_{i=1}^{k-1}{\delta _{i}^{2}} \right) -1 \right) =\left( \exp \left( \frac{\alpha M^2}{4\left( n-1 \right) \beta} \right) -1 \right) \\ \leqslant \left( \exp \left( \log \left( 1+\epsilon \right) \right) -1 \right) =\epsilon$

这两个结论比较显然，但一味的增加采样点，会带来计算负担。一味的增大$\beta$，会导致尖峰函数变得不尖。于是一个很好的想法是在这两者之间找到一个平衡。

基于此，VolSDF的作者再次发力，根据这两个结论提出一个采样的策略。这个采样的目的是构造一个误差在我们控制范围内的$\hat O[i]$序列。

首先，先初始化采集$n$个点，文中是128，然后根据第二条结论，选取一个比较大的$\beta_{+}$来满足$\epsilon$。注意，此时，训练好的网络本身是有一个$\beta$的。但显然$\beta$是不满足结论2的，即$\mathcal{B} _{\mathcal{T} ,\beta}> \epsilon $。

只要$\mathcal{B} _{\mathcal{T} ,\beta}> \epsilon $，并且还没到最大迭代次数，就进入一个循环体。由于$\beta_+$是从最开始的$\mathcal{T}_0$里计算出来的，从而$\mathcal{B} _{\mathcal{T} ,\beta_{+}}\leqslant \epsilon $也一定是绰绰有余的。然而$\mathcal{B} _{\mathcal{T} ,\beta}> \epsilon $，所以根据介值定理，一定有一个$\beta_{\star}\in(\beta,\beta_+)$可以使得$\mathcal{B}_{\mathcal{T},\beta_{\star}}=0$。由于$\mathcal{B}_{\mathcal{T},\beta}$某种意义上可以说是单调的，所以可以用二分查找来找$\beta_{\star}$。之后用$\beta_{\star}$来更新$\beta_+$。

然后接下来，对序列$\mathcal{T}$进行上采样，然后重复上述操作，直到用最开始的$\beta$，就可以满足$\mathcal{B} _{\mathcal{T} ,\beta}\leqslant \epsilon $。通过这样的策略，我们就可以找到在给定$\beta$下，如何采一个误差在$\epsilon$以下的序列$\hat O[i]$了。

然后接下来的事情就是从$\hat O[i]$中进行逆变换采样，然后抽$m$个点，文中是64。得到一个计算负担不那么重，然后误差又相对较小的采样。

所以论文原文里的伪代码“algorithm 1”疑似把upsample和search beta两个部分写反了。

这基本就是VolSDF的内容了。可以看见，VolSDF只是对NeRF的框架进行了很小的修改，然后就是“对麻瓜使用魔法”版的做了数学推导，改进了采样的过程。整个推导走完，观感比NeuS要舒适很多，因为没有很多“天外飞仙”般的“硬植入”的操作。

但VolSDF也确实是“有偏的”，这里的有偏是相对NeuS所提出的无偏来说的，但这不影响整个框架的和谐。然而，由于VolSDF其较为复杂的工序，后面的工作还是以NeuS作为魔改的对象居多。但不得不说，VolSDF的解决方案确实很漂亮。但也属实是学不来，数学功底确实扎实，通篇其实没有用到什么出格的数学工具。只能说是“如听仙乐耳暂明”。

End

“我好想看芙利莲第八集。”——佚名

但其实，这两篇工作里，最为神奇的是，变换函数（无论是$\phi_s(\cdot)$还是$\varPhi_s(\cdot)$）所带来的奇迹般的巧合。在这两篇工作的数学推导里，这两个概率密度函数，无论是单调性还是积分和为1，还是单纯的导函数或原函数形式上的巧合，都成为推导能进行下去的必要因素。有些“妙手偶得之”的意思了。