Neural Radiance Fields


阅读数: 次   
文章目录
  1. 前序
  2. Radon变换
  3. 体渲染
    1. 导出渲染方程
    2. 离散化
    3. 重参数化
  4. 相机与变换
    1. 相机外参
    2. 相机内参
    3. 透视变换与NDC空间
  5. NeRF实现
    1. create_nerf()
    2. get_rays()
    3. render()
  6. Try it!
  7. 扩展讨论
  8. End

​ “在红色警戒2中，尤里国有一个单位叫神经突击车，伊拉克有一个单位叫辐射工兵。所以神经辐射场=神经突击车+辐射工兵。”

​ 神经辐射场（Neural Radiance Fields, NeRF）最早是一种用来解决渲染多视图图像的工具。网上其实有相当多的资料，许多翔实的博客和资料都记录的很好。所以这篇blog是记录我自己学的时候的经历，以及想补充的一些角度。

​ 整体来说，这篇blog将会先从一些背景知识出发，沿途补充一下相关知识，然后到NeRF的整体流程，再到代码实现。适合像我一样的，对计算机图形学毫无了解，数理基础欠佳，有着信号与系统教育背景的人通过一篇blog来掌握NeRF。

前序

​ NeRF解决的任务是“novel view synthesis”，就是有一组相同事物不同角度的照片，如何通过这组照片合成出其他角度下的照片，这其实可以理解为对图片的某种插值。我们可能很容易认为：“如果我可以给出任意角度下某个场景的照片，那我是不是就重建出了一个三维场景？”。可以这么理解，所以NeRF也带动了“3D reconstruction”这个任务的发展。

​ 但在最后我们会讨论，这两者之间虽然紧密联系，但还是有差别的，以及NeRF并不适合进行三维重建。但由于对于没有接触过相关领域的人，我们可能既不了解“novel view synthesis”，也不了解“3D reconstruction”。这就导致NeRF可能是接触到的第一篇跟3D沾边的事物，如果提前不学NeRF而是先一股脑缕清前面的related work，那只会导致“懂的都懂，不懂的说了也不懂”的尴尬局面。所以我们可以暂时认为“NeRF”就是通过实现了“3D reconstruction”，然后由于重建出了整个场景，所以就可以直接“novel view synthesis”。当我们理解了NeRF以后，会自然地再回到这个话题。

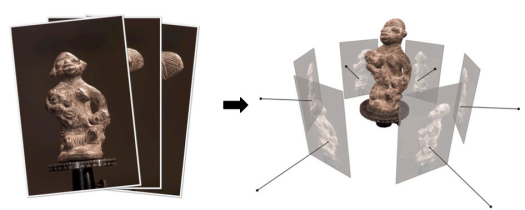
​ 遗憾的是，我们可能对“重建”也知之甚少。然而我突然发觉，之前数学建模中接触到的“计算机断层扫描”，其整个过程的逻辑和背景与NeRF有类似之处，以及其本身也是实现“重建”的一种思路。所以出于对CUMCM2017的致意，同时当作热身，所以会先用CT扫描的理论基础——拉东变换（Radon Transform）来抛砖引玉。

Radon变换

​ 拉东变换被广泛的应用在断层扫描上，与其直接给出一堆公式，我更在意从浅显的例子出发，先对“重建”有个直观的认识。更确切的来说，是对“发起多次测量，就可以重建整个场景”有直观的认识。如果你对此不感兴趣，可以直接跳过这个部分。这一部分也并不是掌握NeRF所必要的知识。

​ 一般而言，CT扫描的目的是为了得到整个切片对X光的吸收率，通过吸收的多少，来观察一些器官或组织的性态。所以本质上也是想估计一个吸收率的”场“。我们先从一个很简单的例子开始：假定材料有一个均匀的衰减系数$\mu$，单位为“强度/米”。那么考虑强度为$I_0$的光线射入衰减系数为$\mu$，厚度为$d$的材料，可以有：

​ 上式其实就是朗伯-比尔定律（Beer-Lambert Law），也是高中化学选修六中所记录的分光光度法测定物质的基本原理。

​ 进一步，如果这个物质实际上是由多个物质复合而成的，衰减系数分别为$\mu_1,\mu_2,…,\mu_n$，厚度分别为$d_1,d_2,…,d_n$。这实际上是对一种衰减系数连续变化的物质的离散化。上式显然会由于指数函数的性质，扩展为：

​ 这里厚度$d_i$是已知的，每次测量后，$I/I_0$也是已知的。所以多次测量会自然地导出一个线性方程组。

​ 显然，为了解决这个方程组，我们需要更多的信息。所以考虑这样的情形：

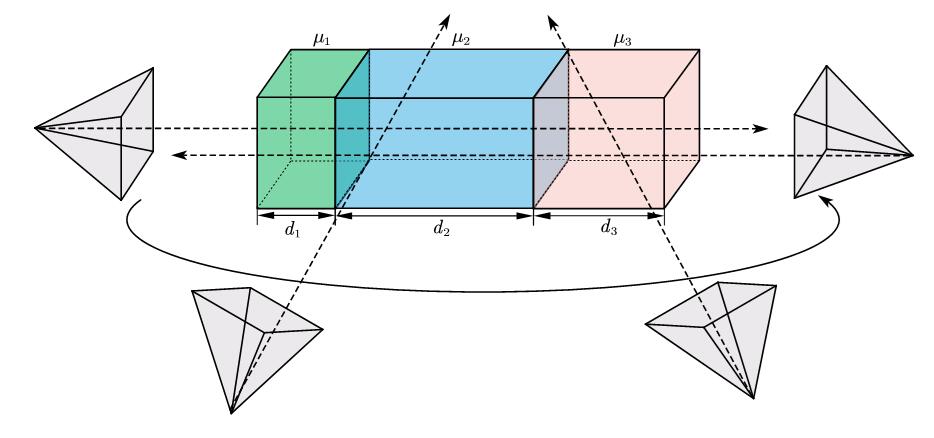
​ 我们可以记录从不同角度射入的光线，在不同光路下行进的光程$s$，只要我们采集$m$个角度，这种离散的情形就可以张成一个线性方程组，我们记$p=\ln \frac{I}{I_0}$：

​ 只要上述线性方程组可以满足列满秩，那么我们就可以得到全部的$\mu_i$。更特殊的，如果我们调整角度，每次沿着宽和高的那面，我们会发现线性方程组变成了一个单纯的对角阵。所以，通过旋转入射角度来增加信息是可行的。

​ 但，如果真正是在扫描比如人的颅腔的某一截面时，我们很难定义“厚度”，因为太复杂了。比如在刚才那个例子里，如果厚度$d_i$也是未知的，那么情况会变得更棘手。但是我们可以将其分成按矩阵排列的若干小的基本单元，这些小单元我们可以称其为体素（Voexl），就像像素（Pixel）一样。我们求取每个体素的$\mu_{i,j}$，这或给出一个很高维，稀疏的矩阵。我们可以用迭代法求这个线性方程组的近似解。

​ 另一种思路是纯解析的，我们考虑对这个网格区域进行细致的扫描，可以用直线的参数方程，来确定此次扫描所沿的线：

​ 所以通过引入信号与系统中的$\delta(\cdot)$​函数，每次扫描的线积分可以形式化为：

​ 实际上$R(\theta,p)$就是拉东变换的意思，所以拉东变换其实就是一个将函数$f(x,y)$转化为参数坐标$(\theta,p)$下的积分变换：

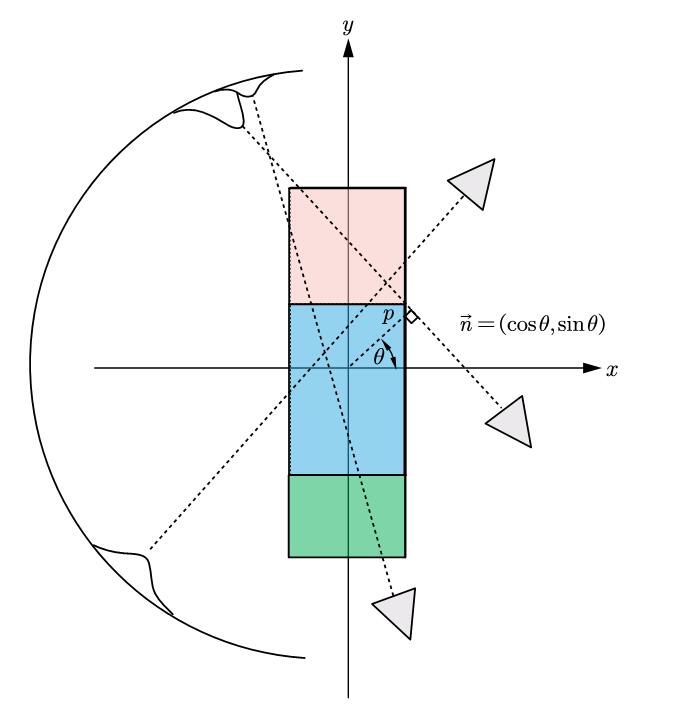
​ 这样作出来的$\theta-p$图，也被称为弦图（sinogram）。为什么这么叫呢？因为假设$f(x,y)$只有一个孤立的点$(x_0,y_0)$的值非零，而其余值均为0。那么此时经过$(x_0,y_0)$的那些有值的$R(\theta,p)$一定满足：

​ $p$和$\theta$的轨迹确实符合一个正弦，所以就叫弦图咯。

​ 我们关心的是，理论上，如何从弦图中获取$f(x,y)$。实际上，我们可以证明$f(x,y)$沿某个方向的投影函数$R(\theta,p)$的傅里叶变换等于$f(x,y)$的傅里叶变换沿着相同方向过原点的切片。这个定理称为中心切片定理，它为拉东逆变换提供了数学基础。简单来说，我们选择某个方向$\theta$，对$p$​应用傅里叶变换：（我们按理说不能随便交换积分顺序，但，whatever）

​ 上面的推导给了通过“通过不断的扫描得到的线积分来复原一个场”一个很坚实的理论基础，它指出：二维函数投影的一维傅里叶变换等于函数的二维傅里叶变换沿与探测器平行的方向过原点的切片。

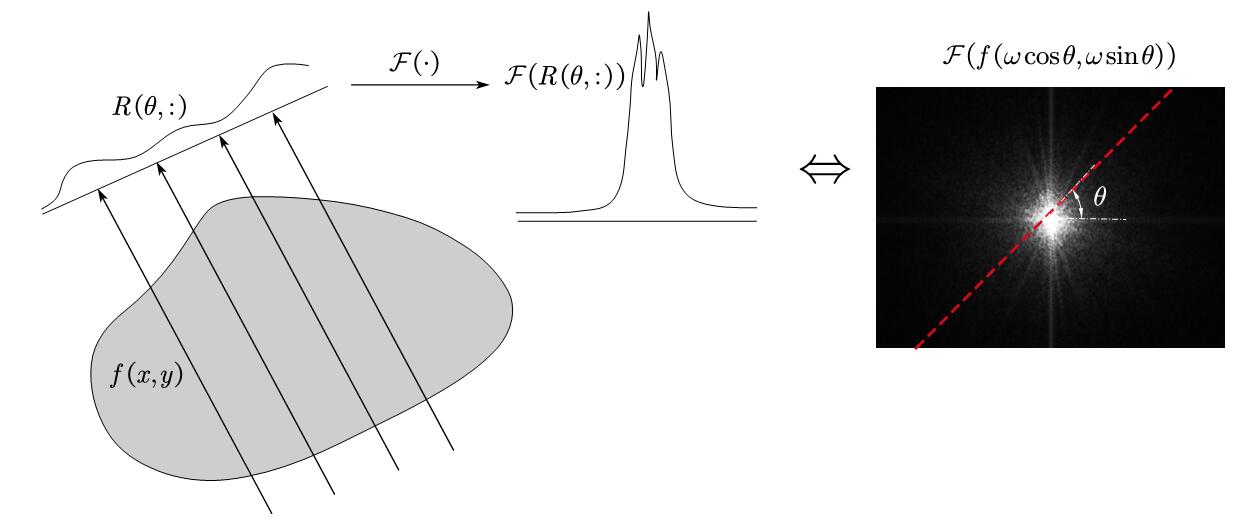
​ 这个定理只是一个理论上的保证，实际操作时可能要引入各种各种工程优化的机制，因为不难看出。为了覆盖完整的区域，需要的$\theta$是无止境的。并且越高频的地方是越不会被覆盖的，这就导致了大量的误差，以及重建的模糊。

​ 所以就有了一些相应的迭代重建算法，滤波反投影，来得到更好的重建效果，这里我们对其不作讨论。

​ 实际上，我们可以发现，上面举的三个不同材质的$\mu_i$的例子，实际上是拉东变换的一个特例。如果一个$f(x,y)$从上到下分为三个部分，每个部分的值都是一个定值。那么其傅里叶变换的非零处基本也只有一根竖线。所以一次切片即可复原，对应的其实就是线性方程组被化简为对角阵时的情形（我们只需沿着“宽-高”的面射一个角度即可）。

​ 拉东变换其实可以扩展为$\mathbb{R} ^n$上的实值函数的拉东变换，其定义为了一个$n-1$维上的积分值。我们刚才介绍的其实就是$\mathbb{R} ^2$，那么$\mathbb{R} ^3$自然也是可以的。

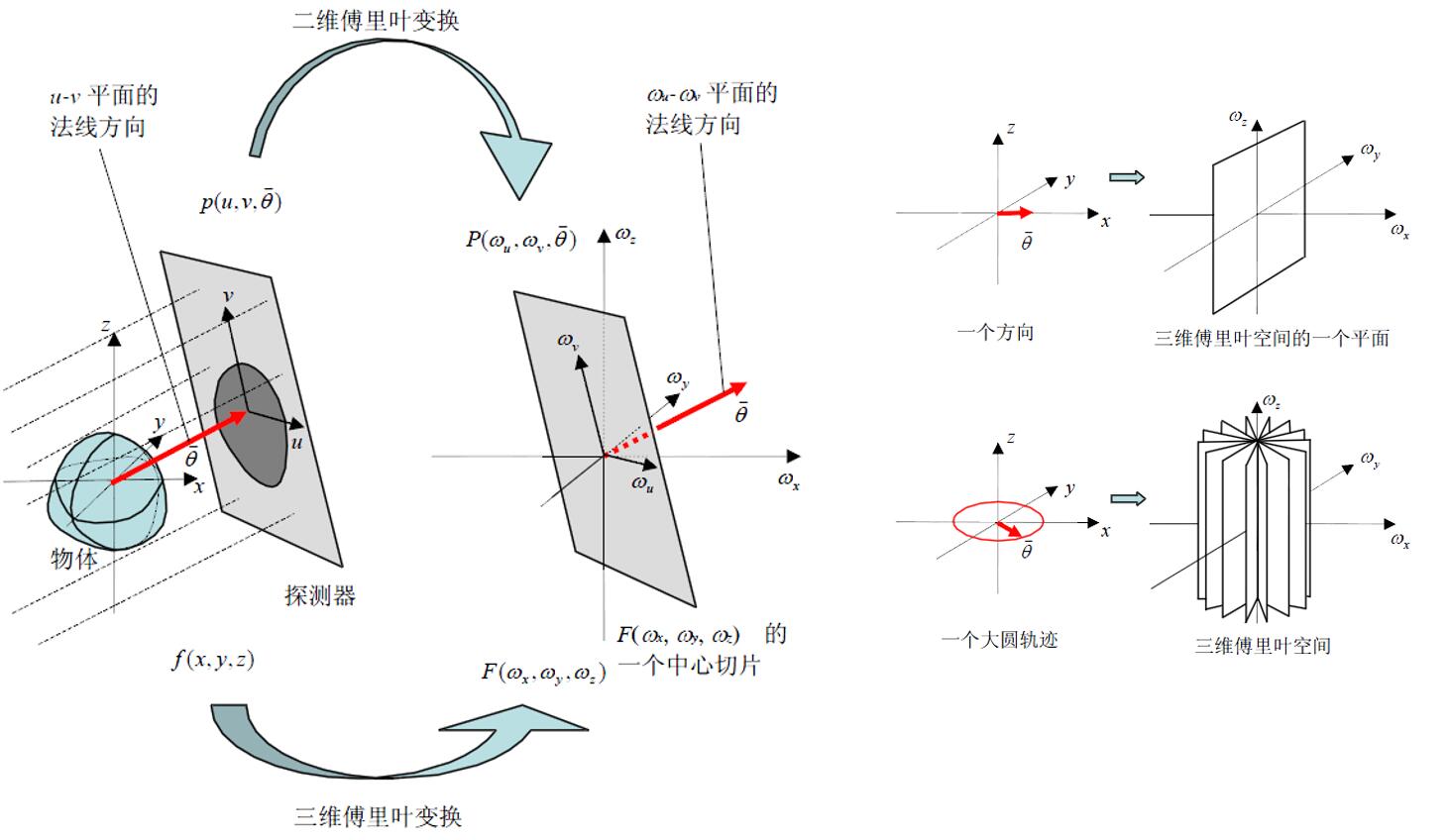
​ 只不过此时在现实生活中就需要用一个足够大的平行板探测器，这基本是不能承受的。所以工程实现时一般是应用例如三维锥形束FDK算法，这就是更复杂的话题了，这里就不予讨论了。

​ 我们明确了这一点后，就可以意识到。如果我们面前现在有一团迷雾$f(x,y,z)$，每个$(x,y,z)$有不同的吸收率。那么作为一个三维函数，它投影的二维傅里叶变换也是它自身傅里叶变换的某个切片。所以我如果选取不同的角度，得到了X光透过它前后的，这个投影，那么我实际上就可以构建它本身。

​ 那么如果把所谓的X光，换成自然光；探测器，换成相机；迷雾$f(x,y,z)$换成一个很一般的三维场景。好像，也很合理。只不过有那么些许的事宜需要再商榷商榷。这就是在这里要花费篇幅讨论拉东变换的目的，让我们对“重建”这个事情有更直观的直觉。

体渲染

​ 现在热身完了，我们继续朝着理解NeRF的方向前进。

导出渲染方程

​ 在CT重建时，人们往往要一个灰度表示就好了，但在真实成像时我们需要颜色。可以使用图形学中一种叫作体渲染（Volume Rendering）的技术来实现这一点，它最初是目的是为了解决一些类似云雾一样的半透明，非刚性物体的渲染。它的一个好处就是天然可微，给反向传播带来了机会。

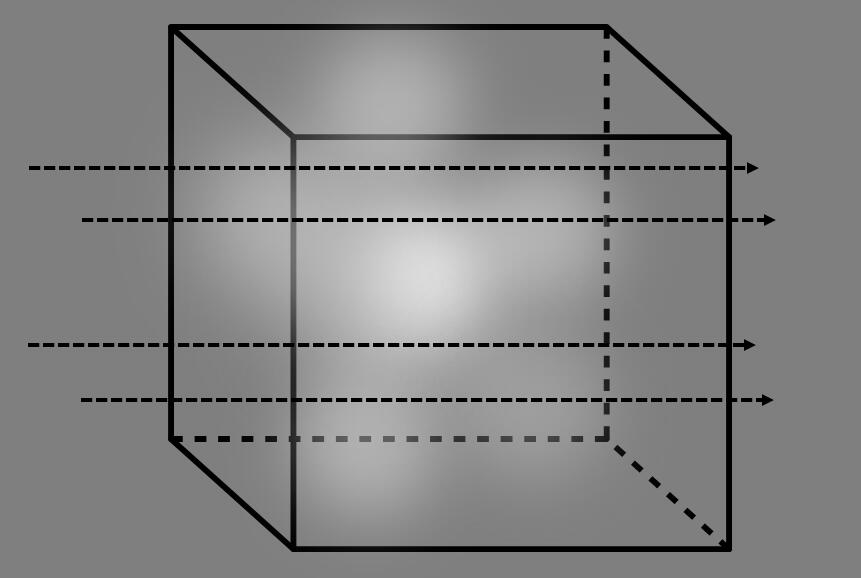
​ 考虑上图，假设整个场景由若干粒子组成，也就是密度$\sigma$，颜色$c$各不相同的粒子。我们认为，光线碰到这些粒子后，会发生吸收，从而导致其光照强度遭到衰减，衰减的部分用于让粒子“发光”。

​ 除了不考虑衍射以外，这个假设可能乍一听都很反直觉，但它其实是完美契合“光路可逆”的一种建模。中学物理告诉我们，光线照射到一个物体上时，一部分色光的光谱会被吸收，剩下的部分再反射进我们的眼里，产生颜色。那么这种反射的性质实际上被直接建模为了颜色$c$，比如一个红色不透明的球面，我们就可以理解为是一个$\sigma$很大的球面，其颜色$c$为红。由于其$\sigma$很大，光线被尽数吸收，所以传递到后面的光线只剩很小的一部分，这就导致球面内部的粒子基本不能被“点亮”，从而产生了不透明。

​ 同时反射分为漫反射和镜面反射，前者是各向同性，后者是各向异性的。所以颜色$c$作为建模反射的手段，也需要根据观测角度的不同而变化。即view-dependent color。

​ 所以整个过程即为，一束强度为$I_0$的光线从$\mathbf{d}$处发射，在$s$处，光线通过粒子密度为$\sigma(s)$的地方后被吸收一部分，吸收的那一部分“点亮”（反射）了粒子本身，产生了颜色$c(s,\mathbf{d})$。粒子密度$\sigma(\cdot)$和颜色$c(\cdot)$是后面NeRF将会学习出来的值，我们可以在下面的推导中认为其已知。根据上文关于吸收定律的讨论，这个过程可以直接写作：

​ 所以当光行进到$s$处时，$e^{\int_0^s{-\sigma \left( t \right) \mathrm{d}t}}$​可以当作一个衰减的系数，由于负指数的性质，这个值必然是介于0~1的。所以我们可以记其为“透明度”：

​ 所以“不透明度”可以记作$1-T(s)$，它指的是从0到$s$被吸收的（用于反射产生颜色部分）系数，也就是一个分布函数。对其求导可以得到密度函数$T(s)\sigma(t)$，于是最后的颜色可以直接积分$\int_0^{\infty}{T\left( s \right) \sigma \left( s \right) c\left( s \right) \mathrm{d}s}$。由于在实际中积分上限不可能真的从0到无穷远，所以会设定一个下限$t_n$和上限$t_f$，取near和far之意。所以给定一个光线$\mathbf{r}\left( t \right) =\mathbf{o}+t\mathbf{d}$，这条光线最后取得的颜色$C(\mathbf{r})$可以写作：

​ 于是就有了NeRF原文中的渲染方程。现在，我们已经知道了一根光线通过一个三维粒子场后，所产生的颜色。由于我们不可能得到上述过程的解析解，我们需要考虑它的离散化情形。

到这里，可能有人会觉得这种技术和现在一些游戏里很流行的“光线追踪”（ray tracing）技术有点像。确实他们都是基于光路可逆的背景下的技术，但NeRF里并不涉及反射，折射的模拟，所以用“光线步进”（ray marching）来形容更加合适。

离散化

​ 我们将积分区间分成$N-1$等份：$\left[ t_n+\frac{i-1}{N}\left( t_f-t_n \right) ,t_n+\frac{i}{N}\left( t_f-t_n \right) \right] $，然后进行朴素的离散化：

​ 对于每一个$C_i(\mathbf{r})$，$\sigma(\cdot),c(\cdot)$可以直接近似为常数。而由于$T(\cdot)$​由于存在一个变上限积分，其导数：

​ 这个导数值不仅与$T(\cdot)$有关，还与$\sigma(\cdot)$​有关，所以不能简单的直接一阶近似。一个有用的观察是利用指数函数的性质，考虑$t$是位于$t_i\sim t_{i+1}$这个小区间里的一个值：

​ 这样，在积分时，$T(t_i)$本身就是个定值了，可以降低积分的误差。其离散化为：

​ 所以$C_i(\mathbf{r})$可以写作：

​ 记$\delta _i=t_{i+1}-t_i$，最终$C\left( \mathbf{r} \right)$的离散形式即为：

​ 现在，所有的努力都是为了给“一根光线穿过一个粒子场后的颜色进行模拟”。实际上，体渲染本身还考虑了散射，内部光源等情况，但NeRF将其省掉了，因为在整个过程中，$\sigma(\cdot),c(\cdot)$其实都是NeRF自己训练出来的。而那些散射，内部光源其实只是在最开始的吸收方程的微分方程上多加了几个同构的项。这对NeRF来说是无所谓的，因为我们只是借用这个框架来得到图像，并不是真的关心光强的动态变化。可以理解为我们只需要整个过程的通解，这个通解就是我们离散化后的那个求解颜色的式子，通解的系数是神经网络自己配的；没必要专门建模一个特解。

重参数化

​ 我们可以从其他的一些视角来观察离散化后的渲染公式：

​ 如果我们直接合并掉系数，整个渲染可以看成采样点颜色的加权和：

​ 我们可以从另一个角度考虑权重的来源，在图形学中，有一种叫作Alpha合成（alpha compositing）的技术。指的是对于半透明物体，我们可以用一个$\alpha$来调整前景和背景RGB的比例，通过这种线性插值来实现过渡和透明。如果我们将上式这$N$个点最后一个点看成背景，那么$C\left( \mathbf{r} \right)$就可以被重参数化为：

​ 由待定系数法，我们可以观察到：

​ 可以得到$\alpha _i=1-\exp \left( -\sigma _i\delta _i \right) $，$\alpha$正是我们直观的对透明度的认识。

​ 我们可能会混淆此时的$\alpha_i$和之前定义的$1-T(s)$。$\alpha_i$考虑的是离散时，第$i$层与第$i+1$层之间混合时的权重。而$T(s)$说的是光线从0传播到$s$，还剩下多少。所以考虑已经被吸收后的光线$I_0T(s)$，再从$s$传播到$s+\delta$，由于负指数性质，会在原有的基础上再衰减$\exp \left( -\sigma \delta \right) $倍。这其实也正好对应了为什么有：

​ 于是自然就有了$\alpha=1-\exp \left( -\sigma \delta \right) $这个定义。

​ 同时这也解释了原文：

This function for calculating $\hat{C(\mathbf{r})}$ from the set of $(\mathbf{c}_i,\sigma_i)$ values is trivially differentiable and reduces to traditional alpha compositing with alpha values $\alpha _i=1-\exp \left( -\sigma _i\delta _i \right) $.

相机与变换

​ 我们现在确定了“从多个角度射入光线可以重建一个场”以及“如何模拟一条光线光路上的颜色”。我们甚至都没有引入“图片”，我们讨论的都只是一条光线。

​ 不同于拉东变换时我们可以想象一个无限大的平板探测器，图像的引入需要借助“相机”，一般指的都是最简单的针孔相机模型：

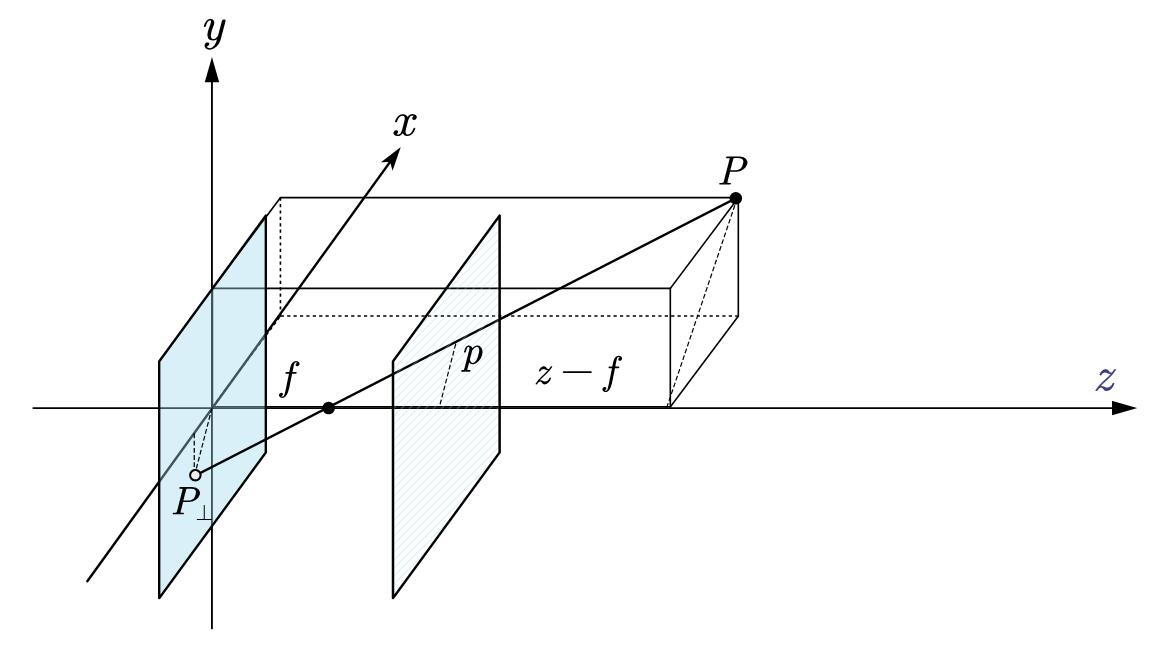
​ 为了分析的方便，经常将成像平面沿小孔（光心）对称处理，使图像不再倒立，如图中蓝色虚线所指平面。

相机外参

​ 现在，我们要公式化一下上述过程：

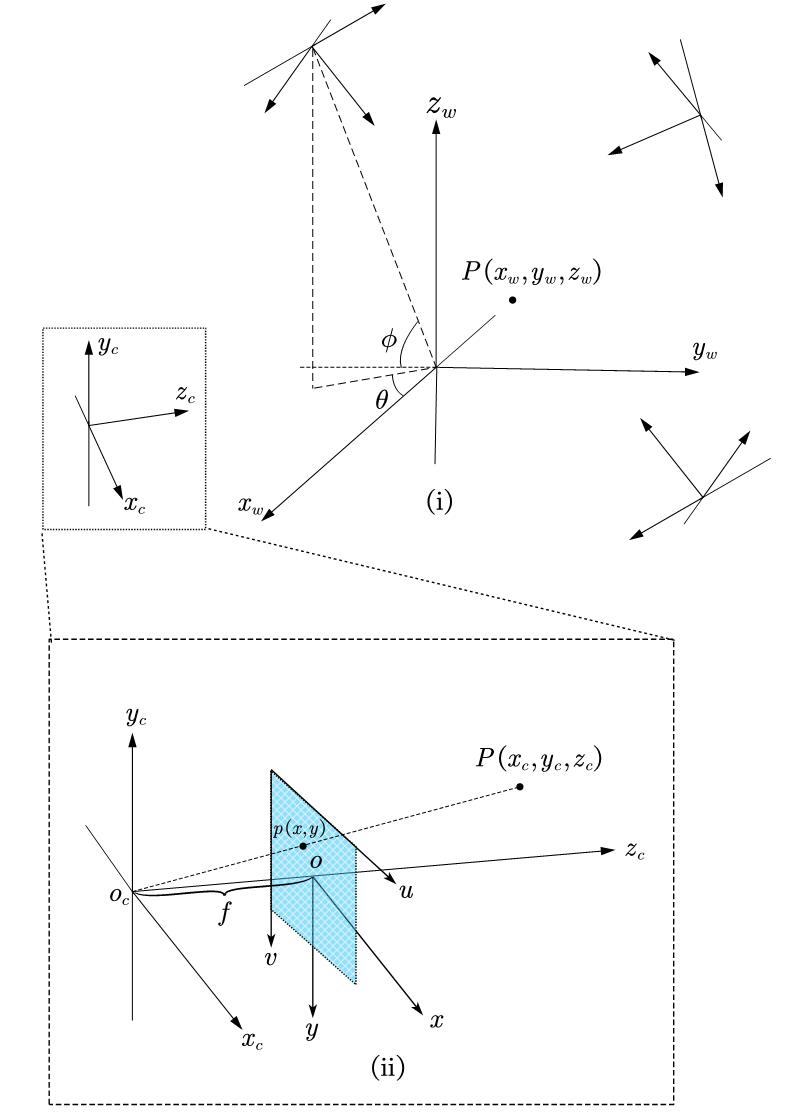
​ 首先，体素所在的（整个场）有一个默认坐标系，称为世界坐标系$O-x_wy_wz_w$。不同的相机可能会从不同的角度进行拍摄，即不同的$\phi,\theta$，以及此时小孔位置的三维坐标。即我们可以通过绕$z_w$轴和绕$x_z$轴旋转坐标系，然后再对坐标系进行平移，来将世界坐标系上的一个点转移到相机坐标系下的表示。假设此时相机的位置是$(x,y,z)$，那么可以先绕$x_w$轴旋转$\phi$，再绕$z_w$轴旋转$\theta$：

​ 同时，平移向量可以表示为$T=[x;y;z]$，那么我们可以通过齐次坐标构造一个位姿矩阵$C$:

​ 矩阵$C$又叫相机外参。这样就能通过左乘将世界坐标转换成相机坐标(w2c)：

相机内参

​ 然后就来到了图中的虚线部分，考虑相机坐标下的$P(x_c,y_c,z_c)$，焦距为$f_{c}$，由相似三角形可以得到：

​ 上式可以写成矩阵形式：

​ 最后得到了投影平面上图像的坐标，但要注意，我们此时仍然在物理坐标系下。即如果现在这些字母都有个单位的话，那么它们应该是米或毫米。距离我们熟悉的图片还有一步：从图像坐标系变换至像素坐标系。为了实现这一点，我们进行了水平和竖直方向的伸缩变换以及平移变换，将坐标系的原点从光心转移到（通常时候）图像的左上角：

​ 这里$u_0$一般近似为$W/2$，$v_0$一般近似为$H/2$​。所以整个的这个变换过程可以整理成：

​ 这里：

​ 表示将物理坐标上的焦距映射进像素尺寸$(\mathrm{d}x,\mathrm{d}y)$中的缩放，然而其实大多数情况下其实都有$\mathrm{d}x=\mathrm{d}y$，即像素是一个正方形。

​ 得到的第一个矩阵简记为$K$，也叫相机内参。获取相机内参和外参的方法即相机标定，但不是这里讨论的重点，这个部分还是交给COLMAP去估计吧，我们直接拿其计算的结果就好了。

​ 所以现在，我们可以从任意一个给定的像素空间出发，建立射线。根据此时相机的位置和角度，计算出其在世界坐标系下的坐标。所以现在我们成功建模了一条光线的位置，角度，以及这条光线最后结算到单个像素的颜色值的机理。

透视变换与NDC空间

​ 注意上文中通过相似三角形来引入内参，最后得到的内参矩阵$K$​。这个过程实际上是一个特殊的透视变换。回顾这个式子：

​ 这其实是一个二维的投影变换，$z$轴充当了齐次坐标。因为我们只考虑投影到$z=1$时的$(x,y)$，所以$K$的第三行最后的1帮忙保存了$z_c$，来使得我们后面可以直接除以$z_c$来得到$(x,y)$。由于：

​ 对于相同的$(x_c,y_c)$，$z_c$越大，其投影出来的$(x,y)$越小。除以$z_c$的这一步也被称为“透视除法（perspective division）”，这正是“近大远小”的物理规律，图来自该视频

​

​ 刚才我们所有的推导，都是基于一个坐标的操作。然而在一个$\mathbb{R}^3$中，摄像机本身其实建立了一个视锥：

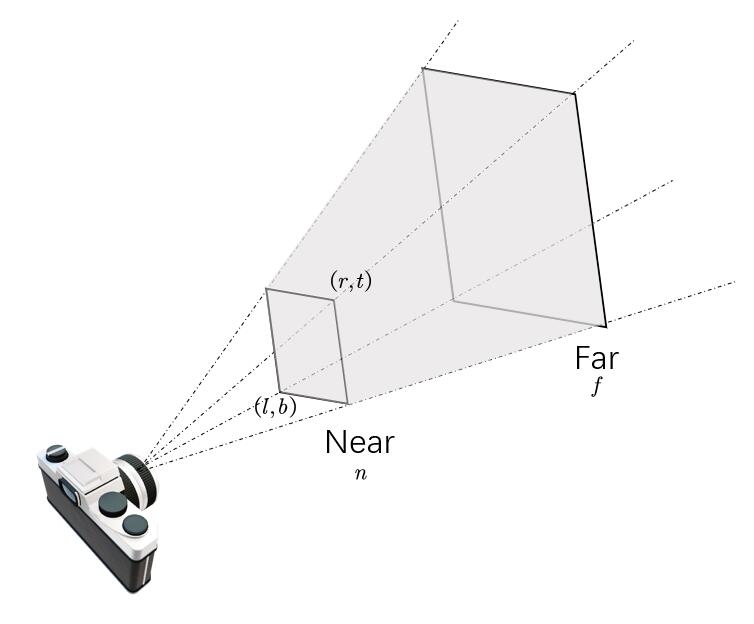
​ 注意我们定义了视锥的left($l$),right($r$),bottom($b$),top($t$),near($n$),far($f$，不要与上文表示焦距的$f_c$混淆)，这个视锥的深度可能很深，比如是一张人的照片，背后是一座大山。山的实际位置可能远得多。如果我们此时用3D坐标来表示的话，可能需要一个值域很大的$z$来表示。所以一种表示是将这个视锥规范化成一个长宽高均在$[-1,1]$内的立方体。这个立方体张成的空间也叫NDC空间（normalized device coordinates）。

​ 不失一般性，我们认为$l=-r,b=-t$。与二维的情形相比，我们需要多引入一个齐次坐标：

​ 为了满足$[-1,1]$的要求：对于$x=\frac{nx_c}{z_c},y=\frac{ny_c}{z_c}$，在分母分别除以$r,t$。所以$a_{11}=n/r,a_{22}=n/t$。

同时，在近平面（near）的物体投影后坐标为-1，远平面（far）的物体投影后的坐标为1。

​ 所以增广后的透视矩阵为：

​ 在传统的坐标系定义下，摄像头指向的方向记为$-z$，所以在标准的透视矩阵下第三列的元素可能多一个负号。由于在NeRF中使用的是带负号的版本下的坐标系，所以我们也遵守这个规矩。

​ 所以，对于一些“facing-forward”的场景，即我们用相机自己拍出的一些真实的图片。我们不会在默认的欧式空间里采样光线，而是在经过变换后的$[-1,1]$立方体中采样。这就产生了一个问题，我们在欧氏空间里采样的光线为$\mathbf{o}+t\mathbf{d}$，在NDC空间里，采样出的光线可能会有一些变化。我们记变换后的光线为$\mathbf{o}’+t’\mathbf{d}’=\mathcal{M}(\mathbf{o}+t\mathbf{d}) $，我们直接计算：

​ 考虑映射后的$\mathbf{o}’$，不失一般性，我们认为将$\mathbf{o}$作映射得到的点$\mathcal{M}(\mathbf{o})$，就是$t’=0$时的$\mathbf{o}’$。

​ 于是$t’\mathbf{d}’$可以直接逐元素作差得：

​ 可以得到：

​ 这里最重要的一个观察是$t’$与$t$成反比关系，或者与倒数成线性关系。这表明在$t’$上线性插值，等价于在$t$上作“倒数线性插值”。后者也被称为“深度（depth）采样”或者“视差（disparity）采样”，这种采样规定了一种特殊的在$z$轴上插值的方法。

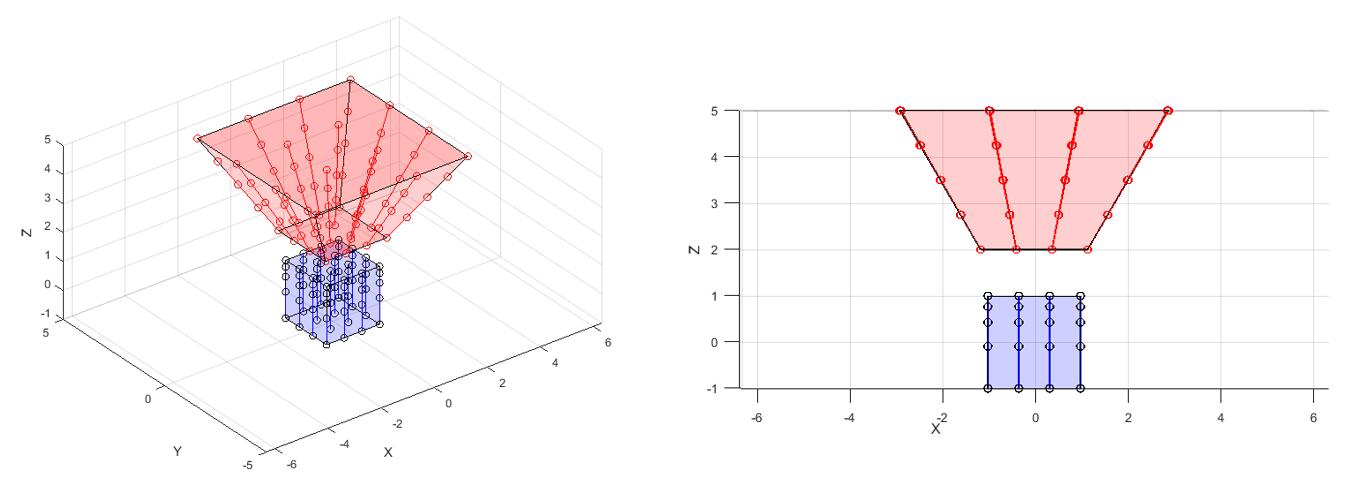
​ 如图所示，如果在原空间均匀采样，那么在NDC空间里就会变得不均匀。

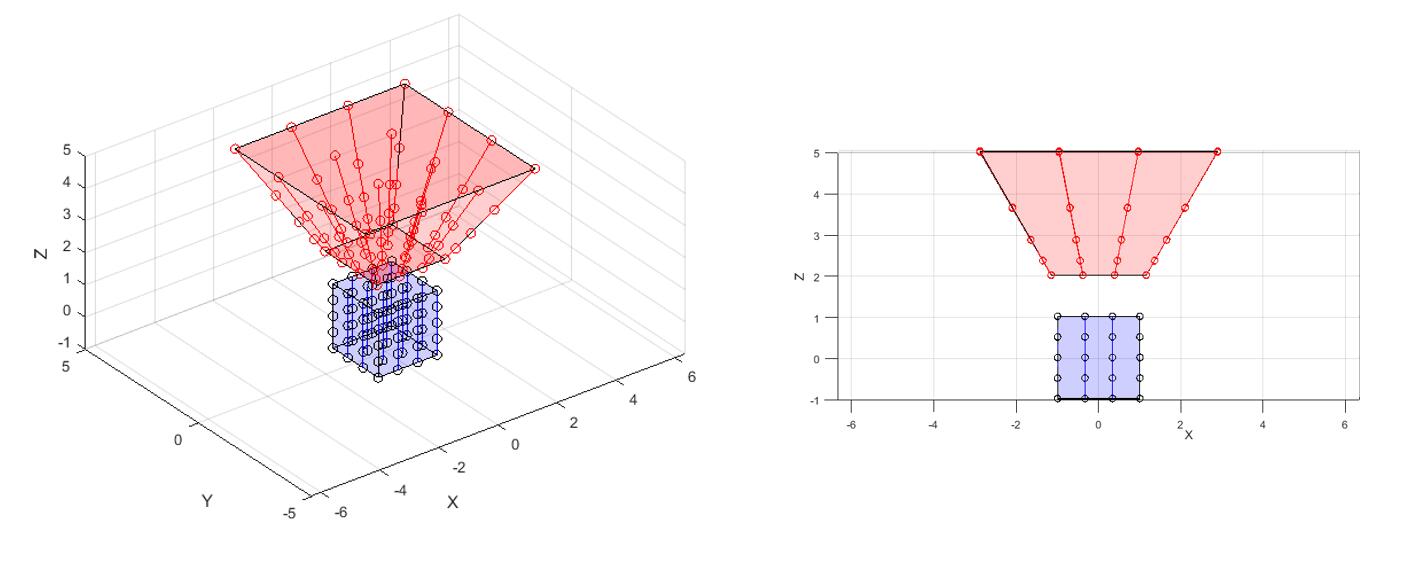
​ 如果在原空间里倒数线性的采样，那么NDC空间里就会变成均匀的线性采样。

​ 在经典的图形渲染管线中，这种采样被用于矫正透视误差。想象一个火车轨道汇聚到地平线一点的照片，虽然火车轨道下的枕木沿轨道是均匀分布的，但它们在图像上的排列却并不等距。但其实NeRF在这里需要处理的不是这个问题。

​ NeRF中的问题是，对于那些“facing-forward”所拍摄的场景，近景和远景之间的距离一般远大于近景到镜头的距离。所以在NeRF这个范式下，我们沿着光线采样若干个点，而近景和远景之间的大部分点事实上都是无意义的。所以，可以正好利用这个倒数线性插值产生的权重，实现在近处密集的采集近景。然后远景就稀疏的采一些点意思意思得了。这对应了后面对光线进行采样时的—lindisp参数，但这样其实并没有解决问题。最早，NeRF的作者们试图直接让网络去表达这种“facing-forward”的场景，但表现的并不好；后来他们尝试了利用倒数线性插值，但问题并没有得到解决。因为NeRF使用的用来克服“spectral bias”的位置编码是在$[-1,1]$有界的，引入超出这个范围的输入显然是有坏处的。所以最后他们对于这种单向的“facing-forward”的场景，采取的措施就是变换进$[-1,1]^3$的NDC空间。

​ 以及非常巧合的是，如果我们预先将原点$\mathbf{o}$移至$z=-n$处，即$\mathbf{o}_n=\mathbf{o}+t_n \mathbf{d},t_n=-(n+o_z)/d_z$。那么此时直接将$t’$从0均匀采样到1，那正是从近平面$n$采到远平面$f$的倒数线性采样。所以变换到NDC空间的这一操作，一箭双雕的解决了问题，在改善效果的同时也避免了显示设定—lindisp。但实际上，这并不能解决全景，即360°的那种“unbounded”的场合，因为在那种场景下，near和far平面不是确定的，是会随着角度变化的。解决360°下的场景，还要靠后人的智慧。

所以在原版NeRF里想渲染360°的真实照片，最好在命令行里追加--no_ndc --spherify --lindisp，这会让这三项在代码里均为true（由于parser设置时是“action=’store_true’”），所以在360°的真实照片下，我们会关闭NDC，将相机位姿球化，同时使用倒数线性插值采集近景，期望可以获得好的结果。

​ 进一步，在NeRF应用的针孔相机模型中，由于NeRF中并不存在“真正的场景”。我们认为“facing-forward”的远平面是无尽的，即$f$设为无穷大。然后，$n/r$这个比例的值实际上和$f_c/(W/2)$是相等的。同理$n/t=f_c/(H/2)$。所以在NeRF中，当生成了在世界坐标系下的$\mathbf{o},\mathbf{d}$后，可以进行如下映射来进入NDC空间：

​ 注意此时定义的方向，$n$应是一个负值。在NeRF的代码中，$n$取1，符号直接吸收进了式子里。直接取1因为NeRF里并不存在真正的“近平面”。

NeRF实现

​ 现在，有了前面的前置储备后。我们终于可以给出NeRF的整个计算流程了！

  • 首先，我们有一个关于一个场景或物体的数据集。这个数据集具体来说就是若干张图片，每张图片对应一组相机参数。同样也会得到关于相机最近和最远距离的两个参数，对应渲染方程中的$t_n,t_f$。
  • 根据相机位置，焦距。我们再从像素平面上选取一个像素点，即可确定一条直线。沿着这个方向确定一条光线，我们可以在$t_n$和$t_f$之间采样$N$个点。
  • 通过将相机坐标系转移到世界坐标系，我们可以得到一个世界坐标系上的三维坐标。然后，我们将每个点的$(x,y,z,\theta,\phi)$输入进一个多层感知机（MLP），输出为该点的体密度$\sigma$以及该点在此时角度下观测的颜色$c$。
  • 我们用MLP计算将这一条光线上的$N$个点都这样计算（或者更贴切地说：“查询”）一遍，然后利用离散的渲染公式，得到这条光线在像素平面的颜色。
  • 然后很简单的用一个平方损失来监督其与真实颜色值的差别。如果是在作推理，那么这个值就是推理出来的值。然后，再选取另一个像素点，构造另一条光线，重复上述过程。

​ 更简短的表述是：

  • 读取图片，相机参数。
  • 根据相机参数，计算每个像素对应的光线。
  • 对rays进行batch训练
  • 渲染，求损失函数，优化。

​ 这个流程也省掉了大量细节，下面我们可以结合代码一点点进行分析，这个仓库是NeRF入门的极佳的PyTorch实现。我们可以先从run_nerf.py切入，直接看train()的实现。

​ 我们这里考虑LLFF形式的数据集：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def train():

    parser = config_parser()
    args = parser.parse_args()

    # Load data
    K = None
    if args.dataset_type == 'llff':
        images, poses, bds, render_poses, i_test = load_llff_data(args.datadir, args.factor,
                                                                  recenter=True, bd_factor=.75,
                                                                  spherify=args.spherify)
        hwf = poses[0,:3,-1]
        poses = poses[:,:3,:4]
        print('Loaded llff', images.shape, render_poses.shape, hwf, args.datadir)
        if not isinstance(i_test, list):
            i_test = [i_test]

        if args.llffhold > 0:
            print('Auto LLFF holdout,', args.llffhold)
            i_test = np.arange(images.shape[0])[::args.llffhold]

        i_val = i_test
        i_train = np.array([i for i in np.arange(int(images.shape[0])) if
                        (i not in i_test and i not in i_val)])

        print('DEFINING BOUNDS')
        if args.no_ndc:
            near = np.ndarray.min(bds) * .9
            far = np.ndarray.max(bds) * 1.
            
        else:
            near = 0.
            far = 1.
        print('NEAR FAR', near, far)

​ 在注册完参数后，load_llff_data()函数会读取按规定存放好的各种数据。这里我们就不分析load_llff_data()的工作流了，只关注返回值。

variable explanation
images [N，H，W，3]，每个角度下拍的照片。
poses [N，3，5]，是对于每张图片的一个3×5的矩阵。前三列是旋转矩阵，第四列是平移向量，在llff格式下，会多出来一个第五列表示图像的高，宽，相机焦距。
bds [N, 2]，每张照片解算出来的积分上下限（near, far）。
render_poses [N_view, 4, 4]，螺旋形路径的位姿序列，用于测试时渲染新视角。
i_test 一个索引，是poses中与平均位姿最接近的那个位姿的索引。

​ 然后是一段比较碎的片段，诸如补充定义内参矩阵$K$​，建立log路径等。然后调用了一个建立nerf的函数：

1
2
# Create nerf model
    render_kwargs_train, render_kwargs_test, start, grad_vars, optimizer = create_nerf(args)

​ 我们有必要打开一下这个函数进行阅读：

create_nerf()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
def create_nerf(args):
    """Instantiate NeRF's MLP model.
    """
    embed_fn, input_ch = get_embedder(args.multires, args.i_embed)

    input_ch_views = 0
    embeddirs_fn = None
    if args.use_viewdirs:
        embeddirs_fn, input_ch_views = get_embedder(args.multires_views, args.i_embed)
    output_ch = 5 if args.N_importance > 0 else 4
    skips = [4]
    model = NeRF(D=args.netdepth, W=args.netwidth,
                 input_ch=input_ch, output_ch=output_ch, skips=skips,
                 input_ch_views=input_ch_views, use_viewdirs=args.use_viewdirs).to(device)
    grad_vars = list(model.parameters())

    model_fine = None
    if args.N_importance > 0:
        model_fine = NeRF(D=args.netdepth_fine, W=args.netwidth_fine,
                          input_ch=input_ch, output_ch=output_ch, skips=skips,
                          input_ch_views=input_ch_views, use_viewdirs=args.use_viewdirs).to(device)
        grad_vars += list(model_fine.parameters())

    network_query_fn = lambda inputs, viewdirs, network_fn : run_network(inputs, viewdirs, network_fn,
                                                                embed_fn=embed_fn,
                                                                embeddirs_fn=embeddirs_fn,
                                                                netchunk=args.netchunk)

    # Create optimizer
    optimizer = torch.optim.Adam(params=grad_vars, lr=args.lrate, betas=(0.9, 0.999))

    start = 0
    basedir = args.basedir
    expname = args.expname

    ##########################

    # Load checkpoints
    if args.ft_path is not None and args.ft_path!='None':
        ckpts = [args.ft_path]
    else:
        ckpts = [os.path.join(basedir, expname, f) for f in sorted(os.listdir(os.path.join(basedir, expname))) if 'tar' in f]

    print('Found ckpts', ckpts)
    if len(ckpts) > 0 and not args.no_reload:
        ckpt_path = ckpts[-1]
        print('Reloading from', ckpt_path)
        ckpt = torch.load(ckpt_path)

        start = ckpt['global_step']
        optimizer.load_state_dict(ckpt['optimizer_state_dict'])

        # Load model
        model.load_state_dict(ckpt['network_fn_state_dict'])
        if model_fine is not None:
            model_fine.load_state_dict(ckpt['network_fine_state_dict'])

    ##########################

    render_kwargs_train = {
        'network_query_fn' : network_query_fn,
        'perturb' : args.perturb,
        'N_importance' : args.N_importance,
        'network_fine' : model_fine,
        'N_samples' : args.N_samples,
        'network_fn' : model,
        'use_viewdirs' : args.use_viewdirs,
        'white_bkgd' : args.white_bkgd,
        'raw_noise_std' : args.raw_noise_std,
    }

    # NDC only good for LLFF-style forward facing data
    if args.dataset_type != 'llff' or args.no_ndc:
        print('Not ndc!')
        render_kwargs_train['ndc'] = False
        render_kwargs_train['lindisp'] = args.lindisp

    render_kwargs_test = {k : render_kwargs_train[k] for k in render_kwargs_train}
    render_kwargs_test['perturb'] = False
    render_kwargs_test['raw_noise_std'] = 0.

    return render_kwargs_train, render_kwargs_test, start, grad_vars, optimizer

位置编码

​ 第一行的get_embedder()就是一个NeRF中应用的技巧，“将输入应用Sinusoidal编码给嵌入进去”。

​ 另一个更为人所知的名字就是：位置编码（position encoding），与当时想编码相对位置的想法不同，这里的位置编码只是单纯的将输入变量的低频变化，利用高频率的三角函数给放大到高频，不然神经网络低通滤波的动力学特性会导致效果的退化。实际上这个议题在“Neural Representations”这个方向下得到了更详尽的讨论，感兴趣可以参见Fourier Feature Networks，SIREN。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def get_embedder(multires, i=0):
    if i == -1:
        return nn.Identity(), 3
    
    embed_kwargs = {
                'include_input' : True,
                'input_dims' : 3,
                'max_freq_log2' : multires-1,
                'num_freqs' : multires,
                'log_sampling' : True,
                'periodic_fns' : [torch.sin, torch.cos],
    }
    
    embedder_obj = Embedder(**embed_kwargs)
    embed = lambda x, eo=embedder_obj : eo.embed(x)
    return embed, embedder_obj.out_dim
    
# Positional encoding (section 5.1)
class Embedder:
    def __init__(self, **kwargs):
        self.kwargs = kwargs
        self.create_embedding_fn()
        
    def create_embedding_fn(self):
        embed_fns = []
        d = self.kwargs['input_dims']
        out_dim = 0
        if self.kwargs['include_input']:
            embed_fns.append(lambda x : x)
            out_dim += d
            
        max_freq = self.kwargs['max_freq_log2']
        N_freqs = self.kwargs['num_freqs']
        
        if self.kwargs['log_sampling']:
            freq_bands = 2.**torch.linspace(0., max_freq, steps=N_freqs)
        else:
            freq_bands = torch.linspace(2.**0., 2.**max_freq, steps=N_freqs)
            
        for freq in freq_bands:
            for p_fn in self.kwargs['periodic_fns']:
                embed_fns.append(lambda x, p_fn=p_fn, freq=freq : p_fn(x * freq))
                out_dim += d
                    
        self.embed_fns = embed_fns
        self.out_dim = out_dim
        
    def embed(self, inputs):
        return torch.cat([fn(inputs) for fn in self.embed_fns], -1)

​ 上面是embed如何实现的代码，这种实现风格在后面也会经常出现。当实现embed时，会先调用get_embedder()，其本身并不会传太多冗余的参数，或者直接传入一个args，大部分embed直接需要的配置都会在子函数里现场定义一个字典embed_kwargs，然后直接用Python动态传参的性质传入类实现。

​ 接着看Embedder类的实现，基本就是从kwargs取参然后完成目的，其实这里有一个有点呆的地方：它最后是初始化的时候用lambda函数给出一个torch.sin(x · freq), torch.cos(x · freq)的列表，忠实的用一个列表生成式遍历，然后计算fn(inputs)，然后torch.cat()在一起。其实是可以写成并行的写法，可能会更有效率一点点。

1
2
3
4
5
6
input_ch_views = 0
embeddirs_fn = None
if args.use_viewdirs:
    embeddirs_fn, input_ch_views = get_embedder(args.multires_views, args.i_embed)
output_ch = 5 if args.N_importance > 0 else 4
skips = [4]

​ 然后，又多定义了一个为了”viewdirs”的embedder，以及给出了一些如output_ch，skips的设置。为了搞清楚这是在干嘛，就要在这里给出NeRF整体的网络结构了：

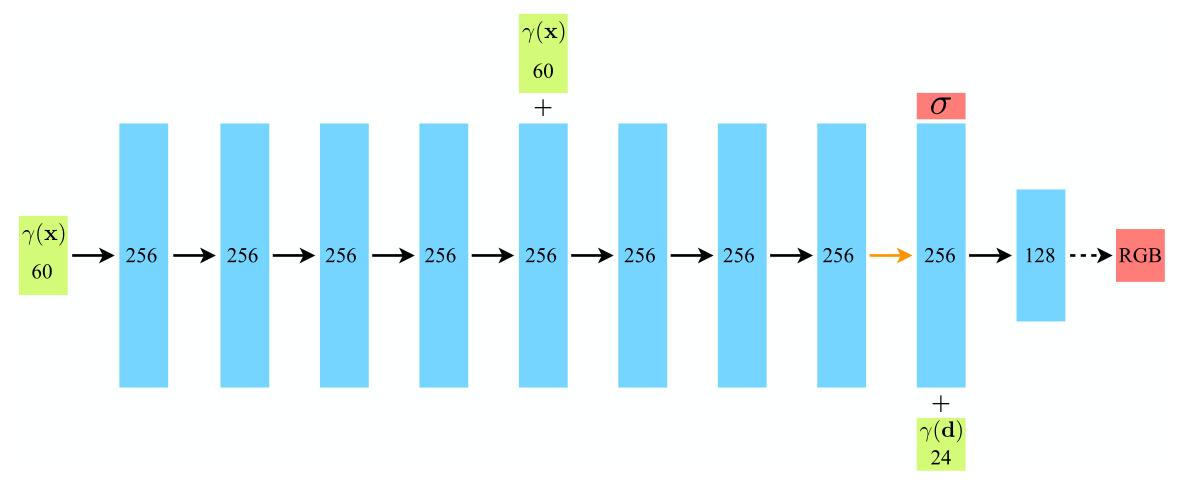
​ 可以看出，NeRF并不是真的把$(x,y,z,\theta,\phi)$直接输入，然后8层MLP直接梭哈。它是先输入$\mathbf{x}=(x,y,z)$位置编码后成为一个长为60的向量，然后送入MLP，中途设一个skips决定跳连位置。

上图中$\gamma(\mathbf{x})$设置的$L=10$，每个频率编码一个正弦和余弦，输入维数为3，所以最后2×3×10=60。如果还保留原有的输入，那就是60+3=63。

​ 8层以后，最后再过一层，映成1维的$\sigma$（代码里称其为alpha而不是sigma。）然后计算$\sigma$的特征向量不要扔，裹上面包糠炸至金黄色，跟$\gamma(\mathbf{d}),\mathbf{d}=(\theta,\phi)$拼一下，然后再过一层线性层，输出RGB，这一步即是前文说的view-dependent color。

编码方向的$\gamma(\cdot)$的$L=4$

​ 所以NeRF这个结构本身的整个PyTorch实现为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class NeRF(nn.Module):
    def __init__(self, D=8, W=256, input_ch=3, input_ch_views=3, output_ch=4, skips=[4], use_viewdirs=False):
        """ 
        """
        super(NeRF, self).__init__()
        self.D = D
        self.W = W
        self.input_ch = input_ch
        self.input_ch_views = input_ch_views
        self.skips = skips
        self.use_viewdirs = use_viewdirs
        
        self.pts_linears = nn.ModuleList(
            [nn.Linear(input_ch, W)] + [nn.Linear(W, W) if i not in self.skips else nn.Linear(W + input_ch, W) for i in range(D-1)])
        
        ### Implementation according to the official code release (https://github.com/bmild/nerf/blob/master/run_nerf_helpers.py#L104-L105)
        self.views_linears = nn.ModuleList([nn.Linear(input_ch_views + W, W//2)])

        ### Implementation according to the paper
        # self.views_linears = nn.ModuleList(
        #     [nn.Linear(input_ch_views + W, W//2)] + [nn.Linear(W//2, W//2) for i in range(D//2)])
        
        if use_viewdirs:
            self.feature_linear = nn.Linear(W, W)
            self.alpha_linear = nn.Linear(W, 1)
            self.rgb_linear = nn.Linear(W//2, 3)
        else:
            self.output_linear = nn.Linear(W, output_ch)

    def forward(self, x):
        input_pts, input_views = torch.split(x, [self.input_ch, self.input_ch_views], dim=-1)
        h = input_pts
        for i, l in enumerate(self.pts_linears):
            h = self.pts_linears[i](h)
            h = F.relu(h)
            if i in self.skips:
                h = torch.cat([input_pts, h], -1)

        if self.use_viewdirs:
            alpha = self.alpha_linear(h)
            feature = self.feature_linear(h)
            h = torch.cat([feature, input_views], -1)
        
            for i, l in enumerate(self.views_linears):
                h = self.views_linears[i](h)
                h = F.relu(h)

            rgb = self.rgb_linear(h)
            outputs = torch.cat([rgb, alpha], -1)
        else:
            outputs = self.output_linear(h)

        return outputs

​ 所以这个网络的输入维度为[B, 6]，6为input_ch + input_ch_views。有人可能会疑惑input_ch_views为什么是3维，不是只有$\theta, \phi$吗？但实际代码实现时没有采用极坐标的表示，采用了基本的点斜式来表示一个三维直线，在get_rays_np()中可以看到：

1
dirs = np.stack([(i-K[0][2])/K[0][0], -(j-K[1][2])/K[1][1], -np.ones_like(i)], -1)

​ 然后输出的维度固定为[B, 4]，前三维是RGB，最后是体密度。

​ 注意到，outputs其实是通过一个output_linear()直接计算出来的，它并没有限制值域。这个部分是后面会提到的raw2outputs()函数中进行的，前三维的颜色会被$\mathrm{sigmoid}(\cdot)$到0~1，体密度会直接$\mathrm{ReLU}(\cdot)$到0至无穷大。

​ create_nerf()中有一行：output_ch = 5 if args.N_importance > 0 else 4。这其实是一个还未修复的失误，可能是早些时候NeRF的作者们在尝试层次化体素采样（后面会提到）时，多输出一个变量来作guidance，或者什么别的原因，导致在应用层次体素采样时，输出维数定为5。但由于后面对NeRF输出的操作都是[:3]或[3]的索引，所以其实设为5也不会有什么影响。

​ 实际上这个结构并不简单，作者们是做了很多消融才最后给定的。关于这个结构的一些深意我们后面再讨论。

层次体素采样

​ 说回代码，现在已经给出个NeRF网络创建的条件，于是后面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
model = NeRF(D=args.netdepth, W=args.netwidth,
             input_ch=input_ch, output_ch=output_ch, skips=skips,
             input_ch_views=input_ch_views, use_viewdirs=args.use_viewdirs).to(device)
grad_vars = list(model.parameters())

model_fine = None
if args.N_importance > 0:
    model_fine = NeRF(D=args.netdepth_fine, W=args.netwidth_fine,
                      input_ch=input_ch, output_ch=output_ch, skips=skips,
                      input_ch_views=input_ch_views, use_viewdirs=args.use_viewdirs).to(device)
    grad_vars += list(model_fine.parameters())

​ 可以看出上述代码实例化了一个NeRF的模型，但有一个分支，是关于args.N_importance的，如果这个值大于0，会再实例化一个model_fine出来，同时将model_fine的参数也加入要求梯度的变量grad_vars中。

​ 这个model_fine实际上是在做“分层体素抽样（hierarchical volume sampling）”，这是一种很直接的优化。具体来说，我们实例化两个模型。一个是粗糙（“coarse”），一个是精细（“fine”）的。我们同时训练它们，先沿着选择的光线的方向随机$N_c$个样本，查询其$T_i\left( 1-e^{-\sigma _i\delta _i} \right) $，记其为$w_i$。由于$w_i$可以保证为非负的，所以我们可以直接归一化为：

​ 然后，我们就得到了沿着这条射线的$\hat{w}_i$的概率密度函数了。这些$\hat{w}_i$是有大有小的，大的说明此处是有物体/密度大，小说明此处是空白的/无意义的。之后我们通过逆变换采样，从这个分布中再采样$N_f$个样本，供model_fine去训练。所以此时整个损失函数为：

​ 最后的渲染结果我们只要fine网络的输出就可以了。这种做法本身是为了避免在没有物体或有遮挡的地方重复采样，那样是没有意义的。这个操作的思想和重要性采样（importance sampling）是一样的。

​ 在实现时，采样$N_f$个点靠的是run_nerf_helper.py中的sample_pdf()函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# Hierarchical sampling (section 5.2)
def sample_pdf(bins, weights, N_samples, det=False, pytest=False):
    # Get pdf
    weights = weights + 1e-5 # prevent nans
    pdf = weights / torch.sum(weights, -1, keepdim=True)
    cdf = torch.cumsum(pdf, -1)
    cdf = torch.cat([torch.zeros_like(cdf[...,:1]), cdf], -1)  # (batch, len(bins))

    # Take uniform samples
    if det:
        u = torch.linspace(0., 1., steps=N_samples)
        u = u.expand(list(cdf.shape[:-1]) + [N_samples])
    else:
        u = torch.rand(list(cdf.shape[:-1]) + [N_samples])

    # Pytest, overwrite u with numpy's fixed random numbers
    if pytest:
        np.random.seed(0)
        new_shape = list(cdf.shape[:-1]) + [N_samples]
        if det:
            u = np.linspace(0., 1., N_samples)
            u = np.broadcast_to(u, new_shape)
        else:
            u = np.random.rand(*new_shape)
        u = torch.Tensor(u)

    # Invert CDF
    u = u.contiguous()
    inds = torch.searchsorted(cdf, u, right=True)
    below = torch.max(torch.zeros_like(inds-1), inds-1)
    above = torch.min((cdf.shape[-1]-1) * torch.ones_like(inds), inds)
    inds_g = torch.stack([below, above], -1)  # (batch, N_samples, 2)

    # cdf_g = tf.gather(cdf, inds_g, axis=-1, batch_dims=len(inds_g.shape)-2)
    # bins_g = tf.gather(bins, inds_g, axis=-1, batch_dims=len(inds_g.shape)-2)
    matched_shape = [inds_g.shape[0], inds_g.shape[1], cdf.shape[-1]]
    cdf_g = torch.gather(cdf.unsqueeze(1).expand(matched_shape), 2, inds_g)
    bins_g = torch.gather(bins.unsqueeze(1).expand(matched_shape), 2, inds_g)

    denom = (cdf_g[...,1]-cdf_g[...,0])
    denom = torch.where(denom<1e-5, torch.ones_like(denom), denom)
    t = (u-cdf_g[...,0])/denom
    samples = bins_g[...,0] + t * (bins_g[...,1]-bins_g[...,0])

    return samples

​ 为了理解这几行代码，我们需要理解逆变换采样。

​ 假设随机变量$X\sim U(0,1)$，一个待求的随机变量$Y$的分布函数为$F_Y(y)$，那么$F_Y(y)$可以由$F_{Y}^{-1}\left( X \right) $这个随机变量函数直接给出。原因是$F_Y\left( y \right) =p\left( Y\le y \right) =p\left( F_{Y}^{-1}\left( X \right) \le y \right)$，对不等式两边同时作用$F_Y(\cdot)$，它是一个单增函数。所以化为$p\left( X\le F_Y\left( y \right) \right) $，又因为均匀分布的分布函数满足$p\left( X\le x \right) =x$，所以式子最后又回到了$F_Y\left( y \right)$。

​ 因为一般能够直接生成的随机数都是均匀分布，所以上面的这个观察就非常有用。只需要生成一批均匀分布的随机数，比如$X$，想要的$Y$就可以通过直接计算$F_{Y}^{-1}\left( X \right) $得出来。例如$X=0.15$，此时我有$F_Y(\cdot)$，我就沿着$y=0.15$找$F_Y(\cdot)$什么时候为0.15，此时的自变量取值即为所求。

​ 体现在上面的代码上就是先对输入的weights（也就是密度）作归一化。然后求cumsum（各行累加值）得到cdf（概率分布函数），注意要在前面加个零以满足定义。然后随机出均匀分布的u，用torch.searchsorted()找到u里每个随机数所在的区间。例如u里的一个数是0.35，那么由于cdf是离散的。其实不一定能有正好等于0.35的值，所以就四舍五入。找出cdf中最后一个小于0.35的索引（比如cdf取0.32时索引为11）和第一个大于0.35的索引（比如cdf取0.40时索引为12）。然后在这个区间，即0.32和0.40里，进行线性插值，即(0.35-0.32)/(0.40-0.32)=0.375，t表示的就是插值后的相对位置：

​ 最后逆变换采样的结果即为$\mathrm{samples}=\mathrm{bins}_\mathrm{g[}…,0]+t\times (\mathrm{bins}_\mathrm{g[}…,1]-\mathrm{bins}_\mathrm{g[}…,0])$。

​ 这样，就可以通过“coarse”模型输出的那一条光线上$N_c$个采样点输出的$\sigma$，采样出$N_f$个更值得采样的点。

network_query_fn()

​ 然后，create_nerf()最后又创建了一个匿名函数：network_query_fn：

1
network_query_fn = lambda inputs, viewdirs, network_fn : run_network(inputs, viewdirs, network_fn, embed_fn=embed_fn, embeddirs_fn=embeddirs_fn, netchunk=args.netchunk)

​ 该匿名函数调用了另一个run_network()函数，其定义为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def run_network(inputs, viewdirs, fn, embed_fn, embeddirs_fn, netchunk=1024*64):
    """Prepares inputs and applies network 'fn'.
    """
    inputs_flat = torch.reshape(inputs, [-1, inputs.shape[-1]])
    embedded = embed_fn(inputs_flat)

    if viewdirs is not None:
        input_dirs = viewdirs[:,None].expand(inputs.shape)
        input_dirs_flat = torch.reshape(input_dirs, [-1, input_dirs.shape[-1]])
        embedded_dirs = embeddirs_fn(input_dirs_flat)
        embedded = torch.cat([embedded, embedded_dirs], -1)

    outputs_flat = batchify(fn, netchunk)(embedded)
    outputs = torch.reshape(outputs_flat, list(inputs.shape[:-1]) + [outputs_flat.shape[-1]])
    return outputs

​ 我们可以发现，直接定义一个句柄函数network_query_fn()可以直接避免后面再次传入embed_fn, embeddirs_fn, netchunk。只需每次传入inputs, viewdirs, fn即可。我们后面会具体讨论inputs和viewdirs。run_network()具体执行了$\gamma(\cdot)$操作，然后对输入数据进行分块批量运算。这一行代码封装了真正运算的那一步：

1
outputs_flat = batchify(fn, netchunk)(embedded)

​ batchify()使用闭包来返回一个函数：

1
2
3
4
5
6
7
8
def batchify(fn, chunk):
    """Constructs a version of 'fn' that applies to smaller batches.
    """
    if chunk is None:
        return fn
    def ret(inputs):
        return torch.cat([fn(inputs[i:i+chunk]) for i in range(0, inputs.shape[0], chunk)], 0)
    return ret

​ 闭包的使用，可以让ret()函数得以访问batchify()所传入的局部变量fn, chunk。batchify(fn, netchunk)(embedded) 使用圆括号调用了所返回的函数ret()，将 embedded 作为参数传递给了 ret() 函数，再用一个列表生成式进行批量运算。

​ 这里的fn，一般都是model=NeRF()时所实例化的那个model，其继承自nn.Module，所以会自动调用forward()函数，完成前向运算。

​ 这一步完成以后，就是一些和checkpoints相关的代码。然后将后面渲染时所用的变量注册进字典render_kwargs_train和render_kwargs_test中，最后悉数返回。

get_rays()

​ 当从create_nerf()返回后，程序将near和far两个值更新进render_kwargs两个字典里。之后是一个render_only的分支，如果我们不需要训练，想直接做inference，程序就会进入这个分支然后结束。

​ 之后no_batching选项会导引光线的生成，如果为true，那么每次都只是随机抽一张图片，然后计算这一张图片发出的光线；如果是false，那么会在正式训练前先遍历所有位姿矩阵，得到所有的rays，然后在训练时从rays里切片得到每个batch。

​ 生成光线，其实生成的是$\mathbf{r}\left( t \right) =\mathbf{o}+t\mathbf{d}$中的$\mathbf{o}$和$\mathbf{d}$。用到的函数为get_rays_np()和get_rays()，后者是torch实现，前者是numpy实现，逻辑都是一样的。这里选取前者：

1
2
3
4
5
6
7
8
def get_rays_np(H, W, K, c2w):
    i, j = np.meshgrid(np.arange(W, dtype=np.float32), np.arange(H, dtype=np.float32), indexing='xy')
    dirs = np.stack([(i-K[0][2])/K[0][0], -(j-K[1][2])/K[1][1], -np.ones_like(i)], -1)
    # Rotate ray directions from camera frame to the world frame
    rays_d = np.sum(dirs[..., np.newaxis, :] * c2w[:3,:3], -1)  # dot product, equals to: [c2w.dot(dir) for dir in dirs]
    # Translate camera frame's origin to the world frame. It is the origin of all rays.
    rays_o = np.broadcast_to(c2w[:3,-1], np.shape(rays_d))
    return rays_o, rays_d

​ 我们发现输入为图像高H，宽W，相机内参K和相机外参的逆c2w（camera to world）。所以get_rays_np()的流程相当于上文“相机与变换”的逆过程。i, j = np.meshgrid()首先生成像素平面上的索引，即：

1
2
3
4
5
6
7
8
9
i = [[0., 1., ..., W-1.],
     [0., 1., ..., W-1.],
     ...
     [0., 1., ..., W-1.]]

j = [[0., 0., 0., 0.],
     [1., 1., 1., 1.],
     ...
     [H-1., H-1., H-1., H-1.]]

​ 然后就像推导相机内参时那样，投影到平面上的点$(x,y,1)$可以按如下计算：

​ 其中$u_0,v_0,f_x,f_y$均是内参矩阵$K$中的元素。由于NeRF和OpenGL所用的坐标系和上式隐含的坐标系有略微区别（RDF->RUB），即$y,z$轴上差一个负号。所以dirs里也加了两个负号。

​ 显然，dirs是定义在相机坐标系下的表示。此时其维数为[H, W, 3]，通过增加一个辅助维度变为[H, W, 1, 3]，可以方便实现其与c2w矩阵的相乘。此时计算出的结果就是世界坐标系下的rays_d，表示光线的方向。rays_o即相机此时的位置，由c2w矩阵最后一列直接给出，只需与rays_d广播成相同的形状即可。

​ get_rays_np()的返回值自动被打包成元组，在train()函数准备ray-batch时：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Prepare raybatch tensor if batching random rays
N_rand = args.N_rand
use_batching = not args.no_batching
if use_batching:
    # For random ray batching
    print('get rays')
    rays = np.stack([get_rays_np(H, W, K, p) for p in poses[:,:3,:4]], 0) # [N, ro+rd, H, W, 3]
    print('done, concats')
    rays_rgb = np.concatenate([rays, images[:,None]], 1) # [N, ro+rd+rgb, H, W, 3]
    rays_rgb = np.transpose(rays_rgb, [0,2,3,1,4]) # [N, H, W, ro+rd+rgb, 3]
    rays_rgb = np.stack([rays_rgb[i] for i in i_train], 0) # train images only
    rays_rgb = np.reshape(rays_rgb, [-1,3,3]) # [(N-1)*H*W, ro+rd+rgb, 3]
    rays_rgb = rays_rgb.astype(np.float32)
    print('shuffle rays')
    np.random.shuffle(rays_rgb)

    print('done')
    i_batch = 0

# Move training data to GPU
if use_batching:
    images = torch.Tensor(images).to(device)
poses = torch.Tensor(poses).to(device)
if use_batching:
    rays_rgb = torch.Tensor(rays_rgb).to(device)

​ 其返回的元组会作为列表生成式的元素，自动合成一个列表作为np.stack()的输入。所以维度为[N, 2, H, W, 3]，2即rays_o和rays_d。这里的N即图片的数量/位姿的数量，接下来会将图片也拼进来（正好RGB也是3个维度）。处理得到rays_rgb，这个数组就可以记录每张图片每个像素点的光线（相机坐标和方向）以及其颜色（即ground truth）。

​ 由于我们知道NeRF本身就是几层MLP，所以我们会将rays_rgb的维数reshape一下，由于1张图片会被hold out出来作测试。所以最后得到的输入的维数即[(N-1)×H×W, 3, 3]，其中第一个3代表rays_o, rays_d和rgb。

​ 在进入训练迭代的循环后，每次都会从中选取N_rand个光线进行训练。

1
2
3
4
5
6
7
8
9
10
11
12
if use_batching:
    # Random over all images
    batch = rays_rgb[i_batch:i_batch+N_rand] # [B, 2+1, 3*?]
    batch = torch.transpose(batch, 0, 1)
    batch_rays, target_s = batch[:2], batch[2]

    i_batch += N_rand
    if i_batch >= rays_rgb.shape[0]:
        print("Shuffle data after an epoch!")
        rand_idx = torch.randperm(rays_rgb.shape[0])
        rays_rgb = rays_rgb[rand_idx]
        i_batch = 0

​ 如果不预先批量化光线，那么就是每次从一张图片的所有光线中随机抽。代码逻辑是类似的，这里就不赘述了。

render()

​ 接下来的render()函数完成了实际意义上的计算：

1
rgb, disp, acc, extras = render(H, W, K, chunk=args.chunk, rays=batch_rays, verbose=i < 10, retraw=True,  **render_kwargs_train)

​ 我们观察一下render()函数在做什么：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
def render(H, W, K, chunk=1024*32, rays=None, c2w=None, ndc=True,
                  near=0., far=1.,
                  use_viewdirs=False, c2w_staticcam=None,
                  **kwargs):
    if c2w is not None:
        # special case to render full image
        rays_o, rays_d = get_rays(H, W, K, c2w)
    else:
        # use provided ray batch
        rays_o, rays_d = rays

    if use_viewdirs:
        # provide ray directions as input
        viewdirs = rays_d
        if c2w_staticcam is not None:
            # special case to visualize effect of viewdirs
            rays_o, rays_d = get_rays(H, W, K, c2w_staticcam)
        viewdirs = viewdirs / torch.norm(viewdirs, dim=-1, keepdim=True)
        viewdirs = torch.reshape(viewdirs, [-1,3]).float()

    sh = rays_d.shape # [..., 3]
    if ndc:
        # for forward facing scenes
        rays_o, rays_d = ndc_rays(H, W, K[0][0], 1., rays_o, rays_d)

    # Create ray batch
    rays_o = torch.reshape(rays_o, [-1,3]).float()
    rays_d = torch.reshape(rays_d, [-1,3]).float()

    near, far = near * torch.ones_like(rays_d[...,:1]), far * torch.ones_like(rays_d[...,:1])
    rays = torch.cat([rays_o, rays_d, near, far], -1)
    if use_viewdirs:
        rays = torch.cat([rays, viewdirs], -1)

    # Render and reshape
    all_ret = batchify_rays(rays, chunk, **kwargs)
    for k in all_ret:
        k_sh = list(sh[:-1]) + list(all_ret[k].shape[1:])
        all_ret[k] = torch.reshape(all_ret[k], k_sh)

    k_extract = ['rgb_map', 'disp_map', 'acc_map']
    ret_list = [all_ret[k] for k in k_extract]
    ret_dict = {k : all_ret[k] for k in all_ret if k not in k_extract}
    return ret_list + [ret_dict]

​ 实际上这里的逻辑很像run_network()，run_network()对输入进行了预处理，然后用一个batchify()封装了计算的过程。在这里render()这里，c2w一般是不输入的，会直接将输入的batch_rays拆成rays_o和rays_d。然后将rays_d作归一化，归一化后记作新的viewdirs，作为$\gamma(\mathbf{d})$中的$\mathbf{d}$。

​ 然后如果要作ndc，那么会将现在在世界坐标系下的rays_o和rays_d都作一次对应的透视变换。ndc和use_viewdirs实际上是在render_train_kwargs里的。对于LLFF格式的数据集，ndc是默认True的。关于这里进行透视变换的原因，在前文已经得到了阐述。ndc_rays()忠实的执行了前文所说的透视变换以及光线原点的搬迁：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def ndc_rays(H, W, focal, near, rays_o, rays_d):
    # Shift ray origins to near plane
    t = -(near + rays_o[...,2]) / rays_d[...,2]
    rays_o = rays_o + t[...,None] * rays_d
    
    # Projection
    o0 = -1./(W/(2.*focal)) * rays_o[...,0] / rays_o[...,2]
    o1 = -1./(H/(2.*focal)) * rays_o[...,1] / rays_o[...,2]
    o2 = 1. + 2. * near / rays_o[...,2]

    d0 = -1./(W/(2.*focal)) * (rays_d[...,0]/rays_d[...,2] - rays_o[...,0]/rays_o[...,2])
    d1 = -1./(H/(2.*focal)) * (rays_d[...,1]/rays_d[...,2] - rays_o[...,1]/rays_o[...,2])
    d2 = -2. * near / rays_o[...,2]
    
    rays_o = torch.stack([o0,o1,o2], -1)
    rays_d = torch.stack([d0,d1,d2], -1)
    
    return rays_o, rays_d

​ 然后，render()里的一些其他代码，会将near, far（它们是create_nerf()后被追加进字典render_train_kwargs的），viewdirs一并跟rays_o, rays_d拼在一起。这其实有点麻，它拼在一起只是为了少传个参，函数接口好看一些。因为实际上在真正处理光线的batchify_rays()里：

1
2
3
4
5
6
7
8
9
10
11
12
13
def batchify_rays(rays_flat, chunk=1024*32, **kwargs):
    """Render rays in smaller minibatches to avoid OOM.
    """
    all_ret = {}
    for i in range(0, rays_flat.shape[0], chunk):
        ret = render_rays(rays_flat[i:i+chunk], **kwargs)
        for k in ret:
            if k not in all_ret:
                all_ret[k] = []
            all_ret[k].append(ret[k])

    all_ret = {k : torch.cat(all_ret[k], 0) for k in all_ret}
    return all_ret

​ 会继续调用render_rays()：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
def render_rays(ray_batch,
                network_fn,
                network_query_fn,
                N_samples,
                retraw=False,
                lindisp=False,
                perturb=0.,
                N_importance=0,
                network_fine=None,
                white_bkgd=False,
                raw_noise_std=0.,
                verbose=False,
                pytest=False):
    
    N_rays = ray_batch.shape[0]
    rays_o, rays_d = ray_batch[:,0:3], ray_batch[:,3:6] # [N_rays, 3] each
    viewdirs = ray_batch[:,-3:] if ray_batch.shape[-1] > 8 else None
    bounds = torch.reshape(ray_batch[...,6:8], [-1,1,2])
    near, far = bounds[...,0], bounds[...,1] # [-1,1]

    t_vals = torch.linspace(0., 1., steps=N_samples)
    if not lindisp:
        z_vals = near * (1.-t_vals) + far * (t_vals)
    else:
        z_vals = 1./(1./near * (1.-t_vals) + 1./far * (t_vals))

    z_vals = z_vals.expand([N_rays, N_samples])

    if perturb > 0.:...

        # Pytest, overwrite u with numpy's fixed random numbers
        if pytest:...

        z_vals = lower + (upper - lower) * t_rand

    pts = rays_o[...,None,:] + rays_d[...,None,:] * z_vals[...,:,None] # [N_rays, N_samples, 3]

#     raw = run_network(pts)
    raw = network_query_fn(pts, viewdirs, network_fn)
    rgb_map, disp_map, acc_map, weights, depth_map = raw2outputs(raw, z_vals, rays_d, raw_noise_std, white_bkgd, pytest=pytest)

    if N_importance > 0:...

    ret = {'rgb_map' : rgb_map, 'disp_map' : disp_map, 'acc_map' : acc_map}
    if retraw:
        ret['raw'] = raw
    if N_importance > 0:...

    for k in ret:
        if (torch.isnan(ret[k]).any() or torch.isinf(ret[k]).any()) and DEBUG:
            print(f"! [Numerical Error] {k} contains nan or inf.")

    return ret

​ 刚才刚拼在一起的rays，viewdirs，near，far，传进render_rays()里时，第一件事就是再拆回来。然后，我们会沿着光线的方向进行采样，有两种方式：线性插值，倒数线性插值（深度插值）。线性插值就是简单的：

​ 倒数线性插值即：

​ 但这个lindisp（linear disparity）默认是False的，在上文讨论NDC的部分，我们已经讨论了倒数线性插值。所以这个开关只是一个时代的眼泪，其实已经被弃用了。

​ 然后，perturb默认是1，一般都会触发对z_vals的再次扰动。让其不是那么严格均匀的，这也是很合理的一个设置。

​ 然后我们根据$\mathbf{r}\left( t \right) =\mathbf{o}+t\mathbf{d}$，就合成出了一条光线上的N_sample个采样点。现在pts（points）和viewdirs都具备了，直接调用先前封装好的network_query_fn即可进行推理。推理得到的raw其实就是run_network中给出的outputs，其实就是继承自nn.Module的NeRF类forward方法的返回值。我们返回去 重新看一下run_network()：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def run_network(inputs, viewdirs, fn, embed_fn, embeddirs_fn, netchunk=1024*64):
    """Prepares inputs and applies network 'fn'.
    """
    inputs_flat = torch.reshape(inputs, [-1, inputs.shape[-1]])
    embedded = embed_fn(inputs_flat)

    if viewdirs is not None:
        input_dirs = viewdirs[:,None].expand(inputs.shape)
        input_dirs_flat = torch.reshape(input_dirs, [-1, input_dirs.shape[-1]])
        embedded_dirs = embeddirs_fn(input_dirs_flat)
        embedded = torch.cat([embedded, embedded_dirs], -1)

    outputs_flat = batchify(fn, netchunk)(embedded)
    outputs = torch.reshape(outputs_flat, list(inputs.shape[:-1]) + [outputs_flat.shape[-1]])
    return outputs

​ 现在我们知道了，inputs其实就是[N_rays, N_samples, 3]的pts，它会被reshape成[N_rays*N_samples, 3]。viewdirs虽然是[N_rays, 3]，但它会切出一个新的维度然后广播成和inputs一样的大小，然后依旧flat。所以一次MLP处理的数据的“batchsize”就是N_rays×N_samples。一般训练时，一个批量的N_rays默认为1024，一条光线上的N_samples为64。这也是run_network的netchunk默认值取1024×64的原因。

​ 最后输出的raw的维度，也会被reshape回来，即[N_rays, N_samples, 4]。

​ 现在，一切离散化的描述都具备了。最后会由raw2outputs()函数完成最后的计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def raw2outputs(raw, z_vals, rays_d, raw_noise_std=0, white_bkgd=False, pytest=False):
    raw2alpha = lambda raw, dists, act_fn=F.relu: 1.-torch.exp(-act_fn(raw)*dists)

    dists = z_vals[...,1:] - z_vals[...,:-1]
    dists = torch.cat([dists, torch.Tensor([1e10]).expand(dists[...,:1].shape)], -1)  # [N_rays, N_samples]

    dists = dists * torch.norm(rays_d[...,None,:], dim=-1)

    rgb = torch.sigmoid(raw[...,:3])  # [N_rays, N_samples, 3]
    noise = 0.
    if raw_noise_std > 0.:
        noise = torch.randn(raw[...,3].shape) * raw_noise_std

        # Overwrite randomly sampled data if pytest
        if pytest:...

    alpha = raw2alpha(raw[...,3] + noise, dists)  # [N_rays, N_samples]
    # weights = alpha * tf.math.cumprod(1.-alpha + 1e-10, -1, exclusive=True)
    weights = alpha * torch.cumprod(torch.cat([torch.ones((alpha.shape[0], 1)), 1.-alpha + 1e-10], -1), -1)[:, :-1]
    rgb_map = torch.sum(weights[...,None] * rgb, -2)  # [N_rays, 3]

    depth_map = torch.sum(weights * z_vals, -1)
    disp_map = 1./torch.max(1e-10 * torch.ones_like(depth_map), depth_map / torch.sum(weights, -1))
    acc_map = torch.sum(weights, -1)

    if white_bkgd:
        rgb_map = rgb_map + (1.-acc_map[...,None])

    return rgb_map, disp_map, acc_map, weights, depth_map

​ 在这个函数中，局部定义了匿名函数raw2alpha，它是将网络输出的用来当作$\sigma$的那一维，祛负然后计算为$\alpha_i$的。dists是对采样序列作差分，对应公式推导中的$\delta_i$。然后每个点的颜色由输出的用来当作颜色的那三个通道，压进0~1后来表示。

​ 在计算颜色（rgb_map）时，代码实现是按照上文提到的Alpha合成的那个风格来实现的，计算$\alpha_i$和$\prod_{j=1}^{i-1}{\left( 1-\alpha _j \right)}$，和$T_i\left( 1-e^{-\sigma _i\delta _i} \right)$本质是一样的。同时会返回视差图（disp_map），深度图（depth_map），累积图（acc_map）以及每条光线上的采样点计算出的权重$w_i$（weights）。

​ 这里有一个一直存在于render_kwargs_train里的一个参数：white_bkgd，终于用上了。这个参数穿越这么多层堆栈，其实只为了是在那种合成出的数据集格式（blender）下补加一个白色背景。（其实设为false出来的结果也差不多，因为图像本身就是白的，但可能psnr会差一点。）

​ 如果N_importance>0，需要进行重要性采样。那么就会拿刚才的weights作为先前sample_pdf()函数的输入，采样出来新的坐标点，训练，渲染，然后更新{‘rgb_map’, ‘disp_map’, ‘acc_map’}。同时coarse网络计算出的结果会标记为rgb_map_0, disp_map_0, acc_map_0，一块传出去来优化。

​ 历经艰险后，我们终于从一堆函数堆栈里跳出来，回到了train()。核心的优化由下面几行代码完成：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
optimizer.zero_grad()
img_loss = img2mse(rgb, target_s)
loss = img_loss
psnr = mse2psnr(img_loss)

if 'rgb0' in extras:
    img_loss0 = img2mse(extras['rgb0'], target_s)
    loss = loss + img_loss0
    psnr0 = mse2psnr(img_loss0)

loss.backward()
optimizer.step()

# NOTE: IMPORTANT!
###   update learning rate   ###
decay_rate = 0.1
decay_steps = args.lrate_decay * 1000
new_lrate = args.lrate * (decay_rate ** (global_step / decay_steps))
for param_group in optimizer.param_groups:
    param_group['lr'] = new_lrate

​ 注意我们是同时优化了coarse和fine。优化器已经在create_nerf()中将两个网络的参数都加进grad_var中了。

“只要计算图成功传回来梯度，一切都会好起来的。” ——佚名

Try it!

​ 就是为了这碟醋而包的饺子！

​ 首先，我们可以用自己的手机对一个场景拍摄若干照片。由于现在智能手机上的相机都是自动对焦的（AF-S，AF-C），为了避免不必要的麻烦，建议改成手动对焦MF。如果拍摄不同照片时相机的焦距不同，可能会导致糟糕的成像质量。因为这会要求网络拟合的场景随着视角的变化是非刚性的。当然，后面也有改进工作去修改它。

​ 之后，用COLMAP去估计相机位姿等信息。

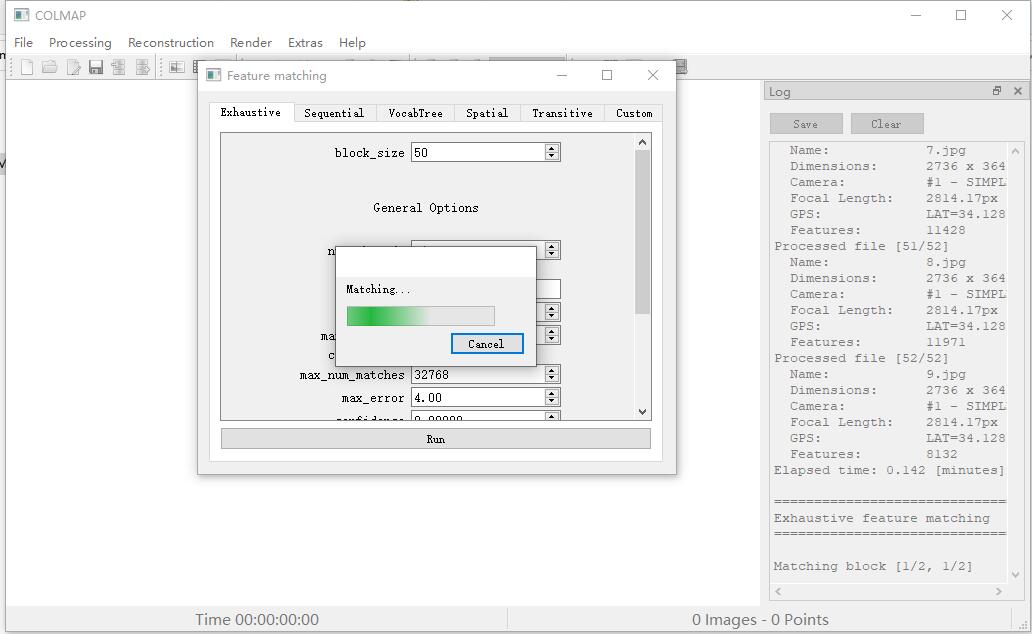
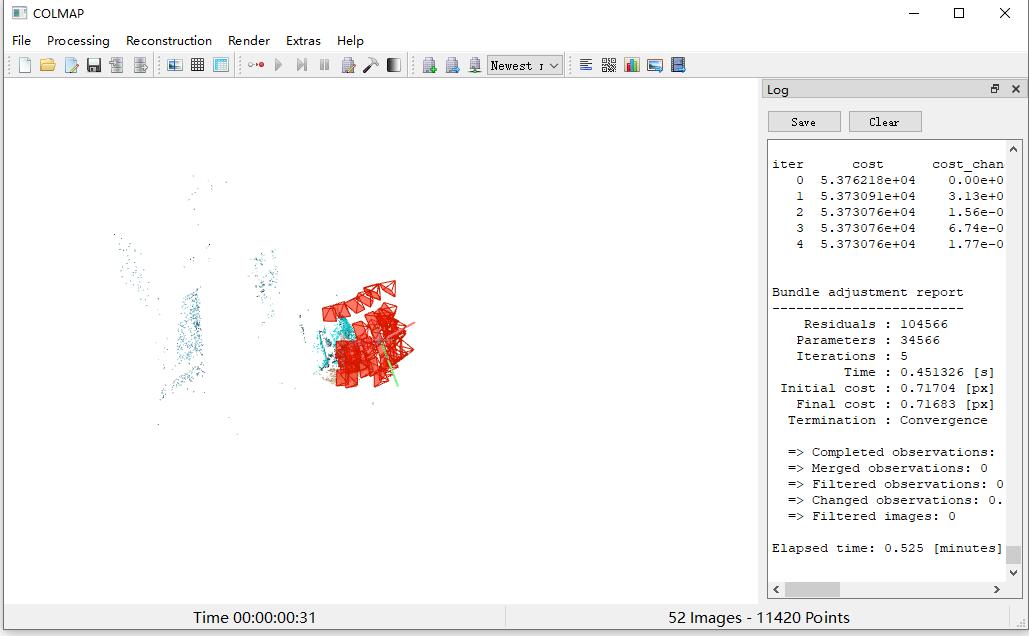
​ 然后使用LLFF中提供的imgs2pose.py，我们就可以得到一个poses_bounds.npy文件：

​ 其是一个N×17的矩阵，里面就是我们要的参数：

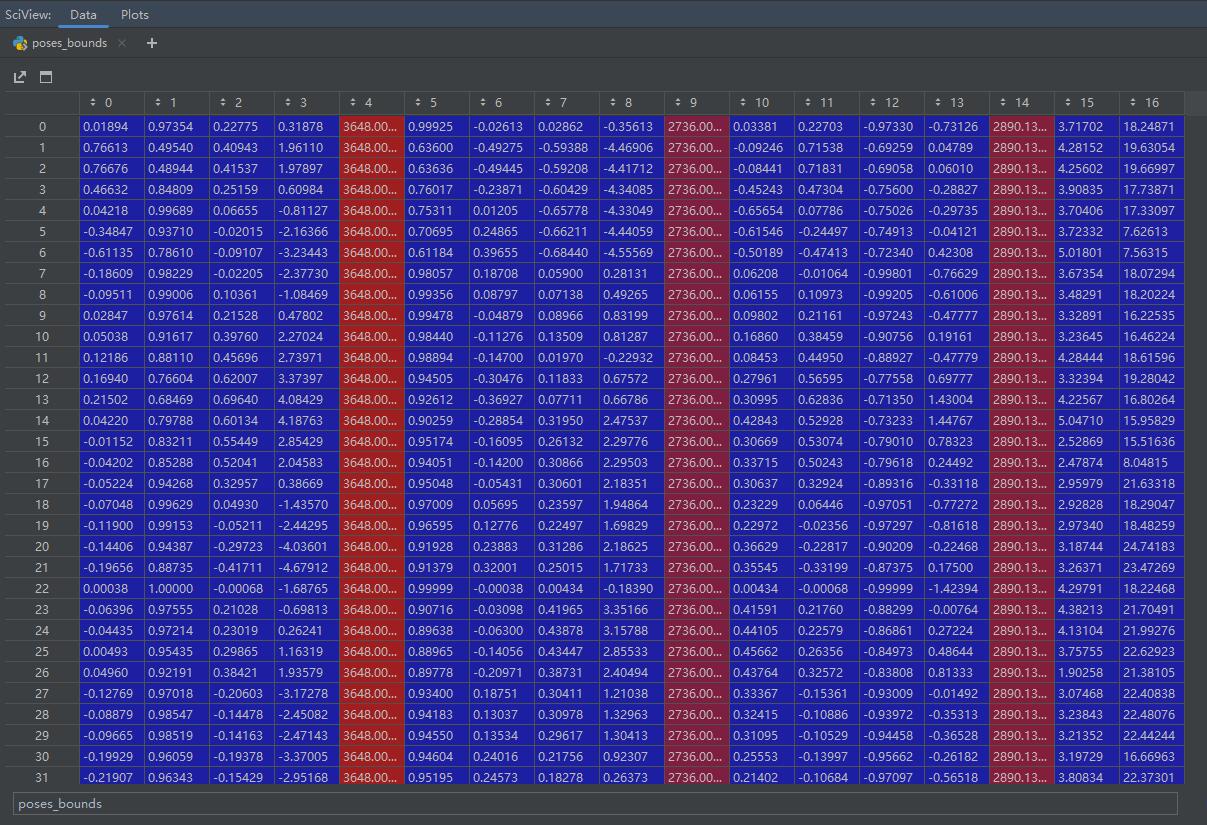
​ 红色的部分从左到右依次是图像的高，宽，和相机焦距。剩下的前三块蓝色部分，根据代码进行重排就可以得到相机的外参矩阵。最后两列是near和far。可以看出手机拍出来的分辨率是很大的，大约4000×3000。所以在训练时会进行8倍的下采样。

​ 然后仿照LLFF格式下的数据集，重写一个自己的数据集下的config，开始训练：

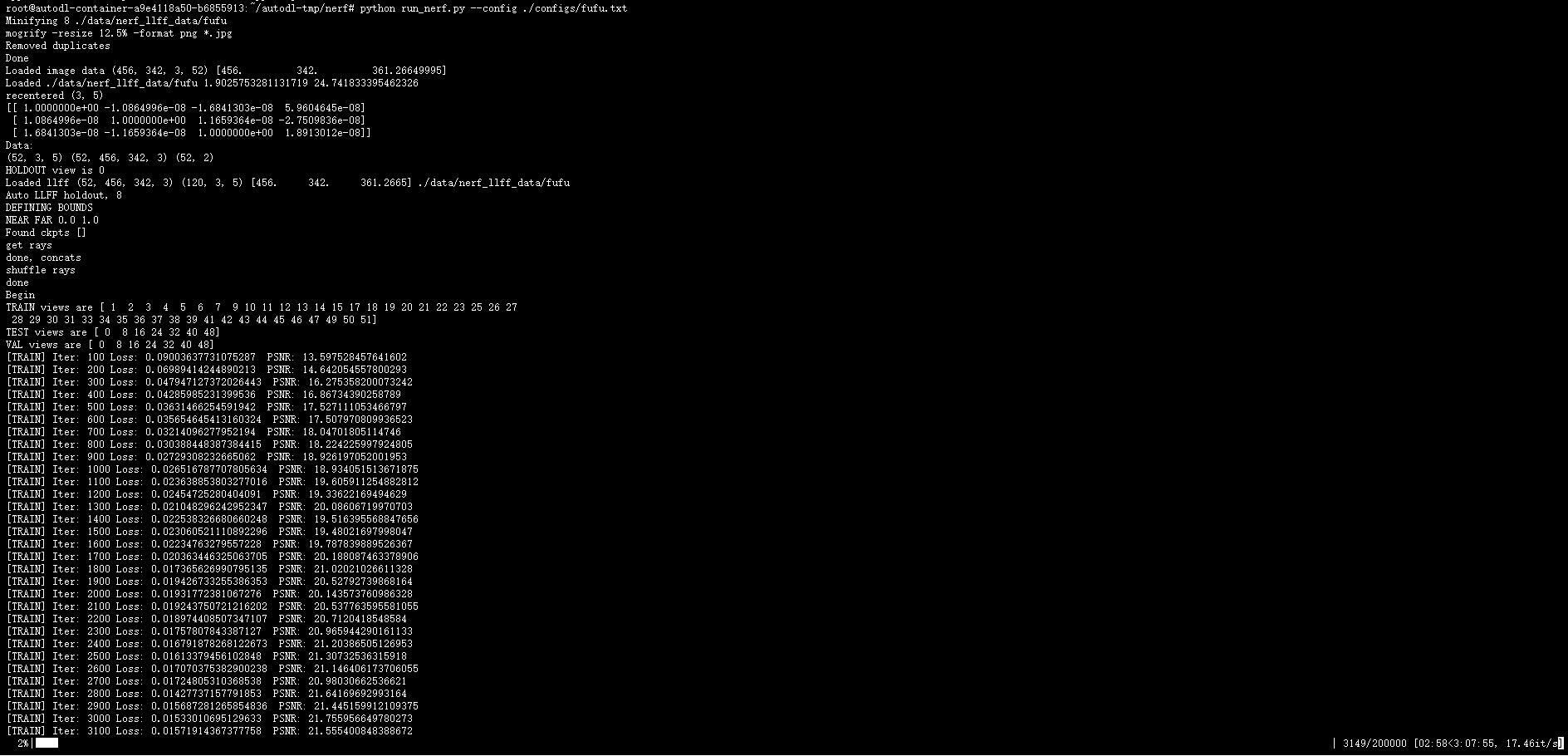
​ 最后剩余的一些生成视角路径的函数会帮忙完成测试：

​ 可见生成的效果还是很不错的。

扩展讨论

​ NeRF惊艳的结果马上引来了大量研究者的关注，随之而来的就是大量的改进工作，和工程上的优化。例如Nerfstudio, Nerfacc，这些库都使用了大量远超我理解范围的技术，对NeRF极其变种的实现做了很多优化。所以如果想实践NeRF，或许可以不从上面vanilla的代码开始了。

​ 如前文所说，NeRF是为了进行新视图合成的，而不是三维重建。因为，NeRF的生成结果，其$\sigma$和$c$，不一定真的是这个场景本身。NeRF只是保证优化出的视图是最贴近的，这并不代表它学到的$\sigma$（也可以叫几何“geometry”）是对的。即如果观察出来的深度图，可能深度图和真实场景相差的非常多，但最后渲染出的RGB图却相差不大。因为损失函数只关心最后计算出的RGB，所以NeRF本身并不能保证学到的几何结构是正确的。一个极端的例子是：如果我拍摄的场景里有一面镜子，那么NeRF是会把镜子重建为一个有着反射高光的几何平面，还是一个有深度，有$\sigma$的几何表示？

​ 在NeRF++中，作者揭示了为什么NeRF可以在学到的几何是错误的情况下，仍然能给出很好的渲染结果（因为一般来说只有几何表示对了才可能有更好的渲染质量）。原因可以概括为，对$\mathbf{x}$和$\mathbf{d}$的处理是不对称的。对位置，它被编码到了更高频的空间（$L=10$）。然而更复杂的几何一般有着更加复杂的颜色变化（或者叫“光场”），而编码$\mathbf{d}$只被映射进了$L=4$，同时只有一层MLP来表示它。所以这保证了对于一般的高光，non-Lambertian的效果，网络可以实现；然而一些更复杂或者充满噪声的光场，网络由于MLP的拟合能力的原因，只能生成一些平滑的光场，这些平滑的光场大多数时候都是符合实际的。所以NeRF其实并不适合三维重建，但后来的NeuS，在NeRF的框架上加入了对几何表面的描述，是真正意义上三维重建的里程碑。

​ 以及在原始的NeRF中，我们一般只会处理有界的合成数据集和“facing-forward”的真实数据集，360°的真实数据集，由于不能应用NDC，所以会有一个两难的境地：如果不建模远景，背景会糊；如果对远景采样，那么在相同采样点数下，近景的分辨率会下降。这个问题先后被NeRF++，Mip-NeRF 360解决。前者是独立的训练两个网络，一个表述近景，一个表述远景，然后将远景进行类似复变函数中学过的反演变换。后者，应该是在Mip-NeRF的基础上做了类似的事情。（Mip-NeRF是一项针对训练和测试时如果分辨率不同，则生成的结果会模糊/锯齿这一问题所进行的改进。）

​ 还有一些对NeRF进行加速的工作，如instant-ngp，其中用到了一种叫作“multi-resolution hash encoding”的技术，同时有着很大的工程价值，我还没看懂。总之它可以将NeRF的生成速度加快很多。

​ 但还有一种路线，是将NeRF作为一个良好的逼近器。例如为了给人脸和人体建模，虽然NeRF本身的几何效果并不佳，但人脸和人体这两个领域本身就有一些参数化的模型如3DMM和SMPL。所以这些参数化模型可以作为一个模板（template），然后NeRF从不同角度射出光线，在模板空间的基础上进行估计。由于人脸和人体一般都会有一些非刚体的特点，所以在这些工作里，往往使用的是Nerfies, D-Nerf，作为整个工作管线的一个小组件。

​ 总之，NeRF的改进一般都是基于一些数学原理或工程优化的角度，我没能把他们每一个都这么细致的看完。TODO list疯狂++。

End

​ 这篇blog详尽的指出了原版的NeRF的原理以及各种技术细节，尤其是在网络里较少被提及NDC和—lindisp。我真希望我一年前做的就是这些，而不是对着model.py“堆积木+缝合”撞大运。

赏

谢谢你请我吃糖果

微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

挟飞仙以遨游，抱明月而长终。<br />知不可乎骤得，托遗响于悲风。