或许我应该给后来的人一些警示,关于“自动调制识别(Automatic Modulation Recognition)”。它有很多的名字,比如“自动调制分类(Automatic Modulation Classification)”,“调制样式识别(modulation identification)”。
从我的教育经历出发,这个问题是一个纯粹的模式识别问题。但实际上我们需要从合适的角度插入一下通信中的一些“domain knowledge”。
为什么是三角函数?
我们从一些信号与系统,数字信号处理的基本知识出发。在学这两门课时,我们有一种冥冥的感觉:“三角函数很重要”。我们可能会说出一些观点来辅证这一点,例如:“三角函数可以构成一组正交基,这在表示信号时很有用。”,“三角函数的傅里叶变换很简单,可以很方便的用来描述特定频率的信号。”
实际上,我们考察$x(t)=e^{j2\pi f_c t}$,我们知道这样的复指数函数的傅里叶变换为$X\left( j\omega \right) = 2\pi \delta \left( \omega -2\pi f_c \right) $。为了让其看得更清楚,我们用频率$f$来作自变量,再由冲激函数的尺缩性质,得$X\left( f \right) =\delta \left( f-f_c \right) $。
我们概括地称这样的复指数函数为“三角函数”,因为傅里叶变换符合线性性质,复指数函数由于欧拉公式的关系,总是可以组合成我们熟悉的三角函数。所以当一个三角函数经过线性系统时,由时域卷积定理,我们知道:
系统的传递函数可以拆解为其幅-频特性和相频特性,同时又因为冲激函数的性质,式子可以重新整理为:
这样就变成了冲激函数乘一对常数,所以最后系统的输出即为:
和$x(t)$相比,整个过程没有改变信号的频率,仅仅是幅度和相位有了变化。这是三角函数优良性质的体现。当我将信息调制到三角函数上时,经过信道这个线性系统。我发射的三角函数的频率并不会变化,只有幅度和相位会发生变化。我只要能获得信道的信息,就可以完成解调了。后面我们会讨论到,其实信道的信息(先验)并不那么容易获得,这里的核心在于“频率不变”。我在A处以100kHz发射一段信号,那么你在B处接受时,也只要处于100kHz即可。
无线电信号?
所以选择三角函数作为描述通信信号,是一个必然的事情。所以,任何一个无线电信号都可以表示为$s(t)=a(t)\mathrm{cos}(2\pi f_0 t+\varphi(t))$。$a(t),\varphi(t)$是人为赋予该信号的幅度调制信息和相位调制信息,我们通过定义不同的$\left\{ a\left( t \right) ,\varphi \left( t \right) \right\} $,就可以实现不同的调制方式。$f_0$我们称为信号载频,或中心频率。关于频率的信息是隐藏在相位调制中的,由于中心频率是一直不变的,所以瞬时频率即相位的变化率:
对上面定义的无线电信号进行离散化,采样间隔为$T_s=1/f_s$。离散化后的式子为:
用索引替代连续时$t$的定义,化简为:
$\omega_0=2\pi f_0 T_s$为数字角频率,由采样定理我们知道,$f_s>2f_0$,所以数字角频率的取值为$0\sim \pi$。接下来,我们用辅助角公式,可以把上面的式子展开:
这个操作的含义很深刻,我们其实可以把它理解中某种“正交分解”。现在$s[n]$被拆解为了两个中心频率$\omega_0$构成的正交基的线性组合。我们记它们的系数为:
其中$I[n]$称为同相(in-phase),$Q[n]$称为正交(Quadrature)。所以自然的,我们可以设想这样的一种调制器:
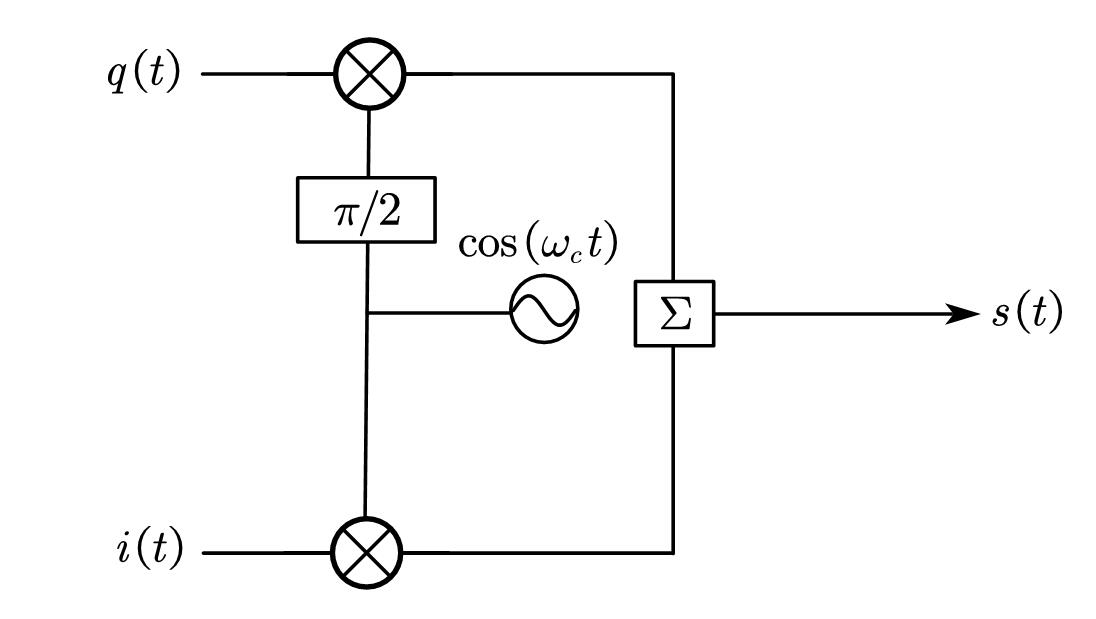
它就可以满足上述公式的构想,我们只需要给定$I[n],Q[n]$,然后给定载波信号的频率$\omega_0$,再用一个移相器来凑$\mathrm{sin(\cdot),cos(\cdot)}$。这就是著名的“IQ调制”。这种架构的提出并不是偶然,其实背后蕴含很深的道理。
比如我们考虑相移键控PSK:$p_{\mathrm{psk}}\left( t \right) =\sum_n{g_{T_s}\left( t-nT_s \right) \exp \left( j\varphi _n \right)}$。在这里:
$T_s$为符号宽度。$\varphi _n\in \left\{ 0,\frac{1}{M}2\pi ,…,\frac{M-1}{M}2\pi \right\} $,为相位调制量。
这里的$g_{T_s}(\cdot)$是基带(矩形)脉冲,我们在后面会连同其他调制方式一起,详细的讨论一下,现在就先习惯它就好。
如果要实现QPSK,即$M=4$,那么根据上面的公式,我们需要生成4个不同的相位(0°,90°,180°,270°)并且能够在正确的时间切换到正确的相位,显而易见的是,当我们要求数据传输的速率越来越快时,这越不容易达到。同样这样也会比较复杂。
然而我们可以利用IQ调制,用两个独立的BPSK($M=2$)来实现QPSK,一个BPSK存在于I通道上,另一个存在于Q通道上。这样每个通道只需处理2个相位(0°和180°),这比直接处理4个相位简单多了。
同样,这种方式可以一次调制两个(独立)的信号,所以有一种理解的角度是:对于单路调制而言,它同时可以调制两个信号,携带的信息量翻倍,而最终调制信号的带宽不变,所以有更高的频率利用率。(这一点实际上是针对相同的调制方式说的。)
现在我们要简单分析一下解调的这个过程:
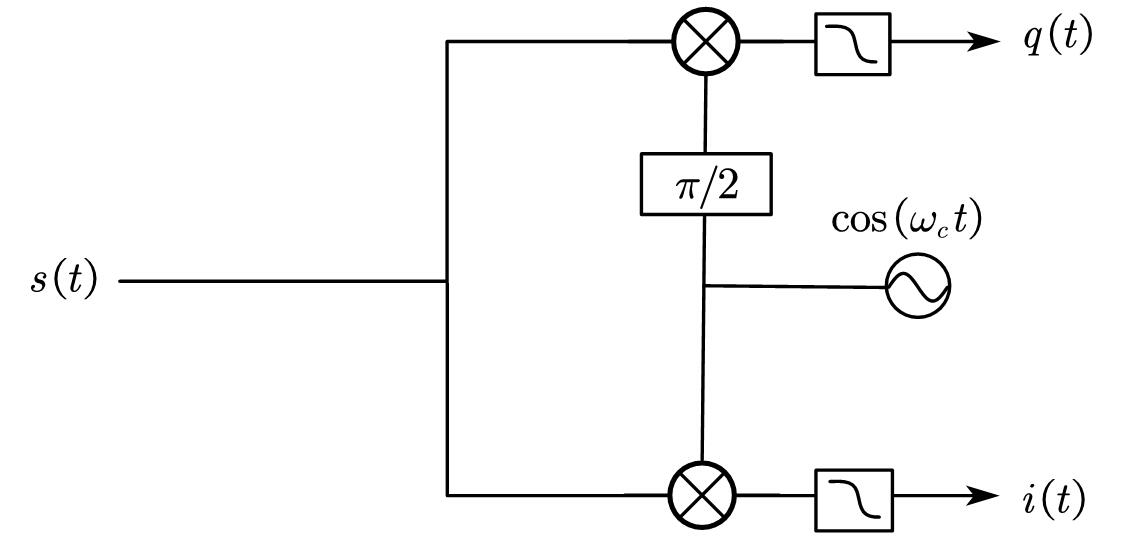
为了叙述的方便,接下来我们仍采用模拟表达式。实际上,考虑接收到的信号$s(t)$,计算:
我们可以发现,产生了一些2次谐波,所以图中用一个低通滤波处理了一下(这里也可以再放大一倍),最后我们就得到了$i(t)=a(t)\mathrm{cos}\varphi (t)$。同理,乘上$\mathrm{sin}(2\pi f_0t)$后,我们也会得到$q(t)$。这样就完成了IQ解调。
刚才我们从发射的角度,得到了一些IQ调制的好处。实际上在接收机段,使用IQ解调也有明显的优点。解调后我们显式得到了$i(t),q(t)$。那么我们可以直接计算其幅度和相位(其实就是$s(t)$的幅度和相位):
假设我们只进行了一次普通解调,那么我们可能只会得到$i(t),q(t)$其中的一个,这样相位信息就比较难获取了。
只是三角函数的技巧吗?
刚才我们从“三角函数是一个经过系统前后频率保持不变的函数”开始,一直推导到“三角函数用于IQ调制”。整个过程用到的数学工具只有高中数学的和差化积,积化和差公式等。那么有没有一种高观点的解释这些事情的工具呢?是有的,而且我们还很有必要在讲述下面更多的技术性细节时着重探讨它。
由于实际存在的信号都是实信号,实信号的频谱具有共轭对称性:
这说明我们只要用其正频率的部分,或者负频率的部分就可以完全描述一个信号。如果我们只取其正频率,生成一个新信号$z(t)$,由于其只含正频率,所以它一定是一个复信号,不是实信号。其频谱可以表达为:
正频率部分加倍是为了保持能量守恒。所以我们可以引入一个阶跃形式的滤波器:
这样,频谱上$Z(f)$和$X(f)$的关系可以写作:
我们知道$H(f)$对应的冲激响应$h(t)$为:
这显然是个非因果系统。这样,根据时域卷积定理,$z(t)$可以写为:
我们将后者的积分运算,称为希尔伯特变换,即:
所以,当给定一个实信号$x(t)$时,我们可以随之计算其仅有正频的复信号$z(t)$,它可以写作:
并且,$x(t)$与$\mathcal{H} \left[ x\left( t \right) \right]$是正交的。我们可以通过交换积分顺序来不严谨的证明这一点。我们称$z(t)$为解析信号,因为它具有一些很良好的特点。它是一个复信号,那么复信号一定可以写成:
那么,瞬时幅度,瞬时相位,瞬时频率均可以从这个框架中导出:
这背后的直觉是:
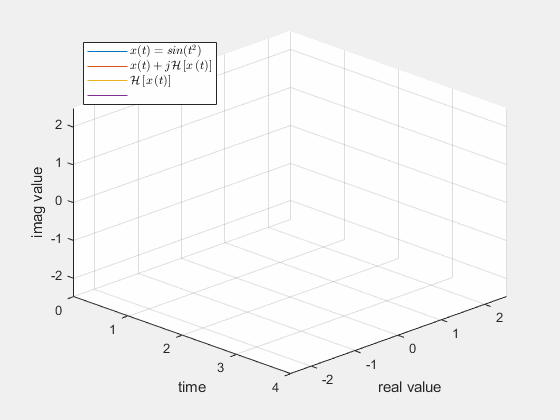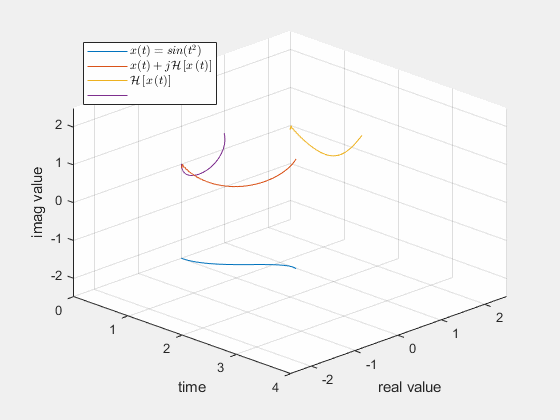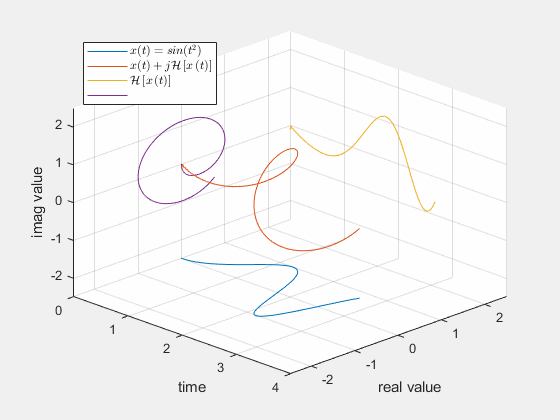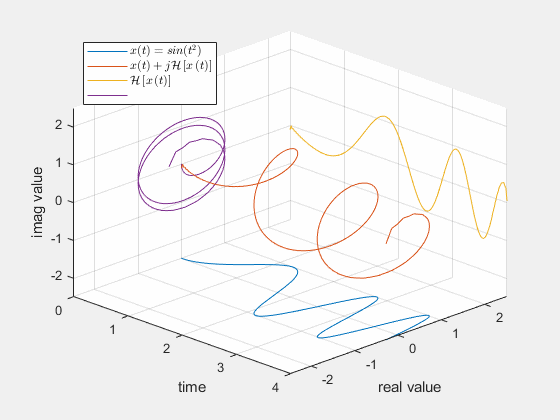
解析信号是原始的实信号的高维表达,而且频谱完全相同。所以用其相位的瞬时变化定义瞬时频率,是合理的。其实也有不同的定义方法,但我们这里不作讨论。
最后衔接希尔伯特变换和IQ调制的,又是欧拉公式。欧拉公式$e^{j\omega}=\cos \omega +j\sin \omega $本来就指出,正弦和余弦是一对希尔伯特变换对。
所以现在,我们清楚了IQ调制的本质。“与其只传输一个实信号,不如传输一个解析信号。”
解调?整个系统?
行文至此,其实我们只是对“为什么是IQ两路信号”做了回答。我们并没有给出整个系统的工作流程,虽然我们也不需要知道。但理解这整个系统,也会帮助我们加深对接下来“调制识别”的体会。
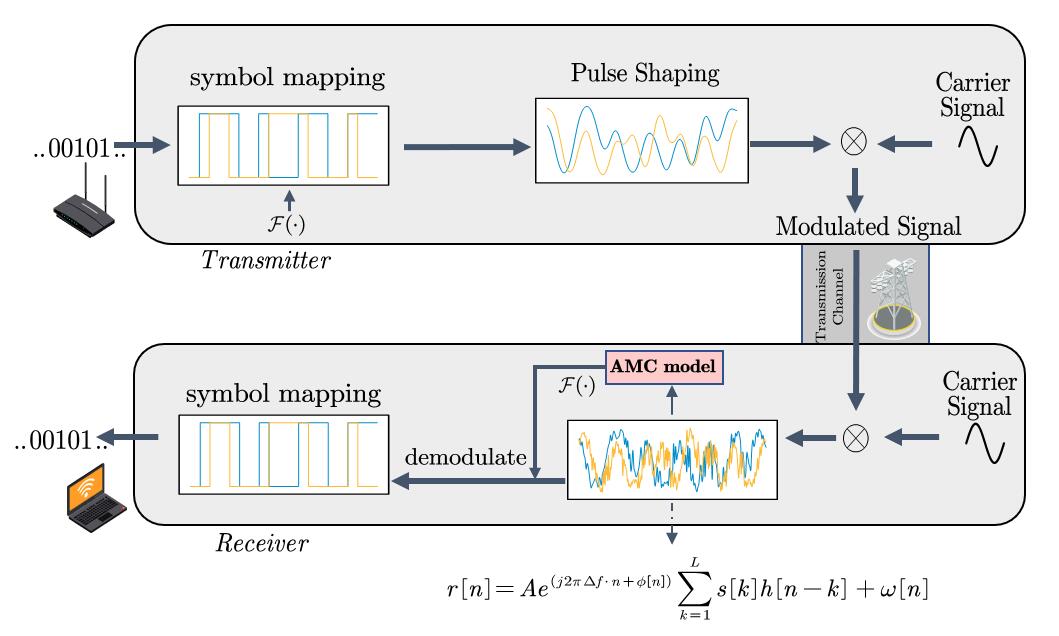
上述过程描述的是一个数字调制信号,产生,发射,接收,识别的整个过程。所以我们需要插播一下模拟调制和数字调制的一些区别,实际上如果我们应用朴素的模拟调制,如调幅(AM),调频(FM),调相(PM)上述流程图会简单许多。这个过程将不会有“symbol mapping”,“phase shaping”。但可想而知,这种方式非常容易受干扰和衰减影响(我们可以联系数字信号和调制信号的区别)。所以这种方式已经逐渐被数字调制替代,比如一些老式收音机,仍然用的是模拟调制。
上述过程中,发射机首先产生一段码流,我们这里并不关心这段码流的具体编码方式,如双相码,曼彻斯特编码。对此感兴趣的话可以查询计算机网络和通信原理等书籍。当得到这段码流的表示后,我们会根据调制方式$\mathcal{F} \left( \cdot \right) $来进行“符号映射”。
例如我们如果选取4-QAM调制,这种方式可以同时将2个码元映射到4个可能的符号上。
| 码元 | 符号 |
|---|---|
| 00 | (+1, +1) |
| 01 | (-1, +1) |
| 10 | (-1, -1) |
| 11 | (+1, -1) |
所以比如二进制码流010111按照这种规则,就会得到(-1, +1)(-1, +1)(+1, -1),即-1, -1, +1为一个通道,+1, +1, -1为另一个。它们自然形成了两路矩形脉冲,对应高低电平。如果是其他的一些调制方式,那可能是形成的是一些跟频率,相位相关的脉冲。
但我们显然不能直接这样发射出去。因为这样得到的频谱往往有很大的跳变,当通过信道这样的有限带宽的系统后,频谱会严重失真。所以我们需要用前文提到的$g_{T_s}(\cdot)$来进行调整,这个操作也称为“脉冲整型”。例如典型的升余弦整形滤波器:
其中$\alpha$称为滚降系数,例如在一个经典的调制信号数据集RadioML2016.10a中,作者就取$\alpha=0.35$。
In our simulated data set we use a root-raised cosine pulse shaping filter with an excess bandwidth of 0.35 for each digital signal.
我们这里对升余弦背后的一些技术细节和选择原理就不作讨论了。接下来记此时得到的两路信号(解析信号)为$s(t)$。最后$s(t)$与高频载波相乘,完成调制。如下图所示,我们实现了一个8ASK的调制方式:
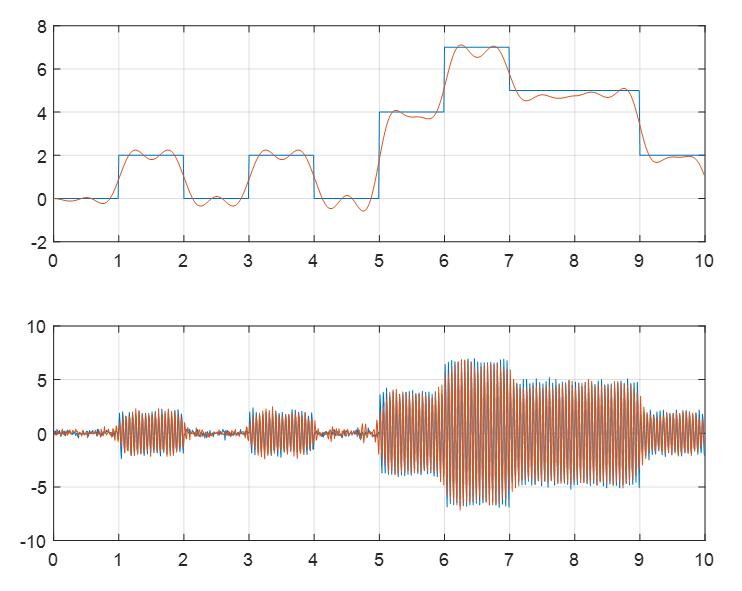
蓝色是原始的信号,橙色是脉冲整形后的信号。可以看到其变得更光滑,同时影响了最终信号的包络。
$s(t)$显然可以由不同的调制方式导出,这里我举我力所能及的几个,并作一些代表性的波形(的实部),帮助读者理解,它们通式都可以表达为:
所以不同之处仅在于$p_{mod}(t)$的形式。
- 幅度键控ASK(Amplitude Shift Keying)
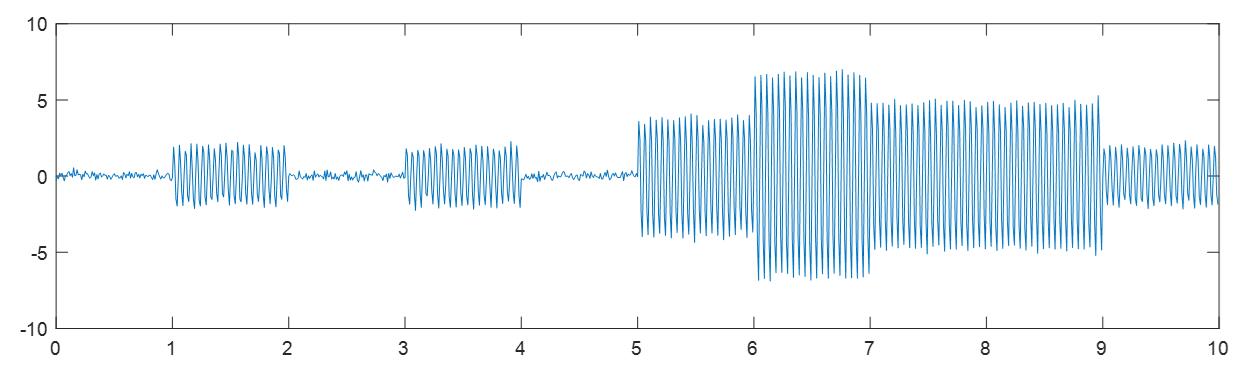
上图所示为8ASK,可以看到幅度分布呈现不同的量级。
- 相移键控PSK(Phase Shift Keying)
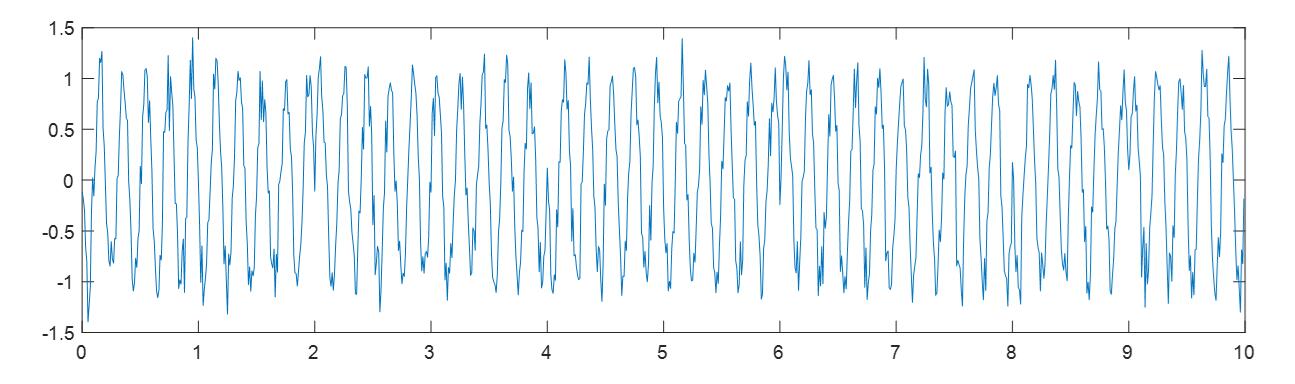
上图显示了BPSK,注意波形上相位的跳变。
- 频移键控FSK(Frequency Shift Keying)
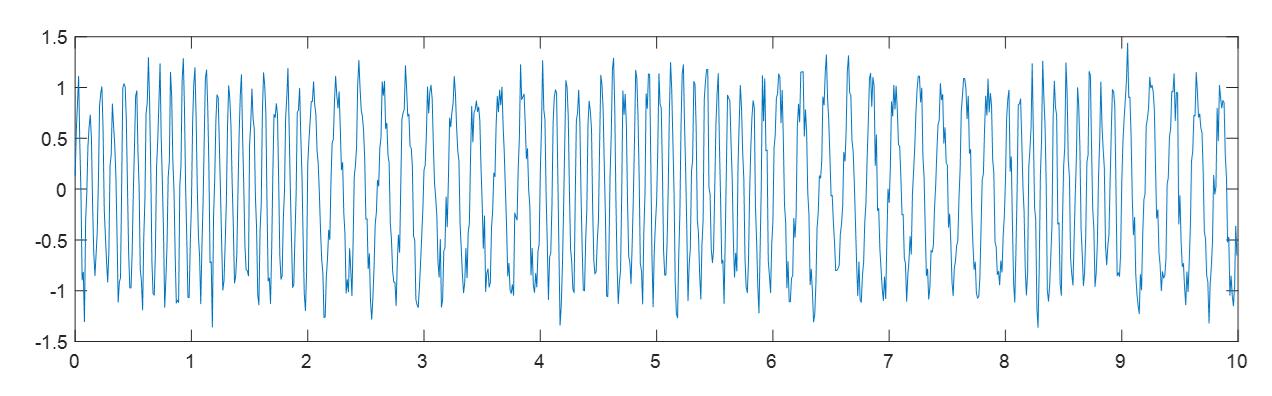
上图显示了2FSK,注意波形的稠密度的变化,这是频率改变的结果。
- 正交幅度调制QAM(Quadrature Amplitude Modulation)
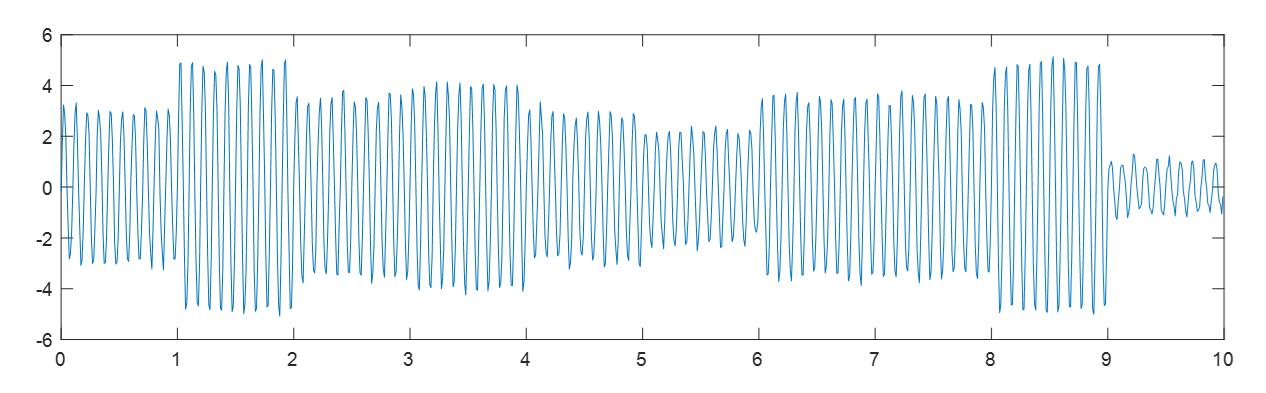
上图显示了QAM16其实部的波形,注意它和单路幅度调制(如ASK)的区别。
我们不需要了解每种调制方式的具体细节,我们只需要知道,阶数$M$越高,信号吞吐量就越高,但越容易受到干扰。同时,不同调制方式之间的抗干扰性本身就有一定差异。
最后,$s(t)$通过信道传输后,离散化,接收到的信号可以表示为:
上面这个式子只是一个形式上对接收到的信号的建模,它基本涵盖了三种信道效应的建模,我们这里简单了解一下。
$\varDelta f$是一个随机步进,它其实是模拟了载波频率的漂移。(Center Frequency Offset)
$\phi[n]$模拟了多径效应的影响,通过引入随机相位来模拟传输过程中的多径效应。
$\omega[n]$模拟接收端的热噪声,即加性高斯噪声。(Additive White Gaussian Noise)
$A$模拟了信道的增益(衰减还是放大)。
$\left\{ h\left[ n \right] \right\} $表示复杂的离散时间信道响应,比如它可能是瑞利衰落信道。那么其是一个复数随机变量,振幅和相位都是随机的。且其振幅服从瑞利分布,比如连续情形下:
上述模型没有体现出的,是采样率的差异。如果接收端和发送端的采样率不太一样,那么得到的波形也会有一定差异。这一点被叫作”Sample Rate Offset“
我们并不需要那么细致的了解这个过程的全部,有很成熟的工具可以模拟信道。例如GNU Radio里实现的各种层次化模块。
我们需要清楚认知的是,当走过了这一整套流程后。其得到的信号已经没有简单的matlab中随手模拟(比如我上文表格中绘制的那样)出来的那么好辨认了。正如2016年那篇原文所说的:
but due to pulse shaping, distortion and other channel effects they are not all readily discernible by a human expert visually.
经过接收机在相同载频下,进行采样。我们最终得到了$r[n]$。接下来就是根据此时$r[n]$的形状,识别出其调制方式,然后根据调制方式进行解调,最后恢复整个传输序列。为了清楚的了解自动调制识别的动机,我们有必要进行如下的背景介绍:
首先,如果是单一式的合作式通信,双方其实会约定同一种调制方式,此时就没有识别的必要了;如果是非合作式的,例如电子攻击与电子对抗环节,我们拦截到敌方的信号后,如果我们可以得知其调制方式,就可以向相同频段,使用该种方式发送大功率干扰信号,同理如果我们可以识别对方的干扰机发送的信号的调制方式,我们就可以切换,来躲避干扰。
除了这两种场合以外,其实还有一种民用场景,即“链路自适应”技术,简单来说,是将发射机的调制器部分换成一个自适应的调制单元。在整个系统初始化期间,自适应调制模块会与接收机进行唯一一次通信,告诉接收机关于它的调制样式备选池的全部信息。然后在整个系统运行时间定期进行信道估计,即侦测信道环境,假如信道比较干净,发射机就可以选用一些吞吐量高的高阶调制方式;如果信道噪声严重且非常复杂,就可以选择一些低阶的更稳定的调制方式。上述过程我们只需要有一个感性的认识,不需要了解具体细节,那大概是通信工程的专业。
现在我们再来说一下解调,这里我们假设,接收机可以和发射机完美同步,并且我们也不关心同步的具体实现。如果关心,可以自行查阅例如数字锁相环,载波估计,码率估计等技术细节。我们现在以一个例子来感受一下解调的这个过程,只有走完了这个过程,我们才能彻底理顺一些事情:
假设我们有一个2ASK调制的信号,已经被我们接收,我们采用IQ解调,那么形式上:
那么由于是2ASK,我们计算其幅度:
根据$a(n)$的表现,我们就可以确认$b_n$的取值,要注意,$b_n$其实是可能被干扰的。观察这个过程,首先,我们能看见使用IQ调制的好处。即使是针对2ASK这种非常简单的方式,由于同时用两路信号来传输,最后计算$a(n)$,可以提高信号的抗干扰性。
之后,从$a(n)$得到$b_n$,是需要进行“抽样判决”的。这是由于传输时,我们可能会给1个符号,采样若干个点,比如8个。就像RadioML2016.10a里所用的那样:
Data is modulated at a rate of roughly 8 samples per symbol with a normalized average transmit power of 0dB.
所以在接收时,我们也会用8个点来综合起来判断,这个符号到底是什么。例如我接收到的符号是:
1 | Received Symbol: [-0.9, -1.1, -1, -1, -1.2, -0.8, -0.9, -1] |
它们的平均值近似为-1,所以我就可以认为这个符号是0(低电平)。有些分析是关于误码率与采样数量的关系,正是出于此。这个事情对调制识别的指导是,“如果信号信噪比非常的低,那即使我正确识别了它的调制方式,是不是有时候也用处不大呢?”(当然,我们上面说过,这在电子对抗时候还是有意义的。)
所以到现在,我们终于走完了一个数字调制信号产生,传输,解调的整个过程。cheers!
数据集?
所以不用我再提,自动调制识别就是一个模式识别的问题。旨在完成寻找一个映射,完成:
然而实际上这个任务也并不轻松,因为它是为了分类一个数据中跟其纠缠(调制)在一起的属性,并不是分类数据本身。就像语音领域的声纹识别一样,关注的重点并不是声源说了什么,而是谁在说。
如果用机器学习的方法论解决它,那第一步就是数据集。常用的数据集有:
| 数据集 | 类别 | 样本数量 |
|---|---|---|
| RadioML2016.10a | 8种数字调制:8PSK, BPSK, CPFSK, GFSK, PAM4, 16QAM, 64QAM, QPSK;3种模拟调制:AM-DSB,AM-SSB,WBFM | 22万(2×128) |
| RadioML2016.10b | 8种数字调制:8PSK, BPSK, CPFSK, GFSK, PAM4, 16QAM, 64QAM, QPSK;3种模拟调制:AM-DSB,WBFM | 120万(2×128) |
| RadioML2018.01a | 19种数字调制:32PSK, 16APSK, 32QAM, GMSK, 32APSK, OQPSK, 8ASK, BPSK, 8PSK, 4ASK, 16PSK, 64APSK, 128QAM, 128APSK, 64QAM, QPSK, 256QAM, OOK, 16QAM;5种模拟调制:AM-DSB-WC, AM-SSB-WC, AM-SSB-SC, AM-DSB-SC, FM, | 255.59万(2×1024) |
下载可以通过访问DeepSig,其实除了这三个以外还有一个数据集:HisarMod2019.1,模拟了一些更复杂的情况,但我自己没有在这上面做过。关于这些数据集的各种参数之类的,网上都可以查到,这里不作赘述。
我们可以检视一下RadioML2016.10a里的样本们:
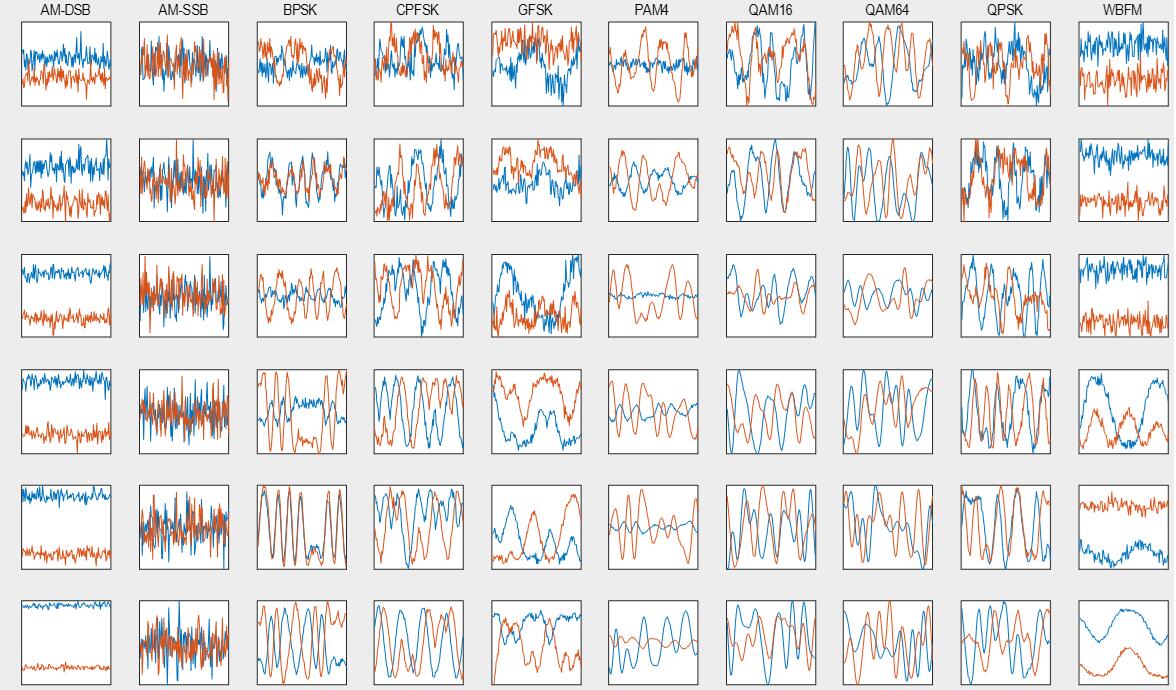
如果你在阅读完上面的内容后,自然地产生了一个疑问:“为什么这个波形和上面生成出来的相差这么多?”。其实是出于一个很自然的原因:“采样率”。在上面模拟每种调制方式时,为了看的清晰,每个符号其实是过采样的,用了甚至100个采样点来表达一个符号。而上述数据集一般都只会过采样2倍,相当于就是4倍于载频,并不会那么高。这是进行调整后的QAM16的例子:
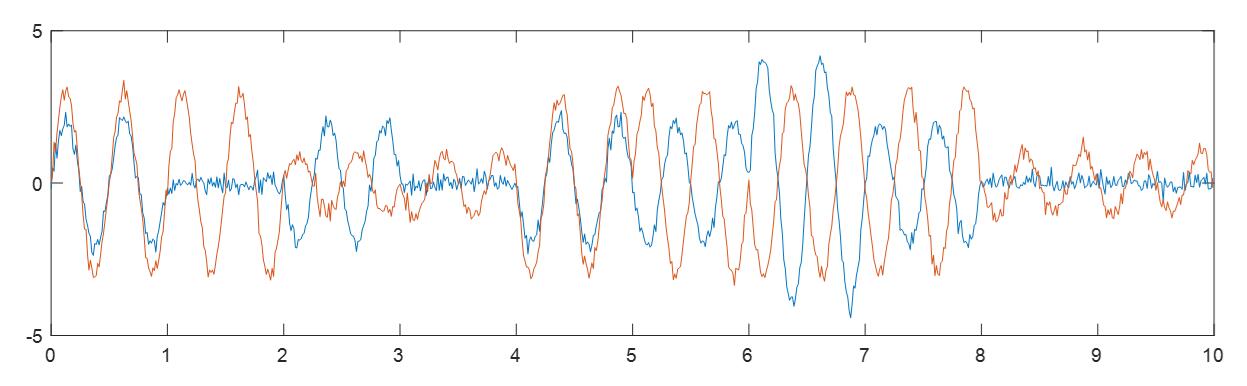
由于没有加入一些信道衰落等因素,还是和样本生成的有一定区别,但已经很神似了。
现在,我们也能完全理解,数据集里的信号是怎么来的了。这点非常重要,因为现在是2023年,再上手的人大概import torch,继承一下torch.utils.data.dataloader就开炼了,然而对自己处理的数据是什么毫无了解!这是非常可笑的。另外,学习一下这整个过程,也可以强化一下一些信号分析上的基础,虽然这都是通信工程专业上入门级别的知识,但也够弥补(如果你和我一个专业且一个学校)一些培养方案上的缺陷。
一些有益的tips?
在这全民炼丹的大时代里,“自动调制识别+深度学习”这个题材还是有一些刊物乐于接收的。比如一些比较二流的“IEEE trans. on cognitive communication and networking”, “IEEE communications letters”, “IEEE wireless communications letters,”, “ICASSP”。也有一些很顶级的期刊和会议,比如”IEEE trans. on communication”, “IEEE INFOCOM”。
以我的经验,最容易上手的是对着网络结构乱调模块,或者把一些计算机视觉,机器学习里的一些新方法直接套用过来。但问题是现在公共数据集(上面那几个)已经没油水可榨了,实在刷不上去。这里一种鸵鸟的办法是自己用T’Oshea et.al提供的脚本自己生成需要的数据集。比如你想讲一个“降低低阶,高阶调制方式之间混淆”的故事,你就自己去生成包含4QAM,16QAM,32QAM,64QAM,128QAM,256QAM的数据集,然后跑baseline和自己的故事。大部分灌水的思路都是这样的。
从网络结构的角度,另一个办法就是在网络里缝入去噪,校正等元素。这里面有一些工作,但都是乏善可陈。
[1]F. Zhang, C. Luo, J. Xu and Y. Luo, “An Efficient Deep Learning Model for Automatic Modulation Recognition Based on Parameter Estimation and Transformation,” in IEEE Communications Letters, vol. 25, no. 10, pp. 3287-3290, Oct. 2021, doi: 10.1109/LCOMM.2021.3102656.
[2]T. T. An and B. M. Lee, “Robust Automatic Modulation Classification in Low Signal to Noise Ratio,” in IEEE Access, vol. 11, pp. 7860-7872, 2023, doi: 10.1109/ACCESS.2023.3238995.
[3]H. Ryu and J. Choi, “EMC2-Net: Joint Equalization and Modulation Classification Based on Constellation Network,” ICASSP 2023 - 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 2023, pp. 1-5, doi: 10.1109/ICASSP49357.2023.10096687.
如果想逃离刷点的困境,我设想过以下几个可行的思路,但可惜没机会实现了。
探索数据生成时的超参数对分类造成的影响。例如升余弦滤波器的滚降系数,这些数据集都设置的是$\alpha=0.35$,以及过采样的倍数。比如如果网络是在$\alpha=0.35$下训练的,那么能否分类$\alpha=0.5$时的数据。如果能,写个报告;如果不能,想办法提升下泛化性。(由于大部分现有工作都是在过拟合,所以大概率是后者。)如果采样的倍数有些许的偏差,那么由于此产生的波形的变化,是否对结果有致命的影响。跟这个类似是一些把深度学习里的对抗攻击与防御拿来的开始水的,其实有些没意思,但是还是有人收的。比如:
[1]R. Sahay, C. G. Brinton and D. J. Love, “A Deep Ensemble-Based Wireless Receiver Architecture for Mitigating Adversarial Attacks in Automatic Modulation Classification,” in IEEE Transactions on Cognitive Communications and Networking, vol. 8, no. 1, pp. 71-85, March 2022, doi: 10.1109/TCCN.2021.3114154.
[2]R. Sahay, C. G. Brinton and D. J. Love, “Frequency-based Automated Modulation Classification in the Presence of Adversaries,” ICC 2021 - IEEE International Conference on Communications, Montreal, QC, Canada, 2021, pp. 1-6, doi: 10.1109/ICC42927.2021.9500583.
将解码的过程,也考虑进神经网络里。毕竟推理一个NN是一个巨量的资源,如果这么大的计算量只花在作一个分类,那也太浪费了。所以其实可以同时对信号进行一些合理的修复,提高解调后过程的解码正确率。这个角度可以follow下面这两份工作,是同一伙人做的,完整版和简略版分别发表在了很顶级的期刊和会议上:
[1]S. Hanna, C. Dick and D. Cabric, “Signal Processing-Based Deep Learning for Blind Symbol Decoding and Modulation Classification,” in IEEE Journal on Selected Areas in Communications, vol. 40, no. 1, pp. 82-96, Jan. 2022, doi: 10.1109/JSAC.2021.3126088.
[2]S. Hanna, C. Dick and D. Cabric, “Combining Deep Learning and Linear Processing for Modulation Classification and Symbol Decoding,” GLOBECOM 2020 - 2020 IEEE Global Communications Conference, Taipei, Taiwan, 2020, pp. 1-7, doi: 10.1109/GLOBECOM42002.2020.9348060.
在一些嵌入式设备(简单起见,tx2,jetson nano)上实际部署一下一些所谓的模型,考察一下latency。一些论文里其实都是在主机,服务器上测的运行速度,这个基本失真严重。然后思考一些推理上更有效率的模型。这个事情说白了就会导向一个整个是CNN的结构,因为卷积在硬件上被优化的很好。一些用了RNN,self-attention算子的模型,其实就很麻,基本属于花瓶,推理很费事。如果学有余力,可以用比较便宜的SDR(software defined radio),例如PlutoSDR,来自己搭建一个简单的调制-解调系统,然后用一个网络分类,看看会发生什么。
但是,这个任务说穿了,也是一个非常基础的分类任务,实现难度并不会很大,适合初学者上手。但是,零食不能当饭吃。当得到了足够的科研训练后,应当去冲击一些更有挑战性的课题。
End
这篇blog简单整理了自动调制识别任务所需要的一些背景知识,以及指出了一些接下来有希望的方向,算是给自己一个收尾。实际上就我个人经验,在升学面试时,老师基本不太关心自动调制识别(AMC)本身,老师大多关心这背后的信号分析的素养是否扎实,你对信号处理的理解是否到位。如果做AMC,做到最后,讲也讲不出来,支支吾吾就会说“两路正交信号”,“注意力机制”,“卷积神经网络”,那无疑是不合格的。


