二叉树2

​ 具有特殊性质的二叉树是实现某些操作的最佳容器，但维护这种特殊性质也并不简单。

​ 在之前的讨论中，我们没有介绍关于二叉树结点的插入(insert)和删除(delete)。因为对于普通的二叉树来讲，这两者其实是任意的(arbitrary)。比如你可以把某个结点插入在父结点和任意一个孩子之间，你可以把它插入在一个叶子节点后。删除时你也可以指定任何一个后继来替代它。

Binary Search Tree

​ 现在我们构造一种特殊二叉树，我们要求它左孩子的值小于根结点的值，右孩子的值大于根结点的值。

     6
   /   \
  3     9
 / \   / \
1   4 7   10

​ 就像这样，我们还可以发现一个特点，由于每个根结点都是这样递归定义的，所以当我们写出它的中序遍历时：1 3 4 6 7 9 10。我们会发现这是一个递增的序列。这种性质带来了查找上的便利。例如和线性搜索数组[1, 3, 4, 6, 7, 9, 10]相比，查找数10只需比较2次即可。这就是二叉搜索树(Binary Search Tree)。

​ 我们先给出搜索/查找(Search)的定义，以便确定我们接下来实现二叉搜索树的哪些功能：

搜索/查找(Search): 给定一个包含$n$个条目的集合，每个条目都与键$x_i$和值$v_i$相关联。(Given a set of $n$ entries, each associated with key $x_i$ and value $v_i$.)

-存储以便快速访问和更新。(Store for quick access and update.)

-假设键是有序且不重复。(Assume that keys are totally ordered and no-duplicated.)

我们将这种数据结构抽象为”字典”。(We abstract this data structure as “dictionary”.)

-insert(key $x$, value $v$)

​ insert ($x$, $v$) in dictionary, no duplicates.

-delete(key $x$)

​ delete $x$ from dictionary. return Error if $x$ is not in dictionary.

-find(key $x$)

​ return a reference to associated with value $v$, or null if $x$ is not there.

​ 然而，事情没有这么简单。二叉搜索树的这种性质导致了我们需要特别处理结点的增加和删除，下面我们开始思考如何建立一颗二叉搜索树。

​ 一个很自然的想法是，我们先将要插入的子结点的键与当前根结点的键作比较，如果子结点更小，那就去左边。如果子结点更大，那就去右边。然后再递归的和根节点的左孩子/右孩子进行判断。

typedef int keytype;
typedef char datatype;

typedef struct node
{
	keytype key;
	datatype value;
	struct node* l_child;
	struct node* r_child;
}bstnode;

bstnode* insert(bstnode* root, bstnode* s)
{
	if(root == NULL)
	{
		root = s;
	}
	else
	{
		if(s->key < root->key)
		{
			root->l_child = insert(root->l_child, s);
		}
		else if(s->key > root->key)
		{
			root->r_child = insert(root->r_child, s);
		}
		else
		{
			printf("key: %d already exists\n", s->key);
		}
	}
	return root;
}

​ 基本思路就是这样的。基于此，我们可以作出一个创建二叉搜索树的函数：

bstnode* CreateBST()
{
	bstnode *root, *s;
	keytype key;
	datatype value;
	root = NULL;
	printf("input -1 as key to end\n");
	scanf("%d", &key);
	while(key != -1)
	{
		s = (bstnode*)malloc(sizeof(bstnode));
		s->key = key;
		s->l_child = NULL;
		s->r_child = NULL;
		scanf(" %c", &value);
		s->value = value;
		root = insert(root, s);
		scanf("%d", &key);
	}
	return root;
}

​ 我们输入一个测试用例，来体验一下：

input -1 as key to end
6 a 2 b 8 c 4 e 9 f 7 g -1
      6
     / \
    /   \
   /     \
  2       8
   \     / \
    4   7   9
<2: b> <4: e> <6: a> <7: g> <8: c> <9: f>

​ 可以看见，我们成功建立了一个二叉搜索树。下面，我们做这样的一个实验：我们修改输入的测试用例的顺序，并不改变键值对之间的匹配关系：

input -1 as key to end
2 b 8 c 6 a 7 g 9 f 4 e -1
              2
               \
                \
                 \
                  \
                   \
                    \
                     \
                      8
                     / \
                    /   \
                   /     \
                  6       9
                 / \
                4   7
<2: b> <4: e> <6: a> <7: g> <8: c> <9: f>
input -1 as key to end
4 e 9 f 6 a 2 b 8 c 7 g -1
                              4
                             / \
                            /   \
                           /     \
                          /       \
                         /         \
                        /           \
                       /             \
                      /               \
                     /                 \
                    /                   \
                   /                     \
                  /                       \
                 /                         \
                /                           \
               /                             \
              2                               9
                                             /
                                            /
                                           /
                                          /
                                         /
                                        /
                                       /
                                      6
                                       \
                                        \
                                         \
                                          8
                                         /
                                        7
<2: b> <4: e> <6: a> <7: g> <8: c> <9: f>

​ 我们发现了一个很糟糕的事情，随着我们改变插入的顺序，二叉树的深度从3变成4，再变成5。然而，实际上，最后输出的中序遍历的键值对表示，这些树其实描述的是同一个结构。

​ 考虑有$n$个元素的搜索情形，如果二叉树像第一个例子一样，是一个很周正的二叉树，我们称之为“平衡(balanced)”，那么搜索的时间复杂度就是这个树的高度，即$O(\mathrm{log}n)$。而如果二叉树像第三个例子那样，是一个非常歪斜(skewed)的结构，那它基本就退化成了线性表，此时的时间复杂度即$O(n)$。

Delete for BST

​ 当我们设法解决这件事之前，我们还有一个遗留问题—删除。

​ 我们在删除时，需要维护二叉排序树的性质。我们一步一步来思考这个问题，二叉树的中序遍历是一个单增序列。如果我们只看这样的一个线性序列，删除非常简单。我们，想删除谁就删除谁就好了。

​ 但唯一的区别就在于二叉树是一个非线性结构，实际上我们可以直观的把中序遍历开成它的垂直投影：

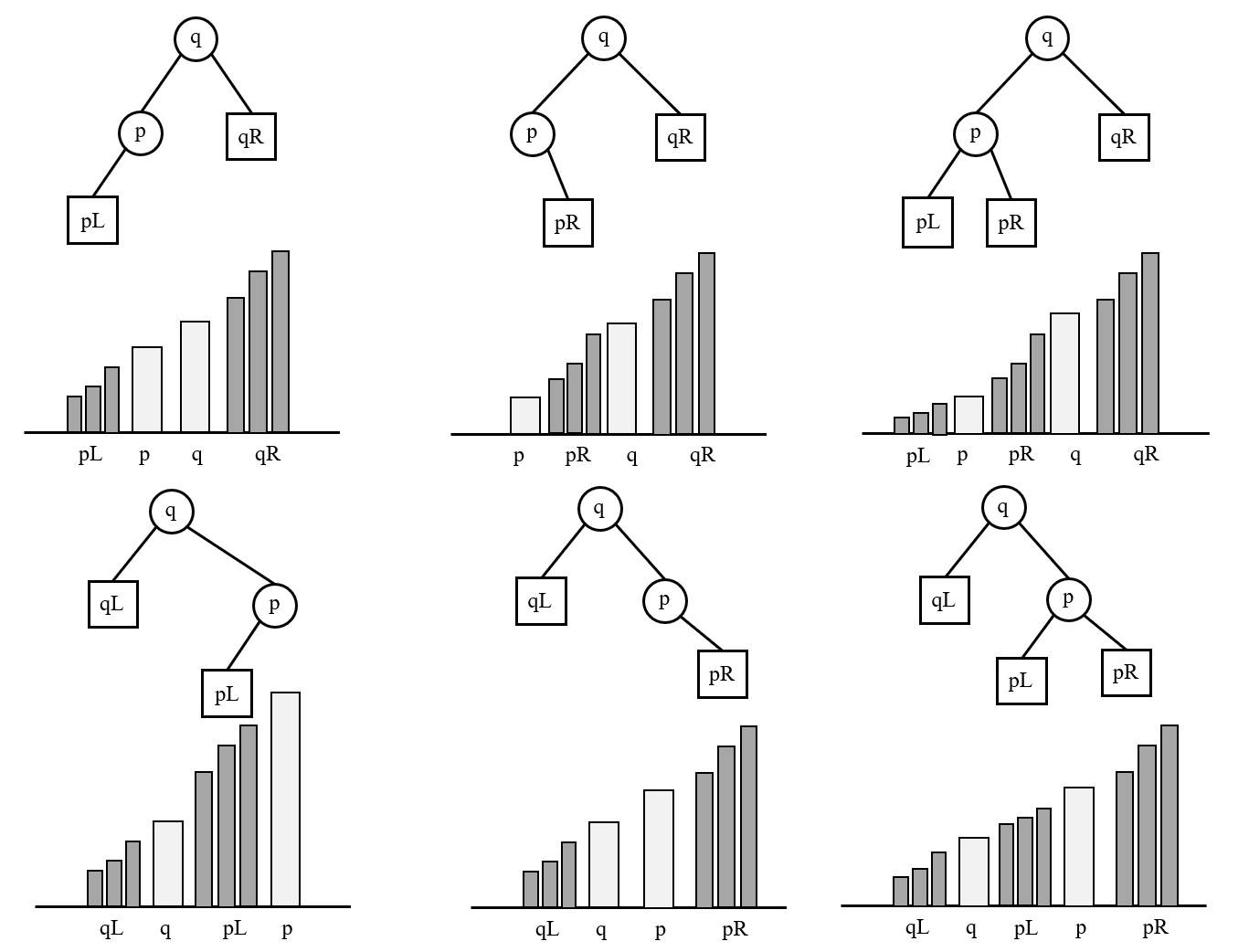
​ 我们思考删除结点p时的情况。逐列来看：

​ 对于第一列，p结点只有左子树。我们发现直接移除p结点，并不会影响投影的单调性。所以对于这种情况，我们只需把q的左或者右孩子直接连成pL的根结点。

​ 在第二列，p只有右子树的情况，也是一样的。直接移除p不会影响单调性。

​ 在这两种情况下，我们要知道为什么会具有这样的便利，比如之前q->r_child == p，为什么我们直接令q->r_child = p->r_child是可以的？因为p->r_child是pR这个子结构的根结点，这个根结点延申的结果本身是符合二叉排序树的性质的。此时，直接连接根节点，会和投影上直接移除p，是等效的。

​ 事情在第三列的情形下会变得有些复杂，此时p同时有左子树和右子树。直观来看我们有两种策略，我们可以找左子树最大的那个，和右子树最小的那个。此时会出现一个和第一列与第二列不一样的情况，假如我们此时是用q->r_child连接pL的根结点，pL本身是一个二叉排序树，但我们此时无法安排pR。

​ 所以此时，我们不能直接连接pL或者pR的根结点，我们以右子树为例。我们需要找到右子树的最小值，然后用它代替待删除结点p。之后再删除这个最小值本身。由于最小值一定是个叶子结点，或者只有右子树（不然他就不是最小值），所以找到并删除它并不费事。

​ 整个过程可以写为：

bstnode* minValueNode(bstnode* node) {
    bstnode* current = node;
    while (current && current->l_child != NULL) {
        current = current->l_child;
    }
    return current;
}

bstnode* delete_key(bstnode* root, keytype key) {
    if (root == NULL) {
        printf("key not found\n");
        return root;
    }
    if (key < root->key) {
        root->l_child = delete_key(root->l_child, key);
    } else if (key > root->key) {
        root->r_child = delete_key(root->r_child, key);
    } else {
        if (root->l_child == NULL) {
            bstnode* tmp = root->r_child;
            free(root);
            return tmp;
        } else if (root->r_child == NULL) {
            bstnode* tmp = root->l_child;
            free(root);
            return tmp;
        }
        bstnode* tmp = minValueNode(root->r_child);
        root->key = tmp->key;
        root->value = tmp->value;
        root->r_child = delete_key(root->r_child, tmp->key);
    }
    return root;
}

​ 我们递归的进行这个操作，首先需要查找所删除的元素。查找到以后，如果它没有左子树，那么就让其右子树的根结点，替代其本身（这个过程是递归进行的）。如果没有右子树，那就用左子树。

​ 如果同时都有左右子树，那么我们先找到右子树里最小的那个结点，通过调用minValueNode()，然后把它的值赋给当前的根结点。然后再递归的从右子树里，删除刚才找到的tmp结点。

​ 现在我们完整的了解了二叉排序树的查找，插入和删除。实际上插入和删除都是基于查找的，他们的时间复杂度最好的时候就是$O(\mathrm{log}n)$，最差的时候就是$O(n)$​了。所以我们称二叉搜索树的完成各种动态操作的时间复杂度为$O(h)$, $h$为树的高度。比如，基于上面的程序，我们可以输入这样一个比较复杂的二叉树：

input -1 as key to end
20 a
10 b
30 c
5 d
15 e
25 f
35 g
3 h
7 i
13 j
17 k
23 l
27 m
33 n
37 o
-1
             20
             / \
            /   \
           /     \
          /       \
         /         \
        /           \
       /             \
      10              30
     / \             / \
    /   \           /   \
   /     \         /     \
  5       15      25      35
 / \     / \     / \     / \
3   7   13  17  23  27  33  37

​ 比如，我们可以删除key为30的结点，根据前面的讨论，我们知道，替代30的将会是它的后继33：

             20
             / \
            /   \
           /     \
          /       \
         /         \
        /           \
       /             \
      10              33
     / \             / \
    /   \           /   \
   /     \         /     \
  5       15      25      35
 / \     / \     / \       \
3   7   13  17  23  27      37

​ 然后，我们可以继续删除35和37，来得到一个只有左子树的结点33：

             20
             / \
            /   \
           /     \
          /       \
         /         \
        /           \
       /             \
      10              33
     / \             /
    /   \           /
   /     \         /
  5       15      25
 / \     / \     / \
3   7   13  17  23  27

​ 此时再删去33，我们知道，25会直接代替它的位置：

             20
             / \
            /   \
           /     \
          /       \
         /         \
        /           \
       /             \
      10              25
     / \             / \
    /   \           /   \
   /     \         /     \
  5       15      23      27
 / \     / \
3   7   13  17

​ 最后，我们再体会一下删除20：

             23
             / \
            /   \
           /     \
          /       \
         /         \
        /           \
       /             \
      10              25
     / \               \
    /   \               \
   /     \               \
  5       15              27
 / \     / \
3   7   13  17

​ 这个过程的动态可视化：

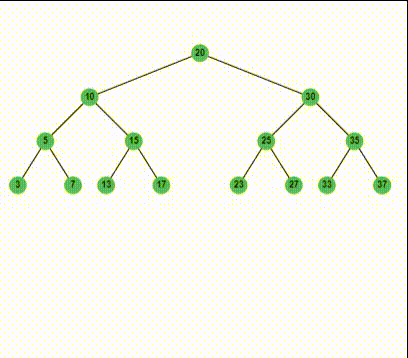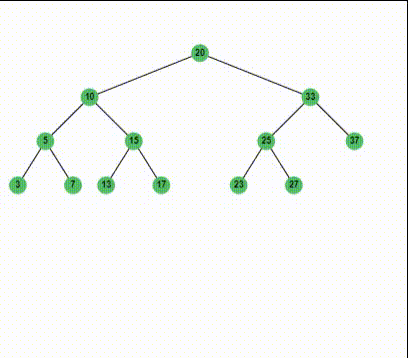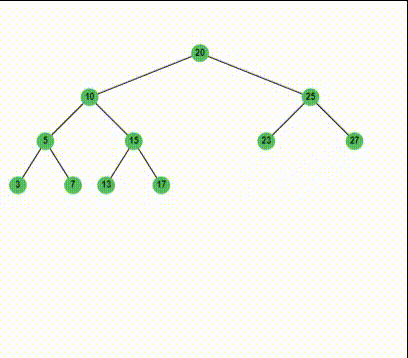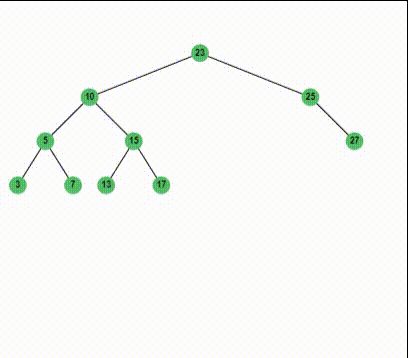
​ 现在，我们就对二叉排序树的删除有了比较清晰的认识。

AVL tree

​ 就像我们在删除部分之前所举的例子，我们插入二叉排序树的顺序，会影响这棵树的形状。实际上，如果我们插入的是一个单调序列，二叉排序树甚至会退化为链表。

​ 我们并不希望这种事情的发生，于是有了平衡二叉树的概念。AVL树是最先发明的一种自平衡二叉搜索树。在AVL树中，每个结点会额外储存一个平衡因子(balanced factor)，这个值是左子树高度和右子树高度之差，它被要求在-1，0，1中。我们称这样的性质为AVL性质。如果AVL树因为插入和删除，破坏了这样的性质。那么需要进行旋转(rotate)来恢复它。

​ 在前面二叉排序树的删除中，我们已经体会到，树的递归性质。由于从一个空结点开始，插入第一个元素，它一定是满足AVL性质的。插入第二个，无论是大于还是小于，也还是满足的，此时根结点的平衡因子为1。只有在此基础上，继续插入元素，才会产生AVL性质的破坏。所以，插入元素的落点只会有4种情况：

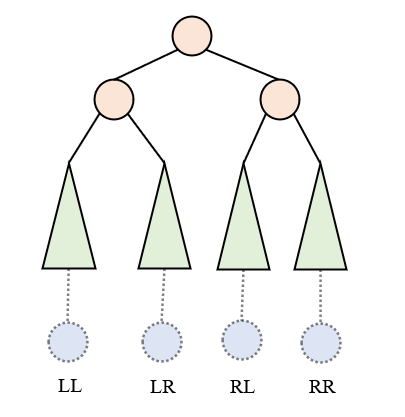
​ 对于LL型和RR型，他们可以通过一次右旋(right rotation)和一次左旋(left rotation)来实现调整：

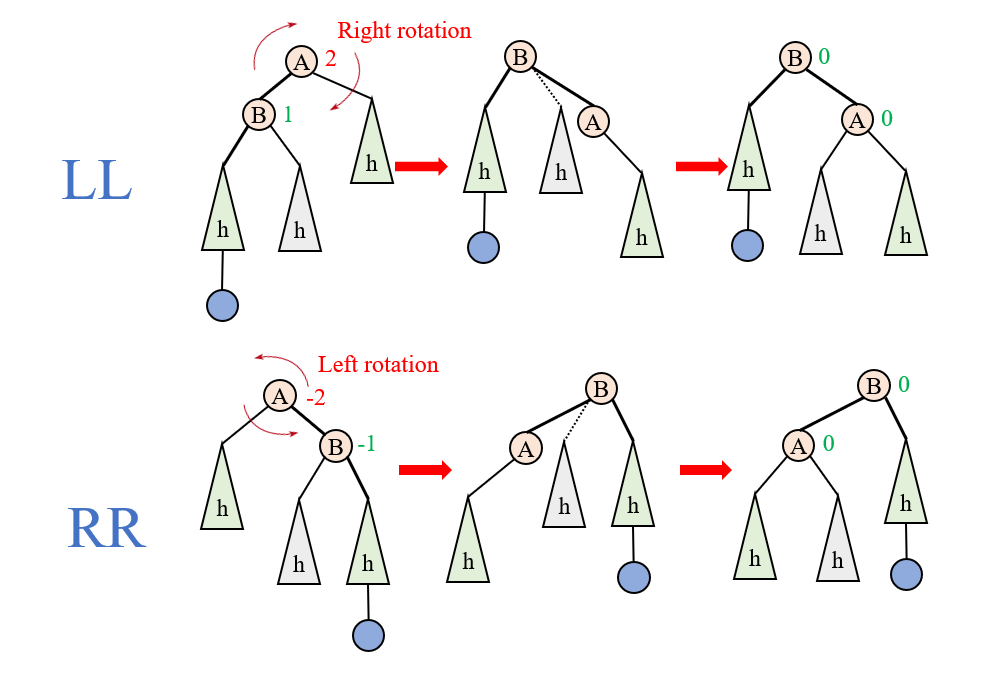
​ 可以看到一次右旋对应的是LL型，一次左旋是RR型。所谓左/右旋，可以形象的理解为，将AVL性质破坏的那个结点，看作方向盘的中心，然后左打/右打方向盘。我们以一次右旋为例，相当于A连同其较短的右子树，统一下降一个高度；B连同其孩子，统一上升一个高度。这样，A的高度差就被填平了。由于B被抬上去成了根结点，而B不能有三个孩子，所以很自然的，B的右孩子过继到A的左孩子（因为这样不影响高度）。

​ 当插入结点为LR和RL型时，情况变得少许复杂：

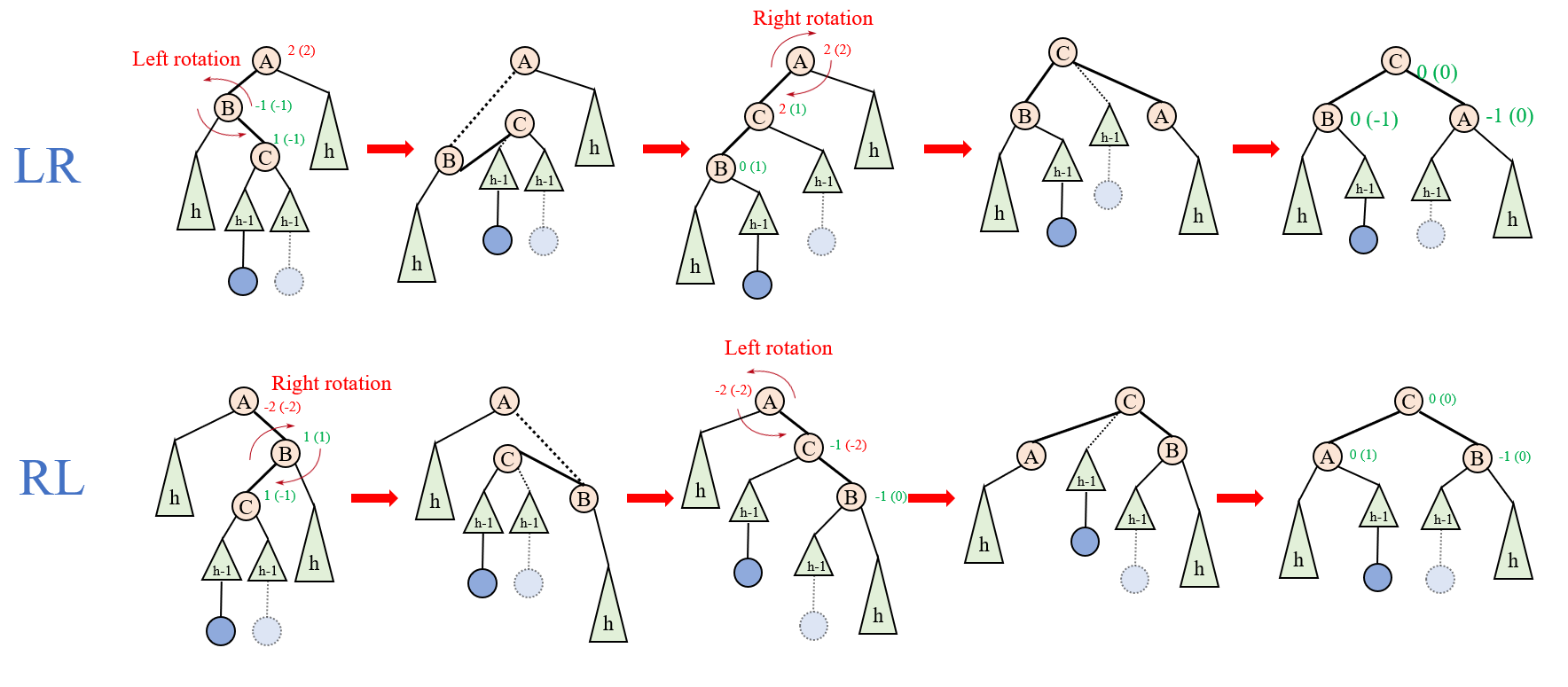
​ 简单来说，就是先左旋/右旋一次，再右旋/左旋一次。这一过程中有许多的对称性，需注意观察。

​ 所以，在原来代码的基础上，我们可以做如下修改，把普通的二叉排序树变成AVL树：

typedef struct node
{
	keytype key;
	datatype value;
	int balance_factor;
	struct node* l_child;
	struct node* r_child;
}bstnode;

​ 首先更新结点的结构体，多加一个平衡因子。

int height(bstnode* node)
{
    if (node == NULL) {
        return 0;
    }
    int left_height = height(node->l_child);
    int right_height = height(node->r_child);
    return left_height > right_height ? left_height + 1 : right_height + 1;
}

int balance_factor(bstnode* node)
{
    if (node == NULL) {
        return 0;
    }
    int left_height = height(node->l_child);
    int right_height = height(node->r_child);
    return left_height - right_height;
}

​ 一个计算结点高度的函数和计算平衡因子的函数，我们需要频繁调用它们。

​ 接下来我们定义左旋和右旋：

bstnode* right_rotate(bstnode* node)
{
	bstnode* new_root = node->l_child;
	node->l_child = new_root->r_child;
	new_root->r_child = node;
	node->balance_factor = balance_factor(node);
	new_root->balance_factor = balance_factor(new_root);
}

bstnode* left_rotate(bstnode* node)
{
    bstnode* new_root = node->r_child;
    node->r_child = new_root->l_child;
    new_root->l_child = node;
    node->balance_factor = balance_factor(node);
    new_root->balance_factor = balance_factor(new_root);
    return new_root;
}

​ 我们逐句的分析一下right_rotate()，因为left_rotate()的逻辑跟它完全一样。对应之前的图可以更易理解：

​ 这里node即是A，new_root即是B。我们先将A的左孩子赋值为了B的右孩子（灰色的h三角），即图中虚线部分所表示的过程。然后将B的右孩子指向A，这一点在图里没有用虚线表示，因为图示中的旋转直接表达了这一点。在这个过程中，只有A和B的平衡因子会发生变动，所以更新了node和new_root的平衡因子。

​ 基于左旋和右旋，我们可以复用他们的代码，来得到RL和LR时的双旋操作：

bstnode* right_left_rotate(bstnode* node)
{
    node->r_child = right_rotate(node->r_child);
    return left_rotate(node);
}

bstnode* left_right_rotate(bstnode* node)
{
    node->l_child = left_rotate(node->l_child);
    return right_rotate(node);
}

​ 之前二叉排序树的插入操作，是递归实现的。每一次递归调用的函数，处理的都是根结点。所以当我们最终，找到插入的位置后。只需在完成插入函数的后面，加一步更新平衡因子和旋转的判断，即可沿着插入的路径不断调整结点：

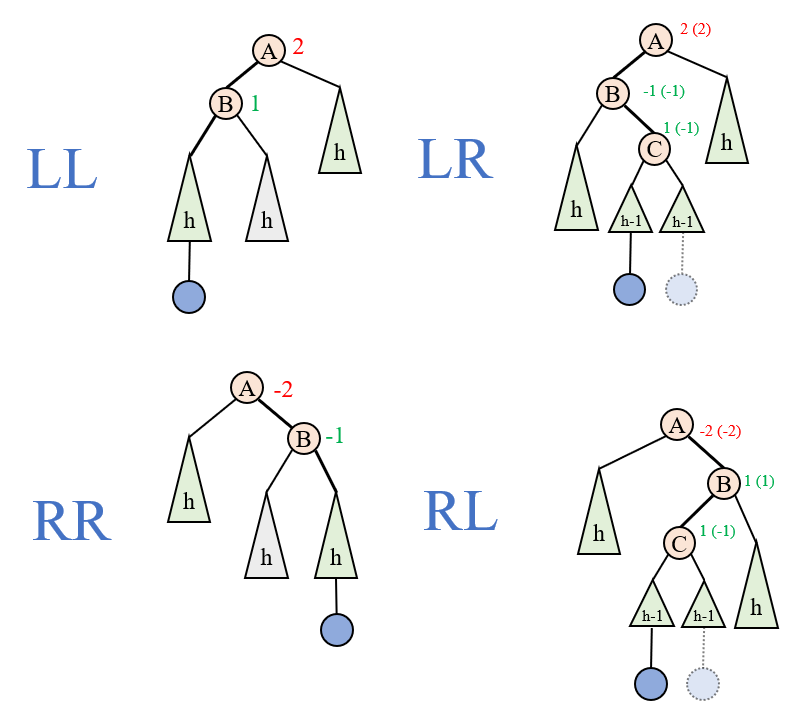
​ 旋转的判断可以根据待旋转结点和其左孩子/右孩子的平衡因子来区分，如图所示。

​ 所以插入函数可以更新为：

bstnode* insert(bstnode* root, bstnode* s)
{
	if(root == NULL)
	{
		root = s;
	}
	else
	{
		if(s->key < root->key)
		{
			root->l_child = insert(root->l_child, s);
			int bf = balance_factor(root);
			if (bf == 2)
        	{
	            if (balance_factor(root->l_child) == 1)
	            {
	                root = right_rotate(root);
	            }
	            else if (balance_factor(root->l_child) == -1)
	            {
	                root = left_right_rotate(root);
	            }
        	}
		}
		else if(s->key > root->key)
		{
			root->r_child = insert(root->r_child, s);
			int bf = balance_factor(root);
			if (bf == -2)
        	{
	            if (balance_factor(root->r_child) == -1)
	            {
	                root = left_rotate(root);
	            }
	            else if (balance_factor(root->r_child) == 1)
	            {
	                root = right_left_rotate(root);
	            }
        	}
		}
		else
		{
			printf("key: %d already exists\n", s->key);
		}
	}
	root->balance_factor = balance_factor(root);
	return root;
}

​ 注意，return之前的更新平衡因子是必要的。虽然旋转函数中自带了更新平衡因子，但这只能保证那些触发了旋转的结点的平衡因子得到更新，而那些可能从1变成0，从0变成-1的合法结点也是需要更新的。

​ 同样，删除函数也是同理：

bstnode* delete_key(bstnode* root, keytype key) {
    if (root == NULL) {
        printf("key not found\n");
        return root;
    }
    if (key < root->key) {
        root->l_child = delete_key(root->l_child, key);
    } else if (key > root->key) {
        root->r_child = delete_key(root->r_child, key);
    } else {
        if (root->l_child == NULL) {
            bstnode* tmp = root->r_child;
            free(root);
            return tmp;
        } else if (root->r_child == NULL) {
            bstnode* tmp = root->l_child;
            free(root);
            return tmp;
        }
        bstnode* tmp = minValueNode(root->r_child);
        root->key = tmp->key;
        root->value = tmp->value;
        root->r_child = delete_key(root->r_child, tmp->key);
    }
    if (root == NULL)
    {
    	return NULL;
	}
	int bf = balance_factor(root);
	if (bf == 2)
	{
        if (balance_factor(root->l_child) == 1)
        {
            root = right_rotate(root);
        }
        else if (balance_factor(root->l_child) == -1)
        {
            root = left_right_rotate(root);
        }
	}
    else if (bf == -2)
    {
        if (balance_factor(root->r_child) == -1)
        {
            root = left_rotate(root);
        }
        else if (balance_factor(root->r_child) == 1)
        {
            root = right_left_rotate(root);
        }
    }
    root->balance_factor = balance_factor(root);
    return root;
}

​ 现在我们再来尝试一下输入一个单增序列：

input -1 as key to end
1 a 2 d 3 c 4 b 5 e 6 f -1
      4
     / \
    /   \
   /     \
  2       5
 / \       \
1   3       6

​ 如果用之前的二叉排序树来作，那就会是一个链表：

input -1 as key to end
1 a 2 d 3 c 4 b 5 e 6 f -1
1
 \
  2                                                                                 
   \
    3                                                                                      \
      4                                                                               		 \
        5
         \
          6

​ 这个插入的过程可以可视化为：

​ 同样，我们可以可视化一下删除过程：

Other trees

​ 除了这两种tree，还有更多的树型结构：

​ 可是我并没有那么长的时间，像学习之前这两者一样，逐一学习，实现，可视化。如果每个都探索，也背离了我写这个blog的初衷，我还有别的事情需要做。

End

​ “吾生也有涯，而知也无涯。”

赏

谢谢你请我吃糖果

微信