二叉树

阅读数: 次 2023-04-18

在没有高人指点的情况下，人没法每一步都踏在鼓点上。总会因为短视，各种原因而犯一些错误。最常见的就是在特定的时间做错误的事情。比如在某个考试的时候把B划成A，在刚入学时报了什么实验班，在大二的时候没有好好学数据结构。

我们在这里重点关注二叉树（binary tree）的创建，操作，递归遍历，非递归遍历。接着我们会将讨论范围沿申到二叉搜索树（binary search tree），平衡二叉树（balanced binary tree）。

二叉树即一种一个父节点（parent nodes）最多有两个孩子结点（child nodes）的结构。它有5条重要的性质（我也是现在才知道他们为什么重要）：

我们约定根节点的层数为1，且对数的底为2（all logarithms are to the base 2）。

在二叉树的第$i$层上最多有$2^{i-1}$个结点。（$1,2,4,8,…,2^{i-1}$）

深度为$k$的二叉树最多有$2^{k}-1$个结点。直接进行等比数列（geometric progression）求和即可。此时我们称它为满二叉树

对于任意一棵二叉树$T$，如果其叶子结点，也就是那些度为0的结点的个数为$n_0$，度为2的结点（即左右孩子都有的结点）的个数为$n_2$，则有$n_0=n_2+1$。

这是由于，对于任意一个二叉树，我们都可以将来自父结点的那条边看成“入“的分支（即使二叉树是无向图），除根节点以外，每个结点都有这个性质。所以总边数$e$与总结点数$n$有：$n=e+1$。同时我们也可以看成每一条边都是度为1和度为2的结点发出，于是$e=n_1+2n_2$，且$n=n_0+n_1+n_2$。所以联立得$n_0=n_2+1$。

具有$n$个结点的完全二叉树的深度为$[\mathrm{log}n]+1$，$[\cdot]$为下取整。

对于$n$个结点的完全二叉树，我们按照从上到下，从左到右进行连续编号$1,2,…,n$。这样可以直接得出线性序列：

若$i=1$，则$i$是二叉树的根；若$i>1$，则$i$的父结点是$[i/2]$

若$2i\le n$，则$i$的左孩子为$2i$，否则无左孩子。

若$2i+1\le n$，则$i$的右孩子为$2i+1$，否则无右孩子。

作为二叉树的一个结点，它需要有左孩子，右孩子，和自己的数据域。所以我们将这样的一个结点定义为一个结构体。

typedef int datatype;

typedef struct tree
{
	datatype data;
	struct tree *l_child;
	struct tree *r_child;
}tree;

我们可以使用前序遍历的方式来创建一个二叉树，当然，现在我们并不知道何为前序遍历。我们可以先手动创建一个二叉树，就像这样：

tree* CreateBinaryTree()
{
    tree* node1 = (tree*)malloc(sizeof(tree));
    tree* node2 = (tree*)malloc(sizeof(tree));
    tree* node3 = (tree*)malloc(sizeof(tree));
    tree* node4 = (tree*)malloc(sizeof(tree));
    tree* node5 = (tree*)malloc(sizeof(tree));
    tree* node6 = (tree*)malloc(sizeof(tree));

    node1->data = 1;
    node2->data = 2;
    node3->data = 3;
    node4->data = 4;
    node5->data = 5;
    node6->data = 6;

    node1->l_child = node2;
    node1->r_child = node4;
    node2->l_child = node3;
    node2->r_child = NULL;
    node4->l_child = node5;
    node4->r_child = node6;

    return node1;
}

int main(){
	tree* mytree = CreateBinaryTree();
	printf("%d", mytree->data);
	return 0;
}

运行后，我们可以得到1，这是我们置于根结点的value。

递归遍历

在二叉树这里，我们重点关注前序，中序，后序遍历。二叉树的层序遍历实际上就是图的广度优先搜索，我们可以到时候再看。

下面，我们可以通过前序(PreOrder)，中序(InOrder)，后序(PostOrder)遍历来对这个二叉树进行线性化：

void PreOrder(tree* root)
{
	if(root == NULL)
	{
		//printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->l_child);
	PreOrder(root->r_child);
}

void InOrder(tree* root)
{
	if(root == NULL)
	{
		//printf("NULL ");
		return;
	}
	InOrder(root->l_child);
	printf("%d ", root->data);
	InOrder(root->r_child);
}

void PostOrder(tree* root)
{
	if(root == NULL)
	{
		//printf("NULL ");
		return;
	}
	PostOrder(root->l_child);
	PostOrder(root->r_child);
	printf("%d ", root->data);
}

我们可以注意到，用递归实现的前序，中序，后序十分简洁和易懂，它们只需交换一些顺序，即可达成不同的遍历方式。

我们可以得到如下的线性化序列：

PreOrder:
1 2 3 4 5 6
InOrder:
3 2 1 5 4 6
PostOrder:
3 2 5 6 4 1

可视化如下：

非递归式的遍历

上述是用递归来实现遍历的，那么自然我们也可以模拟非递归的方式。虽然这个遍历过程，作为对一个非线性结构的线性化，时间复杂度不管是递归还是非递归，都是$O(n)$。然而，后续在计组，微机原理里，我们都知道，如果一直通过递归函数调用自身来实现，每个递归函数的调用需要在系统堆栈中保存一些信息，导致实现的空间复杂度较高。所以我们有必要实现一下非递归的遍历。同时，非递归的遍历涉及到记录访问结点，这在后续也会频繁用到。

我们先考虑前序遍历，直观上，前序遍历是先“处理”（这里就是printf)了中间结点，然后依次“访问”左孩子和右孩子。“访问”左孩子时，会先“处理”左孩子，然后接着“访问”左孩子的左孩子……

所以我们可以先将右孩子入栈，再将左孩子入栈。这样就可以达到我们要的先左后右的要求。然后每一次都让栈顶元素弹出。

这里我们就只用一个tree*的指针数组来模拟栈了，就不去补全栈的代码了。

void PreOrder(tree* root) {
    tree *stack[MAXSIZE], *node;//模拟栈
    int top = 0;
 
    if (root == NULL) {
        printf("树为空树!\n");
        return;
    }
    else {
        top++;
        stack[top] = root;
        while (top > 0) {
            node = stack[top];
            top--;
            printf("%d ", node->data);
 
            if (node->r_child != NULL) {
            	top++;
                stack[top] = node->r_child;
            }
            if (node->l_child != NULL) {
            	top++;
                stack[top] = node->l_child;
            }
        }
    }
}

####output:####
#PreOrder:
#1 2 3 4 5 6

上面就是非递归的前序遍历的实现，接下来，我们考虑如果我们先右孩子后左孩子，如果我们先让左孩子入栈，再让右孩子入栈。这其实相当于“先右后左”的前序遍历，如果我们这样做，设想一下：对于输出出的序列，根结点始终是在最左侧的，由于我们按照“中右左”的顺序，每一个子结构的根结点（也就是中），它们都在子结构在序列的相对位置里的最左侧。

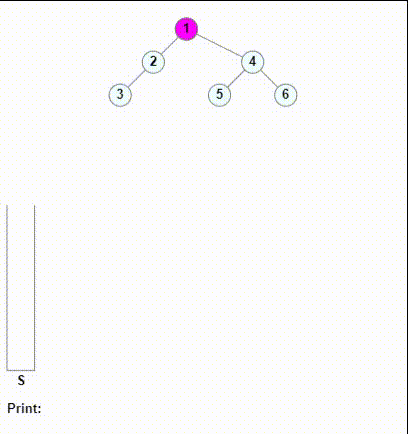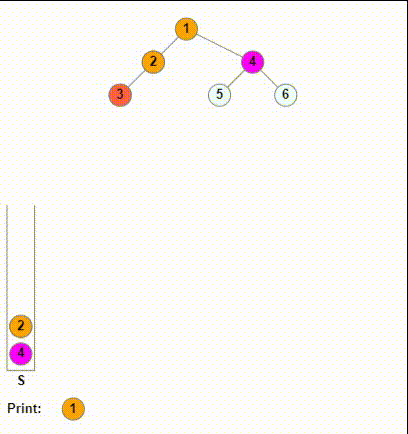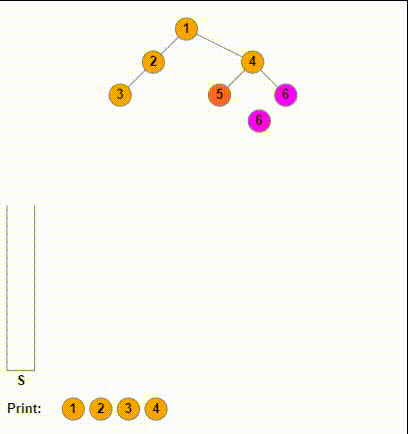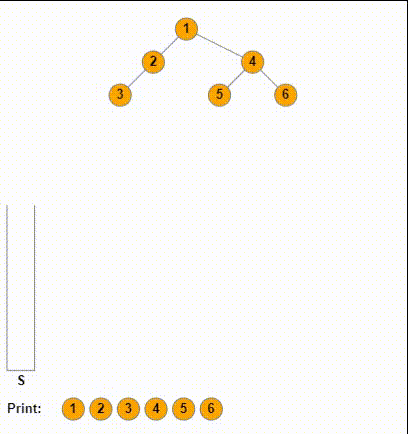
所以我们可以直接翻转我们“中右左”得到的序列，这样就能得到“左右中”的后序遍历的序列。具体来说，我们可以通过一个辅助的栈来实现。

然而如果我们想接着实现非递归的中序遍历，就会有一些问题了。我们再观察前面两个非递归遍历的逻辑，核心在于，对于一个不为空的结点，（我们任何时候都可以视它为一个结构的根结点），这个结点在被访问到的时候，就立刻被处理/输出了。

而中序遍历没有这样的性质，我们虽然也是从初始的根结点开始，但我们需要先遍历完整个左子树，才会输出原来的根结点。所以在刚才的那种逻辑（栈非空时，输出栈顶元素，然后先右后左的让子树入栈）很适合前序和后序，但不适合中序。

所以，我们可以尝试更改一下逻辑：

void InOrder(tree* root)
{
	tree *stack[MAXSIZE], *node;
	int top=0;
	
	if(root == NULL)
	{
		printf("树为空树!\n");
		return;
	}
	else{
		node = root;
		while(node!=NULL || top > 0)
		{
			if(node!=NULL)
			{
				// printf("%d ", node->data); 在这里输出可以实现前序遍历 
				top++;
				stack[top] = node;
				node = node->l_child;  //遍历左子树 
			}
			else
			{
				node = stack[top];
				top--;
				printf("%d ", node->data);  //输出 
				node = node->r_child;  //遍历右子树 
			}
		}
	}
}

这里我们使用类似一路向左的操作，本质上是使用栈记录搜索的路径。然后当探测到接下来的某个孩子为空时，再进行输出。

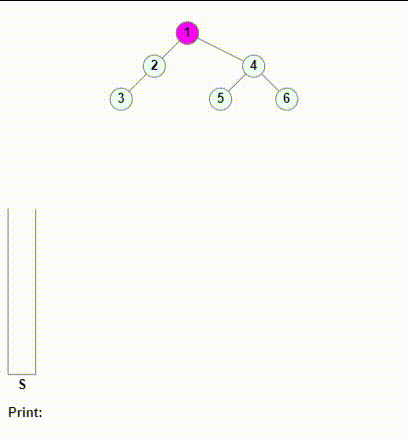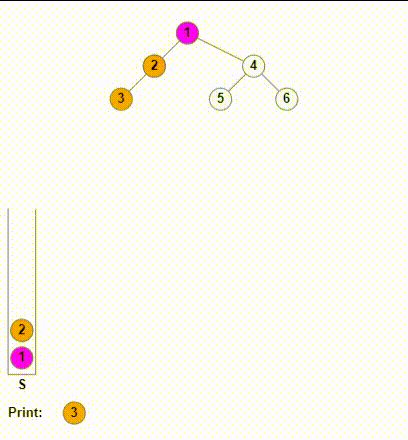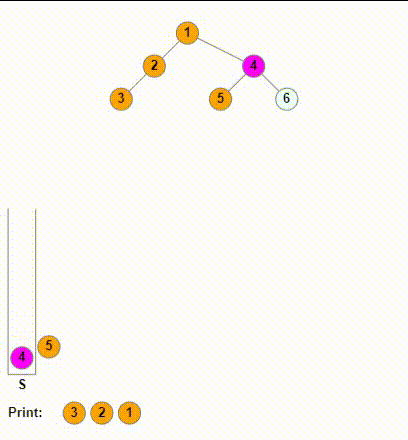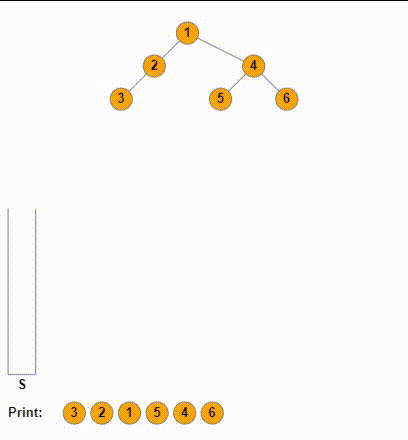
在上面代码的逻辑中，我们是先将一路向左的结点全入栈了，当到叶子结点时，叶子节点的左子树为空。所以我们会走else分支，如果此时我们是在出栈后，进行一次输出，我们就会输出当前的叶子结点。这就是中序遍历；如果我们是把printf放在遍历左子树之前，那么此时我们其实就是先输出了根结点，就是前序遍历。

看起来我们马上可以写出一个更通用的非递归的方式，然而此时一个不好的事情，后序遍历需要先遍历完当前节点的左右子树后再输出当前结点，也就是需要当前结点出栈时，再输出。然而在上面的逻辑中，当前节点出栈后才能访问其右子树，而在右子树遍历完成之前，当前结点已经不在栈中。所以这种写法，可以很好的联系前序和中序，但不适合后序。

自然，我们会想进一步修改一下逻辑：当我们遍历完左子树后，我们先不出出栈，我们接着遍历右子树。自然，我们希望等到右子树也遍历完以后，再输出。我们可以草拟这样的代码：

void PostOrder(tree* root)
{
	tree *stack[MAXSIZE], *node;
	int top=0;
	
	if(root == NULL)
	{
		printf("树为空树!\n");
		return;
	}
	else{
		node = root;
		last_visit = NULL;
		while(node!=NULL || top > 0)
		{
			if(node!=NULL)
			{
				top++;
				stack[top] = node;
				node = node->l_child;  //遍历左子树 
			}
			else
			{
				node = stack[top];
				if(node->r_child == NULL)
            	{
	                //如果右子树为空, 输出节点
	                printf("%d ", node->data);
	                top--;
                    node = NULL;
            	}
				else
				{
					node = node->r_child;  //遍历右子树 
				}
			}
		}
	}
}

然而这样的操作会有一个问题，我们举一个简单的例子来说明：

我们输入根结点1，根据后序遍历，我们先遍历其左子树，我们到达了2。我们将2入栈，然后遍历2的左子树，即4。将4入栈。接着，4没有左子树，执行else。（注意，我们这里是top++;stack[top]=node;node=node->l_child;也就是说，我们先是将栈顶指针+1，然后把4存入栈顶，接着node变为了4的左子树（空），所以下一个循环中，因为node是NULL，所以在else里，stack[top]其实是4，会把4再赋值给node。）

然后，我们发现，4的右子树也是空，于是我们输出了结点数据，即4，然后栈顶指针回退。同时将node设为NULL，强制退栈（不然下一个循环里，会因为node是4不是NULL，而又把node入栈）。此时由于top—;由于node是NULL，所以我们还会来到else这里，此时node=stack[top]会把2赋值给node，然后2的右子树，即5，非空。所以node现在是5了。

node为5以后，走if，入栈。遍历其左子树，发现是空。于是就像刚才4那样，在else里，node变回了5，然后由于5没有右子树，所以此时输出。5出栈，node变为NULL。然后，问题来了，此时node是NULL，我们会走else，然后在else里，node=stack[top]，node又变回了2！虽然这是正常的，但我们现在希望的是，即然已经完成了左右子树的遍历，现在直接输出2就好了。可是在我们程序的设计里，程序本身并不知道此时已经完成了右子树的遍历，它会陷入一个死循环。

一种解决这一死循环的办法是，引入一个辅助指针last_visit。例如在刚才我们所说的，程序即将陷入死循环，此时程序会继续因为2的右子树5不为空，进行else里的else。然而此时，如果我们记录了一个last_visit，就是5。然后把它放在else下的if条件里，我们就可以避免重复的右子树遍历：

void PostOrder(tree* root)
{
	tree *stack[MAXSIZE], *node, *last_visit;
	int top=0;
	
	if(root == NULL)
	{
		printf("树为空树!\n");
		return;
	}
	else{
		node = root;
		last_visit = NULL;
		while(node!=NULL || top > 0)
		{
			if(node!=NULL)
			{
				top++;
				stack[top] = node;
				node = node->l_child;  //遍历左子树 
			}
			else
			{
				node = stack[top];
				if(node->r_child == NULL || node->r_child == last_visit)
            	{
	                //如果右子树为空或已经访问过，就可以输出节点
	                printf("%d ", node->data);
	                top--;
	                last_visit = node;
	                node = NULL;  //将node设为NULL，强制退栈
            	}
				else
				{
					node = node->r_child;  //遍历右子树 
				}
			}
		}
	}
}

然而这种记录路径的方法，好像也没能那么统一。（但是这种记录路径的操作在后面应该熟练掌握）

我们接着考虑会最早给出前序遍历的例子，我们核心关注这个部分：

top++;
stack[top] = root;
while (top > 0) {
    node = stack[top];
    top--;
    printf("%d ", node->data);

    if (node->r_child != NULL) {
        top++;
        stack[top] = node->r_child;
    }
    if (node->l_child != NULL) {
        top++;
        stack[top] = node->l_child;
    }
}

我们之所以不能便捷的通过交换几行代码来实现不同遍历方式的切换，是因为在每个循环的开头，stack都会立刻出栈，并且输出一个内容。它并不知道自己在输出一些什么，只知道那是个有效值。同样，我们也并没有指明，谁是要输出的结点。当然，因为前序遍历的逻辑，被输出的那个一定是根结点。

所以一个很聪明的办法是显式的给出，什么是要输出的结点。具体来说，我们手动对其进行入栈，并且使用一个空指针来标记它：

void InOrder(tree* root)
{
	tree *stack[MAXSIZE], *node;
	int top=0;
	
	if(root == NULL)
	{
		printf("树为空树!\n");
		return;
	}
	else{
		top ++;
		stack[top] = root;
		node = root;
		while(top > 0)
		{
			node = stack[top];
			if(node!=NULL)
			{
				node = stack[top];  //去重
				top--;
                //
				if(node->r_child != NULL)  //右子树
				{
					top++;
					stack[top] = node->r_child;
				}
				//
				top++;
				stack[top] = node;  //待输出的结点(中)
				
				top++;
				stack[top] = NULL;  //空指针作标记
				//
				if(node->l_child != NULL)  //左子树
				{
					top++;
					stack[top] = node->l_child;
				}
                //
			}
			else
			{
				top--;
				node = stack[top];
				top--;
				printf("%d ", node->data);  //输出 
			}
		}
	}
}

我们可以观测栈的变化来理解这段代码的功能，对于我们刚才一直举例子的二叉树：

其栈的变化是：

InOrder:
1
4 1 NULL 2
4 1 NULL 2 NULL 3
4 1 NULL 2 NULL 3 NULL output: 3
4 1 NULL 2 NULL output: 2
4 1 NULL output: 1
4
6 4 NULL 5
6 4 NULL 5 NULL output: 5
6 4 NULL output: 4
6
6 NULL output: 6

最开始，1入栈，为了防止重复同时退栈。接下来以右中左的顺序入栈。得4 1 NULL 2。此时node更新为栈顶元素2，即开始遍历左子树。首先将2弹出一次，防止下面标记时重复。由于2的右子树是空的，所以第一个if没有起效，然后我们又将2入栈，这次连同空指针的标记。然后是2的左子树3入栈。最后得到了4 1 NULL 2 NULL 3

此时，3没有左右子树，我们执行刚才的过程，只会让3出栈以后再入栈，然后再顶一个NULL。于是栈顶元素变成了空指针，触发标记。下一次3和NULL都被输出了。然后输出的就是2，1。这说明左子树遍历完成，且根结点也输出了。现在栈顶元素只剩下了4，也就是1的右子树。所以刚才的过程会再来一遍，来遍历右子树，最终得到了中序遍历的结果。

调整右子树，输出结点，左子树的位置，即可实现不同的遍历方式。比如我们将输出根结点和加标记与下面的遍历左子树交换，运行后可以得到：

PreOrder:
1
4 2 1 NULL output: 1
4 2
4 3 2 NULL output: 2
4 3
4 3 NULL output: 3
4
6 5 4 NULL output: 4
6 5
6 5 NULL output: 5
6
6 NULL output: 6

这就是前序遍历，和我们最早给出的那种方式相比，其实就多了一个NULL。如果是与前面遍历右子树交换，即得：

PostOrder:
1
1 NULL 4 2
1 NULL 4 2 NULL 3
1 NULL 4 2 NULL 3 NULL output: 3
1 NULL 4 2 NULL output: 2
1 NULL 4
1 NULL 4 NULL 6 5
1 NULL 4 NULL 6 5 NULL output: 5
1 NULL 4 NULL 6
1 NULL 4 NULL 6 NULL output: 6
1 NULL 4 NULL output: 4
1 NULL output: 1

至此，我们终于得到了一种，在非递归下也可以通过交换顺序来实现不同种遍历的方法。

遍历算法的应用

虽然我们花费了相当多的时间在非递归的遍历上，但大多数时候我们还是只会应用递归的办法，前者更多的意义在于分析层面。现在我们给出一些遍历算法的应用。

例如，我们可以按照前序遍历的思路，给出一个创建二叉树的方式：

tree *Create_Tree()
{
	tree *root;

	char val;
	
	scanf("%c", &val);//通过输入的ch是否为特殊符号来判断该节点是否有孩子节点
	getchar();
	
	if(val == '#'){	//不存在孩子节点
		return NULL;
	}
	else{
		root = (tree*)malloc(sizeof(tree));
		if(NULL == root){
			printf("创建失败\n");
			return NULL;
		}
		
		root->data = val - '0';
		root->l_child = Create_Tree();//存在左孩子节点，递归调用本函数，使得左孩子节点先被赋值
		root->r_child = Create_Tree();
		return root;
	}
}

以下是几个测试用例的输出来便于理解二叉树：

e.g.1:
1 2 # # 3 # #
PreOrder:1 2 3
InOrder:2 1 3
PostOrder:2 3 1
  1
 / \
2   3

e.g.2:
1 2 # # 3 4 # # 5 # 6 # #
PreOrder:1 2 3 4 5 6
InOrder:2 1 4 3 5 6
PostOrder:2 4 6 5 3 1
              1
             / \
            /   \
           /     \
          /       \
         /         \
        /           \
       /             \
      2               3
                     / \
                    /   \
                   /     \
                  4       5
                           \
                            6

e.g.3:
1 2 3 # # 4 5 # # 6 # # 7 # #
PreOrder:1 2 3 4 5 6 7
InOrder:3 2 5 4 6 1 7
PostOrder:3 5 6 4 2 7 1
              1
             / \
            /   \
           /     \
          /       \
         /         \
        /           \
       /             \
      2               7
     / \
    /   \
   /     \
  3       4
         / \
        5   6

实际上，在最后使用命令行画二叉树时，需要先知道树的深度，才能分配宽和高的内存空间。这其实就是遍历算法的另一个应用：

int DeepTree(tree* T)
{
    if(!T)
    {
        return 0;
    }
    return DeepTree(T->l_child)>DeepTree(T->r_child)?DeepTree(T->l_child)+1:DeepTree(T->r_child)+1;
}

最后return返回时，用到了三目运算符，即(condition)?true:false。当左子树的深度大于右子树的深度时，则返回左子树的深度+1，否则就是右子树的深度+1。（+1是因为我们取根结点所在的那层为1）

此时的遍历其实是后序遍历，这样比较符合人们求解二叉树高度时的思维。

有时我们还想统计一些特定结点的数目，比如叶子结点的数目，度为1的结点的数目，度为2的结点的数目。我们可以按照中序遍历的思想来实现：

int countleaf(tree* root)
{
	if(root == NULL)
	{
		return 0;
	}
	if(root->l_child==NULL && root->r_child==NULL)
	{
		return 1;
	}
	return (countleaf(root->l_child) + countleaf(root->r_child));
}

int countparent(tree* root)
{
	if(root == NULL)
	{
		return 0;
	}
	if(root->l_child!=NULL && root->r_child!=NULL)
	{
		return 1 + countparent(root->l_child) + countparent(root->r_child);
	}
}

###e.g.###
1 2 3 # # 4 5 # # 6 # # 7 # #
              1
             / \
            /   \
           /     \
          /       \
         /         \
        /           \
       /             \
      2               7
     / \
    /   \
   /     \
  3       4
         / \
        5   6
leaf nodes num: 4
parent nodes num: 3

在countleaf中，由于我们统计的是叶子结点，所以我们只在找到叶子结点时返回1。这是由于叶子结点一定是遍历某个子树的最后了。在countparent时，当我们确定了某个结点有两个度后，我们要在加1的同时，继续搜索它的左子树和右子树。这使得两段代码的逻辑有略微的不同。

从输出结果上，我们看到了$n_0=n_2+1$。

此时，仔细观察我们输入一串前序遍历序列，然后构建一颗二叉树的过程。实际上，我们输入的是扩展二叉树的前序遍历序列，即标记了空结点#的那些。前序遍历和后序遍历，我们都能在序列的开头或结尾确定根结点。实际上在输入这个序列时，我们就能感觉的出来：扩展二叉树的前序遍历和后序遍历可以唯一确定一颗二叉树。

那么另一个有意义的问题是，如果我们给出的是普通二叉树的遍历序列，我们如何恢复一个二叉树。在给出具体的策略之前，我们先感受一下两者的不同：

考虑1 2 3 # # 4 5 # # 6 # # 7 # #作为一个前序序列，前序遍历是根左右的，我们可以自然的进行分析：

1一定是根结点，2一定描述的是左子树。将2视作根结点，3一定是它的左孩子。由于3需要有一个交代（因为这里是扩展二叉树），所以3后面的那个不管是什么，都会是3的左孩子。

然后我们发现3的左孩子是空的，所以可以肯定，下一个成员一定是3的右孩子。我们发现3的右孩子也是空的，那么我们可以确定，2的左子树已经遍历完了。

所以4一定是2的右子树，同理，5和6是4的左右孩子，且他们均没有后继（##）。现在我们将2的右子树也探测完了，说明2已经探测完了，也就是1的左子树已经探测完了。接下来下面一个是7 # #。这说明它一定是1的右子树，且后面没有后继结点。

然而，如果#都消失，变成一个普通的前序序列。我们就无法得知关于某个结点在哪里停止这样的情况了。

另一个很显然的观察是：即使有扩展二叉树的中序遍历序列，我们也无法只用中序遍历序列来恢复一颗二叉树。因为我们定位不到根结点。

实际上，对于一颗普通二叉树，我们可以通过前序或后序遍历序列，加上中序序列，来恢复一颗二叉树。这可以看作某种信息的补偿，例如在刚才的例子中：

1 2	PreOrder:1 [2 3 4 5 6] [7] InOrder:[3 2 5 4 6] 1 [7]

我们可以直接恢复一颗二叉树。实际上，这个过程也具有明显的递归性。就像上面的[]标注的一样。现在我们已经处理完了根节点，右子树。现在可以把左子树当成一个整体，继续进行这样的操作：

1 2	PreOrder:1 [2 (3) (4 5 6)] [7] InOrder:[(3) 2 (5 4 6)] 1 [7]

就像我们上面举的这个例子一样，我们可以通过维护一个指向某个子结构（它可能是某个结点的左子树）的子序列（如2 3 4 5 6和3 2 5 4 6, 4 5 6和5 4 6）的指针，来试图编写这样的一个递归程序：

tree *BPI(datatype preod[], datatype inod[], int len)
{
	tree *p;
	p = (tree*)malloc(sizeof(tree));
	if(len == 0)
	{
		return NULL;
	}
	else
	{
		p->data = preod[0];
	}
	
	int m = 0;
	while(inod[m] != preod[0])
	{
		m++;
	}
	
	int len_l = m;
	int len_r = len - m -1;
	
	datatype preod_l[len_l], preod_r[len_r];
	datatype inod_l[len_l], inod_r[len_r];
	
	if(m == 0)
	{
		p->l_child = NULL;
	}
	else
	{
		for(int i = 0; i < len_l; i++)
		{
			preod_l[i] = preod[i + 1];
		}
		for(int i = 0; i < len_l; i++)
		{
			inod_l[i] = inod[i];
		}
		p->l_child = BPI(preod_l, inod_l, len_l);
	}
	if(m == len)
	{
		p->r_child = NULL;
	}
	else
	{
		for(int i = 0; i < len_r; i++)
		{
			preod_r[i] = preod[len_l + i + 1];
		}
		for(int i = 0; i < len_r; i++)
		{
			inod_r[i] = inod[m + i + 1];
		}
		p->r_child = BPI(preod_r, inod_r, len_r);
	}
	return p;
}

上面的代码只是作为一个演示，我并没有完善的实现一个切片操作，只是单纯的演示一下根据根结点找左右子树。上述代码显然会占用更多的空间。

以下是测试样例：

PreOrder:
1 2 3 4 5 6 7
InOrder:
3 2 5 4 6 1 7
              1
             / \
            /   \
           /     \
          /       \
         /         \
        /           \
       /             \
      2               7
     / \
    /   \
   /     \
  3       4
         / \
        5   6

在上述应用中，我们都使用的是递归的方法。但同时，我们也要记住非递归遍历时的思想。因为有时候我们可能被要求用非递归的办法来实现递归的操作。

End

这一篇里给出了二叉树的基本概念。只有掌握了基本概念，我们才能借助这个结构实现更复杂和有效的算法。如果我还有一次重来的机会——可惜没有如果。