大概几个月前,我从零开始上手了一个生成任务。那个任务用到了风头正盛的扩散模型,我当时对此知之甚少,简单入门以后就去做了,边做边学。这篇blog便是对扩散模型的一些更全面的梳理。
这个梳理将会依次介绍在炼丹里,扩散模型的发展历程;本质上是为了全面地理解开源的gaussian_diffusion.py里的代码。因为,假如,你准备开源一个自己的小玩意,结果人家一看发现你的diffusion是自己搓的那种demo的实现,会显得有亿丢丢不专业。而且自己山寨的实现,不容易和后面更为先进的成果结合,复用性不强。主流的做diffusion应用的人们,都会使用openAI的gaussian_diffusion.py,包括后续的加速采样的方法,也是直接照着这个类wrap的。所以有必要看懂那个gaussian_diffusion.py。
然而除了一些语法上的不习惯以外,根本不知道那个代码每个func的功能是最麻的,因为那是在原有的DDPM基础上的极大改进和扩展。所以这篇blog并不能囊括所有关于扩散模型的进阶知识,因为我水平有限,并且,篇幅也有限。
我们先回忆一下,初始的DDPM的大概:
我们建立了一个符合一阶马尔可夫性的噪声链条,我们用正态分布建模了加噪过程$p\left( \boldsymbol{x}_t|\boldsymbol{x}_{t-1} \right) $,并且用重参数化技巧,得到了$p\left( \boldsymbol{x}_t|\boldsymbol{x}_{0} \right) $的表示。这完成了前向扩散的整个过程。接下来引入了热力学里的神奇结论:“逆向扩散时只要步数够小,就可以近似为高斯的”。我们知道了$q\left( \boldsymbol{x}_{t-1}|\boldsymbol{x}_{t} \right) $是可以符合高斯性的,接着我们从$q\left( \boldsymbol{x}_{t-1}|\boldsymbol{x}_{t}, \boldsymbol{x}_{0} \right) $开始推导,得到了我们的优化目标:
回忆了上述DDPM的基础以后,我们开始陆续介绍后续的改进。
Improved DDPM
Improved DDPM简称IDDPM,是openAI提出的优化DDPM的几个至关重要的点。这其中的有些给后续工作带来了很大的启发,但有些,人们很少使用。
Improved Log-likelihood
在之前推理DDPM时,我们有$q\left( x_{t-1}| x_t,x_0 \right) =\mathcal{N} \left( x_{t-1};\tilde{\mu}\left( x_t,x_0 \right) ,\tilde{\beta}_t\boldsymbol{I} \right) $,我们是通过这个式子来进行推导的:
然后我们带入了高斯分布的解析式,进行配方,整理,发现方差是固定的:
在这里稍微暂停一下,因为有个概念至少在我上一篇关于DDPM的blog里并没有说清。首先,我们还是想要建模$q\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t \right)$的,但是这个建模并不容易,因为:
在从始至终的推导中,我们都不知道$q\left( \boldsymbol{x}_{t-1} \right) ,q\left( \boldsymbol{x}_{t} \right) $的表达式,所以引入了$\boldsymbol{x}_0$,得到了$q\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t, \boldsymbol{x}_0\right)$,这个式子是有显式解的。而且距离我们想要的$q\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t \right)$还多了一个$\boldsymbol{x}_0$。
我们之前都是直接说,学习一个模型$p_\theta\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t\right)$来逼近$q\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t \right)$,这个切入的角度有些令人不知所云。其实一个更好的角度是:“我们想用$\boldsymbol{x}_t$来表示$\boldsymbol{x}_0$,这样$q\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t, \boldsymbol{x}_0\right)$中的$\boldsymbol{x}_0$就可以被消去了”。而加噪时,重参数化的式子即是:
所以只要我们有准确的噪声预测,即$\boldsymbol{\epsilon }_\theta \approx \boldsymbol{\epsilon }$,我们就可以一步到位!换句话说,给定网络$t$时刻的$\boldsymbol{x}_t$,网络直接预测的结果就可以直接返回$\boldsymbol{x}_0$,那为什么还要reverse多次呢?我们可以理解为数值分析中的“预估-修正”,就像龙格库塔解微分方程。这其中还有更加深入的原因(有没有一种可能,我是说可能,这个过程本身就是在解一个ODE?),关系到扩散模型的加速采样,这里先按下不表。
我们接着说回来方差固定,实验表明,具体设定那个方差为$\sigma _{t}^{2}=\beta _t$还是$\sigma _{t}^{2}=\tilde{\beta}_t$不太影响生成质量。原因是在step比较大的时候,这俩近似是相等的。这说明,如果扩散步骤非常非常的多,那么方差不会影响样本质量,只有均值来决定数据分布。
但是同时,实验又发现,在step很小的时候,计算的变分下界(可以理解成损失函数的值)往往是比较大的。所以,这就导致了一个问题:如果方差也是可学习的,那么变分下界的值会不会还能低一些?这样生成质量就能更好些。
所以他们提出让模型输出一个向量$v$,用这个$v$来调度待学习的方差:
然后,为了更新方差,让其“可学习”,损失函数被更新为了:
这里的$L_{\mathrm{vlb}}$就是之前推导时,我们还没把KL散度打开时的损失。因为$L_{\mathrm{simple}}$其实是我们“认为”方差是固定所推导出的结果,所以这里再次引入变分下界,可以用来学习方差。$\lambda$当然就靠调参了。
当然,为什么人们一开始就不用$L_{\mathrm{vlb}}$,因为其很难优化。IDDPM中展示直接优化这种loss,梯度噪声极大。所以他们引入重要性采样来缓解,这也是一种方法。
Improved scheduler
同时,这篇论文给出了一种新的噪声调度器,即“余弦”式的,相比于线性调度器,他直观上不会让信息消逝的那么快。具体到个人的实验上有哪个好,主要靠试。典型的除了Linear, Cosine,其实还有Sqrt, Sigmoid等调度器,只不过比较小众。一般用Cosine就挺合适的了。
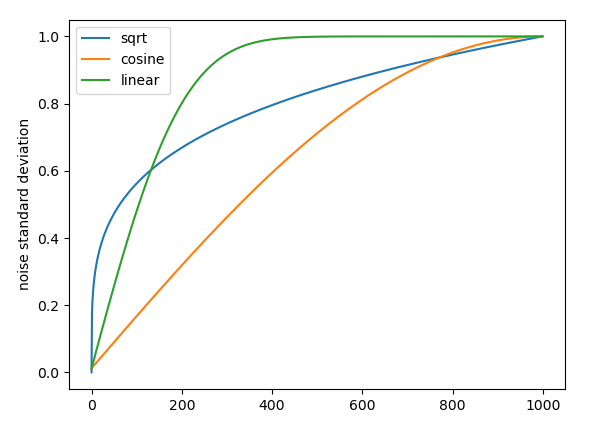
但是根据我的使用经验,具体是什么scheduler还要结合所生成的内容的性质和分布。比如你需要生成的内容最终是低频,光滑的,那么最好就不要用sqrt调度器。因为其在$t$很小时,sqrt的噪声量级仍然很大。但高频,一定程度上也意味着,会有更多的细节(如果被训练的完备的话)。我们很难说对于自然图像,或者序列数据的这个分布,需要额外的噪声来逼近细节是否合理。但如果是latent space的话,谁知道呢?没准有奇效。
Class-condition
这篇论文最后指出,将类别信息和时间步一起,送入model中建模。这样就可以指定类别的生成了。当人们通过这篇论文确定了,这样做是会work以后,铺天盖地的工作就都来了。这些后面再说。
Denoising Diffusion Implicit Models
Denoising Diffusion Implicit Models简称DDIM,这里的Implicit突出一个“隐式”。我们思考一下DDPM最后的结果,在训练时,给出一个样本,重参数化后加噪的$t$步,然后在输入$\boldsymbol{x}_t,t$的情况下预测$\epsilon_t$。采样时,我们从认定一个高斯噪声为$T$时的样本,然后估计其$\boldsymbol{x}_0$,再加噪回$T-1$步,如此往复(这个步骤其实就是$q\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t, \boldsymbol{x}_0\right)$,用训练好的$p_\theta$估计$\boldsymbol{x}_0$)。我们下面依次来看:
在训练时,损失只条件于$\boldsymbol{x}_0$,并不是条件于整个前向过程。也就是说,加噪的那个过程,它可以不是马尔可夫的。最开始,在马尔可夫假设下,随机变量序列的联合概率分布可以写作:
而现在,我们发现训练时,我们并不需要严格按照这个马尔可夫性来操作。我们可以对它进行任意的因式分解,让它不满足马尔可夫假设。只要其边缘分布$p(\boldsymbol{x}_T|\boldsymbol{x}_0)$的形式还是高斯的,我们就仍然可以用原来的损失函数来优化。
在采样时,我们关注了:
我们之前讨论时,是说因为$q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$不好处理,所以再考虑有$\boldsymbol{x}_0$时的条件分布。同时,分子的第一项其实应该是$q\left(\boldsymbol{x}_t | \boldsymbol{x}_{t-1},\boldsymbol{x}_0\right)$,只是由于马尔可夫假设,消去了$\boldsymbol{x}_0$。
但是,引入了$\boldsymbol{x}_0$后可以带来另一个视角。注意$q\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t, \boldsymbol{x}_0\right)$式的意义,给定$\boldsymbol{x}_0$条件下的$\boldsymbol{x}_{t-1}$的分布。那么不妨直接从$\boldsymbol{x}_0$开始:
但采样时我们还是不知道$\boldsymbol{x}_0$,所以我们要用$\boldsymbol{x}_t$来估计:
我们发现,我们并不需要知道$q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1})$,这似乎并不影响我们写出上面的那个式子。我们可以甚至可以跳步取角标,直接列写$q\left( \boldsymbol{x}_{k}|\boldsymbol{x}_s,\boldsymbol{x}_0 \right)$。
通过对训练和采样时的分析,我们意识到,好像$q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1})$可以舍去,也就是说我们可以抛弃马尔可夫性,来进行跳步。我们考虑之前推导$q\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t, \boldsymbol{x}_0\right)$时的公式,这次我们不借助马尔可夫假设:
感性的讲,去掉一个约束$q\left( \boldsymbol{x}_t|\boldsymbol{x}_{t-1},\boldsymbol{x}_0 \right) $,这似乎会“扩大”我们的解空间。在概率论中,我们想移除这一项的约束,只需简单的进行一些变换,对两边进行积分,消去条件概率:
不要忘记条件概率密度函数的性质:
不要被此时突然袭击的教科书符号系统吓到,其实它很好推出来,而且意思其实也很显然:给定$y$条件下,所有$x$出现的概率之和为1。得:
由于在先前,我们忠实的推导DDPM时,我们最后得出的$q\left( \boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0 \right) $是一个正态分布。我们现在破除了一个约束,试探性地,我们设$q\left( \boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0 \right) $为:
同时,$q\left( \boldsymbol{x}_{t-1}|\boldsymbol{x}_0 \right) $和$q\left( \boldsymbol{x}_{t}|\boldsymbol{x}_0 \right) $是已知的:
为什么这里假设其均值是$\boldsymbol{x}_{t-1}$和$\boldsymbol{x}_t$的线性加权,因为之前DDPM里,我们严格推出来的均值正符合这种形式,当时它是:
所以这里的假设是很合理的,我们在不显式的使用“$q\left( \boldsymbol{x}_t|\boldsymbol{x}_{t-1},\boldsymbol{x}_0 \right) $是正态分布”的结论下,探索更一般的$q\left( \boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0 \right)$形式。
回到上面那个左边是积分右边是$q\left( \boldsymbol{x}_{t-1}|\boldsymbol{x}_0 \right) $的方程中。左边的积分,实际上不是一个让我们带入概率密度函数然后一下子开带,或者直接贝叶斯开始代换(那样会代换回去,因为等号两边本来就是相等的)。这个积分式是一个纯粹的数学语言。它是说,对于$q\left( \boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0 \right) q\left( \boldsymbol{x}_t|\boldsymbol{x}_0 \right) $这个联合分布,那些同时满足:
的$\boldsymbol{x}_{t-1}$的分布函数,关键在于,联合分布允许了我们将上式两个式子中的$\boldsymbol{x}_t$进行代换,代换后,根据待定系数法,我们会化简得到:
化简过程中会用到正态分布的叠加性来消掉$\varepsilon _1,\varepsilon _2$。根据上式我们也能看出,三个未知数,但只有两个方程,多了一个自由度,我们取$\sigma_t$为自由度。
最终我们得到了一个十分有趣的结论,将$k_t,l_t$带入,一顿化简,将$\bar{\beta}$全统一成$\bar{\alpha}$后,我们得到:
实际上,这个式子完全就是之前DDPM中:
用一个$\sigma_t^2$来给$\epsilon _{\theta}\left( \boldsymbol{x}_t,t \right) $和$\epsilon $加权,这里可能有同学会纳闷$\epsilon _{\theta}\left( \boldsymbol{x}_t,t \right) $是怎么来的?事实上:
它是这样相互估计来的。$\boldsymbol{x}_0$和$\epsilon _{\theta}\left( \boldsymbol{x}_t,t \right)$是模型的两种输出,模型本身抑或估计噪声抑或估计$\boldsymbol{x}_0$。我们之所以换算成这种形式,是因为这会带来一种很好的视角(注意公式下面的三个文字注解):
我们接下来用一种更直观的图示来理解一下上面的那个式子,就像中学时的尺规作图一样,我们约定刚才的$\boldsymbol{x}, \epsilon…$都发生在二维平面里:
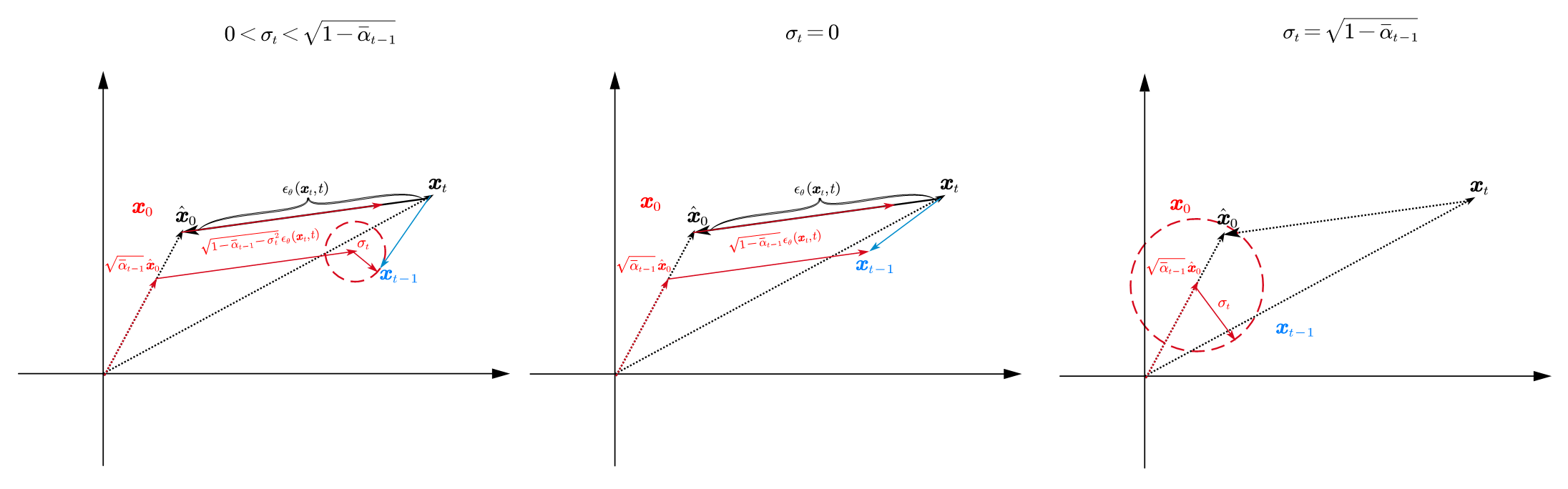
上面三个图展示了在三种$\sigma_t$的情形下,整个去噪过程的形态。首先我们知道,如果噪声预测网络非常的准确,非常的神奇,那么直接就有$\boldsymbol{x}_0=\boldsymbol{x}_t-\epsilon _{\theta}\left( \boldsymbol{x}_t,t \right) $。然而实际上并没有那么容易,所以我们用估计出的$\boldsymbol{\hat{x}}_0$来替代上式的$\boldsymbol{x}_0$。这样,在图上,反映出来的就是$\boldsymbol{\hat{x}}_0$和$\boldsymbol{x}_0$的位置不同,我们可以通过此时的$\boldsymbol{x}_t$和$\boldsymbol{x}_0$来确定预测出的噪声向量$\epsilon _{\theta}\left( \boldsymbol{x}_t,t \right) $。然后,公式中的“direction pointing to $\boldsymbol{x}_t$”,自然就如图所示了。
所以,从$\boldsymbol{x}_t$得到$\boldsymbol{x}_{t-1}$,相当于三个向量相加。当$\sigma_t =0$时,最后的那个噪声项,由于噪声是随机的,我们就视作一个圆吧,就消失了。于是整个过程就是确定性的了。此时就是,DDIM。所以,DDIM的I(implicit),就指的是“隐式的概率模型”,因为它推出来的结果其实是确定性的。
当$\sigma _t=\sqrt{1-\bar{\alpha}_{t-1}}$时,指向$\boldsymbol{x}_t$的向量就消失了。此时就是朴素的DDPM。
当然,如图上所示,我们相加时的三个向量,其中第一个是$\sqrt{\bar{\alpha}_{t-1}}\boldsymbol{\hat{x}}_0$,并不是$\boldsymbol{\hat{x}}_0$本身。自然,这是公式整理出的直接结果。其实,在后面如果有机会,我介绍score-based model时,我们会发现,从这个角度来理解,会对这个$\sqrt{\bar{\alpha}_{t-1}}$有更深的理解。现在我们可以给出一个直接的直觉:考虑用朴素的线性调度器时$\sqrt{\bar{\alpha}_{t-1}}$的曲线:
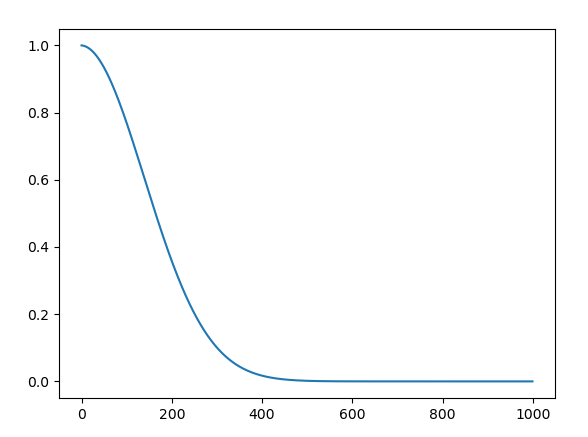
我们发现,当处于比较大的采样步数$t$时,$\sqrt{\bar{\alpha}_{t-1}}$很小,基本就是零。这其实指代的是,在这种比较大的$t$时,预测的$\boldsymbol{\hat{x}}_0$相当不准,所以我们给其分配的权重就比较低。这个地方就先解释到这里了。
所以,在探索了这么多以后,我们其实可以给出一个很简单的DDIM的介绍:
这是最朴素的DDPM的采样公式,而我们只要把$\epsilon$换成$\epsilon _{\theta}\left( \boldsymbol{x}_t,t \right)$,就得到DDIM了:
当然,整个推理过程,我们都没有用到$q(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$,所以我们完全不需要让$t$和$t-1$相邻:
这里我给$\boldsymbol{\hat{x}}_0$加了个角标,写开了是:
所以这自然的引出了“respacing”这个技巧,对于之前的采样序列$\left[ 1,2,…,T \right] $,我们可以跳步的抽取,只采样子序列,比如$\left[ 1,10,…,T \right] $。这样就完成了采样的加速。
总之,学习DDIM有两个目的,从实践的角度来说,它是最容易实现的加速采样;从理论的角度来说,它是理解更深刻的框架的一个基石。
Gaussian Diffusion
接下来要介绍的Gaussian Diffusion并不是一篇论文,只是openAI开源代码里,取的一个文件名叫gaussian_diffusion.py,后来的人们经常基于他们的代码来对diffusion做一些应用,改进。所以得学习一下这个规范diffusion实现。
gassuian_diffusion.py里同时实现了上面介绍的DDIM和IDDPM,所以是一个很好的理论结合实际的例子。
1 | class GaussianDiffusion: |
首先,在初始化方法下,会先注册一些必要的变量,方差的调度器$\beta_t$(betas),模型预测时,均值和方差的类型(“均值”指的是模型是预测噪声$\epsilon$还是预测$\boldsymbol{x}_0$,预测$\boldsymbol{x}_{t-1}$的选项也提供了,但这种方法实践上并不好用;预测方差则就是IDDPM所讨论的,方差到底是不是可学习的。)
我们推导公式时会用到一堆系数,如果这些系数每次都在式子里打一遍,有点呆。所以接下来就是根据betas来计算那些系数,变量名与公式中的对应关系如下:
| 变量名 | 公式 | 备注 |
|---|---|---|
| alphas | $\alpha_t$ | |
| alphas_cumprod | $\bar{\alpha}_t$ | |
| alphas_cumprod_prev | $\bar{\alpha}_{t-1}$ | 初始补一,丢弃最后一位 |
| alphas_cumprod_next | $\bar{\alpha}_{t+1}$ | 末尾补零,丢弃第一位 |
| sqrt_alphas_cumprod | $\sqrt{\bar{\alpha}_{t}}$ | |
| sqrt_one_minus_alphas_cumprod | $\sqrt{1-\bar{\alpha}_{t}}$ | |
| log_one_minus_alphas_cumprod | $\mathrm{log}(1-\bar{\alpha}_t)$ | 在计算可学习的方差时会用到 |
| sqrt_recip_alphas_cumprod | $\frac{1}{\sqrt{\bar{\alpha}_t}}$ | recip即倒数的意思 |
| sqrt_recipm1_alphas_cumprod | $\sqrt{\frac{1}{\bar{\alpha}_t}-1}$ |
接下来是对均值和方差的一些处理:
posterior_variance,后验方差,即我们之前所说的固定的方差:
在DDIM里由于需要对方差取log,同时由于$t=0$时$\beta_0=0$,所以就有了截断的log方差posterior_log_variance_clipped。
posterior_mean_coef1和posterior_mean_coef2分别是这个式子的两个系数:
这个式子其实是最早DDPM时我们要估计的均值,在需要学习方差时,我们需要手动优化$L_{\mathrm{vlb}}$,此时需要计算这一项。
接下来封装了一个被反复用到的静态方法,来广播上面的那些定义好的参数序列:
1 | def _extract_into_tensor(arr, timesteps, broadcast_shape): |
我们下面以q_mean_variance()举例来说明其用处:
1 | def q_mean_variance(self, x_start, t): |
这个函数用来“加噪”,即计算$q(\boldsymbol{x}_t|\boldsymbol{x}_0)$,输入x_start(即$\boldsymbol{x}_0$)和时间步$t$。根据重参数化的结果:
此时的均值即$\sqrt{\bar{\alpha}_t}\boldsymbol{x}_0$,方差即$1-\bar{\alpha}_t$。函数中的_extract_into_tensor即把此时的1-D array抽取第$t$个切片,然后广播成和所要用的张量同一形状,如x_start。
q_mean_variance()并不执行加噪本身,它只是获取此时所需的均值和方差,即获取这个分布。
q_sample()函数则实例化了从这个分布中采样的操作:
1 | def q_sample(self, x_start, t, noise=None): |
q_posterior_mean_variance()用于计算后验分布$q\left( \boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0 \right)$的均值和方差(以及log方差),即$\tilde{\beta}_t, \tilde{\mu}\left( \boldsymbol{x}_t,\boldsymbol{x}_0 \right)$。
1 | def q_posterior_mean_variance(self, x_start, x_t, t): |
接下来的p_mean_variance()就比较复杂了,它是给出实际预测时,$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$的分布。由于此时是预测的反向扩散过程,所以符号标记换成了$p()$。这是第一步引入model来进行预测的函数,而且其实也是最重要的一个函数:
1 | def p_mean_variance( |
值得注意的是,随着model一起输入进来的,还有model_kwargs,这个会一起输入进model的forward里,自动解包成可能需要的condition条件等等。接下来会将(x, t, **model_kwargs)都输入model进行预测。
之后的很多行,其实都是根据最开始,model_var_type和model_mean_type的分支选项。我们这里作简略的分析:由于IDDPM需要预测方差,所以模型的输出会多一倍的通道(用来当作学到的方差),所以model_output会被再分成两部分,一部分是原本意义上的model_output,另一半是model_var_values。
这里如果只是简单的ModelVarType.LEARNED的话,那么就只是简单的把此时的model_var_values当成log方差,然后带入指数函数里,就成了model_variance。如果是限定方差范围的话,就会是:
这个里面的$v$,然后实现方差的更新。
在固定方差的模式下,由于IDDPM论文中,是先对$\beta_t,\tilde{\beta}_t$进行实验,从而发现“让方差也可学习”这一洞见的。由于:
所以$\tilde{\beta}_t<\beta_t$,前者就被称为“小方差”,后者称为“大方差”。于是就有ModelVarType.FIXED_SMALL和ModelVarType.FIXED_LARGE之分了。
所有最后,这一段下来,就得到了$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$的方差。
接下来,就是计算$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$的均值。这个取决于model的类型:如果是直接预测$\boldsymbol{x}_{t-1}$时的均值,那model_mean就是model_output。如果是预测$\boldsymbol{x}_0$和预测$\epsilon$,那需要进行下简单的换算:
如果我们的模型直接预测的就是$\boldsymbol{x}_0$,那么直接将此时的$\boldsymbol{\hat{x}}_0, \boldsymbol{x}_t, t$带入q_posterior_mean_variance()来取后验分布的均值即可。如果预测的是$\epsilon$,那么我们用_predict_xstart_from_eps()来完成噪声和0处的估计的代换即可:
1 | def _predict_xstart_from_eps(self, x_t, t, eps): |
这一段即我们经常写的:
估计的$\boldsymbol{\hat{x}}_0$也是返回字典键的一员。最后返回的字典里,有$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$分布的均值,方差,log方差,以及此时估计的$\boldsymbol{\hat{x}}_0$。
注意,如果我们是直接预测均值的那种方案,那么根据上面的上面的那个式子,我们也可以直接反解出$\boldsymbol{\hat{x}}_0$。这一步被_predict_xstart_from_xprev()完成:
1 | def _predict_xstart_from_xprev(self, x_t, t, xprev): |
同时,我们会发现,在这个方法内部,定义了一个函数process_xstart(),这个函数是用来处理$\boldsymbol{x}_0$的,因为在图像生成中,最后的$\boldsymbol{x}_0$是一个离散的,可能需要截断和一步去噪。
同理,我们还需要一个p_sample()来真正的从$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$进行采样:
1 | def p_sample( |
可以看到,我们在这个函数里调用p_mean_variance()得到了一个字典out,这个字典就包含我们需要的变量。这个式子可能看起来和$\boldsymbol{x}_{t-1}=\mu _{\theta}\left( \boldsymbol{x}_t,t \right) +\sqrt{\beta _t}\epsilon $不太一样。因为代码中sample中的计算同时考虑了$t=0$时不加噪,所以多了一个mask因子。以及为了避免一个分支判断,这里直接使用了log方差。所以根据对数$e^{0.5\log \beta _t}=e^{\log \sqrt{\beta _t}}=\sqrt{\beta _t}$,其实和我们之前认识的式子是一样的。
最后也返回了一个字典,即此时的$\boldsymbol{x}_{t-1}$和p_mean_variance()里估计的$\boldsymbol{\hat{x}}_0$。
行文至此,我们其实已经有了很大的进展,我们已经实现了正向和逆向的采样。最后通过进一步封装一个入口函数p_sample()和一个生成器函数p_sample_loop_progressive(),我们就可以循环进行采样了:
1 | def p_sample_loop( |
DDIM有着相同的函数接口,用法类似。但是显然,我们最希望实施的是DDIM可以跳步采样的能力。这个在编程实现上,是使用一个继承自GaussianDiffusion的类:SpacedDiffusion实现的。具体来说,它通过用一个_WrappedModel类来封装模型(实际上是模型的forward)来实现跳步之后子序列下标的对齐。
SpacedDiffusion里重写了p_mean_variance(),因为我们知道它其实是$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$的核心。重写了它其实就是为了实现跳步$p(\boldsymbol{x}_{m}|\boldsymbol{x}_n)$。但奇怪的是,IDDPM的代码里同时重写了training_losses(),而实际上DDIM的损失函数和DDPM相比之差一个常数,其实可以不重写,直接用原始的时间序列来训练一个扩散模型,然后用DDIM采样。
写的实在是太长了,在这里我就不记录GaussianDiffusion中training_losses()的实现了。因为如果前面能看懂,这个也就看得懂了。当然,由于IDDPM本身是在图片上做操作,所以最后会有一个从连续到离散(RGB空间)的事情需要处理。这里我们可以先跳过不看。
但我想指出一个关于训练的事情,这其实有些反直觉,我在刚上手的时候也很困惑。
实际上,在推loss的时候,不管是KL散度用高斯分布的结论打开,还是不打开。最后的loss都是有个求和号在的($\varSigma$),这个的意思并不是说,我们会把一个样本在所有时刻$t$的loss求出来,然后backward()。没有GPU能这么豪横。
所以其实在实际训练时,都是只优化随机抽取到的时间$t$。这个求和符号只是数学上的意义。这在只用$L_{\mathrm{simple}}$时很直接,我取一个$\boldsymbol{x}_0$,加噪到$\boldsymbol{x}_t$,预测噪声,计算预测噪声和真实噪声的二范数,然后优化。当loss多加一项$L_{\mathrm{vlb}}$,就像IDDPM里一样时,我们也是只计算$t$时的那一项,即$L_{t}$。
End
通过理解DDIM和IDDPM,现在我们对扩散模型有了更进一步的认识,但这还不够。他们的背后可以用更统一的框架来实现,等到有时间的时候再仔细学一下。除去一些理论上的启发和理解外,openAI开源的gaussian_diffusion.py写的也很规范和工整,值得我们学习。


