在这篇blog里,我综合PPT,教材,课外教辅整理一些笔试考试可能考出来的点。
模式识别的定义:
模式识别是研究机器如何能够观察环境,学会将感兴趣的模式与背景区分开来兴趣的模式,并对其类别做出合理的并对这些模式的类别作出合理的决定。
模式识别的核心是:特征提取和分类器设计。
最小错误与最小风险
利用贝叶斯进行分类时,贝叶斯算出后验概率本身,就是最小错误率。
“最大后验概率准则可以保证最小错误率,所以又称最小错误率准则”
最小风险是对后验概率进行加权。有一种一眼看过就不会忘的记忆方法:
由于分母是一样的,我们只要比较前面那个乘积。
而所谓风险的似然量可以记作:
此时,似然量谁小,就属于哪一类。一般的时候,主对角线元素都是0,因为我们并不惩罚分类正确时的结果。所以似然量越大,说明错分的结果越严重,所以是反着的,这点要注意。
在这个情境下,我们可以得到线性决策面(因为更具体的概率密度函数一概不知)。
假设细胞识别正常细胞$\omega_1$的先验概率是0.9,异常细胞$\omega_2$的先验概率是0.1。某待识别的细胞的观测向量为$\boldsymbol{x}$,从类条件概率密度分布曲线上得知,$p(\boldsymbol{x}|\omega_1)=0.2, p(\boldsymbol{x}|\omega_2)=0.4$,并且损失矩阵为:
试利用最小错误率贝叶斯决策和最小风险决策进行分类。
对于最小错误率,直接列写:
带入$p(\boldsymbol{x}|\omega_1)=0.2, p(\boldsymbol{x}|\omega_2)=0.4$,得0.14,所以判定该细胞为正常细胞。
对于最小风险,根据那个矩阵相乘的记法,可以得到:
代入数据,结果为-0.06,故判定为异常细胞。
还有一点要注意,考虑此时二分类的损失矩阵。$\lambda_{12}=6>\lambda_{21}=1$,说明我们认为,将异常细胞错分成正常细胞会产生更严重。我们要清楚这对阈值的影响。显然,我们根据最小风险后的结果计算后,之前觉得是正常细胞的变成错误细胞了。这说明阈值左移了。由于这个影响类条件概率大小的缩放因子,也体现在先验概率中。所以我们要清楚:
先验概率越大的类别,区域向外扩展。
犯了错误以后结果更严重的类别,区域也向外扩展。(因为这样可以少犯错误)
Fisher线性判别
对数据施加一个合适的线性变换有时有奇效,比如PCA,ICA,DFT,DCT等。模式识别课程里要求掌握Fisher线性判别作为一个例子。仅限两类。
考虑$n$维降成1维。在$n$维的$X$空间里,我们定义了总类内离散度矩阵:
此时满足降维的最优投影即:
这样,把$N$维数据就降到了1维,记得复习一下矩阵手动求逆。两边同时作初等行变换!!!
然后一般会根据分类以后的……样子给定一个分类阈值$w_0$:
这里:
那么,如何判断阈值$w_0$左右是哪一类呢?只要记住fisher判别和通常的判别面相反即可,$y>w_0$是$x\in \omega_1$,$y<w_0$代表$x \in \omega_2$。
例如,有两类样本集:
使用Fisher线性判别给出分类面:
其实,这里有个我尚不清楚的事情,为什么fisher线性判别定义的是外积,也就是那些矩阵,然后叫他们“离散度矩阵”。现在最好不要去想他们。
KNN
$k$近邻算法是指给定一个未知标签的样本,在已有的训练集中,找到与该待分类的样本距离最邻近的$k$个训练样本,随后根据这$k$个训练样本的类别,通过一定的决策规则决定该未知样本的类别。
设训练样本集$D=\left\{ \left( \boldsymbol{x}_1, y_1 \right) ,\left( \boldsymbol{x}_2, y_2 \right) ,…,\left( \boldsymbol{x}_m, y_m \right) \right\} $,其中$\boldsymbol{x}_i\in \mathbb{R} ^n$,$y_i\in \left\{ c_1,c_2,…,c_S \right\} $。对于未知样本$\boldsymbol{x}$,按照上述步骤确立$y$:
(1)首先确定一种距离度量,计算$\boldsymbol{x}$与训练集中每个样本$\boldsymbol{x}_i$的距离,选出距离最小,即最近邻的$k$个点,集合记作$N_k(\boldsymbol{x})$。
(2)在$N_k(\boldsymbol{x})$中,作投票,少数服从多数。
$k=1$时算法退化为最近邻算法。
这里的距离就是$p$范数。
K-means and Fuzzy-C-means
$k$-均值是非常经典的聚类算法,这里总结它的步骤:
①初始化:随机选择$k$个样本点,并将其视为各聚类的初始中心$m_1,…,m_k$;
②按照最小距离法则将所有样本划分到以聚类中心$m_1,…,m_k$为代表的$k$个类$C_1,…,C_k$中;
③计算聚类准则函数$J$,重新计算$k$个类的聚类中心(取平均);
④重复②和③直到$J$收敛;
这里要指出一点,由于重新计算聚类中心时,是直接给同一个簇里的”坐标“取平均,此时上一个聚类点并不显式的出现在式子里。但这也导致,如果最开始初始点选的不好,需要迭代很多次……所以如果笔试有手写这个过程,先大概估摸一下,所谓的初始点。这样可以少算一次”全体距离“。
然后,模糊C均值,基本就是套个模糊数学来加权。
怎么回逝呢?$k$-均值里所谓的聚类准则函数$J$,我连提都没提,因为它就是一个二范数之和:
然后,有人提出,我可以给每一类加个权(总之为了要一个0到1的系数整了个什么隶属度的名字出来)
这个,隶属度,有个约束,和要是1。那个$b$,有时候也标为$\alpha$,总之是个超参数,名字是啥众说纷纭,据说取2。对于这个有约束的优化,直接拉格朗日求必要条件:
这坨式子很长,仔细看就发现,其实就是加个权。以及如果要手算,$C=2$,求和其实也简洁很多。
比如$\mathbf{m}_j$,与之前直接的取均值相比,它现在加上了类内的隶属度权重。
至于如何更新隶属度权重,上式表明,如果当前类内的某个样本$\mathbf{x}_i$离聚类中心越近,隶属度越大。为了归一化,分母上就出现了一个它与各个聚类中心的……距离的倒数的和,来加权。
看,非常合理。
所以FCM的算法步骤可以归结为:
①设定聚类数目$C$,参数$b$。
②随机生成隶属度$U$,初始化各个聚类中心。
③根据上式更新隶属度函数
④更新聚类中心
⑤重复③和④直到$J_f$收敛。
Bagging and Boosting
首先,我们要理解,偏置-方差分解。这里我们不加证明:
Bagging旨在降低上式的方差,而Boosting是降低上式的偏差。
Bagging的数据集选择,都遵从放回抽样。假设有$N$个数据,某个数据被选中的概率为$1/N$,则没有被选中的概率为$1-1/N$。所以在$N$次放回抽样中:
放回抽样后的数据集,不包含原数据集中约三分之一的数据。用这些数据集构建具有差异的模型:
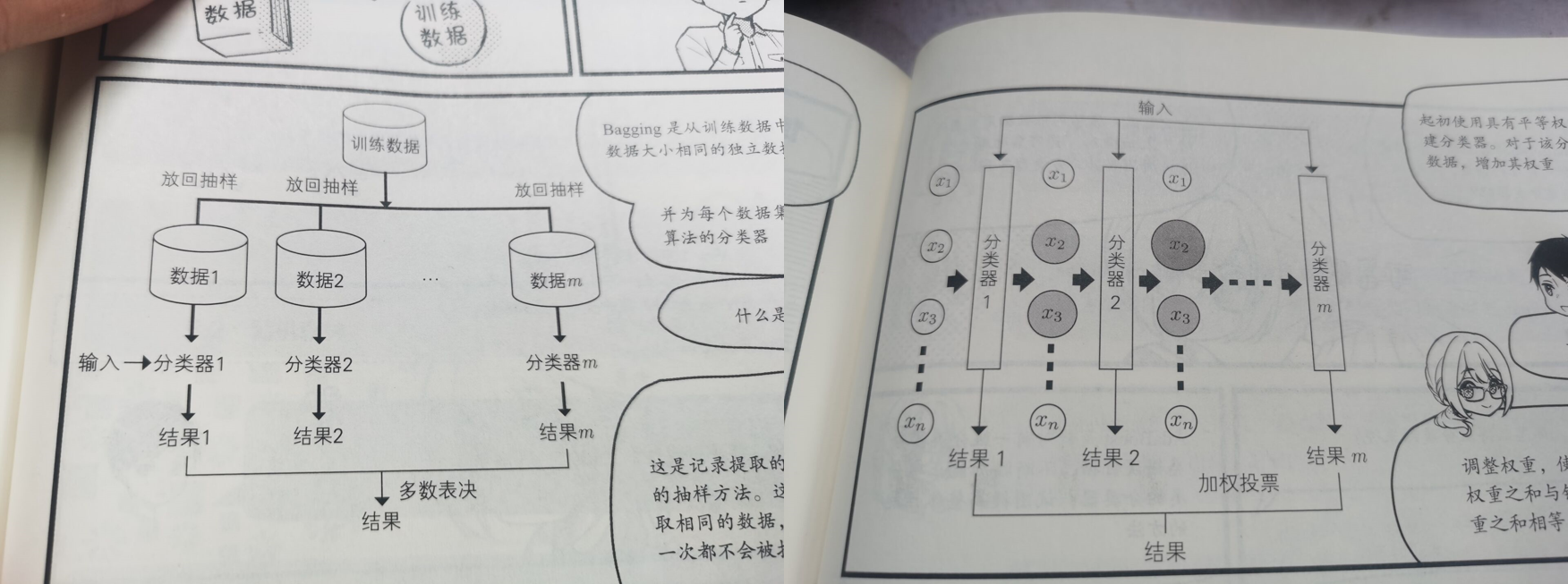
Bagging,体现在分类里,就是投票;在回归里,就是取平均。(上图左侧)
Boosting是通过给弱分类器的表现加权,来强化某些困难样本的表现,最后再综合,见上图右侧。一个很成熟的例子是Adaboost。
这两种方案间存在区别和联系:Bagging随机选择训练集,各轮训练集相互独立。Boosting各轮训练集并不独立,它的选择与前轮的结果有关。Bagging可以并行生成,但Boosting只能串行。但Boosting容易产生过拟合。
SVM
SVM的精华是构造最优分割面,如果考试考计算,那只能是个二维平面。于是不可一世的约束条件和优化函数,就变成了……对着支撑向量找垂直平分线。
比如,给定3个数据点,正例点$x_1=(3,3)^T, x_2=(4,3)^T$,负例点$x_3=(1,1)^T$。求线性可分支持向量机。
首先,我们来一个灵魂call_back,支持向量机的优化问题本来是:
然后,根据,一顿数学推导,线性可分的支持向量机的优化成了:
特别地,最后分割超平面的权值和偏置为:
权值是对偶得来的,这里可以不用管太多。偏置是根据支撑向量算来的(互补松弛)。
所以我们这里有三个坐标点,我们直接代入:
显然,我们用约束条件替换掉$\alpha_3$,目标函数变为:
然后一波正义的偏导为0,梦回大一高数:
然后,啪的一下,很快啊,我们就解出来$\left( \alpha _1,\alpha _2 \right) =\left( 1.5,-1 \right) $,显然不满足大于0的约束条件。所以最值一定在边界上取到(别问,问叶峰。)
当$\alpha_1=0,\alpha_2=0$时依次带入求最小值,得最小值于$\left( \alpha _1,\alpha _2 \right) =\left( 0.25,0 \right) $取得。此时$\alpha_3=\alpha_1+\alpha_2=0.25$,然后,带入对偶的那个式子,得到:
所以,我们得到了,分类面:
我们可以发现,$\alpha_2=0$,其实就是因为它被松弛了。如果我们把$x_1,x_2$画成二维的坐标:
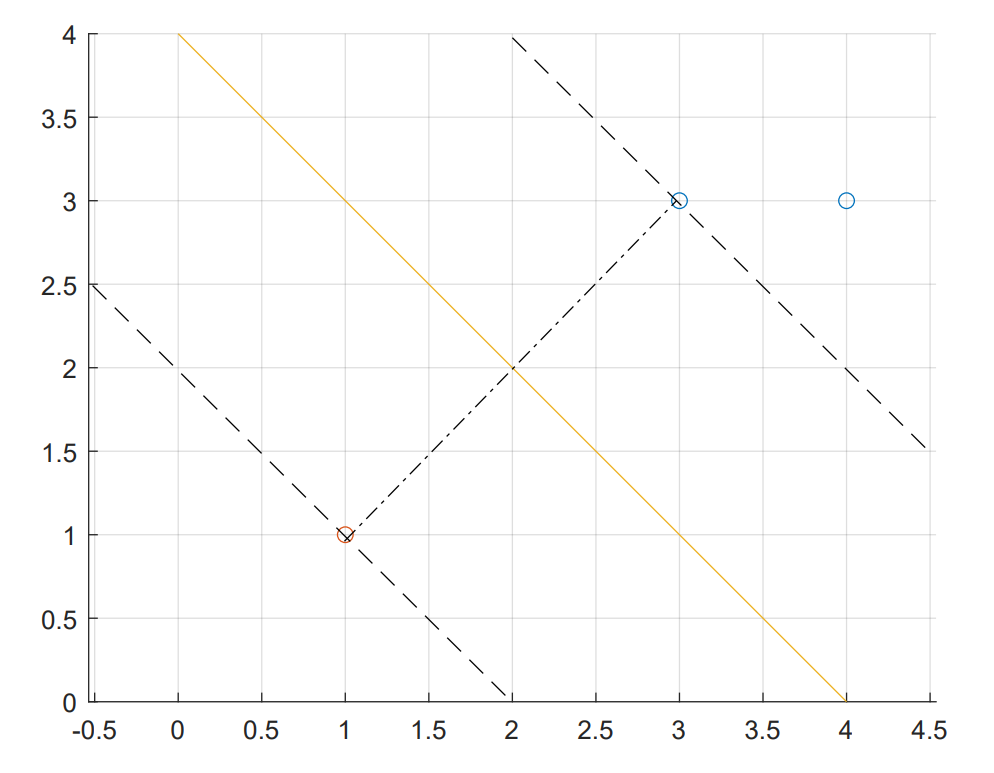
可以看到……确实就是垂直平分线。
但SVM的一个特点在这里会变成一个难绷的事情,他的输入不显式依赖于输入空间的维数。换句话说,如果上述题目变为三维坐标,整个计算过程的拉格朗日乘子的数量还是那么多,就像上面的三个。然而我们不再能够“垂直平分线”一样顶真出答案了。
Kernel Trick是SVM的精髓,上面的操作其实使用的是”线性核函数“:
即上面第一个,下面的是多项式核函数,高斯核函数。由于计算的问题,笔试时肯定不可能考高斯核函数(径向基函数)。最多最多给定一个死的多项式核函数,然后手算一下,计算过程只需替代掉$\boldsymbol{x}_{i}^{T}\boldsymbol{x}_j$。
GMM与EM
高斯混合模型和期望最大算法往往同时出现,我觉得考试不可能考具体计算,太离谱了。我们只要理解其精髓就好了:
对于一个复杂的样本的数据分布,我们假定它服从几个高斯分布的加权和:
这里用看起来很牛逼的$\pi_k$来表示权重,显然:
假如,这里面,这个高斯混合模型的参数是已知的。那我只需要把样本$x$带入上面每一个高斯分布$\mathcal{N}_k$中,我可以认为哪个概率密度函数值最高,$x$就属于哪类。如果重叠的话,那也可以设定一个阈值。
而如果高斯混合模型的参数是未知的,比如这里只有一堆已知的样本。那么就像概率论里学的一样,我们可以通过最大似然估计来拟合这个概率密度函数的参数,我们直接对似然函数取log,然后最大化它。
这样这个问题就变成了$k$个高斯分布的极大似然估计。
然而如果,模型参数未知,样本属于哪些分布也未知,这就乐了。如何处理这个问题,就是EM算法了:
首先,我们设定一堆模型的初始值$\left\{ \pi _k,\mu _k,\varSigma _k \right\} $,然后把样本数据带进去。这样根据此时这个不太完善的模型,我们能大概知道每个样本属于哪个类。这样,我们就有了类别的信息(就像伪标签),这一步称为“E步”。
然后,我们把我们自己估计出的类别信息拿出来,结合原始数据,再去作极大似然估计。更新参数。这一步就是“M步”。
这个过程,非常像,概率论版的k-means。那么这时候可能有人会问,为什么叫“期望最大”呢?期望哪里来的呢?这个就需要推公式了,但现在没时间了,如果有时间我再补上。
正态分布下的统计决策
在正态分布条件下,类条件概率可以用多元高斯分布表达出来:
所以考虑贝叶斯决策时,把分母的归一化系数扬掉,判别函数即:
考试应该会围着这个二次型来复习圆锥曲线。例如:设一个二维空间中的两类样本服从正态分布,其参数分别为:
且先验概率相等。
根据上面的式子,可以直接书写决策面方程:
End
吸收掉上面的这些内容,模式识别大概率就不会挂了。接下来要一晚上速通操作系统。


