第一天考人工智能概论,这门课我根本就没学过。但是我在突击的时候发现,这门课实际上是传统意义的人工智能,对,那些在IJCAI/AAAI运筹分会场头发花白的学者们研究的内容。
所以,秉持着对传统运筹,博弈的尊敬。以及,我要期末考试了。我决定对着每一章的PPT整理一下例题,好记性不如烂笔头。
图搜索策略
这里引入了一个通用的图搜索过程,用OPEN表记录还没有扩展的点,CLOSED表记录已经扩展的点。(选择最左支最先访问,节点12是目标节点)
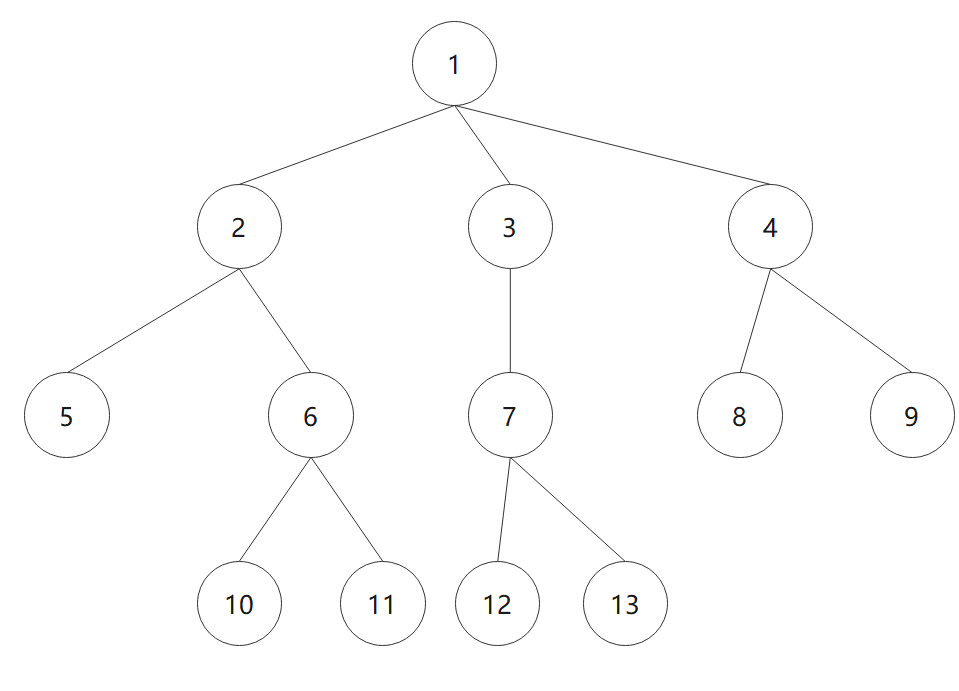
使用DFS访问的open表和closed表:
| OPEN | CLOSED |
|---|---|
| 1 | |
| 2, 3, 4 | 1 |
| 5, 6, 3, 4 | 1, 2 |
| 6, 3, 4 | 1, 2, 5 |
| 10, 11, 3, 4 | 1, 2, 5, 6 |
| 11, 3, 4 | 1, 2, 5, 6, 10 |
| 3, 4 | 1, 2, 5, 6, 10, 11 |
| 7, 4 | 1, 2, 5, 6, 10, 11, 3 |
| 12, 13, 4 | 1, 2, 5, 6, 10, 11, 3, 7 |
| 13, 4 | 1, 2, 5, 6, 10, 11, 3, 7, 12 |
搜索结束,可以看到这个表的意思就是把待扩展的结点放进OPEN表,探索过的结点存进CLOSED表。
如果是BFS时的情形:
| OPEN | CLOSED |
|---|---|
| 1 | 0 |
| 2, 3, 4 | 1 |
| 3, 4, 5, 6 | 1, 2 |
| 4, 5, 6, 7 | 1, 2, 3 |
| 5, 6, 7, 8, 9 | 1, 2, 3, 4 |
| 6, 7, 8, 9 | 1, 2, 3, 4, 5 |
| 7, 8, 9, 10, 11 | 1, 2, 3, 4, 5, 6 |
| 8, 9, 10, 11, 12, 13 | 1, 2, 3, 4, 5, 6, 7 |
| 9, 10, 11, 12, 13 | 1, 2, 3, 4, 5, 6, 7, 8 |
| 10, 11, 12, 13 | 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| 11, 12, 13 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 |
| 12, 13 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 |
| 13 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 |
可以看到,是一样的逻辑。
还存在一些变式,例如代价图。每次探测一个分支是需要考虑代价的。
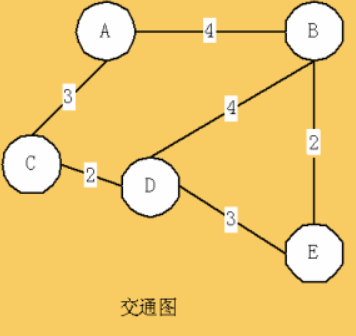
如上图,考虑从A点分别BFS和DFS到E点。那么在OPEN表和CLOSED表里,实际上可以被理解为,在OPEN表中按代价最小来排序。注意在上面的例题中,OPEN表的排序也不是任意的,后面会给出答案。
BFS时的情形:
| OPEN | CLOSED |
|---|---|
| A(0), | |
| C(3), B(4) | A |
| B(4), D(5) | A, C |
| D(5), E(6) | A, C, B |
| E(6) | A, C, B, D |
| A, C, B, D, E |
这时,能发现,走到E的代价是6,他的路径是ABE。实际上,这个例子比较简单,所以E(6)时就是solution。但我们不能认为,OPEN表里第一次出现E时,就可以停止。如果图复杂一些,继续搜索可能会出现小于6的权值,所以要推理到最后。
DFS时:
| OPEN | CLOSED |
|---|---|
| A(0) | |
| C(3), B(4) | A |
| D(5), B(4) | A, C |
| E(8), B(4) | A, C, D |
| B(4) | A, C, D, E |
此时,路径是ACDE,代价是8。
为什么这里的OPEN表不排序呢?因为,在代价树的深度优先搜索中,是从刚扩展出的子节点中选一个代价最小的节点,而这里的图,扩展出来的都是一个点。所以,BFS时,就是从全体节点中选择了代价最小的了。
A*算法
A*算法是一代价树搜索的一个例子,先是PPT上给的八数码问题。假设我们要完成:
搜索树的估价函数是$F(n)=D(n)+H(n)$,$D(n)$表示初始状态的深度,$H(n)$表示不在对应位置上的数码的个数,
所以整个代价图可以画作:
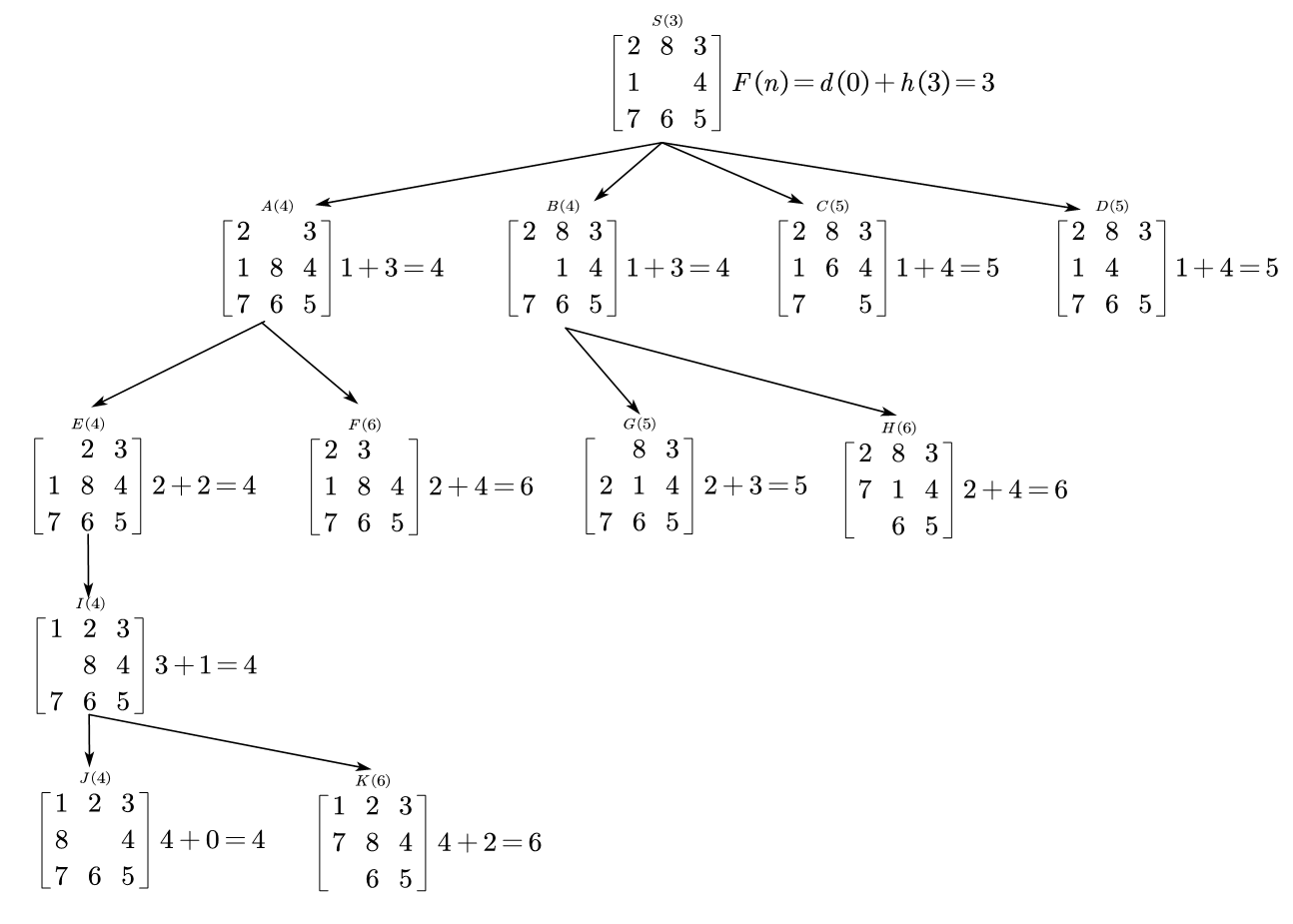
相应的,OPEN表和CLOSED表就是:
| OPEN | CLOSED |
|---|---|
| S(3) | |
| A(4), B(4), C(5), D(5) | S(3) |
| B(4), E(4), C(5), D(5), F(6) | S(3), A(4) |
| E(4), C(5), D(5), G(5), F(6), H(6) | S(3), A(4), B(4) |
| I(4), C(5), D(5), G(5), F(6), H(6) | S(3), A(4), B(4), E(4) |
| J(4), C(5), D(5), G(5), F(6), H(6), K(6) | S(3), A(4), B(4), E(4), I(4) |
| C(5), D(5), G(5), F(6), H(6), K(6) | S(3), A(4), B(4), E(4), I(4), J(4) |
J(4)是相应状态,停止搜索。
行文至此可能有人会意识到,这个搜索怎么这么像代价树的广度有限搜索。这实际上是因为,A*算法的搜索,属于有序搜索。这个搜索的要义是,从OPEN表中选择一个$f$值最小的节点。所以,宽度优先搜索,深度优先搜索,等代价搜索,都是它的特例,区别即$f(\cdot)$的选取。
与或树的搜索
这一部分其实是“基于问题归约的搜索技术”。因为这个部分的搜索意义不是为了“遍历某个空间”,而是确认某个问题是不是有解的。
一个很有意思的例子是求不定积分,我们往往会逐项拆开来处理。如果拆到最后得到了一个例如$\int{e^{-x^2}\mathrm{d}x}$,那就说明,原积分无初等函数的解。把这个例子泛化,就会是与或图的归约问题。此时我们搜索一个与或图,停止的条件就变为“初始节点被标记为可解”或“初始节点被标记为不可解”。
而具体搜索的过程,和前面的搜索是一样的。有一点不同,终叶结点没必要储存在closed表里(因为它们不会被探索),在OPEN表里的那些代表可解or不可解的结点,一旦可以判断一个具体的逻辑,就会从OPEN表里移除。
Max-Min搜索和$\alpha-\beta$剪枝
这一部分其实是博弈树的搜索,分为极大极小搜索和$\alpha-\beta$剪枝两个部分,其实道理很简单。
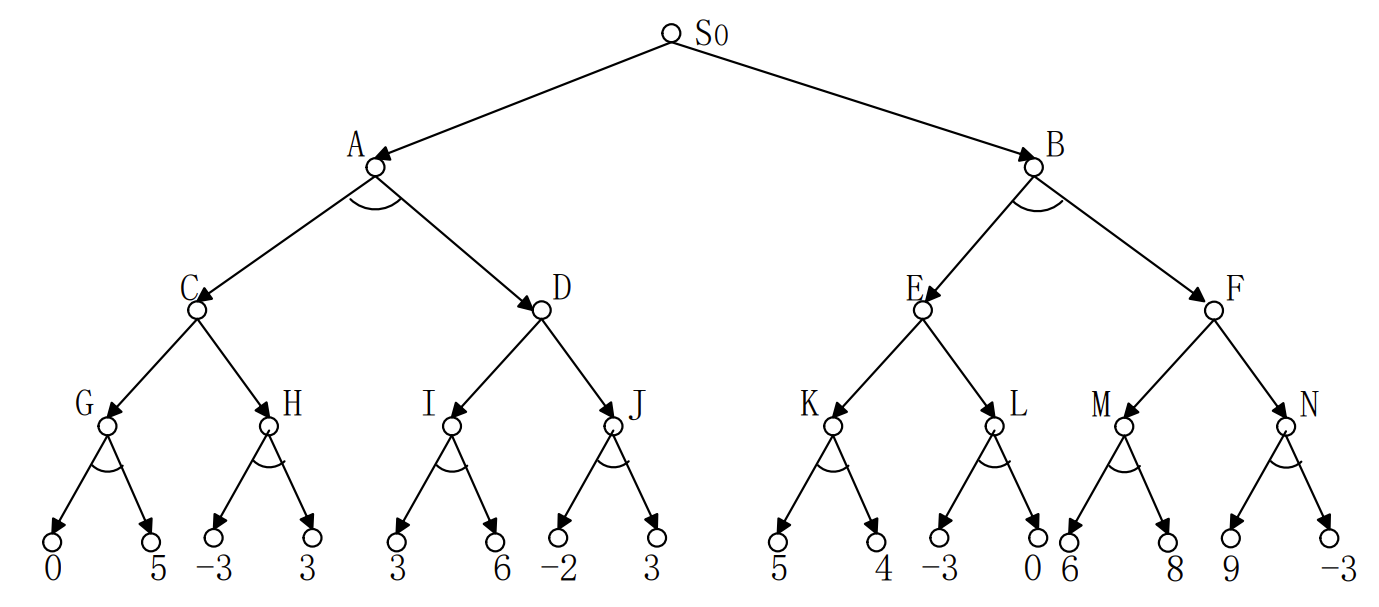
我们先直接看题目,1)计算各节点的倒推值。2)利用$\alpha-\beta$剪枝来剪去不必要的分支。
这个树,描述的是一个博弈的过程。倒数第二层,是MIN,往上是MAX,再往上是MIN。所有带着与的分支,其实都是对手做出的选择,因为我们需要处理对手可能做出的所有的选择,所以是与。最底下的分数是此时的估值。那么倒退的意思其实就是根据“对手想让估值变越小越好,我想要估值变越大越好”来理解。这样就会产生一些不必要的分支。
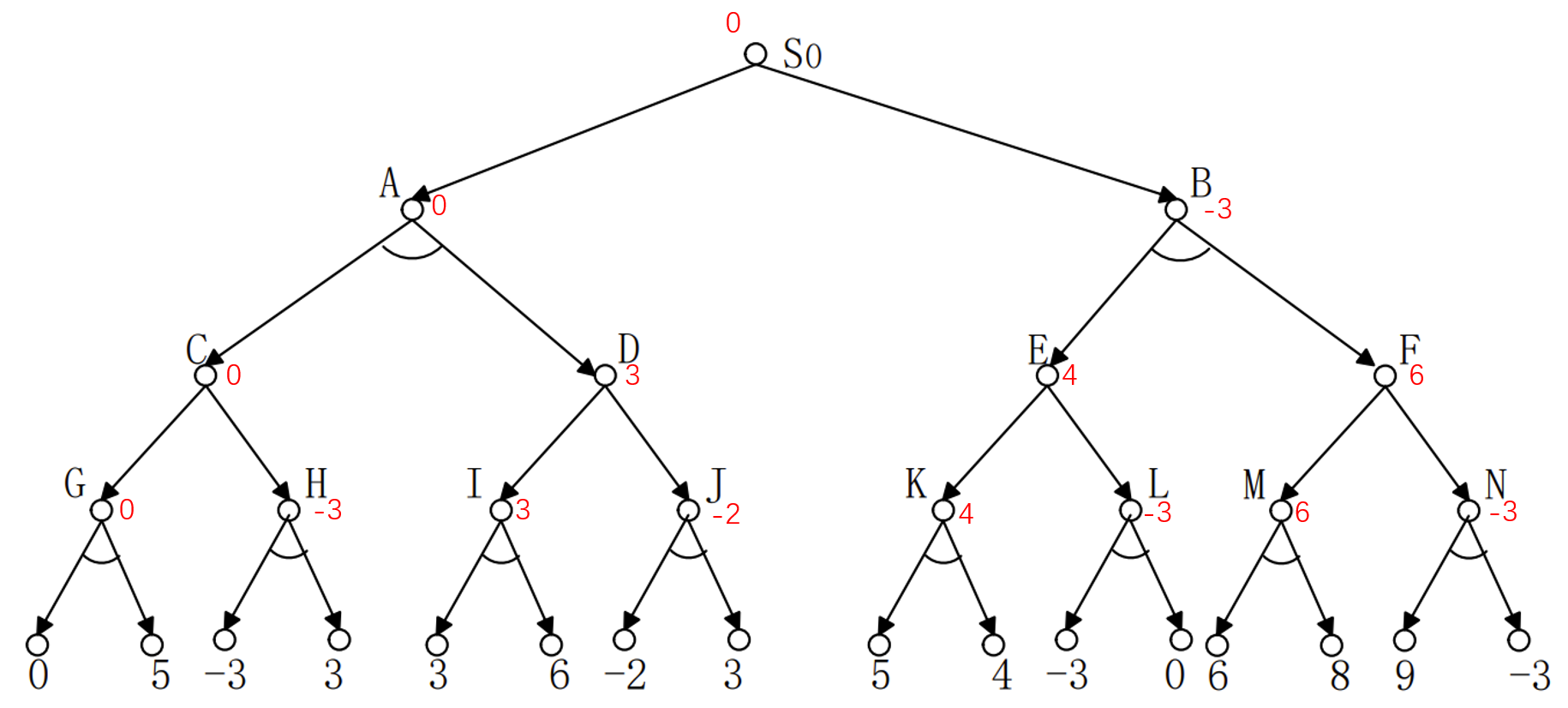
倒推值很简单,与树选最小,或树选最大。例如结点G,结点G演化到0和5两个估值,是我方做的操作导致的。我方一定会做有益的操作,所以在G时的估值肯定是小于等于0的。
那么$\alpha-\beta$剪枝是什么呢?他是在执行搜索时的一个策略。并不是在整个极大极小树被构造之后再用的。
它的逻辑是:首先我们从$S_0$开始,沿着左分支一路走,走到0和5。此时我们会知道G处的结点是小于等于0的。然后我们探测H,进一步探测到-3。此时我们会知道,H处是小于等于-3的。那么我们就不需要探测是3的那一支了(我们当时不知道它是不是3)。我们此时认为我们不知道它是不是3,记作?。
因为,如果?大于-3,那么H结点的值不会变化,因为MIN层要选出最小的那个。如果小于-3,说明H结点的值更小。那样C结点更不会选择H结点,会直接选择G结点,因为那里的值是1。
这样,图上标记的3的那个分支,就被减掉了。这段逻辑用可以概括为:
1)假设有节点$x$,根据$x$的子节点确定了$x$的取值范围
2)节点$x$的父结点,此时可能有取值范围,也可能没有。
3)如果$x$的父结点已经有取值范围了,那么如果$x$的取值范围和$x$的父结点的取值范围没有交集(或只有一个元素),则剪掉此时$x$还没有探测的那些子结点。
所以整个过程为:
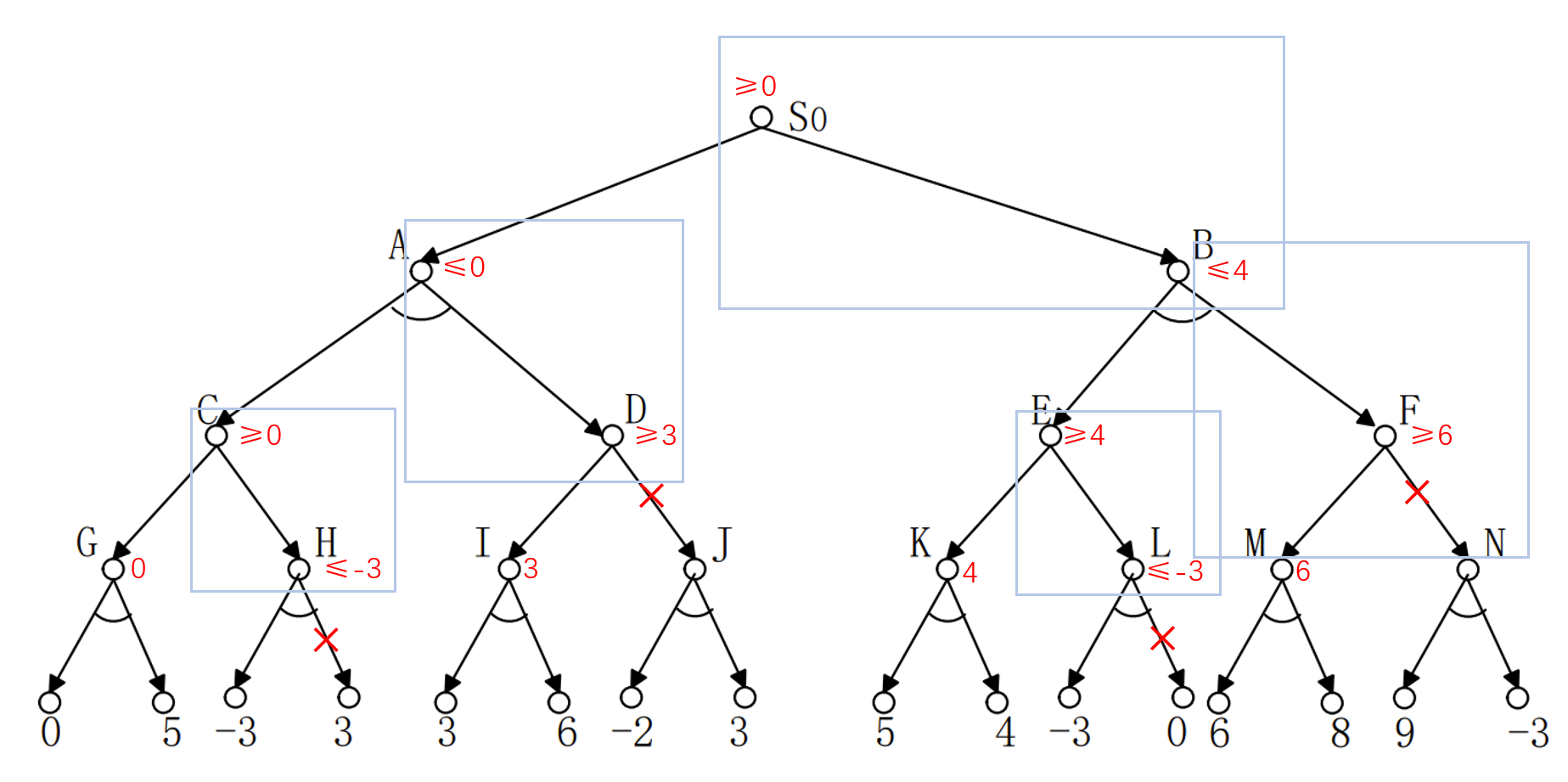
蓝色方框标记着触发剪枝时的取值范围的情景。
谓词逻辑
这里主要是记录两点,一个是翻译逻辑命题时的一个issue。
例如要表示:1)人总是要死的。2)有些人不怕死。
如果论域是全人类,那么$D(x)$表示”$x$是要死的”,$F(x)$表示“$x$是不怕死的”。
那么上述命题非常简单:1)$\left( \forall x \right) D\left( x \right) $, 2)$\left( \exists x \right) F\left( x \right) $
但这样会带来一个问题,当不同的个体变元一起讨论时,用不同的论域会非常不简洁。于是我们采用的是定义一个全总个体域,然后用不同的特性谓词来刻画不同的论述对象。
上面的那个例子中,如果论域是全总个体域,用$M(x)$表示”$x$是人”,那么上述命题变为:
对于特性谓词,使用的规则即:对全称量词,作为蕴含式的前件加入;对存在量词,作为合取项而加入。
其次是对应的大题:
子句集求解
例如:将下列谓词逻辑化为一个子句集:
①消去蕴含符号:
通过如下等下公式,消去公式中的蕴含或等价符号:
所以上式可以写作:
②减少否定符号的辖域:
利用如下逻辑公式,将否定符号控制在单个谓词上:
上式演化成:
③对变元标准化:
换元即可,确保不用重复的符号:
④消去存在量词:
你可以用一个符号不至于混淆的函数,来刻画,一个全称量词内的存在量词。即:
所以我们用$g(x)$来办到这一点,于是式子变为:
其中,$w=g(x)$
⑤化为前束形:
由于上面的步骤已经处理了关于辖域的冲突,所以可以直接把全称量词移到公式左边,这样,前面那个全称量词串称为前缀,后面那个就称为母式。
⑥把母式化为合取范式:
这里常常用分配律:
所以上式变为:
⑦消去全称量词:
此时全称两次的顺序已无关紧要,所以,与其说是消去,不如说是略写掉:
⑧消去合取符号:
用$\left\{ \mathrm{A}, \mathrm{B} \right\} $代替$\left\{ \mathrm{A}\land \mathrm{B} \right\} $,剩下的每个公式的原子公式们的析取:
⑨更换变量名称:
经过这么处理以后,每个子句都对应着一个合取元,每个变元由全称量词量化。所以任意两个不同子句的变量之间实际上不存在任何关系,更换变量名不影响公式真值,所以最后一步即换一下变量名:
总之,这个子句集求解,其实就是离散数学里的,求合取最小项。
消解归结
这个消解归结,就是证明。就是离散数学里那个,如果你要证明$\left( F_1\land F_2\land …\land F_n \right) \rightarrow G$,你可以证明$\left( F_1\land F_2\land …\land F_n \right) \land \lnot Q$是恒假的。这样会推出矛盾,对应在这里叫作“空子句集”。
一个简单的例子是,
前提:$\left( P\rightarrow Q \right) \land \lnot Q$
结论:$\lnot P$
首先建立子句集:$\mathrm{S}=\left\{ \lnot P\lor Q, \lnot Q, P \right\} $
对$S$作归结:
(1)$\lnot P\lor Q$
(2)$\lnot Q$
(3)$P$
(4)$\lnot P$ (1)(2)归结
(5)$NIL$ (3)(4)归结
实际上,这个过程可以写成一颗,树。它被称为“反演树”。
我们现在举一个略微复杂的例子,这个例子同样会给后面的消解反演作铺垫。
前提:每个储蓄钱的人都获得利息。
结论:如果没有利息,那么就没人去储蓄钱。
其中$S(x,y)$表示”$x$储蓄$y$”;$M(x)$表示”$x$是钱”;$I(x)$表示”$x$是利息”;$E(x,y)$表示”$x$获得$y$”;$H(x)$表示”$x$是人”
于是上述命题写为:
注意,运用摩根律,蕴含等价公式,和否定量词,结论也可以写成这种形式(与PPT里类似,但PPT里漏掉了人的谓词)
这个命题并不容易翻译。正确的写出是第一步,第二步,需要正确的求出子句集:
饺子包完了,该上醋了。(上述依次记作子句(1), (2), (3),…)
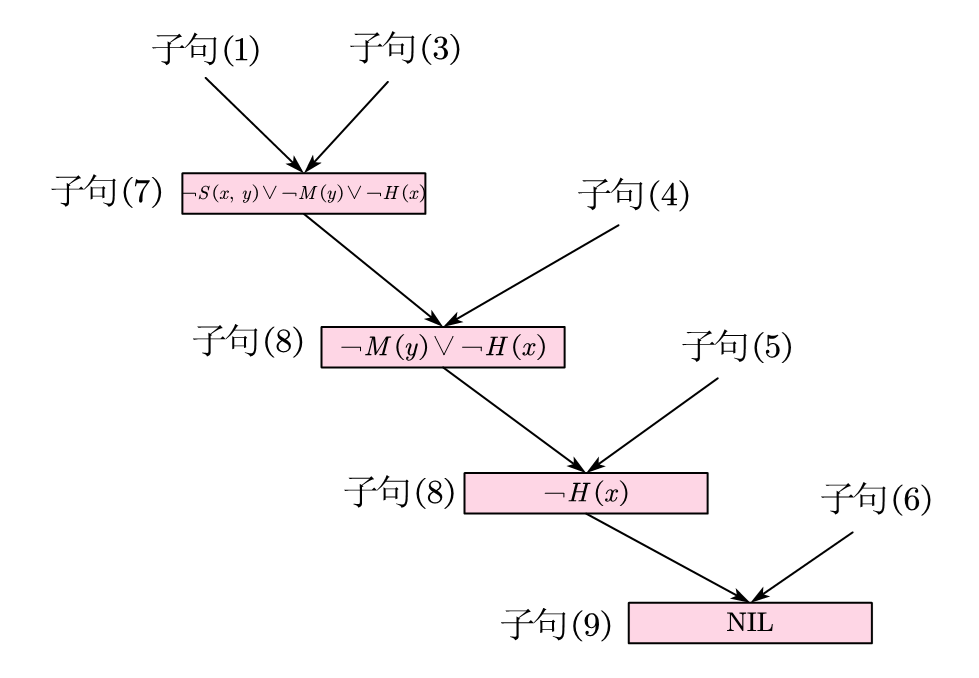
消解反演
消解反演,其实就是上面那个图的反过程,从底部的NIL变换到上面。换句话说,就是从一个NIL出发,能不能到达想要的结论的否定。此处的考察比较简单,例题可见于PPT。
规则演绎系统
这里涉及到规则变化和化为与或形,见于PPT,此处从略。建议考前看一眼,在理解了前面的基础上,很好做。
模糊推理
这整个一章,就是把二元的集合给扩展了一下,来表征模糊。如果数学建模参加的多会见怪不怪。
先是一个称作“逆概率”的点,基本就是贝叶斯公式套皮。
可信度方法(C-F模型)
我们要先记住这种模型的一般表示,实际上写法在规则演绎里是出现过的,但我们可以选择逃课,不影响理解。这种利用产生式规则表示写的知识,格式如下:
IF E THEN H (CF(H,E))
前提E可以是命题,也可以是命题的合取和析取。结论H也可以是单一命题或复合命题。CF(H,E)是确定性因子,取值于-1到1,代表可信程度。
CF的计算公式(就是个故事)考试会给,所以只要知道怎么算就好。命题的合取和析取,就对应着去最小值还是最大值。
这个考题的变式还有,如果给知识加权(由于不确定度),以及给知识的可信度一个阈值$\lambda$。这里我直接把PPT上的题贴上来,通俗易懂。

模糊推理
模糊推理中,用一个0到1上的隶属函数来表达模糊性。就一个“精心设计”的函数罢了,从而在这个模糊的设定下,更新了一系列的简单运算:

这里要注意$\lambda$截集,核,支集的概念。$\lambda$截集只保留了隶属度大于$\ge\lambda$,如果没有等号称为$\lambda$强截集。核就是隶属度等于1的,支集就是隶属度大于0(不等于0)的。
计算模糊度的公式,很好记,前三个都是关于0.5截集的$p$范数,最后是熵表示。
有了模糊的构造,就要有模糊的关系,继而才能有模糊的推理。
一般集合的关系,可以用笛卡尔乘积,例如$U\times V$,那么模糊关系下的是其的推广。如模糊集的笛卡尔乘积:
直接来个例题:
实际上,如果你把上述关系表达成一张数表,那么,这个数表就构成了一个,模糊矩阵。
例如,子女和父母的长相为模糊关系,用模糊矩阵$R$表示为:
父母与祖父母的相似,可以表示为:
所以子女和祖父母的相似程度为:
计算时与矩阵相乘类似,乘法变合取,加法变析取。
这种操作实际上定义了模糊关系的合成,其隶属函数形式化上按:
这样计算。
然后,还会考的就是简单模糊推理,我赌他不考模糊匹配和冲突消解。这里只需要记一个叫扎德法的操作。它意思是对于模糊集$A$和$B$,这样构造$R_m,R_a$:
例如,设$U=V=\left\{ 1,2,3,4,5 \right\} $,$A=1/1+0.5/2, B=0.4/3+0.6/4+1/5$并设模糊知识和模糊证据为:
IF x is A THEN y is B x is A’
A’的模糊集为$A’=1/1+0.4/2+0.2/3$,然后我们,进行计算。
这里$U,V$在计算时是当作全1处理的。然后,模糊结论即:
不要管下标啥意思了,题目让算啥算啥。
上述是针对假言推理时的,即证据为 x is A’,对于拒取式,即y is B’时,换一下A和B即可(角标不变)。
这里还略掉了两个内容,“模糊匹配”和“冲突消解”。打算考前再看PPT,大概率不考,太复杂了。
遗传算法
经典神棍算法,考试会出大题。由于变异和交叉为了答案的统一,都是指定的。包括适应度函数也是给定的。所以题目只会出在根据当前种群的适应度函数值来进行轮盘赌的这个过程中。
例如此时有四个种群,$s_1,s_2,s_3,s_4$,他们的适应度为:
选择概率也是指定的,基本就是归一化的$f(\cdot)$,即:
然后啊,这个式子计算成一个累积概率$q_i$:
这不就轮盘赌了。
这个时候题目给你摇出来的随机数:
然后就可以写表了:
| 染色体 | 适应度 | $P_i$ | $q_i$ | 选中次数 |
|---|---|---|---|---|
| $s_1$ | 169 | 0.14 | 0.14 | 1 ($r_2$) |
| $s_2$ | 576 | 0.49 | 0.63 | 2 ($r_1, r_3$) |
| $s_3$ | 64 | 0.06 | 0.69 | 0 |
| $s_4$ | 361 | 0.31 | 1.00 | 1 ($r_4$) |
End
剩下的杂项,需要接着看PPT,漏掉的大概是“规则演绎系统”,“模糊匹配”,“冲突消解”,后面群智能里的一些常识。建议考前再速记。
人工智能概论和模式识别一天考,所以还是比较紧张的。实在不行,上面那些几项抛弃掉,看懂正文的,也能及格。
得梳理微机原理了,不然该寄了!


