G2Net Detecting Continuous Gravitational Waves

阅读数: 次 2023-01-11

这篇blog来记录一下从Kaggle:G2Net Detecting Continuous Gravitational Waves中学到的一些知识，对我来说非常大开眼界。我充分认识到自己的局限性，尤其是在实验管理方面。

这个竞赛旨在搜寻频谱图中有无连续引力波（Continuous gravitational-wave）存在，相比于在各种科普短视频中看到的由双星碰撞产生的引力波，这种连续引力波更加微弱。

Preparation

主办方提供了pyfstat库使得我们可以扩充训练集，生成不同深度下的信号。下面是一个在近乎无噪声情况下的频谱（幅度）图：

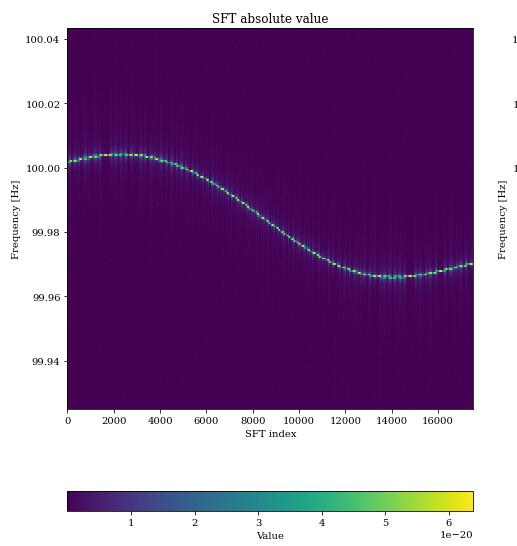
而根据物理学的表达式，引力波应该只是简单的一个正弦曲线。正弦曲线的幅度谱显然不应该是上图这样。通过颜色不一的幅度和发生变化的频率，可以看出引力波信号经过了“调制”。

幅度调制是由于因为地球的旋转，探测器根据接收方向的不同有不同的敏感度。频率的调制一方面是其天体随着引力波的发射，其能量减少，发射的频率降低（这由一个参数$F_1$描述），另一方面是由于地球公转而产生的多普勒频移。有时会发现竞赛所用的频谱图，引力波的频率向上漂变，这可能是一个“周期”中的上升部分，如果再将生成的时间设长一些可以看到：

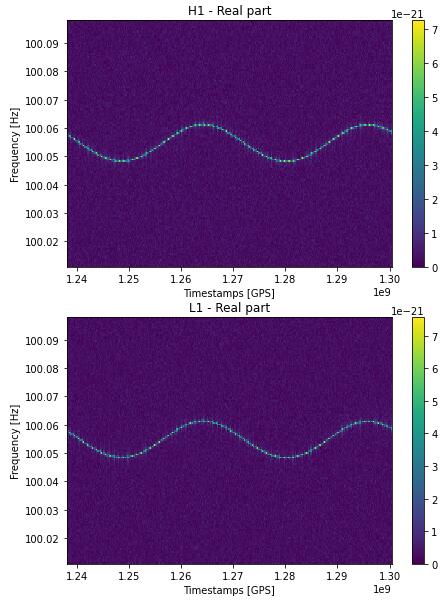
同时还有其他许多参数，共同构成引力波的频谱图。因为这个任务的特殊性，有许多top方案是使用“physical-based”方法，他们通过参数估计，模板匹配等方法进行搜索。其中就利用到了其他的这些参数，而这些在这次的总结了就略过了，因为以后大概率是用不上。

信号的可见程度受信号深度影响，这是一个形象的定义：

$\mathcal{D} =\frac{\sqrt{S_n}}{h_0}$

$\mathcal{D}$越大，说明信号越不可见。在$\mathcal{D}=20$左右就基本丧失了视觉特征，而比赛所用的样本的$\mathcal{D}$广泛分布在10~100，是具有挑战性的。这里$h_0$在某种意义上代表了幅度（因为幅度还与$\cos \iota $有关），$S_n$是噪声的单边功率谱密度。

在简单的模拟中，会使用标准正态分布来生成频谱图中噪声。在这种情况下，功率谱密度和最后分布的实部（虚部）方差的关系为：

$\sigma ^2=\frac{1}{4}T_{SFT}S_n$

这个式子不显然，我在这里一步步拆解一下，当作复习信号与系统了。

在这里，一般$T_{SFT}=1800$，即30分钟，作为短时傅里叶变换的窗长：

$\tilde{x}\left( f \right) =\int_0^{T_{SFT}}{x\left( t \right) e^{-j2\pi ft}dt}$

这样我们就得到了此时信号的双边频谱表示，而且实际上，高斯噪声是一个无限长的功率信号，我们只是对$0\sim T_{SFT}$进行了截取，一般地，时域信号的平均功率定义为：

$P=\underset{T\rightarrow \infty}{\lim}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{\left| x\left( t \right) \right|^2\mathrm{d}t}$

根据帕塞瓦尔定理，信号在时域和频域里能量守恒，所以进一步：

$\underset{T\rightarrow \infty}{\lim}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{\left| x\left( t \right) \right|^2\mathrm{d}t}=\int_{-\infty}^{\infty}{\underset{T\rightarrow \infty}{\lim}\frac{\left| \tilde{x}\left( f \right) \right|^2}{T}\mathrm{d}f}$

那么所谓的功率谱密度，应该满足：

$P=\int_{-\infty}^{\infty}{S_n \left( f \right) \mathrm{d}f}$

于是，我们就得到了信号的功率谱密度：

$S_n\left( f \right) =\underset{T\rightarrow \infty}{\lim}\frac{\left| \tilde{x}\left( f \right) \right|^2}{T}$

由维纳-辛钦定理：

$P_{xx}\left( f \right) =\int_{-\infty}^{\infty}{R_{xx}\left( \tau \right) e^{-j2\pi f\tau}d\tau}$

对于连续随机过程，其自相关函数的傅里叶变换是其功率谱密度。特别地，对于高斯噪声，其功率谱密度是一个常数。所以，不严谨地，在$0\sim T_{SFT}$的情景下：

$\left| \tilde{x}\left( f \right) \right|^2=T_{SFT}S_n$

当我们用单边谱密度来描述时，由于负频域被折了过去，单边谱密度是双边谱密度的两倍。所以更正为：

$\left| \tilde{x}\left( f \right) \right|^2=\frac{1}{2}T_{SFT}S_n$

同时我们知道，零均值的高斯噪声的傅里叶变换仍然是零均值的高斯噪声，同时实部和虚部概率分布相同。所以$\left| \tilde{x}\left( f \right) \right|^2$实际上就是我们关心的频谱中的方差$\sigma^2$，由于计算方差时是同时作用于实部和虚部的，而它们是同分布的，所以对于实部和虚部的方差即为：

$\sigma ^2=\frac{1}{4}T_{SFT}S_n$

运行pyfstat验证一下：

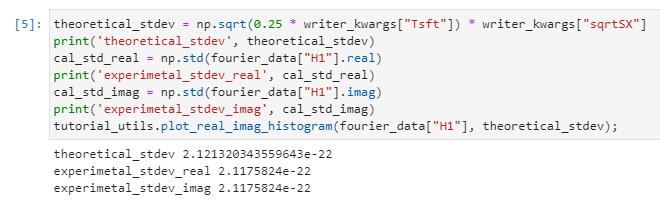
上述推导在实际探索中其实不大重要，因为可以二分出合适的$S_n$，使得自己生成数据的标准差和测试集的一致。只是为了复习一下信号与系统。

如果要模拟一个有引力波的样本，只需要将信号注入噪声背景中，如之前所说，当$\mathcal{D}=20$时，就已经丧失视觉特征了：

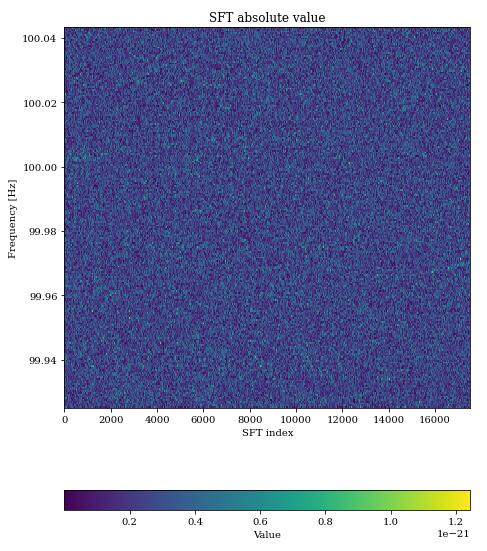
我们的目的就是对样本进行分类，判断这里是否存在引力波。实际上对于用机器学习方法来处理的方案，这同时隐含着“容易拟合噪声”。

Further Analysis

在上面的演示中，绘制的都是绝对值，数量级在10的负21次方左右。为了让引力波在频谱图中显示的更明显，结合实部和虚部是必要的。以一个朴素的正弦波为例：

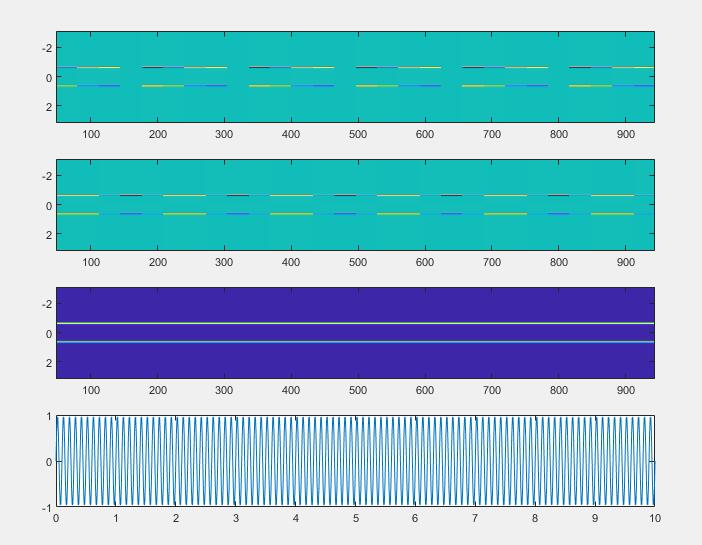
因为短时傅里叶变换的本质是加窗，可以理解成一个频移因子$e^{j\omega}$在作用，我们知道$\mathrm{sin}x$的傅里叶变换应该是一个冲激函数，不应该有虚部，而在$e^{j\omega}$的作用下，可以看到实部和虚部交替出现“涟漪”，而幅度谱就很一致。从这一点出发，结合实部和虚部非常必要。

然而除了幅度谱，还有功率谱，这两个的差别只有一个根号。这在数据预处理中也常见，比如语音的频谱时，我们经常用$\mathrm{log}(\cdot)$来缩放频率值的尺度。在这里，具体是使用幅度谱$\sqrt{\mathrm{Re ^2}+\Im ^2}$还是使用功率谱$\mathrm{Re ^2}+\Im ^2$要根据情况而定，我们进行一波可视化：

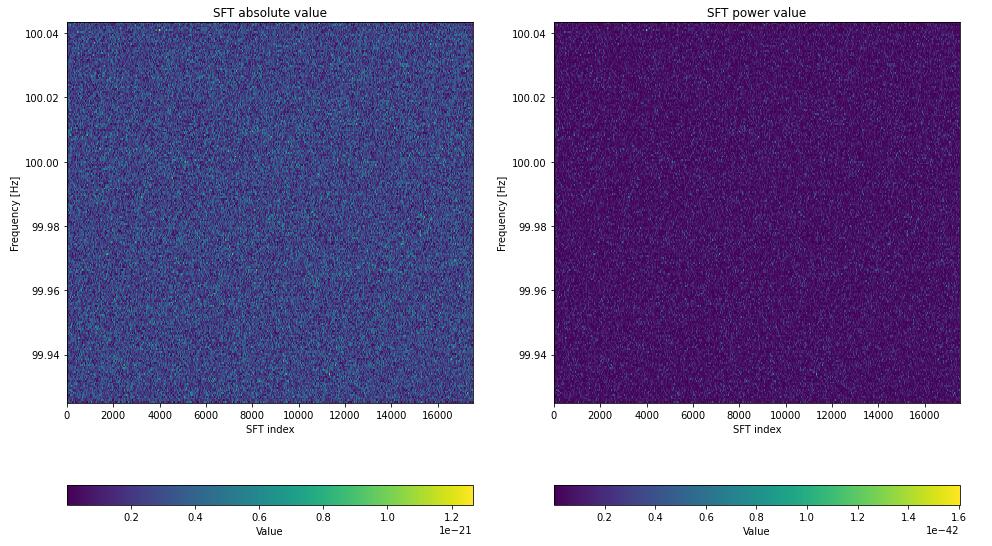
可以看到，功率谱更加稀疏，这可以避免过拟合一些无用的噪声（事实上这在这个任务里十分重要）。所以我们选择功率谱。

然而要小心，float32最小能表达的能到1e-38，而数据的实部和虚部在1e-22。这说明当计算功率谱时，数量级会到1e-44。所以会产生严重的浮点失真。包括在求mean和std时，也要注意这一点。

有些人可能会说：python默认的浮点数是float64啊。这就是一个陷阱，虽然python默认的是float64，但使用的一些非官方的库函数可能在编写时为了储存的方便，是使用float32的。例如这里的get_sft_as_arrays()，如果打印下来可以看到，fourier_data[‘H1’].real.dtype的数据类型是float32！

一个很简单的解决方法，对其频谱数据进行astype(‘complex128’)即可。这就是一个小陷阱，它可能会使人感到困惑。

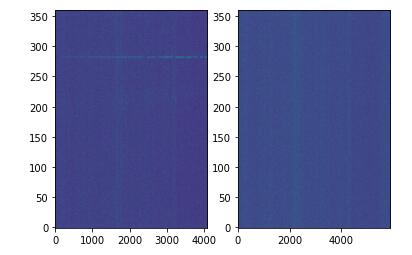
接下来对测试集进行EDA，把训练集和测试集样本中的H1和L1的标准差画出来，会发现如下的事实：

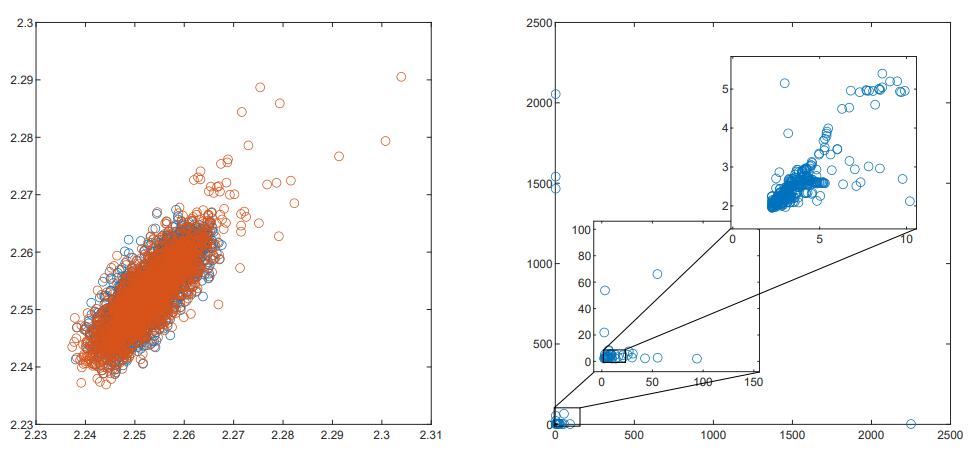
训练集中大部分数据都是使用同一个$S_n$生成的，虽然可以看出，距离中心越远，越可能是注入了信号的（标准差发生了偏移）。然而这是一个很糟糕的估计，因为在测试集里，分布的标准差变得极其广泛。标准差的偏移大概率不是注入信号的原因。

原因是测试集中大约80%是pyfstat库模拟的样本，剩下的20%是比赛官方使用观测站历史数据随机注入的，旨在模拟真实环境下的样本。真实数据中的数据，有着广泛的各种干扰。

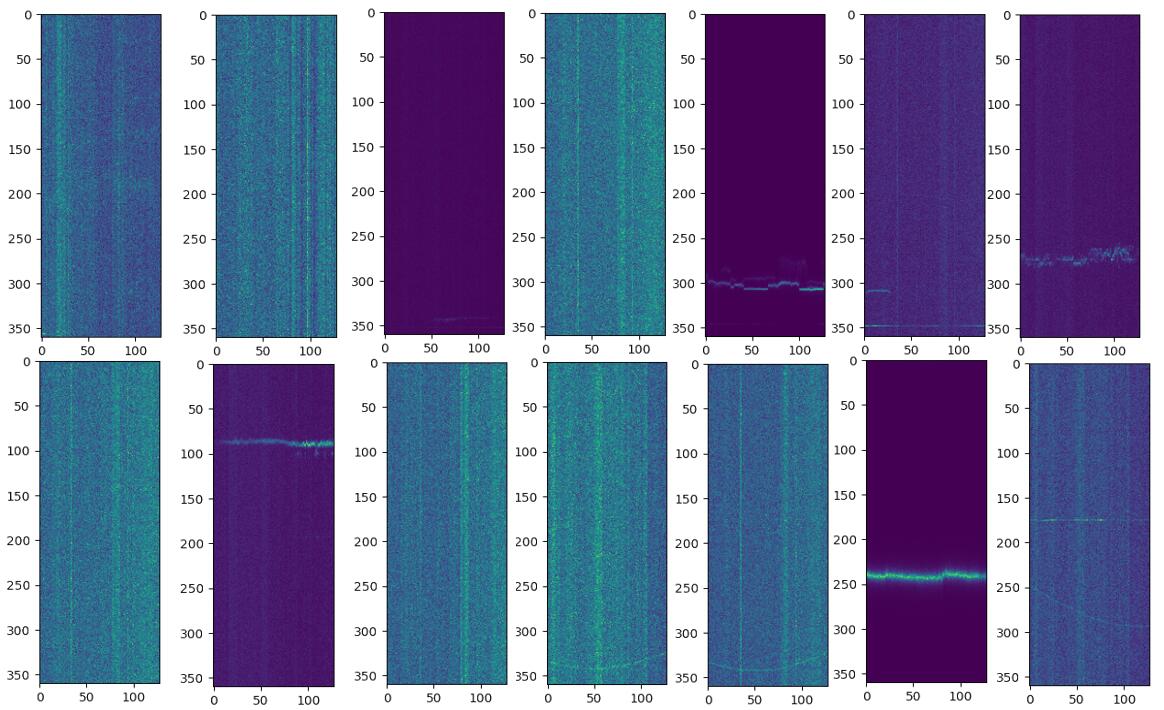
上图中的时间单位以32步取平均，这种操作类似于平滑滤波，实践上可以使得引力波更加可见。上图的样本中，有许多是由仪器产生的伪影，以及由于仪器停机，导致记录的时间戳不齐，使得噪声不均匀。

Normalization

然后就是每个任务都要用到的归一化，前面分析了噪声的性质，其实部和虚部都是服从零均值正态分布的，所以对于功率谱$\xi _{\mathrm{Re}}^{2}+\xi _{\mathrm{Im}}^{2}$其服从$\chi ^2\left( 2 \right) $。我们可以用直方图来check一下：

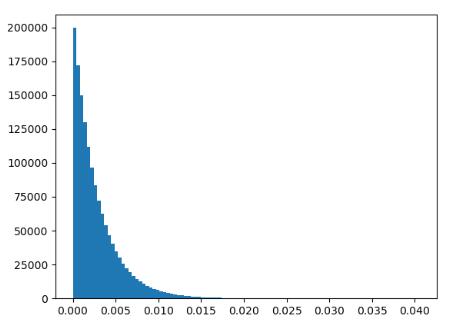
所以一个直接的想法是将其化为标准的由两个$\xi \in \mathcal{N} \left( 0,1 \right) $构成的卡方分布，所以我学到一种新的normalize方法：

def chi_squared_normalize(X):
    X = (X[..., None].view(X.real.dtype) ** 2).sum(-1)
    POS = int(X.size * 0.99903)
    EXP = norm.ppf((POS + 0.4) / (X.size + 0.215))
    scale = np.partition(X.flatten(), POS, -1)[POS]
    X /= scale / EXP.astype(scale.dtype) ** 2
    return X

这种归一化的操作是，找到数据中第POS大的数，然后以POS/X.size作为一个百分位点，寻找此时在标准正态分布中的值。然后通过第POS大的数与查出来的正态分布的值的平方的比，来对功率谱进行归一化。

另外，为了减轻不平衡噪声的影响，可以在进行chi_squared_normalize前先按时间（列）归一化：

1
2
3

def col_normalize(X):
    X /= X.sum(-2, keepdims=True)
    return X

对于之前图中的各种仪器谱线和干扰（他们的值非常的大，使得画出来的图其余部分都是蓝黑色），可以使用sklearn中提供的RobustScaler，它在缩放时会抛弃那些异常值，但我没有用过。

对于一些伪影和仪器谱线，可以从测试集文件中简单地提取出来（检测sigma值）然后写入训练集中，来训练模型对其的鲁棒性。

这里就是一些根据不同类型数据来灵活进行数据处理了，比如上面就是直接检测那些大于3sigma的值，把他们认定为线，然后用同一尺度的高斯噪声替代。

Large Kernel

我在G2Net比赛里学到的另一个知识是：大卷积核。相比于小卷积核提取“材质”等细节特征，大卷积核更关注于形状。实际上，有一个很好的工作：Scaling Up Your Kernels to 31x31: Revisiting Large Kernel Design in CNNs，在RepVGG的基础上提出了RepLKnet，证明大卷积核确实是可行的，是被“错杀”的设计元素。

然而那个工作是一个非常heavy的计算机视觉的工作，我基本无法复现。第一是昂贵的硬件要求，第二是从零开始训练大卷积核需要一些trick，例如重参数化等。然而在这次比赛里我得以体验了一把大卷积核，kaggle的一个用户laeyoung使用一层大卷积的layer，置于传统的backbone之前，训练出了一个很好的大卷积预训练模型。我们可以在它的基础上进行微调。

注意，这里的大卷积核和RepLKnet的基本不同，少了大量的trick，而且也并不是一个“模型设计”，只是一个“主干层”。但仍然能学到很多知识。

class LargeKernel_debias(nn.Conv2d):
    def forward(self, input: torch.Tensor):
        finput = input.flatten(0, 1)[:, None]
        target = abs(self.weight)
        target = target / target.sum((-1, -2), True)
        joined_kernel = torch.cat([self.weight, target], 0)
        reals = target.new_zeros(
            [1, 1] + [s + p * 2 for p, s in zip(self.padding, input.shape[-2:])]
        )
        reals[
            [slice(None)] * 2 + [slice(p, -p) if p != 0 else slice(None) for p in self.padding]
        ].fill_(1)
        output, power = torch.nn.functional.conv2d(
            finput, joined_kernel, padding=self.padding
        ).chunk(2, 1)
        ratio = torch.div(*torch.nn.functional.conv2d(reals, joined_kernel).chunk(2, 1))
        power = torch.mul(power, ratio)
        output = torch.sub(output, power)
        return output.unflatten(0, input.shape[:2]).flatten(1, 2)
    
C = 16
H = 31
W = 255

Large_Kernel = LargeKernel_debias(1, C, [H, W], 1, [H//2, W//2], 1, 1, False).to('cuda')

x = torch.randn((4, 1, 128, 1024)).to('cuda')
x = x ** 2
y = Large_Kernel(x)

这里不使用偏置，继承自torch的nn.Conv2d。实际上，这里计算卷积仍然是靠的torch.nn.functional.conv2d()，然而这里有许多代码，他们的作用其实是为了实现权重衰减。权重衰减确实现在已经很少提了，但是在大卷积里有必要再次引入。

权重衰减，第一反应都是在优化器里设weight-decay和L1-norm，L2-norm。然而此处的大卷积核是在forward里自耦了一个权重衰减。通过target = abs(self.weight)，target = target / target.sum((-1, -2), True)，得到一组新的权重：

$\frac{\left| w_{i,j} \right|}{L_1},L_1=\sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{\left| w_{i,j} \right|}}$

然后将这两组卷积核拼在一起，和输入finput做卷积。记由正常卷积核算出来的部分是output，target变量指的卷积核算出来的是power。然后，这里冗长的reals，是用来创造一个除去padding部分全为1的张量：

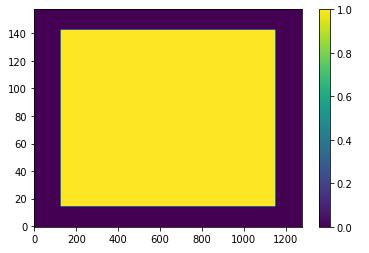
所以ratio = torch.div(*torch.nn.functional.conv2d(reals, joined_kernel).chunk(2, 1))是joined_kernel在和一个大部分为1的张量做卷积。在 reals里为1的区域中，任意一个坐标的值为：

$\frac{\sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{w_{i,j}}}}{\sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{\frac{\left| w_{i,j} \right|}{L_1}}}}=L_1\frac{\sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{w_{i,j}}}}{\sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{\left| w_{i,j} \right|}}}=\sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{w_{i,j}}}$

算这个的作用是什么？我们先可视化一个其分母（上）和随机初始化权重后的ratio（下）：

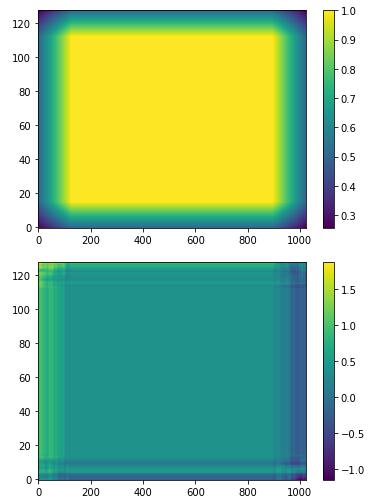
可以看到，在没有padding的部分，分母因为求和式子恰好为1，所以都是1；有padding的部分，由于分子的求和会少一些项，所以出现了衰减。

之后的power = torch.mul(power, ratio)和output = torch.sub(output, power)完成了图穷匕见的过程：power之前是由target指代的卷积核计算的，即$\frac{\left| w_{i,j} \right|}{L_1}$，先乘ratio，ratio近似是权重之和，那么，对于其中一次卷积操作：

$\sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{\frac{\left| w_{i,j} \right|}{L_1}d_{i,j}\varSigma}} \\ \varSigma =\sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{w_{i,j}}} \\ \sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{\left( w_{i,j}-\frac{\left| w_{i,j} \right|}{L_1}\varSigma \right) d_{i,j}}} \\ \sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{\left( w_{i,j}-\frac{\left| w_{i,j} \right|}{L_1}\sum_{m=0}^{H-1}{\sum_{n=0}^{W-1}{w_{m,n}}} \right) d_{i,j}}} \\ \sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{\left( w_{i,j}-\frac{\left| w_{i,j} \right|}{L_1}\left( w_{i,j}+\sum_{m\ne i}^{H-1}{\sum_{n\ne j}^{W-1}{w_{m,n}}} \right) \right) d_{i,j}}} \\ \sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{\left( w_{i,j}-\frac{\left| w_{i,j} \right|}{L_1}w_{i,j}-\frac{\left| w_{i,j} \right|}{L_1}\sum_{m\ne i}^{H-1}{\sum_{n\ne j}^{W-1}{w_{m,n}}} \right) d_{i,j}}} \\ \sum_{i=0}^{H-1}{\sum_{j=0}^{W-1}{\left( w_{i,j}\left( 1-\frac{\left| w_{i,j} \right|}{L_1} \right) -\frac{\left| w_{i,j} \right|}{L_1}\sum_{m\ne i}^{H-1}{\sum_{n\ne j}^{W-1}{w_{m,n}}} \right) d_{i,j}}}$

如此，就实现了某种意义上的权重衰减。我们可以可视化这个H=31，W=255的大卷积核：

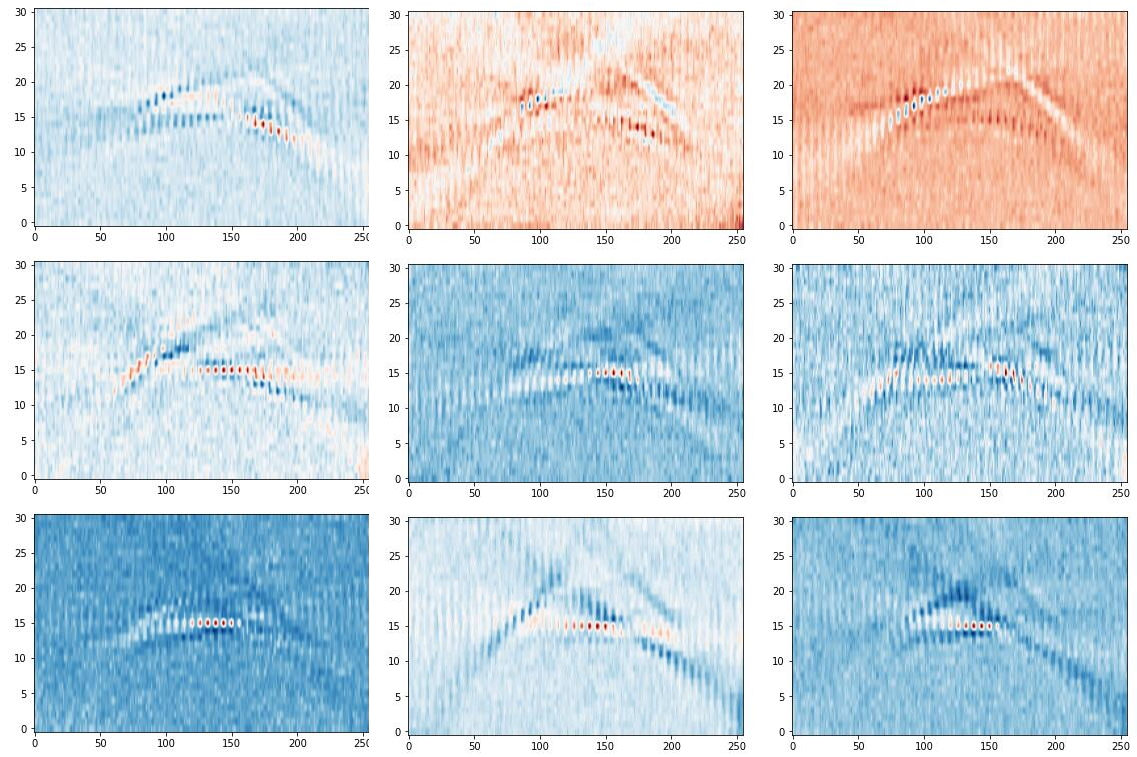
可以看出，权重的分布有些类似边缘检测滤波器。可以看出分为三个方向，与数据分布时不同频率变化的引力波对应。这其实暗示了另一种方法：匹配滤波，这在真实的引力波搜索中是被用到的技术，即使用已知的波形作为模板，也执行这样的“大号卷积核”。不过这是后话了。

除此以外，就像数字信号处理所教的一样，其实使用torch.nn.functional.conv2d()计算大卷积比较低效，我们可以用FFT来加速计算，感兴趣的可以查询https://github.com/klae01/fft-conv-pytorch。

实际上真正应用在CV里的31×31比这个复杂的多，等以后有用到的时候再说吧。

Other Issues

实际上，这个比赛在最后一个月我就基本做不了什么了。现在复盘的时候我意识到，我实验管理太差了……有时候根本就没记下来什么work什么不work，有点类似于狗熊掰棒子。另一个方面是确实没有能力执行大规模的搜超参，搜backbone的任务，梳理好pipeline以后其实能做的只有试点aug，试一些tta。

其实我个人觉得最麻的一件事就是！当时没有弄懂那个chi_squared_normalize，实际上那样以后，再对时间步取平均，可是好上加好，同时极大的减少训练成本（时间，空间）。当时就像美苏冷战被拖垮的苏联一样，每天用2×360×5760训练。

下面的一些是总结的Top选手里的一些我觉得我以后能用到的事项：

①不要迷信本地val metrics，有时候last epoch可能更好。

②训练时采用指数平滑策略（EMA）。

③将模型的第一个卷积层的步幅更改为（1，2）以放大图像分辨率。

④这或许是最重要的，“the intuition task by task”，比如观察到测试集里的timesteps_GPS并不等距，要进行对齐；这种可以生成数据集的比赛里，尽量实现在线生成数据（将噪声和信号随机注入）这样可以天然的防止过拟合。这些小事情不需要4×V100，只是需要“观察到”。

End

大概就写到这里草草结束了，因为事情确实很多。通过这个比赛确实学到很多，最终拿到银牌（Top5%）确实非常开心。至少，它虽然不加分，但我会很自豪的把它写进CV里（相比于一些其他的……）。

与此同时我结识了，不对，我很早就认识的很可靠的伙计，所以我也不能在这里停留太久了。这一篇blog虽然短但是写了很久，因为一直在check和verify一些想法，等等……

提前新年快乐吧！