Understanding Self Attention


阅读数: 次   

​ 从Attention Is All You Need以来，自注意力机制逐渐被应用于各种领域。在我试图将其应用到我自己的任务中时，遇到了一些疑问，遂想进行一些系统的整理。

​ 相比于CNN，自注意力我觉得有些不好理解。CNN可以被很好的理解成带通滤波器，是可学习的卷积核和特征图做自相关。然后再看transformer复杂的结构，各种机制，只能不解其意，然后copy一下代码，对齐tensor的维度，然后就没有然后了。

Dive into the formula

​ 第一步，我们先观察自注意力的式子：

​ 其中，$Q,K\in \mathbb{R} ^{m\times d_k},V\in \mathbb{R} ^{m\times d_v}$

​ 所以$QK^T$会得到：

​ 显然，乘出来的$m \times m$的矩阵是$Q$的行向量与$K$的列向量的内积，也就是他们的相关性。实际上$Q$和$K$只需要有相同的$d_k$即可，在attention is all you need原文中，作者选用了相同大小的$Q$和$K$，其实在$Q\in \mathbb{R} ^{m\times d_k},K\in \mathbb{R} ^{n\times d_k}$时，最后的乘出来是$m \times n$，此时只要$V$从$\in \mathbb{R} ^{m\times d_v}$改成$V\in \mathbb{R} ^{n\times d_v}$即可，非常灵活。

​ 如果我们取$Q=K=V=X$​，例如：

​ 然后，最后一步再乘上$V$（在这里也就是$X$）最后得到：

​ 那么这一堆朴素的代数运算想说明什么呢？我们带入一个情形来获取直观理解。在自然语言处理中，文本被处理成词向量，例如：

​ 那么$XX^T$其实就是在计算“峨”“眉”“峰”三个词向量的相关性，然后这个对称矩阵被Softmax归一化，得到了一个0~1的权重，又乘上$X$​，这个时候：

​ 可以看到，最终的行向量从原来的“峨眉峰”变成了“峨眉峰”与注意力的加权求和。这样做的背景很好理解，如果“峨眉峰”三个字的内积互相是零，那么相当于最后乘了单位阵。如果他们的内积不为0，例如“峨”和“峰”的内积很大，这说明当峨（峰）出现时，峰（峨）也大概率会出现。

​ 这个过程也从$Q,K,V$的字面意义理解，$Q$表示query，$K,V$是熟悉的键值对。比如此时我用$Q$的第一行“峨”去在key里寻址，key里也是“峨”“眉”“峰”，他们计算相似度，这个相似度就是attention score，他反应了要取出的value的重要程度。然后这个相似度与value里的值分别相乘，即对各个value加权求和，最后得到了用“峨”查询的时候的结果。

​ 所以上面的举例和分析其实引导到了一个直观的理解：我们使用 $Q$来查询各个键$K$，每个键有相应的值$V$，最终我们通过$Q,K$来计算注意力，这里的注意力即缩放后的点积注意力，来作为每个$V$的权重，最终输出结果。因为待查询的可以有$m$个，键值对可以有$n$个，$m$完全可以不等于$n$，这就是上文$QK^T$乘出来的矩阵可以是$m\times n$的原因。

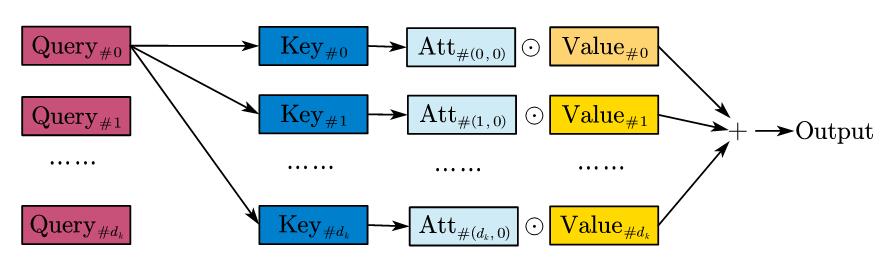
​ 真正实施时， $Q,K,V$ 是用线性层投射来的。特别地，当$X$是方阵，且如果我们令权值矩阵也是方阵，此时的$X$其实就是被矩阵$\mathbf{W}_Q,\mathbf{W}_K,\mathbf{W}_V$换基表示，由于矩阵是可以学习的，所以他们可能会在特定的任务中构建出一组特定的基，刚才我举了一个自然语言处理的例子，这样的例子网上有很多，所以这里我想了另外一个比较有意思的情况：

​ 此时我们取$X$​是由$\mathrm{sin}x$​构成的矩阵，$m=3,d_k=512$​，即：

​ 这里$\mathbf{W}_Q,\mathbf{W}_K$我假设为$3 \times 3$的单位矩阵，即恒等映射。对于$\mathbf{W}_V$取傅里叶变换矩阵，维数是$N\times N$​，相当于做离散傅里叶变换。

​ 由于三角函数的正交性，此时按照自注意力公式，出来的值仍然是各个分量的频谱。相当于我们输入$\mathrm{sin}(20t)$ ，这个“自注意力层”就会给出 $\mathrm{sin}(20t)$

的频谱。这个例子很好的体现了三点：

​ ①自注意力的“自”，我们这里输入的频率是1, 20, 50，实际上最后输出的频谱是就是被输入的频率确定的，不可能输出频率为30的正弦波的频谱。因为$Q$是$X$作线性变换来的，它不可能成为其他频率的基。

​ ②在真正使用self-attention机制时，在pytorch中我们会实例化一个nn.Linear()来构造线性投射，默认的情况下它是带有bias=True的，对于一个$m \times n$ 的映射，它会再上一个$n$维的偏置向量给每一列。这样这个“线性层”就不会是线性映射了。有些开源代码会将bias设成False，在特定的任务里会有一些提升。

​ ③实际上，自注意力的线性投射是：

​ 在上面举的例子里，因为DFT的关系，所以是$\mathbf{W}_V$左乘$X$，而实际是右乘。这里不同的原因是，在$X\mathbf{W}_V$时，我们关注的是$X$的列空间，即采样的时间维度；而当$\mathbf{W}_VX$我们关注行空间，即不同频率的正弦的线性组合。

​ 由于大多数时候我们都在讨论列空间，所以其实nn.Linear()实现的是：

​ 而我们写作$WX$时，是在讨论行空间。这点的不同，催生了“spatial transformer”，“temporal transformer”，通过调整映射的维度，来获取不同维度的信息。nn.Linear()默认是处理张量的最后一个维度。在自然语言处理中（貌似）不会遇到这个问题，因为词向量如果看成行向量，那么逐列看它是没有意义的。但一些别的任务里，比如一个人体动捕数据，一个维度是各个结点的三维坐标，另一个结点是时间（帧），这个时候就要考量一下用self-attention如何建模了。

​ 如果权值矩阵$\mathbf{W}_Q,\mathbf{W}_K,\mathbf{W}_V$非方阵，此时会将输入数据我们所关心的那一维，嵌入到高维或者降维到低维。很有趣的一点是“嵌入”这个词的来源，形象的说，如果我们使用一个矩阵，将一个2维的向量映射到3维。这个过程就可以叫嵌入（embedding），我推测，为什么用“嵌”这个字的原因，是因为被投射的2维向量，只能存在于3维空间的某一特定的平面上，所以就像用一个平面“嵌入”了这个三维空间。

Positional Encoding

​ 我们刚才只是得以直观的理解，$Q,K,V$的核心思想，但还有一些细节没有捋清。

​ 在用RNN来建模时，上一个时刻的状态$h_t$总能以一些方式传递到下一时刻，这样会隐式的给出位置信息。然而，以刚才“峨眉峰”的例子来说，例如输入“雪山千古冷，独照峨眉峰”。假设“雪山”和“峨眉峰”高度相关，那么最后输出的信息，是不能区分“峨眉峰千古冷，独照雪山”还是“雪山千古冷，独照峨眉峰”的。

​ 这不仅在自然语言处理中会遇到，在别的任务中也存在，例如，一个人是到床上躺下了还是从床上坐起来了，如果不关注先后顺序，这两个动作完全可逆。即然self attention算子本身丧失了这种能力，想注入位置信息只能从输入中入手，即位置编码。

​ 位置编码目前还在被许多研究者研究，我们这里不做过多的深入。只需有个概念，想像一下如果我们要对一段序列（语句向量，骨架图数据）做这样的位置编码，第一个想法是在每个时间$t$时的开头或结尾拼上一个“token”，比如整型，1，2，3……

​ 这样的坏处是，位置值会越来越大，而且不能适用于比训练时所用的序列更长的序列（这点多见于NLP），那我们缩放一下，变成$[0,1]$，然而这样，不同长度序列的步长就不一致了。

​ 如果换一个思路，我们不用单个的值，而用一个和输入维度等长的向量相加，最自然的就是二进制编码（@计组）。由于一般的$d_{model}$也比较大，所以$2^{d_{model}}$完全够用，这样的缺点是位置距离不连续，比如$t=0$时我们记token是0000，依次$t=2$是0001，$t=3$是0010。但是它毕竟不是二进制数，是一个向量，计算他们之间的距离会发现其并不连续。

​ 所以一个很聪明的方案是利用有界，连续，简单的周期函数：

​ 这个设计非常的精巧，把它画出来的样子是：

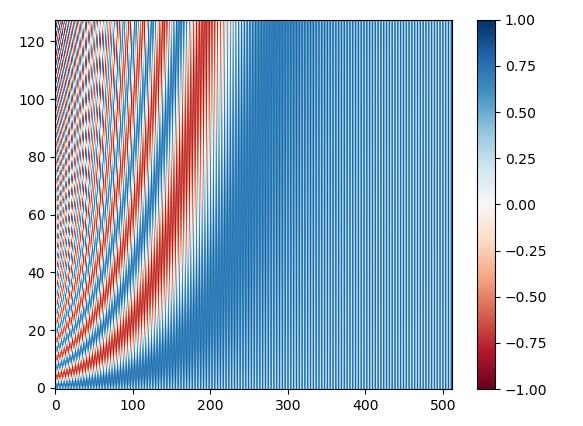
​ 纵坐标指的是“句子长度”或“时间步”为128，每个步的维度为512时的情形，首先我们可以肉眼确认，这确实是一种给不同的步赋予了不同值的编码方法，而且对于$d_{model}$，越大值越小，这个情况对于处理自然语言处理中过长的语句很有帮助，因为这样对于过长的语句不会出现out of distribution。

​ 现在还有两个小问题，第一是为什么要如此约定$w_i$，我们可以理解在同一个时间步的不同位置上要有不同的值，反映到三角函数里就是频率的变化，这其实模拟了二进制编码里的进位，越高位进位越费劲，即高位变化的次数少，可是为什么要用如此小的$w_i$？

​ 简单来说，$w_i$的值很大程度上取决于底数，这里是10000，在$i$很小时，这没什么影响，$w_i t$仍然近似线性增长，所以我们能看到-1；当$i$很大时，此时的$w_i t$几乎接近于0，如果是偶数$i$，那就是$\mathrm{sin(0)}=0$，奇数$i$就是$\mathrm{cos(0)}=1$，他们稳定的交替存在，相当于一块“静止的区域”，就像二进制编码里，总有冗余的高位是0（或是1），这样的高冗余特征实际是一种纠错编码，靠高度冗余保证位置信息，如果在整个$d_{model}$上没有这样的冗余信息，那么注入的位置编码就会被网络忽略（类似于某种噪声）或者过拟合这个噪声。

​ 如果$w_i$没有在$i$增大时变得那么小（即底数取小，例如10），此时的编码就会是：

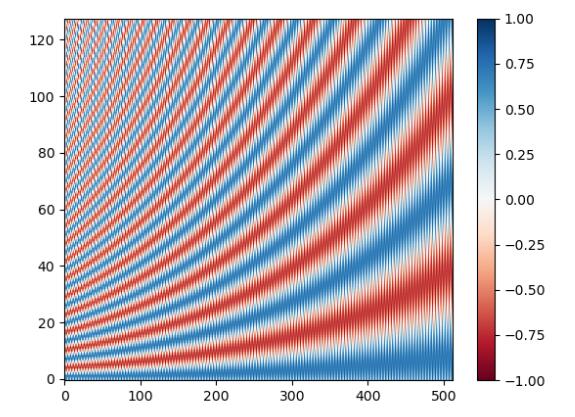
​ 此时冗余的部分几乎没有了，这带来了两个缺点，一个是位置编码与位置编码之间过于致密，第二个是如果维数超过了512，会出现一些超出分布的样本。关于位置编码的致密性，还有一个角度：如果使用频率偏大，那么在$t$偏大时，不同位置的位置向量可能出现重合，例如下面我们取$d_{model}=3$，颜色从蓝到红依次是$t=0$到$t=128$：

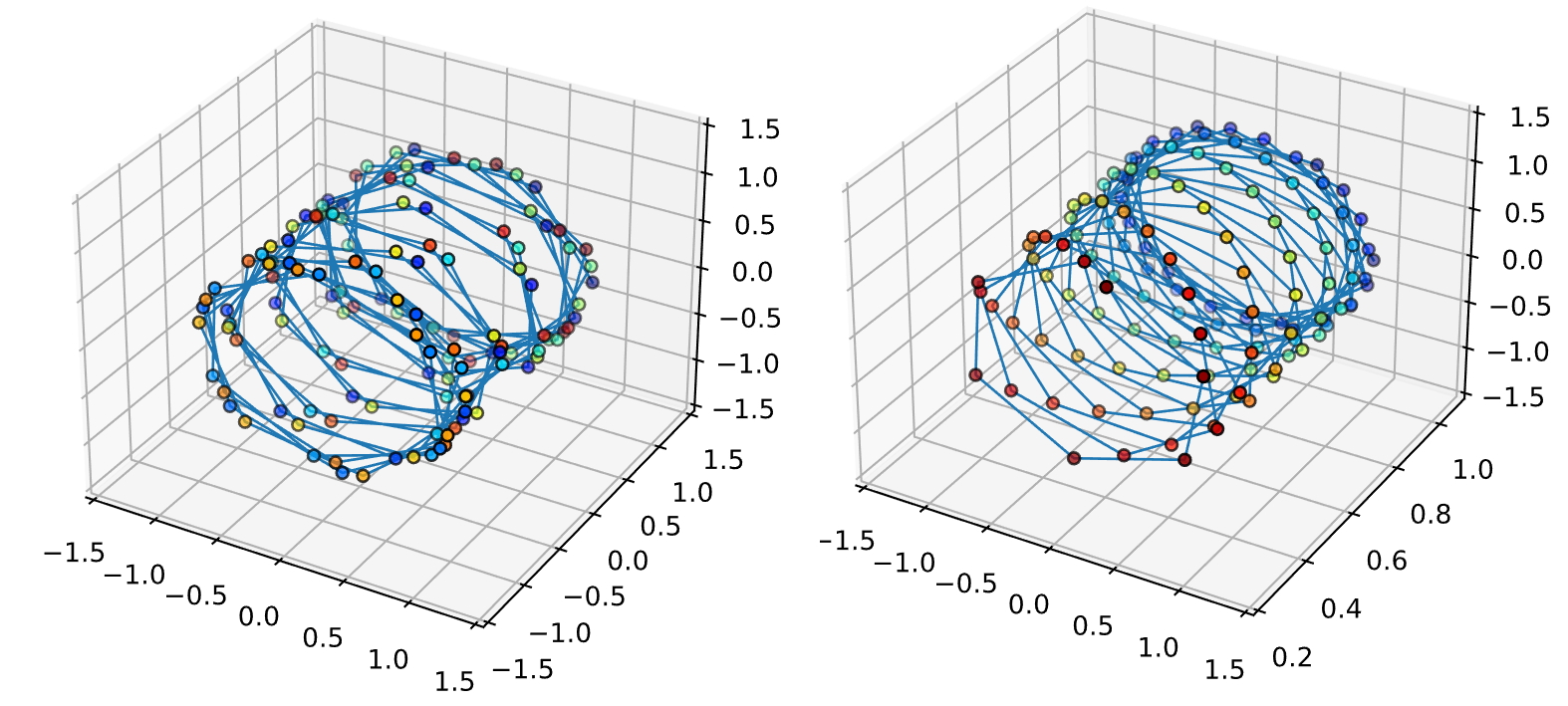
​ 左侧是底数取100，右侧是取10000，会发现左侧出现了大量不同时间的位置向量重叠的情况，而右测的位置向量十分可分。

​ 还有一个问题，余弦函数是怎么来的？为什么要引入余弦函数，而不是一直用正弦？原因其实是高中学的简单的三角恒等变换：

​ 在线性代数中，我们知道了旋转矩阵的概念，和上面的式子是等价的，所以：

​ 为了进一步方便书写，我们将$PE_{t}^{\left( i \right)}$写作$PE_{(pos,2i)},PE_{(pos,2i+1)}$​，即：

​ 所以根据辅助角公式，可以得到：

​ 所以，整个位置向量可以使用一个线性变换，把$t$时间步转移到$t+\varDelta t$：

​ 这样的设计，使得位置编码中不同位置之间，存在线性关系，原作者认为这样可以使得模型较为简单的学习到相对位置信息，从而克服了之前说的二进制编码距离不连续的问题。

​ 现在我们初步探明了这个vanilla的位置编码的设计思想，在最后，我们可以对不同时间$t$下的向量编码计算自相关矩阵，来确认这种设计的唯一性。

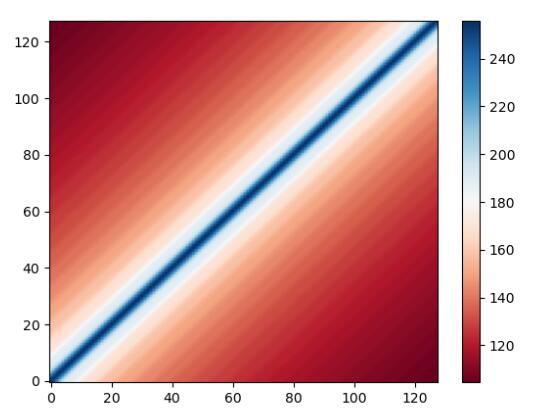
​ （这个”RdBu”配色真的经典,）

​ 现在，还剩最后一个问题，为什么这个位置编码可以直接“加”到所要注入的张量里，这样不会造成什么信息损失吗？实际上，这是一个误解，我们并不是把位置编码直接加在初始的原始输入中，transformer会先对原始输入做一个嵌入，把它映射到高维，然后再加上刚才所讨论的位置编码。这个过程实际等价于，先给原始输入并联(concat)一个代表位置信息的向量，再做嵌入。设一个输入向量$x\in \mathbb{R} ^{\left( 1\times d \right)}$，代表位置的编码向量$PE\in \mathbb{R} ^{\left( 1\times n \right)}$​，他们并在一起做映射：

​ 由于我们上面分析过了，这种利用三角函数实现的编码方式有良好的性质，所以在具体实现时，我们就选择了先对输入向量做嵌入，然后再相加位置编码。也有一些工作使用可学习的编码方式，不过大部分时候差异不大，不是这里的重点。

Strange $\sqrt d_k$

​ 在计算自注意力时，我们将$Q$与$K^T$相乘，然后除$\sqrt d_{k}$来进行缩放，直觉上，这是在防止计算点积时出现过大和过小的项，导致在Softmax时注意力分数的值过于极端。这当然会导致梯度回传的困难，在这里我们稍微深入一下Softmax，看一下这到底会对梯度回传造成多大的影响。

​ 实际上Softmax是将一个$N$维向量映成另一个$N$维向量：

​ 所以对一个多维张量指定Softmax时，需要指定对哪个维度进行计算，由于self attention的思想是用$Q$来查$K$，所以对于$Q\in \mathbb{R} ^{m\times d_k},K\in \mathbb{R} ^{n\times d_k}$的情况，作矩阵乘法后得到$m\times n$的矩阵，我们是指定行向量进行Softmax的，它对应的是长度为$n$的向量，在一般的计算过程中，张量的维度分别是$B\times C\times m \times n$，所以当进行Softmax时往往是对最后一维操作，即F.softmax(dim=-1)。

​ 它具体的计算式子是：

​ 特殊地，当$i=j$时：

​ 所以雅可比矩阵为：

​ 所以当输入的某个值因为其数量级比较大，被赋予一个例如$[1,0,…,0]$的标签时，整个雅可比矩阵的近似为零阵，造成梯度消失。

​ 那为什么用$\sqrt d_k$来放缩，我们可以借此复习一下概率论，假设$Q$和$K$里的元素服从标准正态分布且相互独立，假设随机变量$X\in Q,Y \in K$，由于$X,Y$相互独立，且$f(x)=x^2$是连续函数，所以$X^2,Y^2$也独立，所以我们可以计算$XY$的期望与方差：

​ 所以$D(QK^T)$的方差即为$d_k$个$XY$的叠加，即为$d_k$，所以用$\sqrt d_k$作归一化，比较合适。

​ 我在写这篇blog的时候在网上也查阅一些资料，我发现有人说$QK^T$符合卡方分布，说$D(X)=2n$，这是错误的，卡方分布指的是若干符合标准正态分布的变量的“平方”的累加，$X^2 \ne XY$。

Multi-Head

​ 到目前位置，self-attention算子已经可以实现RNN所实现的功能了，甚至更好，因为RNN不能并行，但它可以。然而与CNN相比，CNN当输入$c_{in}$个channel的特征图时，会用$c_{out}$个滤波器组，每一个有$c_{in}$个滤波器（卷积核），他们对应通道做卷积，然后结果加权，过激活函数。这个过程赋予了CNN与多种通道互相通信的能力，然而目前的self-attention算子，其$Q,K,V$经过训练后，是一个固定的矩阵，他们只能把输入投影到特定的空间。

​ 但是通过多头注意力的机制，也可以使它能并行地计算来自多个空间的注意力。

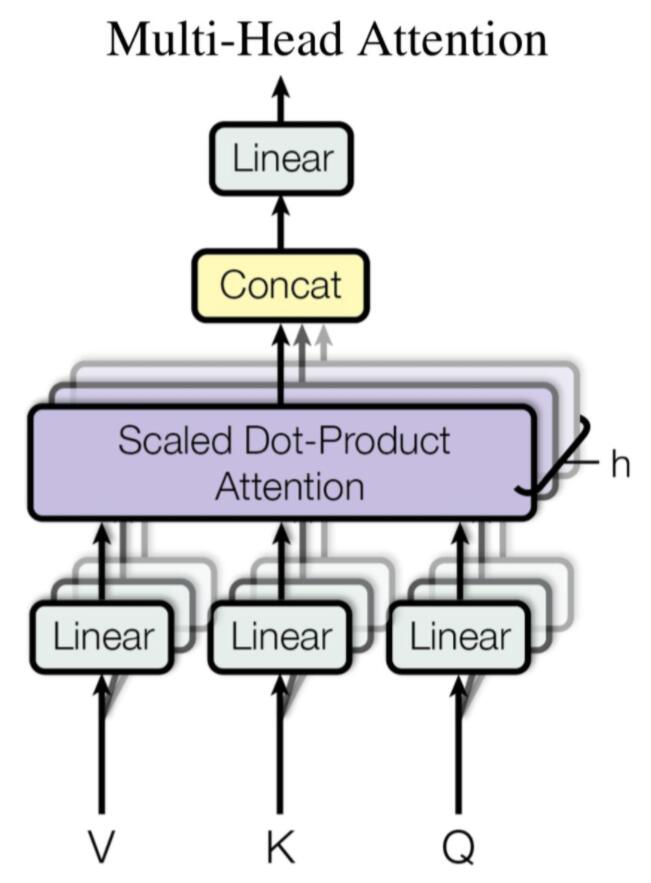
​ 其实操作起来十分简单，之前在得到$Q,K,V$​时，我们是用$W_Q,W_K,W_V$​直接算过来的。其实只要把算过来的结果进行分块，分别做self-attention，再把最后的结果并在一起，这就是多头注意力了，$h$头的注意力可以表示为：

​ 于是self attention算子也有了结合多个子空间进行交互的能力。

LayerNorm

​ BatchNorm的使用让CNN得以快速收敛，在那个年代，这减轻了调参难度，即只要是一个合理的任务，把数据标准化，输入一个CNN，只要CNN里加了BN，总能收敛的不错。而使用self-attention，由于其起源于自然语言处理，所用的是一种叫作LayerNorm的方式，如下图所示：

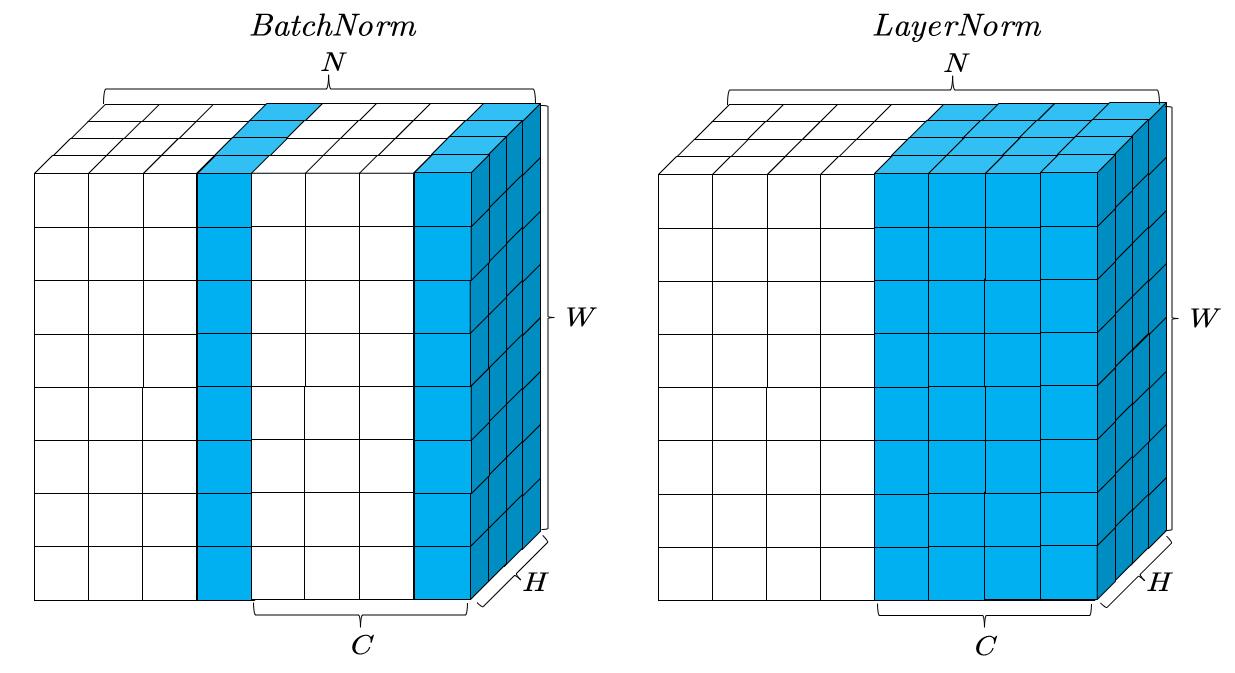
​ 上图展示了一种在更一般的任务中所遇到的情况，由于我们无法画出四维正方体，所以我们将$Batch$维以堆叠并联的方式展示，可以看到，BatchNorm是计算一种feature map在整个Batch里的均值和方差，然后进行标准化。

​ 而LayerNorm是不考虑Batch的，只计算Batch其中一个样本，它所有通道的均值和方差，然后进行标准化。

​ 这还是考虑到在NLP里，样本的句长会发生变化，这里不作过多讨论。

Transformer

​ 现在我们介绍完了一些基本的构件，终于，我们可以引出这个2017年就提出的结构，论文原文画的已经够经典和好看了：

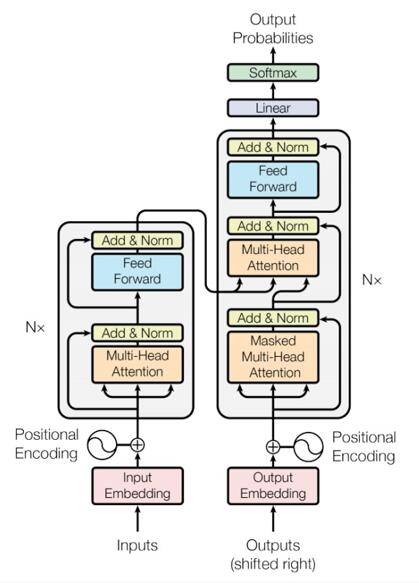
​ 观察这个图，上面有许多前文中熟悉的元素。先对input进行embedding，然后加上我们前面所说的，基于三角函数的positional encoding，然后作多头注意力，同时有一个残差连接，然后LayerNorm，这里的LN实际上是PostNorm，还有一种是PreNorm：

​ 一个明确的结论是：当同一实验设置时，PreNorm更容易训练，而他的效果会稍逊于PostNorm，这个这里不作详细讨论了。

​ 在进行了上图的PostNorm后，会送入一个“Feed Forward Network”，翻译过来是前馈神经网络，它其实就是两层MLP：

​ 经过FFN，再经过残差连接和Norm，这一整个结构就成为了一个“encoder”，这里的残差连接和FFN，是必要的。有一篇工作”attention is not all you need”从理论层面阐述了这一点，感兴趣可以看一下。

​ 注意图里的$N\times$，这说明一共堆叠了$N$层的encoder，这样过了$N$层的encoder后，会送入“decoder”。这里又来了个解码器的原因，是因为transformer最初用于机器翻译，它的训练和推理过程并不一样，如下图所示：

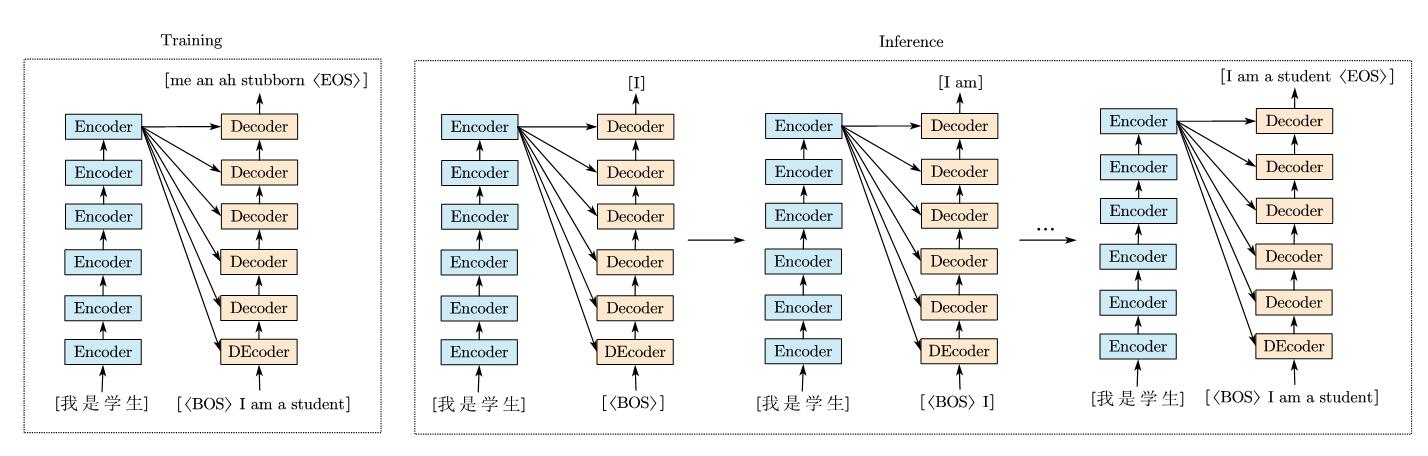
​ 以机器翻译为例，当训练时，encoder和decoder都是可以并行的，可以看到训练时最开始的翻译结果很糟，所以我们进行训练。encoder直接将词向量编码，编码后给decoder去查（注意到encoder后的结果流向了decoder里的一个多头注意力的输入，这里encoder输入的分别作为$K,V$，而decoder的输入是$Q$），在训练时，我们可以直接给出ground truth，即I am a student。然而在推理（测试）时是没有的，所以transformer在这里采取和之前的seq2seq模型一样的方式，进行自回归。其中BOS是begin of sequence，EOS是end of sequence，意思是序列任务中的起始符或结束符，用来预测某一个token预测过程的开始和结束。先输入起始符，结合encoder的结果，给出第一个字，然后结合第一个字，再给出第二个字……所以叫自回归。

​ 在transformer的decoder中，我们可以看到outputs的输入有个shifted right，这个其实就是在添加起始符或结束符，我们不用管它。然后decoder里有一个Masked的多头注意力，这其实是为了与自回归过程对应，把后面的序列的信息先盖住。

​ 实际上在做很多别的任务时，或许并不会忠实的迁移这个decoder过来，比如我如果只是做一个简单的分类任务，我只是希望用encoder部分做特征提取，那也就没有这个decoder的事情了。但为了整个blog的系统性，这里仍然做一下补充。

​ 实际上，如果在训练transformer时就使用串行的方法来训练，那么也就不需要这个masked机制了，但那样太慢了。加上这个mask以后，预测过程就恰好和训练时一致了。同时由于不受后面字词的影响，单词也会符合一个一个输出的自回归模式，否则会出现同一个单词一会儿是这个一会儿是那个的情况。

​ 由于我并不打算做机器翻译以及类似的任务，所以这里就不作过多讨论了。实际上这种特定的机制在不同任务中有不同的体现，例如Swin Transformer中的mask，又是另一套东西了，所以我奉行用到了再说，只要理解本质思想即可。但是，这种用encoder编码，然后decoder来查的思想，在attention is all you need中没有起名，后来的人们起了个名字，叫cross attention。

​ 这个cross attention是一种通用的架构，可以支持一些多种模态输入的任务，比如文本驱动的图像生成啊之类的。

Implement

​ 如上文提到，许多不同的下游任务会“各取所需”，但主要的核心还是要self-attention和cross-attention，这里记录一下爱因斯坦求和约定（einsum）和einops库，以及书写下self-attention的pytorch实现

。（其实主要是为了torch.einsum，einops这点醋包的饺子）

​ 我记得我在最开始的时候，为了让张量对齐，被permute,view,reshape,chunk.cat,squeeze,unsqueeze以及各种切片[:a],[a:],[…,None]整的混沌异常。而einsum可以很大程度上减缓因书写张量变换而引起的头痛。

​ einsum是一个求和“约定”，你可以很方便的告诉计算机一串简单的“符号”，这样就免去了手动指定张量的麻烦。它基于一个很简单的思想：

​ 对于一个$A\in \mathbb{R} ^{m\times k},B\in \mathbb{R} ^{k\times n}$的矩阵乘法，最后计算出的元素可以表示为：

​ 这里，省略掉求和变量$k$并不会影响唯一性，所以我们可以把它记为$ik,kj→ij$，这种方式非常聪明的把下标分为了自由标（输入和输出都出现的下标）和哑标（在输入端出现但输出端不出现的下标）。

​ 我们通过下面的例子理解一些简单的调用：

功能 写法
计算$A$的迹 torch.einsum(“ii -> i”,A)
$A$的转置 torch.einsum(“ij -> ji”,A)
$A$按列求和 torch.einsum(“ij -> j”,A)
$A$全部求和 torch.einsum(“ij -> “,A)
$a,b$的内积 torch.einsum(“i, j -> “, a, b)
$a,b$的外积 torch.einsum(“i, j -> ij “, a, b)
$A,B$矩阵的乘法 torch.einsum(“ik, kj -> ij “, A, B)
$A,B$矩阵乘法后转置 torch.einsum(“ik, kj -> ji “, A, B)

​ 同时它也支持广播机制，比如对于高维矩阵$A,B$​，我只想让后两维相乘，可以写作torch.einsum(“…ik, …kj -> ij”, A, B)。

​ 然后是另一个库，einops，这个库可以彻底的提供灵活且可读的张量操作符。我们主要是用这里的三个函数：rearrange，reduce，repeat。

​ 例如在实现torch中的张量转置时，我们有y=x.transpose(0, 2, 3, 1)，而利用rearrange，可以写为y=rearrange(x, ‘b c h w -> b h w c’)，reduce和repeat其实没有让书写简单特别多，这里就不介绍了。有了这两个工具，self-attention算子可以被方便的书写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Attention(nn.Module):
    def __init__(self, dim, heads=8, dim_head=64, dropout=0.):
        super().__init__()
        inner_dim = dim_head * heads
        project_out = not (heads == 1 and dim_head == dim)

        self.heads = heads
        self.scale = dim_head ** -0.5

        self.attend = nn.Softmax(dim=-1)
        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout),
        ) if project_out else nn.Identity()

    def forward(self, x):
        b, n, _, h = *x.shape, self.heads
        qkv = self.to_qkv(x).chunk(3, dim=-1)  # (b, n(64), dim*3) ---> 3 * (b, n, dim)
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h=h), qkv)  # q, k, v   (b, h, n, dim_head(64))

        dots = einsum('b h i d, b h j d -> b h i j', q, k) * self.scale

        attn = self.attend(dots)

        out = einsum('b h i j, b h j d -> b h i d', attn, v)
        out = rearrange(out, 'b h n d -> b n (h d)')
        return self.to_out(out)

​ 另外，由于现在许多库也都开始用einsum和einops了，所以尽早认识它们也剩的后面看着代码发懵了。

End

​ That’s all，总的来说，这篇blog具体的剖析了2017年的transformer，其实现在的ViT，DETR，AutoFormer，不同任务里的former已经更进一步了，但是就像最开始学习到CNN时，也得先了解CNN的基本思想，才能去追那些各种各样的变种。而self-attention算子是这些各种transformer的变种的基础。

​ 虽然但是，我上学期期末考试的课是一点没学。在家一呆，效率极低。一切责任全在新冠后遗症。我在考虑我要不要现在开始准备考研，再炼俩月丹再说吧。

赏

谢谢你请我吃糖果

微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

挟飞仙以遨游，抱明月而长终。<br />知不可乎骤得，托遗响于悲风。