模式识别,讲到了第八章。而我,抛去绪论只学了第二章。我觉得要出事。所以我又开始学了。
根据老师发的PPT,第三章叫“线性和非线性判别分析”。我看着看着其实发现一个问题,老师为了课时和讲授的方便,其实删减了很多内容。导致了一些不好的结果,比如很多东西就感觉没个由头,看的也半懂不懂。
在上一篇关于贝叶斯的blog里,我们知道,在协方差矩阵均相同的条件下,决策的划分被超平面划分。所以我们先首先假设,已知类别中的所有向量都是线性可分的。这个假设一方面具有实际意义,一方面简单并且便于计算。
此时,由于我们对类条件概率,先验概率等或许知之甚少,所以此时的分类器并不会像贝叶斯分类器一样,使得错误率或者风险最小,称作次优分类器。
换句话说,我们省去了估计类条件概率,当样本量充足时,是有相关的技术来估计类条件概率的,我们后面再提。
在贝叶斯分类中,我们选择最小错误率或最小风险原则,对区域进行划分,那么当采取线性分类器的假设后,那么分类器的参数如何确定?因为此时并不像贝叶斯分类时,权重$\boldsymbol{w}$有一个具体的表达式,可以直接计算。确定参数需要一个准则,就像当时的$g_{ij}(x)$,那这个时候准则的选取就会不同。以及最关键的,如果不是线性可分的怎么办?这些我们一点点来处理。
Perceptron Approach
第一种方法叫作感知器算法,它说的是,假设有两类$\omega_1,\omega_2$线性可分,那么存在一定义为$\boldsymbol{w}^{T}\boldsymbol{x}=0$的超平面,满足:
注意上式是可以包括不过原点的超平面的,只需扩展定义$\boldsymbol{x}=\left[ \boldsymbol{x}^T,1 \right] ^T$以及$\boldsymbol{w}=\left[ \boldsymbol{w}^{T},w_{0} \right] ^T$。
那么需要选择一个合适的代价函数和优化算法来得到$\boldsymbol{w}^{s}$的值,前人定义了一种感知器代价:
这里$Y$是训练集的子集,包含了那些被错分的向量,变量$\delta _x$如下定义:
注意上面关于$\omega_1,\omega_2$的定义,如果属于$\omega_1$,那么值应该是正的,而如果错分了,会是负的,此时乘-1会把符号扭成正的。属于$\omega_2$时,错分的值也是正的,所以这保证$J(\omega)$一值是正的。为了使代价函数最小,可以利用梯度下降法:
实际上,这里要指出:上式并不是真正的梯度下降,因为$J(\omega)$是个分段线性函数,它在某些点不一定有梯度。所以这种算法的收敛性其实需要证明一下,这里就从略了。因为这个算法实际上是1950年左右提出的,当时计算资源很匮乏,所以跟现在直接back propagation然后各种layer一叠比,有种突兀感。我们就不过多的介绍它了,只表以敬意。
Support Vector Machine
感知器算法给出的超平面并不唯一,可能收敛于任何可能的解,并且每一个解其实都完全的分开了训练集(如果线性可分的话),但真正分类时是在测试集上用的,所以我们仍然需要从每个可能的解里选择那些“泛化性”强的解,这样当面对未知数据时,通过超平面得到的结果更可信。这就引入了支持向量机。
支持向量机在网络上可以找到各种层次的详尽的资料,有的深度很深,有的注重几何直观。但是对我自己来说,仍然有整理的必要。因为学习学的其实不是支持向量机这一个事物,学的是学习能力的提升。如果仅仅只是走马观花的看一看一些视频,或者收藏夹吃灰,大概知道了一下“哦我知道,这不就是找个间隔最大的超平面嘛”,是起不到学习的意义的。
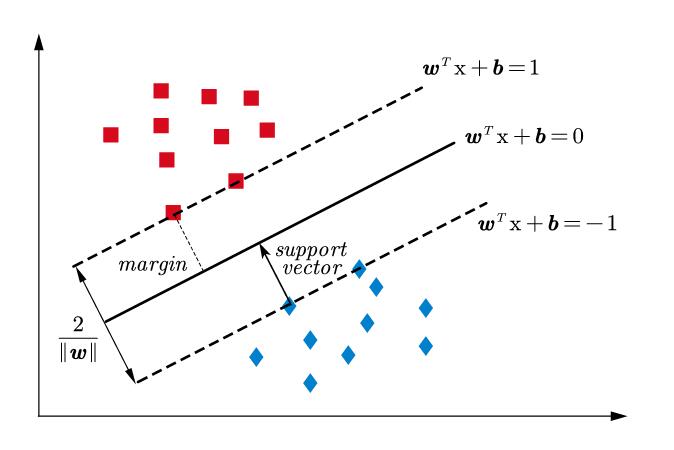
上图画了一个示意图,就像很多的SVM示意图一样。其实SVM这个词我大一就听说过,但是当时我的“学习能力”并不足以支持我理解它,但它的意义就像傅里叶变换之于通信工程和信号处理,是机器学习工程师的护城河。所以我今天鼓起勇气,来看懂它。
最开始我们还是讨论线性可分,我们寻找的是与两类间隔都能最远的超平面,我们认为这样的超平面更加可信一些。注意到对于正样本有:
对于负样本:
我们将正样本的标签置为+1,负样本是-1。那么上面的式子可以归结为一个不等式约束:
同时,我们知道点到超平面距离为:
同时,注意到对于一个超平面,所有的样本点关于它,总是有一个最近距离的。相当于单位化$d$,这对求解最优的$\boldsymbol{w}$是没有影响的,只是为了表达的简洁:
同时注意到,计算距离的公式中的绝对值,其实在二分类时恰好也可以用$y_i\left( \boldsymbol{w}^T\boldsymbol{x}_i+b \right)$来表达,因为$y_i$的符号和$\boldsymbol{w}^T\boldsymbol{x}+b$的符号正好对上了绝对值。这样之前的约束就变得更强了,由于最短距离归一化后成了1,那么:
同时,我们定义几何间隔$\gamma$,即每个样本点到超平面的距离:
记$\gamma =\underset{i=1,2,…}{\min}\gamma _i$,则最大化间隔:
by the way, 这里的$\gamma$也称作”margin”。
由$y_i\left( \boldsymbol{w}^T\boldsymbol{x}_i+b \right) \geqslant 1$可知,$\gamma$为$\frac{1}{\left| \boldsymbol{w} \right|}$,又因为最大化$\gamma$相当于最小化为$\frac{1}{2}\left| \boldsymbol{w} \right| ^2$,因此寻找最大分割超平面的问题就变为了一个有约束的最优化问题:
现在热身结束了,数学上,上面的最优化问题被称作凸二次规划,指的是:
即目标函数是凸二次函数,约束是线性约束。我们可以在这里面先停一下,因为后面的内容全是关于如何具体的求解这个凸二次规划问题。如果先不考虑这个,实际上线性可分的支持向量机就已经结束了。
Lagrange Multiplier Method
下面我们来进一步dive into这个最优化问题,首先要复习一下在大一上学的拉格朗日乘数法,当时只需要记下来做题就好了,但为了方便后续的理解,需要在这里对拉格朗日乘数法有个更直观的理解,拉格朗日乘数法说的是:
对于此类有等式约束下的函数极值,可以构造拉格朗日乘子函数来取得其极值的一阶必要条件:
对拉格朗日乘子函数的自变量求偏导,并令它为0。即对$x$求导,和对$\lambda$求导,得到方程组:
解这个方程组,可得候选极值。这里我们不从直接推公式的角度来理解,注意上式,实际上:
这个式子有一个几何解释:在极值点处目标函数的梯度是约束函数梯度的线性组合。
这个解释看起来很抽象,下面做一些解释:考虑一个二维的情形,这将有助于理解。我们知道,如果这个点的梯度是零,那么它就是一个极值;在等式约束下,极值处的梯度虽然往往不为零,但它一定与约束函数的梯度是共线的,否则就可以沿着与约束函数梯度正交的方向再调整,这样这个点就不是极值点。
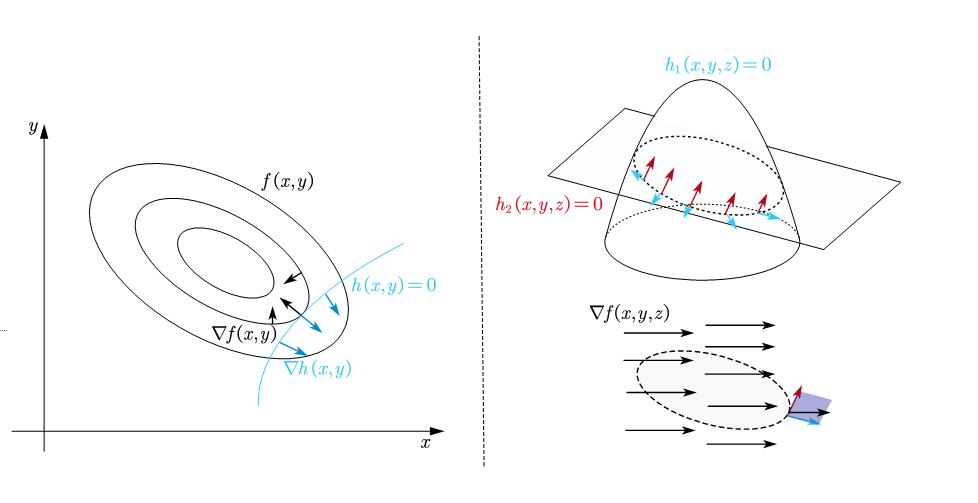
如上图所示,左边演示了高数题中常见的二维情形和一个约束等式,注意到由于左图展示的是等值面,而该点的梯度是与等值面垂直的,能非常直观的看到极值所在的点处的梯度与约束函数共线。
置于多个约束等式时,二维已经不好观察了,因为约束等式必然相交,否则会无解。而两个相交的平面曲线自然导致解空间只有一个点。所以右图画了一个三维的情形,在右图我们能更直观的看出,约束面的梯度构成了一个法空间(outer space),这个空间由各个约束面的梯度的分量张成,只有梯度落在这个法空间里,它才是极值,也就是上式中线性组合的来源。
Lagrange Duality
下面要引入拉格朗日对偶,我们知道,上述的拉格朗日乘数法只能解决等式约束,那么不等式约束的情况下,仍需要进一步探究:
我们仍然仿照拉格朗日乘数法构造一个广义的拉格朗日乘子函数,它的动机在后面会解释:
此时不等式的拉格朗日乘子要满足$\lambda _i\geqslant 0$,关于这一点,回看在拉格朗日乘数法时的插图(左),实际上在那一块,梯度是共线的,但到底是共向还是反向其实没有要求,因为是等式约束。而在不等式约束中,考虑$g_i(x)\le0$,如果对应的$\lambda_i$非零,说明可行解落在约束区域的边界上。
注意,在约束边界上,如果此时目标函数的负梯度指向边界内部,边界内部当然满足$g_i(x)\le0$,那就说明此时边界上的点不是极值点。所以一旦边界上的点是极值点,那么梯度一定指向边界外部,而此时对于约束函数,约束边界外部一定大于0,所以约束函数的梯度也指向外部。此时目标函数的负梯度与约束函数的梯度方向相同。所以$\lambda _i\geqslant 0$。
另外,其实$\lambda _i\geqslant 0$也叫互补松弛条件,在下面关于原问题的描述中,这个条件保证了原问题和我们要求解的问题具有同样的解。
接下来我们定义“原问题”:
原问题的最优解记作$p^{s}$,上面的极大极小,指的是先固定$\boldsymbol{x}$,先求拉格朗日函数对$\boldsymbol{\lambda},\boldsymbol{\nu}$的极大值,消去两个乘子变量后,再对$\boldsymbol{x}$求极小值。
接下来我们可以看到,这个原问题和我们要求解的原始问题有一样的解,记先处理的极大值问题为:
如果$\boldsymbol{x}$不是可行解,比如对于存在$g_i(\boldsymbol{x})>0$,那么取$\lambda_i=+\infty$,会使得$\theta_P$为正无穷;如果违反了等式约束,使得某些$h_i(\boldsymbol{x})\ne0$,那么只需使得$\nu_i=+\infty\cdot\mathrm{sgn}(h_i(\boldsymbol{x}))$,$\theta_P$也会为正无穷。
如果$\boldsymbol{x}$是可行解,那么$h_i(\boldsymbol{x})=0$,并且$g_i(\boldsymbol{x})\le0$,而我们要求$\lambda _i\geqslant 0$,所以此时的极大值就是当$\lambda_i=0$时取,这就导致函数的极大值就是待优化的$f(\boldsymbol{x})$,所以$\theta_P$与原始问题要优化的$f(\boldsymbol{x})$的关系可以表述为:
那么原问题和原始问题,最优化的都是为了最小化$f(\boldsymbol{x})$,所以有相同的解。可以看出$\lambda _i\geqslant 0$这个条件在其中十分重要。
之后定义对偶问题:
可以发现它只是调整了变量求极大值和极小值的顺序。记其最优解为$d^{s}$,注意,假设原问题的最优解为$\boldsymbol{x}_1,\boldsymbol{\lambda }_1,\boldsymbol{\nu }_1$,对偶问题的最优解是$\boldsymbol{x}_2,\boldsymbol{\lambda }_2,\boldsymbol{\nu }_2$,由于原问题先对$\boldsymbol{\lambda},\boldsymbol{\nu}$求极大值,对偶问题先对$\boldsymbol{x}$求极小值,那么:
所以有:
这一结论被称为弱对偶定理(Weak Duality),同样,下面我们以一个直观的几何解释来理解它:
记一个优化问题:$\mathrm{min} f_0(x)$,约束条件为$f_1(x)\le0$,定义域为$D$,mathematically,可以定义集合$G$:
那么原问题的最优解即$p^{s}=\mathrm{inf}_x\left\{ t|\left( u,t \right) \in G,u\leqslant 0 \right\} $,其中$\mathrm{inf}$是下确界。写出拉格朗日乘子函数$L\left( x,\lambda \right) =f_0\left( x \right) +\lambda f_1\left( x \right) $,则对偶函数为:
所以对偶问题的最优解是$d^{s}=\underset{_{\lambda \geqslant 0}}{\mathrm{sup}}g\left( \lambda \right) $,$\mathrm{sup}$是上确界。所以,我作出了这种简单情形下的几何直观:
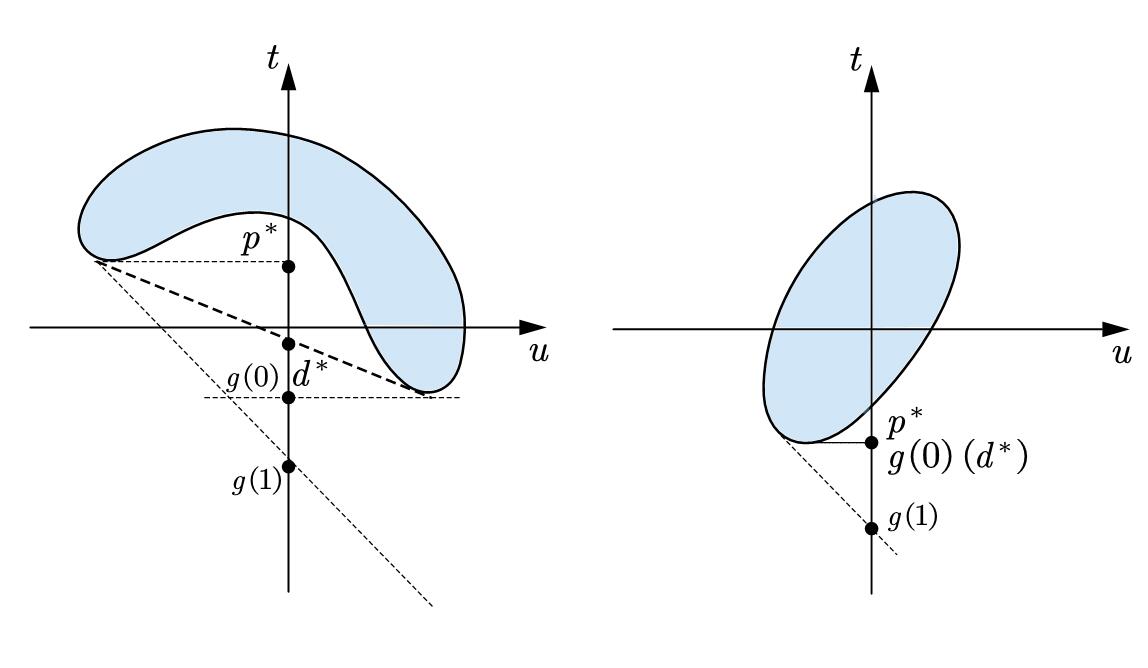
如这张图的左侧,当可行域为凹时,$p^{s}>d^{s}$
是一个弱对偶问题。这张图可能有些不是特别直观,一点点来看,因为$p^{s}=\mathrm{inf}_x\left\{ t|\left( u,t \right) \in G,u\leqslant 0 \right\} $
所以$p^{*}$是好找的,只需要在$u\le0$的点里找$t$最小的即可;但$d^{s}=\underset{_{\lambda \geqslant 0}}{\mathrm{sup}}g\left( \lambda \right) $,而$g\left( \lambda \right) =\mathrm{inf}_{\left( u,t \right) \in G}\left( t+\lambda u \right)$
后面关于$t+\lambda u$的下确界,可以理解成$z=t+\lambda u$的线性规划,找最小的截距,于是就得到了上面的两张图。
特别地,我们发现,当可行域是凸的时候,$p^{s}=d^{s}$
这不是偶然,此时就是强对偶性了。这也是我们关心的。此处引入几何直观,其实是受限于我凸优化知识的欠缺,只得用这种特殊的情形来引出凸可行域和凹可行域时,对偶问题的区别。因为此处严格的证明确实超出了大部分高校的工科培养方案。
我们确实大概的认为,只要可行域是凸集,就可以使得$p^{s}=d^{s}$
只不过,要加入一个条件:Slater条件,它是说,一个凸优化问题如果存在一个候选$x$使得所有不等式约束都严格满足(即对所有的$i$都有$g_i(x)<0$ ),那么就可以有$p^{s}=d^{s}=L\left( \boldsymbol{x}^{s},\boldsymbol{\lambda }^{s},\boldsymbol{\nu }^{s} \right) $
实际上这个条件对于大多数凸优化问题都是成立的。
这个条件对应到上面的几何直观里,即$u\le0$处必须要有点,否则$p^{s}$将无意义
且$d^{s}$会指向整个纵轴。
到了现在,我们基本理解了拉格朗日对偶的含义,但现在有一个问题:为什么要进行对偶。简单来说,实际上在对偶化以后,不等式约束和一些等式约束可以得到消除,从而更好处理。
Karush-Kuhn-Tucker Conditions
现在我们来补全最后一个数学工具,KKT条件。对于带有等式和不等式约束的优化问题,像拉格朗日乘数法一样,KKT条件给出了这类问题取得极值的一阶必要条件:
构造拉格朗日乘子函数:
则极小值满足:
这里的$\mu _ig_i\left( \boldsymbol{x} \right) =0$,和在刚介绍拉格朗日对偶时的$\lambda_i\geqslant0$本质是一样的。如果某一个$g_i\left( \boldsymbol{x} \right)<0$恒成立,那么说明这个不等式约束此时并没有起效,梯度并不会因为它的约束而停下来,故而$u_i=0$。如果某一个$g_i(\boldsymbol{x})$存在$=0$的情况,说明它参与了边界的贡献,此时的$\mu_i$应大于等于0自由取值,来满足目标函数的梯度是约束函数的线性组合。这两种情况下,均有$\mu _ig_i\left( \boldsymbol{x} \right) =0$。所以$\mu _ig_i\left( \boldsymbol{x} \right) =0$
也叫作互补松弛条件。
take a moment,现在解决支持向量机所需要的工具已经完备了。但最后还是那个问题:这三者到底是什么关系?很多资料也有这样的问题,堆砌了Slater条件,拉格朗日对偶,KKT条件,然后就,没了。我认为:KKT条件给出了一般情形下的极值必要条件,就像高数中熟悉的拉格朗日乘子法。在高数习题里我们并不知道什么对偶不对偶的概念,因为当时的问题是好处理的。而在许多等式约束和不等式约束条件下,直接根据KKT条件求解非常困难。所以提出了对偶的思想,定义原问题最优解$p^{s}$和对偶问题最优解$d^{s}$。而当满足Slater条件时:$p^{s}=d^{s}$
此时规划问题是凸的,并且满足强对偶性。可以通过求解对偶问题来得到最优解。
上述论述中仍然缺少了KKT与对偶性的关系,实际上,强对偶性中是蕴含了KKT条件的。如果一个优化问题满足强对偶性,那么KKT条件是取得极值的必要条件,即满足KKT条件不一定是优化问题的解;但如果是优化问题的解一定满足KKT条件。我们记$\boldsymbol{x}^{s}$是原问题的解,$\boldsymbol{\lambda }^{s},\boldsymbol{\nu }^{s}$是对偶问题的解,则:
这可能看起来很困惑,我们回顾一下拉格朗日对偶中的符号标记:
所以第一个不等号是拉格朗日函数的定义,由于$\mu _i\geqslant 0$而在最优解下,不等式约束小于等于0,等式约束等于0,所以:
第二项是个负数,所以$f\left( \boldsymbol{x}^{s} \right) \geqslant L\left( \boldsymbol{x}^{s},\boldsymbol{\lambda }^{s},\boldsymbol{\nu }^{s} \right)$。
第二个不等号是任意一点的函数值都大于等于该函数最小值。后面两个等号是对偶函数$\theta_d$的定义。
而强对偶使得$f^{s}=\underset{\boldsymbol{\lambda },\boldsymbol{\nu }}{\max}\theta _d\left( \boldsymbol{\lambda },\boldsymbol{\nu } \right) $ ,所以取等号。对于第一个不等号,这直接导致$\sum_{i=1}^q{\mu _ig_i\left( \boldsymbol{x}^{s} \right)}=0$,对于第二个不等号,根据极值点的定义可得此处偏导数为0。结合不等式约束,等式约束和$\mu_i \geqslant0$这几个直接给出的条件。就得到了KKT条件。这说明,强对偶蕴含了KKT条件。
至于充分性,此时要加上凸函数的条件。凸函数的条件和强对偶,实际上就是上面说的Slater条件。
由$\sum_{i=1}^q{\mu _ig_i\left( \boldsymbol{x}^{s} \right)}=0$以及强对偶性$p^{s}=d^{s}$ 可得:
由于此时目标函数是凸函数且$\mu _i\geqslant 0$ 且凸函数的非负线性组合还是凸函数,所以$L$也是凸函数,那么由于$L$是凸函数。
根据$\nabla _{\boldsymbol{x}}L\left( \boldsymbol{x},\boldsymbol{\lambda },\boldsymbol{\nu } \right) =0$ 可知此时的极值点一定是最小值点,即:
注意到,此时满足KKT条件,$L\left( \boldsymbol{x}^{s},\boldsymbol{\lambda }^{s},\boldsymbol{\nu }^{s} \right) =f\left( \boldsymbol{x}^{s} \right) $ 所以此时$\boldsymbol{x}^{s}$是原问题的解,同时$\boldsymbol{\lambda }^{s},\boldsymbol{\nu }^{s}$是对偶问题的解。
Go on
现在回过头来看支持向量机的优化问题:
目标函数的海塞矩阵是$n$阶单位矩阵$I$,因此目标函数是凸函数。可行域是由线性不等式围成的区域,是一个凸集。同时由于假设数据是线性可分的,因此一定存在满足约束的$\boldsymbol{w},b$,那么$2\boldsymbol{w},2b$一定严格满足不等式约束:
所以Slater条件成立,进一步,构造拉格朗日乘子函数:
先求解它的对偶问题,控制拉格朗日乘子$\boldsymbol{\alpha}$,注意约束条件$\alpha_i\geqslant 0$调整$\boldsymbol{w}$和$b$,使得拉格朗日乘子函数取极小值。即:
带入拉格朗日乘子函数:
接下来根据拉格朗日对偶,调整乘子$\boldsymbol{\alpha}$,使得乘子函数取极大值,即:
等价于最小化:
这个约束就比原来的问题简单的多了,当计算出$\alpha_i$后,根据互补松弛条件和偏导为零的等式,可以计算出$\boldsymbol{w},b$。我们观察现在被处理过的这个优化问题。
在支持向量机中,$1-y_i\left( \boldsymbol{w}^T\boldsymbol{x}_i+b \right) $相当于$g_i(\boldsymbol{x})$,根据之前在KKT条件中讨论的结论,一定有:
仔细回忆$1-y_i\left( \boldsymbol{w}^T\boldsymbol{x}_i+b \right) $,在前面,我们将样本点关于超平面的距离归一化,那么实际上只有距离超平面最近的样本点满足“不等式约束等于0”,在之前关于拉格朗日乘子法和KKT条件的讨论中,我们知道,只有不等式约束为0,它才参与了边界的贡献,才对极值点有影响。这个性质表明,支持向量机具有稀疏性,它实际上只与少数的距离最近的样本点有关,这些使得$\alpha_i$不为零的样本的特征向量被称为支撑向量(support vector)。
更有趣的一点,对偶化后的问题,特征向量以内积的形式成对的输入。这表明这个代价函数本身不显式的依赖于输入空间的维数。这个性质允许将支持向量机有效的推广到非线性可分的情形。即著名的“核技巧”。
对于线性不可分的情况,本质是一样的,只是加入了一组罚函数。由于篇幅的关系这里就不展开了,只要掌握了前置知识,软间隔下的支持向量机很好理解。
“核技巧”利用了一个大家都习惯的说法:“低维空间上不可分的问题,通过转换可以成为在高维空间上线性可分的问题。”,这将问题引入了“广义线性判别”。
End
在这篇blog里,我介绍了两种著名的线性分类器,实际上我略过了多层感知机(由于篇幅的问题)。如果对照PPT会发现,我没有写“Fisher”线性判别,是因为它与多层感知机,感知器算法,支持向量机有本质的不同:后者都只是被动的使用类别可分性,而并没有度量类别可分的程度。
写这篇blog最大的时间花费在了理解支持向量机的前置条件,值得重申的是,确实,花费一番功夫弄懂这背后的细节,其实并没有什么用。我可能永远都不会使用支持向量机,因为在大多数情况下,召唤几个nn.Linear(),然后nn.Dropout,再来几个PReLU做分类器,能直接走BP而且效果往往都比SVM好。但是这番功夫的重点还是学习能力的提升,我记得我大一的时候,班里有同学看西瓜书,我打开一看,一堆连乘求和下角标,我非常沮丧,尤其是看到支持向量机那一堆密密麻麻的解释,我觉得我可能学不会,最好退学重新高考。但好在经过两年的学习,在学习知识的方法论上得到了提升,知道了如何有效的利用资料,以及如何理解一些新概念。就像怪物猎人:世界里的蛮颚龙,教会新玩家不要贪刀,学走位,被称为“蛮颚龙老师”一样。能弄懂一遍支持向量机,就起到了这样的效果,说明我的理解能力更进了一步。
“倚醉梦提笔,痴人就不必醒。”


