Wavelet Neural Network

阅读数: 次 2022-08-18

“听闻江湖五绝名士，我于之怕只是天地蜉蝣。心想若我哪日亦如此番，那此生再无欲无求。”关于这种类型的模型讨论的较少，但它本身在一些地方又显示出了不错的性能，同时还有一些可以探索的地方。所以在这里整理一下。

注意这里要记录的是：Deep Adaptive Wavelet Network （DAWN），并不是中文搜索出的什么“小波神经网络”（虽然名字一样，但它不能adaptive，它只是把激活函数换了，只能说是前朝遗老。），也不是WaveNet，那是一个用于语音合成的朴素网络。

Background

想要理解这个DAWN，需要一些前置知识，我觉得这个前置门槛导致了它没有被广泛的应用。我简单的陈述一下，在信号分析中，傅里叶变换可以直接转换到频域分析，这完全丧失了时域信息。于是人们加窗，引入短时傅里叶变换，得到一个时频图。但这个时频图的时域和频域的颗粒度（granularity）是固定的，于是人们想出了小波分析：

$WT\left( a,\tau \right) =\frac{1}{\sqrt{a}}\int_{-\infty}^{+\infty}{f\left( t \right) \psi ^{\ast}\left( \frac{t-\tau}{a} \right) \mathrm{d}t}$

注意$a,\tau$的取值，当$a,\tau$变化时，小波基函数（它等同于傅里叶分析中的$e^{-j\omega t}$一样）的尺度和时移就会变化，从而小波分析可以给出一个多尺度的结果。一般地，它在低频区域的时间窗口大，频率窗口小。高频区域的时间窗口小，频率窗口大。这满足了我们分析的要求：低频的变化往往缓慢，且需要区分细节，是信号的主体；高频的变化往往很快且短促，不需要具体区分频率成分，比如噪声。

这里我们对小波基函数不作过多的解释，我们只需知道它们是精心构造出的正交基，本质上是一个带通滤波器，并且不唯一即可，一个常见，易于入门的小波基函数的$harr$小波：

$\psi \left( t \right) =\left\{ \begin{array}{c} 1,0\leqslant t<\frac{1}{2}\\ -1,\frac{1}{2}\leqslant t<1\\ 0,\mathrm{else}\\ \end{array} \right.$

由于尺度变换和时移变换，可以允许小波基函数提取不同时刻下不同尺度的信息。所以一般在小波分析中用尺度来衡量，它与以往的更习惯的频率$f$可以这么换算：

$\mathrm{scale}\times f=F_s\times \omega _{cf}$

我找个例子演示一下，这里面时间和频率（尺度）都作了归一化，采样率直接归一化为1。

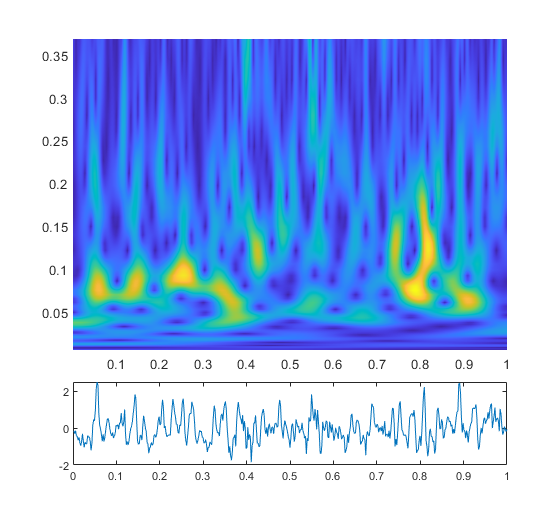
这图是为了给出一个直观印象，这里我们使用了morlet小波。可以发现，高频率（低尺度）的地方显然细长。低频率（高尺度）的地方矮宽。我们这里并不会延申到更深入的地方，只需通过这张图片体会这种多分辨率分析的直觉即可。

我们注意到：其实有些时候我们并不需要如此多的$a,\tau$的结果，只需要一部分，也就是这些带通滤波器并不是完全正交的，其中存在冗余。和提到离散傅里叶变换时类似（也仅仅是类似），我们同时对$a,\tau$离散化。一种常见的离散化方案是对尺度进行二进离散，对时移进行均匀离散：

$a=a_{0}^{m},\tau =n\tau _0a_{0}^{m} \\ \psi _{m,n}\left( k \right) =a_{0}^{-\frac{m}{2}}\psi \left( a_{0}^{-m}k-n\tau _0 \right)$

一般来说，$a_0=2,b_0=1$，这种二进的尺度离散暗合了奈奎斯特采样定理。尺度增加一倍，对应的频带减小一倍，所以采样频率可以相应的减小一倍。所以一般地离散小波变换可以写作：

$DWT\left( m,n \right) =2^{-\frac{m}{2}}\sum_{k=-\infty}^{\infty}{f\left( k \right) \psi \left( 2^{-m}k-n \right)}$

离散小波变换的过程相当于将信号与一个特殊的滤波器组进行作用，这与接下来要给出的多分辨率分析有着密切关系。很遗憾的是，确实没有什么很浅显的方法能把这一块说清楚，我建议是如有需要找相关参考资料，因为那些内容在这篇blog里其实并不是重点。

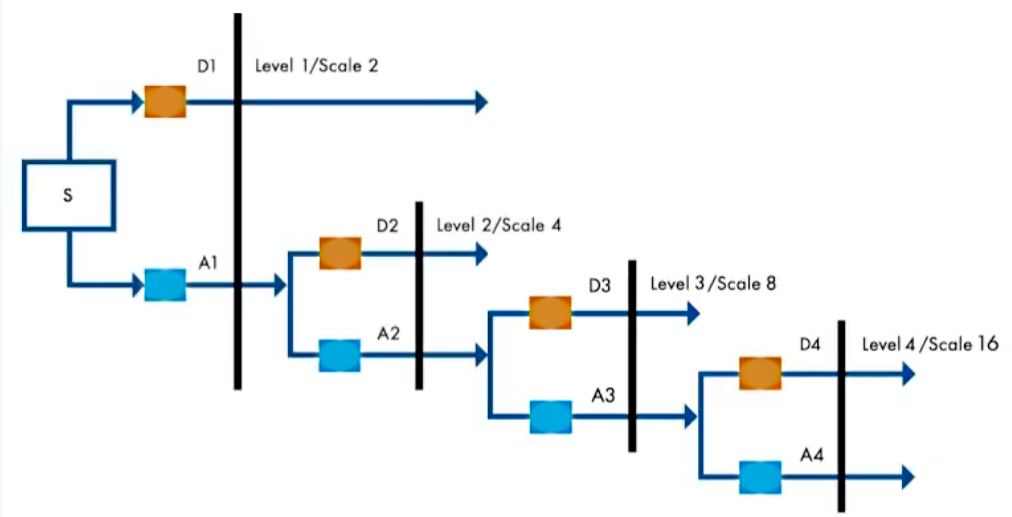
这就是之前说的特殊的滤波器组，它进行了一个多级分解。通过低通滤波器得到近似系数$A_j$(Approximation)，通过高通滤波器得到细节系数$D_j$ (details)。然后进一步下采样，对近似部分继续分解，得到的这些系数就是小波系数。

这个多分辨率的视角很有用，但截止到现在，我们的实现方法都依赖于精心设计的小波基或者滤波器组。所以有了第二代小波（second generation of wavelet），它被称为“提升格式 (lifting scheme) ”它不依托傅里叶变换，可以直接从时域得到一个近似表示，它分为三部分：

1）分裂(spilt)：

我们取一个信号$X=(x[0],x[1],…,x[2k-1])$，它被分为了奇序列和偶序列两部分，这一步有时也叫Lazy小波变换：

$X_{even}=\left( x\left[ 0 \right] ,x\left[ 2 \right] ,...,x\left[ 2k-2 \right] \right) \\ X_{odd}=\left( x\left[ 1 \right] ,x\left[ 3 \right] ,...,x\left[ 2k-1 \right] \right)$

这种分裂，相关性越强越好。

2）预测(Predictor)

预测操作用来抓住高频分量，预测误差即我们上文的细节系数$D_j$，这个步骤用一个预测算子$P(\cdot)$实现：

$D_j=X_{odd}-P\left( X_{even} \right)$

3）更新(Updater)

更新操作，是用$A_j$修正一个子序列，让它包含低频成份，即近似系数$A_j$，由一个更新算子$U(\cdot)$实现：

$A_j=X_{even}+U\left( D_j \right)$

理论可以证明，这种操作保留了上面所说的小波基函数的一些必要的性质，并且运算起来也很方便。只不过，这算子怎么选取也是个问题。但是前人指出：可以BP。这就可以引出一些有趣的事实。

DAWN

论文本身开源了，我在此把它重构一遍，方便以后的使用，同时也理清一些实施细节：

(不得不说，这种赶工public出的开源代码，就像口袋里自己打结的耳机线。这些是可以理解的，毕竟写作啊，等等因素，会导致代码可读性变差，而且也不会有清晰的文档……)

import math
import torch
import torch.nn as nn
import torch.nn.functional as F

# To change if we do horizontal first inside the LS
HORIZONTAL_FIRST = True


class Splitting(nn.Module):
    def __init__(self, horizontal):
        super(Splitting, self).__init__()
        # Deciding the stride base on the direction
        self.horizontal = horizontal
        if horizontal:
            self.conv_even = lambda x: x[:, :, :, ::2]
            self.conv_odd = lambda x: x[:, :, :, 1::2]
        else:
            self.conv_even = lambda x: x[:, :, ::2, :]
            self.conv_odd = lambda x: x[:, :, 1::2, :]

    def forward(self, x):
        """Returns the odd and even part"""
        return self.conv_even(x), self.conv_odd(x)


class LiftingScheme(nn.Module):
    def __init__(self, horizontal, in_planes, modified=True, splitting=True, k_size=4):
        super(LiftingScheme, self).__init__()
        self.modified = modified
        if horizontal:
            kernel_size = (1, k_size)
            pad = (k_size // 2, k_size - 1 - k_size // 2, 0, 0)
        else:
            kernel_size = (k_size, 1)
            pad = (0, 0, k_size // 2, k_size - 1 - k_size // 2)

        self.splitting = splitting
        self.split = Splitting(horizontal)

        # Dynamic build sequential network
        modules_P = []
        modules_U = []

        # HARD CODED Architecture
        size_hidden = 2

        modules_P += [
            nn.ReflectionPad2d(pad),
            nn.Conv2d(in_planes, in_planes * size_hidden,
                      kernel_size=kernel_size, stride=(1, 1)),
            nn.ReLU(),
            nn.Conv2d(in_planes * size_hidden, in_planes,
                      kernel_size=(1, 1), stride=(1, 1)),
            nn.Tanh()
        ]
        modules_U += [
            nn.ReflectionPad2d(pad),
            nn.Conv2d(in_planes, in_planes * size_hidden,
                      kernel_size=kernel_size, stride=(1, 1)),
            nn.ReLU(),
            nn.Conv2d(in_planes * size_hidden, in_planes,
                      kernel_size=(1, 1), stride=(1, 1)),
            nn.Tanh()
        ]

        self.P = nn.Sequential(*modules_P)
        self.U = nn.Sequential(*modules_U)

    def forward(self, x):
        if self.splitting:
            (x_even, x_odd) = self.split(x)
        else:
            (x_even, x_odd) = x

        if self.modified:
            c = x_even + self.U(x_odd)
            d = x_odd - self.P(c)
            return c, d
        else:
            d = x_odd - self.P(x_even)
            c = x_even + self.U(d)
            return c, d


class LiftingScheme2D(nn.Module):
    def __init__(self, in_planes, modified=True, kernel_size=4):
        super(LiftingScheme2D, self).__init__()
        self.level1_lf = LiftingScheme(
            horizontal=HORIZONTAL_FIRST, in_planes=in_planes, modified=modified,
            k_size=kernel_size)
        self.level2_1_lf = LiftingScheme(
            horizontal=not HORIZONTAL_FIRST, in_planes=in_planes, modified=modified,
            k_size=kernel_size)
        self.level2_2_lf = LiftingScheme(
            horizontal=not HORIZONTAL_FIRST, in_planes=in_planes, modified=modified,
            k_size=kernel_size)

    def forward(self, x):
        """Returns (LL, LH, HL, HH)"""
        (c, d) = self.level1_lf(x)
        (LL, LH) = self.level2_1_lf(c)
        (HL, HH) = self.level2_2_lf(d)
        return c, d, LL, LH, HL, HH

这一部分封装了论文中所表述的lifting scheme部分，$U,P$算符本质上被一个小号的非线性网络代替了。这里留了个self.modified的选项，区别目前不得而知。

import math
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
from lifting import *


class BottleneckBlock(nn.Module):
    def __init__(self, in_planes, out_planes):
        super(BottleneckBlock, self).__init__()
        self.bn1 = nn.BatchNorm2d(in_planes)
        self.relu = nn.ReLU(inplace=True)
        # This disable the conv if compression rate is equal to 1
        self.disable_conv = in_planes == out_planes
        if not self.disable_conv:
            self.conv1 = nn.Conv2d(in_planes, out_planes, kernel_size=(1, 1), stride=(1, 1),
                                   padding=(0, 0), bias=False)

    def forward(self, x):
        if self.disable_conv:
            return self.relu(self.bn1(x))
        else:
            return self.conv1(self.relu(self.bn1(x)))


class LevelDAWN(nn.Module):
    def __init__(self, in_planes, kernel_size, no_bottleneck,
                 share_weights, regu_details, regu_approx):
        super(LevelDAWN, self).__init__()
        self.regu_details = regu_details
        self.regu_approx = regu_approx
        if self.regu_approx + self.regu_details > 0.0:
            # L2 loss function with mean
            # Note that might not be ideal for the details
            # as it does not favor sparse solution
            # self.loss_details = nn.MSELoss()
            # Potentially better solution as it less sensitive to outliers
            self.loss_details = nn.SmoothL1Loss()

        self.wavelet = LiftingScheme2D(in_planes, share_weights,
                                       kernel_size=kernel_size)
        self.share_weights = share_weights
        if no_bottleneck:
            # We still want to do a BN and RELU,
            # but we will not perform a conv as the input_plane and output_plare are the same
            # Note that it BN and RELU is to get a more stable training in our case.
            self.bootleneck = BottleneckBlock(in_planes * 1, in_planes * 1)
        else:
            self.bootleneck = BottleneckBlock(in_planes * 4, in_planes * 2)

    def forward(self, x):
        (c, d, LL, LH, HL, HH) = self.wavelet(x)
        x = LL
        details = torch.cat([LH, HL, HH], 1)

        r = None
        if self.regu_approx + self.regu_details != 0.0:
            # Constraint on the details
            if self.regu_details:
                rd = self.regu_details * \
                     d.abs().mean()
                # self.loss_details(d, torch.zeros(d.size()).cuda())
                rd += self.regu_details * \
                      LH.abs().mean()
                # self.loss_details(LH, torch.zeros(LH.size()).cuda())
                rd += self.regu_details * \
                      HH.abs().mean()
                # self.loss_details(HH, torch.zeros(HH.size()).cuda())

            # Constrain on the approximation
            if self.regu_approx:
                rc = self.regu_approx * torch.dist(c.mean(), x.mean(), p=2)
                rc += self.regu_approx * torch.dist(LL.mean(), c.mean(), p=2)
                rc += self.regu_approx * torch.dist(HL.mean(), d.mean(), p=2)

            if self.regu_approx == 0.0:
                # Only the details
                r = rd
            elif self.regu_details == 0.0:
                # Only the approximation
                r = rc
            else:
                # Both
                r = rd + rc

        if self.bootleneck:
            return self.bootleneck(x), r, details
        else:
            return x, r, details

    def image_levels(self, x):
        (c, d, LL, LH, HL, HH) = self.wavelet(x)
        x = torch.cat([LL, LH, HL, HH], 1)

        if self.bootleneck:
            return self.bootleneck(x), (LL, LH, HL, HH)
        else:
            return x, (LL, LH, HL, HH)


class DAWN(nn.Module):
    def __init__(self, num_classes, big_input=True, first_conv=3,
                 number_levels=4, kernel_size=4, no_bootleneck=False,
                 COLOR=True, regu_details=0.01, regu_approx=0.01):
        super(DAWN, self).__init__()
        self.big_input = big_input
        if COLOR:
            channels = 3
        else:
            channels = 1

        self.nb_channels_in = first_conv

        # First convolution
        self.first_conv = True
        self.conv1 = nn.Sequential(
            nn.Conv2d(channels, first_conv,
                      kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False),
            nn.BatchNorm2d(first_conv),
            nn.ReLU(True),
            nn.Conv2d(first_conv, first_conv,
                      kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False),
            nn.BatchNorm2d(first_conv),
            nn.ReLU(True),
        )

        if big_input:
            img_size = 224
        else:
            img_size = 32

        # Construct the levels recursively
        self.levels = nn.ModuleList()

        in_planes = first_conv
        out_planes = first_conv

        for i in range(number_levels):
            bootleneck = True
            if no_bootleneck and i == number_levels - 1:
                bootleneck = False

            self.levels.add_module(
                'level_' + str(i),
                LevelDAWN(in_planes,
                          kernel_size, bootleneck,
                          regu_details, regu_approx)
            )

            in_planes *= 1
            img_size = img_size // 2
            # Here you can change this number if you want compression
            out_planes += in_planes * 3

        if no_bootleneck:
            in_planes *= 1

        self.img_size = img_size
        self.num_planes = out_planes

        self.fc = nn.Sequential(
            nn.Linear(in_planes, in_planes // 2),
            nn.BatchNorm1d(in_planes // 2),
            nn.ReLU(True),
            nn.Linear(in_planes // 2, num_classes)
        )

        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
                m.weight.data.normal_(0, math.sqrt(2. / n))
            elif isinstance(m, nn.BatchNorm2d):
                m.weight.data.fill_(1)
                m.bias.data.zero_()
            elif isinstance(m, nn.Linear):
                m.bias.data.zero_()

        self.avgpool = nn.AdaptiveAvgPool2d((1, 1))

    def process_levels(self, x):
        """This method is used for visualization proposes"""
        w, h = x.shape[-2:]

        # Choose to make X average
        x = x[:, 0, :, :]
        x = x.repeat(1, self.nb_channels_in, 1, 1)
        x_in = x
        print(x_in[:, 0, :, :])

        out = []
        out_down = []
        for l in self.levels:
            w = w // 2
            h = h // 2
            x_down = nn.AdaptiveAvgPool2d((w, h))(x_in)
            x, r, details = l(x)
            out_down += [x_down]
            out += [x]
        return out, out_down

    def image_levels(self, x):
        """This method is used for visualization proposes"""
        if self.first_conv:
            x = self.conv1(x)

        # Apply the different levels sequentially
        # Extract all information
        images = []
        for l in self.levels:
            x, curr_images = l.image_levels(x)
            images += [(curr_images[0], curr_images[1],
                        curr_images[2], curr_images[3])]
        return images

    def forward(self, x):
        if self.first_conv:
            x = self.conv1(x)

        # Apply the different levels sequentially
        rs = []  # List of constrains on details and mean
        det = []  # List of averaged pooled details

        for l in self.levels:
            x, r, details = l(x)
            # Add the constrain of this level
            rs += [r]
            # Globally avgpool all the details
            det += [self.avgpool(details)]
        # At the last level (only) we GAP the approximation coefficients
        aprox = self.avgpool(x)
        # We add them inside the all GAP detail coefficients
        # Finally we concat all before applying the classifier
        det += [aprox]
        x = torch.cat(det, 1)
        x = x.view(-1, x.size()[1])

        return self.fc(x), rs

其中两个image_levels和process_levels是原作者用于可视化结果来讲述story的，我们先不用管它。一般来说，要彻底理解一个Net，看穿它每步的流是第一步：最开始的图片输入进去，经过两层卷积层扩展一下通道数，这里通道数是first_conv，形参上的初始值是3。作者在训练时使用了32，初始值是3估计是为了某种可视化或对比试验的目的。之后使用一个标记变量标记一下输入图片的尺寸，224是指对于ImageNet等，32即CIFAR-10。self.levels用torch提供的ModuleList储存了用于小波分解的结构，它通过一个for循环有顺序的把一个封装好的LevelDAWN输进去。所以很方便的是，在forward中，同样只需要for循环，依次遍历每一个子模块即可。

下面关注LevelDAWN这个类，这个类封装了前面用到的提升方案以及一些正则化。这里面的self.wavelet就是一个由LiftingScheme2D实例化的对象，它最终可以把输入的张量$x\in \left[ N,C,H,W \right] $处理成四个频率成份$LL,LH,HL,HH\in \left[ N,C,H/2,W/2 \right]$。其中的$LL$由于从水平和竖直方向都是近似细节（低频分量），它会再次被进一步分解。而对于剩下的$LH,HL,HH$，总共就是$3\times C$通道的数据，会被GAP后备用。之后$LL$会被过一个bottleneck（或者不），这里原作者含糊其辞。但是我觉得这里贸然对处理好的分量过一个bottleneck并不一定合适。这一部分把正则项的计算放在里面了，那些regu相关的就是正则(regulation)，原文给出的是：

$\mathbf{Loss}=-\sum_{i=1}^P{y_i\log \left( p_i \right)}+\lambda _1\sum_{l=1}^M{\mathbf{H}\left( \mathbb{D} _l \right)}+\lambda _2\sum_{l=1}^M{\left\| m_{l}^{I}-m_{l}^{C} \right\| _{2}^{2}}$

就，我只是忠实的给出原文，我个人认为这一篇文的作者有他当时的局限性，至少思路是有启发的，这就够了。实际上，包括更早以前的那篇文献，我都觉得这个损失函数很扯。至少在ICLR2022的一篇工作用的损失函数就只正则了低频系数和原始输入，这是合理的。对于这一篇实现时用的正则，我们就忠实原文。实际上原文和他开源的代码并不完全匹配，在这里对于细节系数它用的是哈伯归一化，实际上他代码实现的时候只是一个简单的$L-1$归一化。在每一个levels的运算里，正则最后会化成一个系数，在遍历所有levels时相加，最后在外面直接backward掉，这个写法比定义一个loss_function有时要方便。

然后，这篇文章的开源，基本就剩了个train.py，它的写的极其臃肿，令人很麻，简直是屎山。这里的几大槽点就是，我们都知道，炼丹水文里需要有和别的models的对比以及各种baseline。一种显得有点呆但整洁的方式是复制很多副本，然后文件夹归好类等等。但更好一点的是你可以建一个类似.json的文件，把每个模型或者数据集，要用的一些路径啊，参数啊，打包好。但他就不一样了，他直接if-else大师，五个数据集，if-else到底。全堆在一个文件里，我觉得这不太行。

恰好在AMC和那么几次实验里，我都没有好好整理过train.py的模板，今天就写一下。最后它跑出来一个，在CIFAR-10上分类85%，差不多合格了，先不深究了。后面的环节我指出了一些问题（见More discussion）

Sugar

后来发现，全部的代码放进来太蛋疼了。所以就记录一些我觉得在写train.py的时候的一些好的写法吧，这些写法可以让炼丹的过程变得更friendly。

class AverageMeter(object):
    """Computes and stores the average and current value"""

    def __init__(self):
        self.reset()

    def reset(self):
        self.val = 0
        self.avg = 0
        self.sum = 0
        self.count = 0

    def update(self, val, n=1):
        self.val = val
        self.sum += val * n
        self.count += n
        self.avg = self.sum / self.count

定义这么一个类，可以帮助记录和更新变量，尤其在记录损失或者准确率这种需要一直更新，求平均的变量。用法就像代码里表示的一样，很浅显易懂，需要调用的时候，先声明loss = AverageMeter()，然后需要更新时就把更新的值，比如loss_cur，传进去：loss.update(loss_cur)。需要平均值，比如在最后要输出时，就可以直接用loss.avg。这样可以避免一些不必要的错误，比如以往写的时候大多都是loss / num等等，容易出现”笔误“。

这里的class (object)在python3.x的情况下，不写也一样的。在以往的python2.x时，这么写可以才可以继承python内置的一些方法，比如_ _ init _ _等。

class CSVStats(object):
    def __init__(self):
        self.prec1_train = []
        self.prec1_val = []
        self.prec5_train = []
        self.prec5_val = []
        self.loss_train = []
        self.loss_val = []

    def add(self, p1_train, p1_val, p5_train, p5_val, l_train, l_val):
        self.prec1_train.append(p1_train)
        self.prec1_val.append(p1_val)
        self.prec5_train.append(p5_train)
        self.prec5_val.append(p5_val)
        self.loss_train.append(l_train)
        self.loss_val.append(l_val)

    def write(self):
        out = "runs/stats.csv"
        dir = 'runs'
        if os.path.exists(dir) is False:
            os.makedirs(dir)
        with open(out, "w") as f:
            f.write('prec1_train,prec1_val,prec5_train,prec5_val,loss_train,loss_val\n')
            for i in range(len(self.prec1_val)):
                f.write("{:.5f},{:.5f},{:.5f},{:.5f},{},{}\n".format(
                    self.prec1_train[i], self.prec1_val[i],
                    self.prec5_train[i], self.prec5_val[i],
                    self.loss_train[i], self.loss_val[i]))

    def read(self, out):
        raise Exception("Unimplemented")

这个类可以把训练过程中的统计量储存在一个.csv中，记得注意路径是否存在的问题。在我个人的偏好里，我觉得这是最理想的记录方式，自己实现一个实时更新的图窗，迭代次数一多就会卡。用wandb, tensorboard啥的，需要联网。所以最好的方法确实是记到csv里，要画的时候画出来就好了。使用的时候，我们先在训练的循环外面实例化对象 csv_logger = CSVstats()，然后在完成一次训练和验证后，把统计量更新进去就好了：

1
2
3

# Print some statistics inside CSV
csv_logger.add(prec1_train, prec1_val, prec5_train, prec5_val, loss_train, loss_val)
csv_logger.write()

还有一个就是python支持的进度条包：tqdm，我们只需要封装一个任意的迭代器即可为长循环增加一个进度条，使用时就像：

with tqdm(total=len(train_loader), desc=f'Epoch{epoch}/{epoch_max}', postfix=dict, mininterval=0.3) as pbar:
    for i, (input, target) in enumerate(train_loader):
        ...........
                    pbar.set_postfix(**{'train_loss_class': losses_class.avg,
                            'train_loss_regu': losses_regu.avg,
                            'train_loss': losses_regu.avg + losses_class.avg,
                            'Prec@1': top1.avg,
                            'Prec@5': top5.avg})
        pbar.update(1)

一些具体的个性化进度条的方案这里就不赘述了，基本功能就已经够用了。

More discussion

DAWN的想法有些许novel，但是作者的实现上多少有点草率，而且实验不是那么的充分？下面我开始胡言乱语一波，一部分内容是结合ICLR2022的一篇文章总结的。这个lifting scheme的具体细节，很难考证了，原文是很久以前的影印版数学论文，够呛看得懂，只能大概体会一下。首先我们对一个信号使用传统的harr小波试一试，这里我为了演示是直接从matlab里load的内置含噪心电图数据。

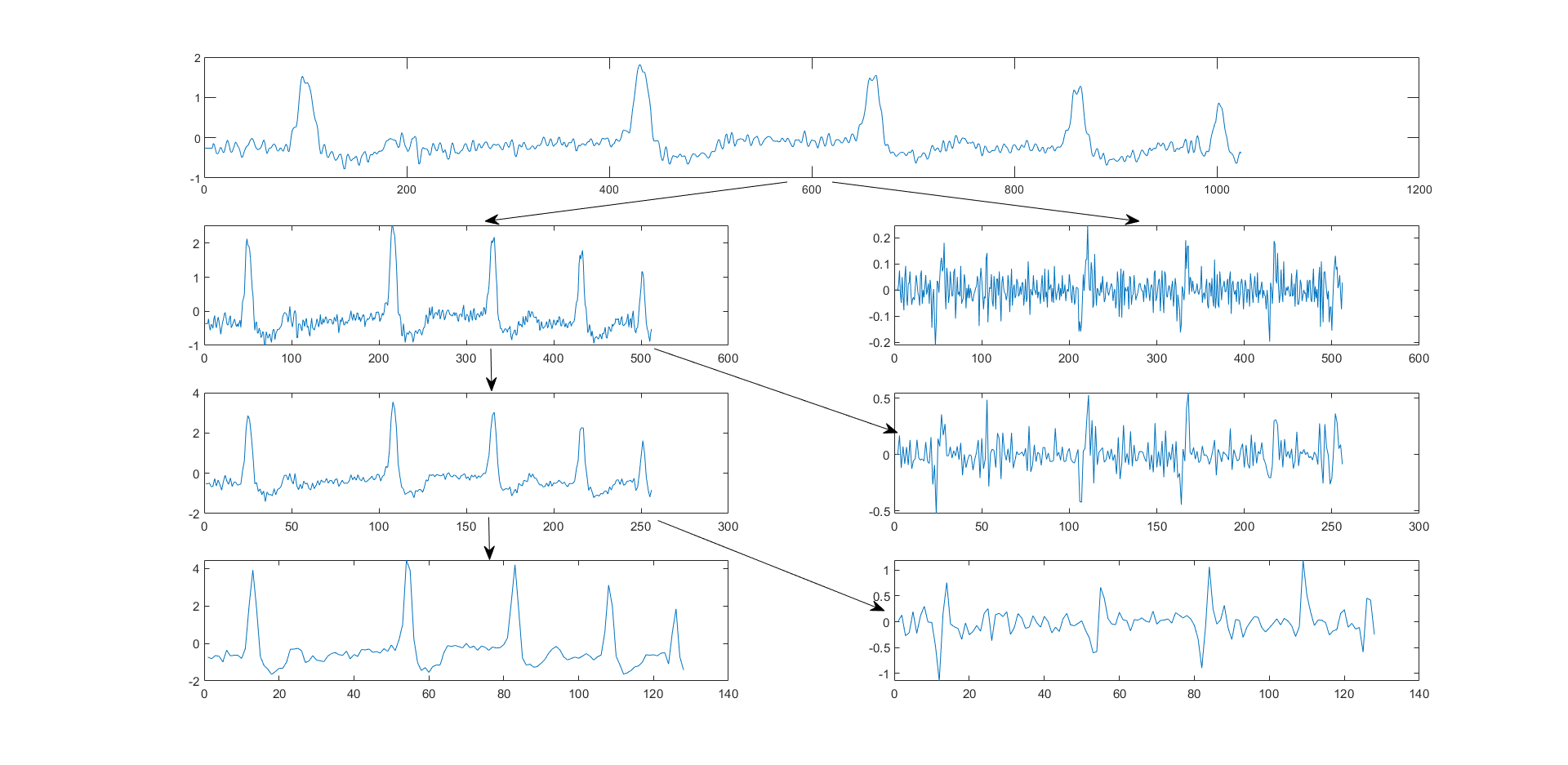
左边是低频（近似），右边是高频（细节），实际上，它们只是低频系数和高频系数，但后面叙述时不作区分。我们注意到每次分解，长度都折半。这是传统的分解方法，实际上这种方法在几年前的计算机视觉中已经被讨论过了。用这种方式替代池化层等等，是不错的故事。而现在考虑lifting scheme的三个步骤：

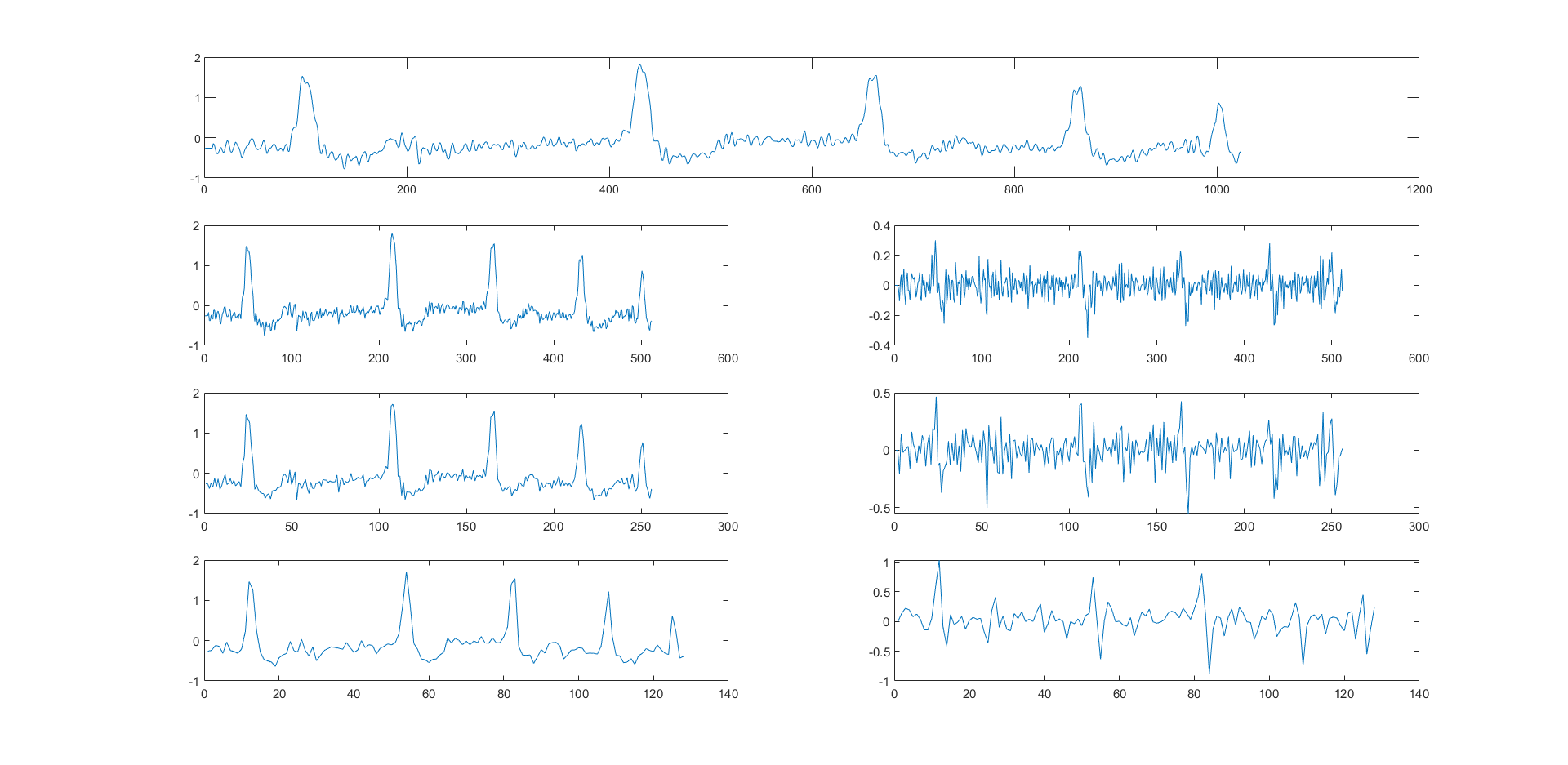
对比前后两张图，发现确实有点那个意思，这里$U(\cdot),P(\cdot)$均是恒等映射，如果我们把代码实现里modified的那个版本写上去，在恒等映射的条件下它们只差一个正负号，所以我们先以上面的来。现在我们关心$U(\cdot),P(\cdot)$的一些性质，查阅资料后我们这里给出一种作为例子：

$P\left[ x_e\left( k \right) \right] =-\frac{1}{8}x_e\left( k-1 \right) +\frac{7}{16}x_e\left( k \right) +\frac{7}{16}x_e\left( k+1 \right) +\frac{1}{8}x_e\left( k+2 \right) \\ U\left[ x_o\left( k \right) \right] =-0.0312d\left( k-2 \right) +0.2813d\left( k-1 \right) +d\left( k \right) +0.2813d\left( k+1 \right)$

这里仅仅给出一个例子，实际上理论分析一般是在$z$域上进行，根本原因是之前传统小波的滤波器组，当其已知时，可以用因式分解把滤波器组的多相矩阵分解为三角矩阵的连乘形式，如：

$\left( \begin{array}{c} \lambda _{j+1}\left( z \right)\\ \gamma _{j+1}\left( z \right)\\ \end{array} \right) =\prod_{i=1}^N{\left( \begin{matrix} 1& 0\\ -s_i\left( z^{-1} \right)& 1\\ \end{matrix} \right) \left( \begin{matrix} 1& -t_i\left( z^{-1} \right)\\ 0& 1\\ \end{matrix} \right) \left( \begin{array}{c} \lambda _j\left( z \right)\\ \gamma _j\left( z \right)\\ \end{array} \right)}$

具体的理论分析这里就不给了，涉及到数字信号处理，一些代数，感兴趣的可以在一些硕士毕业论文里查，我们还是重点关心这个$U(\cdot),P(\cdot)$的刻画，这确实就像一个滤波器组……所以，这么看来…论文原文提供的解决方案：

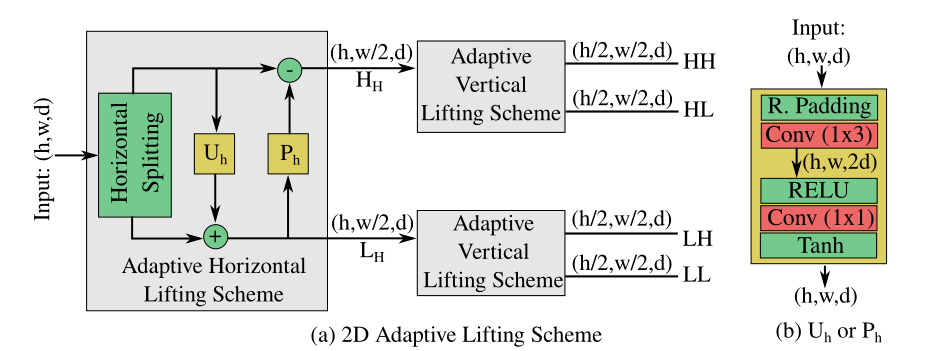
它使用的$U(\cdot),P(\cdot)$并没有起到这样的性质，实际上，我推测它最后可视化以后，真的能产生小波分解的样子，原因第一是数据归一化后的量级在-1到1，以及每层加了BN（这也是那句”we do want a ReLU and BN.“）维持分布一直不变，好让被Tanh作用后的结果和原信号在一个量级上；第二是正则项的添加。总之原作者处理的并不好。

ICLR2022里的一篇文章沿用了这种设置，但是在迭代基础上用一个INN的故事把式子改写为了：

$d=X_{odd}\odot \exp \left( \phi \left( X_{even} \right) \right) -\rho \left( X_{even} \right) ,c=X_{even}\odot \exp \left( \psi \left( d \right) \right) -\eta \left( d \right)$

之后冠以”仿射函数”的名字，说是这种”可逆性“使得它有更好的性质，这当然好于前者，注意到exp中的项其实也是一个类似$U(\cdot),P(\cdot)$的结构，它们同时也在最后收束了一个Tanh……这就导致点乘的缩放其实是一个有界且合适的拟合，这当然会把结果变得更好。

Now, everything I have to say has already cross my mind…

End

当我彻底写完的时候，是8月24号，今天竹园停电，麻了。我对此改进这个dawn萌生了一个比较成熟的想法，打算去试试。不过快要开学了捏，如果写的这个有人看的话，那就祝你新年快乐吧。