CUMCM2021A-"醉里挑灯看剑"

阅读数: 次 2022-08-06

前段时间，有点小忙。结果忙完了数模培训就开始了，然后……摆了，可怜了我一学弟。CUMCM-2021A是永远的痛，当时按照前五年的A题准备的微分方程，然后开题以后直接扑空了。当时甚至没怎么读懂题，也没抓住方向，遂寄。

由于今年的数模培训，我再直面一波自己的翻车历史。但是不管怎么复盘，也不能完全达到初见的状态。这不得不让我有一种“欲买桂花同载酒，终不似，少年游。”的感觉。所以最后我就摆了，然后就一组没交第一次培训，你猜是哪组？

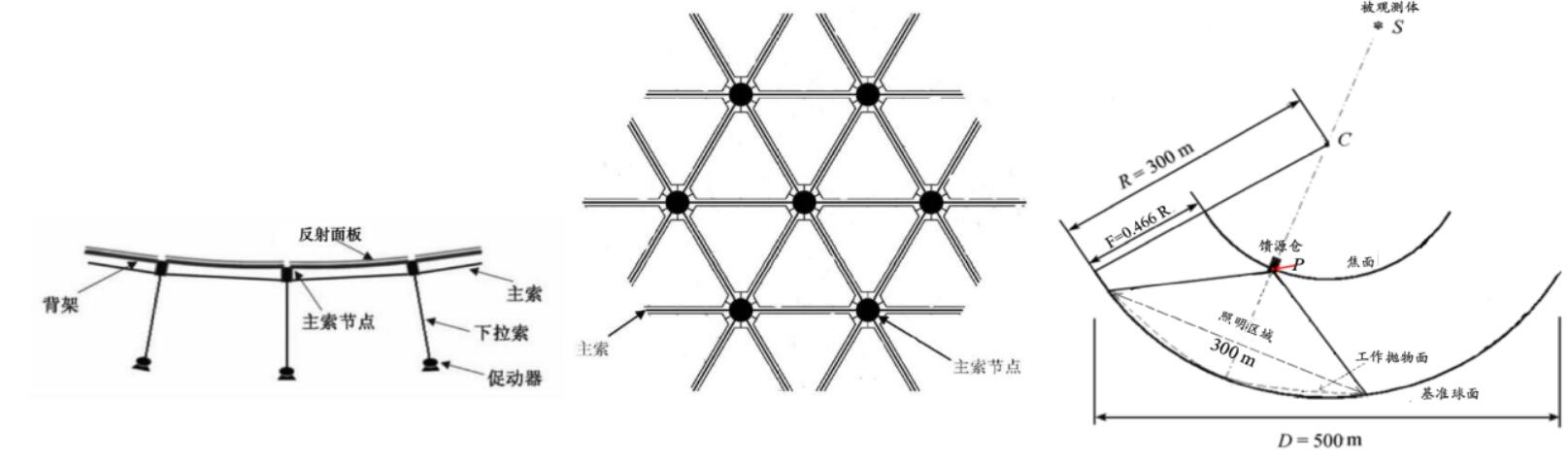
这里引用题目中给的三张插图，其实就可以很简要的概括题目的意图和要求。最开始，从一个球面和抛物面切入，最右边的剖面图给出了一些固定的参数$R=300,F=0.466R,D=500$，即FAST本身是个球面，给出一个坐标，球面的一部分会变成抛物面，这一区域的直径是$300$。之后，这个理论的球面和抛物面肯定不是真实存在的，是若干反射面板拼接近似的。如中图所示。每三个点会确定一个反射面板，结点被称为主索结点。通过调节反射面板的位置，也就是三个主索结点的位置来将球面转成抛物面。但是，如左图所示，有这么几个部件要注意：促动器，下拉索，主索。题目进一步要求，促动器的上下调整幅度为$-0.6$到$0.6$，且下拉索长度不变。主索长度变化不超过$0.07{\%}$。

实际上，如果当时阅读理解够真切，其实就不难，我记得我当时相当错误的理解了$0.07\%$这个条件，我内心加戏加太多了：我以为是每一次迭代(iter)变动不能超过$0.07\%$，稍加思考就会发现这逻辑根本不通。我当时也感觉隐隐不对，结果把自己绕糊涂了。

现在看来，$0.07\%$这个条件其实很直接，他其他的都没说，就是一个简简单单的约束条件罢了。只要和最初的长度比，在这个范围内即可。容易想到这个条件来源于简化后的机械结构，应该是某种应力要求主索不能移动太多。

这个问题还有两个坑点，其中一个是下拉索和促动器并不共线，评阅标准也称之为“不正确的假设”。但现在以上帝视角看，这两个计算结果相差无几。第二个是几乎没被人作出的，即第三问算接收比时要按照曲面三角形处理。

第一问和第二问的前半部分只是简单的代数计算，还不涉及将具体调节纳入考虑中：

注意到附件里其实给了很多坐标，所以直接移用题目所建的坐标系，往往不会出错。注意到第一问是一个完全竖直的抛物面，那么其实可以被归为抛物线来处理。但第二问需要一个旋转后的抛物面。所以我们最好先建立一个抛物面的模型来备用，注意到促动器是可以上下运动的，那么从基准球面到抛物面，就是一部分向下运动，一部分向上运动。所以，跟在二维平面的抛物线类似。我们可以由定义来给出抛物面通式，设抛物面的准平面到基准平面距离为$h$，焦点由图可知，为：$p=\left[ \left( F-R \right) \cos \beta \cos \alpha ,\left( F-R \right) \cos \beta \sin \alpha ,\left( F-R \right) \sin \beta \right] $。

Question-1

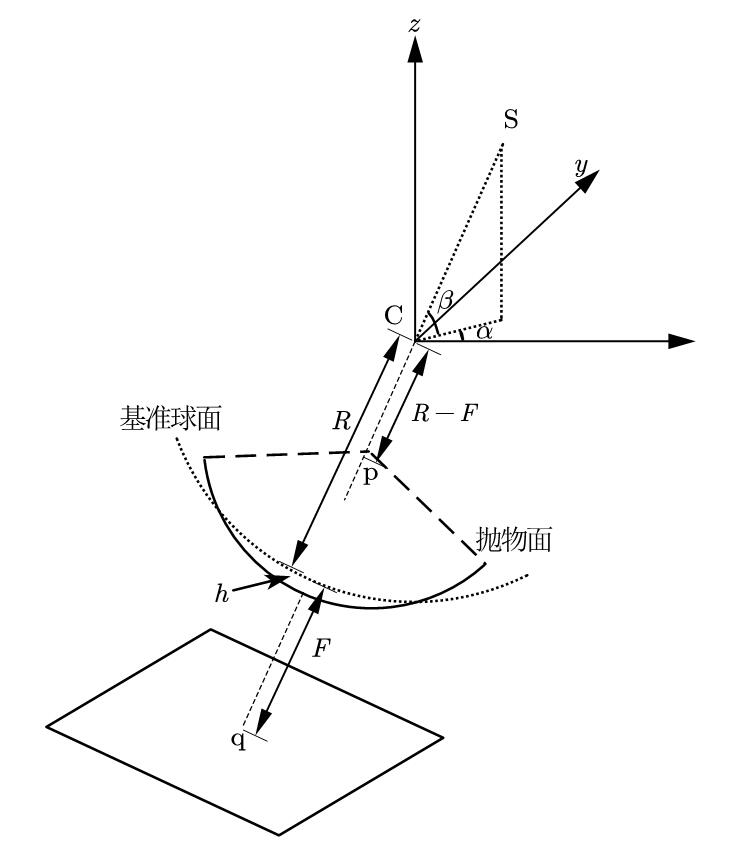
如图所示，准平面与轴线的交点$q=\left[ -\left( F+R+h \right) \cos \beta \cos \alpha ,-\left( F+R+h \right) \cos \beta \sin \alpha ,-\left( F+R+h \right) \sin \beta \right] $

一般地，应该采用旋转矩阵的办法，来得到一般的角度时的抛物面，但这里直接暴力美学了。由抛物面上的点到准平面距离相等：

$\left\{ \begin{array}{c} \left( \psi _1,\psi _2,\psi _3 \right) =\left( \cos \beta \cos \alpha ,\cos \beta \sin \alpha ,\sin \beta \right)\\ \sqrt{\left( x-x_p \right) ^2+\left( y-y_p \right) ^2+\left( z-z_p \right) ^2}=\frac{\left| \psi _1\left( x-x_q \right) +\psi _2\left( y-y_q \right) +\psi _3\left( z-z_q \right) \right|}{\sqrt{\psi _1^2+\psi _2^2+\psi _3^2}}\\ \end{array} \right.$

这波，联立解得（手动肯定解不了，直接上mathematica）：【实际上这样做，后续编程反而更复杂了，但就当练习了。】

$\begin{aligned} &16(F+h) \cos \beta(x \cos +y \sin \alpha)+4 z \sin 2 \beta(x \cos \alpha+y \sin \alpha) \\ &+2 \cos 2 \beta(x \cos \alpha+y \sin \alpha)^{2}+2 x y \sin 2 \alpha+16(F+h) z \sin \beta \\ &+\cos 2 \alpha(x-y)(x+y)-2 z^{2} \cos 2 \beta+16(F+h)(R+h)-3\left(x^{2}+y^{2}\right)-2 z^{2}=0 \end{aligned}$

当$\alpha =0°,\beta =90°$时，方程简化为：

$z=\frac{x^2+y^2}{4\left( F+h \right)}-\left( R+h \right)$

（这里的$R$实际上是300.4，应以附件中的坐标为准。这可能是由于反射面板等结构有一定厚度。）

喜提一个单目标优化问题，初见时非常朴素的认为，只需建立一个基于均方误差的优化函数即可，就是想让基准球面尽可能少的移动就能达到抛物面。但现在结合评阅要点来看，还是要检索中文水刊水报的一些信息，实际上有其他的优化函数，这里我们也就还拿基于均方误差的优化函数举例了，因为现在再把多种优化目标下的都作了没有意义，下次也用不到。同时，我们并不需要用曲面来拟合，因为此时是旋转对称的，直接用二维的计算即可。要注意的是，我们要处理的是径向距离：

$\min z=\sum_{i=0}^{N-1}{\left( \sqrt{x_{i}^{2}+y_{i}^{2}}-R \right)}$

此时最好的$h=0.3609$，带进去，第一问就是：

$z=\frac{x^2+y^2}{561.39}- 300.761$

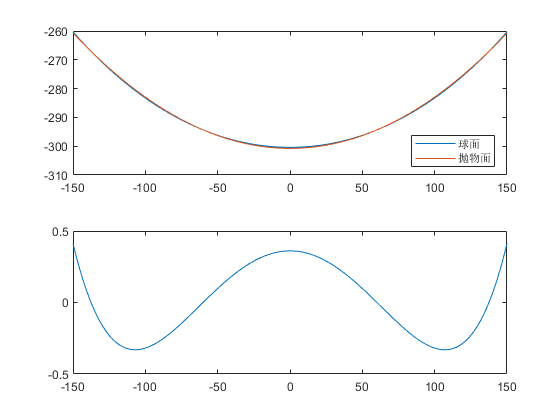
至于第二问的理想抛物面，将$\alpha =36.795°,\beta =78.169°,h=0.3609$带进去，就得到了一个复杂的曲面表达式，此时抛物面的顶点坐标容易写出：

$\left[ -\left( R+h \right) \cos \beta \cos \alpha ,-\left( R+h \right) \cos \beta \sin \alpha ,-\left( R+h \right) \sin \beta \right] = \\ \left[ -49.3793,-36.9337,-294.3717 \right]$

Question-2

接下来就是一些dirty work，因为我们截止到现在，都是一个理想的抛物面，现在要把主索结点和反射面板等实际因素考虑进来。观察附件1，2，3：附件1是主索结点的编号和坐标，附件2是促动器上下端点坐标以及相应编号，附件3是所有反射面板的主索结点编号。分析第二问和第三问，在第二问里，我们需要调整促动器上端点，有±0.6的约束；同时需要计算相邻节点调整后的距离是否在0.07%之内，这要求我们要给出结点之间相连的信息，一般地，一个结点会连6个结点，那么需要一个$k \times 6$的类似邻接矩阵一样的表。以及在这一问里并不是所有的结点都要考虑，我们需要从附件中筛选出在此时$\alpha,\beta$下，调整区域内的结点。第三问，计算反射时，一定是按照反射面板为单元考虑的，此时的情况又略有不同，所以我们需要一个DataProcess.m的程序预处理一下：

clear
clc

appendix_1 = readmatrix('附件1.csv', 'Range', [2, 2]);
appendix_2 = readmatrix('附件2.csv', 'Range', [2, 2]);
% 附件1，2第一列完全相同,是主索结点编号，先不读
appendix_3 = readmatrix('附件3.csv', 'OutputType','string', 'Range',2);

Cord_Nodes = appendix_1;% 主索结点坐标
Cord_lower = appendix_2(:, 1:3); %促动器下端点
Cord_upper = appendix_2(:, 4:6); %促动器上端点
Index_Panel = appendix_3; %反射面板编号集合

Index_Nodes_Motor = readmatrix('附件1.csv', 'OutputType','string', 'Range',2);
Index_Nodes_Motor = Index_Nodes_Motor(:, 1); % 反射结点/促动器 编号


% 筛选符合问题2的结点
% 单位为标准单位制
R = 300.4;
F = 0.466 * R;
L = 300; % 照明区域直径
D = 500; % 球面直径
alpha = 36.795 * pi / 180; % 转为弧度制
beta = 78.169 * pi /180;

% 找到当前焦点位置
P(1) = -(R - F) * cos(beta) * cos(alpha);
P(2) = -(R - F) * cos(beta) * sin(alpha);
P(3) = -(R - F) * sin(beta);

% 初始化
Count = 1;
Cord_Nodes_Q2 = zeros(size(appendix_1));% 主索结点坐标
Cord_lower_Q2 = zeros(size(appendix_2(:, 1:3))); %促动器下端点
Cord_upper_Q2 = zeros(size(appendix_2(:, 4:6))); %促动器上端点
Index_Nodes_Motor_Q2 = string(zeros(size(Index_Nodes_Motor(:, 1)))); % 反射结点/促动器 编号

l_range = sqrt(R^2 + (R - F)^2 - sqrt(1 - (L/2/R)^2) * 2 * R * (R-F)); % 根据焦点得出范围

for i = 1 : length(Cord_Nodes)
    dis = sqrt((Cord_Nodes(i, 1) - P(1))^2 + (Cord_Nodes(i, 2) - P(2))^2 + (Cord_Nodes(i, 3) - P(3))^2);
    if dis <= l_range
        Cord_Nodes_Q2(Count, :) = Cord_Nodes(i, 1:3);
        Cord_lower_Q2(Count, :) = Cord_lower(i, 1:3);
        Cord_upper_Q2(Count, :) = Cord_upper(i, 1:3);
        Index_Nodes_Motor_Q2(Count, :) = Index_Nodes_Motor(i);
        Count = Count + 1;
    end
end

Cord_Nodes_Q2 = Cord_Nodes_Q2(1:Count-1, :);
Cord_lower_Q2 = Cord_lower_Q2(1:Count-1, :);
Cord_upper_Q2 = Cord_upper_Q2(1:Count-1, :);
Index_Nodes_Motor_Q2 = Index_Nodes_Motor_Q2(1:Count-1, :);

% 建立结点间关系矩阵
N = length(Index_Nodes_Motor_Q2); % Q2结点数
D = string(zeros(N, 7)); % 7是因为一次最多连6个结点，第一列是所查询的结点

for i = 1:N
    [row, col] = find(Index_Panel == Index_Nodes_Motor_Q2(i));
    temp = string(zeros(1, 3 * 6)); % 一个辅助矩阵
    for j = 1:length(row)
        temp(3*j-2 : 3*j) = Index_Panel(row(j), :);
    end
    temp_u = unique(temp);
    index_first = find(temp_u == Index_Nodes_Motor_Q2(i));
    temp_store = temp_u(1);
    temp_u(1) = temp_u(index_first);
    temp_u(index_first) = temp_store;
    D(i, 1:length(temp_u)) = temp_u;
end

Q2_Data.nodes = Cord_Nodes_Q2;
Q2_Data.lower = Cord_lower_Q2;
Q2_Data.upper = Cord_upper_Q2;
Q2_Data.index = Index_Nodes_Motor_Q2;
Q2_Data.D = D;

save('Q2_Data.mat', 'Q2_Data')

然后你看，这样就有了Q2要的数据了。接着我们先进行一波分析，首先我们要探明，促动器下端和上端还有主索结点是不是共线的，如果是，三点间的两两斜率几乎就是一样的。同样，我们还要验证这方向是否是径向的，即分别求取单位向量：

$e_{1}^{\left( j \right)}=\mathrm{Norm}\left[ x_{+}^{\left( j \right)}-x_{-}^{\left( j \right)},y_{+}^{\left( j \right)}-y_{-}^{\left( j \right)},z_{+}^{\left( j \right)}-z_{-}^{\left( j \right)} \right] \\ e_{2}^{\left( j \right)}=\mathrm{Norm}\left[ x_{o}^{\left( j \right)}-x_{+}^{\left( j \right)},y_{o}^{\left( j \right)}-y_{+}^{\left( j \right)},z_{o}^{\left( j \right)}-z_{+}^{\left( j \right)} \right] \\ e_{3}^{\left( j \right)}=\mathrm{Norm}\left[ x_{o}^{\left( j \right)}-x_{-}^{\left( j \right)},y_{o}^{\left( j \right)}-y_{-}^{\left( j \right)},z_{o}^{\left( j \right)}-z_{-}^{\left( j \right)} \right] \\ e_{4}^{\left( j \right)}=\mathrm{Norm}\left[ x_{o}^{\left( j \right)},y_{o}^{\left( j \right)},z_{o}^{\left( j \right)} \right]$

我们验证后发现，三者基本共线且指向球心，误差非常的小。所以现在需得到与理想抛物面的距离，在这里，我们是写出了一个一般形式的曲面，由于下拉索长度不变，我们只需让主索结点上下沿径向移动，求取其到抛物面的交点，可以用参数方程来解：

clear
clc

% 计算附件中主索结点到理想抛物面距离

load('Q2_Data.mat')

e = Q2_Data.nodes;
e = e ./ sqrt(sum(e'.^2)');

syms t

N = length(Q2_Data.nodes);
dis_expected = zeros(N, 1);
alpha = 36.795*pi/180;
beta = 78.169*pi/180;
R = 300.4; %笔误 : R  = 300;%
F = 0.466*R;
h = 0.3609;

for i = 1 : N
    m = e(i, 1);
    n = e(i, 2);
    q = e(i, 3);
    x0 = Q2_Data.nodes(i, 1);
    y0 = Q2_Data.nodes(i, 2);
    z0 = Q2_Data.nodes(i, 3);
    f= (R + h)*(16*F + 16*h) - 2*cos(2*beta)*(z0 + q*t)^2 - 3*(x0 + m*t)^2 - 3*(y0 + n*t)^2 - 2*(z0 + q*t)^2 +...
        2*cos(2*beta)*(cos(alpha)*(x0 + m*t) + sin(alpha)*(y0 + n*t))^2 + sin(beta)*(z0 + q*t)*(16*F + 16*h) + ...
        cos(2*alpha)*(x0 - y0 + m*t - n*t)*(x0 + y0 + m*t + n*t) + 4*sin(2*beta)*(z0 + q*t)*(cos(alpha)*(x0 + m*t) +...
        sin(alpha)*(y0 + n*t)) + 2*sin(2*alpha)*(x0 + m*t)*(y0 + n*t) +...
        cos(beta)*(16*F + 16*h)*(cos(alpha)*(x0 + m*t) + sin(alpha)*(y0 + n*t));
    p=sym2poly(f);
    result=roots(p);
    index = find(min(abs(result)) == abs(result));
    dis_expected(i) = result(index);
end

save('Dis_Expected.mat', 'dis_expected')

然后一波计算，发现：

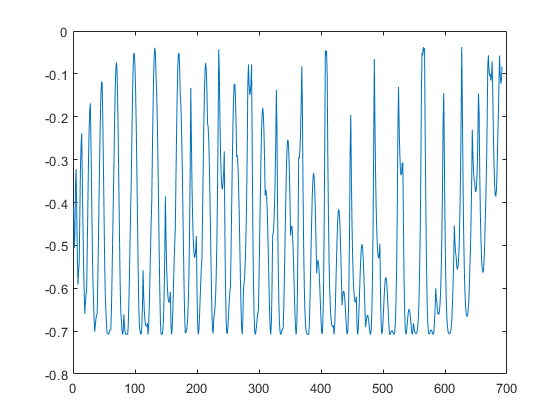
在我们这一版本下，只有少数主索结点的限制超过了0.6。最大约为-0.7。我们以一种折半的方式来迭代，具体来说：我们遍历每一个结点，如果它的调整范围大于0.6，那么我们先将它约束在0.6（正负），然后直接按此时的0.6调整。调整后检查是否符合0.07%的约束，如果符合就更新此时的距离和结点位置，然后继续遍历。直到收敛。这个的实现并不复杂：

clear
clc

load('Dis_Expected.mat')
load('Q2_Data.mat')

N = length(Q2_Data.nodes);

global e
e = Q2_Data.nodes;
e = e ./ sqrt(sum(e'.^2)'); % 方向向量

global Node_origanl
Node_origanl = Q2_Data.nodes; % 一个保留的nodes,用于计算Lo（原始主索长度） 此处待优化

Nodes_fit = zeros(size(Q2_Data.nodes));
step_history = zeros(size(dis_expected));

iter = 20;
Error = zeros(1, iter);
e0 = mean(dis_expected.^2);

for j = 1 : iter
    fprintf('iter:%d\n',j)
    for i = 1 : N
        [step, Nodes_c, step_history] = step_in_constraint(Q2_Data.nodes, Q2_Data.D(i, :), dis_expected, i, Q2_Data.index, step_history); % 输入主索结点，相连矩阵，以及此时的index
        Q2_Data.nodes(i, 1:3) = Nodes_c;
        dis_expected(i) = dis_expected(i) - step;
    end
    Error(j) = mean(dis_expected.^2);
end
Error = [e0, Error];
Nodes_fit = Q2_Data.nodes;


function [h, Nodes_c, step_history] = step_in_constraint(Nodes, D_row, dis, index, Nodes_index, step_history)
    global e
    global Node_origanl
    k_max = 10;
    
    h = dis(index);
    if abs(h) > 0.6    % 由dis_expected的分布知，最大的距离为0.7m
        h = sign(h) * 0.6;
    end
    
    [Index, ~] = find(D_row == Nodes_index);
    Lo_pre = zeros(length(Index) - 1, 3);
    for j = 1 : length(Index) - 1
        Lo_pre(j, 1:3) = Node_origanl(Index(j + 1), 1:3);
    end
    Lo = sum((Lo_pre - Node_origanl(index, 1:3)).^2, 1);
    
    for i = 1 : k_max
        Nodes_changed = Nodes(index, 1:3) + h * e(index, 1:3);
        L = sum((Lo_pre - Nodes_changed).^2, 1);
        ratio = L ./ Lo;
        step_history_temp = step_history(index) + h;
        if  ratio >= 1 + 0.0007 | ratio <=  1 - 0.0007 | abs(step_history_temp) > 0.6
            h = h / 2;
        else
            step_history(index) = step_history_temp;
            Nodes_c = Nodes_changed;
            break
        end
    end
    % 如果失败了的话就ban掉
    if i == k_max
        h = 0;
        Nodes_c = Nodes(index, 1:3);
    end
end

Question-3

然后我们把迭代后的节点存起来做第三问，因为第三问是摆弄主索结点，所以促动器上下端就已经用不到了。特别地，如果把反射面板当成平面，所求的接收比会很低（基准时0.7%~0.8%，调节后1.1%）……总之，要用曲面三角形来做，也就是我们要考虑三点所成的球面的反射。实际上，它比平面处理时仅多了几步工序，其余别无二致：

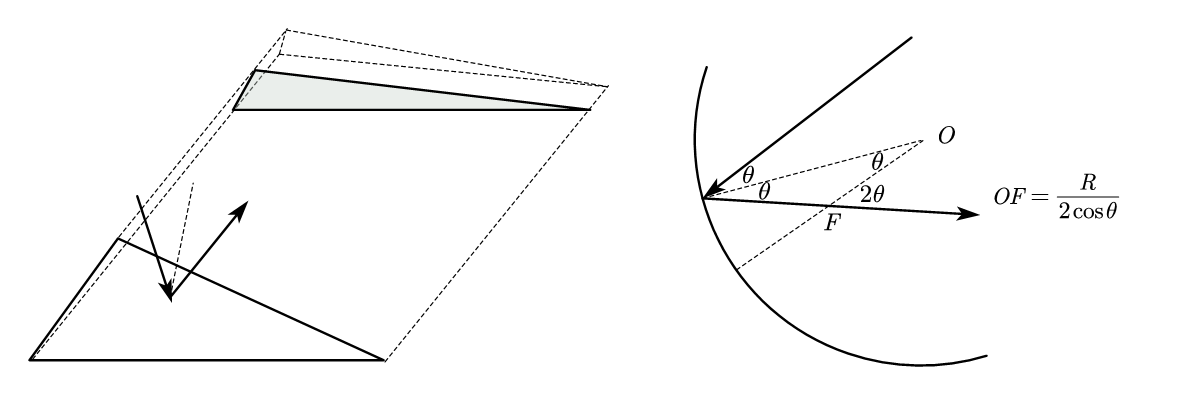
左侧是平面时的情况，馈源舱所在的平面会把反射的三棱柱截成一个三角形，曲面三角形时其实是一样的，这里为了方便画了二维的情形。由于反射和圆的性质，$\theta$越大，$F$点越远离圆心，且张角$2\theta$也越大，所以还是会被一个馈源舱所在平面截成平面。所以思路是直接的，遍历每个反射面板，计算每个反射面板所在球面的球心，球心到端点的向量即为端点的法向量，之后计算沿法向量的反射光线，再计算其与馈源舱所在平面的交点，得到投影三角形。我们先解决反射的问题：

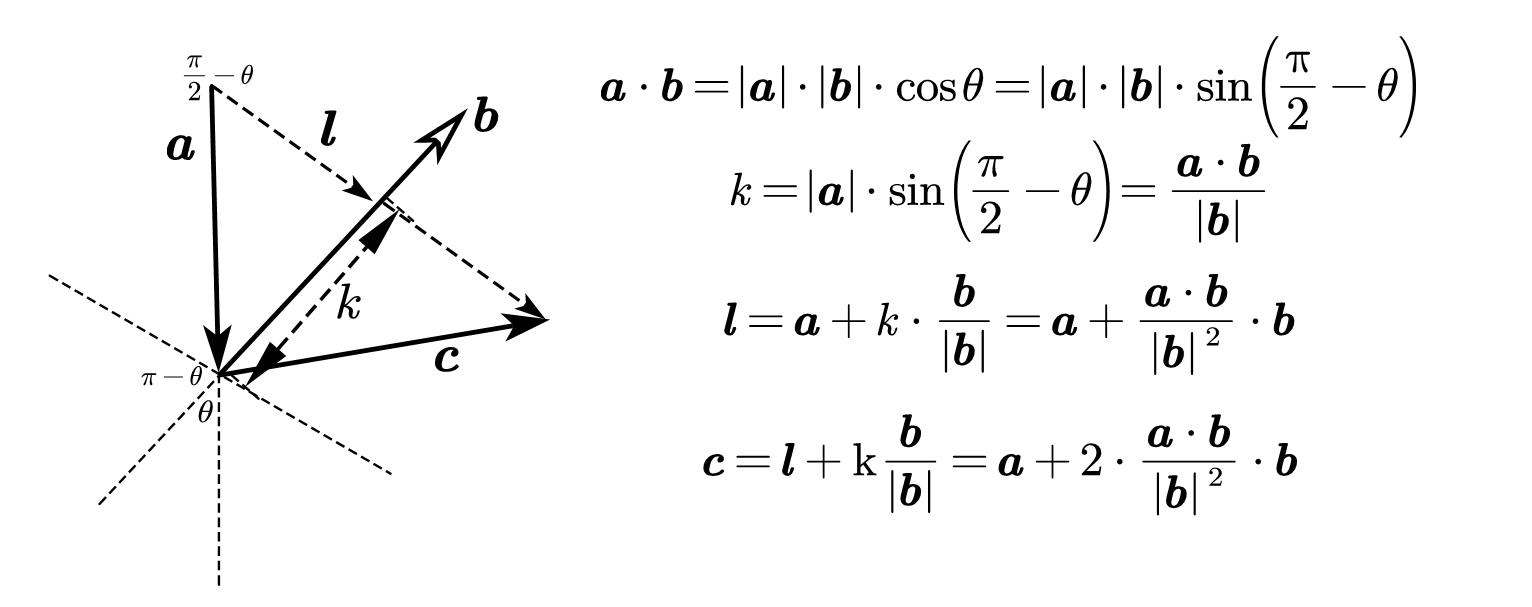
借助简单的向量知识，我们即可找出A向量关于B向量的对称向量C向量。

现在我们考虑寻找法向量，我们需确定此时曲面三角形的球心，很容易我们会这么想：给定空间三点，求三点所确定的球心极半径，于是有三点共面，且三点到空间球心距离相等（此时你可能没有考虑半径$R$到底是个什么情况……）然后你列写：

$\left| \begin{matrix} x_1-x_0& y_1-y_0& z_1-z_0\\ x_2-x_0& y_2-y_0& z_2-z_0\\ x_3-x_0& y_3-y_0& z_3-z_0\\ \end{matrix} \right|=0\Rightarrow A_1x_0+B_1y_0+C_1z_0+D_1=0 \\ \begin{aligned} &A_1=y_1z_2-y_1z_3-z_1y_2+z_1y_3+y_2z_3-y_3z_2\\ &B_1=-x_1z_2+x_1z_3+z_1x_2-z_1x_3-x_2z_3+x_3z_2\\ &C_1=x_1y_2-x_1y_3-y_1x_2+y_1x_3+x_2y_3-x_3y_2\\ &D_1=-x_1y_2z_3+x_1y_3z_2+x_2y_1z_3-x_3y_1z_2-x_2y_3z_1+x_3y_2z_1\\ \end{aligned} \\ \left\{ \begin{array}{c} \left( x_1-x_0 \right) ^2+\left( y_1-y_0 \right) ^2+\left( z_1-z_0 \right) ^2=R^2\\ \left( x_2-x_0 \right) ^2+\left( y_2-y_0 \right) ^2+\left( z_2-z_0 \right) ^2=R^2\\ \left( x_3-x_0 \right) ^2+\left( y_3-y_0 \right) ^2+\left( z_3-z_0 \right) ^2=R^2\\ \end{array} \right. \Rightarrow \left\{ \begin{array}{c} A_2x_0+B_2y_0+C_2z_0+D_2=0\\ A_3x_0+B_3y_0+C_3z_0+D_3=0\\ \end{array} \right. \\ \left[ \begin{array}{c} x_0\\ y_0\\ z_0\\ \end{array} \right] =-\left[ \begin{matrix} A_1& B_1& C_1\\ A_2& B_2& C_2\\ A_3& B_3& C_3\\ \end{matrix} \right] ^{-1}\left[ \begin{array}{c} D_1\\ D_2\\ D_3\\ \end{array} \right]$

写的一气呵成，然后你会发现$R$取什么好像无所谓，带入数据会发现，计算出的球心坐标跟三个顶点很接近，然后算一下半径发现只有7左右。总觉得哪里不太对。实际上是因为，反射面板充当的是整个大球面（$R=300.4$）的一个部分，而这三个点并不完全的在球面上，上述的唯一解并不能指向我们想要的结果。换句话说，对于给定的半径，并非任意三点之间都能满足在球表面上这一条件。但实际上，作为近似，我们可以把$R=300.4$直接带进去，解数值解（vpasolve, solve等），我们会发现对应的球面基本和原点很接近。

然后我们得到了反射光线，有了法向量，由直线的参数方程即可得到被馈源舱所在平面所截的三个坐标点，然后判断其中有多少可以被馈源舱接收。这个判断非常复杂，计算这个比较随机的三角形和圆形的重叠面积有很多种情况，所以：蒙特卡洛！从馈源舱中采点（这样会易于实现且可以复用，如果是在三角形上找点，每次计算出一个新的三角形就要重新生成一次。），然后看看这些点哪些在三角形内，在的数量记为$n_1$，则单个反射面板的接收比为：

$\eta ^{\left( j \right)}=\frac{\pi n_1}{4nS_{\varDelta}^{\left( j \right)}}$

然后把每个面板的算出来，加权求和即可。这里有些琐碎的问题，即给定三个点的坐标求三角形面积，以及如何判断点在三角形内。这两个问题简直是给大一的同学应用高数下里的叉乘最好的例子了：

对于三角形面积，我们关注叉乘后的模，即：

$S_{\varDelta}=\frac{1}{2}\left| \overrightarrow{AB}\times \overrightarrow{AC} \right|=\frac{1}{2}\left| \det \left( \left| \begin{matrix} i& j& k\\ x_B-x_A& y_B-y_A& 0\\ x_C-x_A& y_C-y_A& 0\\ \end{matrix} \right| \right) \right|=\frac{1}{2}\left| \det \left| \begin{matrix} x_B-x_A& y_B-y_A\\ x_C-x_A& y_C-y_A\\ \end{matrix} \right| \right|$

这样就能用计算好的馈源舱所在平面上的坐标直接得到三角形面积了，最后至于判断一个点是否在三角形内，方便起见点记作$P$，三角形记作$ABC$，在平面里，在内部就是说，$P,C$在$A,B$同侧，$P,B$在$A,C$同侧，$P,A$在$B,C$同侧，那么我们注意到向量$AP,BP,CP$，以$BP$为例，由右手螺旋定则，当$BA$叉乘$BP$与$BP$叉乘$BC$同向时（同向即叉乘后的三维向量的第三维的符号），说明$P$在角ABC（小于180°）内，如果此时再满足$\overrightarrow{BA}\times \overrightarrow{PA}$与$\overrightarrow{PA}\times \overrightarrow{CA}$同号，说明$P$在角BAC内。由于ABC围成了一个三角形，所以此时$P$一定在三角形内。

clear
clc

load('Q2_Data.mat')
load('Nodes_reality.mat')

Index_Panel = readmatrix('附件3.csv', 'OutputType','string', 'Range',2);
Panel_Sphere = zeros(length(Index_Panel), 3 * 3); % 以反射面板为单元记录基准状态时主索结点坐标
Panel_Para = zeros(length(Index_Panel), 3 * 3); % 以反射面板为单元记录抛物面状态时主索结点坐标

% 按照反射面板为单位重排
Count = 1;

for i = 1 : length(Index_Panel)
    y = zeros(1, 3);
    for j = 1 : 3
        temp = find(Q2_Data.index == Index_Panel(i, j));
        if isempty(temp)
            y(j) = [];
            break
        else
            y(j) = temp;
        end
    end
    if length(y) == 3
        Panel_Sphere(Count, 1:9) = [Q2_Data.nodes(y(1), 1:3), Q2_Data.nodes(y(2), 1:3), Q2_Data.nodes(y(3), 1:3)];
        Panel_Para(Count, 1:9) = [Nodes_fit(y(1), 1:3), Nodes_fit(y(2), 1:3), Nodes_fit(y(3), 1:3)]; 
        Count = Count + 1;
    end
end

N = Count - 1;
Panel_Sphere = Panel_Sphere(1:Count - 1, :);
Panel_Para = Panel_Para(1:Count - 1, :);

% 重排之后，遍历计算每个反射面板在馈源舱平面截面

% 首先计算馈源舱所在平面
global z_c
global inner_light % 入射光线
alpha = 36.795 * pi / 180; % 转为弧度制
beta = 78.169 * pi /180;
R = 300.4;
F = 0.466 * R;

x_c = - (R - F) * cos(beta) * cos(alpha);
y_c = - (R - F) * cos(beta) * sin(alpha);
r_c = 1 / 2;
z_c = - (R - F) * sin(beta);

inner_light = [cos(beta) * cos(alpha), cos(beta) * sin(alpha), sin(beta)];

% rectangle('Position',[x_c - r_c, y_c - r_c, 2*r_c,2*r_c],'Curvature',[1,1])
% axis equal





% 计算接收比前，先生成馈源舱附近的随机数
x_rand = unifrnd(x_c - r_c, x_c + r_c, 10000);
y_rand = unifrnd(y_c - r_c, y_c + r_c, 10000);
Rand_for_eta = zeros(10000, 2);
eta = 0;
Count = 1;
for j = 1 : 10000
    if (x_rand(j) - x_c)^2 + (y_rand(j) - y_c)^2 <= r_c^2
        Rand_for_eta(Count, :) = [x_rand(j), y_rand(j)];
        Count = Count + 1;
    end
end
Rand_for_eta = Rand_for_eta(1:Count - 1, :);

Panel_selected = Panel_Para;
% Panel_selected = Panel_Sphere;
for i = 1 : N
    
    [x0, y0, z0] = Cal_Sphere_Center(Panel_selected(i, :)); % 得到更新后的球心坐标
    [e1, e2, e3] = Cal_Vector(Panel_selected(i, :), x0, y0, z0); % 计算法向量e1, e2,e3
    [r1, r2, r3] = Cal_Reflect(e1, e2, e3); % 计算反射后的向量
    [p1, p2, p3] = Cal_Cord_in_z0(Panel_selected(i, :), r1, r2, r3); % 计算在馈源舱平面的坐标
    [eta] = Cal_eta(p1, p2, p3, Rand_for_eta, eta);
    
    % if mod(i, 50) == 0
%         hold on
%         plot([p1(1), p2(1), p3(1), p1(1)], [p1(2), p2(2), p3(2), p1(2)])
    % end

%     plot3([0, r1(1)], [0,r1(2)], [0,r1(3)])
%     hold on
%     plot3([0, e1(1)], [0,e1(2)], [0,e1(3)])
%     plot3([0, inner_light(1)], [0,inner_light(2)], [0,inner_light(3)])
end

eta = eta / N;

fprintf('eta:%f',eta)


function [x0, y0, z0] = Cal_Sphere_Center(Panel_Cord)
    x1 = Panel_Cord(1); y1 = Panel_Cord(2); z1 = Panel_Cord(3);
    x2 = Panel_Cord(4); y2 = Panel_Cord(5); z2 = Panel_Cord(6);
    x3 = Panel_Cord(7); y3 = Panel_Cord(8); z3 = Panel_Cord(9);
%     
%     A1 = y1*z2 - y1*z3 - z1*y2 + z1*y3 +y2*z3 - y3*z2;
%     B1 = -x1*z2 + x1*z3 + z1*x2 - z1*x3 - x2*z3 + x3*z2;
%     C1 = x1*y2 - x1*y3 -y1*x2 + y1*x3 + x2*y3 - x3*y2;
%     D1 = -x1*y2*z3 + x1*y3*z2 + x2*y1*z3 - x3*y1*z2 - x2*y3*z1 + x3*y2*z1;
%     
%     A2 = 2*(x2 - x1);
%     B2 = 2*(y2 - y1);
%     C2 = 2*(z2 - z1);
%     D2 = x1*x1 + y1*y1 + z1*z1 - x2*x2 - y2*y2 - z2*z2;
%     
%     A3 = 2*(x3 - x1);
%     B3 = 2*(y3 - y1);
%     C3 = 2*(z3 - z1);
%     D3 = x1*x1 + y1*y1 + z1*z1 - x3*x3 - y3*y3 - z3*z3;
%     
%     Center = - [A1, B1, C1; A2, B2, C2; A3, B3, C3] \ [D1; D2; D3];
%     
%     x0 = Center(1);
%     y0 = Center(2);
%     z0 = Center(3);
%     
%     R = sqrt((x1 - x0)^2 + (y1 - y0)^2 + (z1 - z0)^2);
%     警钟长鸣
    syms x0 y0 z0
    R = 300.4;
    center = [x0, y0, z0];
    
    equ = [(x1 - x0)^2 + (y1 - y0)^2 + (z1 - z0)^2 == R^2,...
        (x2 - x0)^2 + (y2 - y0)^2 + (z2 - z0)^2 == R^2,...
        (x3 - x0)^2 + (y3 - y0)^2 + (z3 - z0)^2 == R^2];
    warning('off', 'symbolic:numeric:NumericalInstability')
    center_vpa = vpasolve(equ, center, [-500, 500; -500. 500; 100. -300]);
    x0 = double(center_vpa.x0);
    y0 = double(center_vpa.y0);
    z0 = double(center_vpa.z0);
end
    
function [e1, e2, e3] = Cal_Vector(Panel_Cord, x0, y0, z0)
    x1 = Panel_Cord(1); y1 = Panel_Cord(2); z1 = Panel_Cord(3);
    x2 = Panel_Cord(4); y2 = Panel_Cord(5); z2 = Panel_Cord(6);
    x3 = Panel_Cord(7); y3 = Panel_Cord(8); z3 = Panel_Cord(9);
    
    e1 = [x0 - x1, y0 - y1, z0 - z1];
    e1 = e1 / sqrt(dot(e1, e1));
    e2 = [x0 - x2, y0 - y2, z0 - z2];
    e2 = e2 / sqrt(dot(e2, e2));
    e3 = [x0 - x3, y0 - y3, z0 - z3];
    e3 = e3 / sqrt(dot(e3, e3));
end

function [r1, r2, r3] = Cal_Reflect(e1, e2, e3)
    global inner_light
    R = inner_light;
    R = R';
    e1 = e1';e2 = e2';e3 = e3';
    r1 = e1 \ R * 2 * e1 - R;
    r2 = e2 \ R * 2 * e2 - R;
    r3 = e3 \ R * 2 * e3 - R;
    r1 = r1 / sqrt(dot(r1, r1));
    r2 = r2 / sqrt(dot(r2, r2));
    r3 = r3 / sqrt(dot(r3, r3));
end

function [p1, p2, p3] = Cal_Cord_in_z0(Panel_Cord, r1, r2, r3)
    global z_c
    x1 = Panel_Cord(1); y1 = Panel_Cord(2); z1 = Panel_Cord(3);
    x2 = Panel_Cord(4); y2 = Panel_Cord(5); z2 = Panel_Cord(6);
    x3 = Panel_Cord(7); y3 = Panel_Cord(8); z3 = Panel_Cord(9);
    
    t1 = (z_c - z1) / r1(3);
    p1(1) = t1 * r1(1) + x1;
    p1(2) = t1 * r1(2) + y1;
    
    t2 = (z_c - z2) / r2(3);
    p2(1) = t2 * r2(1) + x2;
    p2(2) = t2 * r2(2) + y2;
    
    t3 = (z_c - z3) / r3(3);
    p3(1) = t3 * r3(1) + x3;
    p3(2) = t3 * r3(2) + y3;
end

function [eta] = Cal_eta(p1, p2, p3, Rand_Pool, eta)
    M = [1, 1, 1;
        p1(1), p2(1), p3(1);
        p1(2), p2(2), p3(2);];
    S = (1 / 2) * abs(det(M));
    
    in = 0;
    total = length(Rand_Pool);
    
    for i = 1:total
        A = [p1(1), p1(2), 0];
        B = [p2(1), p2(2), 0];
        C = [p3(1), p3(2), 0];
        P = [Rand_Pool(i, 1), Rand_Pool(i, 2), 0];
        
        AB = A - B;
        AP = A - P;
        AC = A - C;
        
        BA = B - A;
        BP = B - P;
        BC = B - C;
        
        BA_BP = cross(BA, BP);
        BP_BC = cross(BP, BC);
        AB_AP = cross(AB, AP);
        AP_AC = cross(AP, AC);
        
        if BA_BP(3) * BP_BC(3) > 0 && AB_AP(3) * AP_AC(3) > 0
            in = in + 1;
        end
    end
    
    eta = eta + (pi / 4) * in / total / S;
end

最后我们把上面说的几个环节小心翼翼地拼接起来，就能得到最终结果了。我运行一次模拟得到的结果是：

（更新于第二天：当我hexo d以后，我发现最后的结果多少有点奇怪，之前的工作态接收比只有30%多。于是我发现了一个错误，它甚至不能被称为一个bug，因为只是一个笔误，这个笔误导致了次优的结果。严谨起见这里面的有些插图需要换一下，但是我就懒得换了，毕竟只是自己的一个树洞，不足为外人道也。如果真的有人看到了这个页面：如果你没有复现这个题的需求，那么不影响看热闹；如果你有，你也很容易能看到问题在哪。）

	基准球面	抛物面工作态
接收比	5.54%	64.95%

与评阅要点中的符合的较好。国赛并不对可视化那么看重，所以我就没整什么花活。最后高低意思意思吧作点基本的可视化：

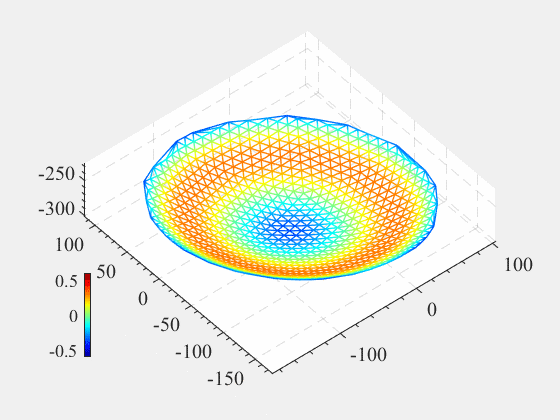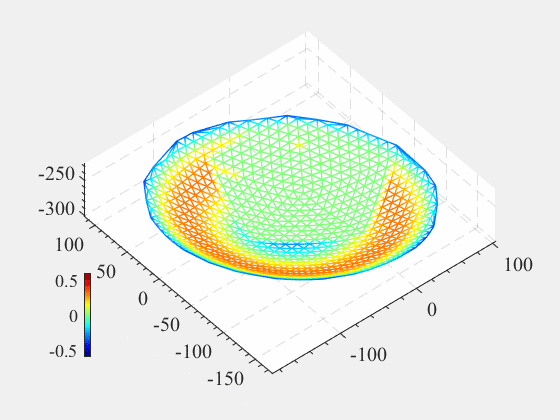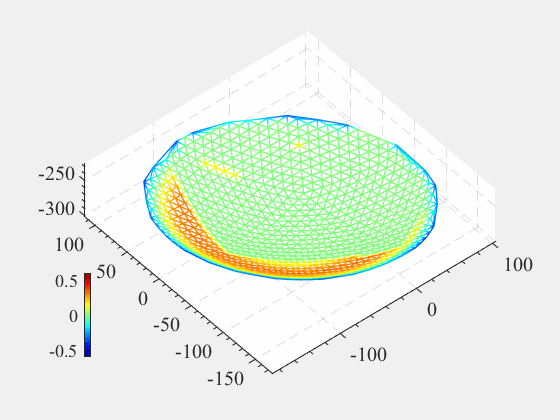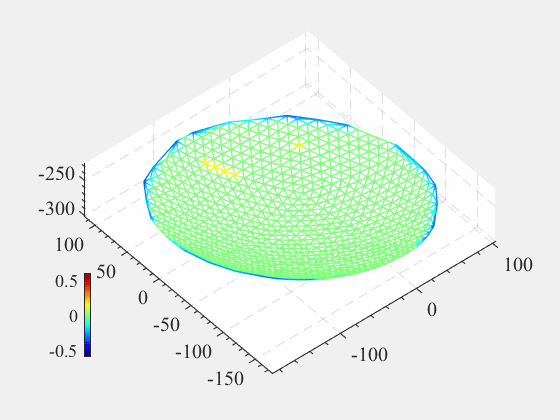
看，我们动态可视化了第二问调整主索结点的过程，可以用来催眠。

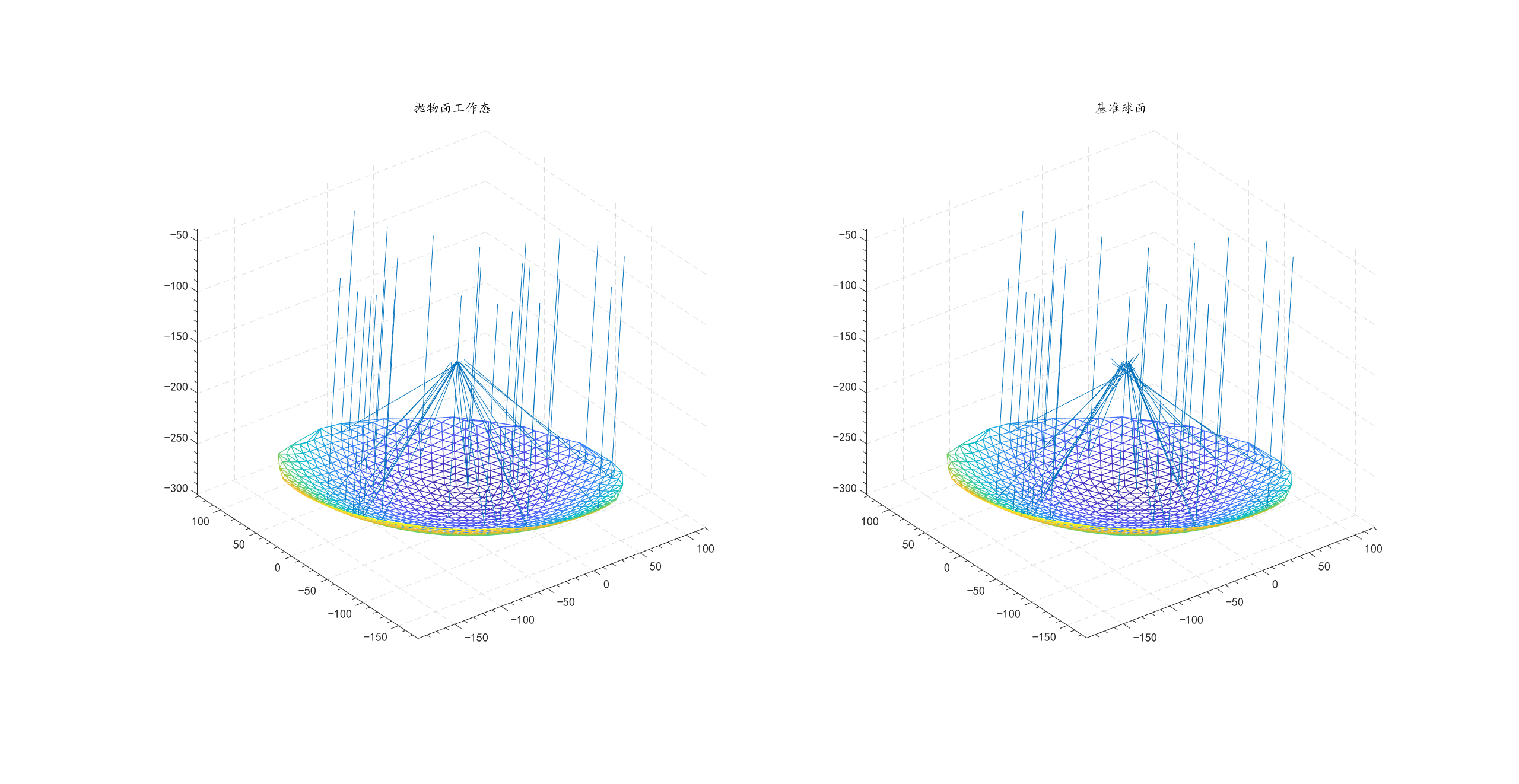
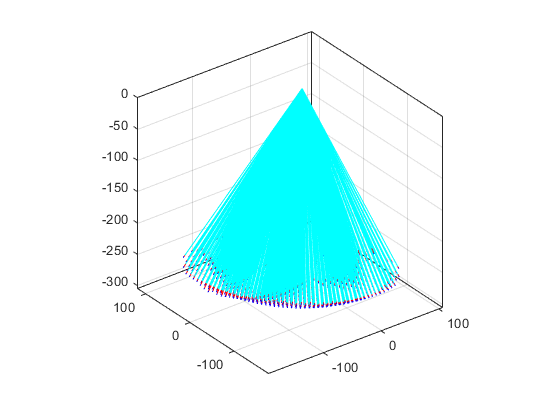
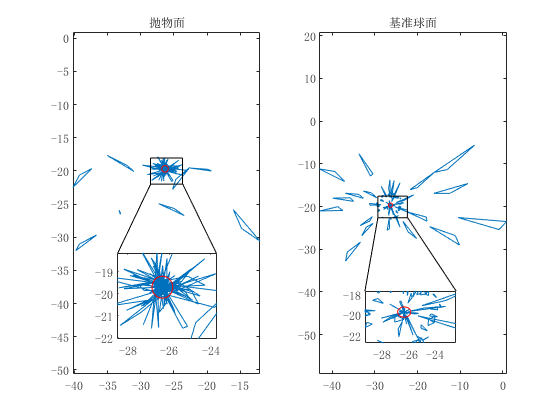
我们抽取了相同的入射光线，将光路可视化，发现抛物面状态下效果确实更优。

馈源舱所在平面可视化，直观的体现了汇聚作用。

End

就像西安交大今年本科招生宣传片《怎样才能达到完美毕业生》，有时候我也在脑补要是能魂穿回大一刚入学或者三河二中，就像《开端》以及其他影视作品里的那样，一定有一个听起来很嗨的最优路径。但是后来越想越觉得，就算是真的，其实不会实现。当我说出那些美好的幻想的时候，实际上是对当前遇到的事情或困难的投影，但等我真的一顿时间穿越修正了它的时候，有些我认识里的好或坏的事情会不发生，然后遇到另一个时间线的福祸，然后继续盼望着另一个最优路径，所以，都一样的。

但毕竟开学就大三了，以前的焦虑现在也没得可焦虑了，因为，寄了啊，当时焦虑那是因为感觉得好好把握机会，现在已经积重难返/大局已定。所以突出一个自己的局限性。接受并和解就好。

至少，感谢现代科技和过去以及将来，我现在晚上能沉迷计算机图形学的伟大作品无法自拔，现代快餐的制成品足以让被接受过精神阉割的我乐一天，我列表里还有同学可以骚扰。所以，让脑筋多转转往好处看看~