傅里叶变换5

阅读数: 次 2022-07-18

信号都考完了，没想到这还能有5吧……我也没想到，因为关于傅里叶变换的故事其实还没有结束，这一篇将会把傅里叶变换更深入的扩展到离散情形下，具有重要的意义。

把一个描述从连续化扩展到离散化，这并不是很显然，比如把微分方程化差分方程，一些数值分析的知识需要引入来保证最后的解收敛。这个也一样，而且由于，学习信号处理时各种资料切入的角度，对于读者背景的不同，会使知识树出现断层。所以就有了这篇blog。当考虑离散情形下的傅里叶变换时，我们首先要把处理的信号从连续的变成离散的点，也就是采样。

Sampling

这里，我们以梳状函数采样为例，简单的复习一下，首先考虑周期信号的傅里叶变换：

$\mathcal{F} \left[ f\left( t \right) \right] =\mathcal{F} \left[ \sum_{n=-\infty}^{\infty}{F_ne^{jn\varOmega t}} \right] =2\pi \sum_{n=-\infty}^{\infty}{F_n\delta \left( \omega -n\varOmega \right)}$

之后把梳状函数带入：

$\delta _T\left( t \right) =\sum_{n=-\infty}^{\infty}{\delta \left( t-mT \right)} \\ F_n=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{\delta _T\left( t \right) e^{-jn\varOmega t}\mathrm{d}t}=\frac{1}{T} \\ \mathcal{F} \left[ \delta _T\left( t \right) \right] =\frac{2\pi}{T}\sum_{n=-\infty}^{\infty}{\delta \left( \omega -n\varOmega \right)}=\varOmega \sum_{n=-\infty}^{\infty}{\delta \left( \omega -n\varOmega \right)}$

所以我们发现，梳状函数的傅里叶变换还是一个周期函数。这点后面会很有用，在之前上课的时候，这个结论一出来，就用来处理周期函数的傅里叶级数了，现在我们要往别的方向发展一下。

现在考察取样信号$f_s\left( t \right) =f\left( t \right) \delta _T\left( t \right) $的频谱函数，由频域卷积定理：

$F_s\left( j\omega \right) =\frac{1}{2\pi}F\left( j\omega \right) \ast \varOmega \delta _{\varOmega}\left( \omega \right)$

我们注意到，$\varOmega$是梳状函数的傅里叶变换的周期，我们称其为采样频率，记为$\omega _s$ 。$T$是梳状函数的周期，我们称它为采样周期，记为$ T_s$。后面会看到为什么这么叫它们，我们展开，由冲激函数的性质，直接计算：

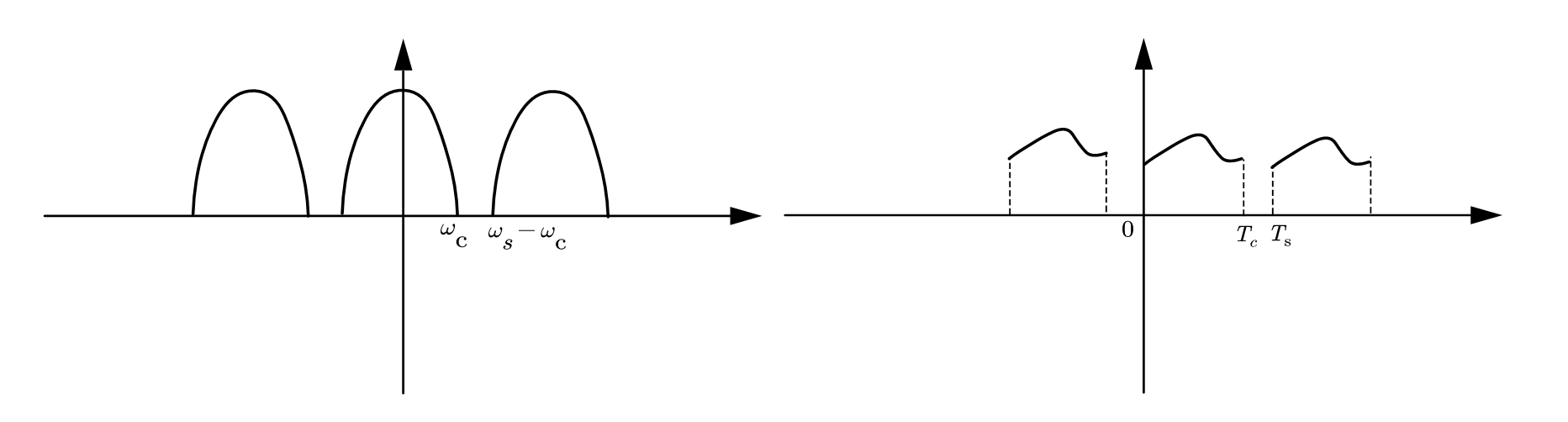
$F_s\left( j\omega \right) =\frac{\omega _s}{2\pi}F\left( j\omega \right) \ast \sum_{n=-\infty}^{\infty}{\delta \left( \omega -n\omega _s \right)} \\ =\frac{1}{T_s}\sum_{n=-\infty}^{\infty}{F\left( j\left( \omega -n\omega _s \right) \right)}$

我们发现，对一个连续信号进行采样，频谱发生了周期延拓，我们设频率响应的截止频率为$\omega_c$，那么为了周期延拓时不发生混叠：

$\omega _c\leqslant \omega _s-\omega _c \\ \omega _s\geqslant 2\omega _c$

我们就得到了习题里的奈奎斯特采样频率。这个现象指出：一个域里的均匀采样，对应另一个域的周期延拓。

对于这个结果，还有一种理解的角度，注意到原始信号的带限频谱被延拓了，这是由于离散的采样让采样点之间的“缝隙”可以用无数高频信号来拟合，虽然减小采样周期看起来貌似能减轻这一现象，但那只是让延拓出的新频谱在更高频的位置，我们能做到的只有确保不发生混叠，而不能说这些采样点里，高频的就不“存在”，只能说低频更符合我们的习惯。例如，对$\mathrm{sin}x$进行采样，采样后的数据点肯定可以想办法用$\mathrm{sin}3x$像连珠一样连起来。并且实际上大多数时候，你得到的一串序列，不一定会知道“采样率”具体是多少，你拿到的只是离散的点。

从频域采样也是一样的，这点是由于梳状函数变换前后都是周期函数，并且卷积和相乘操作有卷积定理作保证。我们下面验证一下频域采样的情形：

$F_s\left( j\omega \right) =F\left( j\omega \right) \delta _{\omega _s}\left( \omega \right) \\ \delta _{T_s}\left( t \right) \leftrightarrow \omega _s\delta _{\omega _s}\left( \omega \right) \\ f_s\left( t \right) =\frac{1}{\omega _s}f\left( t \right) \ast \delta _{T_s}\left( t \right) \\ =\frac{1}{\omega _s}\sum_{n=-\infty}^{\infty}{f\left( t-nT_s \right)}$

当然这里要求信号是时限信号，同样，为了避免混叠：

$T_s>T_c$

（这里是没有2的，因为时域信号不存在类似“负频率”的要素）

这两个定理的意义在于，我们明确了抽样这一操作，建立了连续信号和离散序列的关系，这里先略去了如何从离散序列恢复成连续信号，因为我们先暂时不关心这一点。接下来，有两种思路推出离散傅里叶变换(DFT)，首先我们要明确，DFT它并不严格，只是一种在一定程度近似的条件下，能允许计算机计算有限长序列的傅里叶变换的方法。在下文里我们会发现，频域分析貌似没有我们在连续情形下想的“那么美好”。我们先给出第一种推导：

DFS→DFT

如果我们已知一个连续的周期信号，我们知道它是可以展开成傅里叶级数的，它的幅度谱和相位谱都是离散的，本质上是从复指数函数集里找了最优逼近。之后进行采样，得到了一个周期序列，根据前面的分析它的频域频谱会发生周期延拓。但是，如果我们最开始已知的就是一个周期序列，这个序列不是一个函数，比如可以写成解析式表达的那种，它就是一个简单的$x[1],x[2],..,x[n]$一样的序列。所以，不如直接借坡下驴，既然每一个序列相差1，那我就认为采样间隔是1，然后采样频率是$2\pi *1=2\pi$。

这样处理后，频域的一个周期就是$2\pi$，之后我们把连续傅里叶级数的思想迁移过来。首先要认识到，在之前连续的情形里，我们是用了无穷多个频率的复指数信号来逼近一个连续的函数，而周期信号的谱是离散的，它往往是带限的。我们假设处理的离散信号是没有混叠的，那么也就是说它的截止频率已经被包含进那一个主值序列里了，我们只关注中心的那个主值序列，因为负频和高频远处的那些是完全相同的。所以，此时的复指数就不需要无穷多个频率分量了。

所以，如果我们有$N$个采样点，那么根据线性代数的知识，我们选取的正交基的维度和向量维度应该一样，都要是$N$，且正交基彼此正交，并且能尽可能平分$2\pi$的归一化频谱，根据我们对三角函数集的理解，我们很容易就能给出这样的一组基：

$\left[ 1,e^{j\varOmega _0n},e^{2j\varOmega _0n},...,e^{j\left( N-1 \right) \varOmega _0n} \right]$

其中，$\varOmega _0=\frac{2\pi}{N}$，这就是数字角频率，标准正交基同时要进行单位化，再乘一个$1/N$，就完了。所以我们就得到了离散傅里叶级数的表达：

$f_N\left( k \right) =\frac{1}{N}\sum_{n=0}^{N-1}{F_N\left( n \right) e^{\mathrm{j}n\varOmega k}}$

用这个就可以表达我们一般指代（主值序列）的离散序列的频谱，至于离散傅里叶级数的系数$F_N(n)$的求取，和连续时的办法是一样的，我们定义均方误差：

$E\left( F_N\left( 0 \right) ,F_N\left( 2 \right) ,...,F_N\left( n-1 \right) \right) =\sum_{n=0}^{N-1}{\left( f_N\left( n \right) -\frac{1}{N}\sum_{k=0}^{N-1}{F_N\left( k \right) e^{\mathrm{j}\frac{2\pi}{N}nk}} \right) ^2}$

由极值的必要条件，对某一变量求偏导，这里取$F_N(i)$，令偏导得0，得：

$\frac{\partial E}{\partial F_N\left( 0 \right)}=2\sum_{n=0}^{N-1}{\left[ \left( f_N\left( n \right) -\frac{1}{N}\sum_{k=0}^{N-1}{F_N\left( k \right) e^{\mathrm{j}\frac{2\pi}{N}nk}} \right) \left( -\frac{1}{N}e^{\mathrm{j}\frac{2\pi}{N}ni} \right) \right]} \\ \sum_{n=0}^{N-1}{f_N\left( n \right) e^{\mathrm{j}\frac{2\pi}{N}ni}}=\frac{1}{N}\sum_{n=0}^{N-1}{\sum_{k=0}^{N-1}{F_N\left( k \right) e^{\mathrm{j}\frac{2\pi}{N}n\left( k+i \right)}}}$

然后交换求和顺序：

$\sum_{n=0}^{N-1}{f_N\left( n \right) e^{\mathrm{j}\frac{2\pi}{N}ni}}=\frac{1}{N}\sum_{n=0}^{N-1}{\sum_{k=0}^{N-1}{F_N\left( k \right) e^{\mathrm{j}\frac{2\pi}{N}n\left( k+i \right)}}} \\ =\frac{1}{N}\sum_{k=0}^{N-1}{\sum_{n=0}^{N-1}{F_N\left( k \right) e^{\mathrm{j}\frac{2\pi}{N}n\left( k+i \right)}}} \\ =\frac{1}{N}\sum_{k=0}^{N-1}{F_N\left( k \right) \sum_{n=0}^{N-1}{e^{\mathrm{j}\frac{2\pi}{N}n\left( k+i \right)}}} \\ =\frac{1}{N}\sum_{k=0}^{N-1}{F_N\left( k \right) \frac{1-e^{j\frac{2\pi}{N}\left( k+i \right) N}}{1-e^{j\frac{2\pi}{N}\left( k+i \right)}}} \\ \frac{1-e^{j\frac{2\pi}{N}\left( k+i \right) N}}{1-e^{j\frac{2\pi}{N}\left( k+i \right)}}=\frac{1-e^{j2\pi \left( k+i \right)}}{1-e^{j\frac{2\pi}{N}\left( k+i \right)}}=\left\{ \begin{array}{c} N,k+i=N\\ 0,\mathrm{else}\\ \end{array} \right. \\ =F_N\left( N-i \right)$

将$N-i$代换为$k$，注意到左侧复指数的周期性，得：

$F_N\left( k \right) =\sum_{n=0}^{N-1}{f_N\left( n \right) e^{\mathrm{j}\frac{2\pi}{N}n\left( N-k \right)}}=\sum_{n=0}^{N-1}{f_N\left( n \right) e^{-\mathrm{j}\frac{2\pi}{N}nk}}$

这就是离散傅里叶级数(DFS)，注意，它处理的输入形式仍然是一个无限长的周期序列，而我们试图解决的是有限长序列的，实际上，我们可以尝试直接套用DFS的公式，如果得到的有限长信号确实是周期序列的子周期，那就不会有什么问题，然而，如果不这样呢？就会发生频谱泄露，会出现一些本不应存在的频率。

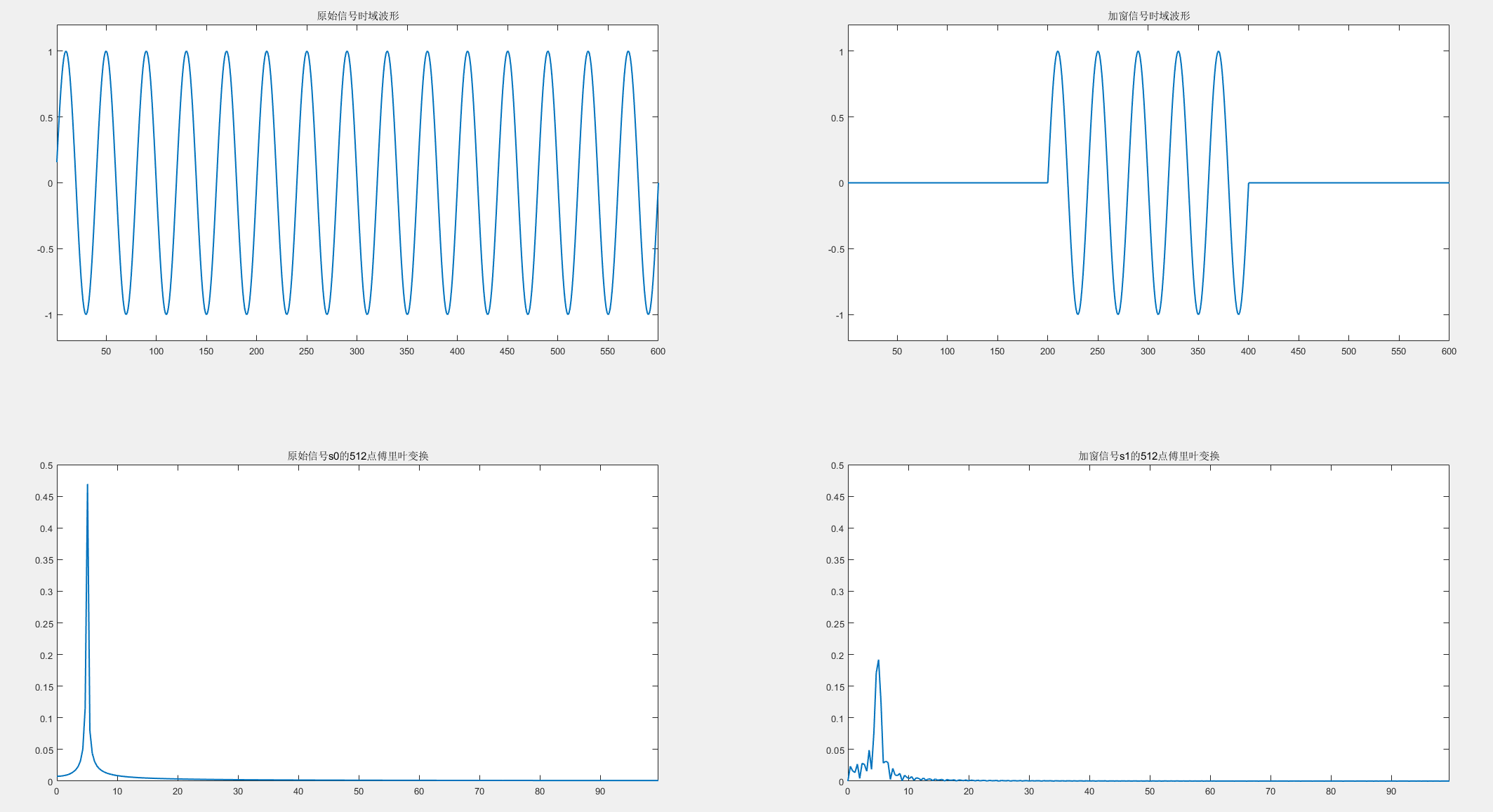
上图，当使用矩形窗加窗后，就发生了频谱泄露，出现了很多本不应出现的频率分量。（实际上不加窗的那个结果本身，也相当于加窗了，所以也出现了一定的泄露。只是额外加矩形窗的那个更严重了。）本质上是因为，我们截取的序列，是从无限长中提取的一部分，由卷积定理，相当于在频域上卷积了一个窗的频谱函数，泄露是无法避免的，对已知信号加一些窗进行衰减，可以减缓频谱泄露。

上图中出现了一个“采样点数”，实际上如果用我们后面说的第二种得出DFT的思路，会更好理解，在这里的话，在介绍第二种思路之前，我们先在这里给出频域分辨率这一概念。实际上，在DFT中，$N$可以看成在单位圆上找共$N$次单位根，$N$越多能表达了频率就越多，所以可以定义一个分辨率：

$\varDelta R=\frac{F_s}{N}$

其实就是$N$越大，分辨率越高，能读出的频谱成份就越多。例如下面这个例子：

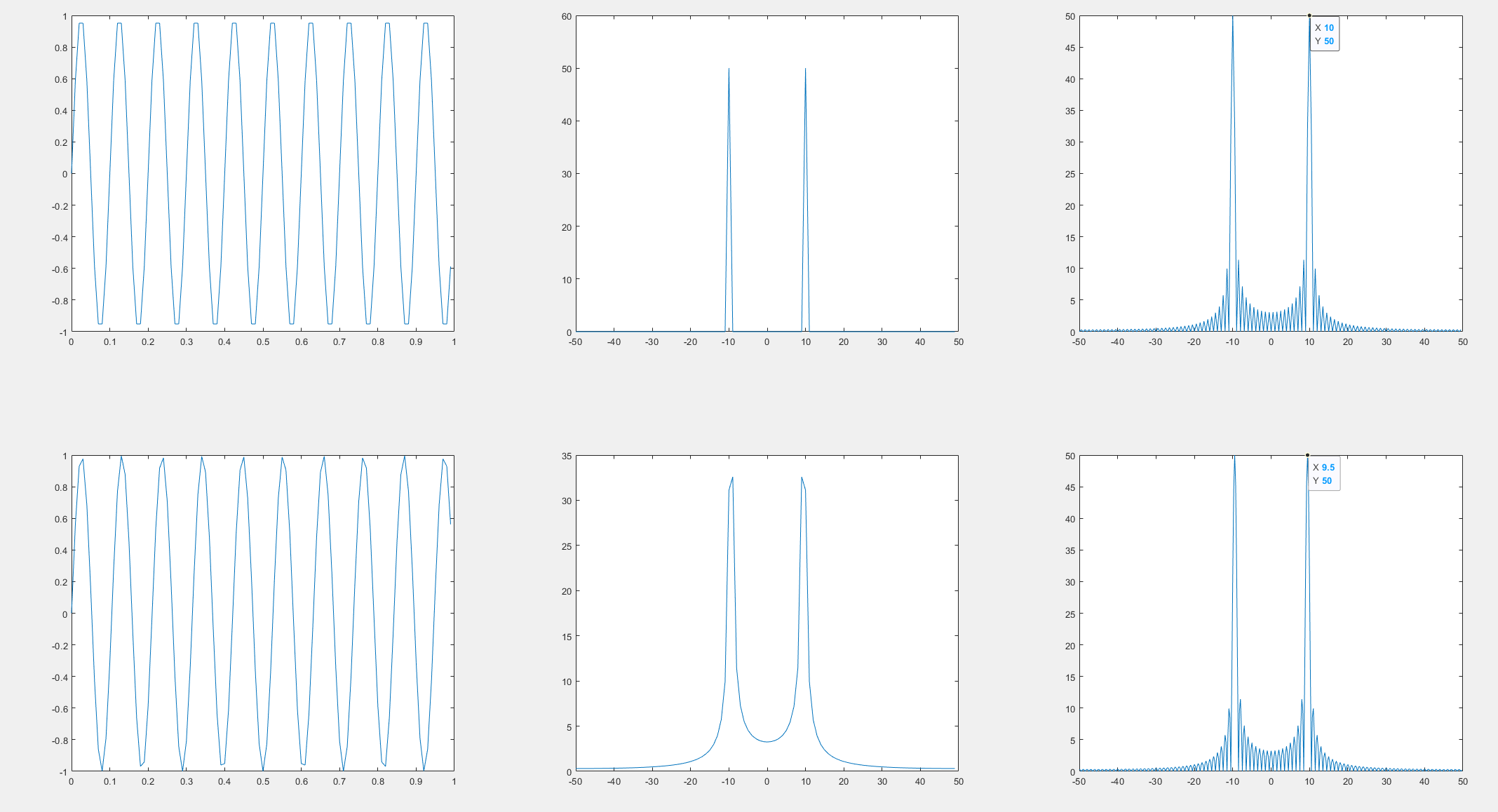
在上面的例子里，采样点数为$N$时的频谱图恰好很干净，这其实是由于此时设置的频率是10，恰好是一个整数倍。当改成9.5后，第二行的结果就显示了严重的畸变，此时不是因为频谱泄露，只是因为之前的频谱分辨率不够，捕捉不到那些分量，当第三列，同时增加采样点数后，频域分辨率得以提升，可以看见出现了明显了频谱泄露，它们看起来很像sinc函数，这其实是有原因的。这里就先不讨论了。

实际上，在操作的时候，如果采样点数大于序列长度，补零即可，这与$N$个正交基的推理并不矛盾。补零这个操作在后面还会遇到。

DTFT→DFT

另一种引入DFT的方法更为直接，对于连续非周期信号的傅里叶变换：

$F\left( j\omega \right) =\int_{-\infty}^{+\infty}{f\left( t \right) e^{-j\omega t}\mathrm{d}t}$

思路很直接，我们就直接对$f(t)$作冲激采样，这不就离散了吗。这样就得到了对离散非周期信号的表示。

$F\left( j\omega \right) =\int_{-\infty}^{+\infty}{f\left( t \right) e^{-j\omega t}\mathrm{d}t} \\ F\left( j\omega \right) =\int_{-\infty}^{+\infty}{f\left( t \right) \delta _T\left( t \right) e^{-j\omega t}\mathrm{d}t} \\ =\sum_{n=-\infty}^{\infty}{\begin{array}{c} f\left( n\varDelta t \right) e^{-j\omega n\varDelta t}\varDelta t\\ \end{array}} \\ =\sum_{n=-\infty}^{\infty}{\begin{array}{c} f\left[ n \right] e^{-j\omega n}\\ \end{array}}$

在最后，我们是把$\varDelta t$归一化成了1，这个写法的意思其实就是把所有的$f(n\varDelta t)$作一次重排，变成一个序列$f[n]$。这样处理完后我们就得到了离散时间傅里叶变换DTFT。特别地，我们要处理的信号，其实是有限的离散信号，与用DFS推的时候类似，它总能被延拓为一个周期信号，我们处理的是延拓后的主值序列。

而现在的一个问题是，得到的频域函数$F(j\omega)$还是连续的，那么我们再对频域进行采样，就可以让两边都离散化了。我们知道，时域抽样对应频域的周期延拓，周期是$2\pi$ ，（复指数关于$\omega$的周期），我们只需要一个周期的即可。所以我们对频域上均匀采样，采$N$个点，得：

$\varDelta \omega =\frac{2\pi}{N} \\ F_N\left( k \right) =\sum_{n=0}^{N-1}{f_N\left( n \right) e^{-\mathrm{j}\frac{2\pi}{N}nk}}$

这里采集点数的要求，就用到了之前的频域采样定理，如果序列有$M$个点，采集点数要大于等于$N$个点，虽然一般我们都会记序列有$N$个点，这里为了匹配以前的公式，就记为$M$个了。当$N>M$时，对序列进行补零操作。这里进行频域采样，是因为我们默认了要处理的是一个有限长的带限序列，所以就都，通了。

这里的补零操作，和前面所说的频谱泄露，频谱分辨率等概念，我只做了简要的描述。实际上它们之间的关系完全解释清楚，那又是一篇blog了。这实际上已经接近数字信号处理的范围了。以及，按照DFT计算，时间复杂度是$O(N^2)$，这是很糟糕的，快速傅里叶变换把时间复杂度降到了$O(\mathrm{nlogn})$，那个算法的深刻洞见非常的神奇，包括他的实现细节，如果我能在学数据结构之前知道这些，我肯定好好学数据结构。其实这一篇就是为了那点醋包的饺子，今天有点事得去下北校区，等到下一篇把它们补完。