本篇记录一些信号与系统中的练习题来备考。“大梦一场三千载,悲喜穿肠莫挂怀。大风翕张浪形骸,疏狂放歌死便埋。”
①已知某LTI连续系统的系统函数为$H\left( s \right) =\frac{s^2}{s^2+2s+1}$ ,其输入激励为$f(t)=\varepsilon \left( t \right) $ ,系统的初始状态为$y\left( 0_- \right) =0,y’\left( 0_- \right) =2$ 。求系统的零输入响应,零状态响应。
解:实际上,我们可以用变换域的方法直接求出全响应,但这样有时并不方便,因为当初始值不为0时,进行拉普拉斯变换容易写错,最安全的做法是用时域方法求解零输入响应,用变换域方法求解零状态响应。
我们观察系统函数,直接写出系统的微分方程:
求解零输入响应,有的同学像我一样经常记不住通解的形式,尤其是共轭时的情况,其实可以现场推出来,只需设$y=e^{rx}$即可,之后用欧拉公式即可得共轭复根的情况。这里用不到,只是说一下。
然后我们用变换域的方法求零状态响应:
如果不能直接写出原函数也没有关系,我们借助部分分式展开来给我们启示:
在这里,求留数时不用求导的那个系数对应分母最高次项的那个。前者很好写,后者带个平方。由$s$域微分性质(这些非时域的微分性质往往会带个负号):
注意这里分母作链式法则也会出一个负号,那么零状态响应即为:
②已知$f\left( t \right) =\sum_{n=-\infty}^{\infty}{e^{jnt}}$ ,$s(t)=\mathrm{cos}(t)$ 。低通滤波器的频率响应为:
求系统响应$y(t)$ 。
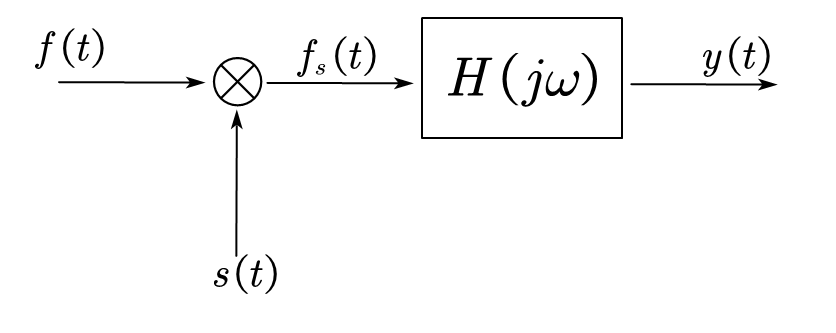
解:这个题实际上开了个玩笑,上述是一个载波调制的基本雏形,但是这里的$s(t)$作用与否不影响结果,当然是因为这是理想状态,首先对于$f(t)$,它天然就是一个傅里叶级数,$F_n =1$,根据周期信号的傅里叶变换:
这里$\varOmega =1$,然后啊,如果乘一个$\mathrm{cos}(t)$ ,那么根据傅里叶变换的性质:
可是你看那个无穷级数,这样整体乘二分之一,左移一位再右移一位加起来。冲激函数的幅度还是没变的。所以,就很乐。
而由于$f(t)$本身又是虚指数信号的线性组合,对于虚指数信号,我们知道零状态响应会有特殊的公式,所以$y(t)$直接就是:
③某稳定因果的连续线性离散系统,其系统函数为$H\left( z \right) =\frac{1}{z^2\left( z-0.5 \right)}$ ,求单位序列响应$h(k)$
解:单位序列响应和系统函数是一个变换对,我们只需求原函数即可。正常的思路是注意到系统函数是一个阶跃信号右移三次产生的,尺度变换为1/2 。然后就得出了答案:
而我这里把它拿出来,有几个小目的,第一个是为了锻炼一下计算能力,第二个是要排除一些错误的刻板印象。在书上教到部分分式展开求逆$z$变换时,往往会对$F(z)/z$进行展开,这样大多数时候分解后会得到一个方便的阶跃变换对。而这种惯性思维有时会阻碍我们对知识的进一步理解,实际上:
这是移位性质的直接应用,我们现在用这个,基于部分分式展开,练习一下计算:
逆变换后:
④判定:$y\left( t \right) =\left| f\left( t \right) -f\left( t-1 \right) \right|$ 的因果性,时变性,线性。
解:我们一项一项的看,因果性说的是,当$f(t)=0,t<0$时,是否有$y(t)=0$,若有则是因果的,反之则是反因果的(响应先于激励发生)。
设$f(t)=0,t<0$,则$f(t-1)=0$ ,可知$y\left( t \right) =\left| f\left( t \right) -f\left( t-1 \right) \right| \equiv 0$恒成立,它是因果性的。
时变性即验证$f(t-t_0)$能否推出$y(t-t_0)$ ,换句话说,即进入系统和时移两者能否对换。这里指出,一般两种情形会带来时变,第一是各项系数出现与时间有关的量,例如$t,\mathrm{sin}(t)$等。第二种是$f(-t)$,这种形式的激励会直接导致不满足时变性,例如形如:
(PS:即使积分上限是$1+2t$也是时变的,读者自证不难。)
这会直接导出$y\left( t-t_0 \right) \rightarrow f\left( -t+t_0 \right) \ne f\left( -t-t_0 \right) $ 。
我们验证发现它也是满足时不变性的。
至于线性,我们在高等代数中验证过许多次了,这里就不作赘述了。
⑤图示某离散$LTI$因果系统的信号流图:
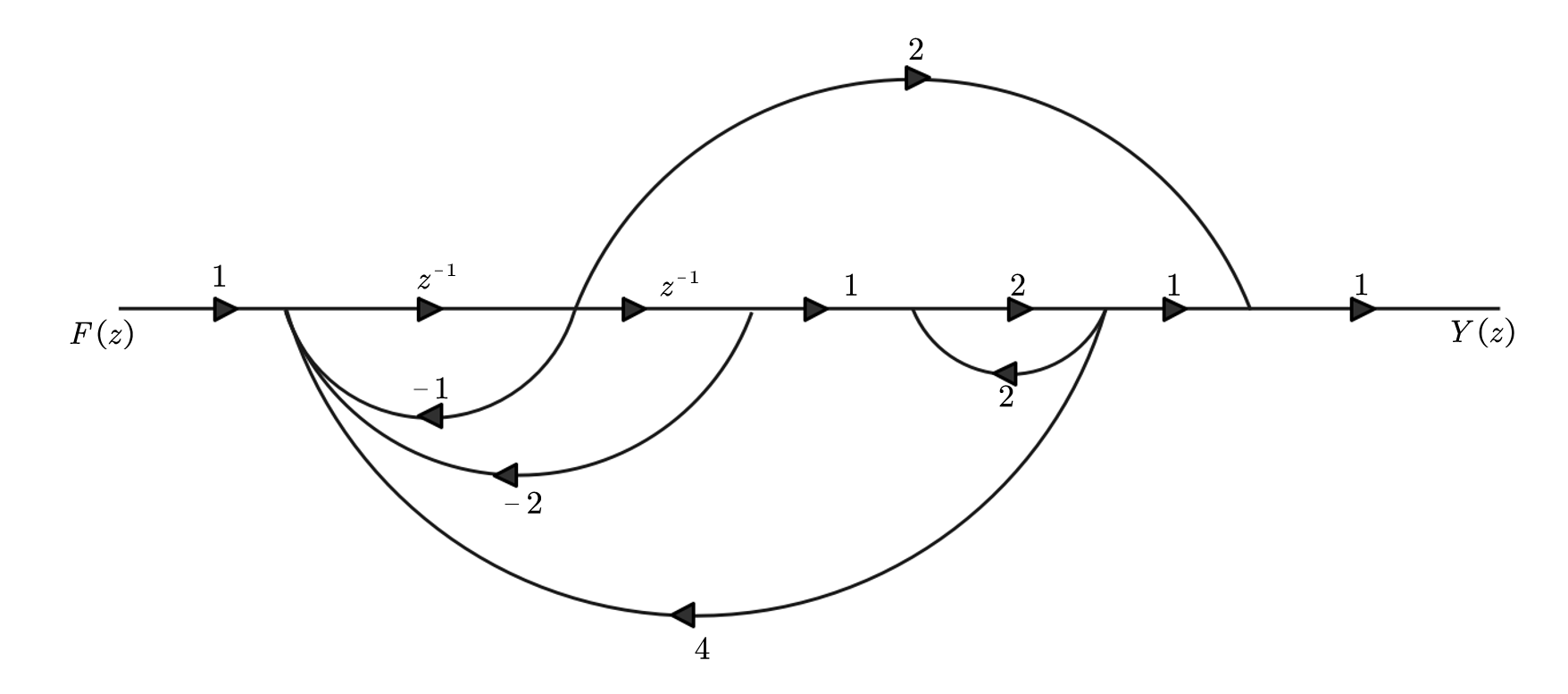
(1)求系统函数$H(z)$
(2)写出输入输出之间的差分方程
(3)判断该系统是否稳定
解:依次写出回路增益,以及互不接触的回路增益的乘积:
一般互不接触的只有两两互不接触的,之后列写特征行列式,以及找出前向增益和其子行列式:
由梅森公式:
由$Y(z)=H(z)F(z)$,展开得:
作逆$z$变换:
对于离散因果系统,我们考虑它极点的位置,若都在单位圆内,说明系统是稳定的。(这一段说来话长了,还是有点故事的。)

(顺带一提这张图中间其实就是信号最后一章状态方程的建立)
求极点,得一对共轭复根都在单位圆外,系统不稳定。
⑥电路如图所示,原已稳定,$t=0$将开关$S$由1打到2,求之后的$u_0(t)$:
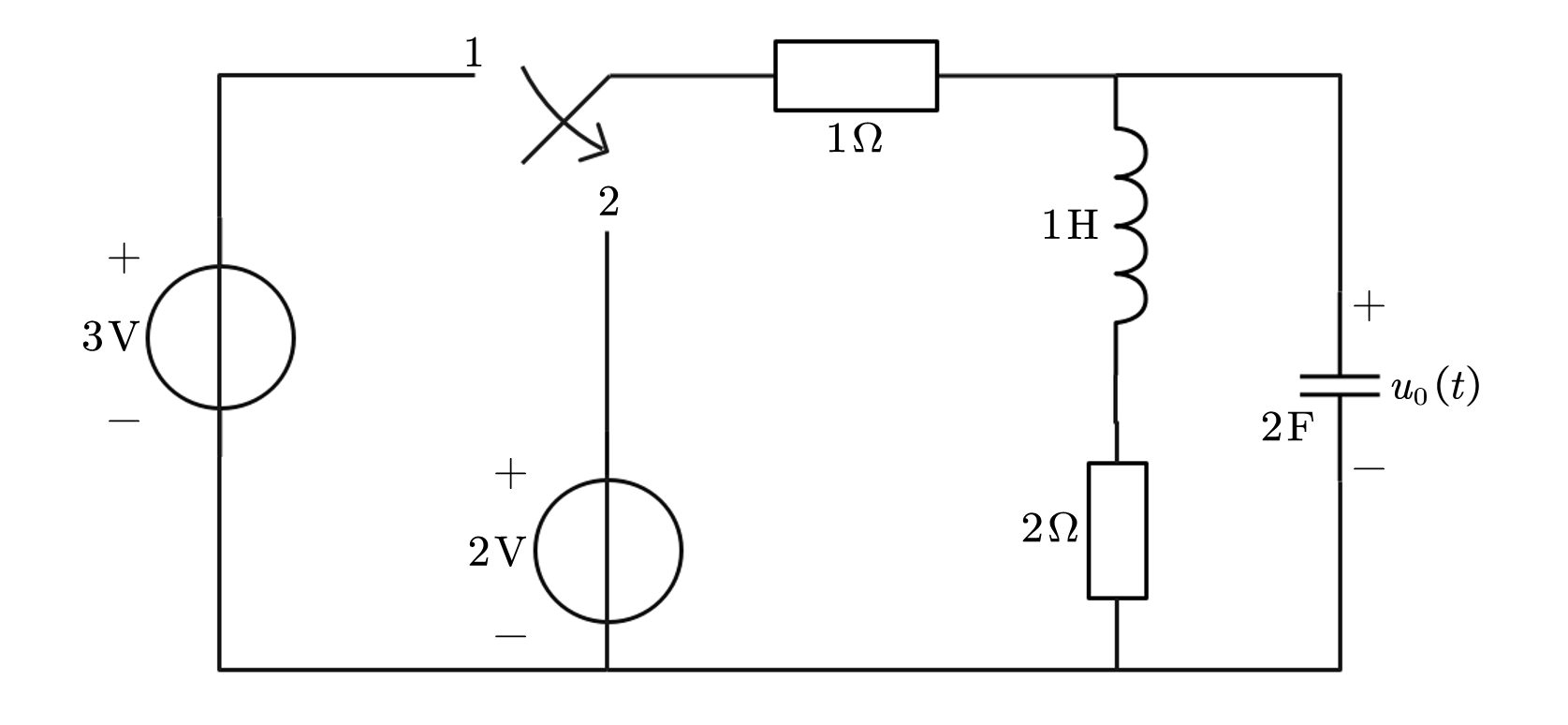
我很不喜欢这个,实际上这个只是套了个皮,本质上是个电路分析,我一般只记微分式变化的,因为那样简单,老记积分的version容易错。
显然初始状态:$i_L\left( 0_- \right) =1\mathrm{A},u_C\left( 0_- \right) =2\mathrm{V}$ ,当$t\geqslant 0$时,$u_S(t)=2\varepsilon(t)\mathrm{V}$ 。然后我们就开始列写式子嗷:
解得:
得:
⑦设因果序列$f(k)$满足方程:
解出序列$f(k)$
解:这个是基本$z$变换的性质,注意到左边的部分和,可以看成$\varepsilon(k-1)$与其卷积,分析得:
右侧道理是一样的,至于$k\varepsilon(k)$应用$z$域微分:
右端得:
所以$F(z)$为:
用熟悉的部分分式展开,得逆变换为:
⑧已知象函数$F\left( z \right) =\frac{z^2}{\left( z+1 \right) \left( z-2 \right)}$ ,其收敛域分别为$|z|>2,|z|<1,1<|z|<2$ ,求其原函数。
解:在之前的整理中,我忽略了收敛域的问题,因为第一这一部分没那么有趣,第二是考核中比较少。实际上,$z$变换就是洛朗级数,不同收敛域下的洛朗级数不唯一,在复变函数中我们有定理来保证,在不同收敛域下我们可以构造收敛的泰勒级数,来构造出洛朗级数的闭式解。在那块会对常用级数求和有着一定要求,但在这里倒不用,我们只需知道一个重要的变换对:
$z$变换中的正幂项是反因果部分,构造$-\varepsilon \left( -k-1 \right)$ 有助于我们作部分分式展开后,在$|z|<1$时构造闭式解。有了这个基础上述问题就很好表达了:
当$|z|>2$时,序列是因果序列,得$f\left( k \right) =\left[ \frac{1}{3}\left( -1 \right) ^k+\frac{2}{3}\left( 2 \right) ^k \right] \varepsilon \left( k \right) $
当$|z|<1$时,序列是反因果序列,得$f\left( k \right) =\left[ -\frac{1}{3}\left( -1 \right) ^k-\frac{2}{3}\left( 2 \right) ^k \right] \varepsilon \left( -k-1 \right) $
当$1<|z|<2$时,序列收敛于一个圆环:$f\left( k \right) =\frac{1}{3}\left( -1 \right) ^k\varepsilon \left( k \right) -\frac{2}{3}\left( 2 \right) ^k\varepsilon \left( -k-1 \right) $

