信号与系统

阅读数: 次 2022-06-13

在以往信号的讨论中我没有提及周期性信号，因为周期性信号有点过于理论，但是今天看完了觉得还是有点说法的，遂记录。

前情回顾，在高数下最后一章，我们学习了，傅里叶级数，简单来说指的是周期性信号可以分解为：

$f\left( t \right) =\frac{a_0}{2}+\sum_{n=1}^{\infty}{a_n\cos \left( n\varOmega t \right)}+\sum_{n=1}^{\infty}{b_n\sin \left( n\varOmega t \right)}$

其中角频率$\varOmega =\frac{2\pi}{T}$，在高等代数中，我们学到由于三角函数系是一个完备的正交函数集，在定义的内积空间下，上式相当于它的最佳逼近，相应的系数可计算为：

$\frac{a_0}{2}=\frac{\int_{-\frac{T}{2}}^{\frac{T}{2}}{f\left( t \right) \cdot 1\mathrm{d}t}}{\int_{-\frac{T}{2}}^{\frac{T}{2}}{1\cdot 1\mathrm{d}t}}=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f\left( t \right) \mathrm{d}t} \\ a_n=\frac{\int_{-\frac{T}{2}}^{\frac{T}{2}}{f\left( t \right) \cos \left( n\varOmega t \right) \mathrm{d}t}}{\int_{-\frac{T}{2}}^{\frac{T}{2}}{\cos ^2\left( n\varOmega t \right) \mathrm{d}t}}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f\left( t \right) \cos \left( n\varOmega t \right) \mathrm{d}t},n=1,2,... \\ b_n=\frac{\int_{-\frac{T}{2}}^{\frac{T}{2}}{f\left( t \right) \sin \left( n\varOmega t \right) \mathrm{d}t}}{\int_{-\frac{T}{2}}^{\frac{T}{2}}{\sin ^2\left( n\varOmega t \right) \mathrm{d}t}}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f\left( t \right) \sin \left( n\varOmega t \right) \mathrm{d}t},n=1,2,...$

接着由欧拉公式，把这串三角级数可以整理成复指数的形式：

$f\left( t \right) =\sum_{n=-\infty}^{\infty}{F_ne^{jn\varOmega t}} \\ F_n=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f\left( t \right) e^{-jn\varOmega t}\mathrm{d}t},n=0,\pm 1,\pm 2,..$

如果故事在这里结束，那不妨是一段佳话，我们知道卷积可以用来算零状态响应：

$y\left( t \right) =h\left( t \right) \ast f\left( t \right)$

根据卷积的定义：

$y\left( t \right) =h\left( t \right) \ast f\left( t \right) =\int_{-\infty}^{+\infty}{h\left( \tau \right) f\left( t-\tau \right) \mathrm{d}\tau}$

结合我们知道的傅里叶级数傅里叶变换，很难不好奇如果激励取成虚指数函数时会发生什么，我们选取$f(t)=e^{j\omega t}$ 。利用指数的性质，发现可以卷积式可以写成：

$\int_{-\infty}^{+\infty}{h\left( \tau \right) e^{-j\omega \tau}\mathrm{d}\tau}\cdot e^{j\omega t}=H\left( j\omega \right) e^{jwt}$

看，积分项突然就变成了傅里叶变换，我们就管他叫频率响应吧，然后零状态响应就，就变成了频率响应与响应激励相乘。这当然只存在于激励是虚指数的时候。我称之为美丽的巧合，因为我之前从未发现，直到考试题考的时候我觉得怎么没什么头绪，才发现。

所以，也就是说，如果输入的信号是写成虚指数形式的，那么直接将它与$H(j\omega)$相乘，就直接得到了零状态响应。以及，如果输入的是三角函数时，我们看一下会发生什么：

$y\left( t \right) =\frac{1}{2}H\left( j\omega \right) e^{jwt}+\frac{1}{2}H\left( -j\omega \right) e^{-j\omega t} \\ =\frac{1}{2}\left| H\left( j\omega \right) \right|e^{j\varphi \left( \omega \right)}\cdot e^{jwt}+\frac{1}{2}\left| H\left( -j\omega \right) \right|e^{-j\varphi \left( \omega \right)}\cdot e^{-j\omega t} \\ =\frac{1}{2}\left| H\left( j\omega \right) \right|\left[ e^{j\left[ \varphi \left( \omega \right) +\omega t \right]}+e^{-j\left[ \varphi \left( \omega \right) +\omega t \right]} \right] =\left| H\left( j\omega \right) \right|\cos \left[ \omega t+\varphi \left( \omega \right) \right]$

通过上式可以看出，如果频率为定值的三角函数输入系统时，其响应也是同频率的三角函数，振幅和相位分别由频率响应的模和幅角决定，此时的响应既是零状态响应，也是稳定响应。

注意推导中的一些小细节，例如当$f(t)=e^{-j\omega t}$时，结果是$H(-j\omega)$，实际上将之前的式子用$-\omega$代换$\omega$即可。以及此时$H(j\omega)$相当于$h(t)$的傅里叶变换，所以幅度谱是偶函数，相位谱是奇函数。（这里默认了激励是实函数哦。）

下面还有两个比较amazing的事实，第一个是无失真传输的条件，这个名词听起来很高大上，实际上就是说我们希望被一个系统作用后的信号，它只有时间上的延迟和幅值的变化，波形不要有变化，那么：

$y\left( t \right) =Kf\left( t-t_0 \right)$

两边作傅里叶变换即可看出无失真传输对系统的要求：

$Y\left( j\omega \right) =Ke^{-j\omega t_0}F\left( j\omega \right) \\ \left| H\left( j\omega \right) \right|=K,\varphi \left( \omega \right) =-\omega t_0$

现在还有另一个，即，最初我们都求解过傅里叶级数，它往往需要计算一个积分，比较繁琐，而常见的傅里叶变换对用起来很方便，所以有没有一种办法联系这两个工具？

首先关于周期信号作傅里叶变换，这点其实已经非常平凡了，由冲激函数变换对和频移特性，知：

$\mathcal{F} \left[ f\left( t \right) \right] =\mathcal{F} \left[ \sum_{n=-\infty}^{\infty}{F_ne^{jn\varOmega t}} \right] =2\pi \sum_{n=-\infty}^{\infty}{F_n\delta \left( \omega -n\varOmega \right)}$

这里有一个比较重要的周期函数的傅里叶变换，即梳状函数（单位冲激函数序列），我们后面会看到它为什么重要，我们先直球计算一下：

$\delta _T\left( t \right) =\sum_{n=-\infty}^{\infty}{\delta \left( t-mT \right)} \\ F_n=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{\delta _T\left( t \right) e^{-jn\varOmega t}\mathrm{d}t}=\frac{1}{T} \\ \mathcal{F} \left[ \delta _T\left( t \right) \right] =\frac{2\pi}{T}\sum_{n=-\infty}^{\infty}{\delta \left( \omega -n\varOmega \right)}=\varOmega \sum_{n=-\infty}^{\infty}{\delta \left( \omega -n\varOmega \right)}$

记最后得到的这个关于$\varOmega$的冲激函数序列为$\delta _{\varOmega}\left( \omega \right) $ ，那么一个重要的傅里叶变换对就有了：

$\delta _T\left( t \right) \leftrightarrow \varOmega \delta _{\varOmega}\left( \omega \right)$

现在我们的准备工作就结束了，我们从一个周期信号中截取一个周期，得到单脉冲信号$f_0(t)$，那么整个周期信号是：

$f_T\left( t \right) =f_0\left( t \right) \ast \delta _T\left( t \right)$

两边作傅里叶变换，得：

$\mathcal{F} \left[ f_T\left( t \right) \right] =F_0\left( j\omega \right) \varOmega \delta _{\varOmega}\left( \omega \right) =F_0\left( j\omega \right) \varOmega \sum_{n=-\infty}^{\infty}{\delta \left( \omega -n\varOmega \right)} \\ \omega =n\varOmega \\ \mathcal{F} \left[ f_T\left( t \right) \right] =\varOmega \sum_{n=-\infty}^{\infty}{F_0\left( jn\varOmega \right) \delta \left( \omega -n\varOmega \right)}$

还记得最开始嘛，我们直接计算得：

$\mathcal{F} \left[ f_T\left( t \right) \right] =2\pi \sum_{n=-\infty}^{\infty}{F_n\delta \left( \omega -n\varOmega \right)}$

对比逐项冲激函数的系数，得：

$F_n=\frac{\varOmega}{2\pi}F_0\left( jn\varOmega \right) =\frac{1}{T}F_0\left( jn\varOmega \right)$

有了这个工具，妈妈再也不用担心我傅里叶级数积不出来了，简直是奇迹，我们看一个例子就能体会到这种方法的优越性：

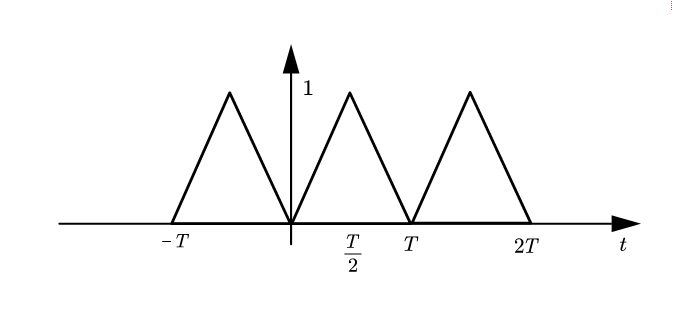
计算它的傅里叶级数，展开成指数型。

可以先把答案抄上来我们看一下：

$F_n=\frac{2\sin ^2\left( \frac{n\pi}{2} \right)}{n\pi ^2}e^{-jn\pi}$

这个如果直接积分，计算非常困难，而我们可以借助傅里叶变换来计算，我们选取$0$到$T$的那个单脉冲为$f_0(t)$，根据三角波的傅里叶变换和时移特性：

$F_0\left( j\omega \right) =\frac{T}{2}\mathrm{Sa}^2\left( \frac{\omega T}{4} \right) e^{-j\omega \frac{T}{2}}$

所以：

$F_n=\frac{1}{2}\mathrm{Sa}^2\left( \frac{n\pi}{2} \right) e^{-jn\pi}$

挺神奇的，现在再看傅里叶级数，就觉得比单调的算积分要有意思一点了。得背脑科学咯，不背要寄了，今天考个2000字大作文的考试，估计是给我写的任督二脉通了，今天有点莫名的嗨。