这一篇整理一下计组的作业题,能学多少学多少。
quiz1:
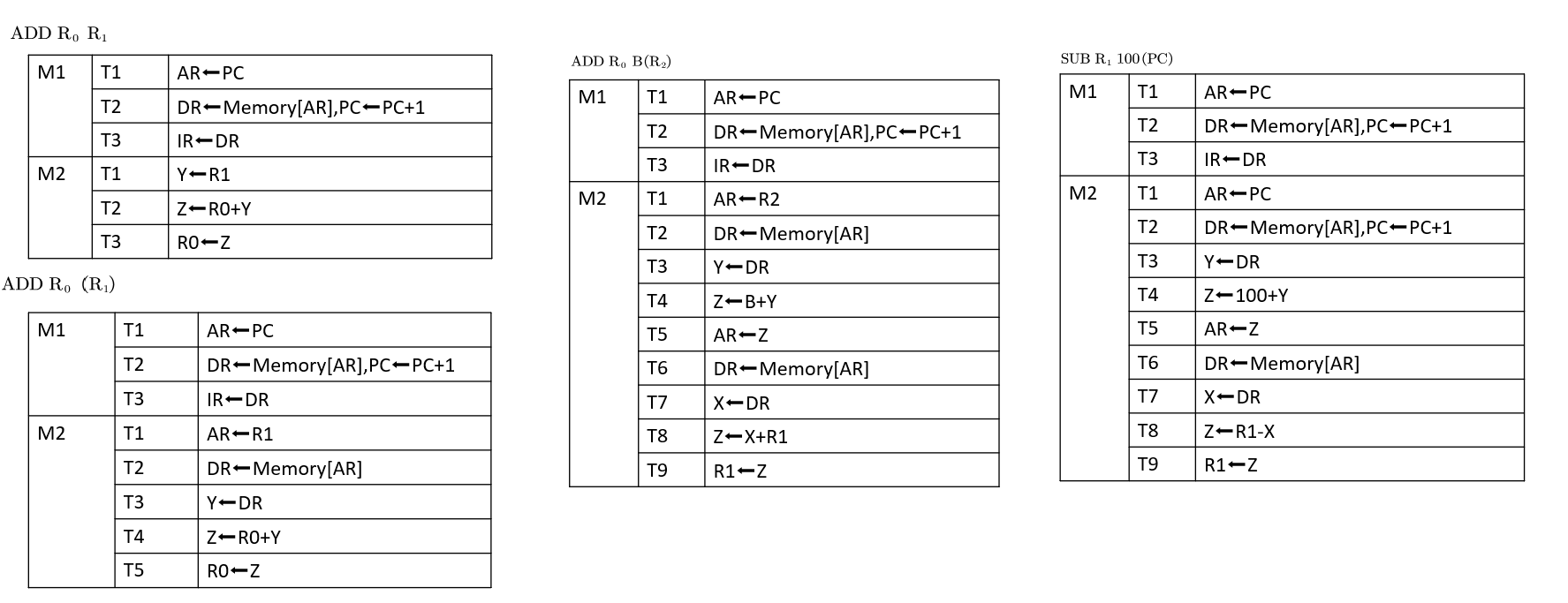
利用6264芯片在8位ISA系统总线上实现00000H~03FFFH的主存区域,试画其连接电路图。若在8086系统总线(16位ISA总线)上实现主存模块,试画其连接电路图:
首先,我们得知道什么是6264芯片,简单来说它有8位数据位,13位地址位。而要实现的主存区域是00000H~03FFFH,我们化成二进制,然后得到主存范围是$2^{14}$,也就是32K。这个时候,数据位8位对8位对上了,我们只需要考虑字,也就是进行字扩展。此时我们需要扩大2倍,所以一个1-2译码器就够了。
注意到所给的主存区域,则总线上应有20位。我们直接作出:
啊,我就懒的画了,直接贴答案了。我们注意左侧8位ISA的情况,对$A_{14}$到$A_{19}$作用一个或门,相当于把它压缩成了0/1一个单元,当它是0以及$A_{13}$是0时,激活下面的芯片,$A_{13}$是1时激活上面的芯片。值得注意的是,$A_{14}$到$A_{19}$实际上是进行一个要求它们全为0的约束,这样的话就能精准实现00000H~03FFFH。
当系统总线的数据位增多时,第二块芯片数据线的连法就可以发生变化,如上图所示,即位扩展。
quiz2:
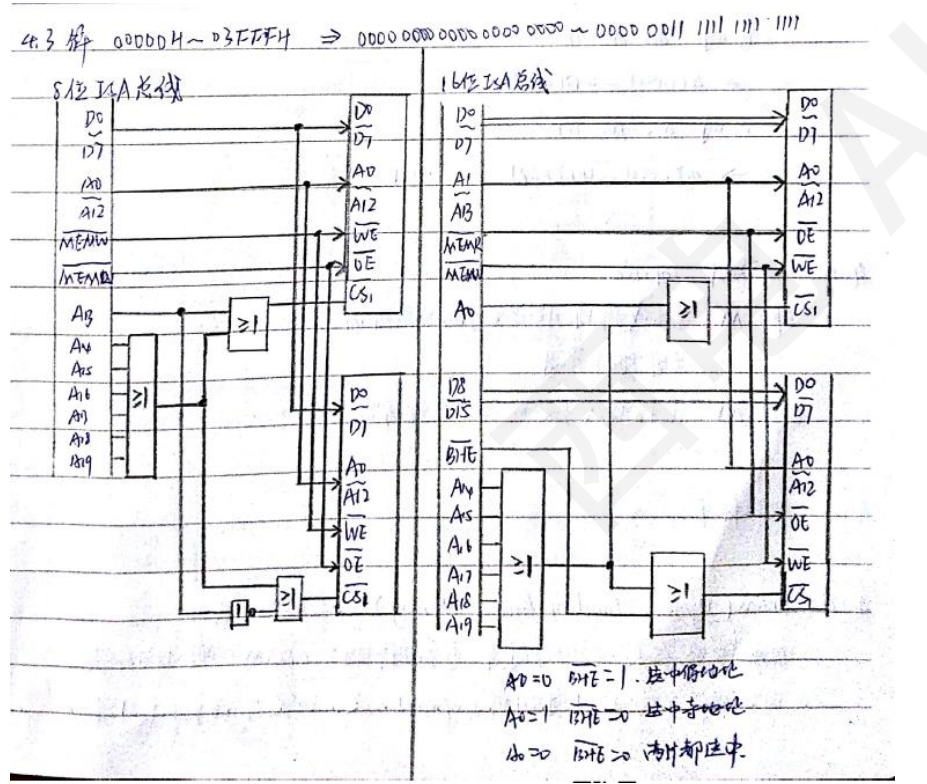
某CPU地址总线为$A_0$~$A_{19}$,数据总线为$D_0$~$D_7$,主存读信号为$\overline{MEMR}$,主存写信号为$\overline{MEMW}$。某SRAM连接电路如图:
(1)分析该图,指出该SRAM芯片占用的主存地址范围。
(2)采用该SRAM芯片实现30000H~33FFFH的主存区域,试画连接图。
这道题就清晰的阐述了上面的思想,我们注意到,片选线是否激活由下面的组合逻辑电路决定,只有在$A_{13}=0$,$A_{14}$~$A_{19}=1$时才能被激活,所以地址范围是1111 110x xxxx xxxx xxxx,换算得FC000H~FDFFFH。
注意到30000H=0011 0000 0000 0000 0000,33FFF=0011 0011 1111 1111 1111,我们发现了范围是0011 00xx xxxx xxxx xxxx,所以按照这个逻辑控制$A_{14}$~$A_{19}$即可。就与前面的quiz1呼应了。
quiz3:
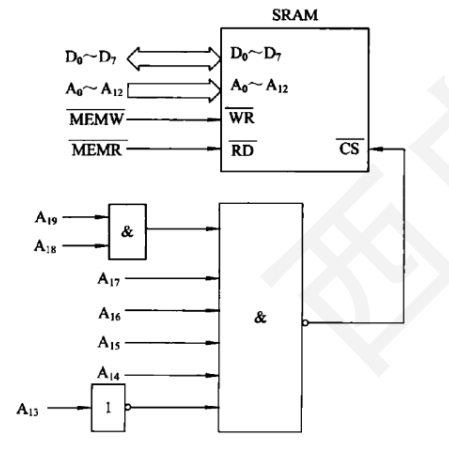
这个Cache和主存的映射关系肯定会考,总的来说,三种不同的映射方式满足下面的关系:
全相联映射:主存物理地址=标记+块内地址
组相联映射:主存物理地址=标记+组号+块内地址
直接映射:主存物理地址=标记+Cache行号+块内地址
在这里写一下我的理解:Cache是把主存的某一块拿过来,存着,为了提速。
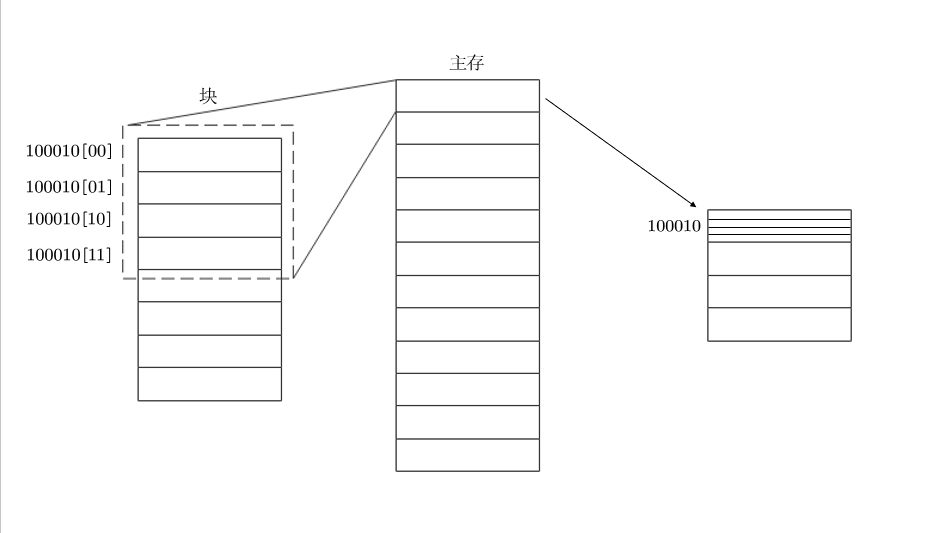
主存是一串二进制数,在这里我们将其分块,例如四个一块,那么一个块中,只会有最后两位不相同。而这四个地址其余部分都相同,所以是一个块,那样把这个块送入Cache后,只需要知道后两个数,就可以取得数据,这后两个数即“块内地址”,前面的那一串块号,就是“标记”,标记唯一指定了一个块。
如果使用直接映射和组相联映射,标记位可以进一步缩短,我们以上面的quiz3为例:
(1)主存1MB,共20位,每块1KB,那么块内地址占10位。四路组相联,即分成了四组,每组2块。那么组号占两位,组内区号占一位。所以标记占20-(10+2+1)=7位。
(2)ABCDEH写成二进制为1010 1011 1100 1101 1110 我们依次读,前7位是区号,即标记。1010101,路号11,组号1,块内地址0011011110。这里关于组号和路号的解释其实是无所谓的,按照书上用的以“路”的概念来解释,组相联时,是分成四路,每路两块(组)。题目中是分成了四个再分两个,可见它是按照路来解释的。这里组号为1,也叫索引(index)。标记tag为1010101连上路号11,为157H.发现它在第三路第一组,命中了,Cache地址为:路号+组号+块内地址1110011011110=
1CDEH,就是从Cache的角度看,索引加原来的块内地址。
我们再看一种经典的找位数分区的题目:
某计算机采用页式虚拟存储管理方式,按字节编址,虚拟地址为32位,物理地址为26位,页大小为4KB,TLB采用全相联映射;Cache数据区大小为64KB,按2路组相联方式组织,主存块大小为64B。
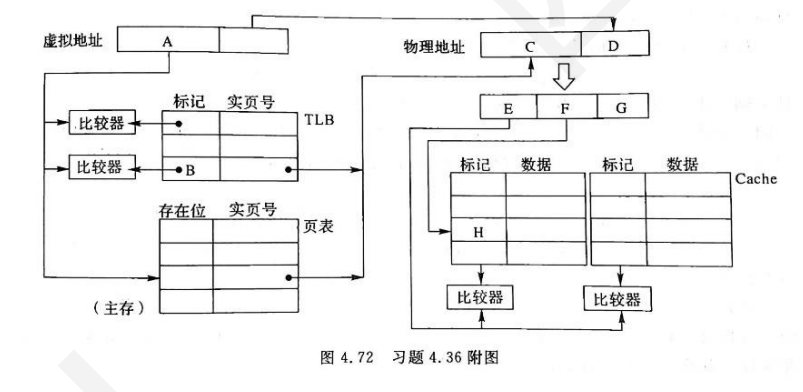
(1)A~G的位数各是多少?TLB标记字段B中存放的是什么信息?
解:
A,B是虚页号,虚拟地址32位,页大小4KB是12位,所以A=B=32-12=20位,D是真实地址中的页内地址,是12位。那么C是26-12=14位。之后考虑主存和Cache,由于是2路组相联,主存块大小为64B,Cache一共64KB大小,那么Cache一共1K块,两路,即512组。所以F(index)是9位,块内地址G是6位(64B),E是26-6-9=11.
quiz4:
根据对PPT和作业的观测,有两种level的设计编码方案的练习题:
①假设某种计算机有14条指令,使用频度由大到小为0.15,0.15,0.14,0.13,0.12,0.11,0.04,0.04,0.03
,0.02,0.02,0.01,0.01。给出定长操作码,霍夫曼编码,只用两种码长的扩展操作码的三种方案。
定长操作码,显然只需4位即可。平均操作码长度也为4。
霍夫曼编码,我们构造霍夫曼树。
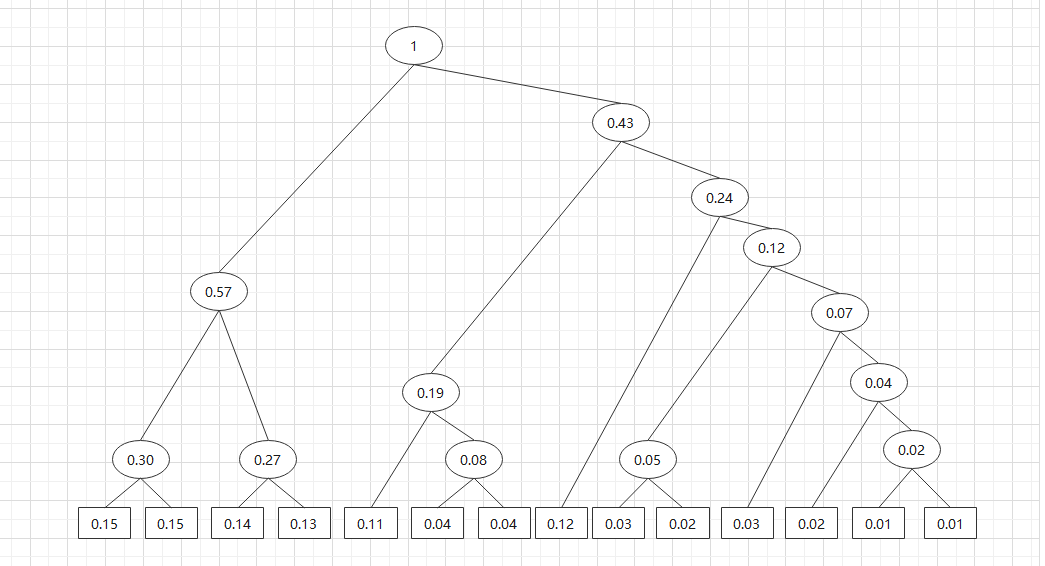
然后求一下平均操作长度:3.38
(这个手算起来好繁琐)
两种码长的扩展操作码,即分成大概率和小概率的,大概率的(大于0.1)有6个,3位就够了。剩下的8个,只能用四位来表示了。
②第二种提法是类似:某指令系统共有200条指令,传送类占5%,使用频度为50%;运算类指令占10%。使用频度为25%;分支跳转类20%,使用频度为15%,其余指令使用频度为10%。用扩展操作码进行编码,给出每类的最短长度及相应编码,并计算平均操作码长度。
这个的道理也是基于,我们让频度高的尽可能短,这样调用时就会更高效。那么50%频度的传送类共有200×5%=10条,我们用0~9(0000~1001)即可表示,四位目前还够用,我们进行+1,在1010后面进行扩展,而剩下的6位不足以表示运算类的20条指令,6*4=24就够了,所以后面补两个00,我们从101000加19,得111011,所以(101000~111011)可以用来表示运算类,同理,此时24个状态里用了20个,加1防止前缀重合,剩余4个状态不够接下来40个的,4×16>40。所以接下来补4位,从111011+”1”=111100补4位,1111000000+”40”到1111100111,最后,64个状态里用掉了40个,还剩24个,24×8才最开始大于130个,所以补3位,编码这里就先略了。
最后计算平均操作码长度为4×50%+6×25%+10×15%+10%×13=6.3位。
quiz5:
寻址方式
一条指令中,地址码的解读方式可能有很多,所以会加入寻址特征,数据寻址的种类如下,其中EA表示effective address。形式地址为A。
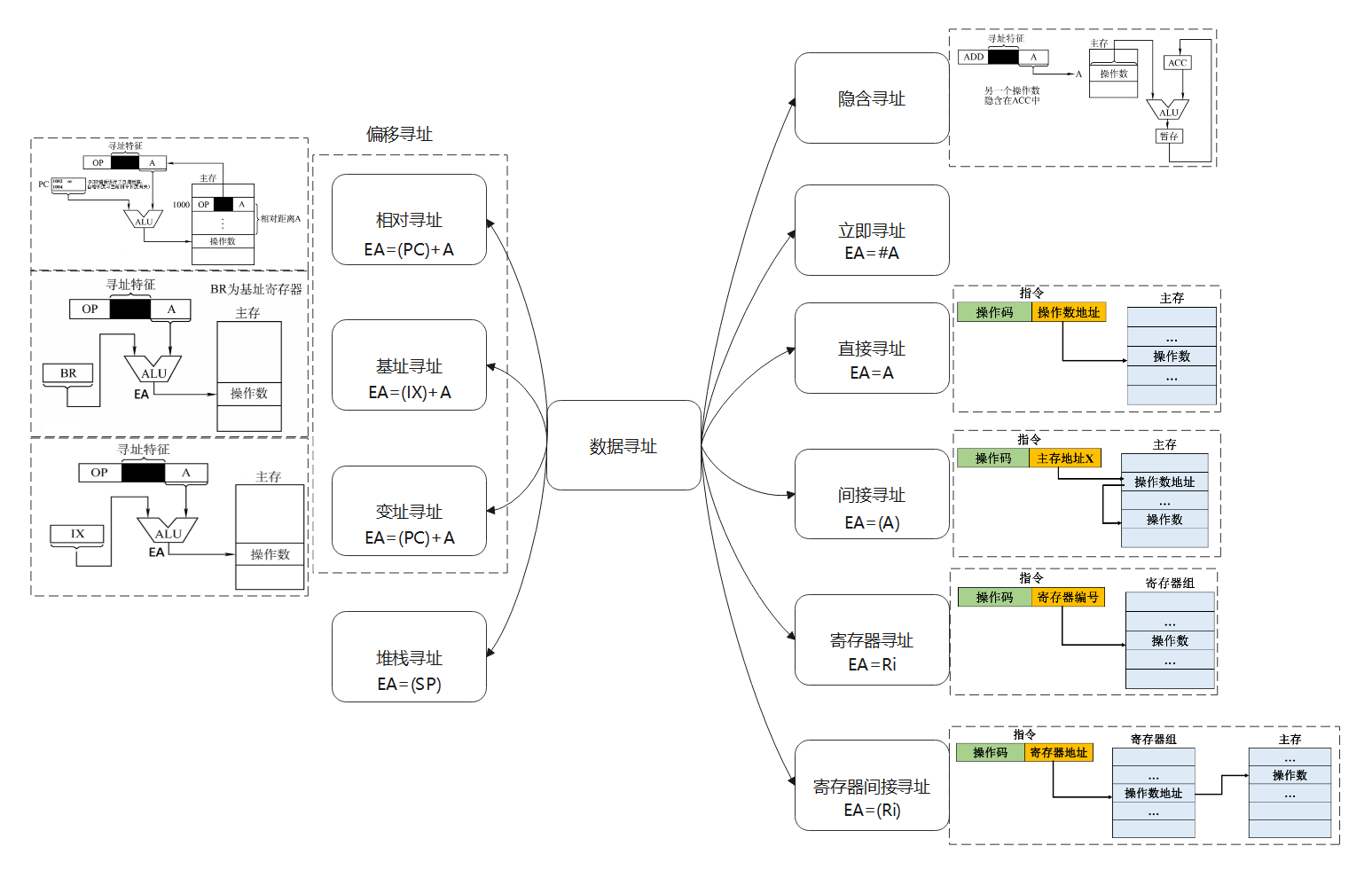
我们会在习题中看见他们的复合,但是只要按照上图捋清楚,都是很直接的。例如:
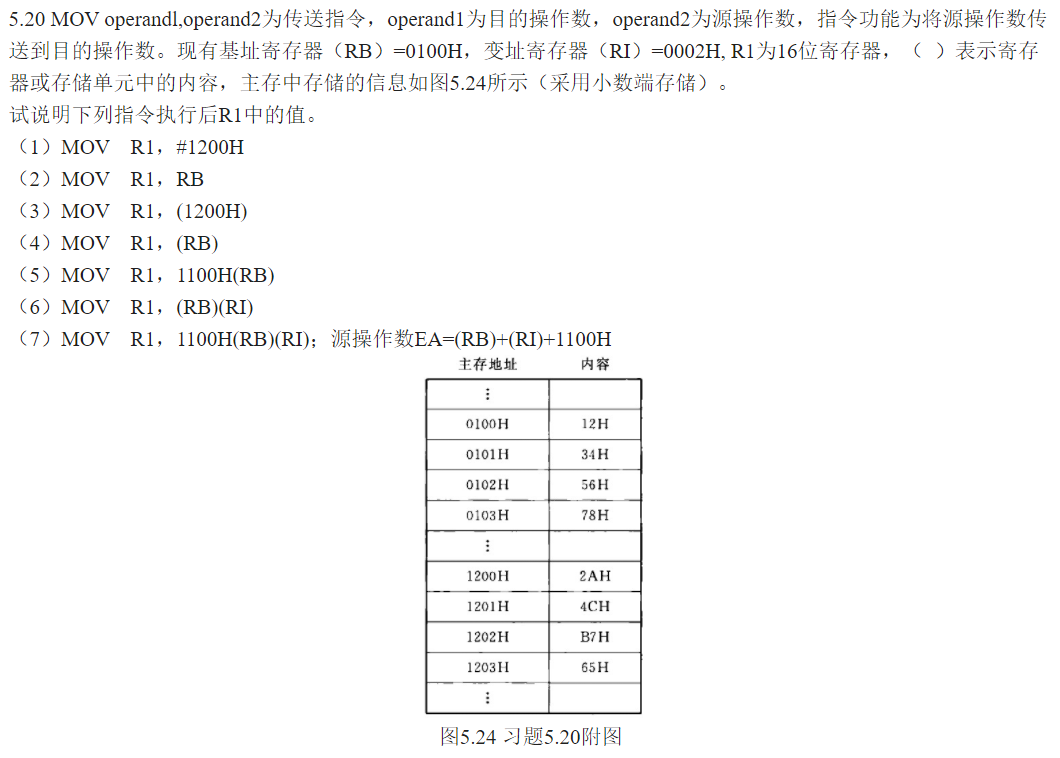
(1)是立即寻址,R1直接等于1200H。(2)是寄存器寻址,R1=0100H。(3)是间接寻址,查表得,注意目标寄存器是16位的数据,采用小端存储,所以4C2AH。(4)是寄存器间接寻址,0100H是12H,0101H是34H,小端存储为3412H。(5)寄存器相对寻址,看到这种表示直接相加即可,1100H与0100H相加,得1200H,是4C2AH。(6)基址变址寻址,看这个意思是两个间接寻址的地址相加,即0100H+0002H=0102H,查表得7856H。(7)EA=0100+0002+1100=1202H,得65B7H。
quiz6:
一些概念性的指标类运算:
CPI(Clock Cycles Per Instruction)
执行一条指令平均需要的时钟周期数:
MIPS(Million Instructions Per Second)
每秒钟CPU能执行的指令总条数:
CPU时间:
$T$为时钟周期,注意CPU的时钟周期单位一般是ns(10的负9次方),转换为时钟频率为GHz。
$Amdahl$定律:
$f_e$是可改进部分的比例,$r_e$是部件加速比。
Cache命中率:
Cache平均访问时间:
磁盘指标:
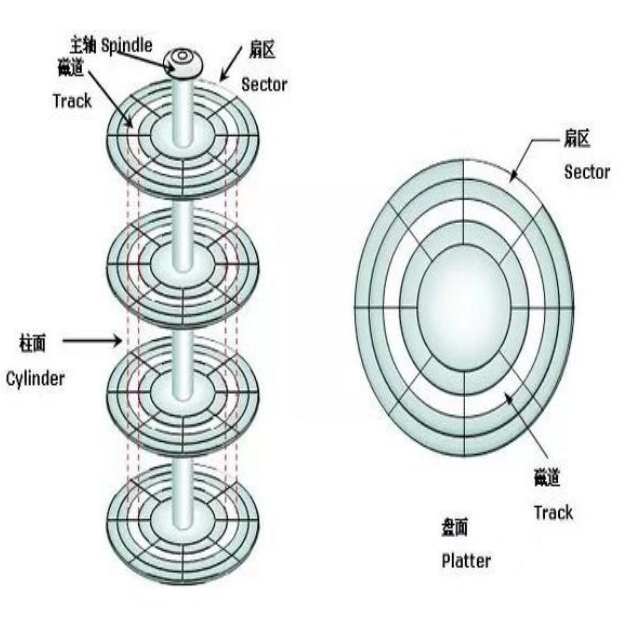
磁头沿盘径向移动,找磁道。磁头不动,盘片旋转,找扇区。最后一个指标是平均访问时间,它分为寻道时间$T_s$,等待时间$T_r$,数据传输时间$T_t$。
$T_s$一般题目给出,$b$是传输的字节数,$N$是一个磁道的字节数。
流水线:
我们假设每个指令的每个阶段都只用一个时钟周期,这样算指标简单。
$n$表示完成了$n$个任务,$m$为流水线段数。
吞吐率:单位时间内流水线完成任务数里,分为实际吞吐率和最大吞吐率:
当各流水线运行时间不等时,
加速比:类比$Amdahl$定律:
效率:占用时空区之比。
quiz7:
第六章考核上给我一种波将金村的感觉,遂记录一下。
某计算机系统简化的CPU结构如下图:
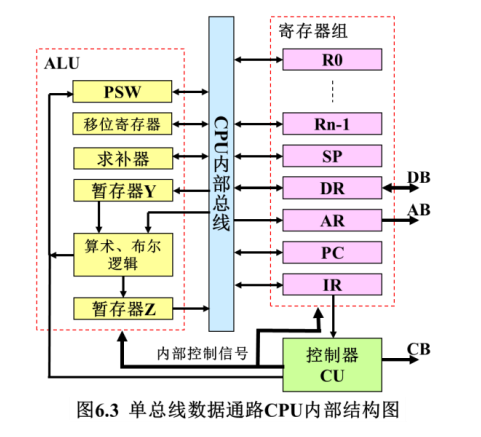
(1)写出ADD R0 R1(功能为$\mathrm{R}_0\gets \left( \mathrm{R}_0 \right) +\left( \mathrm{R}_1 \right) $)的微流程。
(2)写出ADD R0 (R1) 的微流程。
(3)写出ADD R1, B(R2)的微流程。其中B是偏移量。
(4)写出减法指令SUB R1 100(PC)的微流程。
实际上我们可以发现,这一定程度考察了前面的寻址方式。
我们都是先取指令(fetch),在我们这里是直接执行(execute),即二级时序。注意不同寻址方式下的差别。