虽然模电只有两个学分,而且我们院还删减了很多(这很好)。但是就像比如高中学的化学和生物,高考完了就逐渐忘了以及也不会用到。但当时积累的分析方法和思维方式还是有用的。
故事的很大一部分起源于一种新的电子元件的引入:集成运算放大器,一种很好理解的方法就是,把它和电阻,电容一样,想象成一个引入的先验。这是为了方便起见的一个必要的准备,这并不损失什么,就像初三学电阻,老师们只会教欧姆定律,不会教三维拉普拉斯方程。
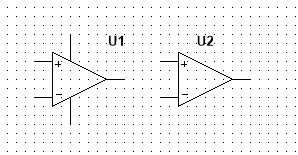
左边上下那两根线代表的是给运放加的电压,运放能输出的最大电压只能是这个数,由于我们正常应用时的都在“放大区”,所以有时也不需要标出加了多大电压。实际上是能量守恒的体现。
这个元器件重要的性质就是“虚短”和“虚断”,实际上就是指正极端口和负极端口电压相同,且两个输入端的电流几乎为零。所以理想情况下,这种器件的输入输出会是一个$k$倍的符号函数,这并不是我们希望的。于是就有了下面两个精巧的设计,在说之前要指明,对于放大器,有三个指标,输入电阻$R_{i}$,输出电阻$R_{o}$,放大倍数$A_{u}$。这些在后面还会遇到。
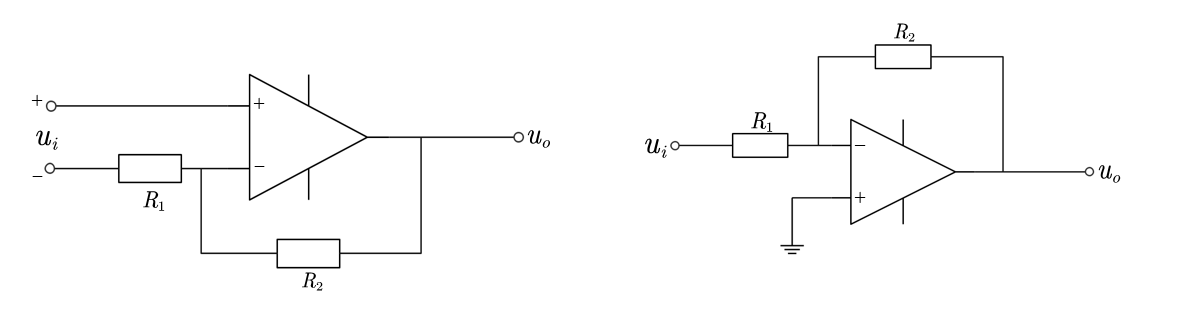
上图展示了同相和反相比例放大器,通过虚短和虚断,我们可以计算出它们的指标:
对于同相比例放大器,+端的电压是$u_i$ ,-端电压根据串联分压规律,为$R1/(R1+R2)$ ,所以由虚短性质,得:
这里的输入电阻和输出电阻是理想运放的性质,稍后再提及如何求解一般情况下的输入电阻和输出电阻。
对于反相比例放大器,道理是一样的:
注意输入电阻,反相时的输入电阻其实是因为虚地点的等效电阻为0,才直接近似成$R_1$了。
下面更有用的内容是利用运放制作相加器,相减器,积分器,微分器。
相加器分为同相和反相,是前面同相放大器和反向放大器的直接应用:
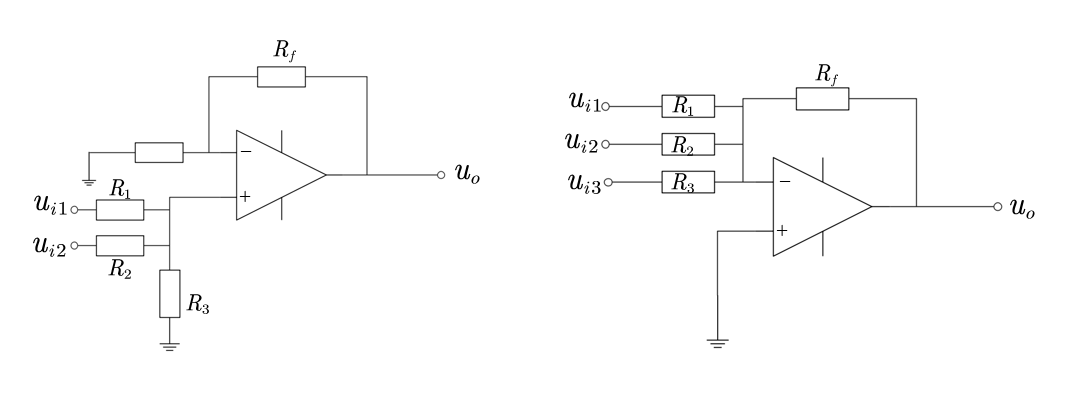
如果你和我一样对这种电位的表示方法没啥直觉的话,你可以像我一样时刻记住把那个小圈和最近的接地点连起来,构造一个闭合回路,这样能增加一点直觉。之后运放的端子看成一个接地,分压与原有的接地相同。我之前一直不知道在这个运算的百慕大三角里到底串联分压是分哪个,这样好多了。
对于这两种加法器,我们通过之前的分析可以知道,这俩一定一个是系数正的,一个是负的。对于同相的:
实际上$R_3$可以被去掉,这样计算也可以得到简化。
反相加法器同相端之前应该加一个直流电阻,直流电阻的值是其余各电阻的并联值。但理想运放的情形下不需要,我们会发现道理是一样的,也是应用叠加性质:
观察这两个相加器,实际上它们的组合就是基本相减器:
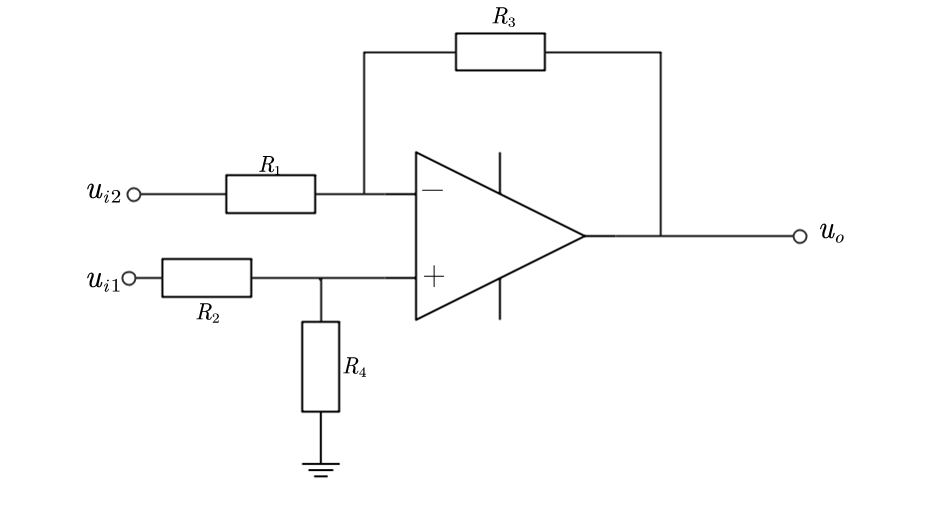
我们容易写出,输出电压为:
这样就实现了相减。那么如果将一些电阻换成电容会发生什么呢?为了简单起见我们考虑电容初始值为0。我们考虑一个反相相加器,如果输入电阻被换成一个电容,那么当$u_i$通直流的时,根据电容通交流阻直流的特性,$u_o$什么都不会采集到。而如果$u_i$发生变化,那么$u_o$将产生相应,这是一个微分器。反之如果将反馈电阻改成电容,会得到一个积分器。
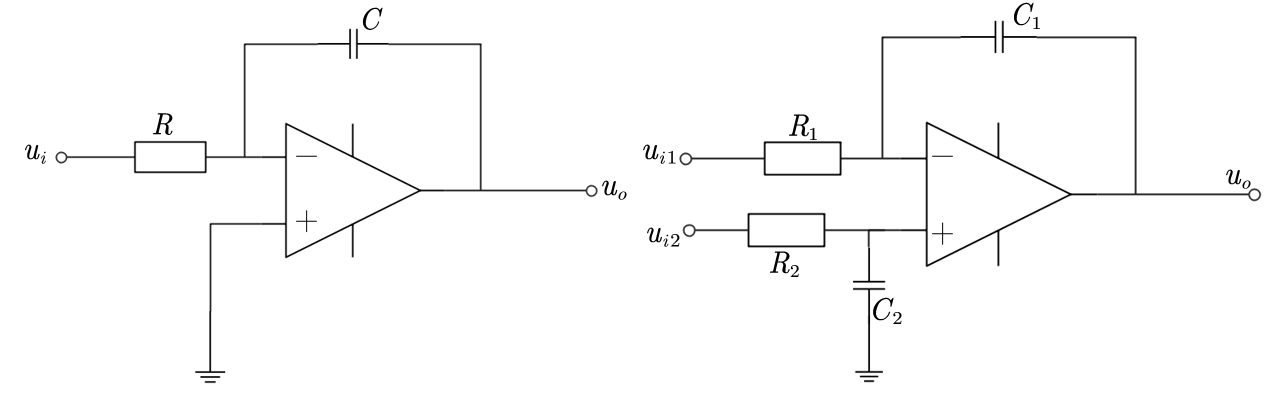
左边是一个经典的积分器,它的输出结果会带一个负号,我们利用虚地点的性质来进行推导:
右边一般情况下,是个正向积分器,这种情况下先置$u_{i1}$为$0$ ,也就是那端接地,那么直接计算:
如果$R_2C_2=R_1C_1$ 上式得以进一步化简,得:
进一步,加上$u_{i1}$ ,那样那一级是一个负向积分器,就有了差动积分器的基本形式:
至于我们考核下的频域函数,就用电路分析里的相量法,把电容写成$1/j\omega C$就好了,其实是一个傅里叶变换。
微分器就是把电容和电阻的位置对换一下,由于用的比较少,这里就不再单独指出了。微分器当遇到高频噪声的跳变,容易饱和,所以应尽可能不用微分器。
通过引入电容,不仅可以实现积分微分运算,还可以进行有源滤波。对于一阶有源$RC$滤波器,道理很简单,也是把电容换成$1/j \omega C$然后计算即可。二阶有源$RC$滤波器以$Sallen-Key$为首。但二阶的情形我们的考核里一般只考判断是低通高通带通还是全通,具体的方法其实很简单,把原输出端接地,去掉管子,看看信号能不能到原定的输入端。
最后用一道作业题练习一下:
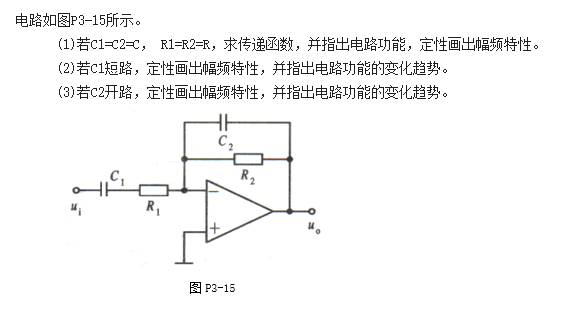
我记得最开始学的时候,当时疫情网课期间,根本没学,看答案看不懂,当时不知道为啥要写成$s$ ,现在知道是拉氏变换了,快速解答的话,观察这个形式是一个类似反相放大器的情形。那么直接写出:
是带通滤波器,如果看不出来的话可以简单算一下幅频特性。如果$C_1$短路,那就只是个低通滤波器。如果$C_2$开路,那就是个高通滤波器。

