拉普拉斯变换2

阅读数: 次 2022-05-30

“请同我，大声唱；唱风霜，唱春光；唱悲伤，唱希望；歌声绕，歌声绕；踏过天高山水长~”

这篇或许可以解答一些按照《信号与线性系统分析》（吴大正第五版）学习拉普拉斯变换时的困惑，在学习$s$域分析时，书上直接讨论单边拉普拉斯变换，这是出于现实考量的，下面为了叙事的完整，我们现在讨论的双边拉普拉斯变换：

$F_b\left( s \right) =\int_{-\infty}^{+\infty}{f\left( t \right) e^{-st}\mathrm{d}t} \\ f\left( t \right) =\frac{1}{2\pi j}\int_{\sigma -j\infty}^{\sigma +j\infty}{F_b\left( s \right) e^{st}\mathrm{d}s}$

这些积分式，它们必须绝对收敛（记住这个直觉），下面我们在这个基础上进行$z$域分析。自然地，我们用梳状函数作采样：

$f_s\left( t \right) =f\left( t \right) \delta _T\left( t \right) =f\left( t \right) \sum_{k=-\infty}^{\infty}{\delta \left( t-kT \right)}=\sum_{k=-\infty}^{\infty}{f\left( kT \right) \delta \left( t-kT \right)}$

同时$\mathcal{L} _b\left[ \delta \left( t-kT \right) \right] =e^{-ksT}$ ，但是这里先停一下，我想用之前一个变换对引发一个问题：

$\sum_{k=0}^{\infty}{\delta \left( t-kT \right)}=\delta \left( t \right) +\delta \left( t-kT \right) +\delta \left( t-2kT \right) .... \\ \delta \left( t \right) \leftrightarrow 1,\delta \left( t-T \right) \leftrightarrow e^{-Ts},...,\delta \left( t-kT \right) \leftrightarrow e^{-kTs} \\ \mathcal{L} \left[ \sum_{k=0}^{\infty}{\delta \left( t-kT \right)} \right] =1+e^{-Ts}+...+e^{-kTs}+...=\frac{1}{1-e^{-Ts}},\mathrm{Re}\left[ s \right] >0$

结合上面这个关于从0时开始的冲击序列的单边变换以及上面那个双边变换，我想让一个现象变得更加清晰：对于下面的三个式子，我们可以认为，我们在求一个阶跃函数被采样后的的单边拉普拉斯变换，此时的收敛域是$\sigma>0$。现在我们把上面的上面那个式子的$f(kT)$换成1，然后分析得到的这个级数：

$\sum_{k=-\infty}^{\infty}{\delta \left( t-kT \right)}=..+\delta \left( t+kT \right) +\delta \left( t \right) +\delta \left( t-kT \right) ....$

然后作双边变换……然后我们？我们得到了一个双向的等比级数，我们发现让它收敛的条件不能同时取得，因为正幂项要求$\sigma>0$ 负幂项要求其小于0。这个结论是正常的，因为我们选取的直流分量本身就不满足绝对可积条件，而用负指数来削减，削弱正半轴时就会放大负半轴。写到这里，我们会发现，如果在一个更一般的条件下，我们需要关注正幂项和负幂项什么时候收敛，以及各种问题。此时在$s$域处理起来就不太方便，所以我们作一个精巧的操作：

$z=e^{sT}$

我们知道，$exp(z)$在复平面上处处解析，因此在整个复平面上是共形的，它会把直线映成圆：

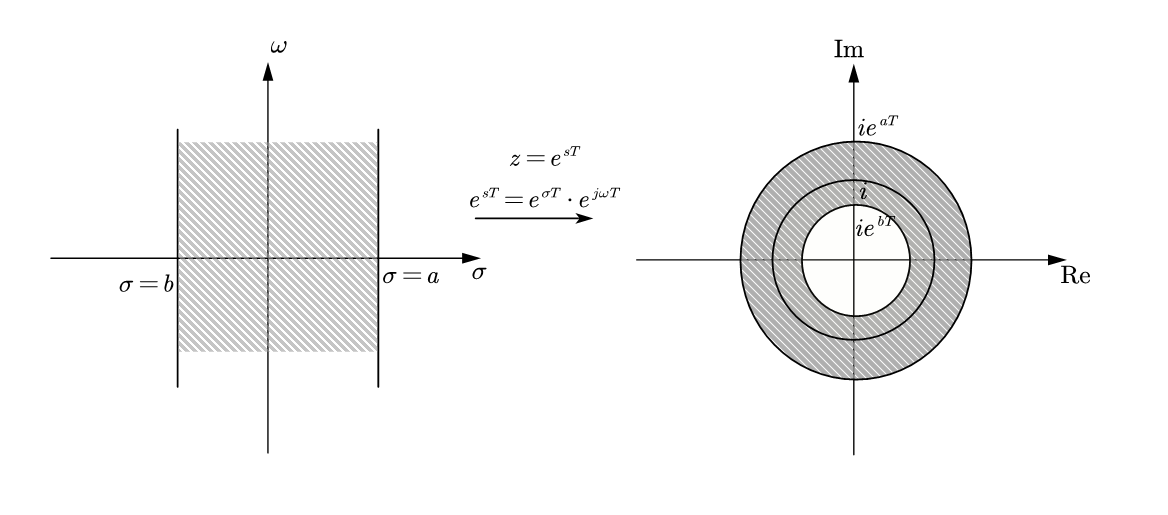
当$Re[s]<0$时，会被映射到单位圆内部。反之映射到单位圆外部，由之前的那篇我们知道，我们往往希望$Re[s]<0$，因为这样说明有的是负指数成分，这个系统会稳定。现在通过这种更直观的表示，我们可以把“在虚轴哪一边”变成“在单位圆里还是外”。

更重要的是，这样换域后，原式就变成了一个复变函数的洛朗级数：

$F\left( z \right) =\sum_{k=-\infty}^{\infty}{f\left( kT \right) z^{-k}}$

这里的$f(kT)$变成了洛朗函数的系数，如果我们能像一些经典的级数展开一样求上面的级数和，那么所有事情都很nice，我们可以得到系统函数以及一些别的什么。或者找这个级数的零点，来作极点分析。

鉴于后面要用到的离散时的性质，考试要考，而且如果不推一遍不会对$z$域上的事情变得敏感。（我这里特别想吐槽，我依稀记得离散傅里叶变换是不讲的，那为什么这里要讲离散时的拉普拉斯变换？考试还考？我反而觉得离散傅里叶变换里的循环卷积，以及蝶形单元工程里更有用。）但是我们先回望一下傅里叶变换：

现在我们知道，离散时的像函数可以写作在原点展开的洛朗级数：

$F\left( z \right) =\sum_{k=-\infty}^{\infty}{c_kz^{-k}},c_k=\frac{1}{2\pi i}\oint_C{\frac{f\left( z \right)}{z^{k+1}}\mathrm{d}z}$

那么我们喜闻乐见的指数形式的傅里叶级数是：

$\varphi \left( \theta \right) =\sum_{k=-\infty}^{+\infty}{c_ke^{ik\theta}},c_k=\frac{1}{2\pi}\int_0^{2\pi}{\varphi \left( \theta \right) e^{-ik\theta}\mathrm{d}\theta}$

实际上……如果取$z=e^{i\theta}$……那么：

$z=e^{i\theta},\mathrm{d}z=ie^{i\theta}\mathrm{d}\theta ,c_k=\frac{1}{2\pi i}\int_0^{2\pi}{\frac{f\left( \theta \right)}{e^{\left( k+1 \right) i\theta}}ie^{i\theta}\mathrm{d}\theta}=\frac{1}{2\pi}\int_0^{2\pi}{f\left( \theta \right) e^{-ik\theta}\mathrm{d}\theta}$

一切都这么自然，并且和谐。傅里叶变换上一篇里只是一个虚轴，它现在变成了一个单位圆。是的捏，直线映成圆。

在这里需要补充一下：如果我们的序列是个因果序列，即右边序列，那么我们会发现，由于此时$z$的幂次是负的，所以收敛域其实是边界圆周外，即$z$“越大”才收敛。如果是反因果序列，则是边界圆周外，而对于一般的双边序列，就是上面的圆环了。也就是说因果序列对应洛朗级数的负幂项，反因果序列对应正幂项。

现在有了这个insight，我们开始推导常用的那些性质：

线性性质我们就不推了。

我们现在来看移位特性，实际上，在连续的积分形式下，当时推那些性质最好的办法还是计算，但是变成级数和了，就很好办了：

$f\left( k \right) \leftrightarrow F\left( z \right) \\ f\left( k\pm m \right) \leftrightarrow z^{\pm m}F\left( z \right)$

这个道理非常朴素，$f(k)$本来和$z$的各幂次方一一对应，原本的$f(k)$变成了$f(k+m)$，那么对应的$z$的各幂次方也要移动，就相当于$f(k)$向左平移$m$单位，$z$也要一次向左平移，只不过平移的是$z$的幂次。所以多乘一个$z^m$。这是双边的情况，也就是$z$的幂从负无穷一直到正无穷。那么如果是单边的，我们一般单边都会保留因果序列那一侧，没什么别的缘由，就是看着欢喜，或者右撇子多。

单边的时候，如果是$f(k-m)$，相当于序列右移，我们需要把序列看成两部分，其中一部分是右移前就在正半轴上的，那么根据上面的逻辑，对于这一部分，我们只需找到之前的像函数$F(z)$，然后乘一个$z^{-m}$ 。还没完，由于右移以后，一些在负半轴上的样点可能会来正半轴上，这样根据线性性质，我们需要把它们加上，$z^{-m}F(z)$的最高次幂是$-m$ （注意我们这里的级数展开和洛朗展开并不完全一样，洛朗展开一般是记作$z^n$ ，而我们是$z^{-k}$ ），所以剩下的那一部分自然是$z^0$对应$f(0-m)$，$z^1$对应$f(1-m)$…一直到$f(m-1-m)z^{m-1}$。根据线性性质，两者相加，所以此时的情形为：

$f\left( k-m \right) \leftrightarrow z^{-m}F\left( z \right) +\sum_{k=0}^{m-1}{f\left( k-m \right) z^{-k}}$

对于$f(k+m)$的情况，道理是一样的，只是我们这次是需要减掉那些进入到负半轴的，由于我们按照左移$z$的幂次后，得到的$z^m F(z)$中会含有一些本不应存在的正幂项，它们的系数分别是原来的$0,1,…,m-1$ 。所以我们需要依次减去这些多出来的正幂项，$f(0)$对应$-0+m$, $f(1)$ 对应$-1+m$ …$f(m-1)$ 对应$-(m-1)+m$ :

$f\left( k+m \right) \leftrightarrow z^mF\left( z \right) -\sum_{k=0}^{m-1}{f\left( k \right) z^{-k+m}}$

之后是尺度变换，这个非常的显然，对$f(k)$乘$a^k$，最后可以吸收进$z^{-k}$次方中：

$a^kf\left( k \right) \leftrightarrow F\left( \frac{z}{a} \right)$

卷积定理的形式也和傅里叶中的完全相同，此处就不交换求和次序来证明了。

$z$域微分，实际上就是对级数逐项求导，每一项求导会拿出来一个$-k$, 再将幂函数求导多出来的$z^{-1}$拿出来，即可：

$kf\left( k \right) \leftrightarrow -z\frac{\mathrm{d}}{\mathrm{d}z}F\left( z \right)$

$z$域积分就稍微有些复杂了，实际上，我觉得，叫它$z$域积分并不明显，就像傅里叶变换里频域里的微分和积分定理一样，不如就叫他（序列除$k+m$）。我并不能解释它的动机，我只能说出一种合乎情理的出发点或方式：

考虑当$f(k)/k$时的变换如何构造，我们先进行列写：

$\frac{f\left( k \right)}{k}\leftrightarrow \sum_{k=-\infty}^{\infty}{\frac{f\left( k \right)}{k}z^{-k}}$

我们希望清除掉分母上的$k$ ，一个可行的办法是积分一下，我们尝试一下，首先我们不能直接拿$F(z)$进行积分，为了让积分出的常数正好与之抵消，我们选取$F(z)/z$ ，我们举其中一个例子看一下：

$f\left( 3 \right) \rightarrow f\left( 3 \right) z^{-3} \\ \frac{f\left( 3 \right)}{3}\rightarrow f\left( 3 \right) \int_z^{\infty}{z^{-4}\mathrm{d}z}=-\left( -\frac{f\left( 3 \right)}{3} \right)$

个人建议不要对这里的敛散性思考太多，会变得不幸，总之按照这样的思路，可以得到：

$\frac{f\left( k \right)}{k}\leftrightarrow \int_z^{\infty}{\frac{F\left( \eta \right)}{\eta}}\mathrm{d}\eta \\ \frac{f\left( k \right)}{k+m}\leftrightarrow z^m\int_z^{\infty}{\frac{F\left( \eta \right)}{\eta ^{m+1}}}\mathrm{d}\eta$

虽然这种变下限积分的写法我觉得很奇怪，但是这里要说明很多时候它确实有效，例如我们求解序列$\frac{1}{k+1}\varepsilon \left( k \right) $ 的$z$变换：

我们首先很容易计算出$\varepsilon \left( k \right) \leftrightarrow \frac{z}{z-1}$ ，那么直接应用积分性质：

$\frac{1}{k+1}\varepsilon \left( k \right) \leftrightarrow z\int_z^{\infty}{\left( \frac{\frac{\eta}{\eta -1}}{\eta ^2} \right) \mathrm{d}\eta}=z\ln \left( \frac{z}{z-1} \right)$

什么？你说不想用积分性质？你了不起！你清高！那么可以这样：

$\varepsilon \left( k \right) =\left( k+1 \right) \frac{1}{k+1}\varepsilon \left( k \right) =\frac{k}{k+1}\varepsilon \left( k \right) +\frac{1}{k+1}\varepsilon \left( k \right) \\ \frac{1}{k+1}\varepsilon \left( k \right) \leftrightarrow F\left( z \right) \\ \frac{k}{k+1}\varepsilon \left( k \right) \leftrightarrow -z\frac{\mathrm{d}}{\mathrm{d}z}F\left( z \right) \\ \therefore -z\frac{\mathrm{d}}{\mathrm{d}z}F\left( z \right) +F\left( z \right) =\frac{z}{z-1}$

先求齐次解，容易看出$F(z)=Cz$ , 之后用常数变易法，$F(z)=C(z)z$ ，带入计算，得：

$C'\left( z \right) =\frac{1}{z}-\frac{1}{z-1} \\ C\left( z \right) =\ln \left( \frac{z}{z-1} \right) +c \\ F\left( z \right) =z\ln \left( \frac{z}{z-1} \right) +cz$

然后我们需要确定常数$c$ ，由初值定理，我们得：

$\underset{z\rightarrow \infty}{\lim}F\left( z \right) =\underset{z\rightarrow \infty}{\lim}\left[ z\ln \left( \frac{z}{z-1} \right) +cz \right] =1$

所以$c=0$ ，所以也算出来了，但这样更加复杂。

还有一个$k$域反转的性质，肯定只在双边情况才有效，把$f(k)$换序后，$z$换序的方法就是$(z)^{-1}$…这个很好理解。

之后和级数里一样，我们有时要研究序列$f(k)$部分和的$z$变换，注意到部分和实际上可以写作$f(k)$与$\varepsilon (k)$的卷积，那么由卷积定理就直接得到了：

$\sum_{i=-\infty}^k{f\left( i \right)}\leftrightarrow \frac{z}{z-1}F\left( z \right)$

注意收敛域的变化，最后是我们之前用的初值定理以及它的伙伴终值定理，为了更好的记忆我们此时最好把$s$域下的初值和终值定理一并写出：

$f\left( 0_+ \right) =\underset{s\rightarrow \infty}{\lim}sF\left( s \right) \\ f\left( \infty \right) =\underset{s\rightarrow 0}{\lim}sF\left( s \right)$

注意，初值定理时$F(s)$是个真分式，这保证极限存在，当然大多时候都是真分式。应用终值定理时，要保证$s=0$在收敛域内。

那么在$z$域中，我们说的初值和终值定理都是适用于因果序列，我们知道，$f(k)$的$z$变换$F(z)$由$z$的非正幂项构成，那么$z$趋于无穷时，只剩下$f(0)$ 这就是初值定理，如果计算的是另外一个$k=M$时的情形，相当于整体左移，由上面的移位可得：

$f\left( 0 \right) =\underset{z\rightarrow \infty}{\lim}F\left( z \right) \\ f\left( m \right) =\underset{z\rightarrow \infty}{\lim}z^mF\left( z \right) -\sum_{k=0}^{m-1}{f\left( k \right) z^{-k+m}}$

终值定理没有那么显然，我们观察：

$F\left( z \right) =f\left( 0 \right) +f\left( 1 \right) z^{-1}+f\left( 2 \right) z^{-2}+...$

我们希望得到$z^{-\infty}$ 时候的系数，这不像初值定理里那么简单，但是我们如果假设$z=1$在收敛域内，错位相减，再用$z=1$替换上式，事情就变得好了起来：

$z^{-1}F\left( z \right) =f\left( 0 \right) z^{-1}+f\left( 1 \right) z^{-2}+f\left( 2 \right) z^{-3}+... \\ \left( 1-z^{-1} \right) F\left( z \right) =f\left( 0 \right) +\left[ f\left( 1 \right) -f\left( 0 \right) \right] z^{-1}+\left[ f\left( 2 \right) -f\left( 1 \right) \right] z^{-2}+... \\ z\rightarrow 1 \\ \underset{z\rightarrow 1}{\lim}\left( 1-z^{-1} \right) F\left( z \right) =f\left( \infty \right)$

通过这个简约的过程，我们会发现，同时要求$f(k)$在无穷处收敛，否则无意义。

“上山岗, 上山岗; 轻轻唱, 轻轻唱; 唱时光, 唱时光; 唱悲伤, 唱悲伤; 不孤单, 不孤单; 因为我们都一样~”