对抗攻击与防御

阅读数: 次 2022-05-28

对抗攻击与防御对于深度学习有重要意义，本文陆续整理自学时的遇到的攻击与防御。

这个领域目前已经扩展到了许多任务中，比如生成，切割等。但我还是先从最简单的分类开始学习。本篇主要记录一些攻击方式，直观地理解就是，对输入样本故意添加一些人无法察觉的细微干扰，导致DNN误判。以及本着认识的角度，先介绍白盒攻击。

《Intriguing properties of neural networks》(2014)是这一领域的开山之作，阅读以后我发现，对抗样本的发现来自于作者对神经网络两个反直觉现象的发现。

①神经网络包含的语义信息是一个空间，而不是一个独立的神经元。

②DNN的输入-输出映射在很大程度上是不连续的。

对于第一点，我当时觉得相当反直觉，我最早接触时所接受的思想一直是：最后一层的节点可以形成一个基，这个基对提取特征非常有用。

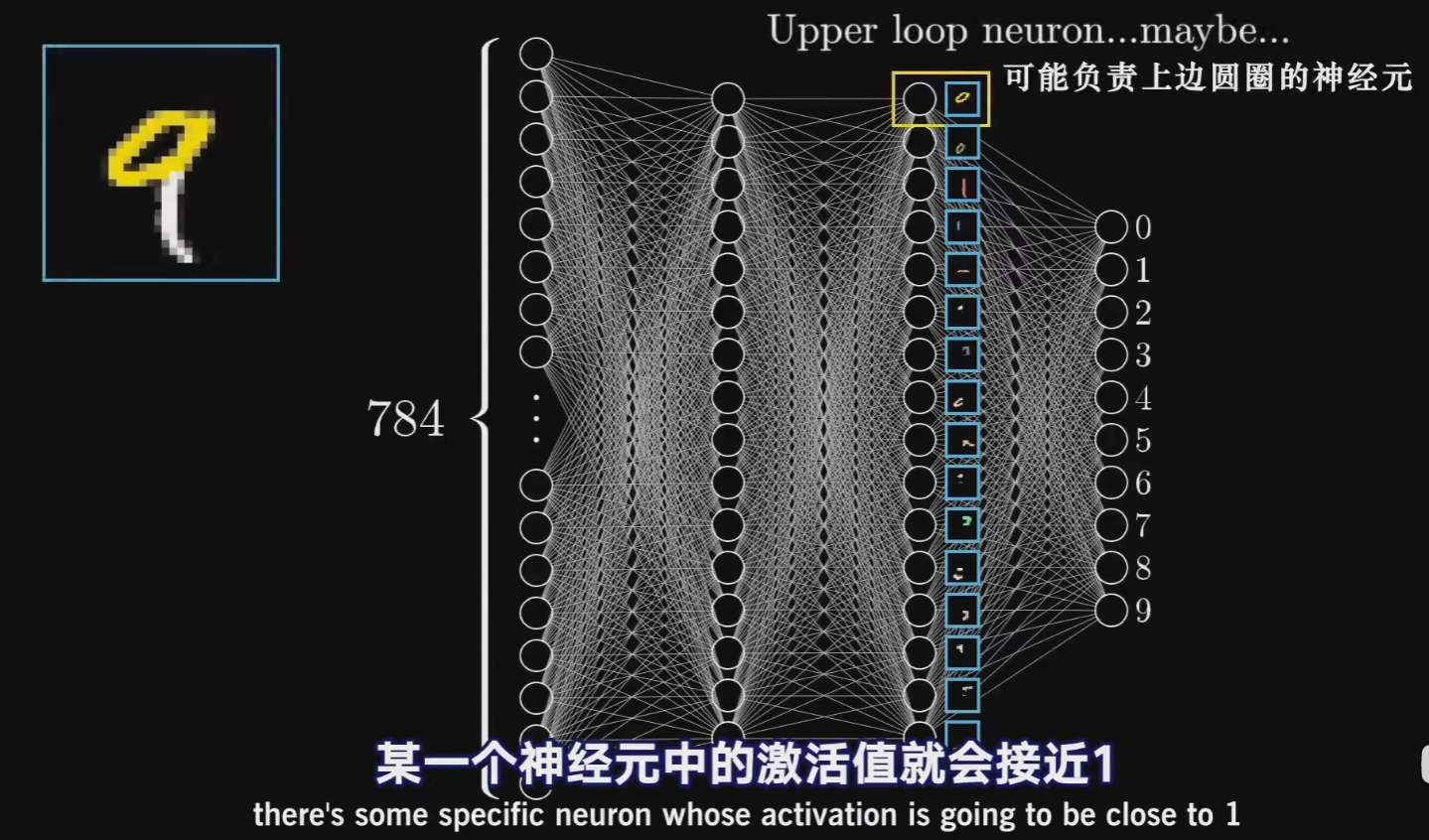
就像3blue1brown视频里解释的一样，最后面的隐藏层包含着某种部件的信息，它们的组合可以得到到底是1，2，3..0中的哪一个。形式上，这种说法指的是：

$x'=\underset{x\in \mathcal{I}}{\mathrm{arg}\max}\left< \phi \left( x \right) ,e_i \right>$

选取一些自然向量基$e_i=(0,1,0,…,0)$ 找出数据集中激活层与其最接近的。那么它们应该代表一个独特的特征，结果发现不同向量最大激活下的样本显示出了相同的语义信息，将自然向量基换成随机向量后，也能找到具有语义信息的图片。这个实践说明，单个结点并不表征语义信息，结点张成的子空间表征了语义信息。

对于第二点，我其实是有一些心理预期的，第二点是对抗样本存在的原因。作者提出了这样的一个有约束的优化问题：

$\min \left\| r \right\| _2\,\,subject\,\,to: \\ \left\{ \begin{array}{c} f\left( x+r \right) =l\\ x+r\in \left[ 0,1 \right] ^m\\ \end{array} \right.$

这里的字母比较形式化，$f$是指将输入映射到离散标签集的分类器$R^m\rightarrow \left\{ 1…k \right\} $ ，标签为$l$ ，$r$即为加的扰动，我们希望加的扰动越小越好，并且$x+r$需要在一定范围内，例如如果是灰度那就是0到1。以及这个任务只有在$f(x) \ne l$时才有意义，即分类出错。这个优化本身是困难的，作者使用有约束的L-BFGS进行近似，将分类器的损失函数引入进来构造罚函数，转化为如下问题：

$\min c\left\| r \right\| _2+loss_f\left( x+r,l \right) \,\, \\ subject\,\,to:x+r\in \left[ 0,1 \right] ^m$

这样可以得到一个近似，这个近似已经可以生成确切的攻击样本了。在这里我想补充一下关于L-BFGS的一些知识，毕竟这是一种很好用的二阶优化方法，解决了牛顿法中海塞矩阵可能不可逆或者计算量大的问题。本质上，我们对一个多元函数$f\left( \boldsymbol{x} \right) $作二阶泰勒展开，忽略高次项：

$f\left( \boldsymbol{x} \right) \approx f\left( \boldsymbol{x}_{k+1} \right) +\nabla f\left( \boldsymbol{x}_{k+1} \right) ^T\left( \boldsymbol{x}-\boldsymbol{x}_{k+1} \right) +\frac{1}{2}\left( \boldsymbol{x}-\boldsymbol{x}_{k+1} \right) ^T\nabla ^2f\left( \boldsymbol{x}_{k+1} \right) \left( \boldsymbol{x}-\boldsymbol{x}_{k+1} \right)$

为了建立当前迭代点$\boldsymbol{x}_k$与$\boldsymbol{x}_{k+1}$的关系，取$\boldsymbol{x}=\boldsymbol{x}_k$ ，两边再取梯度，我们得到：

$\nabla f\left( \boldsymbol{x}_{k+1} \right) -\nabla f\left( \boldsymbol{x}_k \right) \approx \nabla ^2f\left( \boldsymbol{x}_{k+1} \right) \left( \boldsymbol{x}_k-\boldsymbol{x}_{k+1} \right) \\ \boldsymbol{g}_{k+1}-\boldsymbol{g}_k\approx \boldsymbol{H}_{k+1}\left( \boldsymbol{x}_{k+1}-\boldsymbol{x}_k \right)$

令：

$\boldsymbol{s}_k=\boldsymbol{x}_{k+1}-\boldsymbol{x}_k,\boldsymbol{y}_k=\boldsymbol{g}_{k+1}-\boldsymbol{g}_k$

那么就可以简记为：

$\boldsymbol{y}_k\approx \boldsymbol{H}_{k+1}\boldsymbol{s}_k$

由于海塞矩阵以及它的逆矩阵均对称，所以近似的矩阵也应该对称。以及为了运算的速度，通常还要求近似矩阵正定。BFGS方法采用如下算法构造近似矩阵：

$\boldsymbol{B}_{k+1}=\boldsymbol{B}_k+\varDelta \boldsymbol{B}_k \\ \varDelta \boldsymbol{B}_k=\frac{\boldsymbol{y}_k\boldsymbol{y}_{k}^{T}}{\boldsymbol{y}_{k}^{T}\boldsymbol{s}_k}-\frac{\boldsymbol{B}_k\boldsymbol{s}_k\boldsymbol{s}_{k}^{T}\boldsymbol{B}_k}{\boldsymbol{s}_{k}^{T}\boldsymbol{B}_k\boldsymbol{s}_k}$

具体的推导过程等到整理最优化的blog的时候再慢慢写，总之用这种方法可以构造出正定的近似矩阵，剩下的步骤就与常规的牛顿法是一样的了，一维搜索确定步长，迭代，更新矩阵，最后的L-BFGS的核心是为了减少空间消耗，本质是不储存完整的近似矩阵，只储存$\boldsymbol{s}_k,\boldsymbol{y}_k$ 。

这个方法的原理很好理解，但我有的一个问题是：“梯度$g$从哪里来？”，我简单翻阅了一些实现中的源代码，例如scipy中的fmin_l_bfgs_b，好像内部定义了一个“_prepare_scalar_function”类来将输入的”fun”处理成一个标量函数，我对这个表示很诧异，因为本质上，我的输入可以是一个样本$x$，比如MINST中的一张3，然后我优化这个$x$，导致目标函数（上面所说的，其中$r$范数是前后的均方误差，$loss_f$一般是交叉熵）发生变化。而$loss_f$需要经过一个相对复杂的系统（DNN）才能得到，所以我很好奇梯度是怎么来的，比如如果我在做一个最优化课程的作业，让实现这个方法的时候，往往是给出一个有解析的式子，然后梯度可以人工计算出来。那么有时间我一定要研究一下源码的实现。当然，如果用pytorch实现，我们可以调用backward方法然后直接取grad，但别的情况呢？

《Explaining and Harnessing Adversarial Examples》(2015)进一步指出，只要输入维度越大，线性性质足以导致分类器被对抗样本影响，原文给出了很有利的论述：数据例如图像，是存在舍入误差的，如果是8位像素，只要增加的扰动在1/255之内，图像本身其实是不变的，而这样微小的性质，足以导致神经网络分类出错，作者以点积操作举例，论证了这一点，从这个角度出发，FGSM（Fast Gradient Sign Method）被提出，该方法给出增加的扰动只需是：

$\eta =\epsilon \mathrm{sign}\left( \nabla _xJ\left( \theta ,x,y \right) \right)$

$\epsilon $ 用于调整攻击的强度，而 $\nabla _xJ\left( \theta ,x,y \right) $ 是损失函对样本求导得到的梯度值，取 $\mathrm{sign}$ 得到其梯度方向。其思想是简单的：由于是无目标攻击，我们只需要让损失值越来越大即可，在用梯度下降优化时，我们往往是减去学习率乘上梯度，这正好背道而驰，相当于每个被well-trained的参数都被拽了回去，导致损失变大分类效果变差。

《DeepFool: a simple and accurate method to fool deep neural networks》中从决策边界的角度出发，提出了一种可以度量以及精确的攻击方法，我们现在考虑线性分类器，首先先给出点到超平面的距离推导，这在后面会用到：

设点$x_0$在超平面上的正交投影为$x_{0}^{‘}$,记：$\mathcal{F} :f\left( x \right) = w^Tx+b = 0$ 那么$f(x_{0}^{‘})=0$ ，那么我们直接计算即可：

$w \cdot \overrightarrow{x_{0} x_{0}^{\prime}}=w^{1}\left(x_{0}^{\prime}-x_{0}^{1}\right)+w^{2}\left(x_{0}^{\prime 2}-x_{0}^{2}\right)+w^{3}\left(x_{0}^{\prime 3}-x_{0}^{3}\right)+\ldots \\ =\left[w^{1} x_{0}^{1^{\prime}}+w^{2} x_{0}^{2^{\prime}}+w^{3} x_{0}^{3^{\prime}}+\ldots+b-b\right]-\left[w^{1} x_{0}^{1}+w^{2} x_{0}^{2}+w^{3} x_{0}^{3}+\ldots\right] \\=-b-\left[w^{1} x_{0}^{1}+w^{2} x_{0}^{2}+w^{3} x_{0}^{3}+\ldots\right]$

所以点到超平面的距离即为：

$\left\|\overrightarrow{x_{0} x_{0}^{\prime}}\right\|=\frac{\left|f\left(x_{0}\right)\right|}{\|w\|_{2}}, \overrightarrow{x_{0} x_{0}^{\prime}}=\frac{\left|f\left(x_{0}\right)\right|}{\|w\|_{2}} \frac{w}{\|w\|_{2}}$

所以对于简单的线性分类器，是存在最小扰动的解析解的：

$r_*\left( x_0 \right) =\frac{\left| f\left( x_0 \right) \right|}{|w|_{2}^{2}}w$

对于非线性分类器的情况下，就行BFGS里一样，我们往往没有别的方法，只能进行线性近似：

$f\left( \boldsymbol{x} \right) \approx f\left( \boldsymbol{x}_0 \right) +\nabla f\left( \boldsymbol{x}_0 \right) ^T\left( \boldsymbol{x}-\boldsymbol{x}_0 \right)$

这样正交基就成了 $\nabla f\left( \boldsymbol{x}_0 \right) $ ，此时的最小扰动即为：

$r_*\left( x_0 \right) =\frac{\left| f\left( x_0 \right) \right|}{\left\| \nabla f\left( \boldsymbol{x}_0 \right) \right\| _{2}^{2}}\nabla f\left( \boldsymbol{x}_0 \right)$

一次计算后如果不能使得分类器错判，那就再进行线性近似，直到找到（牛顿法）

之后多分类的情况稍微有些复杂，但道理是一样的，只是一些几何上的语言可能不太习惯。多分类时我们记$\mathcal{F} _k$是第$k$类与$x_0$所属类的划分超平面，此时的多分类器记作：

$f\left( x \right) =W^Tx+b$

我们记$x_0$本所属的类为$s$ ，那么此时$x_0$与第$k$个类之间的划分超平面为：

$\left( w_k-w_s \right) x+\left( b_k-b_s \right) =0$

这是由于此时代表$k$与$s$的决策边界为$f_k(x)-f_s(x)=0$ ，展开即得上式，其实就是重合区域的意思。所以最小扰动距离在线性多分类时即记作：

$r_*\left( x_0 \right) =\frac{\left| f_k(x)-f_s(x) \right|}{\left\| w_k-w_s \right\| _{2}^{2}}\left( w_k-w_s \right)$

非线性的时候，道理是一样的，继续线性近似即可：

$r_*\left( x_0 \right) =\frac{\left| f_k(x)-f_s(x) \right|}{\left\| \nabla f_k\left( \boldsymbol{x}_0 \right) -\nabla f_s\left( \boldsymbol{x}_0 \right) \right\| _{2}^{2}}\left( \nabla f_k\left( \boldsymbol{x}_0 \right) -\nabla f_s\left( \boldsymbol{x}_0 \right) \right)$

就先写到这里，最近事情有点多，有空再把相关的API用法和实现方式写上来。