我们即将看到,拉普拉斯变换是傅里叶变换的一种推广,这里有个乐子,有一次我做梦,梦见我是个调和分析大师,然后我就醒了,然后我发现我自己孑然一身P都不会。
如果顺着傅里叶变换来看,拉普拉斯变换是其的扩展。如果一个信号不符合傅里叶变换的条件,那么可以通过强加一个负指数衰减让它符合,这个思路非常直接。(但这里想说一下,如果单从这个角度看,拉普拉斯变换的理论意义远大于实际意义,因为大部分信号都会符合傅里叶变换的,从时频分析的应用来看,拉普拉斯变换并没有很明确的作用,但这不影响它在其他方面的作用。)
既然是强加一个负指数衰减,那么根据衰减的强弱,可以根据原积分是否收敛来划分收敛域。由于遇到的信号都有初始时刻,不妨设初始时刻为坐标的原点。这样就得到了单边拉普拉斯变换,我们下面谈到的拉普拉斯变换就都默认是单边的了,那么正变换和逆变换即:
F(s)=L[f(t)]=∫∞0−f(t)e−stdtf(t)=L−1[F(s)]={0,t<012πj∫σ+j∞σ−j∞F(s)estds,t>0 其中正变换包含0−原因是原函数中可能存在着冲激函数簇,我们先计算三个常见函数的拉普拉斯变换:
F(s)=L[δ(t)]=∫∞0−δ(t)e−stdt=1,Re[s]>−∞ 注意到对于冲激函数来说,收敛域覆盖了整个复平面。
F(s)=L[ε(t)]=∫∞0−ε(t)e−stdt=(−e−sts)|∞0=limt→∞(−e−sts)+1s=1s,Re[s]>0 由于负指数衰减的性质,此时的收敛域是Re[s]>0 。
最后是常见的指数函数:
F(s)=L[e−s0t]=∫∞0−e−(s0+s)tdt=(−e−(s0+s)ts0+s)|∞0=limt→∞(−e−(s0+s)ts0+s)+1s0+s=1s0+s,Re[s]>Re[−s0] 注意此时的收敛于发生了变化,以及在简单的推导中,我们可以看出,收敛域真正关心的是实部,当s0=0时,上式退化为刚才的阶跃函数。我们稍后会解释这里的insight。值得指出的是,由欧拉公式,正弦函数和余弦函数的拉普拉斯变换也可得:
F(s)=L[cosω0t]=∫∞0−cosω0te−stdt=cosω0t(−e−sts)|∞0−ω0s∫∞0−sinω0te−stdt=1s−ω0s∫∞0−sinω0te−stdt∫∞0−sinω0te−stdt=sinω0t(−e−sts)|∞0+ω0s∫∞0−cosω0te−stdt=ω0s∫∞0−cosω0te−stdtI=1s−(ω0s)2I→I=ss2+ω20,Re[s]>0 注意到两者之间的关系,正弦函数的拉普拉斯变换即得:
F(s)=L[sinω0t]=ω0s∫∞0−cosω0te−stdt=ω0s2+ω20,Re[s]>0 确实,当然可以用欧拉公式展开,然后应用指数函数的拉普拉斯变换得到正余弦函数的变换对,只是想复习一下分部积分。
拉普拉斯变换作为和傅里叶变换形式类似的积分变换,也有相应的性质,大多的证明大同小异,我们这里先略去这些琐碎的点,突出一下拉普拉斯变换的重点。
许多时候,像函数F(s)会是一个实系数有理真分式,将其利用留数定理进行分解将有利于作拉普拉斯逆变换:
F(s)=B(s)A(s)A(s)=(s−s1)p(s−s2)...(s−sn)F(s)=K1,p(s−s1)p+K1,p−1(s−s1)p−1+...+K1,1(s−s1)+K2(s−s2)+...Kn(s−sn) 那么系数Ki,j的求法即为:
Ki,j=1(p−j)!dp−jdsp−j{(s−si)pB(s)A(s)}|s=si,j=1,2,3,...,p. (呜呜呜当时没好好学复变函数)
我们找一个例子试一下:
F(s)=s+3(s+1)3(s+2)K1,1=12!(1+1s+2)(2)|s=−1=1K1,2=(1+1s+2)(1)|s=−1=−1K1,3=(1+1s+2)|s=−1=2K2=(s+3(s+1)3)|s=−2=−1F(s)=2(s+1)3−1(s+1)2+1s+1−1s+2 分解之后就可以很容易的用上面推得的正变换得到原函数f(t)
f(t)=[(t2−t+1)e−t−e−2t]ε(t) 实际上可能由于基础的不扎实,会有疑问,为什么我按照算留数的那个式子,可以得到……系数,并且针对多级极点的情况下,为什么是这么排列的?实际上道理非常简单:
f(z)=P(z)(z−a1)(z−a2)...(z−an)(z−b)m=A1z−a1+A2z−a2+...+Anz−an+B1z−b+B2(z−b)2+...+Bm(z−b)m=A1(z−a1)−1+.... 留数的一个定义就是洛朗展开的-1次项,那么对于Ak,很显然就可以这么计算留数来得到系数:
Ak=Res[f(ak)]=limz→ak(z−ak)f(z) 对于B1也是一样的,那么对于Bk呢?实际上对f(z)乘以(z−b)k−1就可以看出来了,理解了这个就很好记忆K1,1,K1,2,K1,3到底对应哪个因式的系数了。
还记得正弦余弦的拉普拉斯变换吗?它们的像函数里会带来复数的根,将两个事情联合在一起看,我们就会发现:拉普拉斯变换的极点告诉了我们该信号所含的频率成分以及指数成分。实部为0的那条线就是傅里叶变换。
但是回忆傅里叶分析时,积分下限是从负无穷开始的,有些时候这样是正好的,比如无边界的扩散问题。有些时候这样是不合适的,例如要考虑0时刻初始值时,而单边拉普拉斯变换恰好满足了这一条件,又有微分性质和积分性质,使得我们可以把线性动力学的问题转化为代数问题:
u(t)=Ldi(t)dt↔U(s)=sLI(s)−LiL(0−)i(t)=Cdu(t)dt↔I(s)=sCU(s)−CuC(0−)↔U(s)=1sCI(s)+uC(0−)s 我们通过时域微分性质,就得到了在s域电容和电感的表达,现在我们将这个技术应用一下,在我们所学的青春版模电的第三章讲过一些无源滤波器,我们现在着手计算一个Butterworth三阶低通滤波器:已知L=1H,C=2F,R=1Ω ,求系统的H(s)=U2(s)/U1(s) 。
进行拉普拉斯变换后,初始状态均为0。由s域下的戴维南定理,开路电压和等效阻抗可以很方便的列写:
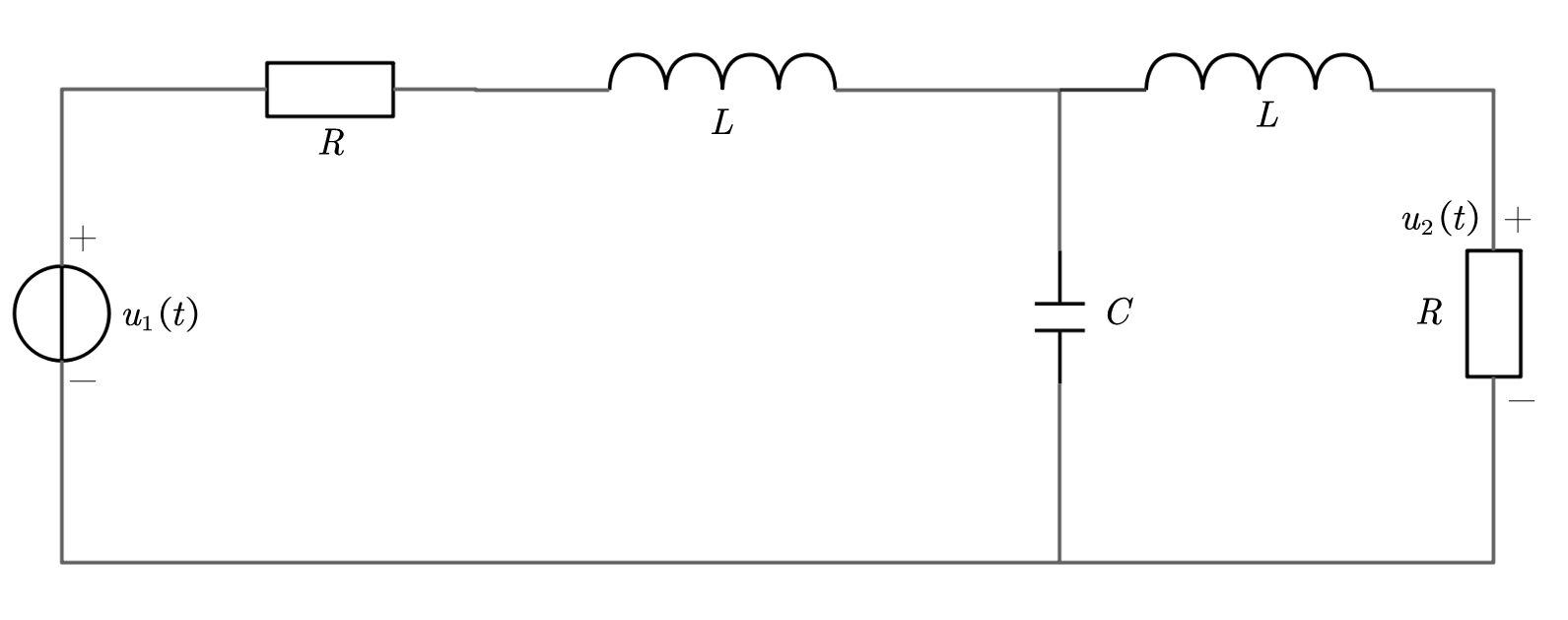
UOC(s)=1sCsL+R+1sCU1(s)=12s2+2s+1U1(s)Z0(s)=sL+(sL+R)1sCsL+R+1sC=2s3+2s2+2s+12s2+2s+1U2(s)=RZ0(s)+RUOC(s)=12(s3+2s2+2s+1)U1(s)H(s)=U2(s)U1(s)=12(s3+2s2+2s+1) 如果把s换成jω ,那么就是之前电路分析里学的相量法,只不过写在s域对于更复杂的问题有更好的效果,我们取s为纯实数,作出H(s)我们会发现一些有用的事实:
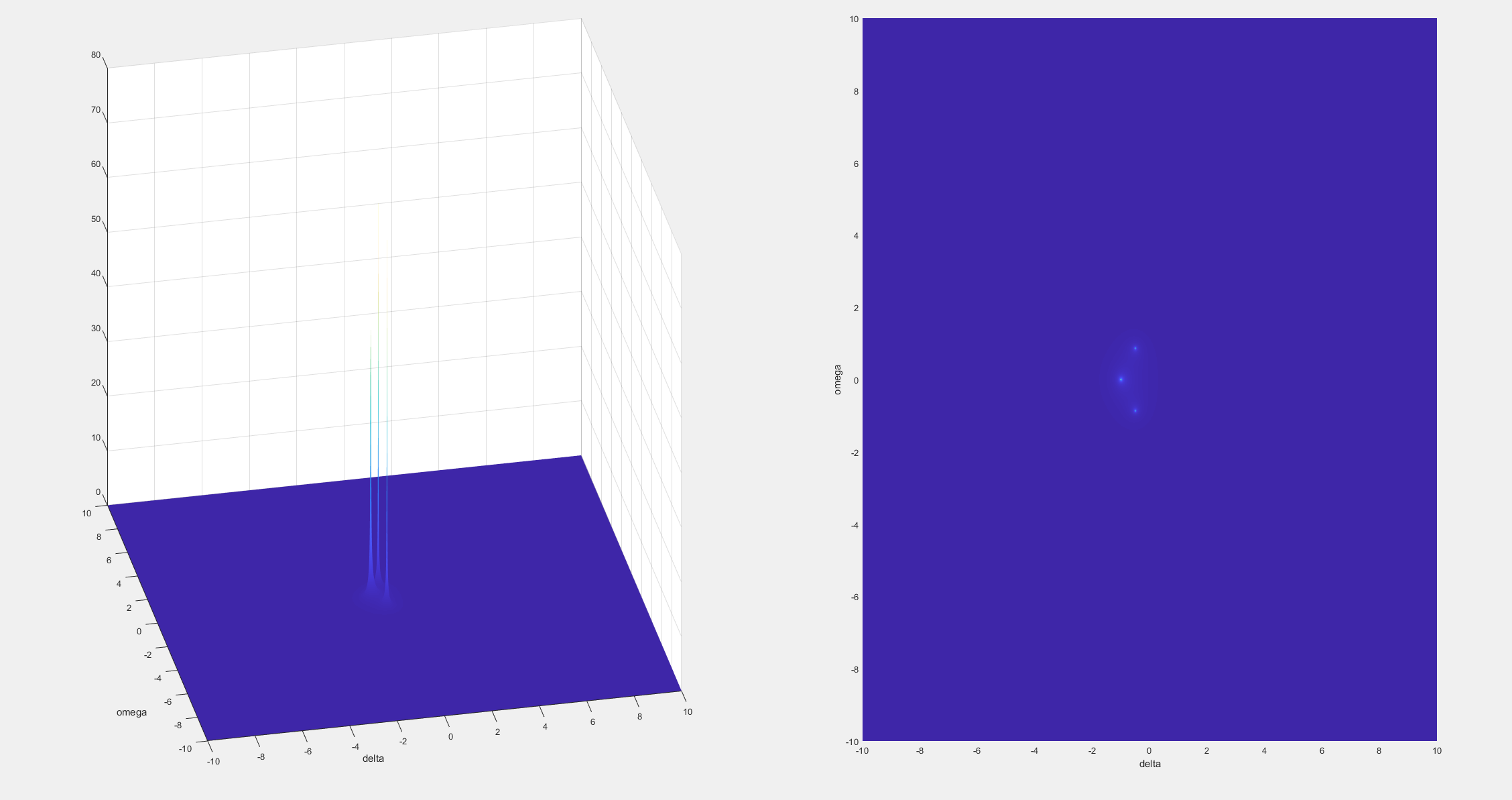
左边三维曲面的高度代表Hs的幅度,其中一个坐标轴代表实部另一个代表虚部。根据上面的叙述我们知道其实实部就是σ (我坐标轴写成delta了)虚部就是频率ω 。左侧图非常直观的告诉我们,其实除了极点处以外,s域的其他区域大部分都是平凡的。以及通过分析极点的位置,在不进行复杂计算的前提下,我们即可知道原函数含有的一定信息。而模电教材里的滤波器曲线是怎么来的呢?实际上只需要取实部为0,观察那个切片即可(正是傅里叶变换):
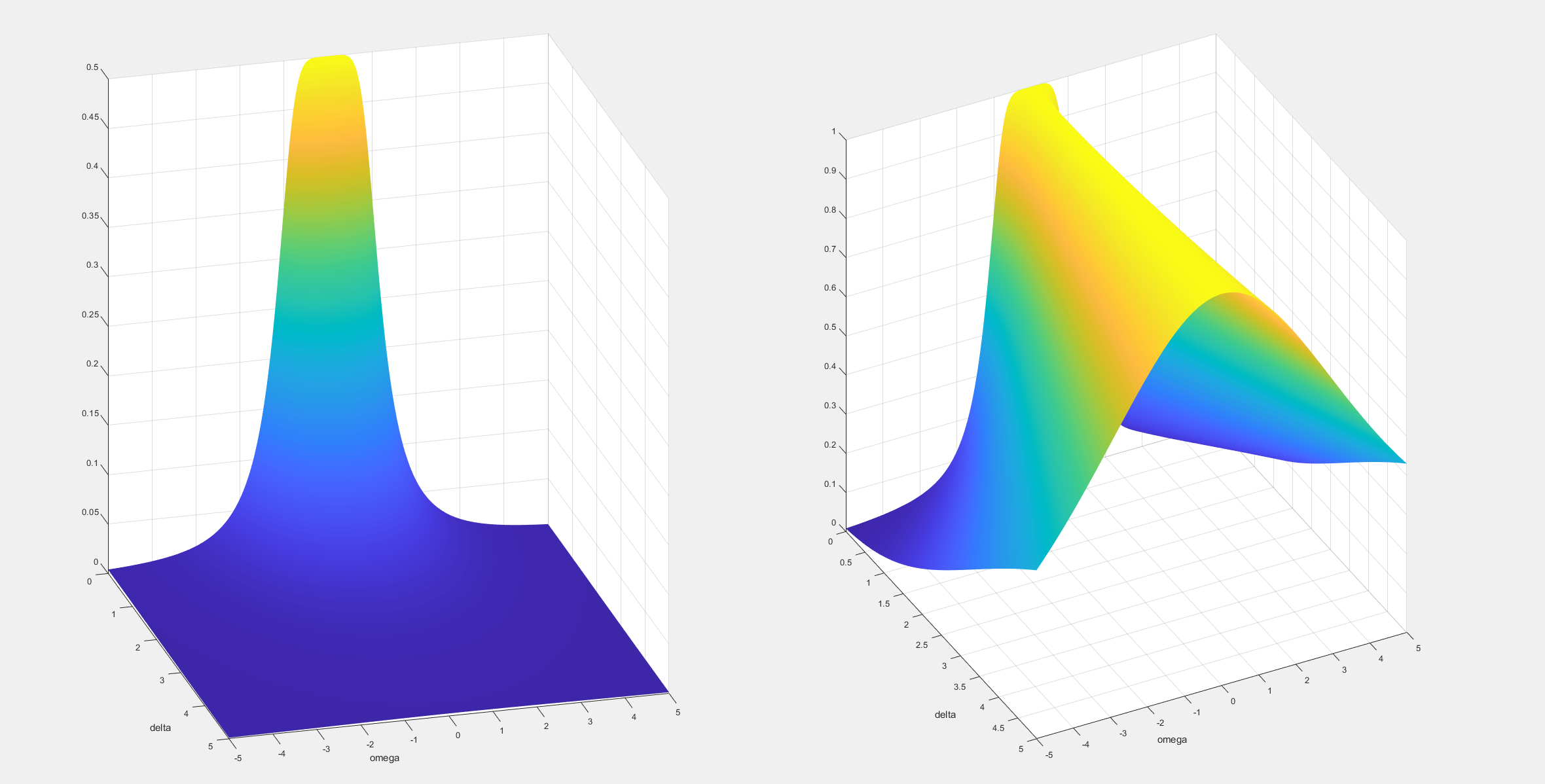
现在再去看模电第三章就不会一眼发懵了,因为那些曲线其实就是特定系统的频率响应,而书上非要分析的传递函数其实就是系统的拉普拉斯变换,包括为什么模电书会对极点念念不忘,现在都有了答案。
下面再引入一个高中历史遗留的问题,来加深印象:质量为m的物体竖直挂在劲度系数为k的弹簧上,零时刻静止,当受外力f(t)自x=0处开始向下运动,求运动规律x(t) 。
如果我在高中,那我肯定是不会的,我只知道它是简谐运动。后来大一了,叶峰教我微分方程,我知道了,它可以解出来,然而我只能解一些特定“激励”下,比如重力等等。再后来,我知道了数值分析,我根本不用管那些,直接龙格库达求数值解就好了,反正不是刚性的。现在,又有了新的办法:
md2xdt2+kx(t)=f(t),x(0)=0,x′(0)=0X(s)=L[x(t)],F(s)=L[f(t)]ms2X(s)+kX(s)=F(s)→X(s)=1ms2+kF(s) 下面这一步可能需要一些insight,不过还好,看不出来关系不大,我们只是体验一下拉普拉斯变换在处理微分方程时的威力,记ω0=√km ,之后得:
X(s)=1mω0ω0s2+ω20F(s)sinω0t↔ω0s2+ω20 由时域卷积定理得:
x(t)=L−1[X(s)]=1mω0[sinω0t∗f(t)] 看,如果f(t)=K是个常数,比如mg ,那样根据卷积的运算性质:
∫+∞−∞sinω0τ⋅mg⋅ε(t−τ)dτ=mg∫t0sinω0τdτ=mgω0(1−cosω0t)x(t)=gω20(1−cosω0t) 如果用时域上的特征根法解决,有一对共轭复根,我们直接计算:
yg=C1cosω0t+C2sinω0typ=mgk=gω20{C1+gω20=0ω0C2=0→{C1=−gω20C2=0y=yg+yp=gω20(1−cosω0t) 看,结果是一样的。如果f(t)=Aδ(t)这种情形,那么卷积的性质会带来更大的便利。
如果是别的复杂的情形,也是可以计算的。
当然我还没有整理一些偏向应试内容,比如那些性质和s域分析,再说吧。
2022-6-12,现在整理一下常用的拉普拉斯变换性质(单边),这些性质对理解变换本身和期末考试都很重要。

我们一条条来过,有些和傅里叶变换时特别相似的就不推了,(1)是定义式,(2)是线性性质,(3)是尺缩性质,值得注意的是,这里的a已经要求大于0了,在傅里叶变换中开出来的常数是a的绝对值分之一,(4),(5)和傅里叶变换中的线性性质完全一致,(6)和载频性质完全一致,注意符号是相反的。
之后的(7)(8)(9)(10)是拉普拉斯变换下的时域积分和微分性质,这里就与傅里叶变换有点不大一样了,因为傅里叶变换直接从负无穷积到正无穷,而单边拉普拉斯变换不是,我们直接计算:
L[f(1)(t)]=∫∞0−df(t)dte−stdt=e−stf(t)|∞0−+s∫∞0−f(t)e−stdt=limt→∞e−stf(t)−f(0−)+sF(s)=sF(s)−f(0−) 虽然没有严格证明,但是可以知道,这里的微分特性也要求信号无直流分量,将上式往高阶导数上推广,即可得(8)。当信号是因果信号时,其在0−的值和各阶导数值都为0,表达式会简洁许多。
对于(9)(10)这里需要更细致的解释,和傅里叶变换不同的是,我们这里要讨论积分下限为负无穷和0−的两种情况。和之前一样,我们将下限从负无穷开始,记为f(−n)(t) ,而从0开始的单独写出:
L[∫t0−f(x)dx]=∫∞0−[∫t0−f(x)dx]e−stdt=−e−sts∫t0−f(x)dx|∞0−+1s∫∞0−f(t)e−stdt=−1slimt→∞e−st∫t0−f(x)dx+1s∫0−0−f(x)dx+F(s)s=F(s)s 当信号是因果信号时,负无穷的时候也会简单一些,此处就略去了。最后两项是s域下的微分和积分,他们有时会用到,但不如z变换里的对应版本,证明也很简单:
F(s)=∫∞0f(t)e−stdtdF(s)ds=dds∫∞0f(t)e−stdt=L[(−t)f(t)] 在傅里叶变换时,由于s变为了jω,所以并不会“突出”那个负号,它会被j吸收进分母。
积分时的情况,又是一波极意玄学强行交换积分次序:
∫∞sF(η)dη=∫∞s[∫∞0f(t)e−ηtdt]dη=∫∞0f(t)[∫∞0e−ηtdη]dt=∫∞0f(t)te−stdt=L[f(t)t] 这些与z域里的z域微分,序列乘k。z域积分,序列除k交相辉映。


v1.5.2