最近有亿点忙以至于没时间写blog自娱自乐,但最近一次的信号大作业是如此的有趣以至于我还是想整理一下。
实际上这次的信号大作业跟信号与系统本身并没有太大的关系,意在盲源分离。处理这种问题有一种方法:独立成分分析(ICA)。最开始做这个作业,是想直接复刻Andrew Ng布置的作业,但是后来一看这种朴素的机器学习方法,还是比搭积木炼丹要更亦可赛艇一点,遂记录。
(前排提醒,实际上大作业里使用的基于负熵的独立成分分析已经是好多年前的理论和成果了(当时的人真聪明),以现在很多的refer来看或多或少都不太严谨,但就像教高中生,逻辑自洽即可。要现在的我一口气赶上前人的智慧,也不现实。)
独立成分分析是希望分开的成分尽可能的“独立”,也就是统计意义上的独立。
首先要明确一个定理:Darmois-Skitovitch定理,假设$S_1,S_2,…,S_n$是相互独立的声源,对于两个随机变量$X,Y$:
如果$X,Y$独立,那么一定对于任意的$\alpha_i\beta_i \ne 0$,且$S_i$一定是高斯分布。
换句话说,如果$S_i$不是高斯分布,那如果$X,Y$独立,则$\alpha_i\beta_i = 0$。这一点是我们得以分离的基础。这个定理的证明比较复杂,就不管了。总之我们应用ICA时,信号一定要是非高斯的。当然,各个信号本身也要是独立的,这是一个很基本的假设。
基于上面的定理,我们考虑一种特殊的情形:
由线性代数知,我们可以找一个旋转矩阵$W$,使得旋转后的$X,Y$独立,而又因为$DS$定理,旋转后的$\alpha_i\beta_i =0$,因为我们假设信号$S$是非高斯的,而$\alpha,\beta$不可能全为0,否则有一个信号就成0了。所以只会有两种可能:
于是我们就找到了分离,就像个奇迹,唯一的缺点就是分离后顺序和幅度不能保证而已,但这问题不大。
所以我们现在找到矩阵$W$就好啦,但是怎么找是个问题。注意到,当我们完成分离后,$X’,Y’$就变成了$S_1,S_2$的常数倍,它们的分布是非高斯的,而在此之前分布都是$S_1,S_2$的线性组合。中心极限定理告诉我们,即使是非高斯的分布,只要组合的够多,也会服从正态分布,那么越组合高斯性肯定越强。(严格来说,我们这里只是为了下面的负熵给出了一个直观的解释,它其实并不能成为一个严谨的论断,但对于我现在的水平,知道到这里就够了。)
而我们知道,所有同一方差下的概率分布中,高斯分布的熵最大,以及,高斯分布是唯一一个满足旋转不变性的分布(结合这个想想前面的$W$就能知道我们为什么要让信号$S_i$是非高斯的了)。所以我们可以利用熵来度量分布的非高斯性。
但是这并不容易,我们先补充一些熵的必要知识:
离散的熵被定义为:
将其连续泛化,得到微分熵的定义:
所以负熵就定义为了:
其中$y_G$是一个与$y$同方差的高斯分布,这是最大熵告诉我们的。
但在ICA计算时,这个理论式子是无法使用的,为此前人提出了各种有效的近似算法,其中一个是:
这个近似非常的不显然,可以参见Hyvärinen当时的论文。其中$G$是一个被选取的非二次函数,$v$是一个零均值单位方差的高斯分布。这里的细节就不好展开讲了。
那么有了上述的铺垫,我们梳理一下我们要做的,原信号记为$X$,混合后的为$Y$,待求的旋转矩阵为$W$,$Y=W^TX$。那么我们要做的其实就是按照$Y$的分量逐个优化,优化函数就是$J(y)$,其中$y=w^Tx$。
那么如何具体的优化呢?我们进一步分析,注意到我们的$x$在优化时是不变的,下面我写的标准一点:
注意,这并不是一个无约束的优化,实际上:
注意,在我们作ICA之前$x$应该已经经过了预处理,那么:
这个是预处理的直接结果,实际上这种预处理叫作白化(球化)。我们后面再提及它。
注意到$J(\mathrm{w})$是引入高斯信号$v$来进行非高斯型的对比,所以$J(\mathrm{w})$的极值和$E\left\{ G\left( w^T x \right) \right\} $的极值在同一处取到,因此由KKT条件,在$E\left[ \left( \mathbf{w}^T\mathbf{x} \right) ^2 \right]=1$的情况下:
其中$\mathbf{w}_{0}^{T}$是最优的$\mathbf{w}$,那么这个搜索根的问题可以用牛顿法来解决,记:
其雅可比矩阵为:
为了简化牛顿法求逆阵时的步骤,注意到此时的$\mathbf{x}$已经是球化后的结果,那么很自然:
所以迭代公式就成了:
每次计算一iter后,$\mathbf{w}$都会归一化一次,于是乎分母并不需要进去计算,所以总的迭代是:
除了基于负熵的独立成分分析法,实际上这个办法相对粗糙,还有基于峭度和极大似然估计的方法,这里先不展开了,有空填坑。但还是很惊讶于依托一个定理和重要的近似,即可有很简短的操作实现如此复杂的功能。下面我们介绍一下之前说的预处理—白化环节:
我们注意到在上面的推导里:$E\left( \mathbf{xx}^T \right) =I$这个结果非常好用,实际上白化就是起到了这样的作用,白化和另一个熟悉的方法—主成分分析法(PCA),其实是一回事。
首先我们对每一个属性字段的数据作零均值化,这是必须的。主成分分析最后希望得到的组分尽可能的“不相关”。实际上就是对协方差矩阵作特征值分解。分解后我们即有了上述所需的性质,即各行向量不相关。这里的详细推导以后有空再整理……
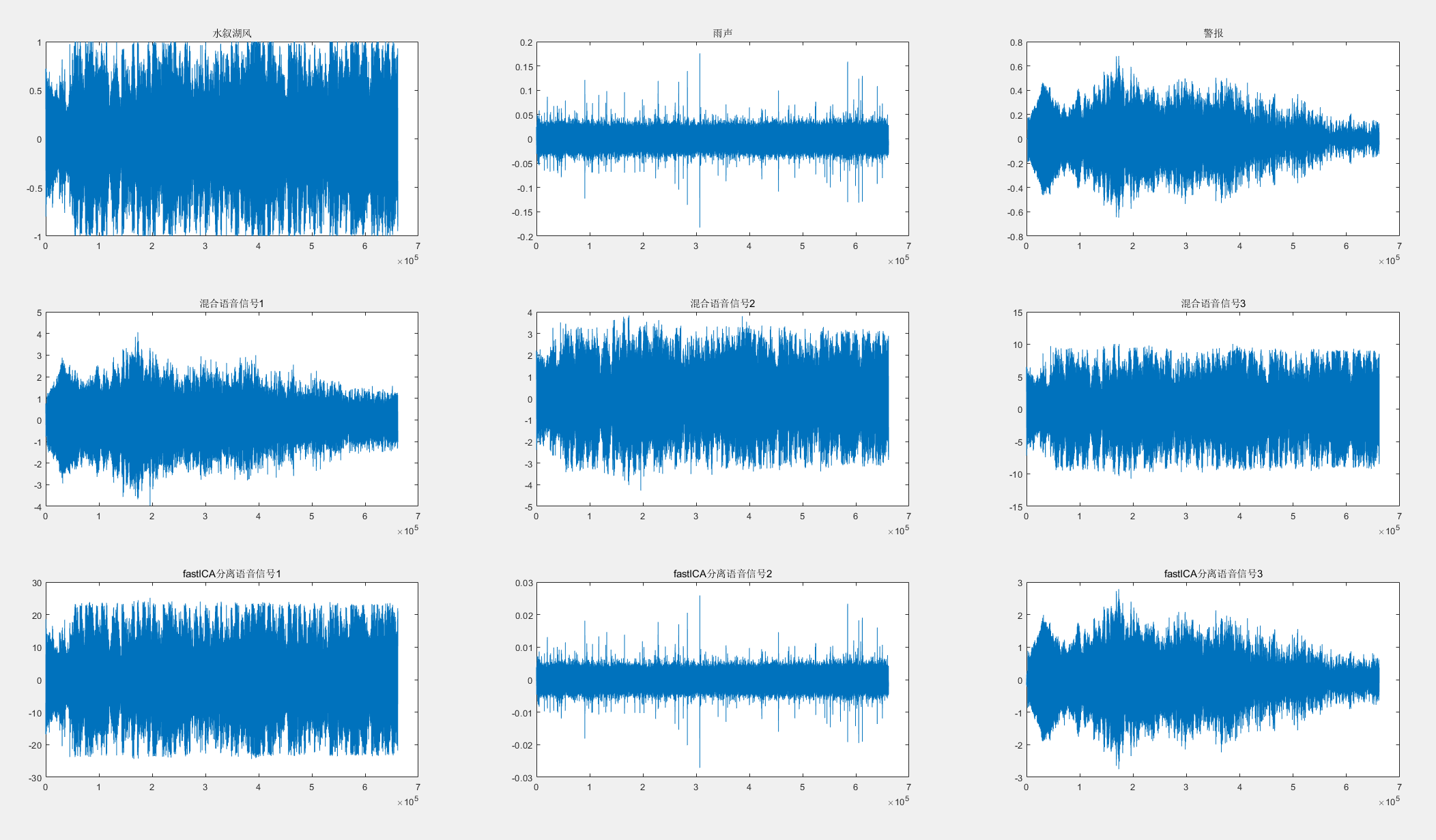
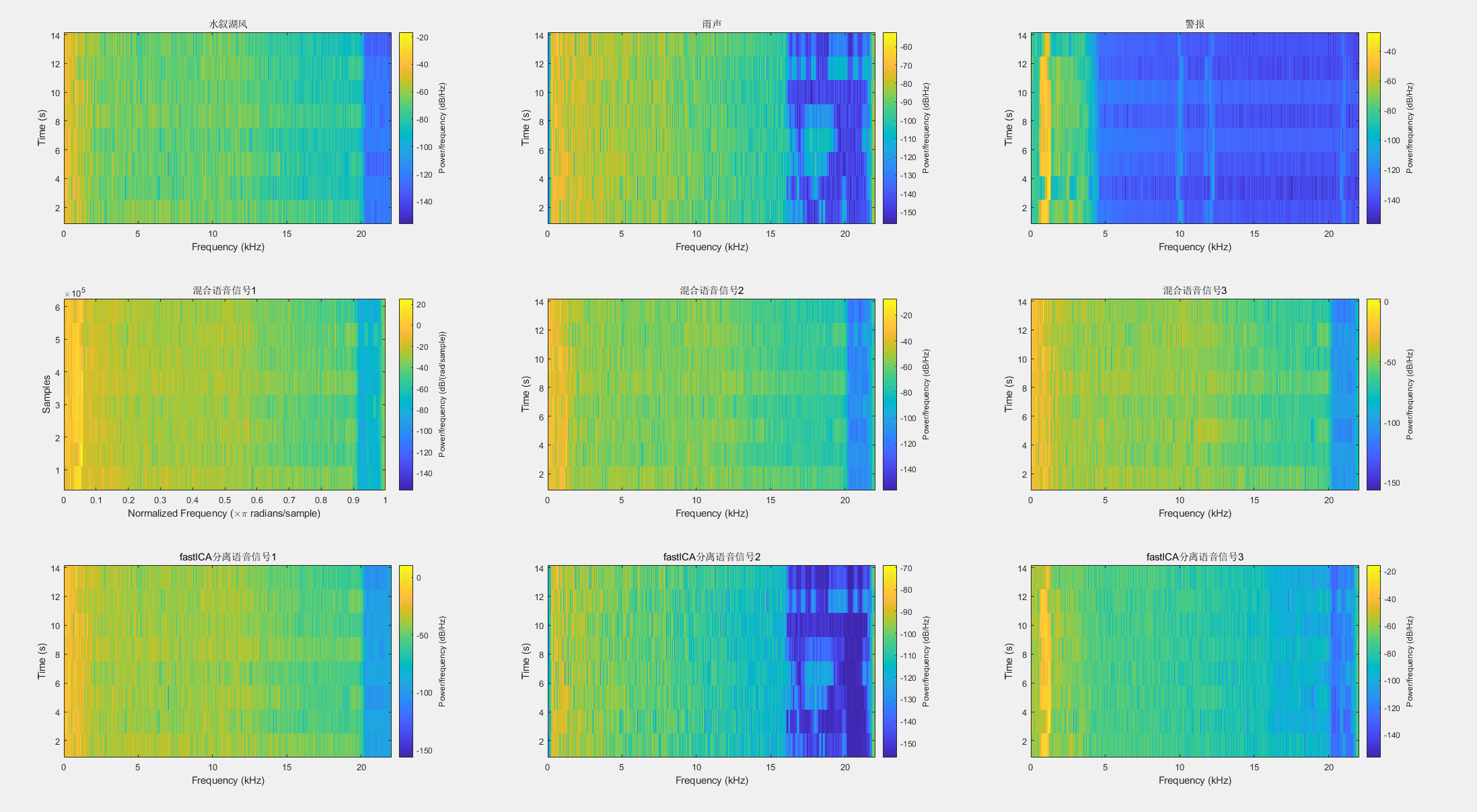
然后大作业作出的时域波形和STFT幅度图如图所示: