这一篇仍然是个插曲,是用来记录一些琐碎的信号与系统课内的知识…应该跟傅里叶变换关系不大,只是为了顺着写就这么写辣
这些查漏补缺是概念将会通过一些检索来的题目进行串联:
①已知系统输入$x(n)=\varepsilon(n-2)-\varepsilon(n-6)$,单位样值响应$h(n)=x(-n)$,求$y(n)=x(n) \ast h(n)$
解:这是在计算离散系统中的卷积和,我们有两种作法,由于$x(n),h(n)$是可列写的,我们可以用不进位乘法来得到答案:
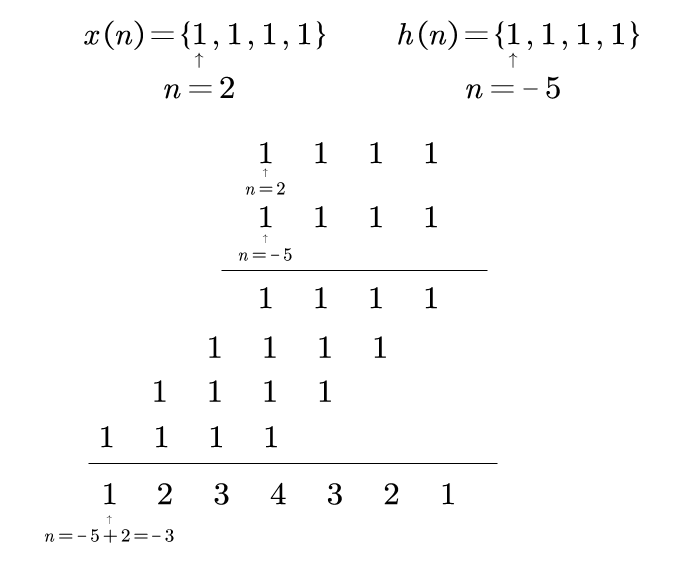
第二种方法就是利用定义和卷积的性质:
$x(n)=\varepsilon(n-2)-\varepsilon(n-6)$,对于$h(n)$,我们直接写出$h(n)=\varepsilon(-n-2)-\varepsilon(-n-6)$,而实际上$h(n)$可以写作$\varepsilon(n+5)-\varepsilon(n+1)$,可以狭隘的理解成$\varepsilon(n)$在0处是1,所以当$h(n)$这种门形序列翻转后,要右移一位。
同时我们知道$\varepsilon(k) \ast \varepsilon(k)=(k+1)\varepsilon(k)$
那样直接计算:
这样也可。
②已知$LTI$连续系统微分方程为$y’\left( t \right) +2y\left( t \right) =f’’\left( t \right) $ ,计算该系统的单位冲激响应$h(t)$:
解决这种问题要利用$LTI$系统的性质,我们利用$LTI$的微分特性,先构造一简单系统使得:
同样,我们要知道,当系统方程右侧出现冲激函数时,左端最高阶导数含冲激,次高阶跃变,再低阶连续。
当$t>0$时,冲激消失,则带入初始值,齐次一阶线性微分方程的解为$y=e^{-2t}\varepsilon(t)$,则题目所求的$h(t)$即对$e^{-2t}\varepsilon(t)$求二阶导数。得:
③计算积分:
这个积分,不讲武德,本来就是个迪利克雷积分了,还平方。正确的解决姿势是将其看作一个$f(t)$的傅里叶变换在$\omega=0$时候的值,所以我们需要求出这个$f(t)$的频谱密度函数$F(j\omega)$:
由频域卷积定理:
由常用的变换对:
④某因果线性时不变系统,当输入信号为$f_1\left( t \right) =e^{-3t}\varepsilon \left( t \right)$,系统的零状态响应为$y_1(t)$,当输入信号为$f_2\left( t \right) =\frac{\mathrm{d}f_1\left( t \right)}{\mathrm{d}t}+3\int_{-\infty}^t{f_1\left( \tau \right) \mathrm{d}\tau}$时,系统的零状态响应为$y_2\left( t \right) =-4y_1\left( t \right) +e^{-2t}\varepsilon \left( t \right) $ 。求该系统的冲激响应$h(t)$
解:这同样是利用$LTI$系统的性质,但我仍然很惊讶于这个问题为什么必定解的出来(后面我会写出来)
第一种方法是利用$LTI$的微分和积分性质,即:
那么$y_2(t)$由微分积分性质可得:
由题目已知条件联立得:
整理后两边求导,这样消去含积分的项:
问题得到了些许解决,因为我们知道$y_1\left( t \right) =f_1\left( t \right) \ast h\left( t \right) $,我们将两式联立,这里要用到卷积的微分和积分性质:
积分性质要注意使用条件,即$f_1\left( -\infty \right) =f_2\left( -\infty \right) =0$,这样才能保证微分积分后仍能还原到$f_1(t),f_2(t)$,我们要作的是微分运算,所以不涉及这个条件。
计算后$f_{1}^{‘’}\left( t \right) +4f_{1}^{‘}\left( t \right) +3f_1\left( t \right) =\delta ‘\left( t \right) +\delta \left( t \right) $,这就是巧合的地方,如果这个式子求出来不是冲激函数或者它的导数们,那么往下就很难进行了。因为是,所以利用卷积的性质,很容易得:
$h\left( 0_- \right) =0$,由积分法,可以得$h\left( 0_+ \right) =1$。最后解这个微分方程,记得加上特解。得:
⑤记得写$t>0(\varepsilon(t))$,正因为这个巧合,直接由卷积积分列写$y_1(t),y_2(t)$最终也可以得到答案。很怪,可能是有意而为之。
某$LTI$因果系统,输入输出间的微分方程为:
(1)求该系统的冲激响应$h(t)$
(2)$f(t)=t \varepsilon(t),y(0_+)=1,y^{‘}(0_+)=3$,求该系统的零输入响应$y_{zi}(t)$和零状态响应$y_{zs}(t)$。
解:(1)为了求解冲激响应,我们将$f(t)=\delta(t)$带入微分方程中,发现含有奇异函数的高阶导数。由待定系数法,我们有:
匹配系数得:
作积分法:
当$t>0$后,冲激函数等奇异函数的作用消失,由特征根法得:
由$A=1$,得最后的$h(t)$为:
同样,我们也可以利用$LTI$系统的性质,构造一个简单系统$y_1(t)$,直接解一个简单系统:
此时两边积分很容易得$0_+$时的值:
易得$h_1\left( t \right) =\left( e^{-t}-e^{-2t} \right) \varepsilon \left( t \right) $,之后的$h(t)$根据方程右端:
(2)由于(1)中计算了冲激响应,一定有人想直接用卷积公式算零状态响应,但是这其实并不方便。简便程度上不如直接解,一定要注意给的初始状态$y(0_+)=1,y^{‘}(0_+)=3$。因为右端有奇异函数,所以零输入和零状态所代入的初始状态要小心:
对于零输入响应,我们要用$0_-$时的初始值:
对于零状态响应,初始值为0,但要注意,这个初始值为0是说$0_-$时候是零,如果有冲激函数,我们仍然要按照积分法来确定$0_+$时的值。并且要加上特解,当$t>0$后,右端是个常数,特解也是个常数。可得$y_p=-1$:
⑥已知某$LTI$离散系统的输入:
其零状态响应为:
求系统的单位序列响应$h(k)$:
解:这是一个离散的系统,我们先进行列写:
根据卷积积分,得:
然后忽然就得到了这么一个差分方程,求特征根,这里要写的仔细一些:
由于我们一般手算的系统最多不超过二阶,一对共轭复根的情况有时会遇到。在这里连续型和离散型的某些形式并不完全一样,这里略去推导直接给出来罢:
| 连续 | 离散 |
|---|---|
| $e^{\alpha t}\left[ C\cos \left( \beta t \right) +D\sin \left( \beta t \right) \right] $ | $\rho ^k\left[ C\cos \left( \beta k \right) +D\sin \left( \beta k \right) \right] $ |
| $\lambda_{1,2}=\alpha \pm j\beta $ | $\lambda_{1,2}=a\pm jb=\rho e^{\pm j\beta}$ |
要注意那个$\beta$,离散情况下,是共轭复根化成指数形式后的$\beta$。
递推得:

