在近一年半来学院同学们的不懈努力之下,我们具有电子信息特色的人工智能学院终于加了“计算机组成与系统结构”这门课。但…也并完全是一件好事。
我对这门课产生不了什么丰富的见解,所以整理的目的只是梳理一下知识点,因为计组的知识点非常的琐碎,哪怕是一个期中考试driven下的整理,也很琐碎。
首先要利用乘基取整和除基取余将十进制转为任意进制,在这个转化中,二进制,八进制,十六进制比较重要。总之视角聚焦到了二进制上。二进制只有0和1,硬件实现上简单。下面的章节里就是在介绍如何用0和1来刻画我们之前的认知。
数据校验
0和1本身的性质化简了很多问题,例如这个位置非0即1,不可能出现别的情况,那么传输的数据的位错误的情况就比较单一。这就引入了数据校验,即如何确认对方发送的数据是否在传输过程中发生了错误。书上介绍了三种方法,每一种方法都很巧妙,他们的共性都是对$n$位数据添加$k$位校验位。
这里要引入汉明码距的概念,任意两个$m$位的码字,其对应位不同的树木称为两个码字的海明码距:
书上在这里介绍了一个关系:$n$位数据,加上$k$位校验位后,一共$m$位,总共有$2^m$种编码方式,其中$2^n$是合法的,在这些合法的编码方式里,两两之间的海明码距的最小值$d_{min}$称为这种编码方式的码距。如果要检测$r$位错误,则$d_{min}$至少需要为$r+1$,这样才能保证$r$位跳变不会跳到另一个合法码字上。如果需要实现纠错,则至少需要为$2r+1$。这种情况下,发生错误的码字与原始数据的码距为$r$,而错误码字与其他任意合法码字的码距大于等于$r+1$。所以此时只需要选取与其码距距离最小的作为正确的码字,即实现了纠错。
例如对于只有4个合法码字的编码为:000000,000111,111000,111111,我们计算这种编码的码距发现是3,那么当$r=1$,即有一位错误时,$3>1+1,3>2+1$,它同时可以完成检测和纠错。而当$r=2$时,它只能检错不能纠错。
实际情况中我们往往只考虑1位错误的情况,发生多位错误的概率很小。当只犯1位错误时,加上校验位后,校验位能表示的编码种类显然有:
奇偶校验,海明校验,循环冗余校验是三种经典的方法:
①奇偶校验的原理很简单,实现容易,就是在$n$位数据前,加一个奇校验位$c$或偶校验位$c$,然后各位作异或。保证$n+1$位中1的个数是奇数。偶校验就是1的个数是偶数。显然这种方法只能检测出1位或者奇数位错误。
例如确定$X=01010100$的偶校验编码和$Y=01010101$的奇校验编码:
②海明码非常的巧妙,详细的说明可以参考3b1b的视频,这里只给出记忆的应试策略:
例如对$D_8D_7D_6D_5D_4D_3D_2D_1=10101110$进行海明编码,一共有8位,根据前面的不等式,我们得出$k$至少为4。将校验位$P_i$插入海明码$H[n+k]$第$2^{i-1}$的位置:
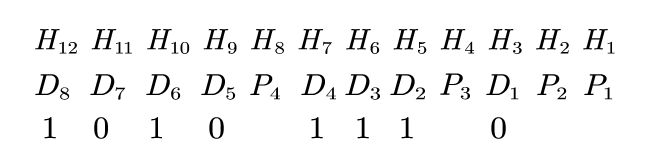
之后将不是校验位的序号用二进制表示,然后从低到高为$1,2,3..$寻找每一列为1的,将对应的拿来作偶校验(异或):
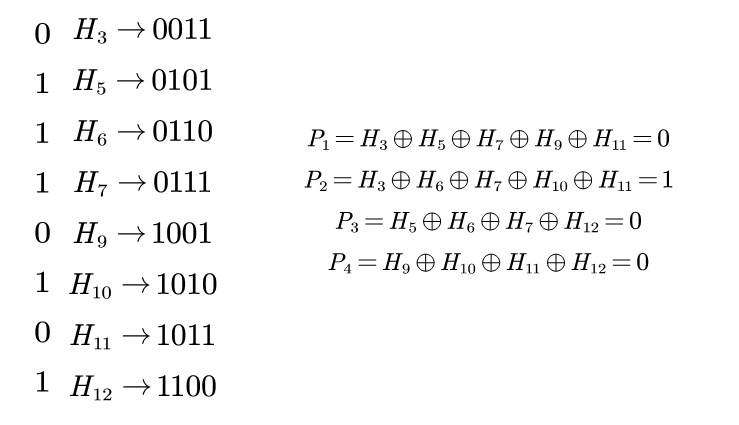
所以最后的海明编码即:101001110010
假设获得的海明编码是101001010010,即第六位跳变,则运行校验方程,即$P_i$分别与对应项进行异或:
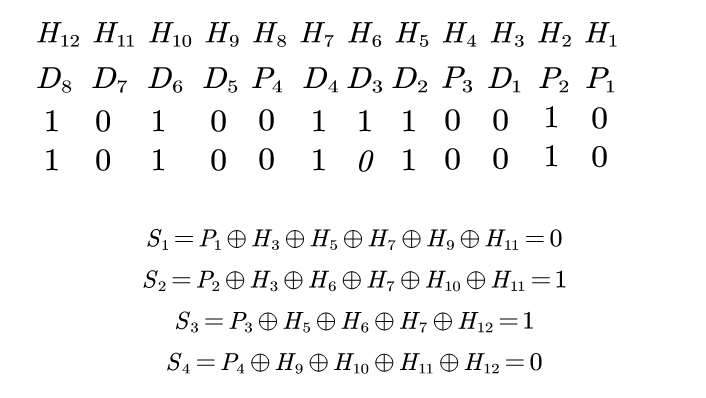
$S_4 S_3 S_2 S_1$不为0,$0110$指出了错误位置在第六位。
③循环冗余校验码简称$CRC$基于模2运算,即不进位的加减乘除,题目会给出一个生成多项式$G(x)$,$G(x)$的系数表示一个编码。将这个编码与信息左移最高次幂低位补零后作模2除,例:
当信息码为101001时,选择生成多项式$G(x)=x^3+x^2+1$,生成多项式的二进制编码为1101,对两者进行模二除,得余数为001。将余数接在101001后面,即得$CRC$码101001001。
可以验证,如果用101001001与约定的生成多项式1101进行模2除,余数为0。若有错误,余数也会像海明码一样表示出错位置,但略有不同。
数据表示
现在我们要着眼于0和1排列所表示的含义,先是定点数,定点数分为定点整数和定点小数。然后就是原码补码反码,对于定点整数,还有移码,这个是后话了。上述内容在大一上导论里已经有接触了,这里就不赘述了。这里强调一下原码补码反码移码的表示范围:
设机器字长为$n+1$,我们考虑有符号位的。
| 整数 | 小数 | |
|---|---|---|
| 原码 | $-\left( 2^n-1 \right) \leqslant x\leqslant 2^n-1$ | $-\left( 1-2^{-n} \right) \leqslant x\leqslant 1-2^{-n}$ |
| 反码 | $-\left( 2^n-1 \right) \leqslant x\leqslant 2^n-1$ | $-\left( 1-2^{-n} \right) \leqslant x\leqslant 1-2^{-n}$ |
| 补码 | $- 2^n \leqslant x\leqslant 2^n-1$ | $-1 \leqslant x\leqslant 1-2^{-n}$ |
| 移码 | $- 2^n \leqslant x\leqslant 2^n-1$ |
规律即原码和反码都遵循等比数列求和,可列出取值范围。由于它们中存在$+0,-0$,所以少表示一个值。补码和移码是保持一致的,但是移码只针对定点整数。
下面重点要指出移位操作:
移位分为三种,算数移位,逻辑移位,循环移位。这里面需要强调的是负数补码的算数移位,其右移高位补1,左移低位补0。
下面我们来分析原码补码的加减乘除,首先原码的加减乘除不用多说,但实现上需要用到减法器,这增加了成本。我们可以用补码来进行加减运算,但要注意溢出。注意,只有正数+正数(上溢变成负数)或者负数+负数(下溢变成正数)才会发生溢出,正数-负数是不会的。
基于此,判断溢出的方法有三种,道理类似:
第一种是双符号位(变形码),利用运算结果的双符号位作异或,如果为1说明溢出,(00是正,11是负)
第二种采用一位符号位,可称作表达式法,记$A$的符号为$A_S$,$B$为$B_S$,运算结果的符号为$S_s$,则溢出的逻辑表达式为:
实际上它枚举了两种溢出的情况,最后取了个或。
第三种是进位判决法,就是对符号位的进位和最高数值位的进位作异或……感觉道理和双符号位类似。
下面是原码和补码的乘除法,这里非常繁琐,如果想过考试需要勤加练习:
结合硬件实现理解起来会简单不少,这里仅作记录。
作原码一位乘法:$X=-0.1101,Y=+0.0110$
自然,被乘数$[X]_原=1.1101,[Y]_原=0.0110$,乘积符号位$1 \oplus0=1$
之后我们对其绝对值进行原码一位乘法:
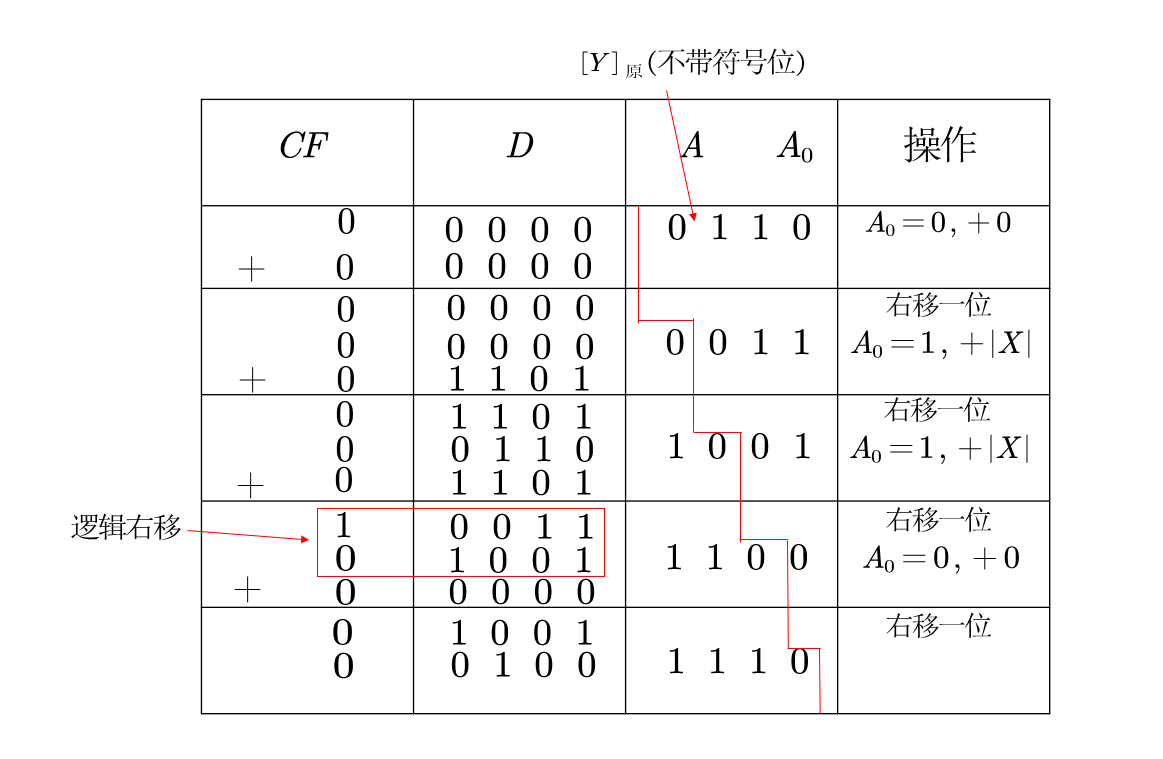
彻底记住这个方法必须手动写一遍,本质上是根据乘数的最后一位来判断加$|X|$还是0,以及进行的是对$CF+D+A$的整体逻辑右移,最后的结果加上符号位就是乘数积$X\cdot Y=1.01001110$
之后是补码的一位乘法,补码比较复杂,观察上面的原码一位乘法,发现他需要进行$n$轮移位和加法,补码的一位乘法还需要多进行一次加法,并且需要引入一个辅助位。基于这样的不同点,我们最好将两者对比起来记忆:
| 原码一位乘法 | 补码一位乘法 | ||
|---|---|---|---|
| 进行$n$轮加法和移位 | 在$n$轮加法和移位上多加一次 | ||
| $+0,+[ | X | _原]$ | $+0,+[X_补],+[-X_补]$ |
| 逻辑右移 | 补码的算数右移(补1还是0需要根据正负) | ||
| 符号位不参与运算 | 符号位参与运算 |
注意,原码一位乘法时用单符号位不会出错,而补码一位乘法时必须用双符号位,我们现在作补码的乘法练习一下,还是用上面那个例子:
$[X]_补=11.0011,[-X]_补=00.1101,[Y]_补=00.0110$
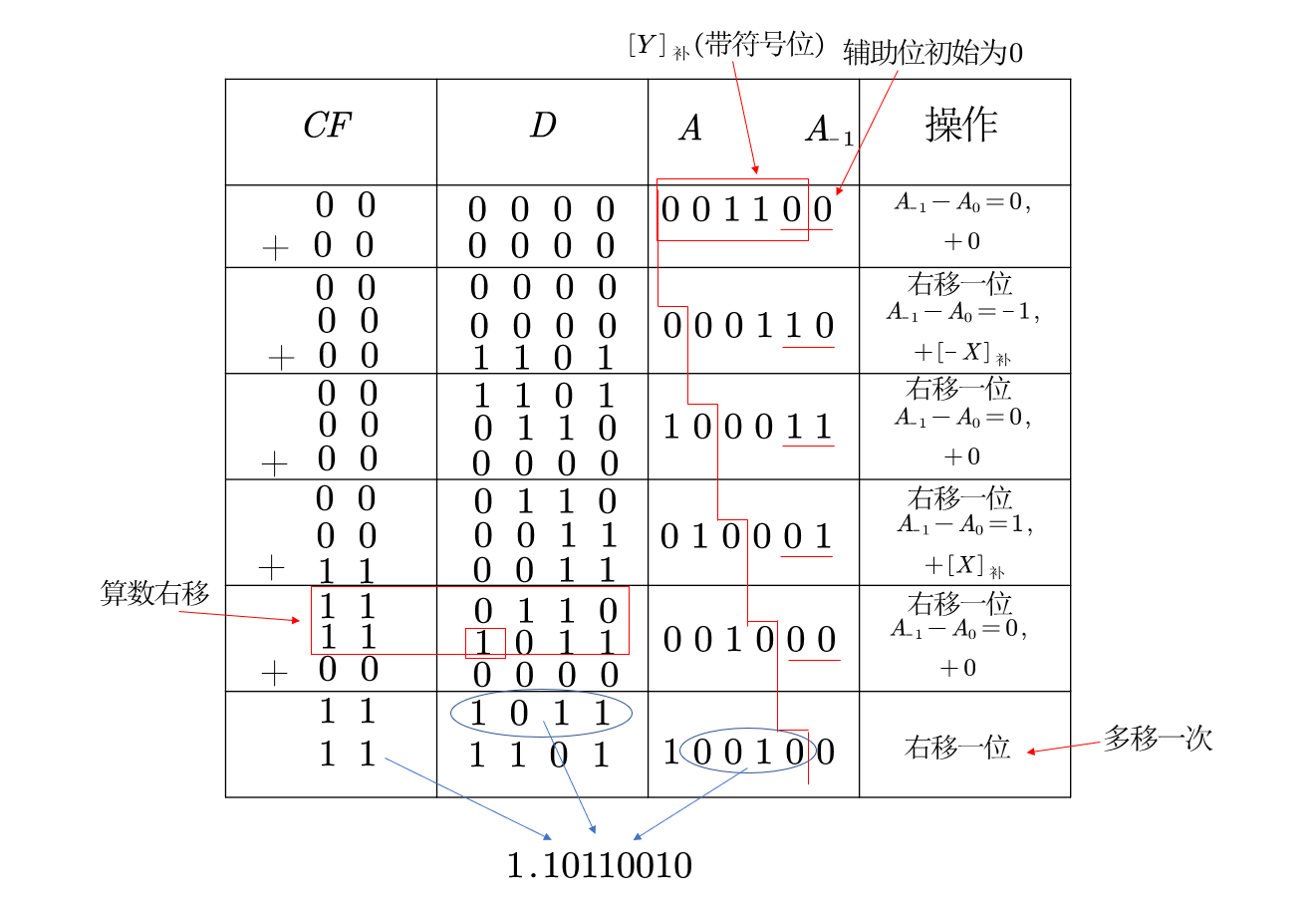
最后得到的结果是1.10110010,将补码转换为原码为1.01001110和上面原码一位乘法是一样的。
最后是除法,和乘法类似,分为原码的除法和补码的除法,我们首先讨论原码的除法,有两种:恢复余数法和加减交替法,其实后者是前者的优化:
我们现在作$X=-0.10001011,Y=0.1110$试用恢复余数法求$X \div Y$的商和余数:
首先我们列写:$[|X|]_原=0.10001011,[|Y|]_原=0.1110,[|Y|]_补=0.1110,[|-Y|]_补=1.0011$
符号位显然可以确定为1:
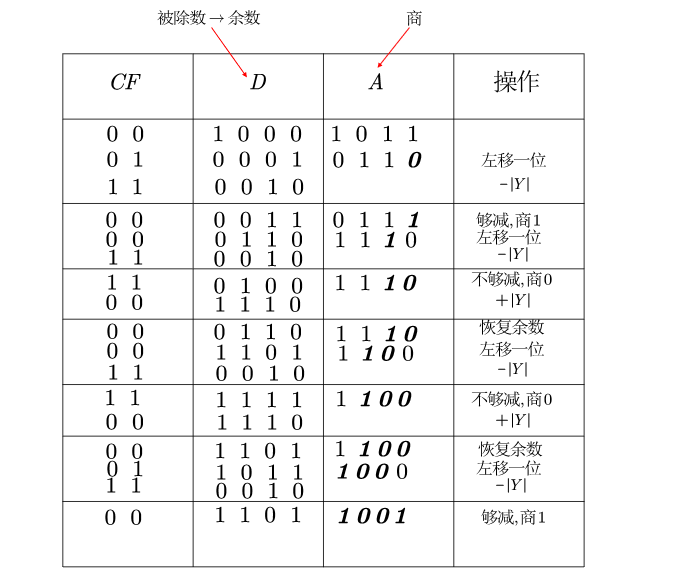
那么商即为1.1001,余数的符号与被除数$X$一致,为$-0.1101\times 2^{-4}$。
加减交替法其实就是当上述过程中,若商为0了,不再进行加$Y$然后左移减$Y$,实际上这个过程等效于直接加左移加$Y$。所以就这样“加减交替”。
补码的除法只介绍了加减交替法,类似于补码乘法,它有它独特的性质,我们仍以上面那个例子为例:$[X]_补=1.01110101,[Y]_补=0.1110,[-Y]_补=1.0010$:
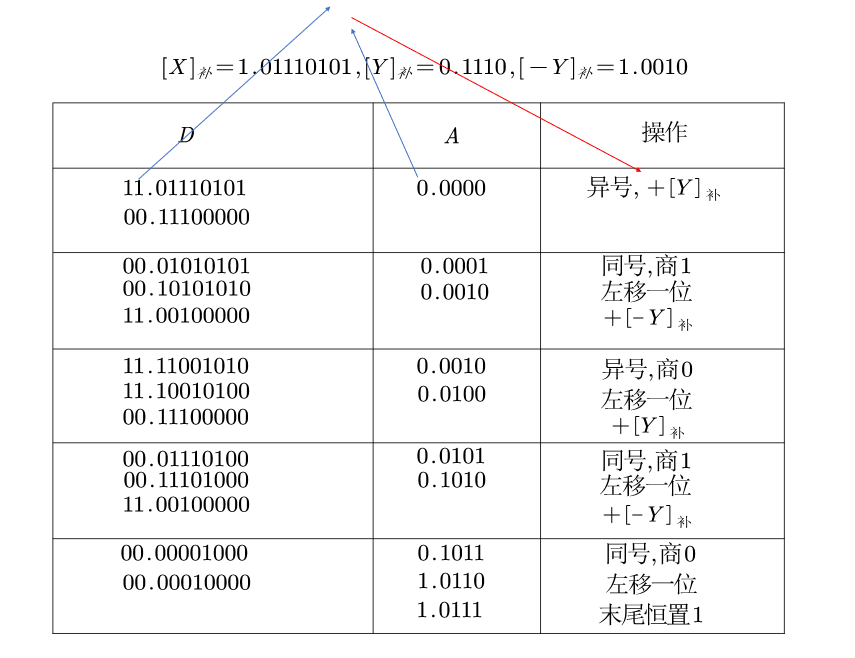
最后算出来的数都是自带符号位的,商虽然对上了但是余数没对上,很怪。我表示很迷,但是不影响应试……这个运算方法太深奥了,应付考试给出的定点小数的特殊情形就已经很难理解了。
然后是浮点数……呜呜呜,浮点数就像是科学计数法,它利用阶码和尾数来表示一个数。阶码是一个常用补码或移码表示的定点整数,尾数是常用原码和补码表示的定点小数。阶符和数符表示它们的正负。浮点数的规格化,就是在存储空间不变的情况下,尽可能多的保持精度。就像科学计数法中让第一位为有效值一样。规格化分为左规和右规:
左规:尾数算数左移1位,阶码减1,直到尾数最高位是有效值。
右规:一般出现在尾数溢出时,即数符双符号位为01或10,将尾数算数右移1位,阶码加1。
但是视尾数用原码还是补码表示的不同,尾数的规格化有一些不一样的要求:
由于规格化后的原码尾数,最高数值位一定是1,所以如果是正数,最大值为0.11…1,最小值为0.10..0。负数的道理也是一样的,最高数值为一定要是1.
当尾数用补码表示时,必须要求规格化后的符号位与数值位一定相反。
现在我们用浮点数的加减这一流程,把这几个概念融合一下。
已知十进制数$X=-5/256,Y=+59/1024$,按机器补码浮点运算规则计算$X-Y$,结果用二进制表示,要求阶符取2位,阶码取3位,数符取2位,尾数取9位。
浮点数的加减运算分为五步:对阶(小阶对大阶),尾数加减,规格化,舍入,判溢出
这样我们得到了原码表示,之后转为题目要求的补码浮点数表示:
可知$X$比$Y$低一阶,对$X$进行对阶,尾数算数右移一位,阶码加1,这里由于是负数的补码的算数右移,高位补1:
然后作$-Y$,得$-Y$的补码表示$11.100,11.000101000$,尾数相减得:
这样$X-Y=11.100,10.110001000$,进行规格化,算数右移1位,由于双符号位最高位是1,所以不1,得$11.101,11,011000100$,然后也不用舍入,看双符号位也没有溢出。所以再转成原码:
刚才我们没有判断舍入的过程,第一种是“0舍1入”,即如果右规丢掉了一个1,就像四舍五入一样,在末位+1,但是如果这样导致尾数又溢出了,那就继续右规。第二种是“恒置1法”,即不管丢掉的是啥,尾数末位恒写为1。
由于阶码也射击加1和减1,当阶码超出上限,则发生上溢,而如果超出下限,则会被记为机器数0。

