傅里叶变换3

阅读数: 次 2022-04-18

前两篇已经介绍了傅里叶变换的一些基础内容，下面我们进一步结合实践延申到短时傅里叶变换，来为最后的小波变换作铺垫。

由于前面我们已经推导出了傅里叶变换的数学表达式，以及阐述了在实际情况下我们用的是离散形式的傅里叶变换，所以下文对这两个概念不作区分，同时也尽量避免数学表达式的出现，多和例子相结合。

fs = 100;%采样频率
t = 0:(1/fs):(10-1/fs);
t_1 = 0:(1/fs):(5-1/fs);
t_2 = 5:(1/fs):(10-1/fs);
S_1 = cos(2*pi*1*t_1);
S_2 = cos(2*pi*5*t_2);

S = [S_1 S_2];
S_cp = [S_2 S_1];

n = length(S);
X = fft(S);
X_2 = fft(S_cp);
f = (0:n-1)*(fs/n);
fshift = (-n/2:n/2-1)*(fs/n);%zero-center化后的频率

subplot(221);
plot(t,S)
xlabel('t');
Y = fftshift(X);%重新排列
powershift = abs(Y).^2/n;%计算频率幅度
subplot(222);
plot(fshift,powershift)
xlabel('f');
subplot(223);
plot(t,S_cp)
xlabel('t');
Y_2 = fftshift(X_2);
powershift_2 = abs(Y_2).^2/n;
subplot(224);
plot(fshift,powershift_2)
xlabel('f');

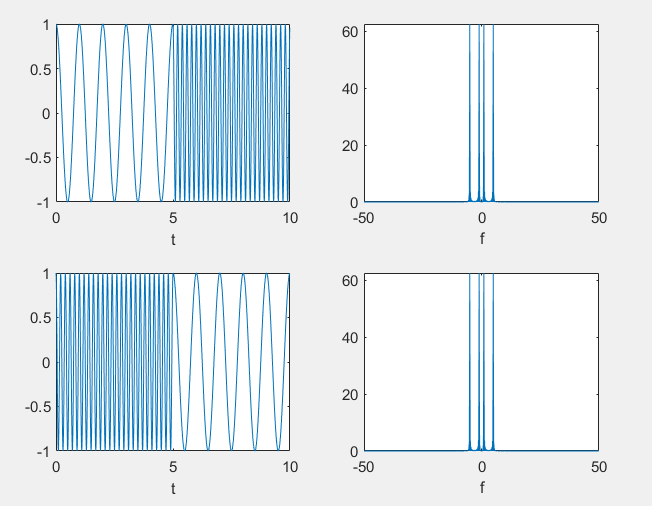
这个例子很好的说明了傅里叶变换的局限性，（实际上我们从傅里叶变换的表达式中可以看到，前一半和后一半的变换结果是共轭的，所以它们的幅度是一样的，这也是为什么我们表示的时候用了fftshift()，否则图像将会以二分之采样频率为对称轴对称。）也就是它将全部的信息从时域变化为了频域，而没有表达出频率随时间的变化，导致两个不同的波形，傅里叶变换后的结果是一样的。

此时我再更新这一篇blog的时候已经是2022年4月18日了，马上要期中考试，本来是想写短时傅里叶变换继而引入小波变换，但是物是人非。现在打算在下面整理一下傅里叶变换的性质并加一些例子便于记忆：

首先，作为一个工科生，我自然不会关心“这积分符号是否可以交换”，“这严谨吗”等等……所以……

首先我们选取经典的$Sinc$函数在时域的波形用于下面的可视化：

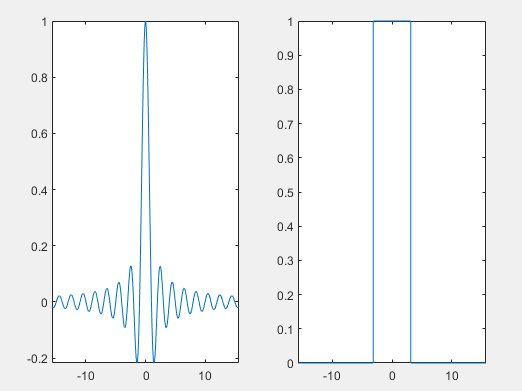
$\mathrm{Sinc}\left( x \right) =\frac{\sin \pi x}{\pi x}$

左边是时域图，右边是频域。可以看出右边是个门函数，至于为什么是门函数我们后面会提到。

线性性质我们这里就默认了，因为傅里叶变换是个线性变换，这个无需赘述。

下面我们考虑时域变量$t$发生线性变换而变为$at+b$的情况：

$\mathcal{F} \left[ f\left( at+b \right) \right] =\int_{-\infty}^{+\infty}{f\left( at+b \right) e^{-j\omega t}\mathrm{d}t} \\ \text{取}x=at+b,\mathrm{d}x=a\mathrm{d}t,\text{先假设}a>0 \\ =\frac{1}{a}\int_{-\infty}^{+\infty}{f\left( x \right) e^{-j\omega \frac{x-b}{a}}\mathrm{d}x}=\frac{1}{a}e^{j\frac{b}{a}\omega}\int_{-\infty}^{+\infty}{f\left( x \right) e^{-j\omega \frac{x}{a}}\mathrm{d}x} \\ =\frac{1}{a}e^{j\frac{b}{a}\omega}F\left( j\frac{\omega}{a} \right) \\ \text{当}a<0\text{时，需要从积分里拿出一个负号。} \\ ==\frac{1}{a}\int_{-\infty}^{+\infty}{f\left( x \right) e^{-j\omega \frac{x-b}{a}}\mathrm{d}x}=-\frac{1}{a}e^{j\frac{b}{a}\omega}\int_{-\infty}^{+\infty}{f\left( x \right) e^{-j\omega \frac{x}{a}}\mathrm{d}x}=-\frac{1}{a}e^{j\frac{b}{a}\omega}F\left( j\frac{\omega}{a} \right) \\ \text{所以}\mathcal{F} \left[ f\left( at+b \right) \right] =\frac{1}{\left| a \right|}e^{j\frac{b}{a}\omega}F\left( j\frac{\omega}{a} \right)$

当$b=0$时，上式变为：

$\mathcal{F} \left[ f\left( at \right) \right] =\frac{1}{\left| a \right|}F\left( j\frac{\omega}{a} \right)$

被称为尺度变换。这个式子表明，当信号$f(t)$被时域压缩$1/a$的时候，频域将展宽，但频率分量的幅度也被削弱，这是能量守恒的体现。比如当快放视频时，会觉得声音发尖，这就是频率展宽后高频分量的作用。我们将上面的$Sinc$函数开个刀试一下：

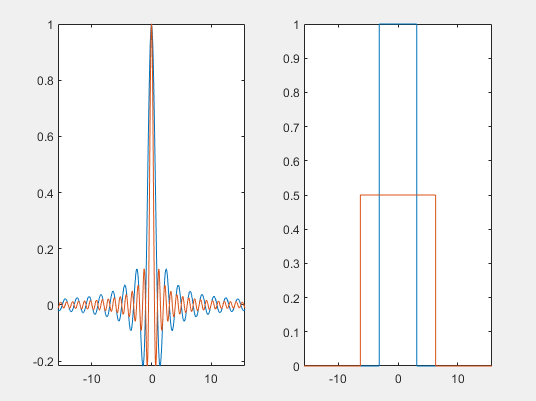
看，确实是这样的。

当取$a=1$时，即没有尺度变换时，称为时移特性：

$\mathcal{F} \left[ f\left( t\pm t_0 \right) \right] =e^{\pm jt_0\omega}F\left( j\omega \right)$

容易看出这个变换不会使得幅度谱发生改变，只会改变相位。这个例子就不能靠$Sinc$函数了，我们找一个平移后的门函数来验证一下：

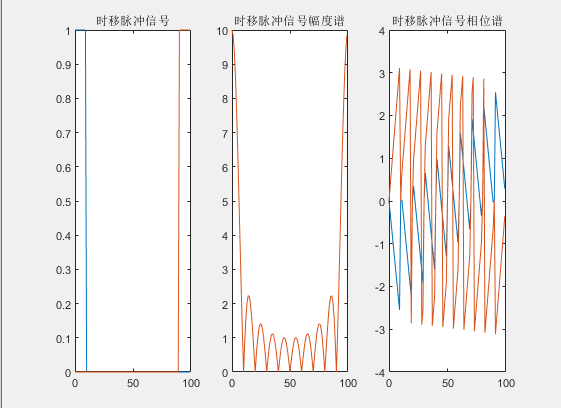
幅度谱没有变化，相位谱变了。并且要注意，如果门函数是完全沿$y$轴对称的，它根本不应该有相位谱，因为变换后的结果是$\tau \mathrm{Sa}\left( \frac{\omega \tau}{2} \right) $没有虚部。通过这一现象我们进一步可以加深对这一性质的理解。

跟时移性质对偶的是频移性质，它是调制的基础：

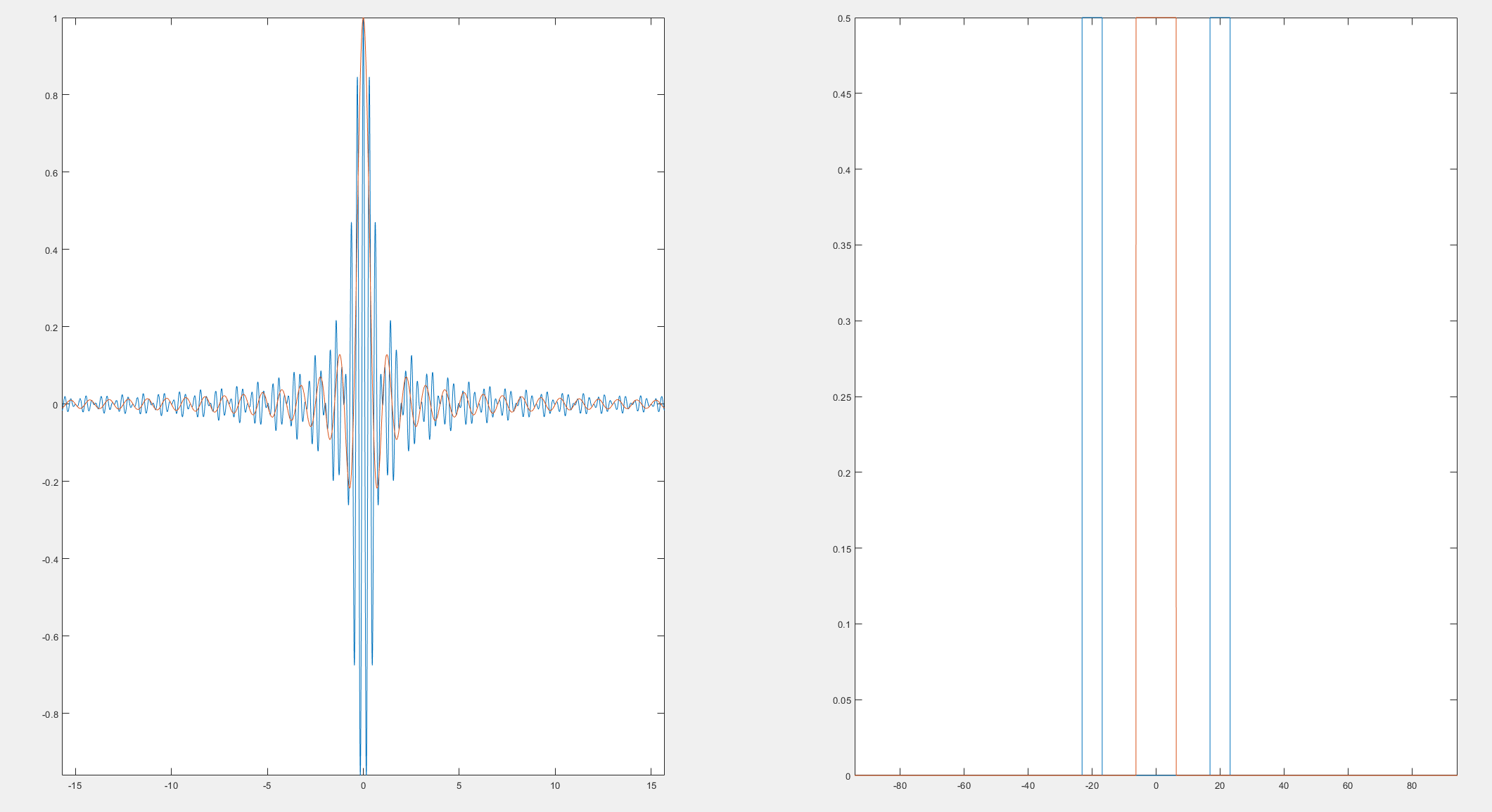
$\mathcal{F} \left[ f\left( t \right) e^{\pm j\omega _0t} \right] =\int_{-\infty}^{+\infty}{f\left( t \right) e^{\pm j\omega _0t}\cdot e^{-j\omega t}\mathrm{d}\omega}=\int_{-\infty}^{+\infty}{f\left( t \right) \cdot e^{-j\left( \omega \mp \omega _0 \right) t}\mathrm{d}\omega}=F\left( j\omega \mp j\omega _0 \right) \\ f\left( t \right) e^{\pm j\omega _0t}\longleftrightarrow F\left( j\omega \mp j\omega _0 \right)$

这里为了可视化的直观，取了一个特殊的情况$\mathrm{cos}(20t)$，可以看到频谱发生了搬移，分向了高频部分。这里的一些细节我们最后再汇总。

实际上，特殊地，我们将信号$f(t)$乘上$\mathrm{cos}(\omega_0t)$或$\mathrm{sin}(\omega_0t)$，此时的频谱会发生搬移，利用欧拉公式展开，可以得下面这俩常用的结论：

$f\left( t \right) \cos \omega _0t\longleftrightarrow \frac{1}{2}F\left[ j\left( \omega +\omega _0 \right) \right] +\frac{1}{2}F\left[ j\left( \omega -\omega _0 \right) \right] \\ f\left( t \right) \sin \omega _0t\longleftrightarrow \frac{1}{2j}F\left[ j\left( \omega +\omega _0 \right) \right] -\frac{1}{2j}F\left[ j\left( \omega -\omega _0 \right) \right]$

下面我们证明对称性质，这一性质极具技巧性但又十分直接：

$\mathcal{F} \left[ f\left( t \right) \right] =\int_{-\infty}^{+\infty}{f\left( t \right) e^{-j\omega t}\mathrm{d}t}=F\left( j\omega \right) \\ \text{由逆变换},f\left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{+\infty}{F\left( j\omega \right) e^{j\omega t}\mathrm{d}\omega},\text{用}-t\text{代换}t \\ f\left( -t \right) =\frac{1}{2\pi}\int_{-\infty}^{+\infty}{F\left( j\omega \right) e^{-j\omega t}\mathrm{d}\omega},\text{将}t\text{与}\omega \text{交换} \\ f\left( -\omega \right) =\frac{1}{2\pi}\int_{-\infty}^{+\infty}{F\left( jt \right) e^{-j\omega t}\mathrm{d}t}=\frac{1}{2\pi}\mathcal{F} \left[ F\left( jt \right) \right] ,\text{即} \\ f\left( t \right) \longleftrightarrow F\left( j\omega \right) \\ F\left( jt \right) \longleftrightarrow 2\pi f\left( -\omega \right)$

特别地，当$f$具有奇偶性质时，该性质十分好用。注意常数因子$2\pi$，这个因子其实是为了能量守恒，如果我们最初定义傅里叶正变换需要乘一个$\sqrt{1/2\pi}$，那对称性就不需要标出常数了。对于这个性质有一个比较high-level的解释方法：

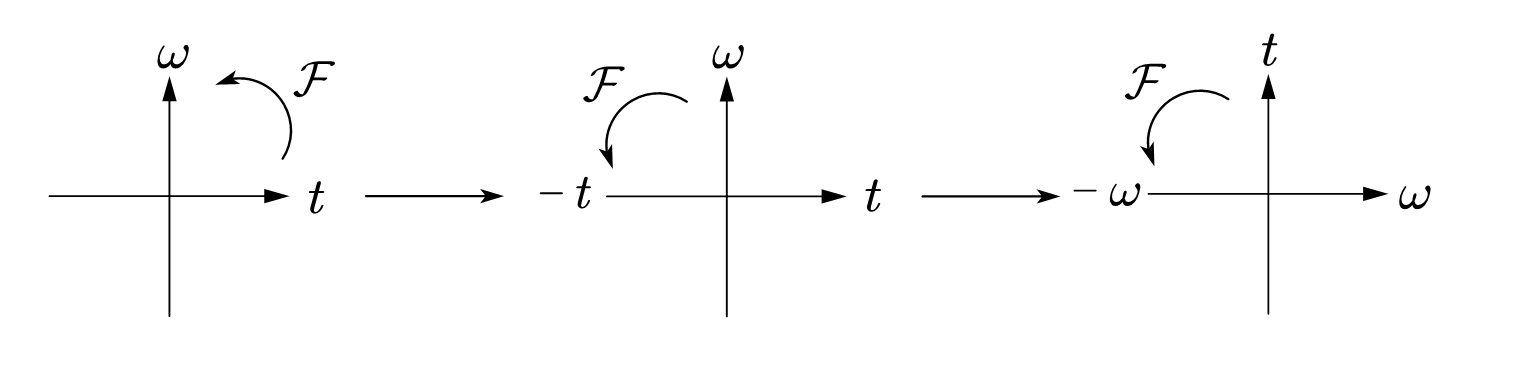
将时域和频域看成一个时频平面，每一次傅里叶变换相当于沿正方向（逆时针）转九十度。那么转两次就会是一个flip，这是可以证明的。而若交换$\omega,t$，就会有对称性的结论，负号正是因为旋转两次，到了一个负方向上。

接下来是时域的微积分性质，微分性质非常直接：

$f\left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{+\infty}{F\left( j\omega \right) e^{j\omega t}\mathrm{d}t} \\ \text{则}\frac{\mathrm{d}f\left( t \right)}{\mathrm{d}t}=\frac{1}{2\pi}\int_{-\infty}^{+\infty}{j\omega F\left( j\omega \right) e^{j\omega t}\mathrm{d}t},\text{也就是说}j\omega F\left( j\omega \right) \text{是}\frac{\mathrm{d}f\left( t \right)}{\mathrm{d}t}\text{的傅里叶变换} \\ \frac{\mathrm{d}f\left( t \right)}{\mathrm{d}t}\longleftrightarrow j\omega F\left( j\omega \right)$

时域的积分性质就不好简单的证明了，这里我们需要引入广义函数的概念，先求出$\varepsilon \left( t \right) $的傅里叶变换。注，它并不是绝对可积的，一种常见的思路是：

$\varepsilon \left( t \right) =\underset{\alpha \rightarrow 0}{\lim}e^{-\alpha t}\varepsilon \left( t \right) \\ \mathcal{F} \left[ e^{-\alpha t}\varepsilon \left( t \right) \right] =\int_0^{+\infty}{e^{-\alpha t}\cdot e^{-j\omega t}\mathrm{d}t}=\frac{1}{\alpha +j\omega} \\ \mathcal{F} \left[ \varepsilon \left( t \right) \right] =\underset{\alpha \rightarrow 0}{\lim}\left[ \frac{\alpha}{\alpha ^2+\omega ^2}-j\frac{\omega}{\alpha ^2+\omega ^2} \right] \\ \text{当}\alpha \text{趋近于}0\text{时},-j\frac{\omega}{\alpha ^2+\omega ^2}\rightarrow +\frac{1}{j\omega} \\ \underset{\alpha \rightarrow 0}{\lim}\frac{\alpha}{\alpha ^2+\omega ^2}=\left\{ \begin{array}{c} 0,\omega \ne 0\\ \infty ,\omega =0\\ \end{array} \right. \\ \text{则}\underset{\alpha \rightarrow 0}{\lim}\frac{\alpha}{\alpha ^2+\omega ^2}\text{显然是个}k\text{倍的冲激函数} \\ \int_{-\infty}^{+\infty}{\delta \left( t \right) \mathrm{d}t}=1 \\ \text{则}\int_{-\infty}^{+\infty}{\underset{\alpha \rightarrow 0}{\lim}\frac{\alpha}{\alpha ^2+\omega ^2}\mathrm{d}\omega}=\left. \pi \underset{\alpha \rightarrow 0}{\lim}\mathrm{arc}\tan \left( \frac{\omega}{a} \right) \right|_{-\infty}^{+\infty}=\pi \\ \underset{\alpha \rightarrow 0}{\lim}\frac{\alpha}{\alpha ^2+\omega ^2}=\pi \delta \left( \omega \right) \\ \text{所以}\mathcal{F} \left[ \varepsilon \left( t \right) \right] =\pi \delta \left( \omega \right) +\frac{1}{j\omega}$

有了这个储备，时域的积分性质就好处理了：

$\mathcal{F} \left[ \int_{-\infty}^t{f\left( \tau \right) \mathrm{d}\tau} \right] =\int_{-\infty}^{+\infty}{\left( \int_{-\infty}^t{f\left( \tau \right) \mathrm{d}\tau} \right) e^{-j\omega t}\mathrm{d}\omega}=\int_{-\infty}^{+\infty}{\left( \int_{-\infty}^{+\infty}{f\left( \tau \right) \varepsilon \left( t-\tau \right) \mathrm{d}\tau} \right) e^{-j\omega t}\mathrm{d}t} \\ \text{交换积分次序}:\int_{-\infty}^{+\infty}{f\left( \tau \right) \left( \int_{-\infty}^{+\infty}{\varepsilon \left( t-\tau \right)}e^{-j\omega t}\mathrm{d}t \right)}\mathrm{d}\tau ,\text{则中间就是求阶跃函数的傅里叶变换，} \\ \text{由时移性质}\mathcal{F} \left[ f\left( t\pm t_0 \right) \right] =e^{\pm jt_0\omega}F\left( j\omega \right) \text{可知}: \\ \int_{-\infty}^{+\infty}{\varepsilon \left( t-\tau \right)}e^{-j\omega t}\mathrm{d}t=\left( \pi \delta \left( \omega \right) +\frac{1}{j\omega} \right) e^{-j\omega \tau} \\ \text{所以}\int_{-\infty}^{+\infty}{f\left( \tau \right) \left( \pi \delta \left( \omega \right) +\frac{1}{j\omega} \right) e^{-j\omega \tau}}\mathrm{d}\tau =\left( \pi \delta \left( \omega \right) +\frac{1}{j\omega} \right) \int_{-\infty}^{+\infty}{f\left( \tau \right) e^{-j\omega \tau}}\mathrm{d}\tau =\left( \pi \delta \left( \omega \right) +\frac{1}{j\omega} \right) F\left( j\omega \right) \\ \text{即}\int_{-\infty}^t{f\left( \tau \right) \mathrm{d}\tau}\longleftrightarrow \left( \pi \delta \left( \omega \right) +\frac{1}{j\omega} \right) F\left( j\omega \right)$

时域的微积分性质可以帮助我们求解一些特定函数的傅里叶变换，同时在数理方程中有着重要作用，例如之前在学习解简单的偏微分方程时。

相应还有频域的微积分性质，道理是一样的：

$F\left( j\omega \right) =\int_{-\infty}^{+\infty}{f\left( t \right) e^{-j\omega t}\mathrm{d}t} \\ \frac{\mathrm{d}}{\mathrm{d}\omega}F\left( j\omega \right) =\int_{-\infty}^{+\infty}{-jtf\left( t \right) e^{-j\omega t}\mathrm{d}t} \\ \mathcal{F} \left[ \frac{\mathrm{d}}{\mathrm{d}\omega}F\left( j\omega \right) \right] =\frac{1}{j}\int_{-\infty}^{+\infty}{tf\left( t \right) e^{-j\omega t}\mathrm{d}t} \\ tf\left( t \right) \longleftrightarrow j\frac{\mathrm{d}}{\mathrm{d}\omega}F\left( j\omega \right)$

频域积分定理和时域积分定理的证明十分类似，这里就直接给出结论：

$\int_{-\infty}^{\omega}{F\left( j\omega \right)}\mathrm{d}\omega \longleftrightarrow \left( \pi \delta \left( t \right) -\frac{1}{jt} \right) f\left( t \right)$

最后的时域和频域卷积定理我们以后再说，利用上述性质可以推出一系列函数的傅里叶变换：

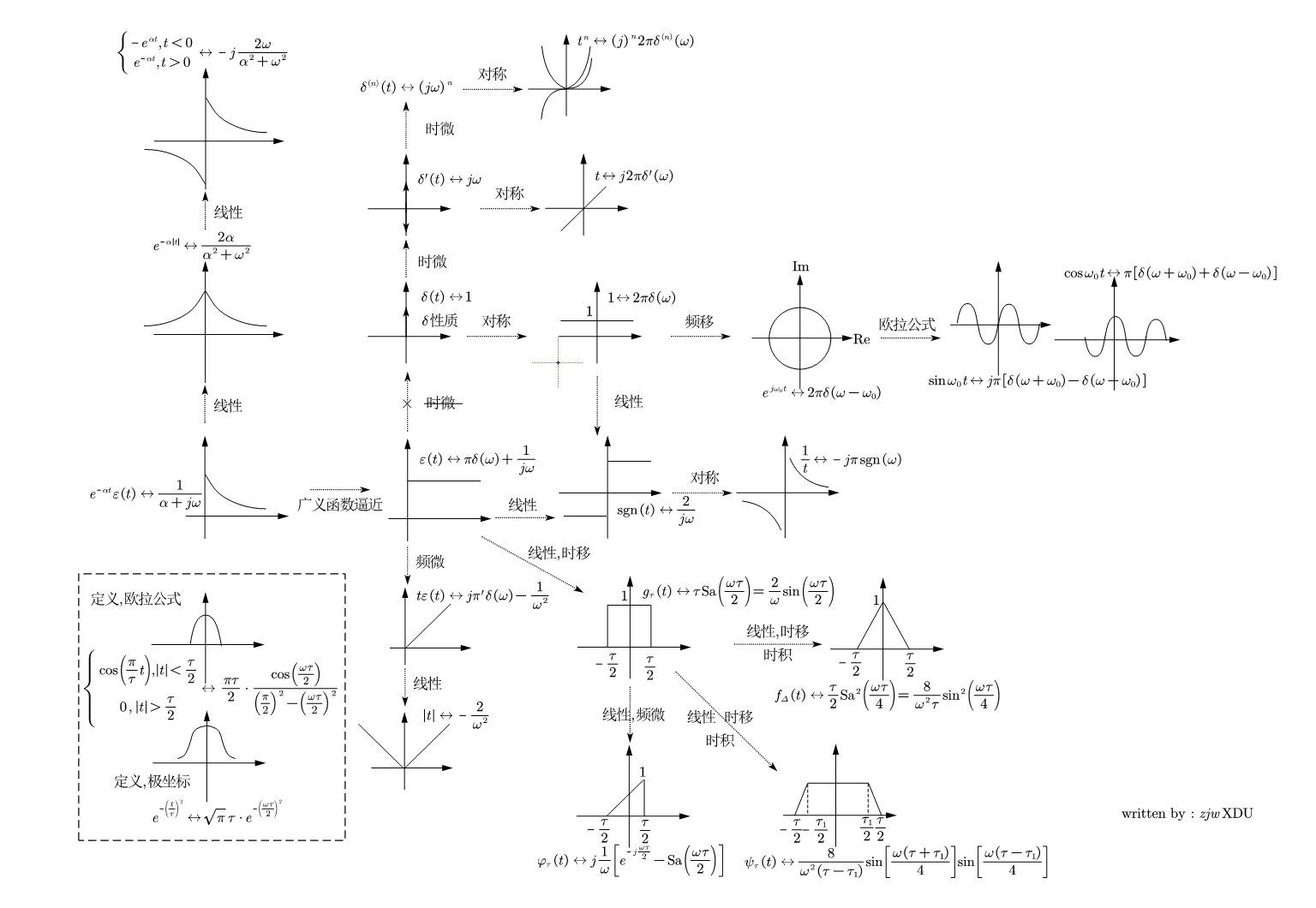
这张图整理了常用的傅里叶变换对以及它们的联系，这里主要要提的是右下角的几个能量信号的傅里叶变换。门函数可以由两个阶跃函数线性表示，所以通过时移性质，尺度变换和线性性质可以从阶跃函数的傅里叶变换导出门函数的傅里叶变换，当然直接用定义计算也不复杂。我们在这里写一下由阶跃函数导出的过程，可以有助于加深对前面性质的应用：

$\varepsilon \left( t \right) \longleftrightarrow \pi \delta \left( \omega \right) +\frac{1}{j\omega} \\ g_{\tau}\left( t \right) =\varepsilon \left( t+\frac{\tau}{2} \right) -\varepsilon \left( t-\frac{\tau}{2} \right) \\ \text{由时移性质},\mathcal{F} \left[ g_{\tau}\left( t \right) \right] =e^{j\frac{\tau}{2}\omega}\left( \pi \delta \left( \omega \right) +\frac{1}{j\omega} \right) -e^{-j\frac{\tau}{2}\omega}\left( \pi \delta \left( \omega \right) +\frac{1}{j\omega} \right) \\ =\frac{e^{j\frac{\tau}{2}\omega}-e^{-j\frac{\tau}{2}\omega}}{j\omega}=\frac{2}{\omega}\sin \left( \frac{\omega \tau}{2} \right) =\tau \mathrm{Sa}\left( \frac{\omega \tau}{2} \right)$

这样我们就知道了，门函数的傅里叶变换是个Sa函数。

对于三角脉冲，我们发现它的导函数是两个平移并且尺度变换后的门相加在一起，直流分量为0。所以我们可以应用时域积分定理：

$g_{\tau}\left( t \right) \longleftrightarrow \tau \mathrm{Sa}\left( \frac{\omega \tau}{2} \right) =\frac{2}{\omega}\sin \left( \frac{\omega \tau}{2} \right) \\ f_{\varDelta}^{'}\left( t \right) =\frac{2}{\tau}\left[ g_{\tau}\left( 2t+\frac{\tau}{2} \right) -g_{\tau}\left( 2t-\frac{\tau}{2} \right) \right] \\ \mathcal{F} \left[ f_{\varDelta}^{'}\left( t \right) \right] =\frac{2}{\tau}\left[ e^{j\frac{\tau}{4}\omega}\frac{2}{\omega}\sin \left( \frac{\omega \tau}{4} \right) -e^{-j\frac{\tau}{4}\omega}\frac{2}{\omega}\sin \left( \frac{\omega \tau}{4} \right) \right] \\ =\frac{4}{\tau \omega}\sin ^2\left( \frac{\omega \tau}{4} \right) 2j \\ \text{由时域积分性质}: \\ \mathcal{F} \left[ f_{\varDelta}\left( t \right) \right] =\left[ \pi \delta \left( \omega \right) +\frac{1}{j\omega} \right] \frac{4}{\tau \omega}\sin ^2\left( \frac{\omega \tau}{4} \right) 2j \\ =\frac{8}{\omega ^2\tau}\sin ^2\left( \frac{\omega \tau}{4} \right) =\frac{\tau}{2}\mathrm{Sa}^2\left( \frac{\omega \tau}{4} \right)$

对于锯齿脉冲，情况稍微复杂一点，我们最好把它利用频域微分性质，得到一个门函数乘$t$的表示，再利用门函数的傅里叶变换，得到锯齿脉冲：

$g_{\tau}\left( t \right) \longleftrightarrow \tau \mathrm{Sa}\left( \frac{\omega \tau}{2} \right) =\frac{2}{\omega}\sin \left( \frac{\omega \tau}{2} \right) \\ \text{由频域微分性质}: \\ tg_{\tau}\left( t \right) \longleftrightarrow j\left[ \frac{\tau}{\omega}\cos \left( \frac{\omega \tau}{2} \right) -\frac{2}{\omega ^2}\sin \left( \frac{\omega \tau}{2} \right) \right] \\ \varphi \left( t \right) =\frac{1}{\tau}\left( tg_{\tau}\left( t \right) +\frac{\tau}{2}g_{\tau}\left( t \right) \right) \\ \text{所以由线性性质}: \\ \mathcal{F} \left[ \varphi \left( t \right) \right] =\frac{j}{\tau}\left[ \frac{\tau}{\omega}\cos \left( \frac{\omega \tau}{2} \right) -\frac{2}{\omega ^2}\sin \left( \frac{\omega \tau}{2} \right) \right] +\frac{1}{\omega}\sin \left( \frac{\omega \tau}{2} \right) \\ =j\frac{1}{\omega}\left[ e^{-j\frac{\omega \tau}{2}}-\mathrm{Sa}\left( \frac{\omega \tau}{2} \right) \right]$

至于梯形脉冲，道理和三角形脉冲完全一致。最后要补充的就是由于直流分量被微分后就变成0了，所以时域微分性质时要单独考虑直流分量。有些时候，去掉一个直流分量，时域函数会变成奇对称的，这时就可以很安全的用时域微分性质，但像门函数，还是不行，那就老老实实积分或者用别的办法。时域积分性质默认指的是变上限积分就是$f(t)$，这是不一定的。我们下面进行一些注解：

$\text{记}f'\left( t \right) =g\left( t \right) \\ \text{则}\int_{-\infty}^t{g\left( t \right) \mathrm{d}t}=f\left( t \right) -f\left( -\infty \right) \\ \text{我们发现当}f\left( -\infty \right) \ne 0\text{时},g^{\left( -1 \right)}\left( t \right) \ne f\left( t \right) \\ \text{所以}f\left( t \right) =f\left( -\infty \right) +\int_{-\infty}^t{g\left( t \right) \mathrm{d}t} \\ \mathcal{F} \left[ f\left( t \right) \right] =2\pi f\left( -\infty \right) \delta \left( \omega \right) +\pi G\left( 0 \right) \delta \left( \omega \right) +\frac{G\left( j\omega \right)}{j\omega} \\ \text{这里}G\left( j\omega \right) \text{是}g\left( t \right) \text{的傅里叶变换}, \\ G\left( 0 \right) =\int_{-\infty}^{+\infty}{g\left( t \right)}=f\left( +\infty \right) -f\left( -\infty \right) \\ \text{所以上式变为}, \\ \mathcal{F} \left[ f\left( t \right) \right] =\pi \left[ f\left( +\infty \right) +f\left( -\infty \right) \right] \delta \left( \omega \right) +\frac{G\left( j\omega \right)}{j\omega} \\ \text{所以区别就在于}2\pi f\left( -\infty \right) \delta \left( \omega \right) \\ \text{同时我们也要注意到}: \\ g\left( t \right) \longleftrightarrow j\omega F\left( j\omega \right) =G\left( j\omega \right) \\ \text{则}F\left( j\omega \right) =\frac{1}{j\omega}G\left( j\omega \right) \\ \text{而}F\left( j\omega \right) =\pi \left[ f\left( +\infty \right) +f\left( -\infty \right) \right] \delta \left( \omega \right) +\frac{G\left( j\omega \right)}{j\omega} \\ \text{可见只有在}f\left( +\infty \right) +f\left( -\infty \right) =0\text{时},\text{积分性质和微分性质} \\ \text{才能同时取得正确的计算结果},\text{即无直流分量}$

这些就是能应付期中考试部分的傅里叶变换内容了……