概率论3

阅读数: 次 2022-02-25

在本篇我们要先对之前说的随机变量做一些补充，之后给出随机变量的数字特征，如方差，期望，协方差。

在考试中往往会遇到二维随机变量函数及其分布，这个问题值得整理，第一是考的多，第二是数理统计里要用到。

求法和之前计算$Y=X^2$时是一样的，都可以用分布函数法来计算，我们先用一般的例子来练习：

$f\left( x,y \right) =\left\{ \begin{array}{c} \frac{1}{2}\left( x+y \right) e^{-\left( x+y \right)},x>0,y>0\\ 0,\mathrm{else}\\ \end{array} \right.$

求$Z=X+Y$的概率密度：

我们直接求分布函数，再对分布函数求导：

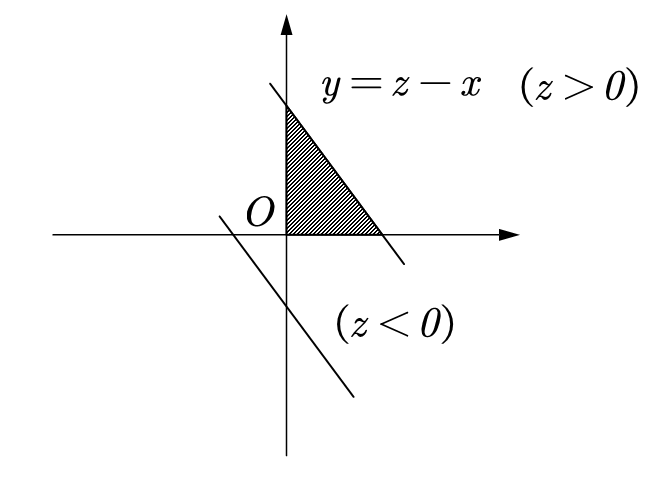
$F_Z\left( z \right) =P\left( Z\leqslant z \right) =P\left( X+Y\leqslant z \right) =\iint_{x+y\leqslant z}{f\left( x,y \right) \mathrm{d}x\mathrm{d}y}$

我们做出了积分区域，这样方便我们计算上式的重积分。我们可以看到，不同的$Z$的取值，结果是不一样的。所以我们往往需要进行分类讨论。

$z>0:\int_0^z{\int_0^{z-x}{\frac{1}{2}\left( x+y \right) e^{-\left( x+y \right)}\mathrm{d}y\mathrm{d}x}}=1-ze^{-z}-e^{-z}-\frac{1}{2}z^2e^{-z} \\ f_Z\left( z \right) =F_{Z}^{'}\left( z \right) =\frac{1}{2}z^2e^{-z}$

一定要记住求完分布函数以后，要求导。因为有时候求分布函数可能需要许多次分部积分，然后最后好不容易算出来，结果就忘了。一定要记住求导求成概率密度函数。

$z\leqslant 0:f_Z\left( z \right) =0$

$z \leqslant 0$时显然概率密度为0。

这种加法实际上十分特殊，可以被推成一个公式，这个公式仿佛信号处理中的卷积：

$f_Z\left( z \right) =\int_{-\infty}^{+\infty}{f\left( z-y,y \right) \mathrm{d}y}=\int_{-\infty}^{+\infty}{f\left( x,z-x \right) \mathrm{d}x}$

如果$X,Y$相互独立，则可以把被积函数拆开成对应的概率密度函数。

这样只用积分一次，会很简洁，例如对上面那道例题：

$f_Z\left( z \right) =\int_{-\infty}^{+\infty}{f\left( z-y,y \right) \mathrm{d}y},z-y>0,y>0\rightarrow 0<y<z \\ =\int_0^z{\frac{1}{2}ze^{-z}\mathrm{d}y=}\frac{1}{2}z^2e^{-z}$

现在我们考虑$X\sim N\left( \mu _1,\sigma _{1}^{2} \right) ,Y\sim N\left( \mu _2,\sigma _{2}^{2} \right) $，求$Z=X+Y$（$X,Y$相互独立）。

$f_X\left( x \right) =\frac{1}{\sqrt{2\pi}\sigma _1}e^{-\frac{\left( x-\mu _1 \right) ^2}{2\sigma _{1}^{2}}},f_Y\left( y \right) =\frac{1}{\sqrt{2\pi}\sigma _2}e^{-\frac{\left( y-\mu _2 \right) ^2}{2\sigma _{2}^{2}}} \\ f_Z\left( z \right) =\int_{-\infty}^{+\infty}{f_X\left( z-y \right) f_Y\left( y \right) \mathrm{d}y}=\frac{1}{2\pi}\int_{-\infty}^{+\infty}{\begin{array}{c} \frac{1}{\sigma _1\sigma _2}e^{-\frac{\left( z-y-\mu _1 \right) ^2}{2\sigma _{1}^{2}}-\frac{\left( y-\mu _2 \right) ^2}{2\sigma _{2}^{2}}}\mathrm{d}y\\ \end{array}} \\ =\frac{1}{2\pi \sigma _1\sigma _2}\int_{-\infty}^{+\infty}{\begin{array}{c} e^{-\frac{\left( z-y-\mu _1 \right) ^2}{2\sigma _{1}^{2}}-\frac{\left( y-\mu _2 \right) ^2}{2\sigma _{2}^{2}}}\mathrm{d}y\\ \end{array}}$

最后的这个积分式子需要一定的技巧，原则上我们要意识到，对于反常积分，大多数时候我们只能由高斯积分计算。

$\int_{-\infty}^{+\infty}{\begin{array}{c} e^{-t^2}\mathrm{d}t\\ \end{array}}=\sqrt{\pi}$

根据这个思想，我们考虑把上式的指数部分凑成一个带有平方的形式：

$a\left( y-b \right) ^2+c \\ =\frac{z^2}{\sigma _{1}^{2}}-\frac{2zy}{\sigma _{1}^{2}}+\frac{y^2}{\sigma _{1}^{2}}-\frac{2\mu _1z}{\sigma _{1}^{2}}+\frac{2\mu _1y}{\sigma _{1}^{2}}+\frac{\mu _{1}^{2}}{\sigma _{1}^{2}}-\frac{y^2}{\sigma _{2}^{2}}+\frac{2\mu _2y}{\sigma _{2}^{2}}-\frac{\mu _{2}^{2}}{\sigma _{2}^{2}} \\ =\left( \frac{1}{\sigma _{1}^{2}}+\frac{1}{\sigma _{2}^{2}} \right) y^2-\left( \frac{2\mu _1}{\sigma _{1}^{2}}+\frac{2\mu _2}{\sigma _{2}^{2}}-\frac{2z}{\sigma _{1}^{2}} \right) y+\frac{z^2}{\sigma _{1}^{2}}-\frac{2\mu _1z}{\sigma _{1}^{2}}+\frac{\mu _{1}^{2}}{\sigma _{1}^{2}}-\frac{\mu _{2}^{2}}{\sigma _{2}^{2}} \\ a=\frac{1}{\sigma _{1}^{2}}+\frac{1}{\sigma _{2}^{2}} \\ b=\frac{\left( \frac{\mu _1}{\sigma _{1}^{2}}+\frac{\mu _2}{\sigma _{2}^{2}}-\frac{z}{\sigma _{1}^{2}} \right)}{\left( \frac{1}{\sigma _{1}^{2}}+\frac{1}{\sigma _{2}^{2}} \right)}=\frac{\mu _1\sigma _{2}^{2}+\mu _2\sigma _{1}^{2}-\sigma _{2}^{2}z}{\sigma _{1}^{2}+\sigma _{2}^{2}} \\ c=\frac{z^2}{\sigma _{1}^{2}}-\frac{2\mu _1z}{\sigma _{1}^{2}}+\frac{\mu _{1}^{2}}{\sigma _{1}^{2}}-\frac{\mu _{2}^{2}}{\sigma _{2}^{2}}-a\cdot b^2 \\ =\frac{\left( z-\mu _1-\mu _2 \right) ^2}{\sigma _{1}^{2}+\sigma _{2}^{2}}$

这对于很长时间不计算的人来说可以是一道非常好的练习题目。然后直接计算：

$f_Z\left( z \right) =\frac{1}{2\pi \sigma _1\sigma _2}e^{\frac{\left( z-\mu _1-\mu _2 \right) ^2}{2\left( \sigma _{1}^{2}+\sigma _{2}^{2} \right)}}\int_{-\infty}^{+\infty}{\begin{array}{c} e^{\frac{a\left( y-b \right)}{2}^2}\mathrm{d}y\\ \end{array}}=\frac{1}{\sqrt{2\pi}\sigma _1\sigma _2}e^{\frac{\left( z-\mu _1-\mu _2 \right) ^2}{\sigma _{1}^{2}+\sigma _{2}^{2}}}$

可见，正态分布具有可加性。更一般的可以推广到有限个独立的正态随机变量的线性组合。实际上考试时候应该不会这么复杂，但还是要记好上面的高斯积分。

最后，当谈及负指数分布的时候，例如某个系统元件的寿命。我们往往要关注这个系统的最值，例如最差的那根保险丝之类的。这个时候往往会涉及一个特殊的分布：极值分布。它说的是$X_1,X_2,…,X_n$是$n$个独立的随机变量，它们的分布函数分别为$F_{X_1}\left( x_1 \right) ,F_{X_2}\left( x_2 \right) ,…,F_{X_n}\left( x_n \right) $，求关于$M=\max \left\{ X_1,X_2,…,X_n \right\} ,N=\min \left\{ X_1,X_2,…,X_n \right\} $。我们仍可以用分布函数法进行计算：

$F_M\left( x \right) =F_{\max}\left( x \right) =P\left( \max \left( X_1,X_2,...,X_n \right) \leqslant x \right) \\ =P\left( X_1\leqslant x,X_2\leqslant x,...,X_n\leqslant x \right) \\ =P\left( X_1\leqslant x \right) P\left( X_2\leqslant x \right) ...P\left( X_n\leqslant x \right) \\ =\prod_{i=1}^n{F_{X_i}\left( x \right)} \\ f_M\left( x \right) =F_{M}^{'}\left( x \right) =\frac{\mathrm{d}}{\mathrm{d}x}\left[ \prod_{i=1}^n{F_{X_i}\left( x \right)} \right]$

对于极小值分布，方法是一样的：

$F_N\left( x \right) =F_{\min}\left( x \right) =P\left( \min \left( X_1,X_2,...,X_n \right) \leqslant x \right) \\ =1-P\left( X_1>x,X_2>x,...,X_n>x \right) \\ =1-P\left( X_1>x \right) P\left( X_2>x \right) ...P\left( X_n>x \right) \\ =1-\left[ 1-P\left( X_1\leqslant x \right) \right] \left[ 1-P\left( X_2\leqslant x \right) \right] ...\left[ 1-P\left( X_n\leqslant x \right) \right] \\ =1-\prod_{i=1}^n{\left( 1-F_{X_i}\left( x \right) \right)} \\ f_N\left( x \right) =F_{N}^{'}\left( x \right) =\frac{\mathrm{d}}{\mathrm{d}x}\left[ 1-\prod_{i=1}^n{\left( 1-F_{X_i}\left( x \right) \right)} \right]$

当它们属于同一个分布函数时，连乘直接化为$n$次方。当引入极值分布后，我们需要对随机变量有一个新的认识，在之前我们学习的过程中，往往会将随机变量认为是一个“未知数”，“自变量”。但当牵扯到多个随机变量的时候，更好的一个观点是把它看成一个“不断变化的数字”，这个数字的出现规律受其概率密度函数约束，当进行一次抽样，这个值将确定下来。这个视角将有助于理解后面的数理统计。

现在引入期望（不加说明我们都说它绝对收敛）：

$EX=\sum_i{x_ip_i}\rightarrow \int_{-\infty}^{+\infty}{xf\left( x \right) \mathrm{d}x}$

以及，随机变量函数的期望可以直接将$X$换成$g(X)$，证明就不管了。这个性质十分重要，也就是：

$Y=g\left( X \right) ,EY=\sum_i{g\left( x_i \right) p_i}\rightarrow \int_{-\infty}^{+\infty}{g\left( x \right) f\left( x \right) \mathrm{d}x}$

这个定理可以让我们在不计算$g(X)$分布律的情况下直接得出期望，十分方便。

二维及高维情况下是一样的。

期望在任何时候都是可加和的：$E(X+Y)=EX+EY$，当独立的时候，乘积可拆分：$E(XY)=EX \cdot EY$。

方差是用于计算偏离程度的统计量，与$E(|X-EX|)$比不带绝对值，性质更好：

$DX=\sum_i{\left( x_i-EX \right) ^2p_i}=\int_{-\infty}^{+\infty}{\left( x-EX \right) ^2f\left( x \right) \mathrm{d}x} \\ DX=E\left( X-EX \right) ^2=EX_2-\left( EX \right) ^2$

协方差用于度量$X,Y$的相关关系：

$\mathrm{cov}\left( X,Y \right) =E\left[ \left( X-EX \right) \left( Y-EY \right) \right] \\ =E\left( XY \right) -E\left( X \right) E\left( Y \right)$

当$\mathrm{cov}\left( X,Y \right)=0$时称两者不相关，期望和协方差间满足：$D\left( X\pm Y \right) =DX+DY\pm 2\mathrm{cov}\left( X,Y \right) $。其他一些比较显然的性质这里就略掉了。相关系数$\rho_{XY}$用于定义$X,Y$的（线性）相关性：

$\rho _{XY}=\frac{\mathrm{cov}\left( X,Y \right)}{\sqrt{DX}\sqrt{DY}}$

实际上相关系数正是二维正态分布里的$\rho$：

$f\left( x,y \right) =\frac{1}{2\pi \sigma _1\sigma _2\sqrt{1-\rho ^2}}e^{-\frac{1}{2\left( 1-\rho ^2 \right)}\left[ \frac{\left( x-\mu _1 \right) ^2}{\sigma _{1}^{2}}-2\rho \frac{\left( x-\mu _1 \right) \left( y-\mu _2 \right)}{\sigma _1\sigma _2}+\frac{\left( y-\mu _2 \right) ^2}{\sigma _{2}^{2}} \right]}$

常用的期望和方差需要记住，我们下面做一些整理：

$X\sim B\left( n,p \right) ,EX=np,DX=np\left( 1-p \right) \\ X\sim P\left( \lambda \right) ,EX=\lambda ,DX=\lambda \\ X\sim U\left( a,b \right) ,EX=\frac{a+b}{2},DX=\frac{\left( b-a \right) ^2}{12} \\ X\sim N\left( \mu ,\sigma ^2 \right) ,EX=\mu ,DX=\sigma ^2 \\ X\sim E\left( \lambda \right) ,EX=\frac{1}{\lambda},DX=\frac{1}{\lambda ^2}$

常用分布的字母表达需要记住，$B$意思是binary，二项分布。$P$意思是Poisson，泊松分布。$U$是uniform，均匀分布。$N$是normal，是正态分布。$E$是exponential，是指数分布。

几何分布和超几何分布这里就略去了，有兴趣的可以查一下咩。

现在我们用一道例题来结束这一篇，严格来说，书上还讲了$n$维随机变量一节，但是考试不会考，虽然在后面的随机过程……贝叶斯优化烂七八糟力会用到它，但是到时候再说吧。

设二维连续型随机变量$(X,Y)$的联合概率密度为：

$f\left( x,y \right) =\left\{ \begin{array}{c} \frac{1}{2}\sin \left( x+y \right) ,0\leqslant x\leqslant \frac{\pi}{2},0\leqslant y\leqslant \frac{\pi}{2}\\ 0,\mathrm{else}\\ \end{array} \right.$

求随机变量$X,Y$的相关系数$\rho_{XY}$：

这个积分运算用到分部积分，比较繁琐，一定要细心算。

$EX=\int_{-\infty}^{+\infty}{\int_{-\infty}^{+\infty}{xf\left( x,y \right) \mathrm{d}x\mathrm{d}y}}=\frac{1}{2}\int_0^{\frac{\pi}{2}}{\int_0^{\frac{\pi}{2}}{x\sin \left( x+y \right) \mathrm{d}x\mathrm{d}y}} \\ =\frac{1}{2}\int_0^{\frac{\pi}{2}}{\left( \left[ -\cos \left( x+y \right) x \right] _{0}^{\frac{\pi}{2}}+\int_0^{\frac{\pi}{2}}{\cos \left( x+y \right) \mathrm{d}x} \right)}\mathrm{d}y \\ =\frac{1}{2}\int_0^{\frac{\pi}{2}}{\left( \frac{\pi}{2}\sin y+\cos y-\sin y \right) \mathrm{d}y}=\frac{\pi}{4} \\ EX^2=\frac{1}{2}\int_0^{\frac{\pi}{2}}{\int_0^{\frac{\pi}{2}}{x^2\sin \left( x+y \right) \mathrm{d}x\mathrm{d}y}} \\ =\frac{1}{2}\int_0^{\frac{\pi}{2}}{\left( \frac{\pi ^2}{4}\sin y+2\left( \frac{\pi}{2}\cos y-\left( \sin y+\cos y \right) \right) \right) \mathrm{d}y}=\frac{\pi}{4} \\ =\frac{\pi ^2}{8}+\frac{\pi}{2}-2 \\ DX=EX^2-\left( EX \right) ^2=\frac{\pi ^2}{8}+\frac{\pi}{2}-2-\frac{\pi ^2}{16}=\frac{\pi ^2}{16}+\frac{\pi}{2}-2$

由于对称性，$EY,DY$和$EX,DX$是一样的。现在还需要计算$E(XY)$：

$E\left( XY \right) =\frac{1}{2}\int_0^{\frac{\pi}{2}}{y\int_0^{\frac{\pi}{2}}{x\sin \left( x+y \right) \mathrm{d}x\mathrm{d}y}} \\ =\frac{1}{2}\int_0^{\frac{\pi}{2}}{y\left( \frac{\pi}{2}\sin y+\cos y-\sin y \right) \mathrm{d}y}=\frac{\pi}{2}-1$

所以相关系数即可计算：

$\rho _{XY}=\frac{\mathrm{cov}\left( X,Y \right)}{\sqrt{DX}\sqrt{DY}}=\frac{E\left( XY \right) -EX\cdot EY}{\sqrt{DX}\sqrt{DY}} \\ =\frac{\frac{\pi}{2}-1-\frac{\pi ^2}{16}}{\frac{\pi ^2}{16}+\frac{\pi}{2}-2}$