时间序列

阅读数: 次 2022-02-01

时间序列是数理统计的一个分支，有其独特的一些内容，本篇记录了一下最经典的ARIMA模型。

介绍$ARIMA$是因为它在应用时间序列分析中意义很深远，并且理论很精巧。并且有很多变式，但是其实只要理解最基本的$ARIMA$那些变形也都很好理解。虽然很多软件，比如SPSS，matlab。以及R语言里都封装好了这一函数，但是如果不对原理做一些了解，运行的结果差了可能也不会改，想直接拿来主义也只能拿张图，然后直接搬来点公式硬套，效果不会很好。

在介绍$ARIMA$之前有两个简单的前置概念要补充，差分算子和延迟算子。

差分算子$\nabla x_t=x_t-x_{t-1}$，这里的差分和微分方程那里不同的地方在于，不用强调向前还是向后，因为我要预测的是下一时刻的值，我肯定只有上一时刻之前的值，将差分后的结果再进行差分，就是高阶差分，记作$\nabla ^dx_t=\nabla ^{d-1}x_t-\nabla ^{d-1}x_{t-1}$，$d$是阶数。当然差分也并不是要求一定要挨着，也可以隔着，这种叫作$k$步差分，差分的用处后面会提到。

延迟算子$x_{t-q}=B^qx_t$，$q$是阶数，起到一个时间回拨指针的作用，在后面的理论部分会用到，只是个符号。

这两个算子可以表达为：$\nabla ^d=\left( 1-B \right) ^d$

$ARIMA$模型分为三个部分，$AR$，$I$和$MA$，它们的名字分别是Auto Regressive, Integrated, Moving Average，我们下面来简单解释：

在介绍之前我们要先强调一个叫作“平稳”的概念，这个概念说的是，对于一个随机变量序列，我们可以多次重复实验，来得到其中每个随机变量更多的样本，但是对于时间序列，它一般是不可重复的，所以我们需要一个强化的条件，比如这一串时间序列它们的均值和方差是一样的，由于均值相同可以作变量代换，所以也就是我们可以估计的时间序列，是零均值并且方差要相同。我们管这样的序列叫平稳的，当然还有一个极端的情况，就是随机白噪声，它也满足我们所说的条件，这引出了随机性检验，简单来说就是要看数据间的自相关系数，如果它们互相都独立，那么我们实际上没有必要再预测了，只需要继续生成白噪声就好了。随机性检验不仅用在了判断一个序列是否值得做预测，也用在了判断后面对时间序列信息的提取得不得当，这个我们后面再说。

我们略去了“平稳”这一概念的数学定义，我们要关注的是，满足平稳这一条件的一个序列$\left\{ \varepsilon _t \right\} ,E\left( \varepsilon _t \right) =0,\mathrm{Var}\left( \varepsilon _t \right) =\sigma _{\varepsilon}^{2}$，它有十分重要的意义，我们后面会沿用这个符号。

$AR$模型说的是：

$x_t=\phi _0+\phi _1x_{t-1}+\phi _2x_{t-2}+...+\phi _px_{t-p}+\varepsilon _t$

注意，这里的$\varepsilon_t$是零均值的白噪声序列，也就是说序列的随机变量相互独立。

当对它进行中心化处理，即：

$\mu =\frac{\phi _0}{1-\phi _0-...-\phi _p},y_t=x_t-\mu$

我们就叫它为中心化的$AR(p)$模型，$p$是阶数。这个时候用上面说的延迟算子$B$，来记成一种更简洁的形式：

$\varPhi \left( B \right) y_t=\varepsilon _t \\ \varPhi \left( B \right) =1-\phi _1B-\phi _2B^2-...-\phi _pB^p$

如果我们不看后面的$\varepsilon_t$这一值，我们很自然的觉得这是由前$p$项作线性回归预测下一项。但是它又有个零均值的平稳序列，如果没有仔细的阅读相关知识，很可能会觉得“这就是加了一个随机扰动”，如果这么想会对后面的理解产生巨大的困难。我们这个时候还没有说到参数估计，但是可以先感性的理解一下：最后的那个式子表明，我们是想让真实值减预测值，满足这么一个序列，而且这个序列最好是白噪声，从信息论的角度看它不包含任何有效信息。更自然的是我们还希望这个白噪声的方差越小越好。也就是说这个值并不是在计算的时候给定的，它更大的意义在于：预测值=确定信息+不确定信息，在此基础上希望不确定信息尽可能小。

那么显然，这里我们是给确定信息可选的阶数$p$，不确定信息始终只有一项，所以这就引出了$MA$模型。

在引出之前，还需要补充一个知识，$AR$模型可以看作一个非齐次的线性差分方程，这里我们就不补充差分方程方面的内容了，直接给出下面的结论：$\varPhi \left( x \right) =0$的解是齐次线性差分方程$\varPhi \left( B \right) x_t=0$的特征根的倒数，并且特征根全部在单位圆内（这个要求其实等价于$AR$模型平稳）。

所以$\varPhi \left( B \right)$可因式分解成$\varPhi \left( B \right) =\prod_{i=1}^p{\left( 1-\lambda _iB \right)}$，所以对于$AR$模型这个非齐次的线性差分方程，特解为：

$x_t=\frac{\varepsilon _t}{\varPhi \left( B \right)}=\frac{\varepsilon _t}{\prod_{i=1}^p{\left( 1-\lambda _iB \right)}}=\sum_{i=1}^p{\frac{k_i}{1-\lambda _iB}\varepsilon _t}$

值得注意的是，我们知道特征根全在单位圆内，由复变函数中的知识，结合求和符号换序：

$=\sum_{i=1}^p{\frac{k_i}{1-\lambda _iB}\varepsilon _t} \\ =\sum_{i=1}^p{\sum_{j=0}^{\infty}{k_i\left( \lambda _iB \right) ^j\varepsilon _t}} \\ =\sum_{j=0}^{\infty}{\sum_{i=1}^p{k_i\lambda _{i}^{j}\varepsilon _{t-j}}} \\ =\sum_{j=0}^{\infty}{G_j\varepsilon _{t-j}}$

上式中的$G_j$称作格林函数，这个式子称为$AR$模型的传递形式，但是很多时候我们并不需要真正求解特征根，由待定系数是可以得出格林函数的系数与我们前面谈论的$\phi _j$的关系，这个并不是我们这里的重点，重点是上面的$x_t=…+\varepsilon _t$可以写成这样一个$\left\{ \varepsilon _t \right\} $的线性组合，这一点最开始会令人觉得有点难以接受，但习惯就好。

有了这个铺垫以后就可以很方便的介绍$MA$模型，$MA$的结构如下所示：

$x_t=\mu +\varepsilon _t-\theta _1\varepsilon _{t-1}-\theta _2\varepsilon _{t-2}-...-\theta _q\varepsilon _{t-q} \\ y_t=x_t-\mu \\ y_t=\varTheta \left( B \right) \varepsilon _t \\ \varTheta \left( B \right) =1-\theta _1B-\theta _2B^2-...-\theta _qB^q$

你看到这个式子会有一种感觉，它好像和$AR$是对偶的，这就对了。同样也可以说，$MA$是“预测值=确定信息+不确定信息”，只是这里的确定信息只有样本均值，而$\varepsilon$有许多，这里的$\varepsilon$也要符合零均值白噪声的要求，但是，讲到现在，要意识到$\varepsilon$不止包含着不可估计的值，也就是在随机数生成之前我并不知道是多少的那种值，也包含着有些确定的预测值与真实值的差，这些差当然也要满足零均值白噪的条件。

$MA$模型抛开变量与$AR$完全一致，上面引出格林函数的过程可以用于引出逆转函数$I$，也就是$MA$的可逆与$AR$的平稳完全对偶。用符号表示也就是，如果$MA$满足可逆性条件，则可以写成这两种形式：

$\left\{ \begin{array}{c} \varTheta \left( B \right) \varepsilon _t=x_t\\ \varepsilon _t=I\left( B \right) x_t\\ \end{array} \right.$

所以我们会发现，这两者其实完全对偶，只不过一个更注重确定信息，比如$x_{t-1}$，一个更注重于不确定性信息$\varepsilon$。将这两个模型合并，就得到了$ARMA$，也就是将等号的两端各自进行扩充，进行更细致的刻画：

$\left. \begin{array}{c} \varPhi \left( B \right) x_t=\varepsilon _t\\ \varTheta \left( B \right) \varepsilon _t=x_t\\ \end{array} \right\} \rightarrow \varPhi \left( B \right) x_t=\varTheta \left( B \right) \varepsilon _t$

要注意，这里指出，如果我们的$ARMA$模型满足平稳和可逆，那么它也可以被写成上面的用到格林函数的这样一种统一的形式，我们即称其为历史观察值的线性函数，只是格林函数取值的递推式上有一些区别，推导过程这里就不展开了，这里给出结果来加深印象：

$AR\left\{ \begin{array}{c} G_0=1\\ G_k=\sum_{j=1}^k{\phi _jG_{k-j}},k\geqslant 1\\ \end{array} \right. ,ARMA\left\{ \begin{array}{c} G_0=1\\ G_k=\sum_{j=1}^k{\phi _jG_{k-j}-\theta _j},k\geqslant 1\\ \end{array} \right.$

构造出这个模型，再进行参数估计，阶数($p,q$)选取，这两个过程这里就略过了。我们可以开始预测，这也是我们最想知道的一点，就是当我们用那些现成的软件和函数时，到底预测值是怎么算出来的，如果只是用$AR$模型，可能还好理解，但是用上$MA$以后，就不太显然了。

我们现在利用之前说的格林函数和逆转函数进行分析，容易导出：

$x_t=\sum_{i=0}^{\infty}{G_i\varepsilon _{t-i}} \\ \varepsilon _t=\sum_{j=0}^{\infty}{I_jx_{t-j}}$

将两式联立，可以得到：

$x_t=\sum_{i=0}^{\infty}{\begin{array}{c} \begin{array}{c} G_i\left( \sum_{j=0}^{\infty}{I_jx_{t-i-j}} \right)\\ \end{array}\\ \end{array}=\sum_{i=0}^{\infty}{C_ix_{t-1-i}}}$

也就是说，$t+l$时的序列值可以被$t+l-1,t+l-2…$的历史数据来表示，只是其中有些可能未知而已。这个结论被用于推导预测方差最小原则，这里我们先不管了。所以当用$ARMA$进行预测时：

$x_t\left( l \right) =E\left( \phi _1x_{t+l-1}+...+\phi _px_{t+l-p}+\varepsilon _{t+l}-\theta _1\varepsilon _{t-l-1}-...-\theta _q\varepsilon _{t-l-q}|x_t,x_{t-1},... \right) \\ =\left\{ \begin{array}{c} \phi _1\hat{x}_t\left( l-1 \right) +...+\phi _p\hat{x}_t\left( l-p \right) -\sum_{i=1}^q{\theta _i\varepsilon _{t+l-i}},l\leqslant q\\ \phi _1\hat{x}_t\left( l-1 \right) +...+\phi _p\hat{x}_t\left( l-p \right) ,l>q\\ \end{array} \right.$

当估计值有真实值存在时，估计值就是真实值。所以$\hat{x}\left( t \right) $如果是已知的序列值，就会是相应的序列值，如果不是就会再迭代计算。同样，当预测步长比$MA$的阶数$q$小的时候，$\varepsilon$是可以有已知的值的，当步长超出$q$时，由于序列$\varepsilon$均值是零，所以就不计了。所以要预测长期数据的时候，可以选择短期多步预测，将预测值记作真实值继续运算，可以证明这样会减少预测方差。

至于$I$，可以将其狭隘的理解成差分操作，具体细节这里不做展开，它的目的是将非平稳序列变成平稳的来进行分析，所以三者凑在一起，变成了$ARIMA$。它被简记为：

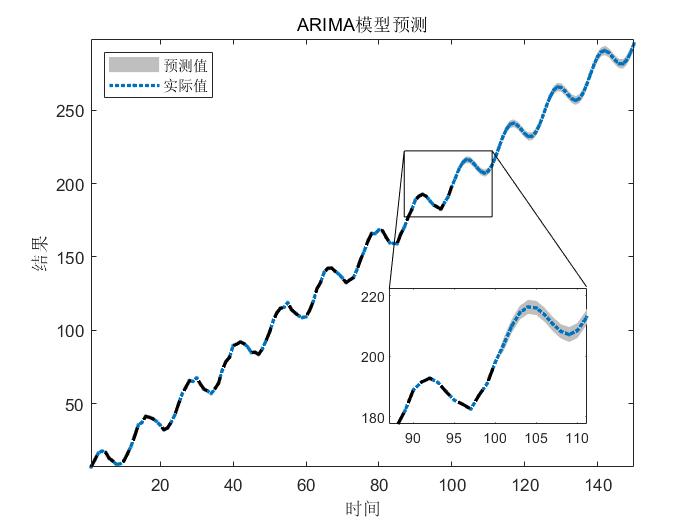
$\nabla ^dx_t=\frac{\varTheta \left( B \right)}{\varPhi \left( B \right)}\varepsilon _t$

上图展示了一个简单的预测的demo，灰色块代表了预测的置信区间。

实际上在很多时候，我们拿到的都是上面demo中的这样的数据，它有一个线性趋势，再有一个周期变化。真正对于预测一个序列，在许多时候，$ARIMA$只是起到了一个使故事更完整的角色，就像刚才那个demo里，实际上用一个形如$f(x)=ax+bsin(cx)$完全可以回归出来，差别也不会很大。而回归出的直线，去做预测，也可以，但是多少缺点理论知识。如果用$ARIMA$，不仅可以写几个公式上去，还可以给它把置信区间画一画，再讲讲故事，何乐而不为呢。

就像有些时候炼丹，构造新的误差函数，并不能够明显起到什么好的结果，但是只要不坏，就可以说上去，可以让故事叙事变得完整。