考试又推回去了,也不知道能不能回家,结果最先考的从概率论变成了复变函数,整理一些复变函数的知识加以理解,由于考核主要考计算,所以会略去大部分的理论内容,着重于直观理解。
复数的前置知识高中都学过了,这里补充并强调下面几点,我们经常习惯把复数看成一个二维向量,实际上可以证明,复数域$\mathbf{C}$作为实数域$\mathbf{R}$上的维数为2的向量空间。
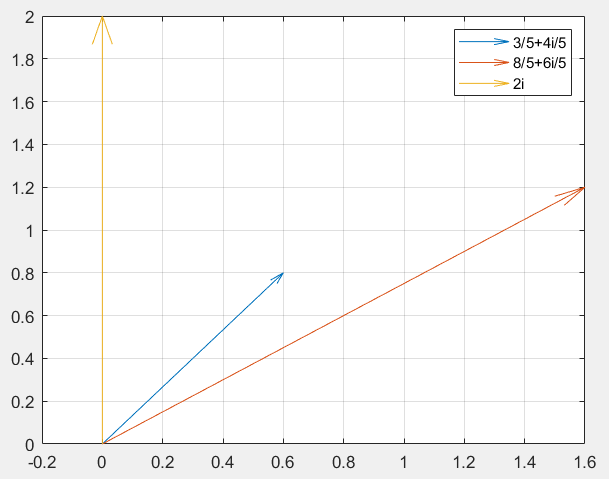
在上面那个例子中,计算的是红色复数和蓝色复数的乘积,实际上就是模长乘积,辐角相加,如果是复数作除法,那模长就是两模长作除法,这个可以通过计算结果直观的看到,而如果由复变函数中的欧拉公式:
则就十分显然了,基于此定义了复数的幂与根,当我们取$r=1$,计算$z=cos\theta+isin\theta$的$n$次方,容易写出:
上式为棣莫弗公式。
下面我们定义要讨论的复变函数,实际上就是一个新的映射:将复数$x+iy$的集合$G$按照一个法则,有一个或多个复数$u+iv$与其对应,那么就记复数$w$是复数$z$的函数,简称复变函数,记作$w=f(z)$。
在后面的讨论中,如果无特殊说明,定义$G$是一个平面区域(复平面),讨论的函数为单值函数。
下面我们要讨论复变函数的连续性和极限,粗浅的来讲,这里与二元函数别无二致,例如如果在$z_0$连续,那么是以任何方式趋近于$z_0$,都有一个相同的极限;在$z_0$可导,也是一样的道理。在复变函数理论中真正关注的是解析函数,在$z_0$解析说的是在$z_0$及其邻域内处处可导,如果在区域$D$内每一点都解析,则记$f(z)$是$D$内的一个解析函数,如果$f(z)$在$z_0$不解析,那么$z_0$称为奇点,这个概念在后面要经常用到。
通过上面解析的定义可以知道,在某一区域内处处可导和处处解析是等价的,但是在某一点的解析和可导不是等价的。
下面我们讨论$f(z)=z^2,g(z)=x+2yi,h(z)=|z|^2,q(z)=1/z$的解析性来加深理解:
这里我们浅显的来讲,复变函数有两种表示方法:$w=f(z),w=u+vi$,其中$u,v$是两个实函数。一般情况下,写成$f(z)$形式的……求导时可以直接看成一元函数,直接套用之前的求导法则即可。而后一种形式往往都不可导。
所以$f(z)$处处可导,则也在复平面上处处解析。
不难发现,$g(z)$处处不可导,所以在复平面上处处不解析。
可见$h(z)$只有在$z=0$点处可导,而在其他点均不可导,所以在复平面内处处不解析。
对于$q(z)$,$q’\left( z \right) =-1/z^2$,所以在除$z=0$外的复平面内,函数$w=1/z$处处解析,而$z=0$是它的奇点。
实际上,对于直接写成$w=f(z)$的复变函数,我们较为熟悉利用求导法则判断他们的解析和可导,但对$f(z)=u(x,y)+iv(x,y)$这样的复变函数,根据上面的例子我们往往只能列出极限表达式,然后进行判断,实际上关于这种形式下的解析有一个充要条件,即满足柯西-黎曼方程:
严格来讲,即$u(x,y),v(x,y)$在$(x,y)$可微,且满足上面的柯西-黎曼方程,则就在定义域$D$内成立,反过来也成立。当然上面两种形式的复变函数是可以互相转换的,这里不管那么多了,最后要指出:
对于满足柯西黎曼方程($C-R$方程)的复变函数$f(z)=u(x,y)+iv(x,y)$在点$z=x+iy$处的导数公式为:
下面将一些初等函数推广到复变函数中,并给出一些相同点和不同点。这里我们就直接给出了,关于初等函数推广到复变函数的结果,一定要分清,否则在后面会引起混淆。
指数函数:
这个定义实际上就要求了$\exp z$的模长为$e^x$,辐角为$Arg(\exp z)=y+2k\pi$,这个定义保证了我们希望的三点,一在整个复平面内处处解析,二是导函数等于原函数,三是当虚部为0时,退化为$e^x$。
实际上……如果不这么指出来你也大概会写出这个表达式,因为:
而那些美好的性质不过是$e$的巧夺天工。由于$e^{iy}$的引入,$\exp z$有实变函数时不具有的周期性。
最后要指出一点,这里的$e^z$没有幂的意义。
对数函数:
和实变函数的时候一样,我们通过对$e^z$取反,来得到对数函数。
但是注意到$\theta$其实是多值的,它具有周期性。所以我们需要的对数函数$w$即为:
记作$Lnz$,它是一个多值函数,但是如果规定上式中的$Argz$取主值$argz$,那么$Lnz$就变成了一个单值函数,记作$lnz$,称为$Lnz$的主值。
这其实也和我们直观写出的想法是一样的,因为:
对数函数保持了在实变下相加和相减的性质,但乘积和商没有保持,后面在介绍复变函数中的幂函数时会说明原因。但是与$e^z$不同,此时定义的$Lnz$并不能在复平面上处处解析,对于其主值的$ln|z|$而言,它在除原点以外的其他点都是连续的。而$argz$在原点与负实轴上都不连续(当$x<0$时,从$y$的不同方向逼近0辐角的左右极限分别为$\pi,-\pi$,所以不连续。)
总上,今后我们使用$Lnz$时,指的都是去除原点和负半轴的某一单值分支。
幂函数:
下面我们定义幂函数$a^b$通过$e^{bLna}$,所以这就导致了上面我们说的,对数函数乘积和商的性质未必会保持,由于$Lna$是多值的,所以$a^b$也将会是多值的。
当$b$为整数时,我们将$e^{bLna}$展开,发现:
因为$2kb\pi i$实际上是旋转了整数圈,所以此时$a^b$是个单值函数。
当$b$是个不可约分数$p/q$时,这里$q>0$,上面的$2kb\pi i$作为一个旋转,其中的$b=p/q$,则就将会有$p$个值。
当$b$是相对一般的情况时,$a^b$有无穷多的值。
换句话说,上面的论述更有意义的一点在于,当$b$取$n,1/n$时,其中$n$为正整数,此时$a^b$的意义与$a$的$n$次幂及$a$的$n$次根是一样的。更一般的,根据此我们可以正式给出$z^n$,$z^{1/n}$。
$z^n$在复平面内是单值解析函数,$z^{1/n}=\sqrt[n]{z}$在除去原点和复实轴上是解析函数。这里就不再赘述了,本质上都是因为引入复数后,多出辐角这一概念。
三角函数:
三角函数可以由欧拉公式通过指数函数来给出:
它们仍保有周期性,以及保持着平方和公式,和差化积公式等三角函数的性质,但有界性不再保证。当$z$取纯虚数时,结构恰好蜕变成了双曲函数,这并不是重点。
反三角函数和反双曲函数见课本,此处从略。
上面点缀的那些内容,意义在于,我们要认识到复变函数和实变函数的不同,不能模模糊糊的把复变函数简单的理解成把$e^x$变成$e^z$等,这样不便于后面的理解。
下面我们来研究在复变函数,也就是复数的映射中的一些现象。
自然,对于一元函数,我们所说的映射,将一组数单值的映射给了另一组数,可以绘制成一个图像,但当我们用一组复数映射给另一个复数时,由于表示一个复数就需要一个平面了,这样往往会有一些奇妙的几何性质。
下图中红色线段表示过某点的切线,就是在复平面上符合我们直接理解的切线。而蓝色线段表示$(x,y)$与原点的连线,我们知道,这实际上是模长。我们即将看到它带来的神奇的性质,对于$f(z)=1/z$可能看起来不是很方便,我们先选取一个更为简单的$f(z)=2z$。
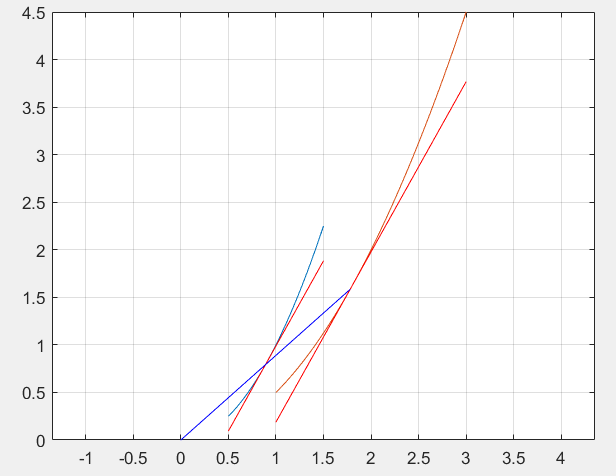
蓝色线段是有两条的,但是它俩重叠了,我们发现映射后蓝色线段的长度恰好是原来的两倍,而红色线段的斜率没有变化,下面我们将映射改为稍微复杂的$f(z)=(1+i)z$。
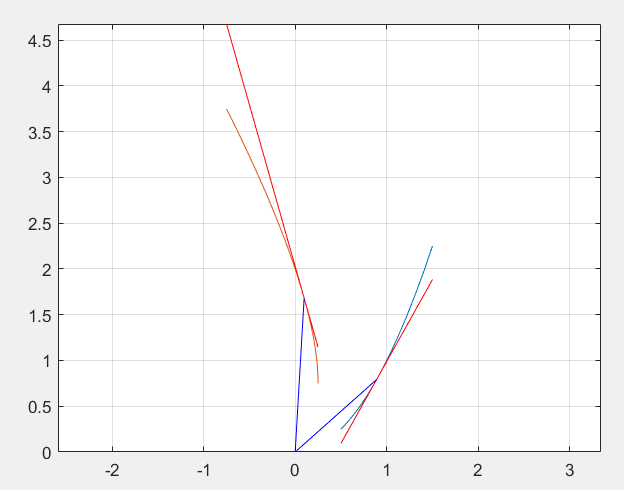
此时我们发现,红色线段的夹角为$45°$,而蓝色线段的长度变为了原来的$\sqrt 2$倍。这与$1+i$的系数和辐角吻合。下面我们考虑映射$f(z)=1/z$。
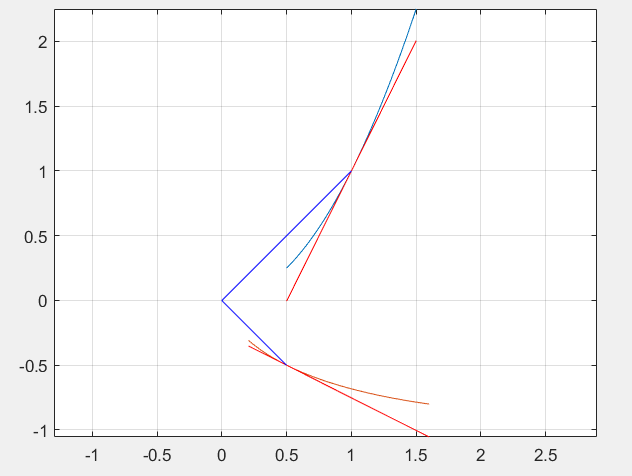
蓝色线段变成了原来的一半,而角度顺时针旋转了90度。如果我们计算$f’\left( z \right) =-1/z^2$,将$z=1+i$代入,会发现结果为$0.5i$,模长正好为0.5,辐角为90度。而上面那个例子$f(z)=2z,f(z)=(1+i)z$求导后,也符合这个规律。
这里我引入这个结论比较生硬,因为确实不想铺垫那么多了,所以我们就能得到一个结论:对于一个复平面内的有向连续曲线,对它作用一个复变函数,切线转动角为$\mathrm{Arg}f’\left( z_0 \right) $,模长以系数$f’\left( z_0 \right)$伸缩。当然这些是建立在$f’\left( z_0 \right) \ne 0$的条件上。
而更神奇的是,实际上上面那个结论并不局限于“切线”,“切线”只是引入时的一个例子,实际上它是指通过$z_0$的任何曲线,都会有相同的转动角和伸缩率,这被记作保角性和伸缩率的不变性。
这样就进一步引出了共形映射的概念,书上清晰的给出了相关内容,这里不再赘述,书上最后给了一个例子,我现在将这个例子作出来来便于理解:
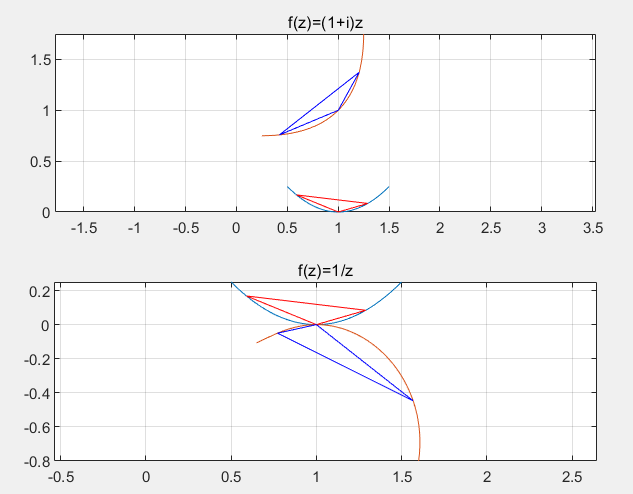
直观上,共形映射将一个三角形,旋转缩放成了另一个相似的三角形。同理,如果作用的是一个圆,它可以进一步缩放,旋转这个圆。
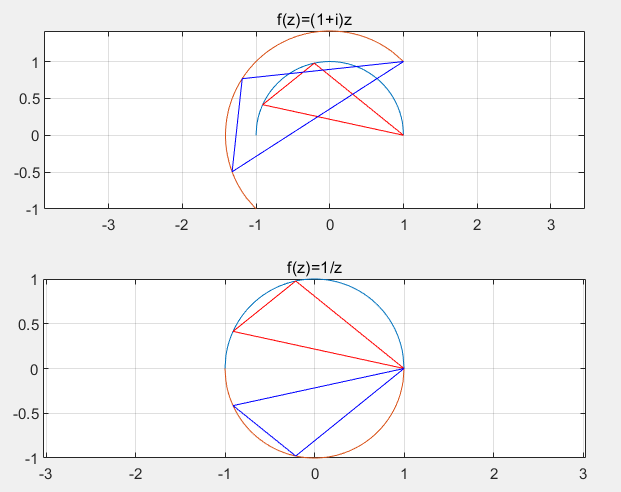
后面我们将进一步挖掘,不同形式的映射起到的作用,例如上图中的$f(z)=1/z$,它将上半平面的圆周映到了下半圆周,等等这一系列性质。如果不是为了考试,这将是非常有趣的内容。

