由于种种原因之前写的内容等寒假再补齐,现在先恶补期末考试,这里直接接数理统计部分了。
数理统计部分书上写的非常的冗长,这里对其中的内容进行一些压缩和个人理解,其实它所讲的故事是:这里有一个总体$X$,我可能清楚它的分布,但我不可能获取$X$的所有内容,我只能作部分抽样,获得一组样本值,即管中窥豹,但是我要尽可能多的从这么一组样本值里来获得总体$X$的信息,这就是我们要理解的内容。下面用一个例子来帮助理解上面的说法。
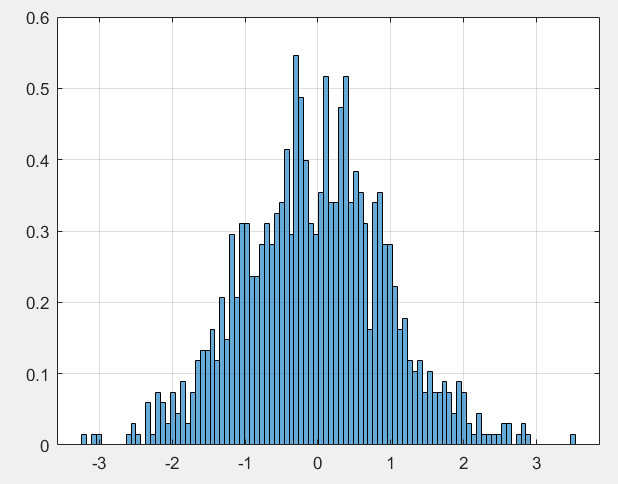
利用计算机生成1000个满足0~1正态分布的随机数,我们发现它们满足这样的概率密度分布,它们每个的取值可以看横坐标,也就是说我们抽样后,可能只是拿到了一组类似1.31,1.29,0.31,0.22,0.01这样的值,但一般的时候我们都是知道数据分布的(大数定律作支撑),所以我们许多时候认为数据符合正态分布,并期望通过已有的样本获取尽可能准确的$\mu \text{,}\sigma ^2$ 。
例如我们已经知道$X$服从0~1正态分布,并且获得了如下的数据:
我们对它们求平均数,我们一直以来都是这么干的,求出值为$0.0162$,根据我们知道的方差公式,我们会计算出:
这已经非常准确了,如果我们抽取更多的样本,比如1000个,结果会更加精确,以及其他$k$阶中心距也可以直接套用我们熟悉的方式计算。这都和我们的第一直觉相差不多,但只有一个例外:
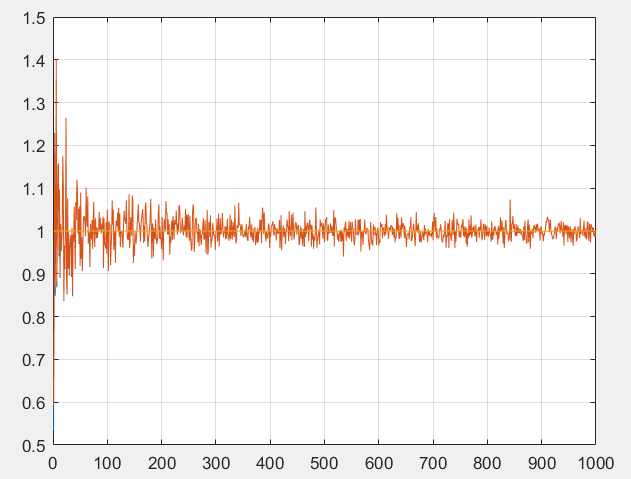
这是在抽取不同大小的样本时计算出的方差,当抽取样本较大的时,这个结果在1附近震荡,但实际上有上面杂乱曲线是两条曲线,其中一条是按照分母为$n$计算的,另一个是$n-1$,确实它们的差异相当的小,但是如果计算它关于标准方差的误差平方和,会发现后者大多数时都小于前者。所以以后我们计算样本方差时分母都使用$n-1$。后面我们会给出原因,实际上上面做的实验是不严谨的,下面为了不与我们之前的认识混淆,我们要声明以下概念:
设$X_1,X_2,…,X_n$为来自总体$X$的一个样本,$x_1,x_2,…,x_n$是$X_1,X_2,…,X_n$的样本值,值得注意的是,$X_1,X_2,…,X_n$也是随机变量,后面会用到:
样本均值及其样本值:
样本方差及其样本值:(标准差只需开个根号):
在此基础上,要引入一个比较显然的定理:样本均值的期望等于总体期望,样本均值的方差等于总体方差除以$n$,样本方差的的均值等于总体方差,写成公式就是说:
注意,样本均值,样本方差的期望和方差是其作为随机变量的属性,我们利用计算机模拟加以理解:
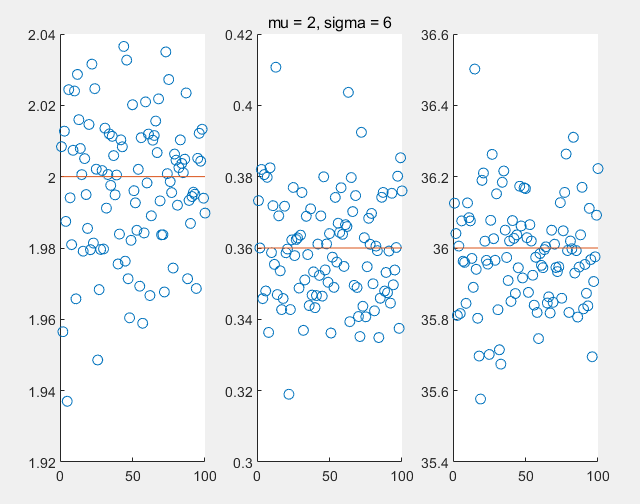
可以看出,它们对样本真实属性的估计,至于样本均值的方差为什么是总体方差除以$n$,不加计算可以这么理解:多次抽样获得的样本均值,一定程度上削弱了样本的波动性,削弱了多少则需要进行推导。
详细证明见课本,这里从略了。上面的三个定理在后面经常会用到。
但是实际上我们刚才的例子都是说,在已经知道分布是正态分布的情况下,我们作的推断,等等,而实际上,在真实情境中,我们只是“估计”总体是个正态总体,并不是百分百确定(这里涉及正态性检验,先略去),所以与其关注于所谓精确的分布,不如关心由已知量构成的那些分布,这里的已知量指的就是上面的统计量。
首先要介绍四个基础的分布,本着备考的原则,个人建议没必要纠结每一个基础分布的概率密度函数等细节,只要知道它们的定义即可,因为它们的具体推导需要另一些基础知识,在前面的学习中一般都略去了,如果有时间我后面将会整理出来。(主要是许多分布之间的关系)
①标准正态分布:$N\sim\left( 0,1 \right) $
它的概率密度函数还是要记得的:
②卡方分布:$\chi ^2\ \sim \chi ^2\left( n \right) $
设随机变量$X_1,X_2,…,X_n$相互独立且同服从标准正态分布$N(0,1)$,则称:
的分布为服从自由度$n$的卡方分布,记为$\chi ^2\text{-}\chi ^2\left( n \right) $
这里我们只需要对独立的随机变量相加这个事情有概念就好了,实际上它可以被视作一种卷积。下面的几种分布也是基于随机变量间的“加减乘除”,如果记的不清可以翻前面的章节。我们只需将它记为“$n$个符合正态分布的随机变量的平方的加和”。
③$t$分布:$T\ \sim t(n)$
设随机变量$X\text{-}N(0,1),Y\text{-}\chi^2(n)$,且$X,Y$相互独立,则:
为服从参数$n$的$t$分布。
④$F$分布:$F\ \sim F(n_1,n_2)$
设随机变量$X\text{-}\chi^2(n_1),Y\text{-}\chi^2(n_2)$,且$X,Y$相互独立,则:
称其为服从参数$(n_1,n_2)$的$F$分布。
这四种分布因为在前人的研究和探索中,发现它们很常见或有意义,所以发展至今,这里建议把它们从公式“字面意义”上理解成由正态分布引发的随机变量的复合。
后面在我校的教材上,通过这四大分布又引出了“八大分布”,非常的不利于接受,现在以一种更合理的角度重新给出。
首先给出三大抽样分布定理:
(首先要补充的是,正态分布的线性组合仍是正态分布)
设$X_1,X_2,…,X_n$是来自正态总体$N(\mu,\sigma^2)$,则:
(1)是显然的,因为各个样本也服从$N(\mu,\sigma^2)$,所以它们的线性组合$\bar X$也服从$N(\mu,\sigma^2)$,这正是上面提到的那个“显然的定理”,即:
所以有:
去均值除标准差即有了(1)
(2)和(3)并不显然,我校教材上并没有证明,但这个证明是必要的,否则很不便于后面的理解:
直接计算:
上面的过程很长,实际上就是将要证明的式子展开成一个$n$元二次型。
将上面这个二次型的矩阵记为$A$,$A$是一个实对称矩阵,那么可以将其对角化:
$B$将是一个对角线为$A$的特征值的对角矩阵,$T$为正交化单位化的特征列向量组成的矩阵。求$A$的特征多项式,得到它的特征值为$\lambda _1=0,\lambda _2=…=\lambda _n=1$,我们对$X$施以线性变换$T$,则二次型矩阵$A$将变为$B$,$B$除了对角线上有$n-1$个1外其余全是0,则变换后的形式即为:
其中随机变量$Y$服从$N(0,\sigma^2)$,分母上除以$\sigma^2$后结论即得到了证明,这个并不显然,下面作一些注解:
当$\lambda_n=1$时,$A-\lambda_nI$经过行初等变换可化为:
解右边的齐次线性方程组得到$n-1$个特征向量,它们分别是:
当$\lambda=0$时,同样,矩阵$A-\lambda I$进行初等变换后,求解齐次线性组得到特征向量。齐次线性方程组只有一个解,即特征向量$\alpha _n=\left( 1,1,…,1 \right) ^T$。
对这$n$个特征向量作施密特正交化处理,对于已经快忘了线性代数的同学来说计算比较困难,计算过程这里就略去了,计算后我们会发现,构成的正交阵$T$是:
所以进行正交变换后,即:
最后那一项正好由于主对角线上的唯一的一个0消去了,所以上面的结论就得到了证明。
同样我们可以计算$Y_i$与$\bar X$的协方差,自然发现它们全为零,所以独立也得到了证明,至此我们就完成了对抽样分布定理证明。
下面对于其他分布的证明,就简单了许多:
这两个与前面的三大抽样分布定理结合起来,就形成了书上说的关于单正态总体的四大分布。
后面是双正态总体的四大分布,道理是一样的:
双正态总体时:$X\sim N(\mu_1,\sigma_1^2),Y,\sim N(\mu_2,\sigma_2^2)$,(样本容量分别为$n_1,n_2$):
上面的公式的推导看起来非常的繁琐,其实相对简单,均是一些直接的应用,可能会有两点没有提及到,这里补充一下:
①卡方分布具有可加性,即$\chi ^2\left( n_1+n_2 \right) \sim \chi ^2\left( n_1 \right) +\chi ^2\left( n_2 \right) $
②$F$分布:$\frac{1}{F\left( n_1,n_2 \right)}\sim F\left( n_2,n_1 \right) $
这八个分布要非常熟悉,最好看一遍上面的推导过程,对后续理解置信区间,假设检验有很大的帮助。

