傅里叶变换

阅读数: 次 2021-10-22

由于在要做的事情上要用到时频分析，在此之前只是简单的接触了一下傅里叶变换，可是那点程度完全不够用。所以写个blog记录一下从傅里叶变换到小波变换的过程。

在此之前要再认识一下傅里叶变换，实际上在此之前已经学到了足够多的预备知识，在学习偏微分方程时就已经知道，傅里叶变换可以用于解偏微分方程，但是从本篇起我们要换一个方向，来具体介绍傅里叶变换以及基于傅里叶变换的其他变换在时频分析中的用处。

令$C[a,b]$是定义在$[a,b]$上一切连续实函数所成的向量空间，设$f\left( x \right) ,g\left( x \right) \in C\left[ a,b \right] $

$\left< f,g \right> =\int_a^b{f\left( x \right) g\left( x \right) \mathrm{d}x}$

由定积分的性质可知，这个运算符合内积的性质，这样就引入了一种度量，也就是说当$\left< f,g \right>=0$时就像两向量垂直一样，有两个这样的函数$f(x),g(x)$也是“垂直”的，只不过并不是在我们习惯的$V_2$空间，而是在上面定义的欧氏空间中。

而且我们在学习傅里叶级数的时候，就接触过三角函数系这个概念。

$1,\cos x,\sin x,...,\cos nx,\sin nx \\ \int_{-\pi}^{\pi}{\cos mx\cos nx\mathrm{d}x}=\left\{ \begin{array}{c} \pi ,m=n\\ 0,m\ne n\\ \end{array} \right. \\ \int_{-\pi}^{\pi}{\sin mx\sin nx\mathrm{d}x}=\left\{ \begin{array}{c} \pi ,m=n\\ 0,m\ne n\\ \end{array} \right. \\ \int_{-\pi}^{\pi}{\sin mx\cos nx\mathrm{d}x}=\int_{-\pi}^{\pi}{\sin n\mathrm{d}x}=\int_{-\pi}^{\pi}{\cos n\mathrm{d}x}=0$

实际上这一组函数在上述欧氏空间中是正交的（完备正交基），实际上在这里，我们已经看出了一种类似“过滤器”的机制，只有当积分的两个函数相同时，结果才非零。所以只需要对此时的信号作这样的运算，就可以得到频率成分：

$\int_{-\pi}^{\pi}{f\left( t \right) \cdot \sin \left( t \right) \mathrm{d}t}=0 \\ \int_{-\pi}^{\pi}{f\left( t \right) \cdot \sin \left( 1.8t \right) \mathrm{d}t}=3.0936 \\ \int_{-\pi}^{\pi}{f\left( t \right) \cdot \sin \left( 2t \right) \mathrm{d}t}=3.1416 \\ \int_{-\pi}^{\pi}{f\left( t \right) \cdot \sin \left( 2.5t \right) \mathrm{d}t}=1.7778 \\ \int_{-\pi}^{\pi}{f\left( t \right) \cdot \sin \left( 3t \right) \mathrm{d}t}=0$

实际上上面的$f(t)=sin(2t)$，所以只有当和其进行积分运算的信号与$f(t)$的频率相近时，积分值才会明显变大。这样我们其实就得到了$f(t)$的频域信息，如果以频率为横坐标，积分值为纵坐标，我们就可以得到各频率强度的图像。

但是如果将$f(t)$改成$cos(3t)$，那么如果我们只从$1,sin(t),sin(2t)…,sin(nt)$里找，会发现积分值都是0，这是由于$sin$和$cos$在这个空间里是正交的，所以我们这样对频率的筛选，可能需要在两个维度（sin维度和cos维度）都计算一遍……既然如此，那为什么不同时来算一下呢？

我们知道：

$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}...+\left( -1 \right) ^{n-1}\frac{x^{2n-1}}{\left( 2n-1 \right) !}+R\left( n \right) \\ \cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}...+\left( -1 \right) ^{n-1}\frac{x^{2n-2}}{\left( 2n-2 \right) !}+R\left( n \right) \\ e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+...+\frac{x^n}{n!}+R\left( n \right)$

将$e^x$换成$e^{ix}$，即有了复变函数中的欧拉公式：

$e^{ix}=1+ix-\frac{x^2}{2!}-\frac{ix^3}{3!}+\frac{x^4}{4!}+... \\ =\cos x+i\sin x$

利用这个方程，我们就可以选取基函数$e^{ix}$来作为“滤波器”，比如我们直接计算：

$\int_{-\pi}^{\pi}{f\left( t \right) \cdot e^{it}\mathrm{d}t}=0+0i \\ \int_{-\pi}^{\pi}{f\left( t \right) \cdot e^{i2t}\mathrm{d}t}=0+3.1416i \\ \int_{-\pi}^{\pi}{f\left( t \right) \cdot e^{i3t}\mathrm{d}t}=3.1416+0i \\ \int_{-\pi}^{\pi}{f\left( t \right) \cdot e^{i4t}\mathrm{d}t}=0+0i$

这里我选择的$f(t)=sin(2t)+cos(3t)$，所以我们看出，如果这么计算，得到的实部是与$cos(wt)$的内积（相似度），虚部是与$sin(wt)$的相似度，上面的结果也告诉我们，这种方法效果很明显。

这里要说明，在对于有周期的情况下，比如我们知道周期是$T$，那么我们根据$T=2\pi /\omega _0$可以计算出$\omega _0$，这是有意义的，因为我们知道，这一段周期信号是若干信号的叠加，因为即使，两个不同周期的信号叠加，它们的周期并不简单的等于周期中取最大的那个，实际上是它们的最小公倍数，这个最小公倍数就是我们观测到的周期$T$，它一定大于各个成分的$T_i$，所以它具有最小的$\omega$，所以我们称此时计算的$\omega_0$为基频率，而我们所选取的“基函数”就是$e^{inw_0t}$，而我们在频谱上看，就是若干各离散的点。

也就是说，根据上面的分析，结合我们知道的“周期函数可以用傅里叶级数表示”，我们就有了这么一种的做法：

$f_T\left( t \right) =\sum_{n=-\infty}^{\infty}{c_ne^{in\omega _0t}},\omega _0=\frac{2\pi}{T} \\ c_n=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f_T\left( t \right) e^{-in\omega _0t}\mathrm{d}t}$

（如果你觉得这个写法很不好理解，尝试结合上面说的欧拉公式，和下面这个熟悉的版本进行推导）

$\text{设}f\left( x \right) \text{是周期为}2\pi \text{的周期函数，可展开为} \\ f\left( x \right) =\frac{a_0}{2}+\sum_{k=1}^{\infty}{\left( a_k\cos kx+b_k\sin kx \right)} \\ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \cos nx\mathrm{d}x}\quad \left( n=0,1,2,3,\cdots \right) \\ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \sin nx\mathrm{d}x}\quad \left( n=0,1,2,3,\cdots \right)$

注意上面的$c_n$，这个运算就是前面我们一直分析的，也就是说，实际上傅里叶级数的系数，正是那个筛选频率的方法，而它的含义，是在某个内积空间下，函数作为向量的度量。（只是我们之前为了过高数考试一直不在意这个罢了）

至于周期函数，傅里叶级数以及上面的分析已经给出圆满的答案，但是很多时候我们遇到的信号序列可能不是周期的，但即使在这种情况下我们也想得到它的频率成分，对于这种非周期的函数，“just roll in”，我们认为它的周期区域无穷大，直接将积分上下限变为无穷，并且此时我们知道，对于无穷大的周期，此时我们上面讨论的离散的点，就发生了一些有趣的变化：

$\varDelta \omega =\left( n+1 \right) \omega _0-n\omega _0=\omega _0=\frac{2\pi}{T} \\ \lim_{T\rightarrow \infty} \varDelta \omega =0$

而作一些等价变形：

$f_T\left( t \right) =\sum_{n=-\infty}^{\infty}{\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f_T\left( t \right) e^{-in\omega _0t}\mathrm{d}t}e^{in\omega _0t}} \\ =\sum_{n=-\infty}^{\infty}{\frac{\varDelta \omega}{2\pi}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f_T\left( t \right) e^{-in\omega _0t}\mathrm{d}t}e^{in\omega _0t}} \\ =\frac{1}{2\pi}\int_{-\infty}^{\infty}{\int_{-\infty}^{\infty}{f_T\left( t \right) e^{-i\omega t}\mathrm{d}t}e^{i\omega t}}\mathrm{d}\omega \\ \left( n\omega _0\rightarrow \omega \left( \text{一个连续变化的变量} \right) ,\sum_{-\infty}^{\infty}{\varDelta \omega}\rightarrow \int_{-\infty}^{\infty}{\mathrm{d}\omega} \right)$

注意推导出的最后一个式子中关于$t$的积分：

$\mathcal{F} \left( \omega \right) =\int_{-\infty}^{\infty}{f_T\left( t \right) e^{-i\omega t}\mathrm{d}t}$

这就是傅里叶变换，它将一段连续的时频数据变化为了连续的频域数据，而最后一个式子：

$\mathcal{F} ^{-1}\left( \omega \right) =\frac{1}{2\pi}\int_{-\infty}^{\infty}{\mathcal{F} \left( \omega \right) e^{i\omega t}}\mathrm{d}\omega$

这就是傅里叶逆变换，它会将频域信息再变回去，这里的$1/2\pi$实际上是归一化因子，在不同地方会有不同写法，比如可能根号一下放在傅里叶变换中，这对我们的目的是无所谓的。

现在唯一的问题就是，这个积分往往不是很好计算，而计算机又无法直接处理反常积分，以及实际采样获得的信号，也并不是连续的，都只是离散点。所以后面就有了离散傅里叶变换（DFT），这是下一篇要介绍的内容了，但实际上它们的原理完全一致。

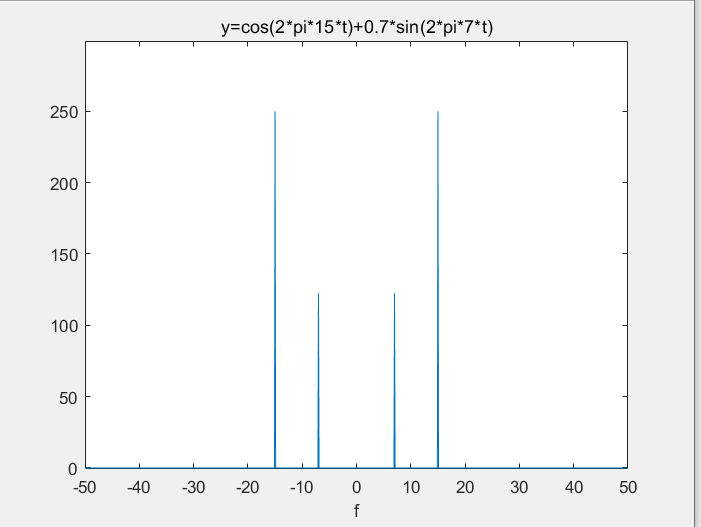
这是利用matlab进行傅里叶变换的结果，可以直观的看到，信号的频率确实被直观的提取了出来。