大学物理4

阅读数: 次 2021-10-21

第四篇主要总结下考试会考到的静磁场，由于非相关专业，只是为了过考试，会省略许多内容。

人们发现通电导线在磁场中受力的作用，这些高中已经学过了，在这里再作下补充。实际上，磁感应强度正是由这个现象而定义的，我们更习惯用“左手定则”来进行方向的判定。

$B=\frac{\mathrm{d}F_{\max}}{I\mathrm{d}l}$

（这里对$F_{max}$就不作赘述了，实际上按照高中被教的方式，到这里其实已经形成一个闭环了，没必要打破它。）

但是实际上我们最好用叉乘来记忆，这样更规范一些（右手从电流方向绕向磁感应方向，大拇指所指为磁感应强度方向）：

$\mathrm{d}\boldsymbol{F}=I\mathrm{d}l\times \boldsymbol{B}$

正如静电场中的点电荷之于库仑定律一样，静磁场中这样的角色是电流元，电流元在某点$P$产生的磁场可以由毕奥-萨伐尔定律给出：

$\mathrm{d}B=\frac{\mu _0}{4\pi}\frac{I\mathrm{d}l\sin \theta}{r^2},\mu _0=4\pi \times 10^{-7}\mathrm{N}/\mathrm{A}^2$

其中$\mu_0$为真空磁导率，这里的$sin\theta$是由电流元指向$P$的位矢与电流源的夹角，而$r$是$P$与电流源的距离，方向由从电流元到$P$小于$\pi$的位矢确定，利用这个公式再进行积分，就可以得到简单通电几何体的磁感应强度。

其中一个是载流直导线。

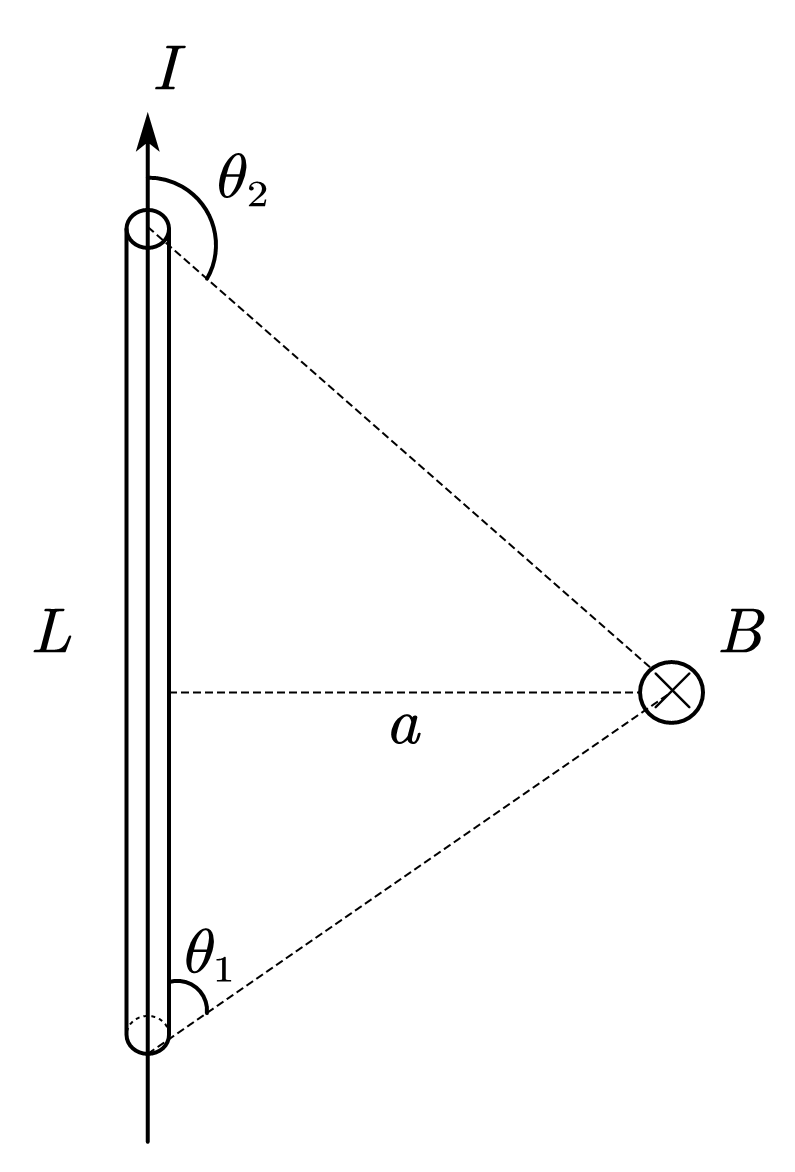
由毕奥-萨伐尔定律可以判断出磁感应强度微元方向均垂直指入纸面，积分过程中$\theta,r,l$都在变化，需要统一积分变量：

$r=a\csc \theta ,l=-a\cot \theta \\ \mathrm{d}l=a\csc ^2\theta \mathrm{d}\theta$

注意在这里$\theta,l$的正负要匹配，所以：

$B=\frac{\mu _0I}{4\pi}\int_{\theta _1}^{\theta _2}{\frac{a\csc ^2\theta \sin \theta \mathrm{d}\theta}{a^2\csc ^2\theta}}=\frac{\mu _0I}{4\pi a}\left( \cos \theta _1-\cos \theta _2 \right)$

对于无限长的导线，$\cos \theta _1=1,\cos \theta _2=-1$,此时有用的结果是

$B=\frac{\mu _0I}{2\pi a}$

另一个特殊的几何体是位于环形电流对称轴线上的点的磁感应强度。

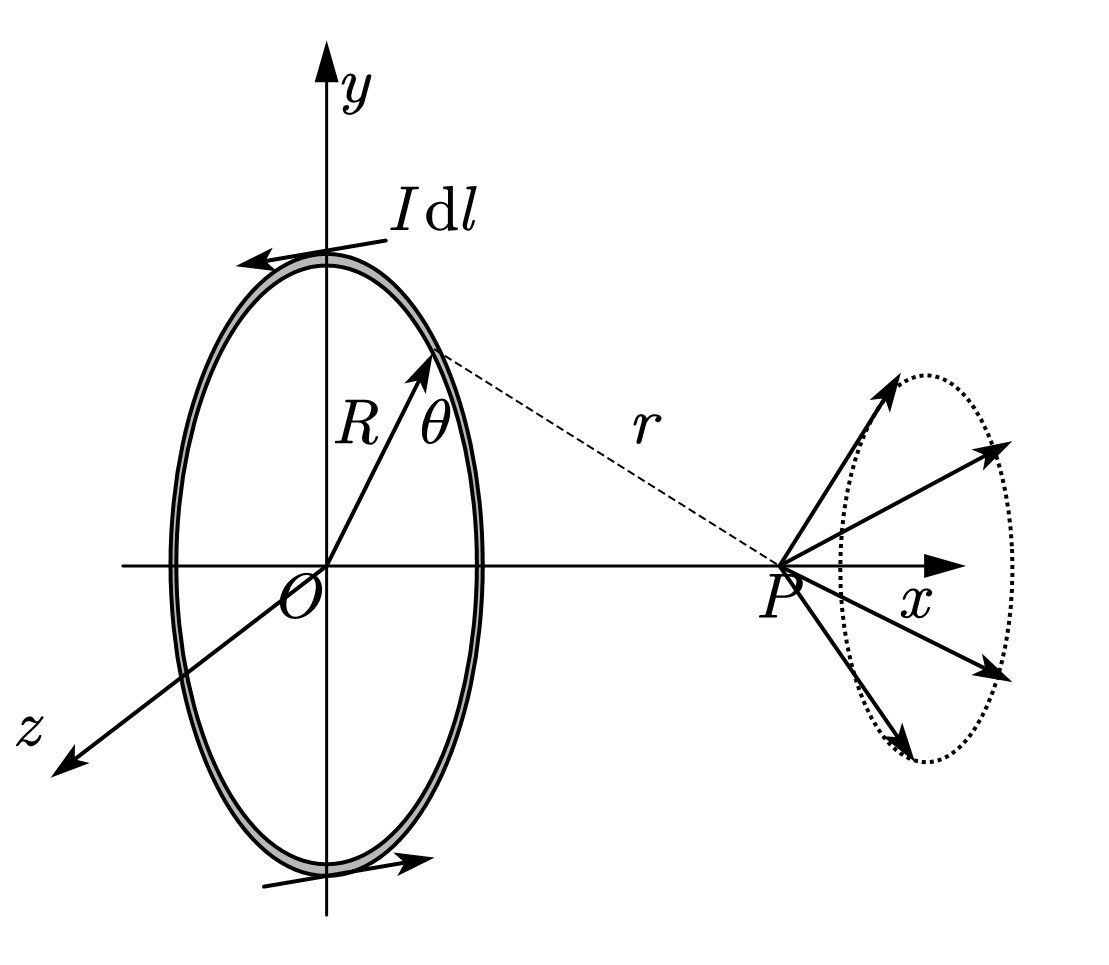
我们将环形电流的电流元带入进行计算，发现电流元一周形成的磁感应强度呈一个圆锥，由于$y,z$方向互相抵消，只需计算$x$方向。

(由立体几何知此时毕奥-萨伐尔公式中的$sin\theta=1$)

$B=\frac{\mu _0I}{4\pi}\int{\frac{\mathrm{d}l}{r^2}\cos \theta}=\frac{\mu _0IR^2}{2r^3}=\frac{\mu _0IR^2}{2\left( R^2+x^2 \right) ^{3/2}}$

当$x=0$时，即圆心处，磁感应强度为：

$B=\frac{\mu _0I}{2R}$

与电偶极子类似，在这里，环形电流就起到这样一个角色，当上式$x\gg R$时，此时的磁感应强度为：

$B=\frac{\mu _0IR^2}{2x^3}=\frac{\mu _0IS}{2\pi x^3}$

这里引出了一个重要概念：磁矩，即$\boldsymbol{p}_m=IS\boldsymbol{n}$，其中$\boldsymbol{n}$为线圈平面正法线方向上的单位矢量，这个概念后面会有很大的作用。

接下来是与静电学中平行的两个定理，安培环路定理和静磁场的高斯定理。

$\oint_L{\boldsymbol{B}\cdot \mathrm{d}l=\mu _0\sum_{\left( \text{内} \right)}{I_i}}$

当磁感应强度和电流方向符合右手定则时电流取正，反之取负。当有磁介质存在时，安培环路定理中的$\mu_0$直接替换为$\mu_0 \mu_r$。

$\oint_S{\boldsymbol{B}\cdot \mathrm{d}\boldsymbol{S}}=0$

静磁场的高斯定理说明，磁场是无源场。

最后要说明关于求磁力矩和磁力所做的功的计算方法，关于磁力矩，确实可以依照具体问题，求出安培力，然后根据力矩计算公式来计算，但是这个一般只在直载流线情况下方便，对于任意形状的平面载流线圈，用如下这个式子。

$\boldsymbol{M}=\boldsymbol{p}_m\times \boldsymbol{B}$

磁场做功的一般公式（电流恒定时）

$A=I\varDelta \varPhi$

这个的好处是不管对于磁场力做功还是磁力矩做功，都可以用这个式子来计算。下面举个例子来说明：

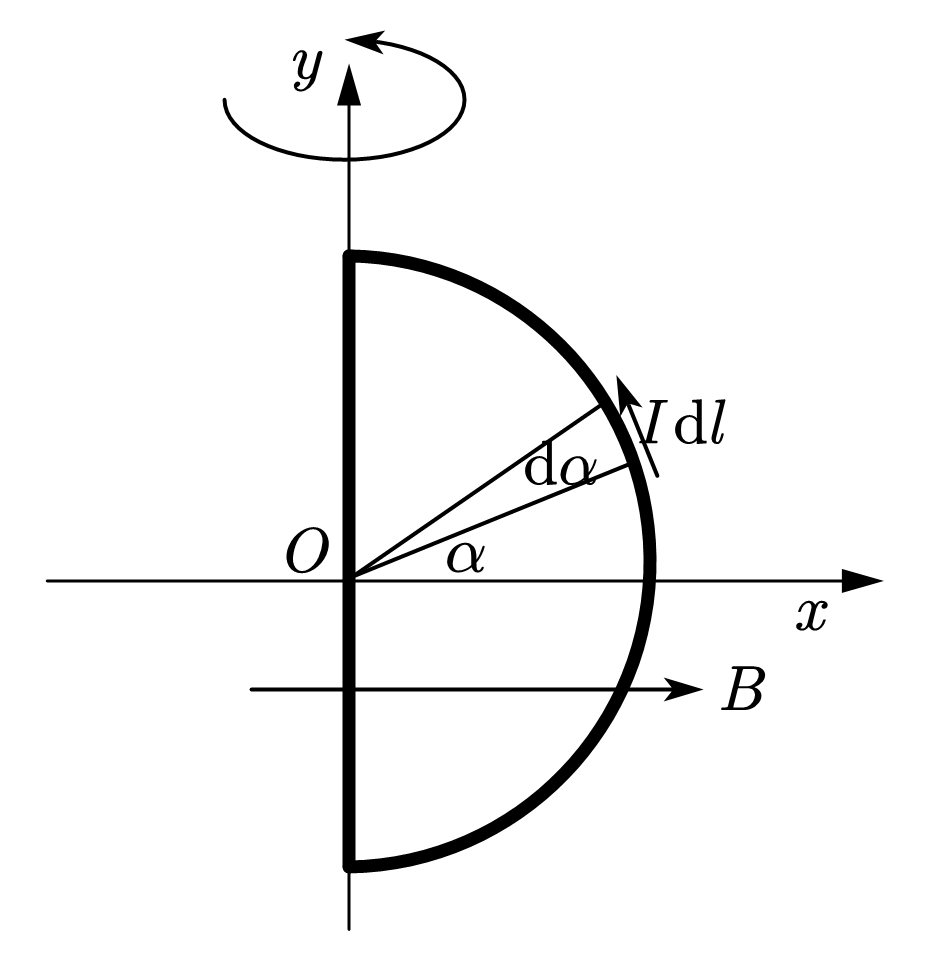
半径为$R$的半圆形闭合载流线圈，通有电流$I$，放在均匀磁场中磁感应强度与$Ox$方向平行，计算此时磁力对$y$轴的力矩，在此力矩作用下线圈转过$90$度磁力矩做的功。

$\mathrm{d}M=x\mathrm{d}F=xBI\mathrm{d}l\sin \left( \frac{\pi}{2}-\alpha \right) \\ x=R\cos \alpha ,\mathrm{d}l=R\mathrm{d}\alpha \\ \mathrm{d}M=BIR^2\cos ^2\alpha \mathrm{d}\alpha \\ M=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}{\mathrm{d}M=}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}{BIR^2\cos ^2\alpha \mathrm{d}\alpha}=\frac{\pi BIR^2}{2}$

但是如果用上面的公式，直接计算：

$M=ISB=\frac{\pi BIR^2}{2}$

此时做的功也应用上述公式：

$A=I\varDelta \varPhi =\frac{\pi BIR^2}{2}$