大学物理3

阅读数: 次 2021-10-20

最后再补充一下关于电容和电介质的内容，之后静磁场的内容与这三篇完全一致，就可以应付期中考试了。

实际上均匀带电体在实际中很难存在，更多时候关注的是静电平衡下的导体，由于在外加电场的作用下（这里只举感应起电的例子，因为考试也只有感应起电），导体内部的自由电荷作定向移动，直到达到静电平衡状态，此时导体内部场强处处为0（内部各点散度处处为0），净电荷只存在于外表面。

利用高斯定理，我们也可以对于静电感应时的某些特殊情况作定量解释，这个会在后面的练习中体现。

后来人们发现静电平衡时，带电量$q$的导体有一定的电势$u$，当所带电量增加时，电势也增加，将其比例记为电容，这个属性与器件本身性质有关，特别地，对于平行板电容器：

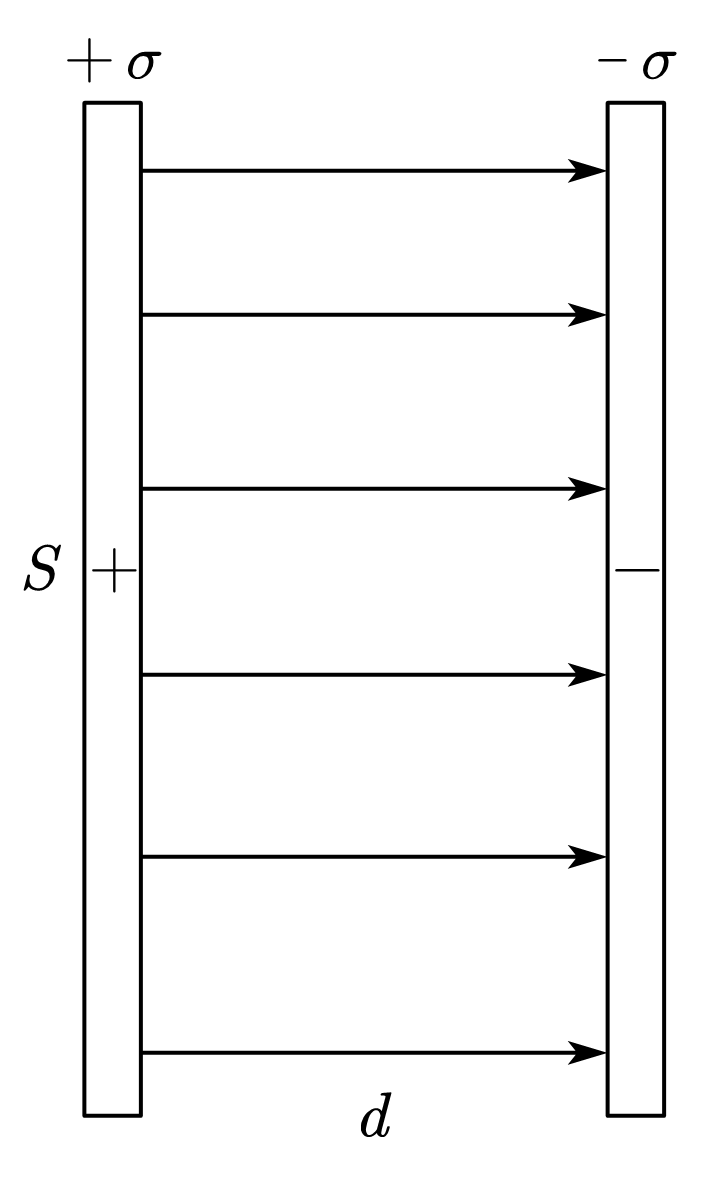
现在我们由高斯定理，可以计算出板间强度，继而计算它的电容：

$E=\frac{\sigma}{\varepsilon _0},\varDelta u=Ed=\frac{\sigma}{\varepsilon _0}d=\frac{qd}{\varepsilon _0S} \\ C=\frac{q}{\varDelta u}=\frac{\varepsilon _0S}{d}=\frac{S}{4\pi kd}$

（注意：实际计算电容时，由于孤立导体不存在，都是用的$C=\frac{q}{u_1-u_2}$）

但是我们发现，上面推导的结果和高中时要求背的公式好像差了一个相对介电常数$\varepsilon_r$。这实际上是因为，我们在推导时认为中间是真空，而实际情况下的电介质中，不可避免的有一些电介质分子，他们在受到外加电场作用时，也会定向移动，从而在极板上产生一层与极板极性相反的的束缚电荷，它的密度一般记作$\sigma’$，在这里我们不管一些细节，只需要了解到，在这个现象下。

$\sigma '=\left( 1-\frac{1}{\varepsilon _r} \right) \sigma _0$

这样在考虑有束缚电荷下的高斯定理时：

$\oint_S{\boldsymbol{E}\cdot \mathrm{d}\boldsymbol{S}=\frac{1}{\varepsilon _0}\left( \sigma _0-\sigma ' \right) S}=\frac{1}{\varepsilon _0\varepsilon _r}\sigma _0S$

此时在有电介质情况下的高斯定理就可以写成：

$\oint_S{\boldsymbol{D}\cdot \mathrm{d}\boldsymbol{S}=q},\boldsymbol{D}=\varepsilon _0\varepsilon _r\boldsymbol{E}$

这里的$D$称作电位移矢量，这样我们就有了可以应用在有电介质情形下的高斯定理。

最后还要提一下静电能的计算，实际上根据功能关系，这是非常容易的，这里直接给出结果：

$W=\frac{1}{2}QU$

一个更加重要的结论是：电场能量密度为：

$w=\frac{1}{2}\varepsilon _0E^2$

即单位体积下如果存在电场$E$，则就有这么多的能量。要注意到，上面直接用$Q,U$计算的那个方程，其中$Q,U$有特殊的含义，只是大学物理作为引入后面的方程的一个特殊例子。而下面能量密度的表达式更为通用，而它的推导已经远远超出了普物的范围，我们只需要记住，计算时避免用第一种，直接用第二种。

下面是一些练习：

① 沿$x$轴放置的长度为$l$的不均匀带电细棒，其电荷线密度为$\lambda =\lambda _0\left( x-a \right) $，取无穷远处为电势零点，求坐标原点$O$处的电场强度和电势。

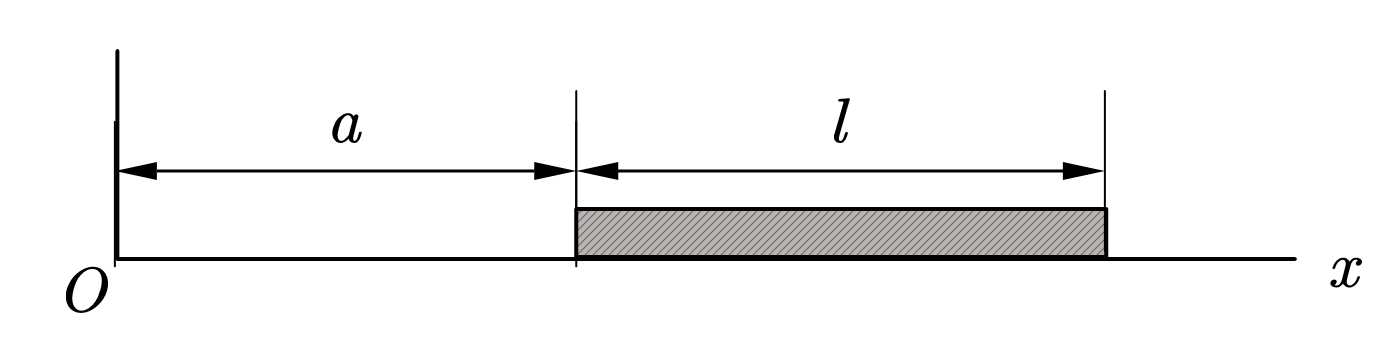
我们选取一段带电微元，且由于均匀细棒不记厚度，可以将该微元视作点电荷，直接积分计算：

$\mathrm{d}q=\lambda _0\left( x-a \right) \mathrm{d}x \\ \mathrm{d}E=\frac{\mathrm{d}q}{4\pi \varepsilon _0x^2}=\frac{\lambda _0}{4\pi \varepsilon _0}\left( \frac{1}{x}-\frac{a}{x^2} \right) \mathrm{d}x \\ E=\int{dE=}\int_a^{a+l}{\frac{\lambda _0}{4\pi \varepsilon _0}\left( \frac{1}{x}-\frac{a}{x^2} \right) \mathrm{d}x=}\frac{\lambda _0}{4\pi \varepsilon _0}\left( \ln \frac{a+l}{a}-\frac{l}{a+l} \right)$

电势是一样的：

$\mathrm{d}\phi =\int_x^{\infty}{\boldsymbol{E}\cdot \mathrm{d}\boldsymbol{l}}=\int_x^{\infty}{\frac{\mathrm{d}q}{4\pi \varepsilon _0t^2}\cdot \mathrm{d}t}=\frac{\mathrm{d}q}{4\pi \varepsilon _0x}=\frac{\lambda _0}{4\pi \varepsilon _0}\left( 1-\frac{a}{x} \right) \mathrm{d}x \\ \phi =\int_a^{a+l}{\frac{\lambda _0}{4\pi \varepsilon _0}\left( 1-\frac{a}{x} \right) \mathrm{d}x=}\frac{\lambda _0}{4\pi \varepsilon _0}\left( l-a\ln \frac{a+l}{a} \right)$

②一内外半径分别为$a,b$的带电量为$Q$的导体球壳，在球壳空腔内距离球心$O$为$r$处有一点电荷$q$。设无穷远处为电势的零点，则导体球壳的内表面上的电荷量为？外表面上的电荷量为？球心$O$处的电势为？

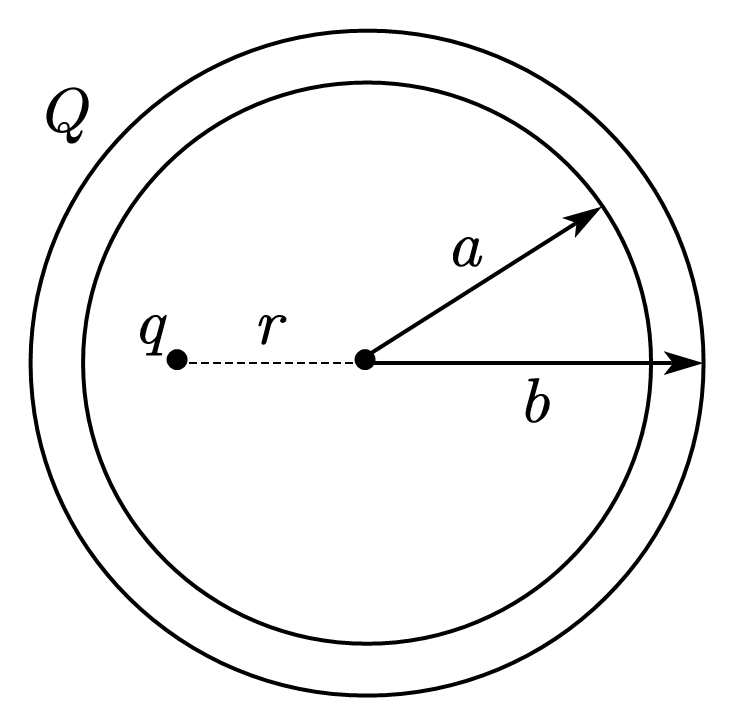
作紧贴内表面的高斯面，由静电平衡可知此时球壳内外之间的电场强度为0，则电通量也为0，说明内表面上感应产生了$-q$的电荷，它的分布是不均匀的，由电荷守恒，此时外表面的电荷量为$Q+q$。

此时计算球心处电势，首先考虑球壳外，由高斯定理可以得：

$\oint_S{\boldsymbol{E}\cdot \mathrm{d}\boldsymbol{S}=4\pi r^2E=\frac{Q+q}{\varepsilon _0}},E=\frac{Q+q}{4\pi \varepsilon _0r^2}$

且球壳为等势体，内表面电势和外表面电势相同（内外表面之间的场强为0），则球壳的电势为：

$\phi _1=\int_b^{\infty}{E\cdot \mathrm{d}l}=\int_b^{\infty}{\frac{Q+q}{4\pi \varepsilon _0r^2}\mathrm{d}r}=\frac{Q+q}{4\pi \varepsilon _0b}$

考虑点电荷在球壳内部产生的电势：

$\phi _2=\int_r^a{E\cdot \mathrm{d}l}=\int_r^a{\frac{q}{4\pi \varepsilon _0r^2}\mathrm{d}r}=\frac{q}{4\pi \varepsilon _0}\left( \frac{1}{r}-\frac{1}{a} \right)$

所以$O$点电势即为：

$\varPhi =\frac{1}{4\pi \varepsilon _0}\left( \frac{Q+q}{b}+\frac{1}{r}-\frac{1}{a} \right)$

③三个无限长的同轴导体圆柱面$A,B,C$半径分别为$R_a,R_b,R_c$，其中圆柱面$B$带电荷，$A,C$接地，求$B$的内表面上电荷线密度$\lambda_1$和外表面上电荷线密度$\lambda_2$的比值。

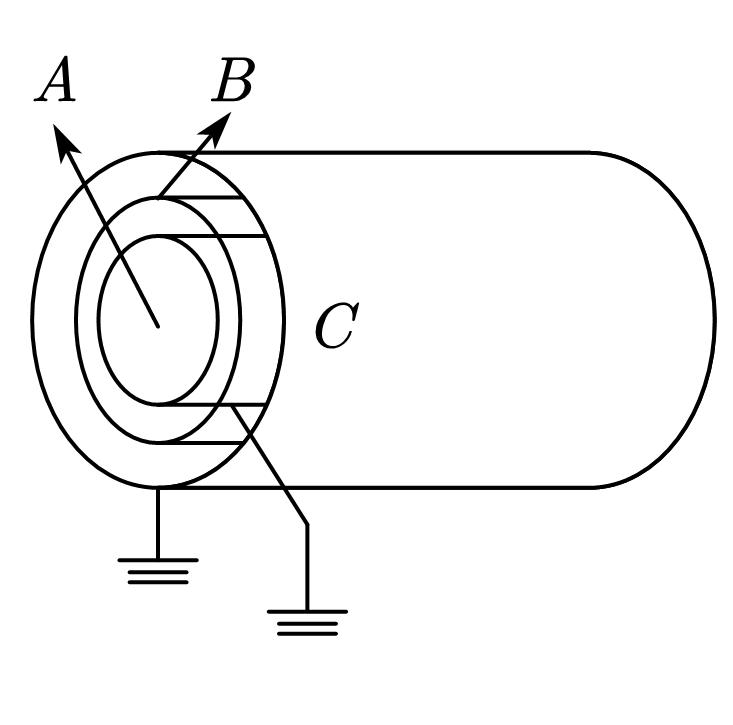
由于$A,C$接地，当静电平衡时$B$的内外表面等势，所以构造圆柱形高斯面得到场强后直接计算：

$E_1=\frac{\lambda _1}{2\pi r\varepsilon _0},E_2=-\frac{\lambda _2}{2\pi r\varepsilon _0} \\ \int_{R_b}^{R_a}{\frac{\lambda _1}{2\pi r\varepsilon _0}\mathrm{d}r}=-\int_{R_b}^{R_c}{\frac{\lambda _2}{2\pi r\varepsilon _0}\mathrm{d}r} \\ \frac{\lambda _1}{\lambda _2}=\frac{\ln \left( \frac{R_b}{R_c} \right)}{\ln \left( \frac{R_a}{R_b} \right)}$

一定要注意到两个电场强度方向相反，计算电势时代数上差一个符号，否则算出的比值会是负的。

④半径为$R_1$的导体球带有电荷$+q$，球外有一个内半径为$R_2$外半径为$R_3$的同心导体球壳，球壳上带有电荷$+Q$。试求系统的静电能量，再计算当外球壳接地时，计算球和球壳各自的电势。

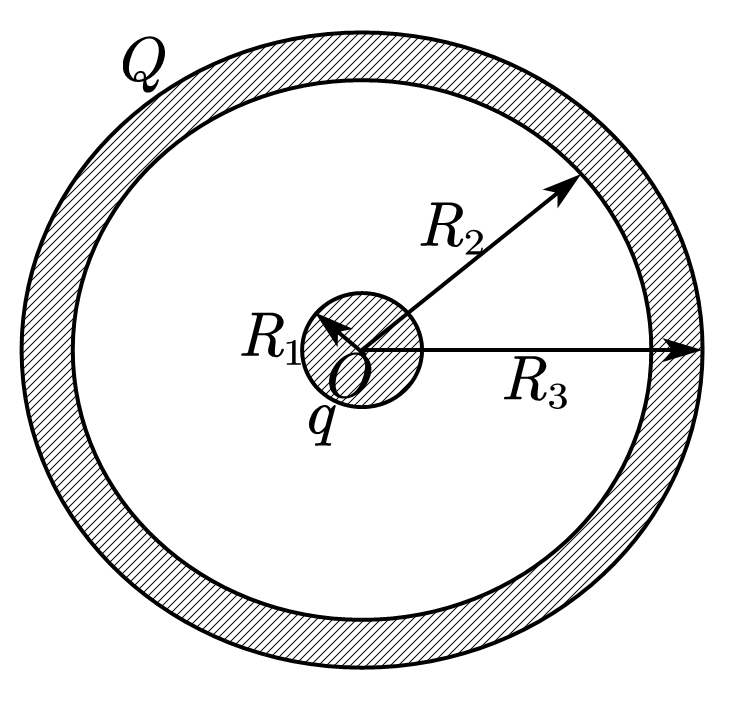
计算静电能，对电场能量密度进行积分即可，首先由高斯定理计算球体与球壳间，球壳外的场强。

$E_1=\frac{q}{4\pi \varepsilon _0r^2},R_1<r<R_2\\ E_2=\frac{Q+q}{4\pi \varepsilon _0r^2},R_3<r\\$

之后再计算静电能：

$W=\int_{V_1}{\frac{1}{2}\varepsilon _0E_{1}^{2}}\mathrm{d}V+\int_{V_2}{\frac{1}{2}\varepsilon _0E_{2}^{2}}\mathrm{d}V \\ =\int_{R_1}^{R_2}{2\varepsilon _0E_{1}^{2}}\pi r^2\mathrm{d}r+\int_{R_3}^{\infty}{2\varepsilon _0E_{2}^{2}}\pi r^2\mathrm{d}r \\ =\frac{q^2}{8\pi \varepsilon _0}\int_{R_1}^{R_2}{\frac{1}{r^2}}\mathrm{d}r+\frac{\left( Q+q \right) ^2}{8\pi \varepsilon _0}\int_{R_3}^{\infty}{\frac{1}{r^2}}\mathrm{d}r \\ =\frac{q^2}{8\pi \varepsilon _0}\left( \frac{1}{R_1}-\frac{1}{R_2} \right) +\frac{\left( Q+q \right) ^2}{8\pi \varepsilon _0}\cdot \frac{1}{R_3}$

接地后球壳电势视为0，只需计算球体的电势，直接计算：

$\varPhi =\int_{R_1}^{R_2}{\frac{q}{4\pi \varepsilon _0r^2}\mathrm{d}r}=\frac{q}{4\pi \varepsilon _0}\left( \frac{1}{R_1}-\frac{1}{R_2} \right)$

⑤两同轴导体圆筒组成的电容器，内外筒半径分别为$R_1,R_2(R_2<2R_1)$其间有两层均匀电介质，分界面半径为$R$，内层介质相对介电常数为$\varepsilon_{r1}$,外层相对介电常数为$\varepsilon_{r2}$，且$\varepsilon_{r2}=\varepsilon_{r1}/2$。两层介质的击穿场强都是$E_M$。当电压升高时哪层介质先被击穿？两筒间能加的最大电压是多少？

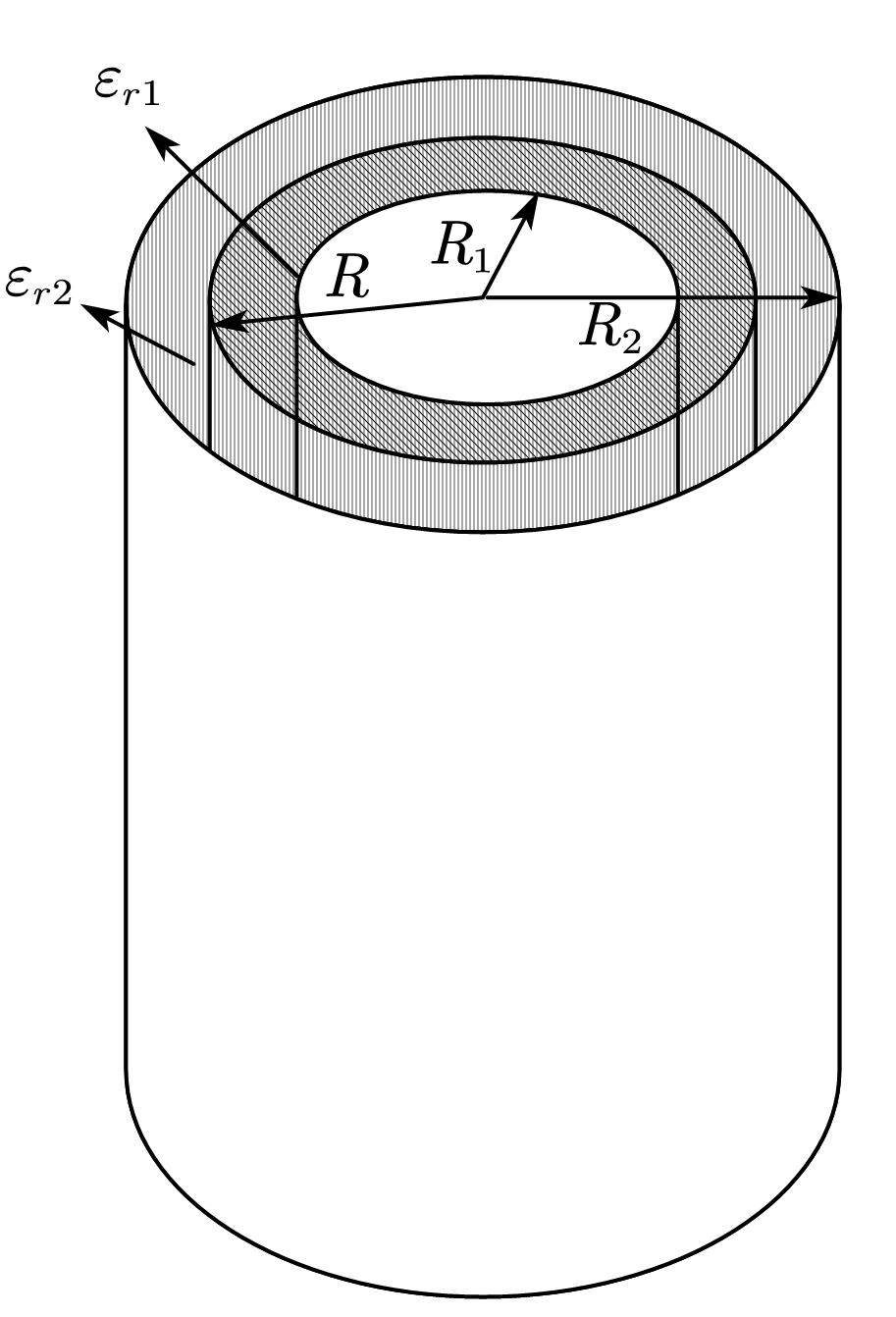
实际上加电压将会改变圆柱体线密度$\lambda$。先由高斯定理，构造圆柱形高斯面，可以计算得到内层到边界的场强和边界到外层的场强。

$\oint_S{\boldsymbol{D}\cdot \mathrm{d}\boldsymbol{S}}=\sum{q}\rightarrow 2\pi r\varepsilon _0\varepsilon _rE=\lambda \\ E_1=\frac{\lambda}{2\pi \varepsilon _0\varepsilon _{r1}r},E_2=\frac{\lambda}{2\pi \varepsilon _0\varepsilon _{r2}r}$

在这里$\lambda$是一个参数，这里要解释一下，对于圆柱体的$\lambda$很多时候是相对圆柱的高来说的，即是单位长度下的圆柱面的带电量，并不是将圆柱面按照圆心细分出的“线”，这里严格来说其中一个圆柱面的线密度是$+\lambda$，另一个是$-\lambda$，这个结论可以由前面的作紧贴表面的高斯面得到。

所以我们比较两个区域的最大场强：

$E_{1}^{\max}=\frac{\lambda}{2\pi \varepsilon _0\varepsilon _{r2}R_1},E_{2}^{\max}=\frac{\lambda}{\pi \varepsilon _0\varepsilon _{r1}R} \\ \frac{E_{1}^{\max}}{E_{2}^{\max}}=\frac{R}{2R_1}<1$

所以外层先被击穿。

当给定$E_M$时，$\lambda$就可以求解了，此时两筒间的电压即为最大电压。

$\lambda =E_M\pi \varepsilon _0\varepsilon _{r1}R \\ E_{\text{内}}=\frac{E_M\pi \varepsilon _0\varepsilon _{r1}R}{2\pi \varepsilon _0\varepsilon _{r1}r}=\frac{E_MR}{2r} \\ E_{\text{外}}=\frac{E_M\pi \varepsilon _0\varepsilon _{r1}R}{\pi \varepsilon _0\varepsilon _{r1}r}=\frac{E_MR}{r} \\ \varPhi =\int_{R_1}^R{\frac{E_MR}{2r}\mathrm{d}r}+\int_R^{R_2}{\frac{E_MR}{r}\mathrm{d}r} \\ =\frac{E_MR}{2}\ln \frac{R}{R_1}+E_MR\ln \frac{R_2}{R}$

由于这个原题并没有给出哪里是正极板哪里是负极板，所以只要最后计算出的电压是正的就好了。