大学物理2

阅读数: 次 2021-10-18

这一篇主要是引入两个电磁学的基本定理，以及一些记录一些作业的课后题用来过考试。

当高中计算磁通量时，经常要将倾斜的面处理成与场强方向正交的投影面，对于曲面来说这个规律也一样适用，因为可以将曲面细分，但是这是在匀强场时的时的情况，下面考虑一个点电荷$q$,而一个半径为$r$的球面包裹着它，由电场的性质，我们可以求得此时的电通量为：

$\oint_S{E\cdot \mathrm{d}\boldsymbol{S}}=\frac{1}{4\pi \varepsilon _0}\frac{q}{r^2}\oint_S{\mathrm{d}\boldsymbol{S}}=\frac{q}{\varepsilon _0}$

所以在这种情形下通量的计算结果其实与半径无关，直观上感受，电通量的值好像不仅与半径无关，还与电场强度有关，好像是取决于电场线的数量，这是由于对于点电荷来说，它的电场强度的$r^2$与此时与电场垂直的微元面积中的$r^2$互相抵消，不影响最后的结果。

基于此，实际上在这个闭合曲面包裹内，即使点电荷不在球中心，结果也是一样的。

现在我们考虑点电荷不在球面内部的情况：

$\oint_S{E\cdot \mathrm{d}\boldsymbol{S}}=\frac{1}{4\pi \varepsilon _0}\oint_S{\frac{q}{r^2}\mathrm{d}\boldsymbol{S}},\text{化为第二类曲面积分} \\ =\frac{q}{4\pi \varepsilon _0}\oint_S{\frac{1}{r^3}\left( x\mathrm{d}y\mathrm{d}z+y\mathrm{d}x\mathrm{d}z+z\mathrm{d}x\mathrm{d}y \right)},\text{由高斯公式} \\ =\frac{q}{4\pi \varepsilon _0}\iiint_V{\left[ \frac{\partial \left( \frac{x}{r^3} \right)}{\partial x}+\frac{\partial \left( \frac{y}{r^3} \right)}{\partial y}+\frac{\partial \left( \frac{z}{r^3} \right)}{\partial z} \right]}\mathrm{d}x\mathrm{d}y\mathrm{d}z=0\left( \text{散度为零} \right)$

上述结果扩展到多个点电荷时自然也成立，所以静电场的高斯定理即为：

$\oint_S{E\cdot \mathrm{d}\boldsymbol{S}}=\frac{1}{\varepsilon _0}\sum_{\left( \text{内} \right)}{q_i}$

由这个定理，可以计算许多具有良好对称性的带电体的场强，只需构造合适的高斯面即可。

实际上对于闭合曲面内电荷连续分布的情况，并且如果电荷密度$\rho$处处为有限值。那么可以得到：

$\oint_S{E\cdot \mathrm{d}\boldsymbol{S}}=\frac{1}{\varepsilon _0}\iiint_V{\rho \left( r \right) \mathrm{d}V} \\ \nabla \cdot E=\frac{\rho}{\varepsilon _0}$

第二个定理即静电场的环路定理：

$\oint_{}{\boldsymbol{E}\cdot \mathrm{d}\boldsymbol{l}}=0$

这个定理实际上可以由格林公式说明，但感性理解起来也不生硬。实际上静磁场的环路定理有更大的功用，这个实际上我们已经“默认”了。

剩下的一些关于电势，电势差，电势能在此不作赘述。

下面是一些练习：

①下面的球面（半球面）半径均为$R$,电荷密度为$\sigma$，对于半球面，求球心$O$点的电场强度。对于球面，求电场强度随$x$的变化。

对于半球面时的情况，利用球坐标系。记$xOy$平面上关于$x$正半轴方向夹角为$\varphi$,记与$Oz$夹角为$\theta$。那么面积微元$\mathrm{d}S=R^2\sin \theta \mathrm{d}\varphi \mathrm{d}\theta $。

由对称性，只需计算$-z$方向的电场强度分量。

$dE_z=\frac{1}{4\pi \varepsilon _0}\frac{\sigma \mathrm{d}S}{R^2}\cos \theta \\ E=\frac{1}{4\pi \varepsilon _0}\int_0^{2\pi}{\mathrm{d}\varphi}\int_0^{\frac{\pi}{2}}{\sigma \sin \theta \cos \theta \mathrm{d}\theta}=\frac{\sigma}{4\varepsilon _0}$

方向沿$z$轴负方向。

对于球面时的情况，直接作球形高斯面：

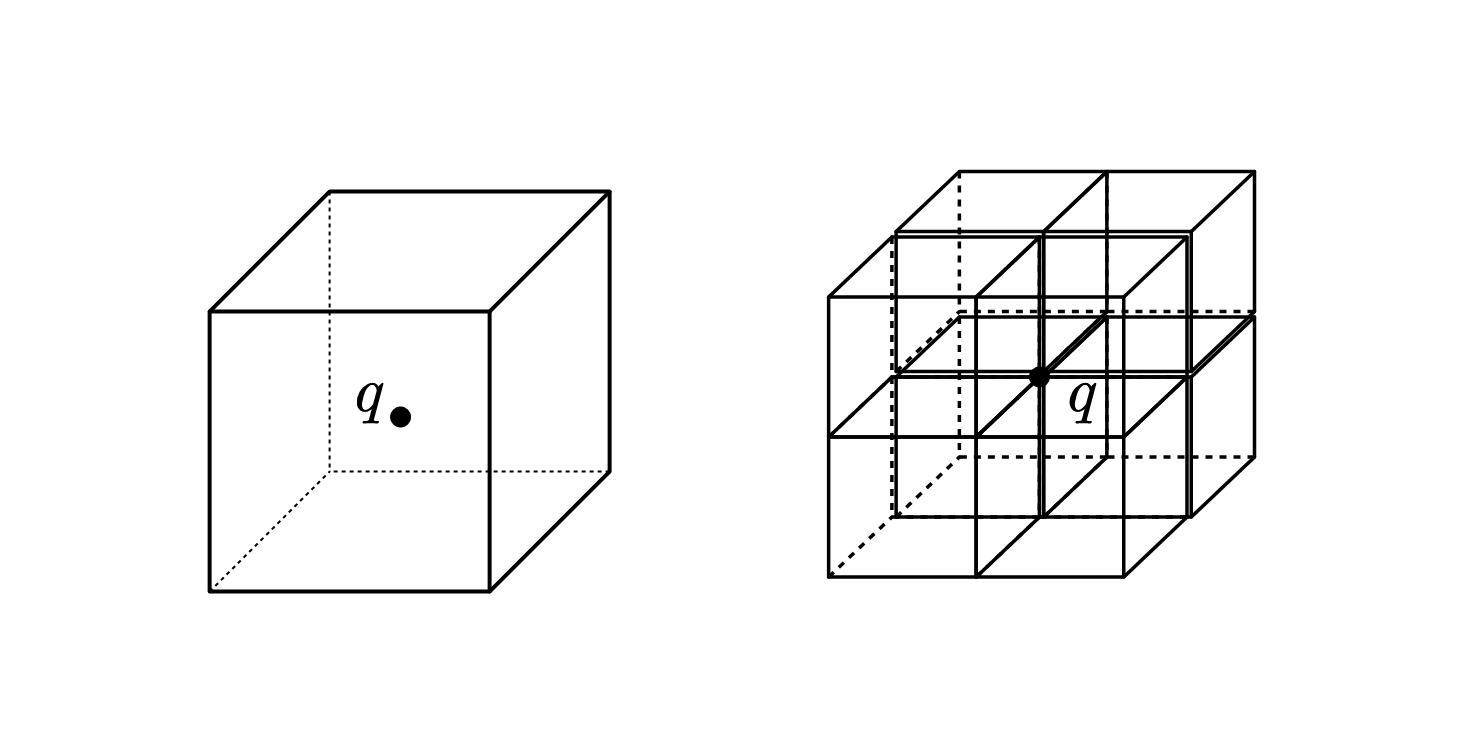
$\oint_S{E\cdot \mathrm{d}\boldsymbol{S}}=4E\pi r^2=\left\{ \begin{array}{c} \frac{1}{\varepsilon _0}\sigma 4\pi R^2,r>R\\ 0,r\leqslant R\\ \end{array} \right. ,E=\left\{ \begin{array}{c} \frac{\sigma R^2}{\varepsilon _0r^2},r>R\\ 0,r\leqslant R\\ \end{array} \right.$

②一个点电荷$q$位于边长$a$的正立方体的中心，通过此立方体的每一面的电通量为？将该电荷移到正立方体的某一个顶点上，那么通过每个面的电通量又为？

直接取立方体形高斯面，在2问时构造8个正方体，选取大正方体共24个小面为高斯面。

$\varPhi =\oint_S{E\cdot \mathrm{d}\boldsymbol{S}}=\frac{q}{\varepsilon _0},\varPhi _1=\frac{q}{6\varepsilon _0},\varPhi _2=\frac{q}{24\varepsilon _0}\text{或}0$

③一个半径为$R$,长为$L$的均匀带电圆柱面，其单位长度的带电量为$\lambda$。在带电圆柱的中垂面上有一点P，它到轴线的距离为$r(r>R)$,则当$r\ll L$时，电场强度为？当$r\gg L$时，电场强度为？

当$r\ll L$时，用高斯定理处理，取圆柱形高斯面：

$\oint_S{E\cdot \mathrm{d}\boldsymbol{S}}=\frac{\lambda L}{\varepsilon _0}=2\pi rLE,E=\frac{\lambda}{2\pi r\varepsilon _0}$

当$r\gg L$时，按照点电荷处理，由库仑定律：

$E=\frac{1}{4\pi \varepsilon _0}\frac{\lambda L}{r^2}=\frac{\lambda L}{4\pi \varepsilon _0r^2}$

④设气体放电形成的等离子体在圆柱内的电荷分布可表示为

$\rho \left( r \right) =\frac{\rho _0}{\left[ 1+\left( \frac{r}{a} \right) ^2 \right] ^2}$

$r$是到圆柱轴线的距离，$\rho_0$是轴线处电荷体密度，$a$是常量。试计算其在圆柱外的电场强度分布。

$\mathrm{d}q=\rho \left( r \right) 2\pi rl\mathrm{d}r=\frac{2\pi rl\rho _0}{\left[ 1+\left( \frac{r}{a} \right) ^2 \right] ^2}\mathrm{d}r \\ q=\int_0^r{\frac{2\pi rl\rho _0}{\left[ 1+\left( \frac{r}{a} \right) ^2 \right] ^2}\mathrm{d}r=\frac{\pi rl\rho _0a^2}{1+\left( \frac{a}{r} \right) ^2}} \\ 2\pi rlE=\frac{\pi rl\rho _0a^2}{\varepsilon _0\left( 1+\left( \frac{a}{r} \right) ^2 \right)},E=\frac{\rho _0a^2}{2\varepsilon _0r}\frac{1}{1+\left( \frac{a}{r} \right) ^2}$

可以看出，运用高斯定理，可以方便的求解一些有对称性的带电体的电场强度。