大学物理

阅读数: 次 2021-10-17

为了应付期中考试，要预习大学物理了。由于大物只是个凑学分的课，所以不会纠的太深，能过个考试就得了。

其实第十章和第十一章的内容可以被总结的十分简洁，先从第十章开始。首先我们要对库仑定律进行改写：

$\boldsymbol{F}=k\frac{q_1q_2\boldsymbol{r}}{r^3}=\frac{q_1q_2\boldsymbol{r}}{4\pi \varepsilon _0r^3}$

也就是我们将高中学的静电力常数$k$改写成一个别的形式，这个形式是由高斯定理得来的，证明需要用到立体角，我们不必关心具体细节，在这里$\varepsilon _0\approx 8.85\times 10^{-12}\mathrm{C}^2\cdot \mathrm{N}^{-1}\cdot \mathrm{m}^{-2}$。

并且在以后的一些表达式里，会更多的将表达式写成矢量式的形式，因为这样才是规范的，但在实际上应付考试和写作业的时候，由于处理的问题都很简单，其实……没啥太大的必要。

电场强度的定义与高中完全相同，这里引入一种说法：电偶极子。

说的是高中时经常遇到的两个大小相等的异号点电荷$+q,-q$相距$l$,要计算的电场强度的各场点相对这一对电荷的距离$r\gg l$时，这样一对点电荷称为电偶极子。这个定义十分的形象，

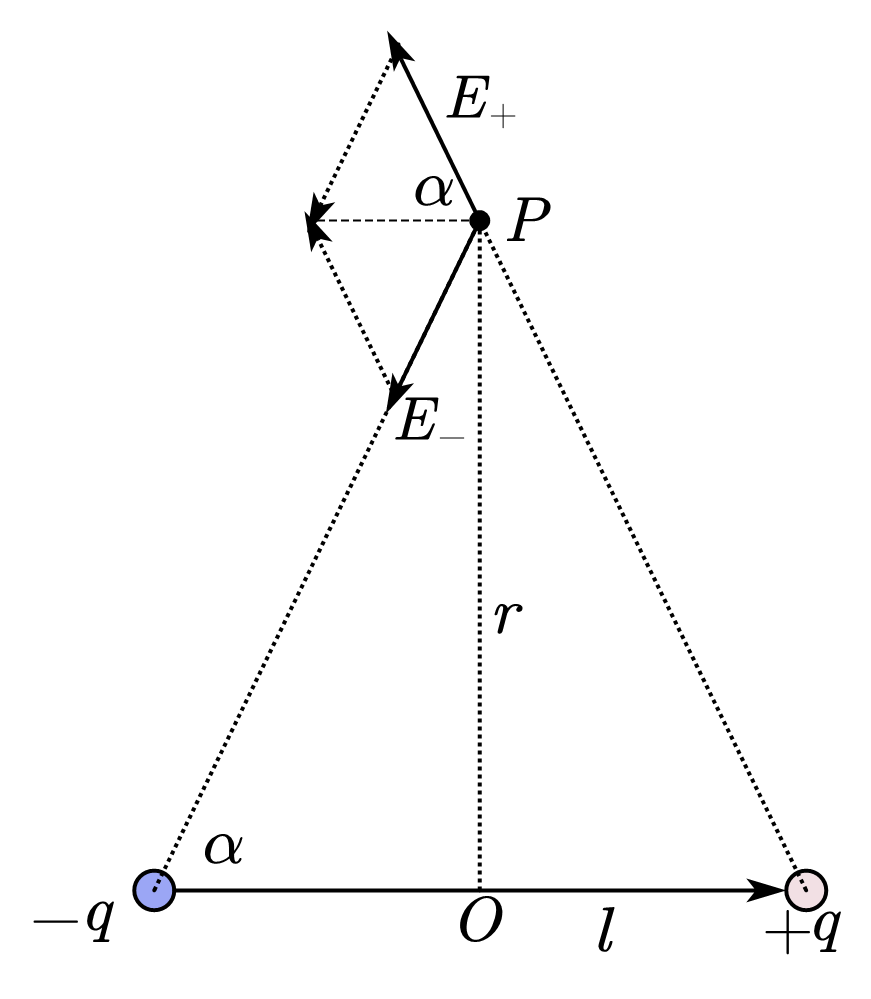
利用平行四边形法则可以计算出：

$E_p=2\cos \alpha E_{+/-}=2\frac{l/2}{\sqrt{r^2+l^2/4}}\frac{1}{4\pi \varepsilon _0}\frac{q}{r^2+l^2/4} \\ E_p=\frac{1}{4\pi \varepsilon _0}\frac{ql}{r^3\left( 1+\frac{l^2}{4r^2} \right) ^{\frac{3}{2}}}$

考虑到在此时$\left( 1+\frac{l^2}{4r^2} \right) ^{\frac{3}{2}}\approx 1$，且注意到，我们实际上是定义了$l,E$的方向，且它们的方向是相反的，则可以定义$\boldsymbol{p}=q\boldsymbol{l}$。

这样公式可以简化成：

$\boldsymbol{E}=\frac{1}{4\pi \varepsilon _0}\frac{\boldsymbol{p}}{r^3}$

但对于很多时候的带电体，电场强度都需要利用矢量积分来求解，将矢量积分转化为标量积分然后求解。下面举一个可以延伸到很多种情形的例子。<下面不加特殊说明，$q$代表带电体总电量，$\lambda ,\sigma ,\rho $依次代表电荷的线密度，面密度，体密度>

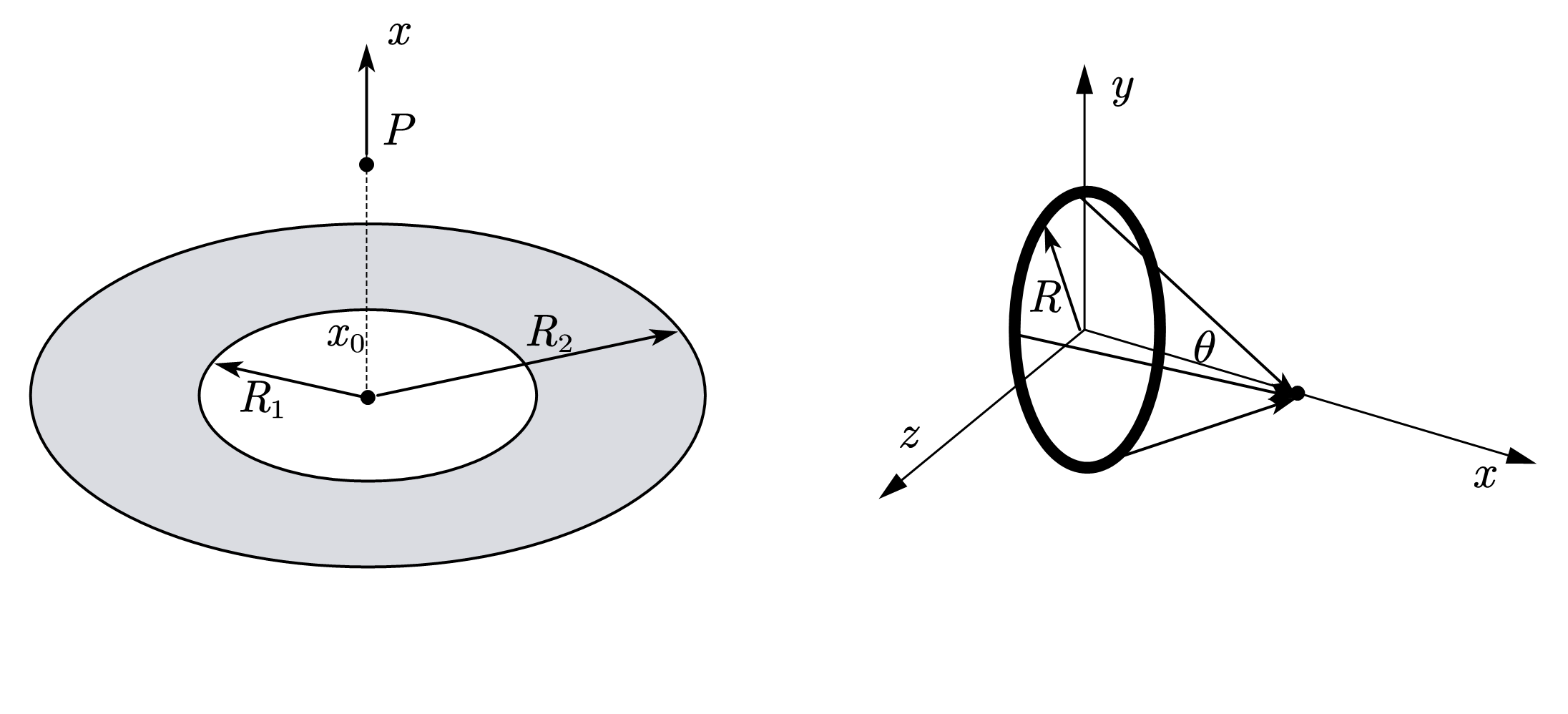
首先要处理右边的细圆环时的情形，由于对称性，$zOy$平面的电场强度分量互相抵消，只需计算$Ox$方向。在下面的介绍中我们均认为带电体电荷分布均匀，这是一个理想化的做法。那么对于圆环，可以得：

$E_{ring}=\int{dE_x}=\frac{1}{4\pi \varepsilon _0}\int{\frac{\cos \theta}{r^2}dq}=\frac{1}{4\pi \varepsilon _0}\frac{q\cos \theta}{r^2}=\frac{1}{4\pi \varepsilon _0}\frac{qx}{\left( R^2+x^2 \right) ^{\frac{3}{2}}}$

有了这个前置结果，对于左侧的同心圆环带电体，自然可以将其看作若干细圆环的叠加，则有：

$dq=2\pi r\sigma \mathrm{d}r,\sigma =\frac{q}{\pi \left( R_{2}^{2}-R_{1}^{2} \right)} \\ \mathrm{d}E=\frac{1}{4\pi \varepsilon _0}\frac{\mathrm{d}qx}{\left( R^2+x^2 \right) ^{\frac{3}{2}}}=\frac{x\sigma}{2\varepsilon _0}\frac{r\mathrm{d}r}{\left( r^2+x^2 \right) ^{\frac{3}{2}}} \\ E=\int{dE}=\frac{x\sigma}{2\varepsilon _0}\int_{R_1}^{R_2}{\frac{r\mathrm{d}r}{\left( r^2+x^2 \right) ^{\frac{3}{2}}}}=\frac{x\sigma}{2\varepsilon _0}\left( \frac{1}{\sqrt{R_{1}^{2}+x^2}}-\frac{1}{\sqrt{R_{2}^{2}+x^2}} \right)$

（这里复习一下换元积分法，其实也能直接看出原函数。）

$r=x\tan \theta ,\mathrm{d}r=x\sec ^2\theta \mathrm{d}\theta \\ \frac{x\sigma}{2\varepsilon _0}\int_{R_1}^{R_2}{\frac{r\mathrm{d}r}{\left( r^2+x^2 \right) ^{\frac{3}{2}}}}=\frac{\sigma}{2\varepsilon _0}\int_{\theta _1}^{\theta _2}{\sin \theta}\mathrm{d}\theta ,\theta _1=\mathrm{arc}\tan \frac{R_1}{x},\theta _2=\mathrm{arc}\tan \frac{R_2}{x} \\ =\frac{x\sigma}{2\varepsilon _0}\left( \frac{1}{\sqrt{R_{1}^{2}+x^2}}-\frac{1}{\sqrt{R_{2}^{2}+x^2}} \right)$

分析得到的结论，实际上当改变$R_1,R_2$的值，会得到一些其他的结论：

①当$R_1=0,R_2\rightarrow \infty $时，可以认为是无限大均匀平板，场强公式为

$E=\frac{\sigma}{2\varepsilon _0}$

②当$R_2\rightarrow \infty$,认为是有孔的无限大平板。场强公式为

$E=\frac{x\sigma}{2\varepsilon _0}\frac{1}{\sqrt{R_{1}^{2}+x^2}}$

③当$R_2-R_1=O(R)$，认为是细圆环，由导数定义，场强公式退化为

$g\left( R \right) =\frac{1}{\sqrt{R^2+x^2}},g'\left( R \right) =-\frac{R}{\left( R^2+x^2 \right) ^{\frac{3}{2}}} \\ \frac{1}{\sqrt{R_{1}^{2}+x^2}}-\frac{1}{\sqrt{\left( R_1+\varDelta R \right) ^2+x^2}}=-g'\left( R_1 \right) \varDelta R=\frac{R_1\varDelta R}{\left( R_{1}^{2}+x^2 \right) ^{\frac{3}{2}}} \\ \sigma =\frac{q}{\pi \left( \left( R_1+\varDelta R \right) ^2-R_{1}^{2} \right)}=\frac{q}{2\pi R_1\varDelta R} \\ E=\frac{x}{2\varepsilon _0}\frac{q}{2\pi R_1\varDelta R}\frac{R_1\varDelta R}{\left( R_{1}^{2}+x^2 \right) ^{\frac{3}{2}}}=\frac{1}{4\pi \varepsilon _0}\frac{qx}{\left( R_{1}^{2}+x^2 \right) ^{\frac{3}{2}}}$

和之前的结果是一致的。

还有一个比较重要的理想模型是均匀带电直线杆

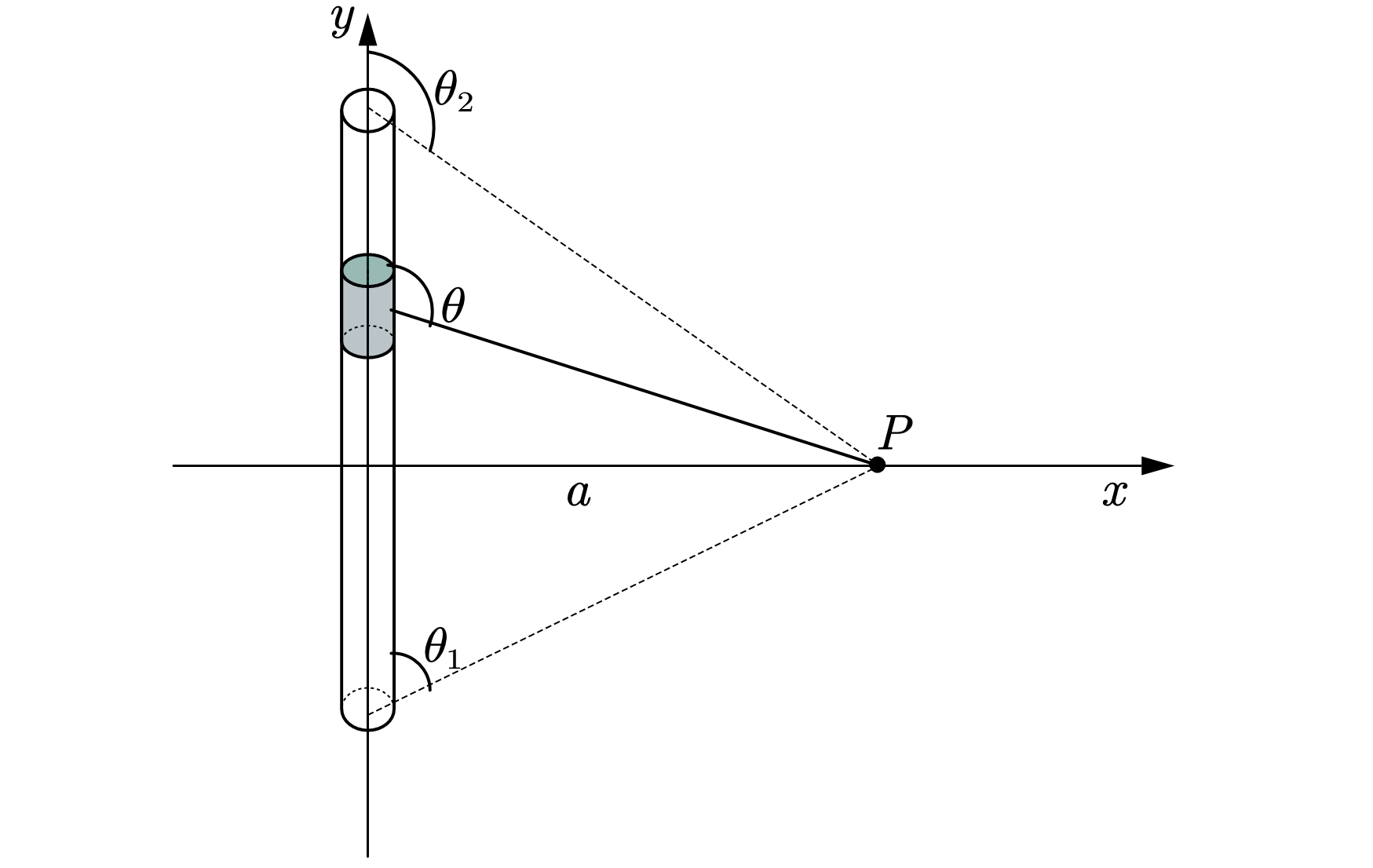
由于$\theta_1,\theta_2$并没有给出特殊关系，所以对称性不能得到保证。所以要分$x,y$方向计算。

$\mathrm{d}q=\lambda \mathrm{d}y \\ \mathrm{d}E=\frac{1}{4\pi \varepsilon _0}\frac{\lambda \mathrm{d}y}{r^2},r^2=a^2+y^2=a^2\csc ^2\theta \\ y=-\frac{a}{\tan \theta}=-\mathrm{a}\cot \theta ,dy=a\csc ^2\theta \mathrm{d}\theta \\ \mathrm{d}E=\frac{1}{4\pi \varepsilon _0}\frac{\lambda \mathrm{d}y}{r^2}=\frac{1}{4\pi \varepsilon _0a}\lambda \mathrm{d}\theta \\ \mathrm{d}E_x=\mathrm{d}E\sin \theta ,\mathrm{d}E_y=\mathrm{d}E\cos \theta \\ E_x=\int_{\theta _1}^{\theta _2}{\frac{1}{4\pi \varepsilon _0a}\lambda \sin \theta \mathrm{d}\theta}=\frac{1}{4\pi \varepsilon _0a}\left( \cos \theta _1-\cos \theta _2 \right) \\ E_y=\int_{\theta _1}^{\theta _2}{\frac{1}{4\pi \varepsilon _0a}\lambda \cos \theta \mathrm{d}\theta}=\frac{1}{4\pi \varepsilon _0a}\left( \sin \theta _2-\sin \theta _1 \right)$

许多时候是考虑当杆无限长时，此时积分上下限变为$\pi,0$。得到较为有用的结论：

$E_x=\frac{\lambda}{2\pi \varepsilon _0a},E_y=0$

以圆环和直杆的结果出发可以求解多种几何体的电场强度，后面还会有另一种简洁的求电场强度的方法，在此就从略了。

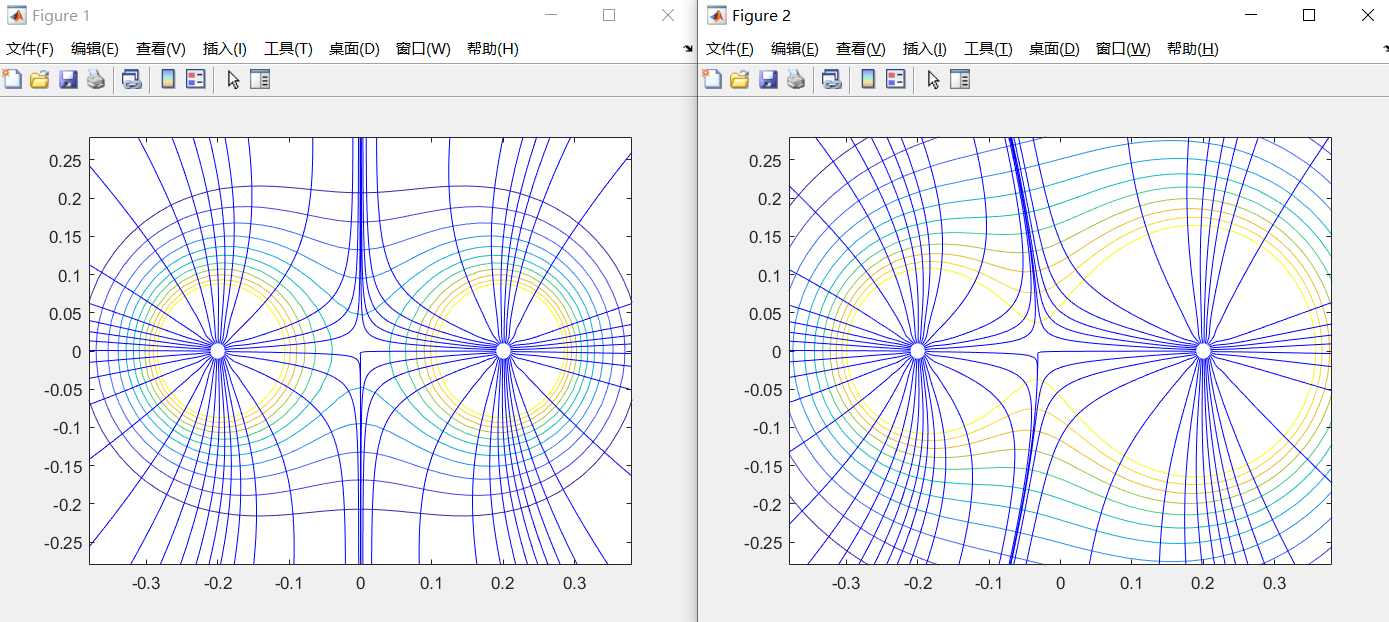
今天先写到这里，以后有空把一些可以可视化的作出来，上面是等量同种电荷和不等量同种电荷的图像，我希望我的高中老师在我上高中的时候也能画出这个来给我们看，但很遗憾他没有。