数值积分

阅读数: 次 2021-09-08

我们都十分希望有个“解析式”，这样把把变量的值带入就能得到想要的数值。在求定积分时，我们希望可以直接用牛顿莱布尼茨公式得到答案，但是对于多种情况都要借助数值积分。

对于数值积分的大多数实践方法其实和之前对微分方程的处理是十分相似的，因为抛去理论的分析，在数值求解上，这两者近乎就是完全一致的。

有许多效果很好的数值积分方法，比如多项式逼近，辛普森方法，并且matlab已经封装了许多完好的数值积分器，自己造的轮子性能是跟商业化的比不了的。对于实际操作时，其实用一些基础的方法就够了。

关于数值积分有一道经典的问题：CUMCM2010A储油罐的变位标定，这个问题具有非常好的现实意义，但是放在今天看难度已经太低了，问题简单说来就是由于加油站地下地基的变位导致的储油罐油浮子高度导出的体积的变化，需要对原有的表格重新标定，基于此要建立纵向和横向偏角对体积方程。

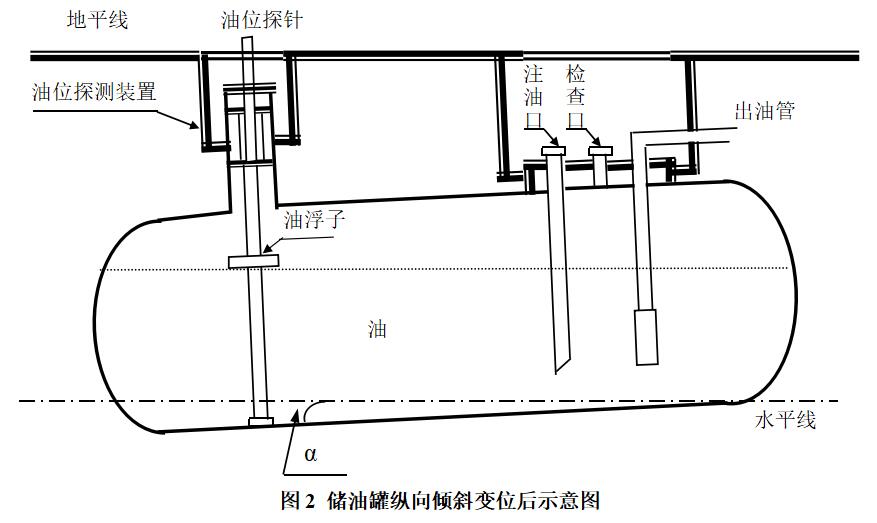
罐体的具体参数在题目原件里已经给出，实际上在解决这个两端是球缺中间是圆柱的比较复杂的情况之前，题目用一个小的椭圆柱形的小储油罐进行了过渡。

我们先考虑一种特殊的，即没有发生任何变位时，小储油罐的情况。

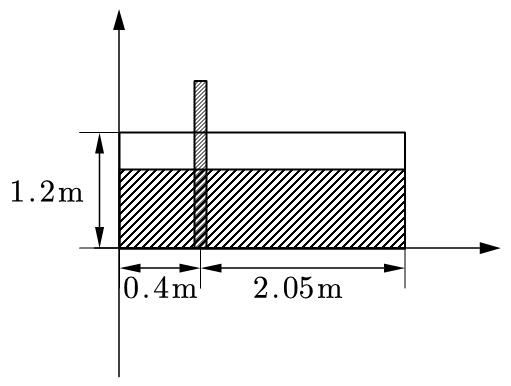
这是我们第一反应会建立的模型，此时积分也并不复杂：

$V=\int_0^{2.45}{\int_{-b}^{-b+h}{a\sqrt{1-\frac{y^2}{b^2}}dydx}}$

给定一个$h$就可以计算出此时的体积，但是当有变位时，上述公式就不适用了，容易分析出，变位$\beta$实际上只是对高度的改变，在实际的储油罐中，$\beta$作用下从截面上看液面仍然水平，所以通过简单的几何关系可以导出：

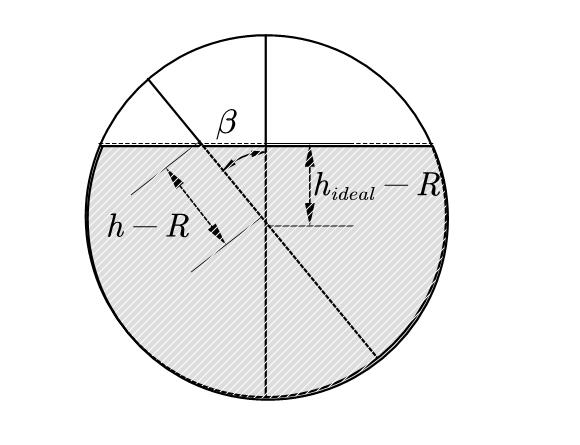
$h_{ideal}=\left( 1-\cos \beta \right) R+h\cos \beta$

要注意，这么写实际上是为了解耦，利用上面的关系，就可以将$\beta$的影响转化为对$h$的更新。对于$\alpha$问题变得稍微复杂了一些，因为实际上由于倾斜，第一直觉就是：在$h=0$时仍然会有油。并且由于倾斜，两端不再对称，两端的边界条件会导致这个问题复杂化。比如当倾起一个角度时，当油比较多时，较低端已经被注满，所以需要分类讨论。

但运用一些比较显然的技巧，可以帮助简化整个过程。

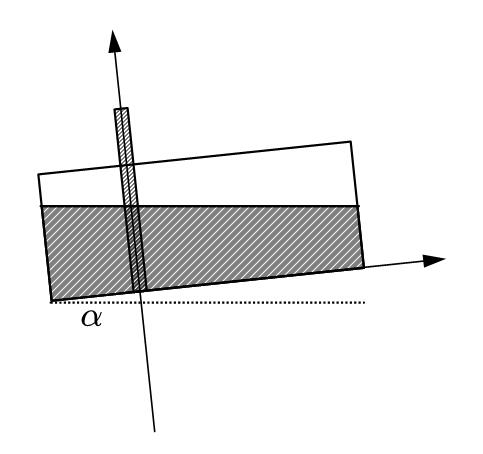
如果将坐标系改成这种形式，问题就会得到简化。但仍然有一个问题，若左端有油而油不够多，右端没有油，则仍然要分类讨论，实际上是不需要的，此时的积分会积出一个复数，它的实部是零，虚部对我们没有意义，此时一个积分式就可以完成第一问，这个积分的方式可以理解为“切片”。

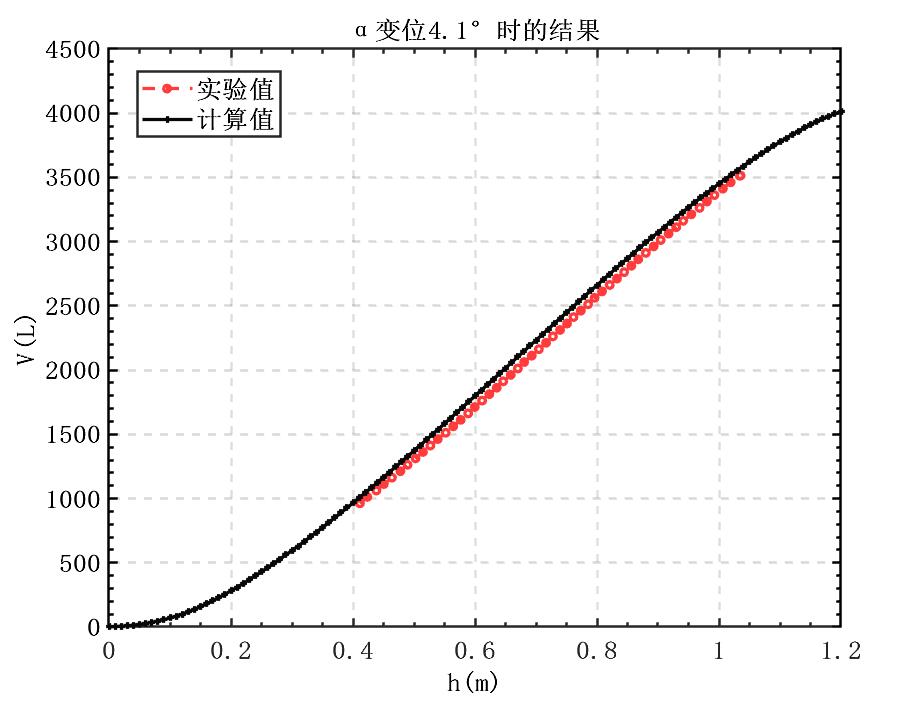
计算得到的4.1°时的结果与实际数据的比较，考虑到实际的储油罐是有厚度的而题目并没有给相关的信息，误差是可以接受的。

而第二问是一个反问题，加之变成了两端是球缺的储油罐，难度增加。此时通过第一问的铺垫，可以直接推出此时应该建立的坐标系是：

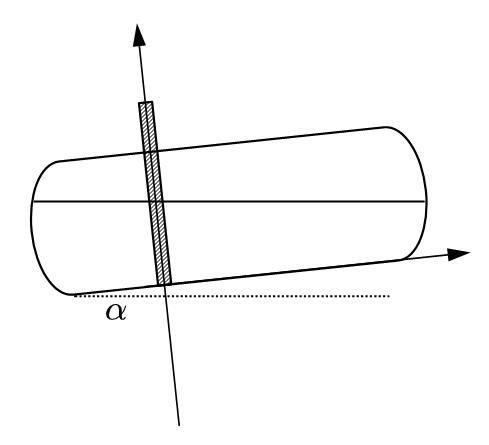
此时对于给定的一个$h$,体积可以如下求得：

$\left\{ \begin{array}{c} x\in \left[ -3,-2 \right) \left\{ \begin{array}{c} \begin{array}{c} \begin{array}{c} \begin{array}{c} S=\int_{-\sqrt{2R\left( x+3 \right) -\left( x+3 \right) ^2}}^{h-x\tan \left( \alpha \right) -1.5}{2\sqrt{2R\left( x+3 \right) -\left( x+3 \right) ^2-y^2}dy}\\ V_{left}=\int_{-3}^{-2}{S\left( x \right) dx}\\ \end{array}\\ \end{array}\\ \end{array}\\ \end{array} \right.\\ x\in \left[ -2,6 \right) \left\{ \begin{array}{c} \begin{array}{c} S=\int_{-1.5}^{h-x\tan \left( \alpha \right) -1.5}{2\sqrt{R_{b}^{2}-y^2}dy}\\ V_{mid}=\int_{-2}^6{S\left( x \right) dx}\\ \end{array}\\ \end{array} \right.\\ x\in \left[ 6,7 \right) \left\{ \begin{array}{c} \begin{array}{c} \begin{array}{c} \begin{array}{c} S=\int_{-\sqrt{2R\left( 7-x \right) -\left( 7-x \right) ^2}}^{h-x\tan \left( \alpha \right) -1.5}{2\sqrt{2R\left( 7-x \right) -\left( 7-x \right) ^2-y^2}dy}\\ V_{right}=\int_6^7{S\left( x \right) dx}\\ \end{array}\\ \end{array}\\ \end{array}\\ \end{array} \right.\\ V=real\left( V_{left}+V_{mid}+V_{right} \right)\\ \end{array} \right.$

由于上述的积分式都很难得到解析解，所以数值解是出路。但是数值解一定会带来误差，此时附件的数据就起到了作用，这个问题的有趣之处是要分辨清楚附件中所给数据的意义。对于附件2来说，此时的“显示油量容积”是不准确的，这是由于此时变位后导致高度的“畸变”，此时高度和体积的关系对应的是$\alpha,\beta$均为零时的体积，我们可以利用此数据与数值积分的结果进行校验，来选取合适的积分步长$dx$

并且由于附件2中没有给初始油量的体积，所以仅从附件2是无法知晓储油罐内当时的准确体积的，所以试图用$h-V$来进行最小二乘的解法都是不正确的。应该从附件2中提取$\varDelta h-\varDelta V$的关系进行最小二乘，接下来的问题就是如何选取合适的数据进行最小二乘，实际上这个的计算速度不是很快，处理时需要进一步考虑选取哪些数据点对进行最小二乘，以及对用matlab的计算代码进行加速处理。

function [Error]=Lsq_oil(alpha,beta,V_cur,H)

alpha=alpha*pi/180;
beta=beta*pi/180;

dx=0.005;
R=1.625;

n=length(H);
H=(1-cos(beta))*R+cos(beta).*H;

V=zeros(n,1);
delta_V=zeros(n-1,1);

for i=1:n
    h=H(i);
    V_l=0;
    V_m=0;
    V_b=0;
    S_front_pre=0;
    S_stable_pre=0;
    S_behind_pre=0;
    for x=-3:dx:-2
        f=@(y) 2*sqrt(2*R*(x+3)-(x+3).^2-y.^2);
        S_front_cur=real(integral(@(y)f(y),-sqrt(2*R*(x+3)-(x+3).^2),h-x*tan(alpha)-1.5));
        S_consider=(S_front_cur+S_front_pre)/2;
        S_front_pre=S_front_cur;
        V_l=V_l+S_consider*dx;
    end
    for x=-2:dx:6
        g=@(y) 2*sqrt(1.5*1.5-y.^2);
        S_stable_cur=real(integral(@(y)g(y),-1.5,h-x*tan(alpha)-1.5));
        S_consider=(S_stable_cur+S_stable_pre)/2;
        S_stable_pre=S_stable_cur;
        V_m=V_m+S_consider*dx;
    end
    for x=6:dx:7
        z=@(y) 2*sqrt(2*R*(7-x)-(7-x).^2-y.^2);
        S_behind_cur=real(integral(@(y)z(y),-sqrt(2*R*(7-x)-(7-x).^2),h-x*tan(alpha)-1.5));
        S_consider=(S_behind_cur+S_behind_pre)/2;
        S_behind_pre=S_behind_cur;
        V_b=V_b+S_consider*dx;
    end
    V(i)=V_l+V_m+V_b;
    if i~=1
        delta_V(i)=V(i-1)-V(i);
    end
end
V=V*1000;
delta_V=delta_V*1000;
Error=sum(V_cur-delta_V(2:n)).^2/(n-1);

由于这个问题是我与我的一个队友这三天利用临近比赛每晚一到两小时左右进行处理的，上述代码哪怕用matlab都有很大的加速空间，但由于这里只是作为一个数值积分的例子就先不管了，如果用这个直接进行遍历搜索，且数据点对选取附件2中第一次加油前的所有数据，粗略计算出的$\alpha=2.6°$，$\beta=0°$，这个结果与评阅标准中的“$\alpha=2°$左右，对$\beta$不敏感。”仍然有一定差距，但对于用6个小时计算出的结果，已经可以接受了。

这里值得一提的是，对于数值积分来说，任务已经完成了。但是对于该问题，实际上选取合适的数据点对是重要的，如果选取的很多，拟合的效果可能过头，并且计算的时间会显著变长。合理的处理方法实际上在高中的物理课上就学过：选取间隔长的数据。即对数据进行稀疏化，效果会变好一些，且得到的参数将会更稳定。

实际上我愧对我两个队友，因为无条件的做A题是我的想法，功利的来讲，去广撒网的，浅尝辄止的学一些C题要用的评价类，预测类，调包等等，画点华而不实的图，从功利的角度上看这是上策。但是我当时心里想：“如果都这么水，和咸鱼有什么区别。”，心一横就敲定A了，他俩也没啥意见。结果到临头我甚至有点怂，“如果推进的时候遇到一些我没遇到的问题怎么办？如果解方程解出来发散了而我又不清楚步长怎么选怎么办？”等等，我希望我一个假期学到的数值方法和数学工具，应付明天的A题够用。

确实数学建模在一些大佬眼里，处于鄙视链最低端。因为做这个无非就是想混个加分什么的，和同级加分的比赛比技术含量还是最低的，或许在他们眼里我一个月学那些内容他们两天就上手了，或许他们根本不屑于用matlab这种傻瓜式的软件来写这个的代码。我根本达不到他们的高度，差的太多了，我毕竟不是他们啊，我是我啊。“世间只有一种英雄主义，那就是看清生活的真相之后依然热爱生活。”，至少我回看我发的第一篇博客的时候，回想起当时PDE都不会列的我，还是有一些收获的，这就够了。