今天是2021年9月4号,星期六。而我宿舍里就我一个人,另外三个连人带包都没了,不知道是去扫楼招新还是去卷了。在宿舍太无聊了所以就随便写点。
第一次认识最小二乘来源于高中数学的第19题,有时会给出$\hat{a},\hat{b}$的表达式和一些被初步计算过的数据,来进行算数,即“线性回归”。回归的思想在别的领域也有很大的用处,但不是本文的内容了。由于当时高中受水平限制,老师并没有给出一个较圆满的解释,但“通俗”的解释也足够把我从一个考个一本都不得了的地方送到这里(然后一上网冲浪985遍地走211遍地爬,重开吧)。
实际上在系统的阐述之前要复习一个定理,说的是:
设$A$是一个$m$行$n$列矩阵,则$A$一定可以通过行初等变换和第一种列初等变换将其形式变为:
这里$r$代表什么现在已经很清楚了,考虑其增广矩阵和$r$,我们能写出线性方程组解的情况。现在我们关注这样的一种情况:当$rank(A)\ne rank(A,b)$时,线性方程组无解。此时将其称为矛盾方程组,但如果能找到一组向量$x$使得$f\left( x \right) =\left| Ax-b \right| _2$最小,那么就称$x$是$Ax=b$的最小二乘解。
计算其2-范数:
由极值必要条件,求得极值需要保证关于$x$的偏导为0,因为:
可得线性方程组:
这看起来是个无奈之举,因为此时原线性方程组已经无解了,就像三个必不共线的点一样,只是勉强的找出了一个和三个点距离之和最小的直线。但实际上这个作法是很有意义的。
对于给定的一组数据$\left\{ \left( x_i,y_i \right) \right\} _{i=1}^{m}$,假设拟合函数为:
这里$\varphi_i(x)$线性无关,则希望误差平方和最小(这一点被高斯和勒让德详细论述过),即:
希望$\frac{\partial E\left( a_0,a_1,…,a_n \right)}{\partial a_i}=0$,记:
上述向量组$a$是待求参数,再令$A=\left[ a_{ij} \right] _{m\times \left( n+1 \right)},a_{ij}=\varphi _j\left( x_i \right) $,那么:
所以拟合某一曲线的问题就转化为了超定线性方程组$Aa-y$的最小二乘解的问题,即:
此时要求$A$列满秩,在此情况下我们对最小二乘法作简单的几何解释。此时列满秩,则行数必然大于等于列数($m\geqslant n$),则$A$的所有列张成了一个$m$维线性空间中的$n$维子空间,即$Im(A)$,而又知道$y$不能被$A$的基线性表示,则由推导出的式子:$A^T\left( Ax-y \right) =0$,由内积的几何意义(显然可以证明这个向量空间满足欧氏空间)可以说明$A^T$与$Ax-y$正交。则$Ax$就是向量$y$在$Im(A)$的投影,这个情形,与高等代数中对最佳逼近继而推出傅里叶级数的操作如出一辙。也就是说,最小二乘相当于一个高维向量在低维空间的投影。
此时$\left( A^TA \right) ^{-1}A^T$的作用就相当于在有解情况下$Ax=b,x=A^{-1}b$中$A$的逆一样,称为广义逆,当$A$非列满秩时,广义逆的形式稍作改变。
基于此对最小二乘进行改造,第一种是加权法,考虑到不同方程的重要性不同,可以给出一个对角阵$W$,继而优化$E=\left| W(Aa-y) \right| _{2}^{2}$,此时求解的线性方程组就变为了:$\left( A^TW^TWA \right) x=A^TW^TWy$。
第二种是阻尼法,这时考虑到当$A$非列满秩时,理论证明此时一种可行的替代途径是阻尼法,此时$A^TA$的行列式为零,则考虑$\mu I+A^TA$,对于任意的$\mu >0$显然$|\mu I+A^TA|\ne$0,其中$\mu$称为阻尼参数,修正后的矩阵便可逆了。此时满足的方程组为$(\mu I+A^TA)x_\mu=A^Ty$,自然在这种情形下,要合适的选择阻尼参数$\mu$。(Levenberg-Marquardt方法)
现在可以看到,对最小二乘拟合曲线的求解,最终归结为了对线性方程组的求解,从而对线性方程组求解的所有数值方法均可使用。(后面专门写个数值分析的系列,现在先鸽着)。
这里举一个Gauss-Newton迭代法的例子:
此时的函数是$y=f(x,\beta)$,其中$\beta=(\beta_1,\beta_2,…,\beta_n)$,在这里已知点的数目$m>n$,这也与实际情况相符。目的是找到最优解使得$S=\sum_{i=1}^m{r_{i}^{2}}$最小,那么自然希望:
但多数情况下,这个条件不能直接求出,只能迭代求解:$\beta _j\approx \beta _{j}^{k+1}=\beta _{j}^{k}+\varDelta \beta _j$,对$\beta^k$处由泰勒级数展开:
此时残差写作:
带回极值的必要条件:
考虑所有的$j$,写成矩阵形式为:
所以最终得到迭代公式为:
其中$J$是关于参数向量组$\beta$的雅可比矩阵。写一个简单的例子,来由$y=e^{ax^2+bx+c}$拟合$y=e^{x^2+2x+1}$。
1 | clear all; |
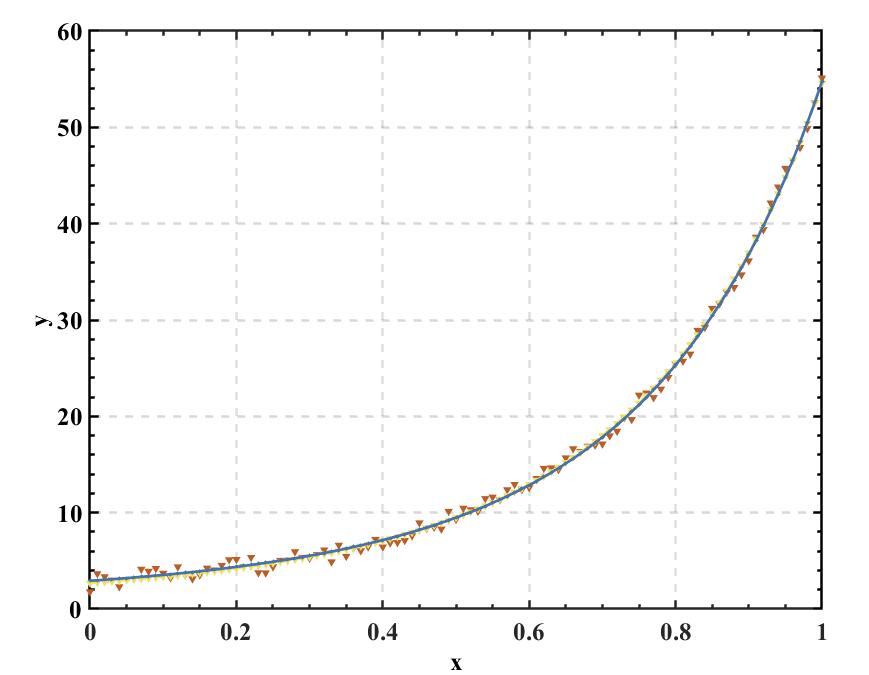
利用加噪后的数据拟合出的效果与真实曲线仍符合的很好,并且这种做法也要比暴搜要更……优雅?毕竟当参数得不到有效估计时直接搜索实数空间$R$不是什么好办法。
在CUMCM的题目中有许多时候都涉及到了这个问题,例如2015A太阳影子定位,通过基本地理知识和几何关系可以推出影子长度$d$满足:
上述问题就化为了与实验数据进行最小二乘确定各参数(纬度,经度,杆长),由于完成该操作的代码过于琐碎,这里从略了。可以看出计算的结果:
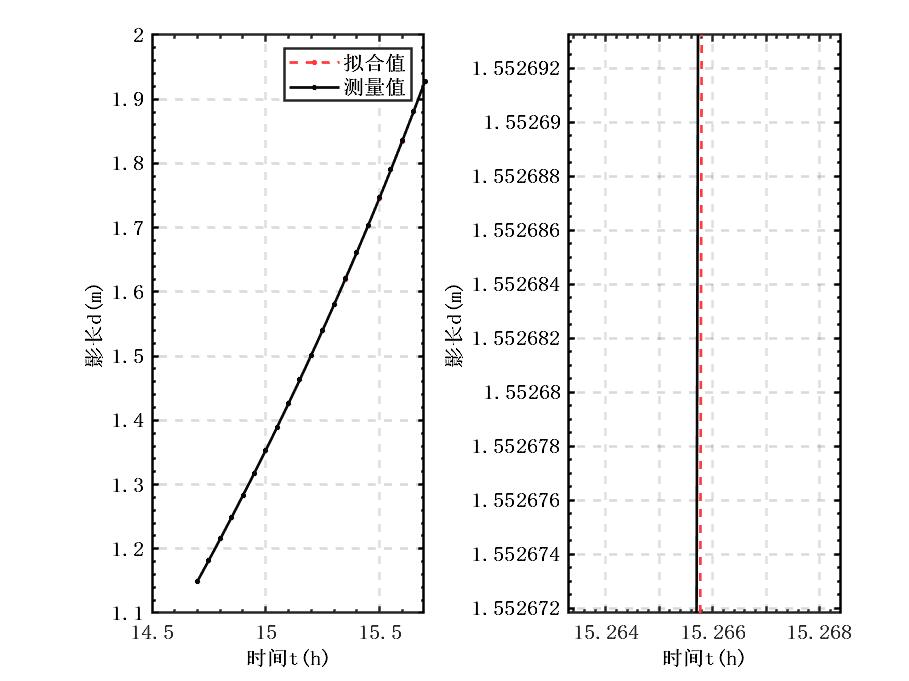
可以看出拟合效果很好。并且重要的一点是:运行时间短,如果遍历搜索,每多一个参数就要多一个循环,时间复杂度难以承受。而编写一些迭代算法,可能又会依具体问题出现一些不可预料的错误,例如不收敛,或者报错等等。这个确实是值得度量的,因为可能有用传统方法编写代码的时间,遍历早搜出可以接受的解了。
实际上对于这类参数反演问题,联合使用多种方法是最合适的,例如对某些问题,确定的参数数量不多且区间较小,暴搜的时间在比赛时间内可以接受,用暴搜也是可以的。
写完的时候已经是9月5号了,昨天晚上发生了一个非常恐怖的事情:我舍友吃错药了,真吃错药了。基于此,我想下一篇写一个关于血药浓度的微分方程模型……

