多目标优化

阅读数: 次 2021-08-31

多目标优化在大多数情况下比单目标有更重要的意义，下面介绍一些典型的多目标优化方法。

多目标优化遇到的情景更加普遍，例如实际情境中，导弹的射程和战斗部的优化，这两者的最优解无法同时取得，而多数情况下，这个多目标指的就是两个目标。

对于该问题有一个很经典的例子：

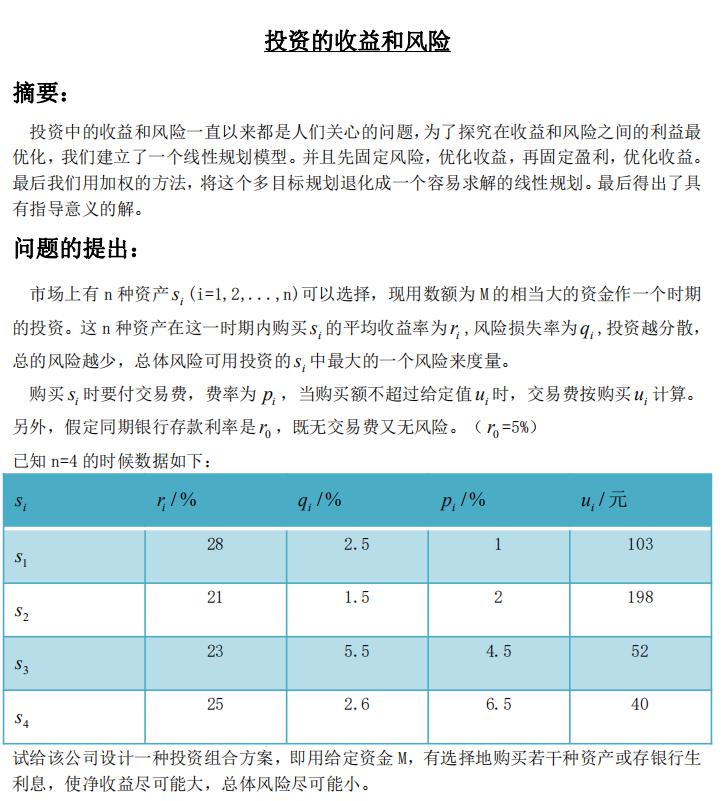
这个问题选自选修课上的数模作业，它的做法是固定的：先固定风险水平，优化收益，再调整风险的强度，作出许多收益的散点；再固定盈利水平，优化风险，然后调整盈利水平，作出许多风险的散点；最后给风险和盈利加权，改变权重来得到多组风险和盈利的值。可以理解为“遍历”了线性规划的最优解，实际上这种做法就是将多目标问题转化为了单目标问题，下面将系统的介绍这些做法。

传统方法：

①加权法

$\sum_{i=1}^p{w_i}=1 \\ opti:u\left( x \right) =\sum_{i=1}^p{w_if_i\left( x \right)}\,\,or\,\,\prod_{i=1}^p{\left( f_i\left( x \right) \right) ^{w_i}}$

权重的来源参考评价类模型，要注意，这里不同的$f_i(x)$往往是被标准化后的，量纲或数量级有差异时的加权是无意义的。

②偏差函数法（罚函数法）

选定一组理想点$\left( \bar{f}_1,\bar{f}_2,…,\bar{f}_p \right) $，将原问题归结为：

$opti:u\left( x \right) =\sqrt{\sum_{i=1}^p{\left( f_i\left( x \right) -\bar{f}_i \right)}^2}$

在这里理想点的选取一般为题目给定，或以主观偏好选取。

(实际上罚函数这个词广义上是将有约束的规划问题利用罚因子转化为无约束的这一方法，例如拉格朗日数乘法。)

③测度法：

该方法提供了一个与①同质的方法，实际上它对每个子函数$f_i(x)$作归一化（normalization）

$d_i\left( x \right) =\frac{f_{i,\min}-f_i\left( x \right)}{f_{i,\max}-f_{i,\min}} \\ opti:u\left( x \right) =\sum_{i=1}^p{d_i\left( x \right)}$

要指出，这种方法对原有子函数的形态有要求，这是因为归一化方法只取决于其极值，如果存在过于偏差的极大点和极小点，会出现问题。

与归一化类似的是标准化：

$X=\frac{x-\mu}{\sigma}$

称为z-score方法，将原有序列转化为一个均值为0，方差为1的分布（不一定是正态分布）。

实际上，归一化方法对指标的不同，不止有上面简单的线性形，也有非线性归一化方法，在一些情况下，选择合适的非线性归一化方法，与指标更匹配。这里不作赘述。

④约束法

在多个目标中选定一个主要目标，而对其他目标设定一个期望值，在要求结果不比期望值坏的情况下，求主要目标的最优值。之前投资与风险的例题使用的就是这一的方法。

⑤分层序列法

这个方法可行性十分有限，意思就是将多个目标按照重要程度进行排序，先求第一个目标的最优解，找到此目标的条件，然后在这个条件下求第二个目标的最优解，以此类推。但是实际上，这个“条件”很难找到。

启发式算法：

利用启发式算法，可以得到帕累托前沿解（Pareto Front），我们遇到的多目标问题，许多函数往往是互相冲突的，此时只能寻找帕累托解（非支配解），所谓支配的定义是指：如果A，B为问题的两组解，A的各项指标都优于B，就说A支配B，否则A和B就是非支配的关系。而帕累托解就是在解空间里不被其他任何解支配（全方位碾压）的解。

此算法目前已经被matlab集成，算法原理是基于遗传算法的NSGA-II，详细原理此处从略。

下面用一个小规模的例子来进行举例。

某厂共有工人300名，生产A，B，C，D四种化工原料，要求每人每周平均生产时间在40~48小时内，C为国防用产品，每周至少生产150公斤，而每周最多可提供能源20吨标准煤。其他数据如下表：

产品	最大产量(kg/周)	销售量(kg/周)	成本(元/kg)	售价(元/kg)	能耗(吨煤/kg)	生产时间(h/kg)
A	270	300	190	200	0.015	13
B	240	300	210	230	0.02	13.5
C	460	600	148	160	0.018	14
D	130	200	100	114	0.011	11.5

如何安排每周的生产，可以使纯利润最高，而能耗最少？

记利润函数为$f_1$,能耗函数为$f_2$,四种产品分别为$x_1,x_2,x_3,x_4$,那么可以写作：

$\max f_1=10x_1+20x_2+12x_3+14x_4 \\ \min f_2=0.01\times \left( 1.5x_1+2x_2+1.8x_3+1.1x_4 \right) \\ s.t.\left\{ \begin{array}{c} 40\times 300\leqslant 13x_1+13.5x_2+14x_3+15x_4\leqslant 48\times 300\\ 0.01\times \left( 1.5x_1+2x_2+1.8x_3+1.1x_4 \right) \leqslant 20\\ x_1\leqslant 270,x_2\leqslant 240,150\leqslant x_3\leqslant 460,x_4\leqslant 130\\ x_i\geqslant 0\left( i=1,2,3,4 \right)\\ \end{array} \right.$

用传统方法，使用约束法，考虑希望能耗最少，则能耗必然有一个限度$t$,则将上述关于能耗的条件更新为$0.01\times \left( 1.5x_1+2x_2+1.8x_3+1.1x_4 \right) =t$,遍历$t$。

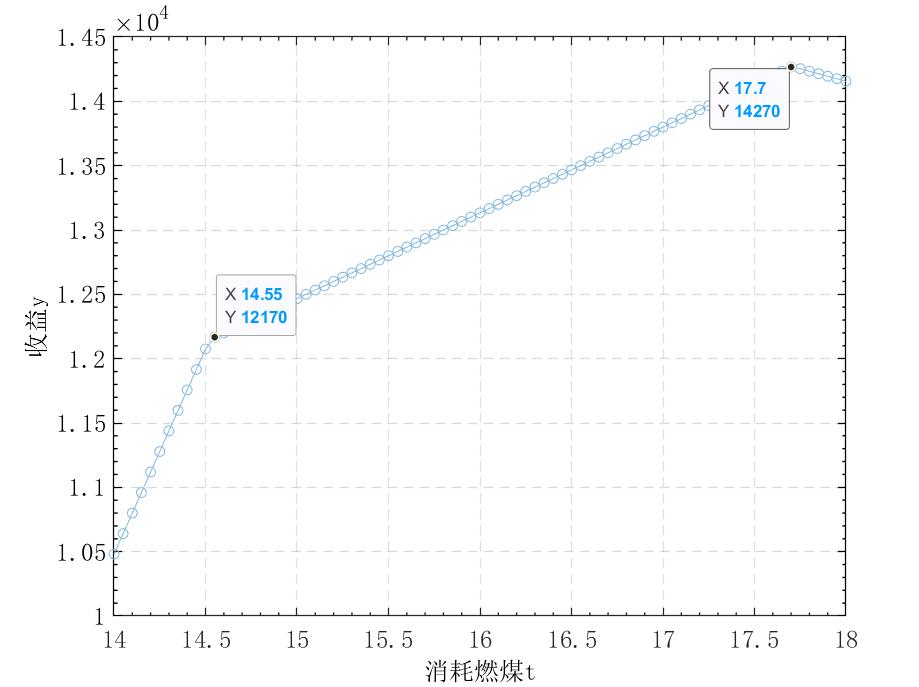
clear all
clc
c=[10 20 12 14];
A=[-13 -13.5 -14 -15;13 13.5 14 15];
b=[-12000,14400];
Aeq=[0.015 0.02 0.018 0.011];
lb=[0 0 150 0];
ub=[270 240 460 130];
Result=[];
box=[];
for t=14:0.05:20
    beq=[t];
    [x,fval]=linprog(-c,A,b,Aeq,beq,lb,ub);
    if fval~=0
        box=[t,-fval];
        Result=[Result;box];
        hold on
    end
end
plot(Result(:,1),Result(:,2));

用启发式算法，可以得到类似的结果：

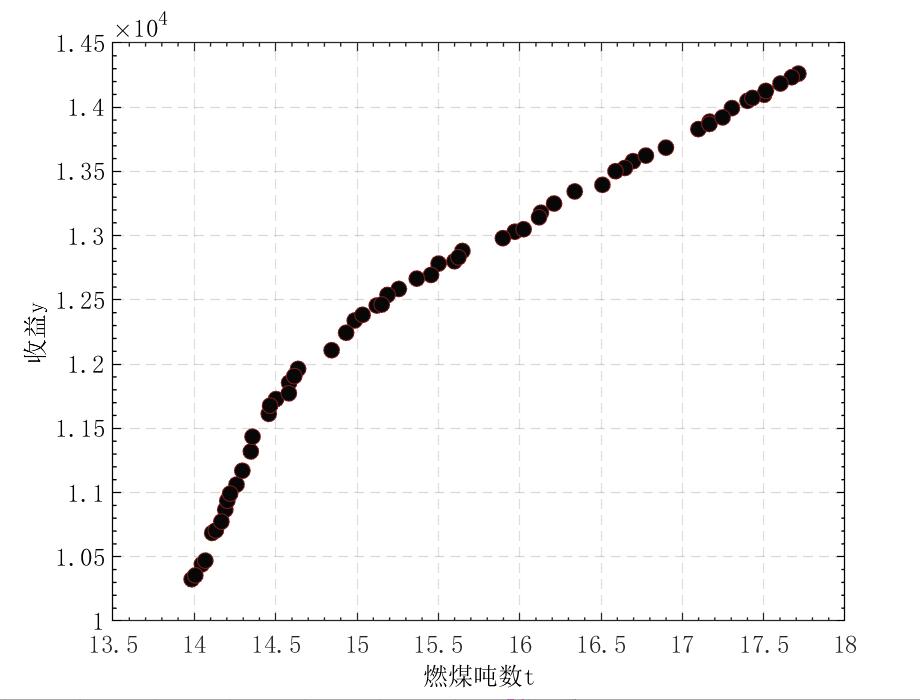
clear all
clc  
fitnessfcn=@example2Fun;  
nvars=4;  
A=[13,13.5,14,15;-13,-13.5,-14,-15;1.5,2,1.8,1.1];  
b=[48*300 -40*300 2000]';  
Aeq=[];  
beq=[];  
lb=[0,0,150,0];  
ub=[270 240 460 130];  
options=gaoptimset('paretoFraction',0.3,'populationsize',200,'generations',300,'stallGenLimit',200,'TolFun',1e-10,'PlotFcns',@gaplotpareto);  
[x,fval]=gamultiobj(fitnessfcn,nvars,A,b,Aeq,beq,lb,ub,options)

function y=example2Fun(x)  
y(1)=-10*x(1)-20*x(2)-12*x(3)-14*x(4);  
y(2)=0.01*(1.5*x(1)+2*x(2)+1.8*x(3)+1.1*x(4));

图像的拐点的意义更大，可以帮助做决策。此时传统方法和启发式算法的效果相差不大，但实际上对一些复杂的非线性问题，后者解决起来更加方便，但可解释性差。实际上两幅图所表示的就是帕累托前沿。

多目标优化在这里是个优化类问题，实际上在博弈和决策上也起到作用，有时间会研究一下如何用多目标优化写一个简单的五子棋程序。