偏微分方程OVA

阅读数: 次 2021-08-26

快开学了噻，也不知道写啥了，随便写一个最开始写的偏微分方程的OVA吧，本文以药物扩散分布建模为例，实现一个基于偏微分方程的模型问题。

问题说的是：由于血脑屏障的原因，很多精神类药物无法被循环到大脑，例如治疗帕金森症时注射的多巴胺。为此必须精确估计药物影响的脑部区域，他们必须顾及注射后药物在脑内分布区域的大小和形状。

研究数据包括50个圆柱体组织样本的每个样本的药物含量的测定值，每个圆柱体样本的长为0.76mm,直径为0.66mm,这些互相平行的圆柱体的中心位于网格距为1mm×0.76mm×1mm的格点上，注射是在最高计数的那个圆柱体的中心附近进行的，自然在圆柱体之间以及圆柱体样本区域外也有药物。

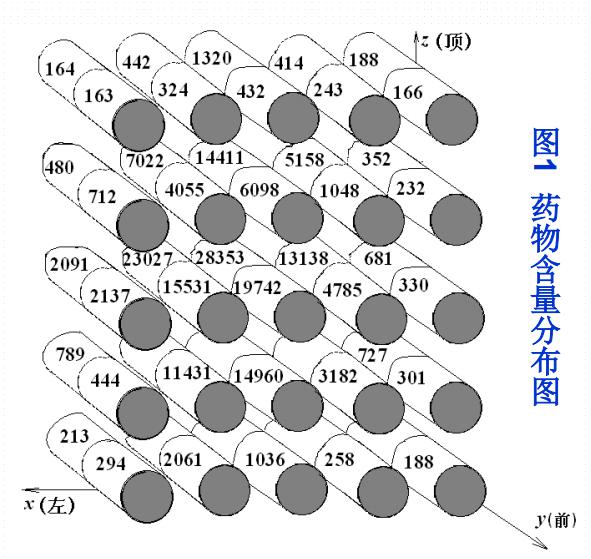
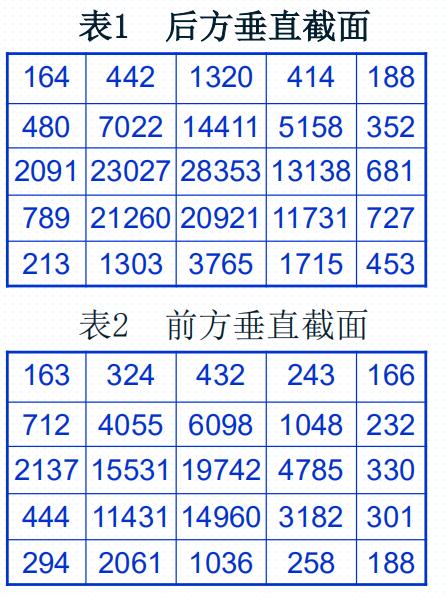
上表的数据是经过折算后的单位，如19742就代表该圆柱体有19742单位的药物。试给出药物分布的数学模型。

自然地，为了研究的方便，给出下面合理的假设：

①组织中原有的药物含量忽略不计。

②不考虑组织的边界，即忽略边界条件。

③考虑扩散和衰减的影响，忽略对流。

④假定一次性注射，不考虑注射和取样的时间和影响，并且注射位点在含量最高的那个位置圆柱中心处附近。

无论要作怎样的处理，第一件事都是要确定注射点的坐标，由于我们缺失相当多的沿y轴变化的数据，这里就给定注射点的y坐标为$y_0=0.38$,下面确定$x_0,z_0$。

根据扩散现象，可以知道这两个点其实就是数据极值点所在的位置，只是数据本身由于圆柱体的位置等限制，数据量很少，则下面我们考虑的就是对数据进行拟合使它连续。之后取拟合后数据的极大值点，即可以估计注射的位置。

方向	$x_0$	$z_0$
后方	3.245	2.861
前方	3.207	2.826
平均值	3.226	2.844

下面来给出平衡时的分布：

由于药物有游离的和吸收住的，我们认为当分布达到平衡时，所有药物都被细胞吸收（固定）住了（不考虑被分解），记$v(x,y,z,t)$为$t$时刻$(x,y,z)$处游离的药品浓度；且吸收系数$h$可以认为与浓度成正比，且先假设扩散系数各向同性，为$k$,那么：

$\frac{\partial v}{\partial t}=k\left( \frac{\partial ^2v}{\partial x^2}+\frac{\partial ^2v}{\partial y^2}+\frac{\partial ^2v}{\partial z^2} \right) -hv$

被固定住的药物浓度记为$w(x,y,z,t)$，则上式变为：

$\frac{\partial v}{\partial t}=\frac{k}{h}\frac{\partial}{\partial t}\left( \nabla w \right) -\frac{\partial w}{\partial t}$

将上式两端从对$t$作从0到正无穷的积分，记平衡时的药物浓度$u(x,y,z)=w(x,y,z,\infty)$,则积分后的方程化为

$-\frac{k}{h}\nabla u+u=v\left( x,y,z,0 \right)$

再考虑各向异性，方程可修正为：

$-a^2\frac{\partial ^2u}{\partial x^2}-b^2\frac{\partial ^2u}{\partial y^2}-c^2\frac{\partial ^2u}{\partial z^2}+u=v\left( x,y,z,0 \right)$

接下来考虑$v(x,y,z,0)$,实际上只有当给药瞬间它才不为零，其余时刻均为零，也就是说相当于在大部分点浓度均为零时，对注射点赋一个浓度，这个浓度记作$M$,之后方程的右侧就变为零了。此时右侧就可以通过有限差分法来进行迭代求解，这个办法确实可行，迭代格式是：

$u\left( i,j,k \right) =\frac{1}{t}\left( A+B+C \right) \\ A=\frac{a^2}{\left( \varDelta x \right) ^2}\left( u\left( i-1,j,k \right) +u\left( i+1,j,k \right) \right) \\ B=\frac{b^2}{\left( \varDelta y \right) ^2}\left( u\left( i,j-1,k \right) +u\left( i,j+1,k \right) \right) \\ C=\frac{c^2}{\left( \varDelta z \right) ^2}\left( u\left( i,j,k-1 \right) +u\left( i,j,k+1 \right) \right) \\ t=\left( \frac{2a^2}{\left( \varDelta x \right) ^2}+\frac{2b^2}{\left( \varDelta y \right) ^2}+\frac{2c^2}{\left( \varDelta z \right) ^2}+1 \right)$

但是直接求解起来并不容易，即使为了粗判断参数的量级，暂时视为各向同性，仍然有两个丝毫不知范围的参数$M,k$,并且上述迭代方程何时收敛需要到时候来尝试，以及步长的确定，均不容易。实际上，借助傅里叶变换，我们是可以写出分布函数稳定状态下的解析解的：

$u\left( x,y,z \right) =\frac{M\cdot \exp \left( -\sqrt{\frac{1}{a^2}\left( x-x_0 \right) ^2+\frac{1}{b^2}\left( y-y_0 \right) ^2+\frac{1}{c^2}\left( z-z_0 \right) ^2} \right)}{\sqrt{\frac{1}{a^2}\left( x-x_0 \right) ^2+\frac{1}{b^2}\left( y-y_0 \right) ^2+\frac{1}{c^2}\left( z-z_0 \right) ^2}}$

这个解析解的好处是它可积，从而可以估计参数数量级，首先考虑各向同性，令$a=b=c=1/\lambda$,类比质心，计算得：

$\iiint{u\left( x,y,z \right) dxdydz=\frac{4\pi M}{\lambda ^3}} \\ \iiint{\sqrt{\left( x-x_0 \right) ^2+\left( y-y_0 \right) ^2+\left( z-z_0 \right) ^2}u\left( x,y,z \right) dxdydz=}\frac{8\pi M}{\lambda ^4}$

而我们有有限的数据点，记$r(i,j,k)$为某点相对注射点的欧式距离，$\bar{u}\left( i,j,k \right) $为估计的该点的浓度，即用圆柱体浓度作近似，所以参数可以确定为：

$\frac{2}{\lambda}\approx \frac{\sum_{i,j,k}{r\left( i,j,k \right) \bar{u}\left( i,j,k \right)}}{\sum_{i,j,k}{\bar{u}\left( i,j,k \right)}}$

编程计算为：

load('Front.mat')
load('Behind.mat')

x_o=1:1:5;
y_o=1:1:5;
[x_o,y_o]=meshgrid(x_o,y_o);

x0=3.226;
y0=0.38;
z0=2.844;

for i=1:5
    for j=1:5
        for k=0.38:0.76:0.38+0.76
            %x-z-y
            if k==0.38
                k_coord=1;
            else
                k_coord=2;
            end
            r(i,j,k_coord)=sqrt((i-x0)^2+(k-y0)^2+(j-z0)^2);
        end
    end
end

u=cat(3,Behind,Front);

int_A=sum(sum(sum(r.*u)));
int_B=sum(sum(sum(u)));

lambda=2*int_B/int_A;

计算得$\lambda=1.5885$,则$a,b,c$的量级均在0.62附近，这个信息十分有用。基于此，待确定的参数只有M的数量级未知，但单个参数的数量级是好通过遍历得到的。

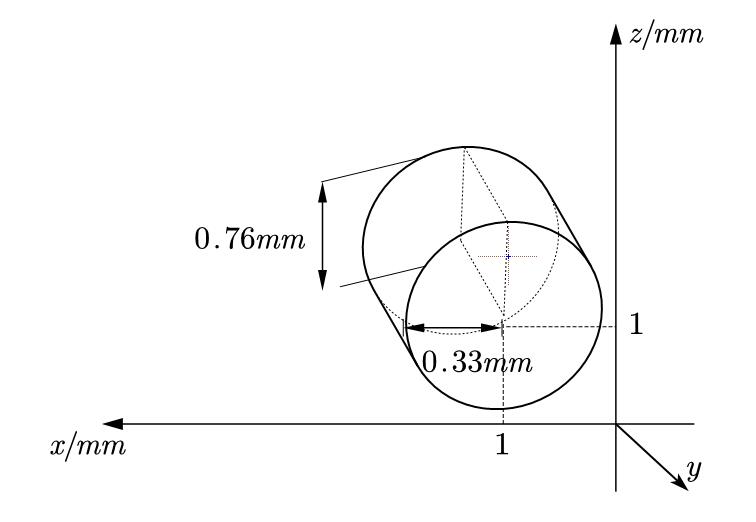
根据此坐标编写程序进行老一套的最小二乘，并最小化残差平方和。但是直接最小二乘拟合后，效果并不好，一方面来源于数据量少，另一方面，将每次求解的结果与真实数据作对比，发现梯度变化明显不同，原因是，所给数据未必达到了平衡状态，所以考虑将原椭圆型方程改进成抛物线型方程。

即考虑：

$\frac{\partial u}{\partial t}-\left( a^2\frac{\partial ^2u}{\partial x^2}+b^2\frac{\partial ^2u}{\partial y^2}+c^2\frac{\partial ^2u}{\partial z^2}-k^2u \right) =\delta \left( x-x_0,y-y_0,z-z_0,t \right)$

同样是借助傅里叶变换得到解析解，并定义取样时间$t=1$,此时参数的选取的自由度比较高，$a,b,c$的数量级之前已经确定，仅需确定$M,k$。再编程求解后，得到的效果变好了许多。

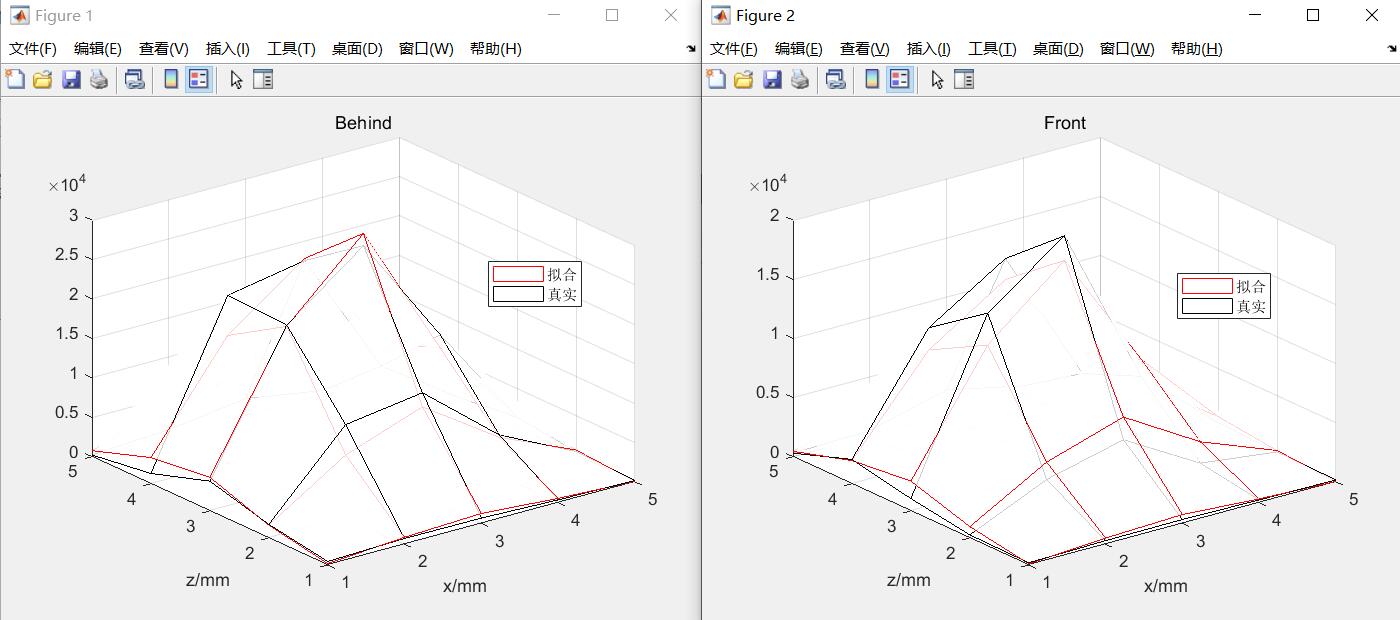
实际上，扩散问题与热传导问题，虽然遵从的规律相同，但是在实际求解中还是有不同点，在热传导问题中，参数的范围可以从边界条件很好的估计出来；而扩散问题往往要借助傅里叶变换，或者是给定初始点源浓度，之后的扩散系数和点源浓度对于结果的影响是耦合的，所以搜索起来比较困难，此外，由于扩散问题的数据往往比较少，且误差可能比较大，也造成了一定的影响。

对于这个问题，用傅里叶变换求解析解是方便的，因为它一没有边界条件二是三维的（不便于写有限差分法），如果对于二维或者一维问题来说，用有限差分法还是最合适的，因为解析解可能求不出来。

当我写完的时候，我四级成绩也出来了，反正是过了，过了就行，过了就行。去做核酸了……要开学了。