变分法2

阅读数: 次 2021-08-23

在有了上一篇的铺垫以后，下面来简单介绍无约束条件和有约束条件的泛函极值问题，简单介绍完这一部分就告一段落了，在此前还要明确几个概念。

①自变量函数的变分：

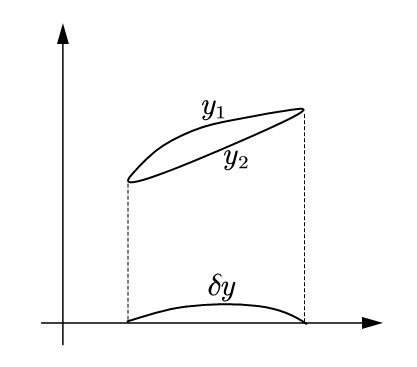
考虑自变量函数$y(t)$,那么$\delta y=y_1\left( t \right) -y_2\left( t \right) $，其中的$y_1(t),y_2(t)$是同属于函数类$\left\{ y\left( t \right) \right\} $的两个函数，在这里$t$最后变为了类似自变量的存在，当取$y(t)$为一维函数时，意思就是说：

②最简泛函及其变分：

最简泛函这个概念是从我们之前讨论过的最速降线的问题导出的，它是说：设$F\left( x,y\left( x \right) ,y’\left( x \right) \right) $是三个独立变量在区间$[x_0,x_1]$上的已知函数，且二阶连续可微。（其实确定了$y(x)$,$y’(x)$也就随之确定。），那么泛函：

$J\left[ y\left( x \right) \right] =\int_{x_0}^{x_1}{F\left( x,y\left( x \right) ,y'\left( x \right) \right) dx}$

称为最简泛函，其中函数$F$称为泛函的核，那么考虑$y(x)$的变分$\delta y=y_1\left( x \right) -y\left( x \right)$以及它的一阶导的变分，则根据定义我们写出泛函$J$的增量：

$\varDelta J=J\left[ y_1\left( x \right) \right] -J\left[ y\left( x \right) \right] =J\left[ y\left( x \right) +\delta y \right] -J\left[ y\left( x \right) \right] \\ =\int_{x_0}^{x_1}{F\left( x,y+\delta y,y'+\delta y' \right) dx}-\int_{x_0}^{x_1}{F\left( x,y,y' \right) dx} \\ =\int_{x_0}^{x_1}{F\left( x,y+\delta y,y'+\delta y' \right) -F\left( x,y,y' \right) dx} \\ =\int_{x_0}^{x_1}{\left( F_y\delta y+F_{y'}\delta y' \right) dx}+...+\int_{x_0}^{x_1}{\frac{1}{n!}\left[ \left( \delta y\frac{\partial}{\partial y}+\delta y'\frac{\partial}{\partial y'} \right) ^nF \right] dx}+R_n$

取其线性主部为该泛函的变分，即$\int_{x_0}^{x_1}{\left( F_y\delta y+F_{y’}\delta y’ \right) dx}$，记作$\delta J$。

这里存在一个定理：

$J(X)$在$X=X^{\ast}$处有极值的必要条件是对于$X^{\ast }$在此处的变分，有$\delta J\left( X^{\ast },\delta X \right) =0$。实际上为了判断是极大还是极小，要计算二阶变分，但是由于实际问题中很容易判断是极大还是极小，所以没必要计算二阶变分。这个定理的意思实际上是说，当我们对一个$X^{\ast }$施加扰动，而此时将这一附近的$X^{\ast }$的函数带入泛函进行计算，泛函的值几乎不变，这是有意义的。

所以对我们前面分析出的线性主部，即泛函的变分，考察它为0的时候，根据上一篇我们的推导，它计算后的结果是：

$\delta J=\int_{x_0}^{x_1}{\left( \frac{\partial F}{\partial y}-\frac{d}{dx}\left( \frac{\partial F}{\partial y'} \right) \right) \delta ydx-\left. \frac{\partial F}{\partial y'}\delta y \right|}_{x_0}^{x_1}=0$

在这个方程中，它的一种情况我们已经见过，即满足欧拉-拉格朗日方程，且第二项为零，但是之前讨论时，我们固定了两个端点，即最速降线下落的起点和终点，在这两点的$x,y$坐标是给定的，所以对第二项要做更进一步的说明：

$\left. \frac{\partial F}{\partial y'}\delta y \right|_{x_0}^{x_1}=\left( \frac{\partial F}{\partial y'} \right) _{x=x_1}\cdot \delta y\left( x_1 \right) -\left( \frac{\partial F}{\partial y'} \right) _{x=x_0}\cdot \delta y\left( x_0 \right)$

当端点固定，即两个变分为零时，第二项自然为零。但当两个变分不为零，即端点不是固定的而是自由的时候，第二项如果仍为零，就要补加条件：

$\left( \frac{\partial F}{\partial y'} \right) _{x=x_1}\cdot \delta y\left( x_1 \right) =0 \\ \left( \frac{\partial F}{\partial y'} \right) _{x=x_0}\cdot \delta y\left( x_0 \right) =0$

该条件称为横截性条件。通过补充这些，我们进一步完善了对于无约束的泛函求极值的问题，同样我们也能很简单的将其推广成自变量函数为向量函数时的情景，但是很多时候遇到的问题是有约束的，例如最初想解决的最优控制问题，我们进一步考虑将有约束的问题转化成无约束的问题来进行求解。

首先明确的一点是：最优控制问题一般有三种性能指标，但理论可以证明，三种性能指标可以互相转换，即它们是等价的，这里就举一个对于拉格朗日问题的例子：

考虑系统

$\dot{x}\left( t \right) =f\left[ x\left( t \right) ,u\left( t \right) ,t \right] ,x\left( t \right) \in R^n,u\left( t \right) \in R^r;$

给定时间$t\in \left[ t_0,t_f \right] ,x\left( t_0 \right) =x_0$,且终端$x_f$自由，性能泛函为：

$J=\int_{t_0}^{t_f}{L\left[ x\left( t \right) ,u\left( t \right) ,t \right] dt}$

欲求最优控制$u(t)$使得系统得以从初始状态转移到终端状态，并使得性能泛函取极值。这个例子实际上就是燃料最优的一种情况。

将状态转移方程写成约束方程形式：$f\left[ x\left( t \right) ,u\left( t \right) ,t \right] -\dot{x}\left( t \right) =0$，在多元函数求极值问题时，我们用到过拉格朗日数乘法，来将有约束的问题转化成无约束的问题，在这里我们也应用拉格朗日乘子法，构造泛函：

$J'=\int_{t_0}^{t_f}{L\left[ x\left( t \right) ,u\left( t \right) ,t \right] +\lambda ^T\left( t \right) \left[ f\left[ x\left( t \right) ,u\left( t \right) ,t \right] -\dot{x}\left( t \right) \right] dt}$

其中的$\lambda^T(t)$就是待定的拉格朗日乘子形成的n维向量，前人在此基础上想出了这样的方法：

定义哈密顿函数：

$H\left[ x,u,\lambda ,t \right] =L\left[ x,u,t \right] +\lambda ^Tf\left[ x,u,t \right]$

那么增广泛函$J’$可以作如下变形(分部积分)：

$J'=\int_{t_0}^{t_f}{\left\{ H\left[ x,u,\lambda ,t \right] -\lambda ^T\dot{x}\left( t \right) \right\} dt} \\ =\int_{t_0}^{t_f}{\left\{ H\left[ x,u,\lambda ,t \right] +\dot{\lambda}^Tx\left( t \right) \right\} dt}-\lambda ^T\left. x \right|_{t_0}^{t_f}$

就像我们先前用拉格朗日数乘法解决多元函数求极值的问题时一样，这里我们也要研究增广泛函取极值时的情况，即增广泛函的变分为零，那么根据上文的泛函的变分公式，此时我们变分的对象有控制$u$和轨线$x$,即是计算由$\delta u,\delta x$引起的$J’$的变分，即：

$\delta J'=\int_{t_0}^{t_f}{\left[ \left( \delta x \right) ^T\left( \frac{\partial H}{\partial x}+\dot{\lambda} \right) +\left( \delta u \right) ^T\frac{\partial H}{\partial u} \right]}dt-\left( \delta x \right) ^T\left. \lambda \right|_{t_0}^{t_f}$

上式要为零，会得到如下等式：

$\left\{ \begin{array}{c} \frac{\partial H}{\partial x}+\dot{\lambda}=0 ......\left( 1 \right)\\ \frac{\partial H}{\partial \lambda}=\dot{x}\,\,......\left( 2 \right)\\ \frac{\partial H}{\partial u}=0 ......\left( 3 \right)\\ \left. \lambda \right|_{t_0}^{t_f}=0 ......\left( 4 \right)\\ \end{array} \right.$

(1)式称为伴随方程或协态方程，$\lambda$称为伴随矢量或协态矢量。

(2)即系统的状态方程，它是直接对哈密顿函数求$\lambda$偏导的结果（再结合状态方程）。

(3)称为控制方程。

(1),(2)联立称为哈密顿正则方程。

(4)为横截性条件，用于补充边界条件，例如当终端自由时，由于$\delta x(t_f)$任意，所以$\lambda(t_f)=0$。

但是后面的过程就很复杂了，有些时候里面的量是解耦的，但有些时候不是；有些时候形成的微分方程组变得十分复杂只能迭代求解，但是这种方法不好的地方就是，如果初值和真实值相差的比较大，则结果不易收敛；而且就算收敛，要解的方程组也是一个两点边值性质的微分方程组，这大大加大了求解的难度，尤其是两点边值这个问题，我直接被锤爆了，所以下面我只举一个比较简单的例子，难一点的例子求解起来，属实不大行，我太垃圾了。

考虑一个竖直的动力着陆过程，主要依靠发动机来反冲，最后要使得在给定的一个时间，着陆器安全降落：

$J=\frac{1}{2}\int_0^{t_f}{a^2dt}$

边界约束条件${G}$为：

$\begin{equation} G=\left\{ \begin{array}{l} r( t_f ) =0,r( 0 ) =2000\\ v( t_f ) =0,v( 0 ) =80\\ \end{array} \right. \end{equation}$

构造哈密顿函数：

$\begin{equation} H=\frac{1}{2}a^2+\lambda _rv+\lambda _v( g+a ) \end{equation}$

控制方程：

$\begin{equation} \frac{\partial H}{\partial a}=0 \end{equation}$

协态方程：

$\frac{d\lambda _r}{dt}=-\frac{\partial H}{\partial r}=0 \\ \frac{d\lambda _v}{dt}=-\frac{\partial H}{\partial v}=-\lambda _r$

下面考虑将给定的时间${t_f}$分为${n}$等分，考察其中的区间${[t_i,t_f]}$，在这一区间内求解上述方程。

$\begin{equation} \int_t^{t_f}{d\lambda _v=}\int_t^{t_f}{-\lambda _rdt} \end{equation}$

由于${\lambda_r}$是常值函数：

$\begin{equation} \lambda _v( t ) =( t_f-t ) \lambda _r+\lambda _v( t_f ) \end{equation}$

由控制方程：

$a = -\lambda_v\\ = (t_f - t)\lambda_r + \lambda_v(t_f)$

记$t_g=t_f-t$，则只要求解出${\lambda _r}$与${\lambda_v(t_f)}$就可以根据此时的${t}$得到最优的加速度，进而推算出此时的推力和燃料消耗，对加速度进行积分，与边值条件进行联立，得到：

$a=-\frac{6r}{t_{g}^{2}}-\frac{4v}{t_g}-g$

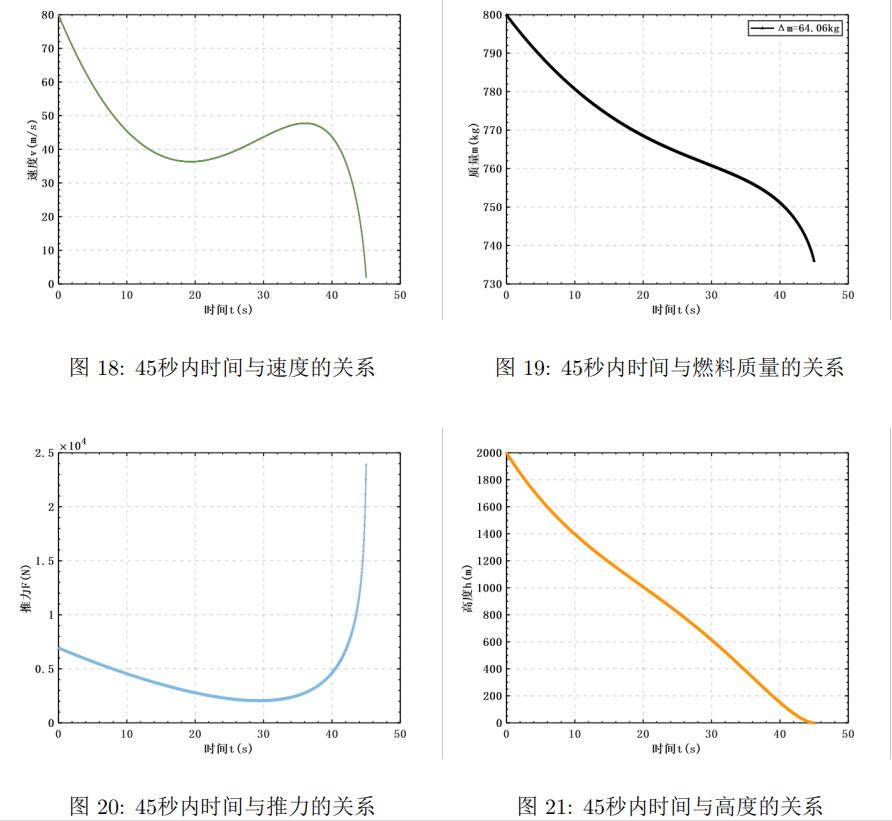
这个坑就先挖了不填了，可能以后如果遇到无人车或者无人机之类的方面我再填一填，实际上根据2014A的结果来看，CUMCM直接拿最优控制来处理也并不是加分项，可能是这样专业性太强，实际上当时的许多队伍选择了离散化轨道和一些别的数值方法，得到的效果虽然并不相同，但对于当时的2014A评阅要点并未对结果有要求，应该是基于无穷维优化简化为有限维后精度的丢失。通过深圳杯和2014A也简单的对泛函和变分有了一定的了解，接着摆烂了。