七夕和我这个死宅没有什么关系,但第一次培训作业终于是写完了。太阳影子定位的命题不复杂,求解也比较简单,但是还是挖掘到了一些有用的内容,透视变换和费马原理。
透视变换
太阳影子定位的问题四要求我们从给定的一段40分钟视频中获取影子长度的信息,再反演出可能位置。这里就涉及到了透视变换。
由于高中立体几何的影响和我们潜意识的惯性思维,我们现在设想一个正方体,我们会作出这样的一个图形(左),但实际上它应该是(右)
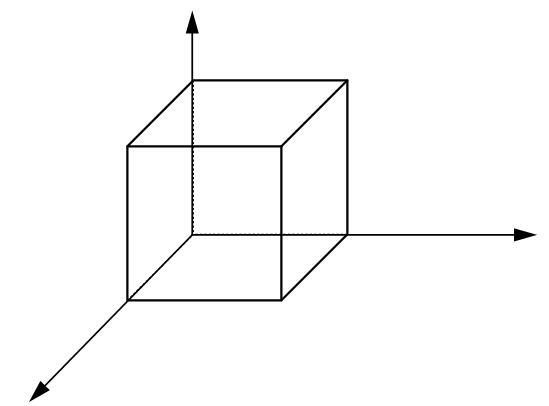

因为左边的直接用坐标行而有效的表示,更能体现出一个几何体的特点,所以我们都很习惯这种表示。但在实际情况中,如果观察一个正方体,它的情况确实是右边的样子,如果拍成右边那样的照片,量取上面的各个边,会发现他们的长度并不都相等。
这个原理很简单,但是有意思的地方在于:当你真的习惯用坐标系来度量的时候,你拿起一个正方体,各个视角的观察,你眼睛接受的图像,还是传递给你一种他们“边长”都相等的错觉,即使如果把此时你看到的景象拍下来,用尺子量,确实是不相等的。问题就在于,原本在立方体的平行的结构,在三维的空间上,它们两条线的平行关系是会延申到无限远的,但是由于图片是二维的,在二维中会产生信息的损失,就像铁轨在远处看去汇聚成一点一样,在图片上看上去,它们不再是“平行”的,这个汇聚的点在相关领域被称为“消失点”,消失点所在的一条与视角平行的线称为“视平线”。
知道这个以后我们来修正视频中的影长,如果我们仅仅根据已知信息,计算图中的杆顶和杆底的在像素坐标系下的距离,得到缩放系数,然后根据同样的道理计算影长,这样会带来不小的误差,我们现在试图来进行修正。这就像对于正方体而言,如果你只注意它离你最近的面,只要它的视位面对于拍出来的图片的视线是垂直的,那么它就是没有被扭曲的。

但是我们如何实际的办到这一点呢,我是说,我们非常熟悉对一个图片进行各种操作,比如平移,拉伸,旋转,在这里我可就要讲一下我两学期拉跨的高等代数了嗷!
实际上对于二维的坐标变换,它的完整形式是对于(x,y,w)进行形如如下的变换:
最后$x’=\frac{u}{w’},y’=\frac{v}{w’}$才是完整变换后的坐标
这里为什么要引入z=w这个虚量呢,实际上这一步被称为齐次化处理,因为我们能想到的平移并不能写成一个向量与矩阵的乘积的形式(可以证明,平移变换和透视变换不是线性变换),但是齐次化处理后就不会有这样的问题。这个变换被称为透视变换,是用来处理二维平面上图像的。
如果单独拿出$T_1$,这就是我们常说的仿射变换,它只包含旋转,翻折,缩放。
所以我们的思路是,只要我们确定好透视变换矩阵$T$,对整个图片中的所有坐标都如此作用,就可以简单修正误差了。
费马原理
我安排彭师傅做模型的改进,显然光线进入大气层会发生折射现象,但是大气层各处密度不均匀等等,折射率也会有微小的差异,考虑到这一点,为了得到光最终的路径以便求出角度的变化,这里引入了费马原理,费马原理说的是光会沿着光程差最小的路径前进,实际上更精确的表述是对于从P到Q的光线:
实际上我们至多只用考虑一维时的情形,此时光线方程的表达式可以写成一个不定积分的形式:
但这并不是重点,重点是它与一种重要的数学方法:变分法有关,以及和那“最小作用量原理”也有深刻联系(但是后者已经和我关系不大了)但是举一个物理中的例子也是很形象的:
如果我们不考虑空气阻力,扔一个小球,当给定初始的物理状态,我们利用牛顿第二定律可以计算小球的整个运动过程,但是,这里有另外一个观点:为什么从起点到终点的路径那么多,小球只选了这么一条。这实际上就与最小作用量原理有关。
在这里我就省略掉繁琐的数学证明和计算了,最重要的是这个思想,它不仅仅只针对一个函数,而是将可行的所有函数拿来讨论,“以函数为自变量的函数(泛函)”,在此基础上有许多成果,变分法将原来的微分方程问题,转化成一个求泛函极值的问题。比较简单的例子有证明最速降线是摆线以及证明摆线的等时性,再复杂的例子就与我无关了,那是物理专业的事情了。

