元胞自动机

阅读数: 次 2021-08-10

很多情况下，一些复杂系统并不能直接用数学或物理方程来描述，也不能很好的用统计学来表征。甚至量化它们就是个问题。我们希望一种方法，用简单的规则来实现复杂的系统。

实际上确实有这么一种方法：元胞自动机，元胞自动机是上世纪计算机科学家的伟大创造，现在已经在许多领域发挥了重要的用途。我在这里就不重复那些理论性的内容，重点放在如何编程实践。

这里的元胞和在许多高级语言中的元胞其实意义上并不相同，在这里元胞只是对“cell”这个词翻译过来的，它是说元胞是元胞自动机最小单元，且所有元胞的状态都按照元胞规则不断演化。我们如果取其中一个元胞来分析，它的下一个状态由本身的当前状态和它的“邻居”的状态通过一定的规则来确定。

我们现在考虑经典的森林火灾问题，这个问题，我们很难用一些机理建模的方法，写出一个函数来分析，用计算机仿真处理它是最合适的。为了简单起见，我们将起火原因归结为一个随机因素，将树木的生长也归结为一个随机因素，即如果满足了特定条件，元胞会发生变化：

①如果某树木元胞的4个邻居有燃烧着的，那么下一状态该元胞也燃烧（我们这里默认使用了Von Neumann邻居）

②一个燃烧着的元胞下一刻变为空元胞（烧完了）

③所有树木元胞以一个低概率开始燃烧（模拟起火）

④所有空元胞以一定概率开始生长（模拟其生长）

我们很自然的想到这样的一种流程：遍历当前的元胞矩阵，根据每个元胞的上下左右元胞的情况进行判断，将判断的结果存入另一个矩阵，这样通过储存两个矩阵，我们进行迭代，就可以得到进行元胞的演变。实际上对于元胞自动机，它的边界的情况是无关紧要的，因为边界只有那么两行两列，并且真实情况下边界外的影响对边界本身也是未知的，以及我们模拟的是数据的宏观变化，将其可视化还需要借助别的一些工具，我们仍然要考虑的是如何从宏观的动态变化中提取我们需要的信息。

但是对于一个简单的例子并不需要这么复杂，下面演示的是基础的森林火灾：

(这个例子由于比较简单，演化的过程直接用&和|完成了)

clear all
clc
%空元胞为0，燃烧元胞为2，树木元胞为1
n=300;
P_fire=0.001;
P_tree=0.000001;
upper_left=[n 1:n-1];%这两个矩阵是来后面求邻居元胞状态的
down_right=[2:n 1];
judging_matrix=0.7*ones(n);
random_matrix=rand(n,n);
Zone=double(random_matrix>judging_matrix);%初始化元胞空间
img=image(cat(3,Zone,Zone,Zone));%作图
run=1;
plotbutton=uicontrol('style','pushbutton','string','Pause', 'fontsize',12,'position',[100,400,50,20],'callback','run=-1');
stopbutton=uicontrol('style','pushbutton','string','Stop', 'fontsize',12,'position',[200,400,50,20],'callback','run=0');
for i=1:100000
    if run==0
        close all
        break
    end
    if run==-1
        pause
        run=1;
    end
    neigbor=(Zone(upper_left,:)==2)+(Zone(:,upper_left)==2)+(Zone(down_right,:)==2)+(Zone(:,down_right)==2);
    Zone=(Zone==1)+((Zone==1)&(neigbor>0 | (rand(n,n))<P_fire))+((Zone==0)&(rand(n,n)<P_tree));
    Tree_num=length(find(Zone==1));
    Fire_num=length(find(Zone==2));
    Tree(i)=Tree_num;
    Fire(i)=Fire_num;
    set(img,'cdata',cat(3,(Zone==2),(Zone==1),zeros(n)));
    drawnow
    figure(2)
    plot(Tree);
    hold on
    plot(Fire);
    legend(['树的数量',num2str(Tree_num)],['火源数量',num2str(Fire_num)]);
    title(['天数=',num2str(i),'天']);
    hold off
end

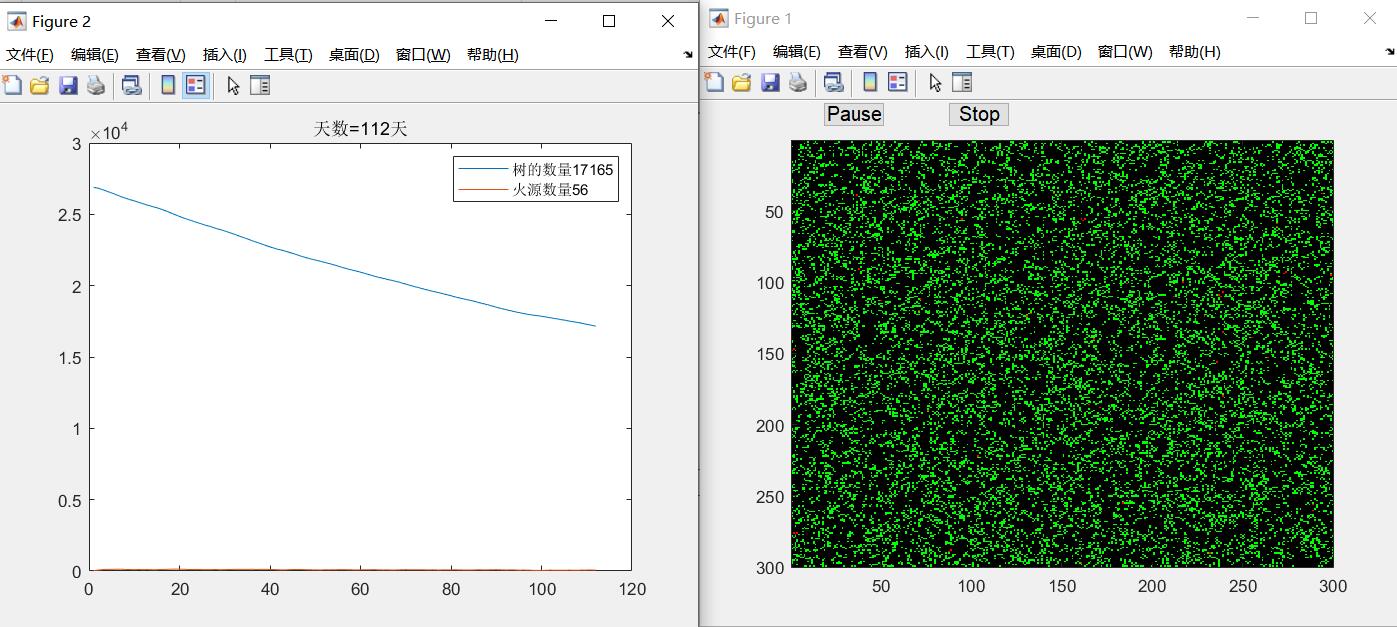
但是这个简单的例子与实际情况还是有差距，因为我们只考虑了一个元胞的上下左右，并且认定只要邻居是燃烧的，下一时刻该元胞就燃烧，实际上，燃不燃烧还不一定呢。以及斜对角也是有可能燃烧的，并且火焰传播与风力及方向关系很大，所以上面的模型是不太合理的。我们更加细致的进行改进，纳入风力和不同方向的火焰传播。得到这样的示意图。

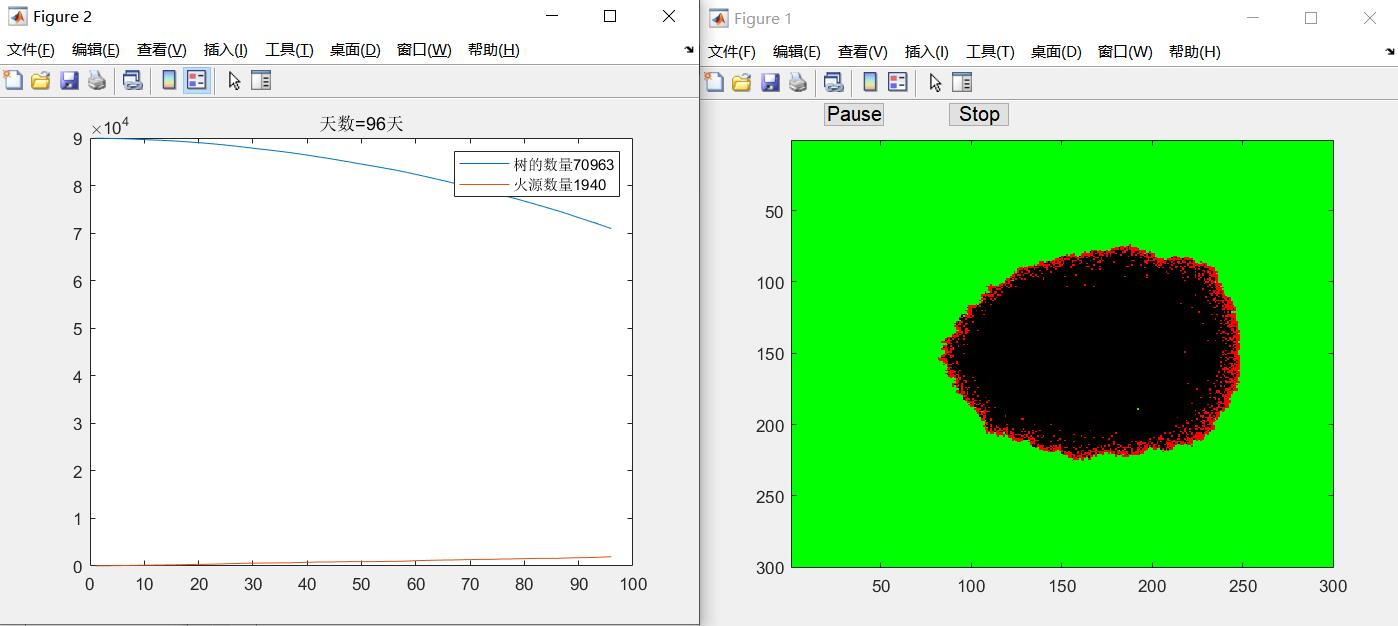
下面我们举一个稍微复杂的例子，淡水养殖时因藻类的聚集可能会出现水华现象，严重损害生态环境和经济利益。有资料指出：构建一个以鱼，虾，蟹，藻为基础的生态养殖池可以很好的避免水华现象，我们这里按照五级制转换后的数据来表示藻类密度值，同时设鱼，虾，蟹的养殖量为300kg,500kg,500kg，考虑养殖池为一个长度为50单位的正方形即可。

	I	II	III	IV	V
藻类密度值	0~15	15~50	50~150	150~500	500以上

为了简便起见，用二维元胞自动机模拟这一过程：

考虑到养殖池水体的特性，这里用Moore型邻居模拟比较合适。并且由于三种生物移动性均很强，我们这里就将他们视作整体，将它们各自个体对藻类的影响归结为整体对藻类的影响，并且如果藻类密度不同，那么生物对藻类的消耗也不同，以及我们所说的下一状态下特定元胞的藻类密度不仅与Moore邻居有关，也与该元胞该状态下的密度有关，它们影响的权重并不相同。综合上面几点我们总结出：

$\left\{ \begin{array}{c} c_{i,j}=\left( w_1c_{i,j}\delta _{multiply}+w_2\sum_{around}{c_{i,j}} \right) \times \lambda\\ \lambda =1-rand\times \left( \rho _t \right) \times \alpha _i,i=1,2,..,5\\ \rho _{t+1}=\rho _t\times \beta _i,i=1,2,...,5\\ \end{array} \right.$

编程求解，我们模拟出了藻类密度随着时间的动态变化，以及三种生物数量随着时间变化：

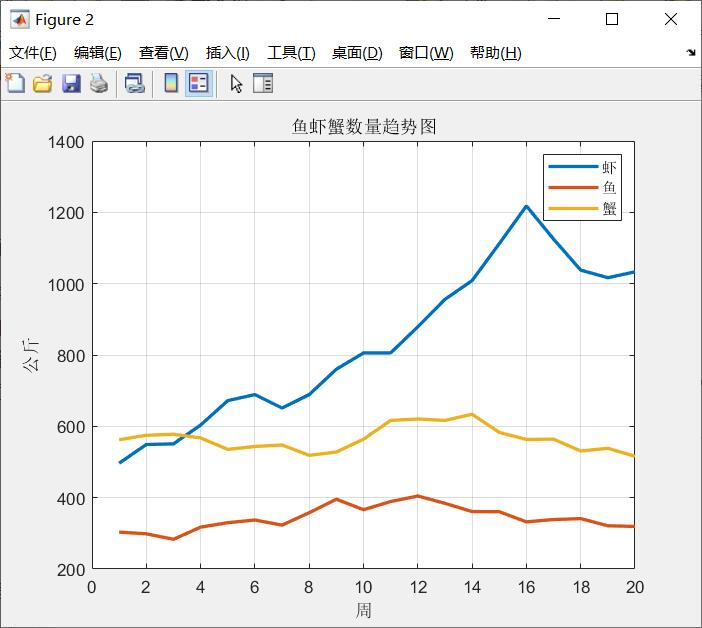
在这里颜色越接近深绿色，说明藻类密度越大；颜色越接近青色，说明藻类密度越小，可以看到引入这样的生物链确实可以抑制水华。

上面两个例子均是元胞自身随时间的影响，实际上元胞自动机还可以对随机游走进行模拟，在考虑真实的随机模拟前，我们先考虑一种规则比较确定的单方向游走模型，即它在交通流领域的应用，这个也可以扩展到人流等不同的流现象中，由于这部分内容如果细致分析，涉及到交通上的很多理论以及概率论，所以这里我们就用最常用的nasch规则进行模拟，先是单车道：

在时间t到t+1的过程中，元胞自动机如此演化：

加速，$v_n\rightarrow \min \left( v_n+1,v_{\max} \right) $

减速,$v_n\rightarrow \min \left( v_n,d_n \right) $,$d_n$是距离前面车之间的空元胞数，即为了避免相撞而进行减速。

随机慢化，以概率$p$发生，$v_n\rightarrow \max \left( v_n-1,0 \right) $,由各种不确定性造成的减速。

运动，$x_n\rightarrow\ x_n +v_n $,其中$x_n$表示第n辆车的位置，车辆按照上述规则调整后的速度向前行驶。

我们依照上面的规律编程模拟：

clear all
clc
hf=figure('Position',[100,300,1200,170],'Resize','off','menubar','none','Name','Nagel-Schreckenberg model','NumberTitle','off');
plotbutton=uicontrol('style','pushbutton','string','Run','position',[250,130,50,20],'callback', 'run=1;');
erasebutton=uicontrol('style','pushbutton','string','Stop','position',[350,130,50,20],'callback','freeze=1;');
quitbutton=uicontrol('style','pushbutton','string','Quit','position',[450,130,50,20], 'callback','stop=1;close;');

n=3;%行数，这里因为留出两条边当人行道，所以是3
m=60;%列数，其实就是模拟的道路的长度
Base=ones(n,m);
imh=image(cat(3,Base,Base,Base));%初始化图片
grid on;%这样就直接打上格子不用另外plot了

axis equal;
axis tight;
set(gca,'XTick',0.5:m+0.5,'YTick',0.5:n+6.5);
set(gca,'GridLineStyle','-','LineWidth',1,'FontSize',1);%隐藏掉坐标

Base_1=Base;
Base_2=Base;
Base_3=Base;%创建RGB三通道
GrayLine=[1 3];%人行道两边着色
Base_1(GrayLine,:)=0.5;
Base_2(GrayLine,:)=0.5;
Base_3(GrayLine,:)=0.5;

set(imh,'cdata',cat(3,Base_1,Base_2,Base_3))
drawnow;

stop=0;
run=0;
freeze=0;

cars=zeros(1,m);
v=zeros(1,m);
colors=zeros(1,m);
global vmax p q cars_in cars_out cars_on;
vmax=4;
p=0.1;%随机慢化的概率
q=0.9;%入口出现新车的概率

cars_in=0;
cars_out=0;
cars_on=0;

while(stop==0)
    if(run==1)
        [cars,v,colors]=develop(cars,v,colors);
    end
    %给中间马路的颜色进行更新
    Base_1(2,:)=1;
    Base_2(2,:)=1;
    Base_3(2,:)=1;
    for i=1:m
        if cars(i)==1
            Base_1(2,i)=colors(i);
            Base_2(2,i)=colors(i);
        end
    end
    set(imh,'cdata',cat(3,Base_1,Base_2,Base_3));%更新图片内容
    if (freeze==1)
        run=0;
        freeze=0;
    end
    drawnow;%更新现在展示的图片
    pause(0.5)
end

function [cars_new,v_new,colors_new]=develop(cars,v,colors)
global vmax p q cars_in cars_out cars_on
[~,col]=size(cars);
cars_new=zeros(1,col);
v_new=zeros(1,col);
colors_new=zeros(1,col);%给下一状态初始化
for i=col-1:-1:1%第col个位置如果有车，下一时刻认为必定出去，这里就写成col-1了
    if cars(i)==1%搜索到小车，开始依规则进行演变
        d=0;%重新初始化下车间距，下面具体求d
        if cars(i+1:col)==0
            d=vmax;%这车前面一辆车都没有时
        else
            for j=i+1:col%搜寻车距
                if cars(j)==0
                    d=d+1;
                else
                    break;
                end
            end
        end
        v_temp=min([v(i)+1,vmax,d]);%综合考虑加速和减速
        if rand<p;%随机慢化
            v_temp=max(v_temp-1,0);
        end
        if i+v_temp<=col%如果小车还没驶出，需要在下一状态的矩阵上更新他的信息
            cars_new(i+v_temp)=1;
            v_new(i+v_temp)=v_temp;
            colors_new(i+v_temp)=colors(i);
        else
            cars_out=cars_out+1;
        end
    end
    if cars(col-1)==1
        v_old=v(col-1)
        car_state=cars_new(col-1)
        v_new_single=v_new(col-1)
    end
    if rand<q
        %判断是否生成新车
        if cars(1)==0%如果生成新车，要给各属性赋值
            cars_new(1)=1;
            v_new(1)=randi(vmax);
            colors_new(1)=randi(80)/100;
            cars_in=cars_in+1;
        end
    end
    cars_on=sum(cars);
end
end

我们在此基础上进行改进，再加一条车道，并且加上对变道超车的内容，可以得到双车道时的模拟：

对于更加一般的游走模型，举这样的一个例子：由于大西洋水温的改变会使得某些区域的水温不再适合鲱鱼（对，就是鲱鱼罐头的鲱鱼）生活，鲱鱼群由此会进行迁移，据资料显示鲱鱼生活适宜海温在9~12摄氏度。试模拟苏格兰区域的鲱鱼迁移活动。

为了简化起见，鱼群的迁移认为只与海洋温度有关，并且鲱鱼会向适合生存的水温方向游动，如果存在两个以上适合的方向，会随机走向其中一个，即：

①如果鱼群周围八个元胞的温度都不在在9到12摄氏度，那么鱼群不移动。

②如果鱼群周围八个元胞只有一个元胞在9到12摄氏度，那么鱼群向这个元胞移动。

③如果鱼群周围多个元胞均满足适宜温度，那么鱼群在这几个格点进行随机选择。

实际上鱼群的转移还与欲转移至的元胞是否有鱼群有关，但是这里就不展开讨论了。所以下图最开始，只有一个红色小方块，说明只考虑了单个的鱼群，它们迁移到过哪里，就将那块海域标红。

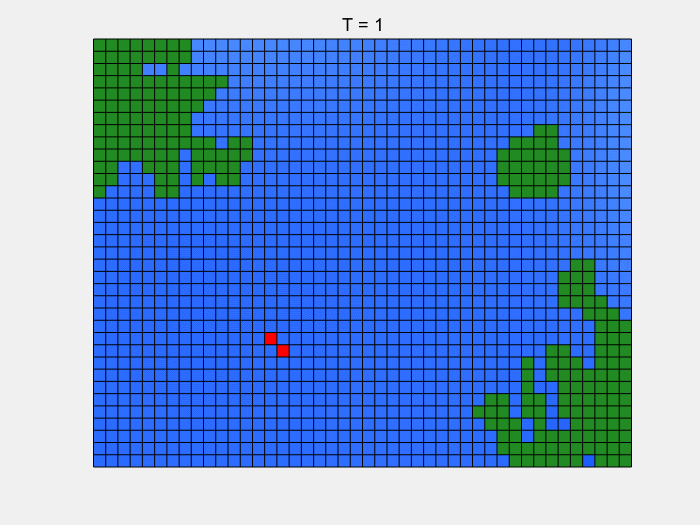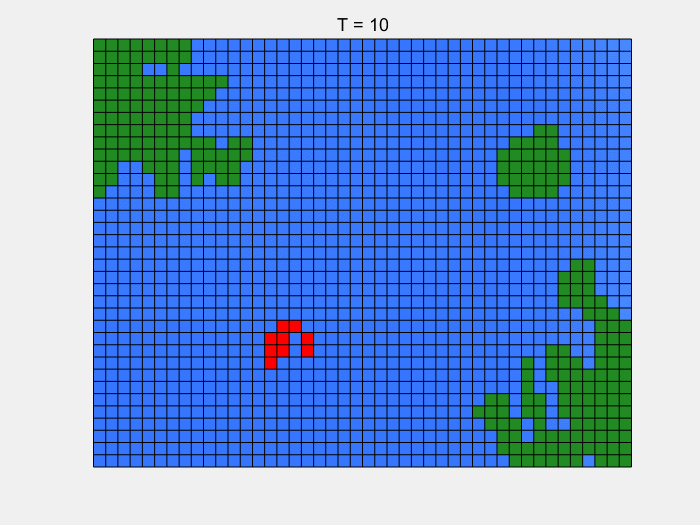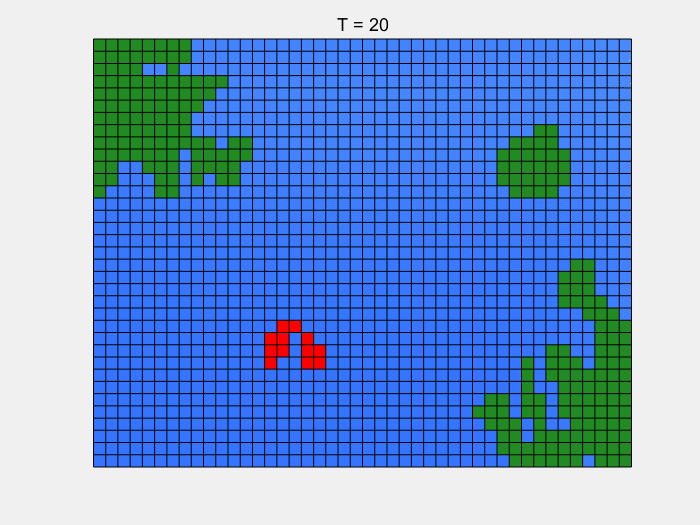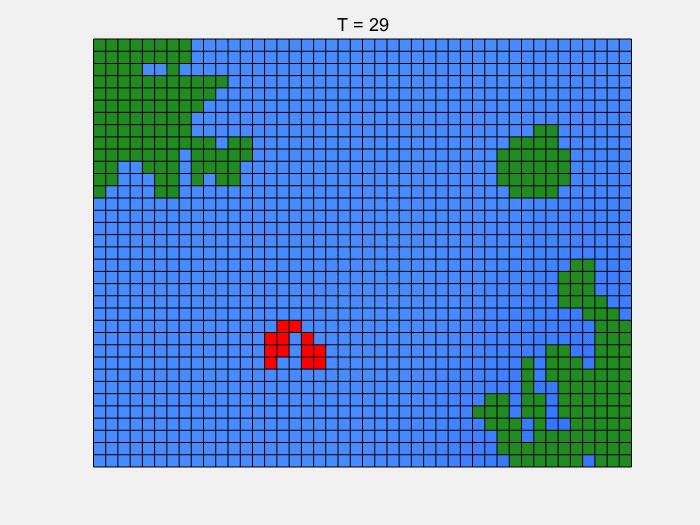
我们多次模拟，最终得到鲱鱼会固定游走在一个范围内，得出这个范围可以帮助我们最大化捕捞鲱鱼的利益。

实际上这个例子节选自MCM2020A，处理这个问题真正的难点在于如何处理较大规模的海洋温度数据……实现这个元胞自动机的时间远远短于从六十多万行的矩阵中处理海洋温度的时间。

最后考虑一个比较复杂的例子：MCM2021A中要求参赛者对碳循环中的真菌进行分析，这个情景应该先依据给出的数据对真菌的不同特征进行一些类似PCA的操作，考虑种间因素应用比如Lotka-Volterra模型进行分析等等。但我当时并没有做这道题，如果仅为了实现一次元胞自动机就将这个问题从头到尾推一遍，代价有点高，所以我在这里作一些比较似然的假设，然后对其中34种真菌分解木质素这一过程进行仿真。

①认为菌落以圆形在培养基表面扩张，忽略扩张时其中菌株含量对在该小块分解木质素效率的影响

②不同类型的真菌由于受培养基环境影响，有不同的竞争系数$\beta_i$,由于竞争能力强的真菌摄取有机物的能力相对也更强一些，认为不同类型的菌株分解木质素的效率与竞争系数成正比

③当多种真菌同时占领了一块区域时，木质素被消耗的速度是各自真菌摄取木质素的总和，同时除该区域竞争系数最大的菌种以外，其他在该区域的菌株的分解能力被指数削弱，即：$e^{1-\frac{\beta _{\max}}{\beta _i}}$

（由于上面所说的原因，这里34种真菌的竞争系数$\beta$就以生成的0~1随机数表示了，这样也能适配上面的假设③）

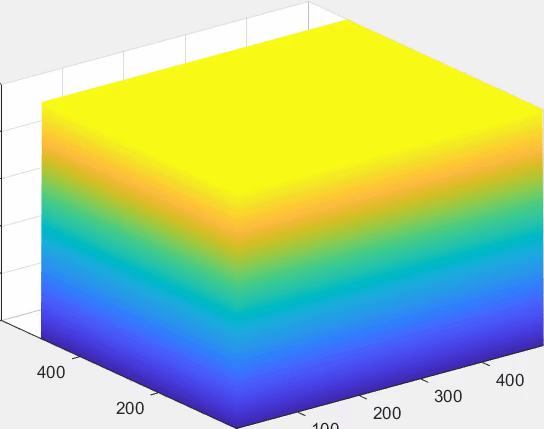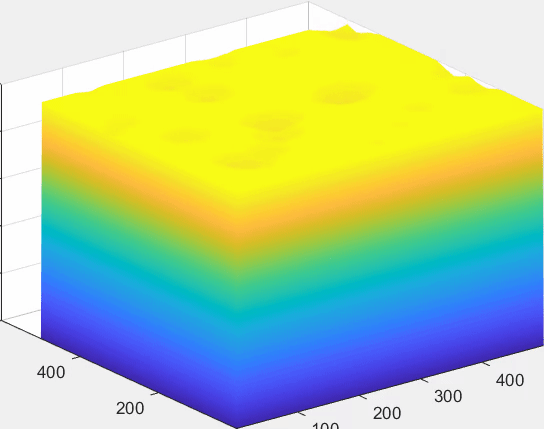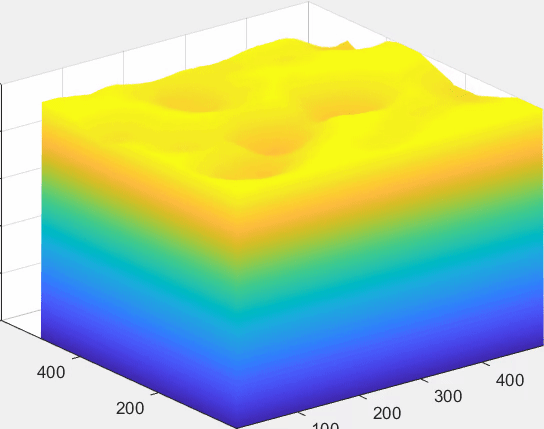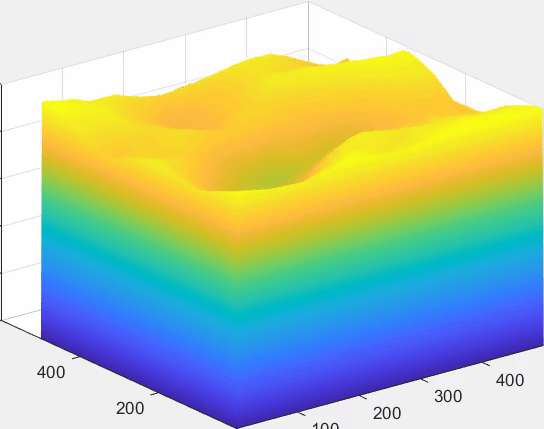
最后关于元胞自动机，它其实有一个令人着迷的一点，哪怕是一些规则最为简单的元胞自动机，如”Conway life game”,它们都是“不可计算”的，我们并不能研究出一个算法，让它帮助我们判定，某一初始的分布最后会导向什么结果，这个又和哥德尔不完备性定理有些许关系，如果我能早半年了解这些，或许大一下学期的时候就会好好学离散数学。

当写完这篇blog时，其实学校的数模培训已经布置作业了，所以我也不能再在这里耗下去了，但是在我不在的时候，我的两个队友发挥了相当强的主观能动性，他们做了很多有用的工作，也因此估计以后更新也不勤了，现在我也要去研究那“太阳影子定位”问题了。